Introduction

Hydraulic conductivity is one of the most important mechanical properties of soil, influencing both long-term consolidation deformation and soil stability (Shen et al. 2003; Zeng et al. 2011; Chai et al. 2011). Many challenges in geotechnical engineering are related to the hydraulic conductivity of soil, including the design of foundation pit dewatering (Ma et al. 2014), the estimation of foundation settlement and the analysis of soil consolidation (Shen et al. 2013; Shen and Xu 2011; Xu et al. 2008, 2012, 2013; Horpibulsuk et al. 2011). Hitherto, numerous research projects have been dedicated to methods of hydraulic conductivity measurement (Randolph and Wroth 1979; Clarke et al. 1979; Baligh and Levadoux 1980; Leroueil and Jamiolkowski 1991; Robertson 1990; Jefferies and Davies 1993; Lunne et al. 1997; Elsworth and Lee 2005; Elsworth and Lee 2007; Cai et al. 2007; Robertson 2009; Chai et al. 2011; Wang et al. 2013; Wang and Shen 2013; Zou et al. 2014). One widely used, economic and efficient method to determine in situ hydraulic conductivity is the piezocone penetration test (CPTU; Campanella and Robertson 1988; Lunne et al. 1997; Mitchell and Brandon 1998), providing near-continuous measurements of tip resistance q t, sleeve friction f s and pore water pressure u at the shoulder, face or shaft of the cone. The test can provide a quantitative measurement of various soil properties, including soil stratigraphy, soil mechanical properties, soil type and the distribution of soil saturation (Douglas and Olsen 1981; Robertson 1990; Lunne et al. 1997; Mitchell and Brandon 1998; Lu et al. 2004; Cetin and Ozan 2009; Cai 2010; Shen et al. 2010, 2015; Wang et al. 2013; Wang and Shen 2013).

The utility of equations derived from piezocone soundings and employed to describe the hydraulic conductivity of soils can be classified into three types. The first involves introducing a relation for the coefficient of consolidation of soils via the dissipation test, then indirectly deriving a further equation for hydraulic conductivity (Gupta and Davidson 1986; Robertson et al. 1992; Danziger et al. 1997; Burns and Mayne 1998; Baligh and Levadoux 1980; Leroueil and Jamiolkowski 1991; Cai et al. 2007), a method that is both time-consuming and labour-intensive. A second possible approach is to apply the soil behaviour index proposed by Robertson (1990, 2009). This index, however, is empirical and may cause large errors in various parameters.

The final method involves theoretical analysis based on a combination of dislocation analysis, Darcy’s law and cavity expansion theory (Elsworth and Lee 2005; Elsworth and Lee 2007; Chai et al. 2011; Wang et al. 2013; Wang and Shen 2013; Zou et al. 2014). Elsworth and Lee (2005, 2007) first proposed a semi-rigorous method and an explicit equation. After that, Chai et al. (2011) presented a modified method based on a half-spherical flow assumption. Yet, numerical simulations of piezocone dissipation tests (Yi et al. 2012a, b; Mahmoodzadeh et al. 2014, 2015; Ceccato and Simonini 2016) indicate that the distribution of excess pore pressures is more suitable for cylindrical flow in the horizontal direction, while the negative exponent distribution of initial excess pore water pressure satisfy the test results closely (Baligh and Levadoux 1980; Roy et al. 1981; Zhu and Tang 1986; Tang et al. 2002; Zhu et al. 2005; Ma et al. 2007).

The objective of this paper is to propose an approach in order to estimate the hydraulic conductivity. First, existing approaches are briefly reviewed and discussed. A new method is thereby presented in detail and compared with existing approaches using piezocone data from Yangtze Delta deposits through a graphical and statistical methodology.

Modification methods for predicting hydraulic conductivity

Brief review of Elsworth’s method

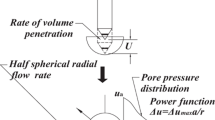
In order to evaluate the hydraulic conductivity directly from piezocone tests, Elsworth and Lee (2005) presented a method (hereafter referred to as Elsworth’s method) based on a dislocation model (Elsworth 1991), as shown in Fig. 1a, where a is the radius of the cone, i a is the hydraulic gradient at radius r = a, k is hydraulic conductivity, U is the rate of cone penetration, u a is the absolute pore water pressure measured by the piezocone and u s is the initial static pore water pressure. The following assumptions are substantially adopted: (1) during piezocone penetration, ‘dynamic steady’ spherical flow of pore water will form around the tip of the cone; (2) excess pore water pressure in the soil around the cone has a power function distribution for radial distance; and (3) the diameter of the spherical cavity is assumed to be the same as the diameter of the cone, while the rate of spherical flow of pore water through the periphery of the cavity is assumed to be equal to the rate of volume penetration \( \vartriangle \dot{V} \) of the cone. An explicit equation was derived to calculate the hydraulic conductivity, using Darcy’s law and assuming that zero excess pore water pressure exists at an infinite distance from the cone.

Fig. 1
figure 1

Basic concept of a Elsworth’s method (recreated from Chai et al. 2011) and b Chai’s method (modified from Chai et al. 2011)

Full size image

In an infinite porous medium, on the condition that excess pore water pressure is zero for radial distance r → ∞, the distribution of pore water pressure u can be expressed as:

$$ u - u_{\text{s}} = (u_{\text{a}} - u_{\text{s}} )a/r. $$
(1)

Then, the hydraulic gradient at radius r = a may be deduced by way of

$$ i_{a} = \frac{1}{{\gamma_{\text{w}} }}\frac{{{\text{d}}u}}{{{\text{d}}r}}|_{r = a} = \frac{{u_{\text{a}} - u_{\text{s}} }}{{a\gamma_{\text{w}} }} = B_{\text{q}} Q_{\text{t}} \frac{{\sigma '_{\text{v0}} }}{{a\gamma_{\text{w}} }}, $$
(2)

where γ w is the unit weight of water, and B q and Q t are the dimensionless pore water pressure ratio and dimensionless tip resistance, respectively, defined as (Wroth 1984)

$$ B_{\text{q}} = (u_{2} - u_{0} )/(q_{\text{t}} - \sigma_{\text{v0}} ), $$
(3)
$$ Q_{\text{t}} = (q_{\text{t}} - \sigma_{\text{v0}} )/(\sigma '_{\text{v0}} ), $$
(4)

In which q t is the static point resistance, u 0 is hydrostatic pressure, u 2 is pore water pressure on the cone shoulder, σ v0 represents the total overburden stress (Teh and Houlsby 1991; Lu et al. 2004) and σ′ v0 is the initial vertical effective stress.

Spherical radial flow around the cone per unit time can be obtained using:

$$ q = 4\pi a^{2} i_{a} k. $$
(5)

Cone penetration amount per unit time is given by

$$ \vartriangle \dot{V} = \pi a^{2} U $$
(6)

Substituting Eq. (2) into Eq. (5), and assuming \( \vartriangle \dot{V} = q \), one can obtain the equation:

$$ 4kB_{\text{q}} Q_{\text{t}} \frac{{\sigma '_{\text{v0}} }}{{a\gamma_{\text{w}} }} = U. $$
(7)

A dimensionless hydraulic conductivity coefficient is defined herein as:

$$ K_{\text{D}} = 1/B_{\text{q}} Q_{\text{t}} . $$
(8)

Combining the above equations, the in situ value of k is expressed by:

$$ K_{\text{D}} = \frac{{4k\sigma '_{\text{v0}} }}{{a\gamma_{\text{w}} U}}\;{\text{or}}\;k = \frac{{\gamma_{\text{w}} K_{\text{D}} U}}{{4\sigma '_{\text{v0}} }}. $$
(9)

Subsequently, the line K D = 1/B q Q t does not provide the best fit to the measured data. As a consequence, Elsworth and Lee (2007) modified the K D − B q Q t relation:

$$ K_{\text{D}} = \frac{\alpha }{{(B_{\text{q}} Q_{\text{t}} )^{\beta } }}, $$
(10)

Where α and β are constants. Elsworth and Lee (2007) suggested suitable values for α and β of 0.62 and 1.6, respectively.

Chai’s method

On the basis of Elsworth’s method, Chai et al. (2011) presented a half-spherical flow approach (hereafter referred to as Chai’s method), as shown in Fig. 1b. In this approach, the following hypotheses are assumed: (1) a half-spherical flow of pore water covers the tip of the cone because pore water cannot flow into the cone; and (2) the rate of half-spherical flow of pore water through the periphery of the cavity is linearly proportional to the rate of volume penetration of the cone (Shen et al. 2015). Chai et al. (2011) modified Elsworth’s method in terms of a bi-linear relation defined by

$$ K_{\text{D}}^{'} = \left\{ \begin{aligned} &1/B_{\text{q}} Q_{\text{t}} ,\quad \quad \quad \quad B_{\text{q}} Q_{\text{t}} < 0.45 \hfill \\ &0.044/(B_{\text{q}} Q_{\text{t}} )^{4.91} ,\,\,\,B_{\text{q}} Q_{\text{t}} > 0.45 \hfill \\ \end{aligned} \right.. $$
(11)

Compared to Elsworth’s method, it was deduced:

$$ K_{\text{D}}^{'} = \frac{{2k\sigma '_{\text{v0}} }}{{a\gamma_{\text{w}} U}} = \frac{{K_{\text{D}} }}{2}. $$
(12)

Moreover, Chai’s approach is applicable to both normally or lightly over-consolidated clayey deposits as well as loose sandy deposits.

Zou’s method

Owing to the stratification commonly observed in natural soil deposits, the hydraulic conductivity in the horizontal direction, k h, is often larger than that in the vertical direction, k v (Leroueil et al. 1990). In fact, whereas most laboratory consolidation tests are conducted with the samples cut in the vertical direction with respect to the in situ condition, pore pressure dissipation occurs mainly in the horizontal direction. As a result, Zou et al. (2014) proposed an explicit equation (see Fig. 2a), assuming radial flow normal to an improved cylindrical surface, which is given by

Fig. 2
figure 2

Basic concept behind: a Zou’s method (Zou et al. 2014); b the method proposed in the present paper

Full size image
$$ K_{\text{D}}^{''} = \left\{ \begin{aligned} &1/B_{\text{q}} Q_{\text{t}} ,\quad \quad \quad \quad \,B_{q} Q_{\text{t}} < 0.35 \hfill \\ &0.017/(B_{\text{q}} Q_{\text{t}} )^{4.64} ,\;\;B_{\text{q}} Q_{\text{t}} > 0.35 \hfill \\ \end{aligned} \right.. $$
(13)

Assuming that the rate of ‘dynamic steady’ flow through the periphery of the cavity with a radius a of a cylinder is linearly proportional to the rate of volume penetration of the cone, one can obtain:

$$ 2\pi a \cdot h \cdot k \cdot i_{a} = \pi a^{2} U = \vartriangle \dot{V}. $$
(14)

The proposed method

The direction and value assumptions of excess pore water pressure distribution are fundamental and substantial for a reliable method, yet, the previous methods emphasized pore water pressure distribution assumptions in a finite local area, hence, the improved assumptions are as follows (shown in Fig. 2b):

  • A dynamic steady cylindrical flow of pore water will form around the tip of the cone.

  • The diameter of the cylindrical cavity is assumed to be the same as the diameter of the cone.

  • Excess pore water pressure in the soil around the cone has a negative exponential function distribution for radial distance, and there is no excess pore water pressure at an infinite distance.

Based on the assumption \( q = \vartriangle \dot{V}\;\left( {{=}\pi a^{ 2} U} \right) \), the mathematical function adopted in this case is:

$$ 2\pi a \cdot \eta h \cdot k_{h} \cdot i_{a} = \pi a^{2} U = \vartriangle \dot{V}. $$
(15)

As shown in Fig. 3, based on the numerical simulation of piezocone dissipation tests (Ceccato and Simonini 2016), the scope of excess pore water pressure dissipation is not confined to the filter thickness h, but instead extends to a larger range ηh (where η is a parameter calibrated with the experimental and simulation values). Yet, it could not be considered in previous methods.

Fig. 3
figure 3

Excess pore pressure distribution around the cone (Ceccato and Simonini 2016)

Full size image

It is essential to determine the distribution of initial excess pore water pressure during penetration, hence, a number of laboratory and field tests (Fig. 4) are carried out which revealed that the negative exponent distribution of initial excess pore water pressure near the tip fit the test results closely (Baligh and Levadoux 1980; Roy et al. 1981; Zhu and Tang 1986; Gupta and Davidson 1986; Tang et al. 2002; Zhu et al. 2005; Ma et al. 2007). Therefore, under the condition that excess pore water pressure is zero for radial distance r → ∞, the distribution of pore water pressure u can be expressed as:

Fig. 4
figure 4

Fitting curve between initial pore water pressures with negative exponent distribution (modified from Wang and Shen 2013)

Full size image
$$ u - u_{\text{s}} = (u_{2} - u_{\text{s}} )e^{ - \theta (r/a - 1)} , $$
(16)

Where θ is a soil parameter: 0.35 < θ ≤ 1.5 for clay, 0.3 < θ ≤ 0.35 for silt and 0.1 < θ ≤ 0.3 for sand (Zhu and Tang 1986; Ma et al. 2007; Shen et al. 2015). According to Darcy’s law, the hydraulic gradient on the surface of the cylinder i a can be expressed by,

$$ i_{a} = \theta \frac{{u_{2} - u_{\text{s}} }}{{a\gamma_{\text{w}} }}e^{ - \theta (r/a - 1)} |_{r = a} = \theta B_{\text{q}} Q_{\text{t}} \frac{{\sigma '_{\text{v0}} }}{{a\gamma_{\text{w}} }}. $$
(17)

Chai et al. (2011) considered that K D values (and, thus, the value of k) deduced from CPTU tests mainly represent the hydraulic conductivity of a natural deposit in the horizontal direction. The results obtained from a series of classical numerical simulations of piezocone dissipation tests and in situ tests (see Figs. 3, 5a, b for conventional CPTU), indicated the surface area for water flow could be cylindrical in shape around the cone at larger scales, even though this area seems spherical in shape only in a finite local area, whereas the half-spherical surface area assuredly is more suitable for spudcans (Fig. 5c) and piezoballs (Fig. 5d). More conformity of the surface area and the distribution of initial excess pore water pressure with actual conditions increase the possibility of accuracy. Hence, the cylindrical surface is more suitable for conventional CPTU primarily.

Fig. 5
figure 5

Distribution of excess pore pressures: a Yi et al. (2012a); b Mahmoodzadeh et al. (2015); c Yi et al. (2012b); d Mahmoodzadeh et al. (2014)

Full size image

Substituting Eq. (17) into Eq. (15), one can obtain:

$$ k_{h} = \frac{Ua}{2\eta h} \cdot \frac{1}{{i_{a} }} = \frac{a}{2\eta h} \cdot \frac{1}{{B_{q} Q_{t} \theta }} \cdot \frac{{Ua\gamma_{w} }}{{\sigma '_{v0} }}. $$
(18)

Defining K D″′ = 1/B q Q t, k h is expressed as:

$$ k_{\text{h}} = \frac{a}{2\eta h} \cdot \frac{{K_{\text{D}}^{'''} }}{\theta } \cdot \frac{{Ua\gamma_{\text{w}} }}{{\sigma '_{\text{v0}} }}. $$
(19)

Comparing with Elsworth’s method, the relationship is given by

$$ K_{\text{D}}^{'''} = \theta \eta hK_{\text{D}} /2a. $$
(20)

Based on previous methods (Elsworth and lee 2005; Chai et al. 2011; Wang et al. 2013; Wang and Shen 2013; Zou et al. 2014), it follows that:

$$ K_{\text{D}}^{'''} = \left\{ \begin{aligned} 1/B_{\text{q}} Q_{\text{t}} ,\quad \quad B_{\text{q}} Q_{\text{t}} < \varepsilon \hfill \\ \alpha /(B_{\text{q}} Q_{\text{t}} )^{\beta } ,\;\;B_{\text{q}} Q_{\text{t}} > \varepsilon \hfill \\ \end{aligned} \right., $$
(21)

where ɛ is a constant parameter. According to international standards for CPTU cones, their height should be equal to 5 mm and their radius to 17.85 mm. Considering Ma et al. (2007) found the value of θ equal to 0.3, the data provided by Elsworth and Lee (2005; see Fig. 6) can be employed to obtain values of η = 8 and ɛ = 0.98. Equation (21) can then be expressed as follows:

Fig. 6
figure 6

Relationship between the proposed bi-linear K″′ D − B q Q t (data from Elsworth and Lee 2007)

Full size image
$$ K_{\text{D}}^{'''} = \left\{ \begin{aligned} &1/B_{\text{q}} Q_{\text{t}} ,\quad \quad \quad \;\;B_{\text{q}} Q_{\text{t}} < 0.98 \hfill \\ &0.87/(B_{\text{q}} Q_{\text{t}} )^{7.81} ,\;B_{\text{q}} Q_{\text{t}} > 0.98 \hfill \\ \end{aligned} \right.. $$
(22)

Data

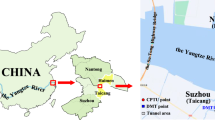
The area of the Yangtze River Delta (including Shanghai, Suzhou, Wuxi, Changzhou and other cities) is located in the eastern part of China, with seven sites across the region

(four in Suzhou: Yushan Station, Xinghui Road Station, Hongzhuang Station and Zhuhui Road Station; two in Nanjing: Jiangbei work well and the fourth Yangtze River Bridge; and the Yangtze Bridge in Taizhou) selected for the present study, as shown in Fig. 7. A summary description of these sites is also provided in Table 1. Typical profiles of CPTU measurements, including cone tip resistance (q t), side friction resistance (f s), and pore water pressure (u 2 ) versus depth recorded at Hongzhuang Station in Suzhou are presented in Fig. 8. At each of the investigated sites, high-quality piston samples were taken at different depths that corresponded to the depths of piezocone dissipation tests undertaken in comprehensive laboratory testing. Soil samples were collected by means of a stationary piston sampler, 76 mm in diameter, at 1.0-m intervals below ground level. Once the stationary piston sampler was withdrawn from the borehole, the soil at both ends of the tube was excavated for wax sealing. Horizontal permeability tests were carried out in the laboratory on undisturbed samples of cohesive soils obtained from high-quality thin-wall samplers, with field pumping tests also performed in boreholes located on cohesionless soils. Groundwater tables at the sampling sites are located at 0–5 m and with depths ranging from 12 to 40 m.

Fig. 7
figure 7

Map of the Yangtze River Delta showing the seven CPTU site locations

Full size image
Table 1 Soil properties and description of sites
Full size table
Fig. 8
figure 8

Typical CPTU soundings recorded at Hongzhuang Station, Suzhou

Full size image

The CPTU device used throughout the study was produced by Vertek-Hogentogler and Co., USA, and comprised a versatile piezocone system equipped with advanced digital cone penetrometers fabricated with a 60º tapered, 10-cm2 tip area cone, which provided measurements of q t, f s and u 2 with a 5-mm-thick porous filter located just behind the cone tip. The rate of penetration for all tests was 20 mm/s, enabling one set of readings to be obtained for every 50-mm penetration. Shear wave velocities were measured at intervals of 1.0 m, corresponding to successive rod additions during advancement of the penetrometer.

Analysis and discussion

Qualitative analysis

Hydraulic conductivity values obtained using the aforementioned methods were subsequently compared with the laboratory and field pumping results (see Fig. 9 through Fig. 16). The fact that more than 90% of data points are scattered above the bi-linear line in Figs. 9 and 11 and below the perfect line displayed in Figs. 10 and 12 indicates that both Elsworth’s method and Chai’s method substantially underestimate the hydraulic conductivity of saturated soils. In contrast, more than half of the data points obtained using Zou’s method lie above the bi-linear in Fig. 13 and below the perfect line shown in Fig. 14, which implies that the predicted accuracy of this particular method is higher. However, the results shown in Figs. 15 and 16 reveal that the proposed modified method is most applicable to Yangtze Delta soils due to the proximity of the line and data points. It is obvious that the values of k h for soils ranging from partially drained silt through to undrained clay may be continuously and reasonably evaluated from piezocone sounding records using the modified method. As can be seen from Fig. 16, the data points are evenly distributed around the perfect line y = x, which implies that the proposed method produces the best agreement.

Fig. 9
figure 9

Bi-linear K D − B q Q t relationship for Elsworth’s method

Full size image
Fig. 10
figure 10

Measured versus predicted k h values for Elsworth’s method

Full size image
Fig. 11
figure 11

Bi-linear K′ D − B q Q t relationship for Chai’s method

Full size image
Fig. 12
figure 12

Measured versus predicted k h values for Chai’s method

Full size image
Fig. 13
figure 13

Bi-linear K″ D − B q Q t relationship for Zou’s method

Full size image
Fig. 14
figure 14

Measured versus predicted k h values for Zou’s method

Full size image
Fig. 15
figure 15

Bi-linear K″′ D − B q Q t relationship for the modified method

Full size image
Fig. 16
figure 16

Measured versus predicted k h values for the modified method

Full size image

Quantitative analysis

The reliability of the adopted correlations is assessed on the basis of four existing and one new criteria: root mean square error (RMSE; Grima and Babuška 1999), the first (mean) and second moment (standard deviation) statistics of the ratio of the estimated to test-determined shear wave velocity (K; Briaud and Tucker 1988), ranking index (RI; Briaud and Tucker 1988), ranking distance (RD; Cherubini and Orr 2000) and a new relative error index (RE).

RMSE is the square root of the average of the squared difference between true values and the corresponding observed values. Errors in RMSE are squared before they are averaged; consequently, a relatively high weight is given to large errors. This means that the RMSE is most useful when large errors are particularly undesirable, with the lower the RMSE value, the better the model performance. RMSE is determined via the following equation:

$$ {\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {(h_{\text{l}} - h_{\text{c}} )^{2} } } , $$
(23)

where n is the number of data points, h c is the hydraulic conductivity calculated from empirical equations and h l is the hydraulic conductivity measured directly from tests.

The first (mean μ) and second moment (SD standard deviation) statistics of the ratio of estimated to measured hydraulic conductivity is denoted by K and determined via the following equation:

$$ K = h_{\text{c}} /h_{\text{l}} $$
(24)

whereas the accuracy of a method refers in this case to its ability to predict the measured hydraulic conductivity and is represented by the mean of K (Briaud and Tucker 1988; Cherubini and Orr 2000; Giasi et al. 2003), method precision refers to the scatter around the mean and is quantified by the standard deviation of K (Briaud and Tucker 1988; Cherubini and Orr 2000; Giasi et al. 2003; Onyejekwe et al. 2015). Theoretically, K ranges from 0 to infinity with an optimum value of one; this results in the nonsymmetric distribution of K around the mean and, thus, also an unequal weight of underprediction and overprediction (Briaud and Tucker 1988).

The ranking index (RI) is also one of the two methods proposed by Briaud and Tucker (1988) with which to alleviate the problem of nonsymmetrical distribution of K data. Hence, RI values can be used to express an overall judgment regarding the quality of a correlation whilst simultaneously accounting for the mean value and SD of all K data. The ranking index is obtained via the following equation (Briaud and Tucker 1988):

$$ {\text{RI}} = \left| {\mu_{\ln (K)} } \right| + \sigma_{\ln (K)} , $$
(25)

where μ and σ represent the mean and SD of the series of analysed data, respectively. RI has been used by several investigators (e.g. Briaud and Tucker 1988; Cherubini and Orr 2000; Giasi et al. 2003) to evaluate the performance of empirical equations.

RD, first proposed by Cherubini and Orr (2000), is another method enabling users to make an overall judgment as to the quality of a calculation method, again taking into consideration the mean value and standard deviation of all K data. RD represents, on a plot with mean (μ) values on the x axis and SD (σ) on the y axis, the distance of the point representing a computation using a particular correlation from the point representing the optimum condition (μ = 1 and σ = 0). RD is determined as follows (Cherubini and Orr 2000):

$$ {\text{RD}} = \sqrt {(1 - \mu_{K} )^{2} + \sigma_{K}^{2} } . $$
(26)

RD and RI provide different evaluations of the suitability of a given correlation equation to fit a measured value (Cherubini and Orr 2000). For correlation equations where the precision (as indicated by the SD), mean value and accuracy are similar, RD gives a better result than RI, while for those that are either very accurate or very precise, RI provides the best result. RD gives equal weight to accuracy and precision, and has been used by several investigators (e.g. Cherubini and Orr 2000; Giasi et al. 2003) to evaluate the performance of empirical equations.

Relative error (RE), a new statistical criterion proposed in the present paper, is the ratio of the absolute difference between the measured value and the estimate of the measured hydraulic conductivity; the lower the RE value, the better the model performance. RE is mainly used to assess the pros and cons of different methods and is expressed as follows:

$$ {\text{RE}} = \left| {h_{\text{l}} - h_{\text{c}} } \right|/h_{\text{l}} = K - 1. $$
(27)

Results and discussion

In the following section, both the observed and calculated data are presented in logarithmic form due to the fact that the obtained values of hydraulic conductivity varied by up to six orders of magnitude; with the more logarithmic the result, the lower the original hydraulic conductivity (that is always less than 1). A summary of the RMSE, K, RE, RI and RD values obtained for the Jiangsu clays is presented in Table 2. RMSE, RI and RD data are also illustrated in Fig. 17 in log form, while those for RE are shown graphically in Fig. 18.

Table 2 Results for RMSE, K, RE, RI and RD
Full size table
Fig. 17
figure 17

Results for RMSE, RI and RD

Full size image
Fig. 18
figure 18

Results for RE

Full size image

In terms of RMSE, the best performing correlation was provided by the proposed method (RMSE = 0.940). However, regarding general overestimation (K > 1 or RE > 0), all methods produced more than 50% of K values greater than 1, indicating that all underestimated the hydraulic conductivity of the studied saturated soils. In terms of accuracy (based on the closeness of the mean of K to 1 or RE to 0), the proposed method again produced the best performance, with a K mean of 1.003. Similarly, regarding RI values, as well as the σ of K and RE, the proposed method provided the most accurate evaluation (RI = 0.070). However, both RMSE and RI have certain shortcomings, with the former highlighting only substantial errors (i.e. low accuracy) and the latter considering both accuracy and precision but not assigning an equal weight to them. In contrast, RD, which gives equal weight to accuracy and precision, is a better parameter with which to compare the suitability of different correlation equations (Onyejekwe et al. 2015). In terms of RD, the best method for the analysed Jiangsu soft clays was the proposed method (RD = 0.068). Considering a common allowable limit of relative error (ALE) of 5%, the percentage relative error less than ALE (PRELA) is shown graphically in Fig. 18 for each method, with the higher the PRELA value, the better the correlation performance. Again the proposed method achieved the best performance (PRELA = 78%), followed by Zou’s method (64%). In summary, the most efficient of the four studied methods is that proposed in the present paper.

Conclusions

Despite several recent improvements, evaluation using conventional CPT-based methods continues to underestimate the in situ hydraulic conductivity of soil. In order to obtain more accurate values of this parameter, the present paper has outlined a new method based on the analysis and comparison of existing methods. A comparison of the results obtained by the proposed method and existing approaches using piezocone, field pumping and laboratory data for Quaternary deposits in the Yangtze Delta region was conducted. The most important findings of our study can be summarized as follows:

  1. 1.

    Existing methods mainly assume spherical or half-spherical radial flow around the cone or/and a power functional distribution. Yet, the surface area for water flow seems to be cylindrical rather than spherical in shape around the cone, with the exception of regions very close to the cone, while the surface area seems to be a half ellipsoid or spherical shape for spudcans and piezoballs according to the numerical simulation of piezocone dissipation tests. A number of laboratory and field tests were also carried out demonstrating that the negative exponent distribution of initial excess pore water pressure near the tip fits these results closely. These new hypotheses yielded a new method that builds on existing approaches.

  2. 2.

    Obtained using a graphical method for the analysis of field data, the results of measured versus predicted k h values for the four analysed methods indicate that the proposed method can evaluate the hydraulic conductivity of soil (based on the CPTU test) more accurately.

  3. 3.

    In terms of the general overestimation (K > 1 or RE > 0) of k h, the methods of Elsworth and Chai fundamentally underestimate the hydraulic conductivity of soils. In terms of RI and RD, Zou’s method (RI = 0.101 and RD = 0.078) and the newly proposed method (RI = 0.070 and RD = 0.068) provide more accurate evaluations regarding the allowable limits of relative error (ALE) (5%); however, the proposed method achieved a percentage RE less than ALE (PRELA) value 14% greater than that of Zou (at 78 and 64%, respectively). Generally speaking, the most efficient method is the proposed one in the present paper. This method has been selected thanks to its larger accuracy and truthfulness compared with other possible approaches.