1 Introduction

As an economic and efficient site investigation method, the piezocone penetration test (CPTU) always provides near-continuous measurements of tip resistance, sleeve friction, and pore water pressure at the shoulder, face, or shaft of the cone [1–3]. It can also give a quantitative measurement of various soil properties in situ, such as soil stratigraphy, soil mechanical properties, soil type, and the distribution of soil saturation.

Hydraulic conductivity may influence consolidation deformation [4–6], the design of pit dewatering [7], the estimation of foundation settlement, and the analysis of soil consolidation [8–12]. Therefore, numerous researchers have been dedicated to studying methods of hydraulic conductivity measurement [13–25].

Generally speaking, there are three types of methods to describe the hydraulic conductivity of in situ soils derived from piezocone soundings. The first approach involves applying the Soil Behaviour Index proposed by Robertson [18, 19]. The second refers to an indirect way to introduce a relation for the coefficient of consolidation of soils via the dissipation test [26–29], which is time-consuming and labour-intensive. The third involves a semi-theoretical method based on dislocation analysis, Darcy’s law, and cavity expansion theory [6, 21–25]. Elsworth and Lee [21, 22] first proposed an explicit equation on the basis of a spherical flow assumption. Subsequently, Chai et al. [6] modified the method using a half-spherical flow assumption, which can be used for normally or lightly overconsolidated clayey deposits and loose sandy deposits. Zou et al. [25] proposed an explicit equation with radial flow normal to an improved cylindrical surface. Yet, numerical simulation of piezocone dissipation tests [30–33] shows that the distribution of excess pore pressures is more suited for a combination of cylindrical and half-spherical (cylindrical-half-spherical) flow rather than simplex half-spherical flow or cylindrical flow [15, 34–36].

The aim of this paper was to apply the assumption of cylindrical-half-spherical flow and a negative exponent distribution to estimate the in situ hydraulic conductivity of soil.

2 Modification Methods

2.1 Brief Review of Elsworth’s and Chai’s Method

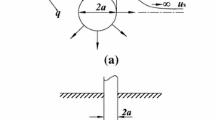
To evaluate the hydraulic conductivity directly from piezocone data, Elsworth and Lee [21] first presented a spherical flow method (hereafter referred to as Elsworth’s method) based on a dislocation model [37]. To improve the accuracy of the model, Chai et al. [6] proposed a half-spherical flow approach (hereafter described as Chai’s method), as shown in Fig. 1.

Fig. 1
figure 1

(modified from [6])

Basic concept of Chai’s method

Full size image

The following assumptions are essentially adopted (Fig. 1): (1) during piezocone penetration, ‘dynamic steady’ semi-spherical flow of pore water will form around the tip of the cone; (2) excess pore water pressure around the cone has a distribution of power function for radial distance; and (3) the rate of half-spherical flow of pore water through the periphery of the cavity is linearly proportional to the rate of volume penetration of the cone [38].

The hydraulic gradient at radius \(r=a\) may be deduced by way of

$${{i}_{a}}=\frac{1}{{{\gamma }_{w}}}\frac{\text{d}u}{\text{d}r}{{|}_{r=a}}=\frac{{{u}_{a}}-{{u}_{s}}}{a{{\gamma }_{w}}}={{B}_{q}}{{Q}_{t}}\frac{\sigma {{'}_{v0}}}{a{{\gamma }_{w}}}$$
(1)

where \({{B}_{q}}\) and \({{Q}_{t}}\) are the dimensionless pore water pressure ratio and dimensionless tip resistance, respectively [39]:

$${{B}_{q}}=({{u}_{2}}-{{u}_{0}})/({{q}_{t}}-{{\sigma }_{v0}})$$
(2)
$${{Q}_{t}}=({{q}_{t}}-{{\sigma }_{v0}})/(\sigma {{'}_{v0}}).$$
(3)

Half-spherical radial flow around the cone per unit time can be obtained using the following equation:

$$q=2\pi {{a}^{2}}{{i}_{a}}k.$$
(4)

Cone penetration amount per unit time is given by the following equation:

$$\vartriangle \dot{V}=\pi {{a}^{2}}U.$$
(5)

Substituting Eq. (1) into Eq. (4), and assuming \(\vartriangle \dot{V}=q\), one can obtain the following equation:

$$2k{{B}_{q}}{{Q}_{t}}\frac{\sigma {{'}_{v0}}}{a{{\gamma }_{w}}}=U.$$
(6)

If a dimensionless hydraulic conductivity coefficient \({{K}_{D}}=1/{{B}_{q}}{{Q}_{t}}\) was introduced, Elsworth’s method [21] first gave a bi-linear relation:

$${{K}_{D}}=\left\{ \begin{aligned} & 1/{{B}_{q}}{{Q}_{t}},{{B}_{q}}{{Q}_{t}}<1.2 \\ & 0.62/{{({{B}_{q}}{{Q}_{t}})}^{1.6}},{{B}_{q}}{{Q}_{t}}>1.2 \\ \end{aligned} \right..$$
(7)

And then, Chai et al. [6] modified this in terms of another bi-linear relation defined by the following:

$$K_{D}^{'}=\left\{ \begin{aligned} & 1/{{B}_{q}}{{Q}_{t}},{{B}_{q}}{{Q}_{t}}<0.45 \\ & 0.044/{{({{B}_{q}}{{Q}_{t}})}^{4.91}},{{B}_{q}}{{Q}_{t}}>0.45 \\ \end{aligned} \right..$$
(8)

2.2 Zou’s Method

Considering half-spherical flow may be more suitable for pore water pressure on the cone shoulder, Zou et al. [25] proposed an explicit equation (see Fig. 2a), assuming radial flow normal to an improved cylindrical surface, which is given by the following equation:

Fig. 2
figure 2

Basic concept behind: a Zou’s method [25]; b the method proposed in the present paper

Full size image
$$K_{D}^{''}=\left\{ \begin{aligned} & 1/{{B}_{q}}{{Q}_{t}},{{B}_{q}}{{Q}_{t}}<0.35 \\ & 0.017/{{({{B}_{q}}{{Q}_{t}})}^{4.64}},{{B}_{q}}{{Q}_{t}}>0.35 \\ \end{aligned} \right..$$
(9)

3 The Improved Method

To determine the distribution of initial excess pore water pressure during penetration near the cone tip more precisely, a number of laboratory, field tests (Fig. 3), and numerical simulations (Fig. 4) were carried out. The results derived from Fig. 3 revealed that the negative exponent distribution of the initial excess pore water pressure near the tip could fit the test results more closely [15, 34–36]. In addition, the results obtained from Fig. 4 indicated that the surface area for water flow seems to be more half-spherical–cylindrical in shape. Hence, the improved cylindrical–half-spherical flow assumptions are described as follows (see Fig. 2b).

Fig. 3
figure 3

(modified from Wang et al. [24])

Fitting curve between the initial pore water pressures with negative exponent distribution

Full size image
Fig. 4
figure 4

Distribution of excess pore pressures: a Yi et al. [40]; b Mahmoodzadeh et al. [32]; c Ceccato and Simonini [33]

Full size image

The diameter of the cylindrical and half-spherical cavity is assumed to be the same as the diameter of the cone.

The height of the cylindrical cavity is assumed to be the height of the cone.

The negative exponential function rules the distribution of excess pore water pressure in the soil around the cone.

Based on the assumption \(q=\vartriangle \dot{V}\)(\(=\pi {{a}^{2}}U\)), the mathematical function adopted in this case is as follows:

$$2\pi a\cdot h\cdot {{k}_{h}}\cdot {{i}_{a}}+2\pi {{a}^{2}}\cdot {{k}_{h}}\cdot {{i}_{a}}/\xi =\pi {{a}^{2}}U=\vartriangle \dot{V}$$
(10)

where \(\xi\) is a reduction factor of the half-spherical cavity determined by tests and simulations, because for the conventional CPTU, the surface area for water flow seems to be more half-spherical–cylindrical in shape near the cone and cylindrical–half-spherical in shape around the cone at larger scales than half-spherical or spherical (Fig. 4).

In addition, assuming that excess pore water pressure is zero for radial distance\(r\to \infty\), the distribution of pore water pressure u can be expressed as follows:

$$u-{{u}_{s}}=({{u}_{2}}-{{u}_{s}}){{e}^{-\theta (r/a-1)}}$$
(11)

where \(0.35<\theta \le 1.5\) for clay, \(0.3<\theta \le 0.35\) for silt, and \(0.1<\theta \le 0.3\) for sand [34, 38, 41]. According to Darcy’s law, \({{i}_{a}}\) can be given by

$${{i}_{a}}=\theta \frac{{{u}_{2}}-{{u}_{s}}}{a{{\gamma }_{w}}}{{e}^{-\theta (r/a-1)}}{{|}_{r=a}}=\theta {{B}_{q}}{{Q}_{t}}\frac{\sigma {{'}_{v0}}}{a{{\gamma }_{w}}}.$$
(12)

Moreover, Chai et al. [6] considered that \({{K}_{D}}\) or k deduced from CPTU tests mainly represent the hydraulic conductivity of a natural deposit in the horizontal direction.

Substituting Eq. (12) into Eq. (10), one can obtain the following equation:

$$2(h+a/\xi )\cdot {{k}_{h}}\cdot {{B}_{q}}{{Q}_{t}}\theta \cdot \frac{\sigma {{'}_{v0}}}{a{{\gamma }_{w}}}=Ua.$$
(13)

Defining \({{K}_{D1}}=1/{{B}_{q}}{{Q}_{t}}\), one can obtain

$${{K}_{D1}}=\frac{(h+a/\xi )\theta }{2a}\cdot \frac{4{{k}_{h}}\sigma {{'}_{v0}}}{Ua{{\gamma }_{w}}}\,\ \text{or}\ \ {{k}_{h}}=\frac{2a}{(h+a/\xi )\theta }\cdot \frac{{{K}_{D1}}Ua{{\gamma }_{w}}}{4\sigma {{'}_{v0}}}.$$
(14)

Based on the previous methods, it follows that

$${{K}_{D1}}=\left\{ \begin{aligned} & 1/{{B}_{q}}{{Q}_{t}},{{B}_{q}}{{Q}_{t}}<\varepsilon \\ & \alpha /{{({{B}_{q}}{{Q}_{t}})}^{\beta }},{{B}_{q}}{{Q}_{t}}>\varepsilon \\ \end{aligned} \right..$$
(15)

According to international standards for CPTU cones, their height and radius of filter ring should be equal to 5 and 17.85 mm, respectively. Considering that Ma et al. [41] suggested that the value of \(\theta\) was 0.3, the data provided by [22] (see Fig. 5) can be employed to obtain values of \(\xi\) = 2 and \(\varepsilon\) = 0.9. Equation (17) can then be expressed as follows:

Fig. 5
figure 5

Relationship between the proposed bi-linear KD1 − BqQt (data from [22])

Full size image
$${{K}_{D1}}=\left\{ \begin{aligned} & 1/{{B}_{q}}{{Q}_{t}},{{B}_{q}}{{Q}_{t}}<0.9 \\ & 0.9/{{({{B}_{q}}{{Q}_{t}})}^{7.81}},{{B}_{q}}{{Q}_{t}}>0.9 \\ \end{aligned} \right..$$
(16)

4 Data

The seven sites selected for this study locates at the three cities in the eastern part of China, as shown in Fig. 6. A summary description of these sites is also provided in Table 1. Typical profiles of CPTU measurements, including cone tip resistance (qt), side friction resistance (fs), and pore water pressure (u2), versus depth recorded at Hongzhuang Station in Suzhou are presented in Fig. 7. Soil samples were collected by means of a stationary piston sampler, 76 mm in diameter, at 1.0-m intervals below ground level. Once the stationary piston sampler was withdrawn from the borehole, the soil at both ends of the tube was excavated for wax sealing. Horizontal permeability tests were carried out in the laboratory on undisturbed samples of cohesive soils obtained from high-quality thin-wall samplers, with field pumping tests also performed in boreholes located on cohesionless soils. Groundwater tables at the sampling sites are located at 0 to 5 m and with depths ranging from 12 to 40 m.

Fig. 6
figure 6

Map of the CPTU sites

Full size image
Table 1 Soil properties and description of sites
Full size table
Fig. 7
figure 7

Typical CPTU soundings recorded at Zhuhui Station, Suzhou

Full size image

The CPTU device in the study was produced by Vertek-Hogentogler and Co, USA, and comprised a versatile piezocone system equipped with advanced digital cone penetrometers fabricated with a 60° tapered, 10-cm2 tip area cone, which provided measurements of \({{q}_{t}}\),\({{f}_{s}}\), and \({{u}_{2}}\) with a 5-mm-thick porous filter located just behind the cone tip. The rate of penetration for all tests was 20 mm/s, enabling one set of readings to be obtained for every 50-mm penetration.

5 Analysis and Discussion

5.1 Qualitative Analysis

The hydraulic conductivity of soils obtained using the different CPTU interpretation methods is indicated in Fig. 8 through Fig. 15, compared with the laboratory and field pumping results. The fact that more than most of the data points are scattered below the perfect line (see Figs. 8, 9) shows that Elsworth’s method and Chai’s method underestimate the hydraulic conductivity of saturated soils substantially. In addition, about 60% of the data points using Zou’s method below the perfect line shown in Fig. 10 imply that the predicted accuracy of this particular method is higher than the first two methods. However, as can be seen from Fig. 11, the data points are evenly scared around the perfect line y = x, which implies that the proposed method is most suitable for Yangtze Delta soils.

Fig. 8
figure 8

Measured versus predicted kh values for Elsworth’s method

Full size image
Fig. 9
figure 9

Measured versus predicted kh values for Chai’s method

Full size image
Fig. 10
figure 10

Measured versus predicted kh values for Zou’s method

Full size image
Fig. 11
figure 11

Measured versus predicted kh values for the modified method

Full size image

5.2 Quantitative Analysis

In this paper, five indexes are adopted to assess the reliability of these four above-mentioned methods: root-mean-square error (RMSE) [42–45], the first (mean) and second moments (standard deviation SD) statistics of the ratio of the estimated to test-determined k (K), ranking index (RI) [46], ranking distance (RD) [47], and relative error index (RE).

RMSE is determined via the following equation:

$$\text{RMSE}=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}{{{({{h}_{l}}-{{h}_{c}})}^{2}}}}.$$
(17)

The first (mean μ) and second moment (SD standard deviation σ) statistics of the ratio of the estimated shear wave velocity to the measured shear wave velocity is denoted by K. It is determined using the following equation.

$$K={{h}_{c}}/{{h}_{l}}.$$
(18)

The ranking index (RI) is determined by:

$$\text{RI}\ =\ \left| {{\mu }_{\ln (K)}} \right|\ +\ \sigma _{K}^{2}.$$
(19)

Ranking distance (RD) is another method that takes into consideration the mean value and the standard deviation of all the K data. RD is given by [47]:

$$\text{RD}\ =\ \sqrt{{{(1-{{\mu }_{K}})}^{2}}}+\sigma _{K}^{2}$$
(20)

RD gives equal weight to accuracy and precision, and has been used by several investigators (e.g., [48, 49]) to evaluate the performance of empirical equations.

Scaled relative error is the ratio of the difference between the measured value and the estimate to the measured hydraulic conductivity, while the absolute of it is RE. RE is mainly used to assess the pros and cons of different methods and is expressed as follows:

$$RE=\left| {{h}_{l}}-{{h}_{c}} \right|/{{h}_{l}}=K-1.$$
(21)

The lower the RMSE, K, RE, RI, and RD values are, the better the correlation is.

Actually, the cumulative frequency curve is always applied to the particle-size distribution curve. Yet, it may be used for the assessment of equations in this paper (see Fig. 12), because not only can it reveals the variation range of an equation, but it also presents the variation tendency of an equation.

Fig. 12
figure 12

Scaled relative errors of k predicted

Full size image

6 Results and Discussion

In the following section, the data are presented in logarithmic form due to the fact that the obtained values of hydraulic conductivity varied by up to six orders of magnitude. A summary of the RMSE, K, RE, RI, and RD values calculated by these methods is presented in Table 2. Scaled relative errors and relative error data are shown graphically in Figs. 12 and 13, respectively.

Table 2 Results for RMSE, K, RE, RI, and RD
Full size table
Fig. 13
figure 13

Results for relative error RE

Full size image

In terms of RMSE, the proposed method performs best (RMSE = 0.996). with respect to general overestimation (K > 1), the percentage of the K values greater than 1 for all methods is all above than 50%, indicating that these methods all underestimate the hydraulic conductivity of soils. In terms of accuracy, the proposed method again provides the most accurate evaluation, with a K mean of 0.996. Similarly, regarding RI values, as well as the σ of K and RE, this method produces the best performance (RI = 0.066). Compared to RMSE and RI, RD, which gives equal weight to accuracy and precision, is a better parameter with which to compare the suitability of different correlation equations [49]. In terms of RD, the best method is the proposed method (RD = 0.070). Considering a common allowable limit of relative error (ALE) of 5%, the percentage relative error less than ALE (PRELA) is shown graphically in Fig. 13 for each method, where the higher the PRELA value, the better the correlation performance. Again, the proposed method achieves the better performance (PRELA = 51%), than Zou’s method (44%).

These indexes are all discontinuous and indirect, and hence, new graphical analysis using cumulative frequency is carried out in this paper. It is shown from Fig. 12 that the proposed method gives the least error. In summary, the most efficient of the four methods is the proposed method in the present paper.

7 Conclusions

To obtain more accurate the in situ hydraulic conductivity of soil, the present paper has presented a new method. A comparison of the results obtained by the proposed method and existing approaches using tests in the Yangtze Delta region was carried out. Five different indices and a new graphical analysis were utilized, from which the following significant conclusions can be drawn:

  1. 1.

    The cylindrical–half-spherical radial flow around the cone and the negative exponent distribution of initial excess pore water pressure near the tip are more suitable for the test and numerical results.

  2. 2.

    According to the qualitative graphical analysis, the proposed method can evaluate the hydraulic conductivity of soil more accurately.

  3. 3.

    Five different indices and a new graphical analysis can be utilized to assess the similar equations.

  4. 4.

    The Elsworth’s and Chai’s method fundamentally underestimate the hydraulic conductivity of soils. Although in terms of RI and RD, both Zou’s method (RI = 0.101 and RD = 0.078) and the newly proposed method (RI = 0.066 and RD = 0.070) provide more accurate evaluations, if ALE equals to 5% the proposed method achieves a percentage relative error less than ALE with a value 7% greater than that of Zou’s method (at 51% and 44%, respectively). The results of new graphical analysis using cumulative frequency, the proposed method gives the least error. Generally speaking, the most efficient method is that proposed in the present paper.