A three-stage shearlet-based algorithm for vessel segmentation in medical imaging

Abstract

Dictionaries are known tools used in different branches of image processing like edge detection, inpainting and, etc. Segmentation is the task of extracting an object as the part of a particular image. The common drawback of different segmentation methods is that they perform the extraction task incompletely. Tasks like edge detection, denoising and smoothing, as the parts of segmentation, can be done through applying the dictionaries. In this paper, we propose three new contrast stretching function. Based on one of the stretching functions and shearlets as a dictionary, we improved the previous version of a method that has been used in binary segmentation for magnetic resonance angiography images (MRI). We also introduce a three-stage binary image segmentation algorithm for vessel segmentation in MRI images. There are some disadvantages in recent proposed methods when dealing with extracting vessels of medical images. Our algorithm does the task with a more accurate extraction in detecting vessels having low intensity and weak edges in MRI.

1 Introduction

Segmentation is a process of partitioning an image into distinct parts in which the pixels in each part are homogeneous with respect to a particular feature like intensity. This process is usually applied to extract a target object out of the image. There is a broad application of this procedure in medical sciences, where for example we analyze magnetic resonance angiography images (MRI).

Medical imaging is a noninvasive approach used for observing and studying interior tissues of human body. Segmentation of tube-like objects in 2D images is an important problem, and the result of this task can be used to solve some other problems like vessel segmentation in medical images. The main purpose of this paper is to detect tubular and branching structures , especially for the images with weak edges and intensity close to the background.

There are involved parameters, e.g., varying intensities and thickness, false discontinuities and twisting, when dealing with medical images that make this kind of problems hard to deal with. Furthermore, in this type of images, there are some additional factors, e.g., noise and blur that make the segmentation process complicated. In medical images, contamination of images with blur and noise might occur in any stage of the imaging process. Moreover, we must consider other factors like inhomogeneity and low contrast in the images. Considering segmentation problem, the efficiency of an algorithm is the potential of it when segmenting an image in the presence of all these factors.

Segmentation is a very powerful tool in different branches of medicine, like anatomy identification of a tissue, planning for surgery, discovering of abnormal tissues like tumors, assessing a patient’s condition before surgery, determination of vessels obstruction in heart disease and angiography and, etc.

The segmentation methods that are based on space feature of images can be grouped as:

• 1. Edge-based methods

• 2. Region-based methods

• 3. Pixel- or intensity-based methods .

By this classification, our algorithm is in the first and the second groups.

There are different approaches in the literature for vessel segmentation [1,2,3,4,5,6,7,8,9,10,11]. For some good review on the subject, see [12,13,14]. Below, we give a brief account of some of these methods.

Deformable models are applied to the vessel segmentation [3, 5, 8, 10, 11]. They are initiated from a curve as an object boundary estimation and then a functional depending on the regularity and structure of a surface is minimized by the curve evolution. Explicit deformable models [15] have some disadvantages such as inaccurate computation of normal and curvatures and costly computations. Level-set models, as implicit deformable models, are applied to tubular structure segmentation as well [6, 9, 16, 17]. Similarly, they are computationally expensive methods. The model introduced in [8] for volume data is not capable of detecting the thin vessels with having intensity close to the background [18]. The geometric deformable model in [5] presented for the tubular-like structures segmentation which deforms the distance function by a PDE obtained from a total variation model. Due to the use of diffusion tensor for the governing of directionality, it has the ability in detecting twisted, convoluted and, occluded vessels. However, this method also has difficulty in dealing with the noisy and blurred vessels having weak edges.

Deep learning-based vessel segmentation method proposed in [19] that performed the segmentation task as a pixel classification problem. The model introduced in [20] benefits of cross-modality data from the retinal image to the vessel map and get the label map from all of the given image patch pixels. Not using from a global correlation, it fails in dealing with a local pathological region. Also, due to training and testing phases, it has heavy computational complexity.

In [21], as a retinal vessel segmentation method, the authors addressed the segmentation task as a boundary detection problem using a novel deep learning system, deep vessel, constructed by a convolutional neural network and a conditional random field. The method presented in [22] was specifically designed using U-net [23] as the most promising deep learning frameworks for the segmentation tasks which has shown high performance for the segmentation of biomedical images. Depending on the training data that may not be available, is the important disadvantage of such methods.

Besides the above-mentioned methods, tight-frame-based approaches in texture classification and segmentation are proposed [24, 25]. A minimization model proposed in [4], as a convexed version of the Chan–Vese active contour model [1], has the minimal partition property and multiresolution analysis advantages inherited of the Chan–Vese model and tight-frame systems, respectively. This method performs the segmentation task of complex structures successfully, but it has a weak performance in front of the thin vessels having low intensity [18].

In [18], the authors introduced a novel algorithm for MRIs that estimates the interval included boundary pixels of the vessels and refines it iteratively. Based on the interval, it classified boundary pixels as a vessel or background in each iteration gradually. Recently, several vessel segmentation methods are proposed based on the shearlets frame [26,27,28,29]. In [26], the shearlets frame is applied as a regularizer of a convex multiclass method. We used shearlets frame as a denoising and smoothing tools in [27]. In [28], the authors benefit from the shearlets as a denoising tool in the preprocessing step of a vessel segmentation algorithm. The study [29] proposed a retinal vessel segmentation approach using shearlet transform and indeterminacy filtering. In this way, the green channel of the fundus image is mapped to the neutrosophic domain. Then, indeterminacy filtering is performed on the resulted image to remove uncertain information. Finally, the vessels are detected using a neural network.

We build our algorithm based on the proposed effective method in [18]. Methods presented in [18, 30] are called TFA¹, and their modifications are referred to as TFAE² [27, 31]. In this paper, using shearlets and a novel stretching function, we modify TFA approach which is called SA.³ We then introduce a three-stage binary segmentation algorithm based on the SA algorithm for vessel segmentation in MRI images. We use the fact that in MRI images the intensity value of the vessels is usually higher than the background intensities.

We describe our proposed algorithm as follow:

• Extracting the vessels with high intensity using the SA method.

• Making a new image by combining the result of the first stage and the original image.

• Implementing SA on the new image resulted from the previous stages.

Our algorithm automatically extracts twisted, convoluted and occluded vessels with low intensity and weak edges. It can also extract branching structures with various thickness accurately. Also, due to using shearlets in each stage, this algorithm is more robust against noise. Since our algorithm is based on SA method, it has the convergence property as well. The produced results of our algorithm show the efficacy higher than those from TFA, SA and TFAE when applying to synthetic and real medical images with a, respectively, quantitative and qualitative comparison (see Sect. 5).

We present the rest of the paper as follows. In Sect. 2, we explain shearlets as a dictionary and show some their advantages. In Sect. 3, we explain TFA and TFAE methods as the related works. Three novel contrast stretching functions, our modifications of the TFA algorithm and our proposed algorithm are described in Sect. 4. In Sect. 5, we compare the results of our algorithm with the results of the TFA, SA and TFAE methods. Finally, the conclusions are outlined and possible developments of the algorithm are suggested.

2 Shearlets

In applied mathematical analysis, shearlets are a multiscale framework that allows efficient encoding of anisotropic features in multivariate problem classes. They were introduced for the analysis and sparse approximation of functions $f\in L^2({\mathbb {R}}^2)$. Since wavelets, as isotropic objects, are not capable of capturing anisotropic features such as edges in images and multivariate functions are typically governed by such phenomena, therefore, we need the shearlets as a natural extension of wavelets. Similar to wavelets, shearlets arise from the affine group and allow a unified treatment of the continuum and digital situation leading to faithful implementations. Although they do not constitute an orthonormal basis for ${\displaystyle L^{2}({\mathbb {R}} ^{2})}$, they still form a frame allowing stable expansions of arbitrary functions ${\displaystyle f\in L^{2}({\mathbb {R}} ^{2})}$.

One of the most important properties of shearlets is that they represent a sparse approximation of a function ${\displaystyle f\in L^{2}({\mathbb {R}} ^{2})}$ [32] which means

$$\begin{aligned} \left\| {f - {f_N}} \right\| _{{L^2}}^2 \le C{N^{ - 2}}{(\log N)^3}, \qquad N\longrightarrow \infty \end{aligned}$$

(1)

where $f_N$ is a nonlinear approximation of f using shearlets [33], which is extracted by using N largest coefficients. Shearlets have the following advantages to the other 2D dictionaries that allows faithful implementation:

• Having analogous structures in both continuous and discrete cases.

• Initiating from a group of square integrable functions.

Shearlets have a wide range of applications in image processing like edge detection, denoising, inpainting and, etc, see [34,35,36,37,38]. One of the main properties of shearlets that can result in a faster algorithm is that they can be implemented by fast Fourier transform.

2.1 Continuous shearlets

Let $A_a$, $S_s$ be parabolic scaling and shearing matrices, respectively, defined as

$$\begin{aligned} {A_a} = \left( {\begin{array}{*{20}{c}} a&{}0\\ 0&{}{\sqrt{a} } \end{array}} \right) , a\in {{\mathbb {R}}^ + }, {S_s} = \left( {\begin{array}{*{20}{c}} 1&{}s\\ 0&{}1 \end{array}} \right) , s \in {\mathbb {R}} \end{aligned}$$

(2)

Then, continuous shearlets ${\psi _{a,s,t}}$ is derived by scaling, shearing and translation of the function $\psi \in {L^2}({\mathbb {R}})$ :

$$\begin{aligned} {\psi _{a,s,t}}(x) = {a^{ - \frac{3}{4}}}\psi \left( {{A_a}^{ - 1}{S_s}^{ - 1}(x - t)} \right) ,\qquad t\in {\mathbb {R}}^2 \end{aligned}$$

(3)

which has the following Fourier transformation

$$\begin{aligned} {{{\hat{\psi }} }_{a,s,t}}(\omega ) = {a^{\frac{3}{4}}}{{\mathrm{e}}^{ - 2\pi i\left\langle {\omega , t} \right\rangle }}{\hat{\psi }} \left( {a{\omega _1}, \sqrt{a} (s{\omega _1} + {\omega _2})} \right) . \end{aligned}$$

(4)

For every $f \in {L^2}({\mathbb {R}})$, the corresponding shearlet transformation is defined as

$$\begin{aligned} {{{\mathcal {S}}}{{\mathcal {H}}}_\psi }(f)(a,s,t) = \left\langle {f,{\psi _{a,s,t}}} \right\rangle = \left\langle {{{\hat{f}}},{{{\hat{\psi }} }_{a,s,t}}} \right\rangle . \end{aligned}$$

(5)

For discussions in more details, see [32].

Shearlets have been implemented in different ways [39, 40], the newest of them used the compact support shearlets for the implementation. The related toolbox is available as shearlab4 in [41]. We benefit from this toolbox at the implementation of the proposed algorithm. The difference between shearlets frame and linear piecewise B-spline tight-frame in dealing with the additive noise is presented in Fig. 1. We see the efficiency of the shearlets frame compared to the linear piecewise B-spline tight-frame.

Fig. 1

a Is a noisy MRI b is a denoising by the linear piecewise B-spline tight-frame and c is a denoising by the shearlets frame

3 Related works

In this section, we explain two binary segmentation methods which have been recently introduced for vessel extracting of MRI images. It should be emphasized that the algorithm introduced in this paper is based on TFA method.

3.1 TFA method

TFA is a tight-frame-based method which is designed for blood vessel segmentation in MRI images [18, 30]. This method has advantages, being designed based on simple mathematical structure to other methods like Chan–Vese active contour model [1], frame-based model [4], CURVES method [8] and anisotropic deformable method [5]. It has very simple and precise calculation results, consequently having less computational complexity than the other methods.

TFA method uses a special property of MRI images, the potential boundary pixels are in an interval which does not include pixels of other parts. The main idea is to approximate this interval and update it in each iteration and classify the unclassified pixels according to this interval. Pixels with the values lower than this interval are mapped to zero, those with higher values are mapped to 1 and the pixels inside the interval are stretched by a linear method described in [42]. Using 2D piecewise linear B-spline, it performs smoothing and denoising on the derived image. In fact, this technique gradually moves the given image toward becoming a binary image in each iteration.

The TFA method is described as follow:

Without loss of generality suppose that the values of pixels in the given image are in $\left[ {0,1} \right]$ . The stages of the algorithm are as follows:

Stage 0 (Initialization) Regarding f as the given image,

$$\begin{aligned} {f^0}&= f \end{aligned}$$

(6)

$$\begin{aligned} {\varLambda ^{(0)}}&= \left\{ {j \in \varOmega :{{\left\| {\nabla {f_j}} \right\| }_1} \ge \varepsilon } \right\} \end{aligned}$$

(7)

where $\varOmega$ is the set of image indices, ${\nabla {f}}_j$ is the jth pixel of the discrete gradient of f . ${\varLambda ^{(0)}}$ is the initial estimation of the positions of the potential boundary pixels.

Following stages are the ith iteration steps:

Stage1 (Computing $\left[ {{\alpha _i}, {\beta _i}} \right]$) First, compute the average of ${f^{(i)}}$ On ${\varLambda ^{(i)}}$

$$\begin{aligned} {\mu ^{(i)}} = \frac{1}{{\left| {{\varLambda ^{(i)}}} \right| }}\sum \limits _{j \in {\varLambda ^{(i)}}} {f_j^{(i)}}. \end{aligned}$$

(8)

Set

$$\begin{aligned} B^{(i)}&= \left\{ {j \in {\varLambda ^{(i)}}|f_j^{(i)} \le {\mu ^{(i)}}} \right\} , \end{aligned}$$

(9)

$$\begin{aligned} A^{(i)}&= \left\{ {j \in {\varLambda ^{(i)}}|f_j^{(i)} \ge {\mu ^{(i)}}} \right\} \end{aligned}$$

(10)

and compute the average of ${f^{(i)}}$ on them

$$\begin{aligned} \mu _ - ^{(i)}&= \frac{1}{{\left| B^{(i)} \right| }}\sum \limits _{j \in B^{(i)}} {f_j^{(i)}} \end{aligned}$$

(11)

$$\begin{aligned} \mu _ + ^{(i)}&= \frac{1}{{\left| A^{(i)} \right| }}\sum \limits _{j \in A^{(i)}} {f_j^{(i)}}, \end{aligned}$$

(12)

where ${{\left| . \right| }}$ is the cardinality of the set and ${f_j^{(i)}}$ is the jth pixel value in ${f^{(i)}}$; compute

$$\begin{aligned} {\alpha _i}&= \max \left\{ {\frac{{{\mu ^{(i)}} + \mu _ - ^{(i)}}}{2},0} \right\} \end{aligned}$$

(13)

$$\begin{aligned} {\beta _i}&= \min \left\{ {\frac{{{\mu ^{(i)}} + \mu _ + ^{(i)}}}{2},1} \right\} . \end{aligned}$$

(14)

Stage 2 (Stretching and Thresholding) By setting

$$\begin{aligned} Q^{(i)} = \left\{ {f_j^{(i)}|\alpha _i} \le f_j^{(i)} \le {\beta _i}, j \in {\varLambda ^{(i)}} \right\} , \end{aligned}$$

(15)

if $\vert Q^{(i)}\vert = 0$, then ${f^{(i)}}$ is the binary image and the algorithm is terminated; otherwise, $M_i$ , $m_i$ are computed by

$$\begin{aligned} {M_i} = \max Q^{(i)}, \quad {m_i}= \min Q^{(i)}. \end{aligned}$$

(16)

Finally, stretching and thresholding are performed as below

$$\begin{aligned}\forall j \in \varOmega ,\qquad f_j^{(i + \frac{1}{2})} = \left\{ {\begin{array}{*{20}{l}} 0,&{}\quad {f_j^{(i)} \le {\alpha _i}}\\ &{}\\ {\frac{{f_j^{(i)} - {m_i}}}{{{M_i} - {m_i}}}},&{}\quad {{\alpha _i} \le f_j^{(i)} \le {\beta _i}}\\ &{}\\ 1,&{}\quad {f_j^{(i)} \ge {\beta _i}.} \end{array}} \right. \end{aligned}$$

Here, the indices of unclassified pixels are obtained by

$$\begin{aligned} {\varLambda ^{(i + 1)}} = \left\{ {j| 0< f_j^{(i + \frac{1}{2})} < 1,j \in \varOmega } \right\} .\end{aligned}$$

Stage 3 (Denoising) In this stage, denoising and of $f^{(i + \frac{1}{2})}$ on ${\varLambda ^{(i + 1)}}$ are done.

$$\begin{aligned} f_j^{(i + 1)} = \left\{ {\begin{array}{*{20}{l}} {f_j^{(i + \frac{1}{2})}},&{}\quad {j \notin {\varLambda ^{(i + 1)}}}\\ &{}\\ {{{\left( {{{\mathcal {A}}^T}\left( {{{\mathcal {T}}_\lambda }\left( {{\mathcal {A}}{f^{(i + \frac{1}{2})}}} \right) } \right) } \right) }_j}},&{}\quad {j \in {\varLambda ^{(i + 1)}}} \end{array}} \right. \end{aligned}$$

(17)

where ${\mathcal {A}}$ is the linear piecewise B-spline tight-frame transform [43] and ${{\mathcal {T}}_\lambda } (. )$ is the local soft thresholding operator.

Stop criterion The algorithm is terminated when $f^{(i + \frac{1}{2})}$ is a binary image or equivalently $\left| {{\varLambda ^{(i)}}} \right| = 0$.

A summary of TFA method is provided in Table 1.

Table 1 TFA algorithm

The convergence of TFA method is proved by the following argument:

Assume in ith iteration the set $Q^{(i)}$ is nonempty; therefore, one of the values in this set is certainly equal to $M_i$(or $m_i$), which was mapped to 1 (or 0) in stretching and thresholding stage. Result is that in the ith iteration at least one pixel of the unclassified pixels is reduced. Since the number of pixels is finite, so the method will be convergent.

3.2 TFAE method

This method is a modification of TFA based on following changes on the original method.

Modifying the stage 0 Replace discrete gradient of the image in TFA by convoluting Gaussian kernel derivation with the image and use norm 2 instead of norm 1 in the thresholding step.

Modifying the stage 1 Add the following parameters to the decision parameters of the TFA:

$$\begin{aligned} {\mathrm{mean}}^{(i)} = \frac{{\sum \nolimits _{j \in {\varLambda ^{(i)}}} {\overrightarrow{v}_{p_{\max }}. \overrightarrow{v_j}} }}{{\left| {{\varLambda ^{(i)}}} \right| }} \end{aligned}$$

(18)

where $\overrightarrow{v_j}$ is the eigenvector corresponding to the greatest absolute value of the eigenvalues of the Hessian matrix of the jth pixel of $f^{(i)}$ and $\overrightarrow{v}_{p_{\max }}. \overrightarrow{v_j}$ is the dot product of two vectors that measures the similarity of them. Other elements are defined as

$$\begin{aligned} {\mathrm{grad}}_{\max } = \max {\left\{ {{{\left\| {\nabla {f_j}} \right\| }_2}\mid j \in {\varLambda ^{(i)}}} \right\} } = {\left\| {\nabla {f_{{p_{\max }}}}} \right\| _2}, \end{aligned}$$

(19)

where $p_{\max }$ is the corresponding index to ${\mathrm{grad}}_{\max }$. In fact, ${\mathrm{mean}}^{(i)}$ is the parameter that measures the average of the similarity between eigenvector of ${p_{\max }}$ and other eigenvectors corresponding to the indices in ${{\varLambda ^{(i)}}}$.

Modifying the stage 2 Change the thresholding and stretching function to the following:

$$\begin{aligned} { \forall j \in \varOmega \quad f_j^{(i + \frac{1}{2})} = \left\{ {\begin{array}{*{20}{l}} 0,&{}{f_j^{(i)} \le {\alpha _i}}\\ &{}\\ 1,&{}\quad {\left\{ {f_j^{(i)} \ge {\mu ^{(i)}} , v({p_{\max }}). {v_j} \ge {\mathrm{mean}}^{(i)}} \right\} }\\ &{}\\ {\frac{{f_j^{(i)} - {m_i}}}{{{M_i} - {m_i}}}},&{}\quad {\mathrm{otherwise}}. \end{array}} \right. \,\,{\mathrm{or}}\,\,\left\{ {f_j^{(i)} \ge {\beta _i}} \right\} } \end{aligned}$$

(20)

Modifying the stage 3 Instead of denoising by linear piecewise B-Spline tight-frame, use curvelets.

4 The proposed algorithm

Our work includes three parts as follows:

• 1. Three new contrast stretching functions are introduced

• 2. TFA method is modified by using one of the new contrast stretching functions and shearlet transformation.

• 3. A new three stage segmentation algorithm is constructed based on the contrast stretching function and a modified version of the TFA.

4.1 Novel contrast stretching functions

The main purpose of enhancing the contrast of the image is that the improved image is better than the original image for a particular application, such as segmentation. Improving the contrast of the image improves the interpretation or perception of image information for human beings and makes it more suitable for other processing tasks. Image contrast enhancement techniques usually depend on the in hand problem [42]. This means that a contrast stretching function may work for a specific range of images but no that practical for other type of images.

Contrast stretching methods can be classified into two categories.

• 1. Spatial domain methods

• 2. Frequency domain methods

In the spatial techniques, we deal with the intensity values of the pixels directly. The intensities are given as inputs of a function, and the outputs are considered as the alternative intensity values.

Image enhancement is applied where the images need to be understood and analyzed, such as medical and satellite image analysis.

In this section, we propose three new contrast stretching functions which are classified as the spatial domain methods. They are constructed based on the Sin function and its inversion and called Trigonometric Contrast Stretching (TCS) functions. We describe them as the following:

• 1. The first TCS function we introduce is as follows:

  $$\begin{aligned} \begin{array}{l} f_1:[m,M] \rightarrow [0,1]\\ f_1(x) = \frac{1}{2}(1 + A + \frac{1}{\pi }\sin (\pi A)) \end{array} \end{aligned}$$

  (21)

  where $A = \frac{2x - (m + M)}{M - m}$. This function is made using a regularized version of the Heaviside function [44].

• 2. The second TCS function is defined as

  $$\begin{aligned} \begin{array}{l} f_2:[m,M] \rightarrow [0,1]\\ f_2(x) = \frac{1}{2}(1 + \sin (\pi (A-\frac{1}{2}))) \end{array} \end{aligned}$$

  (22)

  where $A = \frac{x - m }{M - m}$.

• 3. The third TCS function is defined as the inverse of the second TCS function:

  $$\begin{aligned} \begin{array}{l} f_3:[m,M] \rightarrow [0,1]\\ f_3(x) = \frac{1}{2}+\frac{1}{\pi }\sin ^{-1}(2A-1) \end{array} \end{aligned}$$

  (23)

  where $A = \frac{x - m }{M - m}$.

In all of the TCS functions, $[m,M] \subseteq [0,1]$.

In Fig. 2 ,considering $[m,M]=[0,1]$, we plot the TCS functions. Increasing the variance of the intensities in the middle and reducing the variance of the intensities at the beginning and the end of the domain is the main property of the first and the second TCS functions. In other words, they stretch the intensities of the image to begin and end of the domain. In MRI images, the intensities in the middle of the domain are the boundaries of the vessels. The artifacts in the background of MRI images disappear, and the vessels are brighter after applying the first and the second TCS functions. Against them, the third TCS function stretches the intensities of the image toward the middle of the interval. Described properties of the TCS functions are demonstrated in Sect. 5.

Fig. 2

The proposed stretching functions: green is $f_1$, blue is $f_2$, gray is $f_3$ and black is the linear stretching function. All of them are drawn on [0, 1]

Choosing the correct interval [m, M] for the stretching task is the base of the contrast stretching functions. Without loss of generality, let the intensity values of the image be in [0, 1].

Based on the statistical confidence interval, we use the following interval for the TCS functions:

$$\begin{aligned} m = \mu -n\sigma , M = \mu +n\sigma \end{aligned}$$

(24)

where $\mu$ and $\sigma$ are the mean and the standard deviation of the intensities of the image in interval (0, 1). In this paper, we get $n=1.96$. There are some image segmentation technique based on the confidence interval in the literature [45]. We show the effectiveness of our TCS functions in Sect. 5.

4.2 Modified version of TFA: SA method

We improve the TFA method by changing some basic parts of TFA as follows:

• 1. As a preprocessing step, we improve the contrast of the image by using the TCS functions with a 95 percent confidence interval(not necessary for all of the images).

• 2. Contrast stretching and thresholding in TFA (stage 2) replaced by: At first, we do the following computational task:

  $$\begin{aligned} \begin{aligned}&M^1_i = \max Q^{(i)}\\&m^1_i = \min Q^{(i)}\\&M^2_i = {\mathrm{mean}} Q^{(i)}+1.96 {\mathrm{std}} Q^{(i)}\\&m^2_i = {\mathrm{mean}} Q^{(i)}-1.96 {\mathrm{std}} Q^{(i)}\\&m_i = \max \{ m^1_i, m^2_i\}\\&M_i = \min \{ M^1_i, M^2_i\}. \end{aligned} \end{aligned}$$

  (25)

  based on, contrast stretching and thresholding are performed using the second TCS function:

  $$\begin{aligned} f_j^{(i + \frac{1}{2})} = \left\{ {\begin{array}{*{20}{l}} 0,&{}{f_j^{(i)} \le {m _i}}\\ \frac{1}{2}(1 + \sin (\pi (A-\frac{1}{2}))),&{}{{m_i} \le f_j^{(i)} \le {M_i}}\\ 1,&{}{f_j^{(i)} \ge {M_i}} \end{array}} \right. , \forall j \in \varOmega \end{aligned}$$

  (26)

  where $A = \frac{f_j^{(i)} - m_i }{M_i - m_i}$.

• 3. According to Sect. 2, shearlets are better tools compared to wavelets in dealing with 2D signals, and their use in the TFA algorithm makes it robust against the noise. Also, they do smoothing the boundaries of detected vessels, and modifying vessel disconnections in the results, therefore instead of linear piecewise B-spline tight frame we use the shearlet transform ${{\mathcal {S}}}{{\mathcal {H}}}$ in the denoising stage. Since denoising do not make any changes to pixels whose values become 0 and 1 in the previous stages, and just cost us some computational complexity resulting in reducing the speed of the algorithm, we apply these tasks only on those pixels related to ${\varLambda ^{(i + 1)}}$. It must be noticed that we produce an image ($F^{(i + \frac{1}{2})}$) which has nonzero values just to the pixels inside ${\varLambda ^{(i + 1)}}$, i.e., the nonzero components of $F^{(i + \frac{1}{2})}$ are related to the unclassified pixels. By applying these modifications, the relation (17) will be as the following

  $$\begin{aligned} f_j^{(i + 1)} = \left\{ {\begin{array}{*{20}{l}} {f_j^{(i + \frac{1}{2})}}&{}{j \notin {\varLambda ^{(i + 1)}}}\\ {{{\left( {{{{\mathcal {S}}}{{\mathcal {H}}}^T}\left( {{{\mathcal {T}}_\lambda }\left( {{{\mathcal {S}}}{{\mathcal {H}}}{(F^{(i + \frac{1}{2})}})} \right) } \right) } \right) }_j}}&{}{j \in {\varLambda ^{(i + 1)}}} \end{array}} \right. \end{aligned}$$

  (27)

  where $\lambda$, as the thresholding value, is local value depend on image noise.

We called the modified TFA as SA method. We know that the convergence of the TFA method depends on the contrast stretching interval that we changed, so we need to prove the convergence of the SA method.

Theorem 1

(Convergance of SA method) The SA method is converged in finite iterations.

Proof

In order to reduce the unclassified pixels in each iteration, some values out of $[m_i, M_i]$ must be converted to zero or one. According to the relations 25, we have $m^1_i\le m_i,\quad M_i\le M^1_i$; therefore, $[m_i,M_i]\subseteq [m^1_i,M^1_i]$. Since TCS function converts $m_i$ and $M_i$ to 0 and 1, respectively, so at least one pixel is classified in each iteration. Since the number of image pixels is finite, the SA method will be converged at finite iterations. $\square$

To see the effect of the shearlet frame in the modified version of TFA (SA), we run SA with linear stretching function as well as TFA. Both of them are performed on the noisy image represented in Fig. 1 by $\varepsilon =0.05$ as the thresholding parameter in the edge detection stage. Considering the yellow ellipses on the results, we see that the LCS-based SA has been modified false disconnections in the vessels approximately (see Fig. 3). In Sect. 5, we show the advantages of the SA method to the original TFA version by the several experiments.

Fig. 3

a Original image, b TFA result by $\varepsilon = 0.05$ and, c LCS-based SA result by $\varepsilon = 0.05$

4.3 Proposed algorithm

Magnetic resonance angiography technology is based on detecting the flowing blood signals and suppressing the static tissue signals. The vessels in this type of images have high intensities. The main problem here is that this type of images have low contrast, and some thin vessels have intensities close to the background. To maintain the brightness ratio among the details of the image to each other, our idea is using linear contrast stretching (LCS) in the segmentation process. Let pixel values of a given images be in $\left[ {0,1} \right]$. Stretching the interval $\left[ {m,M} \right]$ , where m and M are minimum and maximum of the pixel values, respectively, to $\left[ {0,1} \right]$ is done by the following relation:

$$\begin{aligned} \begin{array}{*{20}{l}} {{{\mathcal {S}}}{{\mathcal {T}}}:\left[ {m,M} \right] \rightarrow \left[ {0,1} \right] }\\ \\ {{{\mathcal {S}}}{{\mathcal {T}}}(x) = \frac{{x - m}}{{M - m}}} \end{array} \end{aligned}$$

(28)

For $\left[ {m,M} \right] =\left[ {0,1} \right]$, this function is the identity function. In MRI images, usually m and M are close to 0 and 1, respectively, so LCS does not effect on the given image. To solve the problem, we separate vessels with high intensity and then perform LCS on other pixel values. Then, by making a new image out of the original image and another one with high-intensity vessels(the binary image), we extract the vessels with low-intensity and weak edges from the new image. We explain the details of our algorithm as following:

Stage 1 (Extracting high-intensity vessels) Extract the high-intensity vessels by performing the SA on the given image f, the result Ft is a binary image:

$$\begin{aligned} Ft = {{\mathcal {S}}}{{\mathcal {A}}}\left( f\right) \end{aligned}$$

(29)

where ${{\mathcal {S}}}{{\mathcal {A}}}$ is the function corresponding to SA.

Stage 2 (Making the new image) Make a new image using the original image and the one resulted from the first stage.

The procedure of making a new image is in this way: first, convert the pixel values related to high-intensity vessels to zero, other pixel values are kept as their values in the original image. We define last image, g, as

$$\begin{aligned} {g_j} = \left\{ {\begin{array}{ll} {{f_j}},&{\quad j \in J}\\ &{}\\ 0,&{}{\quad j \notin J} \end{array}} \right. \end{aligned}$$

(30)

where $f_j, g_j$ are the jth pixel of f and g, respectively, and

$$\begin{aligned} J = \left\{ {j| F{t_j} = 0,\quad j \in \varOmega } \right\} \end{aligned}$$

(31)

where $Ft_{j}$ is the jth pixel of Ft.

Define

$$\begin{aligned} {m_g}&= \min \left\{ {{g_j} | 0< {g_j} < 1, j \in \varOmega } \right\} , \end{aligned}$$

(32)

$$\begin{aligned} {M_g}&= \max \left\{ {{g_j} | 0< {g_j} < 1, j \in \varOmega } \right\} . \end{aligned}$$

(33)

${M_g}$ is much smaller than 1; therefore, LCS is effective. Actually, the vessels with low intensity and weak edges become brighter by LCS. We call the image resulted from LCS of g as G:

$$\begin{aligned} {G_j} = \left\{ {\begin{array}{*{20}{l}} {{g_j}},&{}\quad {{g_j} = 0,1}\\ &{}\\ {\frac{{{g_j} - {m_g}}}{{{M_g} - {m_g}}}},&{}\quad {0< {g_j} < 1} \end{array}} \right. \end{aligned}$$

(34)

where ${G_j}$ is the jth pixel of G. Since LCS increases the pixel values corresponding to the speckle noise in the image as well as the low-intensity vessels, it generates a problem in the segmentation. To solve this problem, denoising is performed applying shearlets. We used the shearlets toolbox as shearlab 4 available in [41]. The resulted image is named H:

$$\begin{aligned} H = {{\mathcal {S}}}{{\mathcal {H}}}^{T}\left( {\mathcal {T}}_{\lambda }\left( {{\mathcal {S}}}{{\mathcal {H}}}(G) \right) \right) . \end{aligned}$$

(35)

Also, we could use deblurring [46] at this stage to make the image more clear, but we did not find it necessary. Next, we make the combination image from H and Ft and call it F:

$$\begin{aligned} F = H + Ft = \left\{ H_j + Ft_j | j {\in {\varOmega }} \right\} . \end{aligned}$$

(36)

It is possible that some of the pixel values end up being outside of $\left[ 0,1\right]$, we need to map those points of F into the interval as well.

Stage 3 (Applying SA on the new image) We perform SA on the new image and call the result Kt:

$$\begin{aligned} Kt = {{\mathcal {S}}}{{\mathcal {A}}}\left( F\right) \end{aligned}$$

(37)

where Kt is the final binary result of our algorithm, within pixels with values zero are the background and those with values 1 are the vessels.

Convergence of our algorithm is inherited from SA method which has proved in the previous subsection. We refer to our algorithm as TSA, all the stage of TSA are summarized in Table 2. Also, a general flow diagram of the proposed method is presented in Fig. 4.

Table 2 TSA algorithm

Fig. 4

A general flow diagram of the proposed method

By this approach, all of the methods in [1, 4, 5, 8] and edge detection methods can be improved as well.

5 Experimental results

5.1 Comparing the results of the TCS functions

Through some practical application of the method, we showed the effect of the TCS functions on different images using their histograms. We applied our TCS functions on natural gray and colorful images as well as medical images. The results of the first and second TCS functions are almost the same, but the result of the third function is different from them. We use the second function that is suitable for our work and MRI images. But, either of them may be appropriate for a different problem.

Fig. 5

Experimental results on natural gray images: first column is the original images with corresponding histograms (a). Second column is the results of the first TCS function (b). Third column is the results of the second TCS function (c). Forth column is the results of the third TCS function (d)

In Fig. 5, the first row is a child’s image, the second row is an areal image of a satellite and the third row is an image of the surface of the moon. In all of the results, the image contrast has improved.

Fig. 6

Experimental results on two type of MRI images: first column is the original images with corresponding histograms (a). Second column is the results of the first TCS function (b). Third column is the results of the second TCS function (c). Forth column is the results of the third TCS function (d)

In Fig. 6, observing the results of our TCS functions on two type of MRI images, we see that the results of the first and the second TCS functions are better than the result of the third function. Because the maximum and the minimum intensity are close to 1 and 0, respectively, LCS will be ineffective in this type of image. Because the maximum and the minimum intensity are close to 1 and 0, respectively, LCS will be ineffective in this type of image.

In Fig. 7, we showed the effect of our TCS functions on the colorful images without their histograms. In the first row, the third TCS function is effective, but the first and the second TCS functions are failed. The second TCS function is more effective than the others in the second and the third rows.

Fig. 7

Experimental results on colorful images: first column contains the original images (a). Second column contains the results of the first TCS function (b). Third column contains the results of the second TCS function (c). Forth column contains the results of the third TCS function (d)

5.2 Quantitative evaluation metrics

Evaluation of segmentation results is an important step in validating a segmentation method that confirms its reliability. Most segmentation results are measured qualitatively and visually. This method of evaluation is either subjective or depends on specific applications. One can judge the performance of a segmentation method objectively.

For quantitative evaluation of a segmentation technique, the results of the segmentation method with its corresponding Ground truth are compared. There are different metrics for this comparison. For example, the ratio of the number of pixels that are correctly detected to the total pixels is one of the metrics. The common metrics used to evaluate segmentation techniques are Accuracy, Sensitivity, and Specificity. Let I be the given image, S be the tissue in the segmented image and G be the tissue in the corresponding Ground truth, the metrics are defined as the following:

$$\begin{aligned} {\mathrm{Accuracy}}&= \dfrac{|S\cap G|+|S'\cap G'|}{|I|}, \end{aligned}$$

(38)

$$\begin{aligned} {\mathrm{Sensitivity}}&= \dfrac{|S\cap G|}{|G|}, \end{aligned}$$

(39)

$$\begin{aligned} {\mathrm{Specificity}}&= \dfrac{|S'\cap G'|}{|G'|} \end{aligned}$$

(40)

Some other common metrics used in the quantitatively evaluations are defined as

$$\begin{aligned} {\mathrm{Dice}}&= \dfrac{2|S\cap G|}{|G|+|S|} \end{aligned}$$

(41)

$$\begin{aligned} {\mathrm{Jaccard}}&= \dfrac{|S\cap G|}{|S\cup G|} \end{aligned}$$

(42)

where |.| is the cardinality of the set. The higher the value of the metrics, the better the segmentation result.

5.3 Experimental results of the proposed segmentation method

We applied our algorithm on some synthetic and real MRI images. Some of them are provided by Azar Mehr Imaging Center Tabriz-Iran, and some others adopted from [18, 47]. Because the proposed method is designed to blood vessel segmentation from MRI images, it has been attempted to select images having the challenges of this field. The first synthetic image simulates circular vascular systems having thin vessels with the intensity close to the background, and the second simulates a branching structure with low intensities in the tips. These are applied to the quantitative evaluation of the proposed method. Experimental real images include some challenges such as twisting branching vessels with false discontinuity, low-intensity and weak edges.

Since the results of TFA and TFAE have been proved as the better results compared to the other methods [18, 31] like Chan–Vese active model [1], frame-based method [4], CURVES vessel segmentation method [8] and anisotropic deformable method [5], we only compare our results with TFA and TFAE.

We tried to take the best results out of TFA and TFAE methods, then compare them with our results. In synthetic images, we compared the results by the metrics described in 5.2. But in real MRI images, the comparison is qualitative, based on the visualizing by taking similar boxes on the resulted images, as there are no ground truth segmentations for those images. Even manually segmentation could not be considered as ground truth since many thin vessels are hard to detect and many faulty detections can be included due to the high noise presented in the data set. These comparisons show that our algorithm has the best performance among them. Our algorithm is capable of detecting the vessels with weak edges and those with intensity close to the background.

The shearlets toolbox used in denoising step in the ${{\mathcal {S}}}{{\mathcal {A}}}$ method is provided from [41]. We set $\sigma = 0.05$ as the standard deviation of the noise in all of the images. SA method has two parameters, one of them is $\varepsilon$, initial edge detection parameter, the other is the standard deviation of the noise level in the image, $\sigma$. We get $\sigma =0.05$ in SA method for all of the images. Our algorithm has two parameters $\varepsilon _1 , \sigma _1$ which both are applied in the first stage; and also there is a parameter related to the second stage which is related to the standard deviation of the speckle noise in the new image $\sigma$, and same as the first stage, we have two parameters, namely $\varepsilon _2 , \sigma _2$ , in the third stage. We assume $\sigma _1 =0.05, \sigma =0.05$, $\sigma _2 =0.001$ and $\varepsilon _1 = 0.1$ in TSA method for all of the examples. The other variable parameter values used in the examples are presented in description of the examples and Table 3. All of the cods related to the SA, TFA and TFAE algorithms are provided by the authors in MATLAB R2018a software.

Table 3 Parameter values used in all of the algorithms

Figure 8 contains a synthetic image with four circles and two diagonal lines of different thicknesses. The line in the minor diagonal of the image has intensities close to the background. The circles are also designed to be scaled down by moving away from the center on circles. This synthetic image simulates the circular vascular systems having thin vessels with the intensities close to the background in MRI images. The blurred and noisy image is obtained by adding a Gaussian noise and Gaussian blur to the clean image. The blur is created by a $3 \times 3$ Gaussian filter with standard deviation 0.5. The Gaussian additive noise is created with the average 0.01 and the variance 0.001. We get $\varepsilon = 0.001$ as the SA parameter and $\varepsilon _1 = 0.1, \varepsilon _2 = 0.01$ as the TSA parameters for this image.

Observing Fig. 8, we see that the SA method have a better performance than the TFA in detecting the exterior circle. All of the TFA, SA and TFAE methods have a weak performance in detecting minor diagonal and exterior circle, but our TSA has a great performance than the others. In Table 4, we compare the results of the methods by using the known measures. According to the table and based on all of the measures, we see that SA (a modified version of TFA) has a better performance than TFA, but TFAE is better than SA and our TSA result is the best. The values with bold values shows higher values in any column.

Fig. 8

a Is ground truth, b is clean image, c is noisy and blurred image and d–g are the results of TFA, TFAE, SA and our TSA, respectively

Table 4 Quantitatively evaluation of the performance of the segmentation methods on the first synthetis image (Fig. 8) using known described measures

Figure 9 is a synthetic image which have a branching structure. The tips of the branches have intensities close to the background and are the challenging points for the segmentation techniques. This synthetic image simulates the branching vascular systems having thin vessels with the weak edges in MRI images. The blurred and noisy image is obtained by adding a Gaussian noise and Gaussian blur to the clean image. The blur is created by a $3 \times 3$ Gaussian filter with standard deviation 0.5. The Gaussian additive noise is created with the average 0.01 and the variance 0.001. We get $\varepsilon = 0.001$ as the SA parameter and $\varepsilon _1 = 0.1, \varepsilon _2 = 0.001$ as the TSA parameters.

Figure 8 illustrates the fact that the SA method has better performance than the TFA in detecting more thin tips of the branches . Our TSA has the best performance in revealing of the tip pixels and the thin branching structures with low intensity and weak edges. In Table 5, we compare the results of the methods by using the known measures. According to the table and based on all of the measures, we see that SA (an improvement of TFA) has a better performance than TFA, but TFAE is better than SA and our TSA has the best performance. The bold values shows a higher values in any column.

Fig. 9

a Is ground truth, b is clean image, c is noisy and blurred image and d–g are the results of TFA, TFAE, SA and our TSA, respectively

Table 5 Quantitatively evaluation of the performance of the segmentation methods on the second synthetis image (Fig. 9) using known described measures

Figure 10 is a real MRI image of a carotid vascular system which is adopted from [18]. In this image, the vessels have low and high intensities and the vessels between two branches are thin having intensities close to the background. The non-uniform intensities in the background remove simple thresholding choice for the segmentation. Intersections partial structures even make a hard segmentation problem. We applied $\varepsilon = 0.001$ and $\varepsilon _1 = 0.1, \varepsilon _2 = 0.01$ as the values of the parameters in SA and TSA methods, respectively. According to the yellow boxes on the results, we conclude that TFA and TFAE have disconnections in detection of the middle vessels, but SA and TSA have not this wrong. The green boxes on the SA and TSA results show the advantage of our TSA with respect to the SA method.

Fig. 10

a Is an MRI image of carotid vascular system and b–e are the results of TFA, TFAE, SA and TSA results

Figure 11 is an MRI image of Kidney vascular system adopted from [18]. Non-uniform intensities in the background and some discontinuity in the vessels are a feature of this image which make a hard segmentation problem. $\varepsilon = 0.001$ and $\varepsilon _1 = 0.1, \varepsilon _2 = 0.06$ are the parameter values for SA and TSA methods. The content of the yellow box show that the SA result is better than the TFA’s. In other words, SA has resolved the discontinuity problem in this image. Some artifacts shown in red boxes are an over-segmentation of TFAE, SA and TSA methods.

Fig. 11

a Is an MRI image of Kidney vascular system and b–e are the results of TFA, TFAE, SA and TSA results

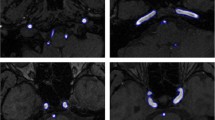
Figure 12 shows three magnetic resonance tomography angiography of human head vessels with the skull removed, viewed from three different orthogonal viewpoints. These images were also adopted from [18]. There are a lot of thin convoluted vessels in these images which increase the difficulty of the segmentation task. $\varepsilon = 0.001$ and $\varepsilon _1 = 0.1, \varepsilon _2 = 0.01$ are the parameter values for SA and TSA methods. Among the results of the first row, TFAE has detected vessels with unusual thicknesses. The results of SA, TFA approximately are the same. Because of completely detecting the tips of the thin vessels, the result of the TSA is the best. In the second row, the vessels in the yellow boxes show the better performance of the SA method with respect to the TFA. Among them, TSA have the best performance, for example see the green box on the result of TSA. The results in the third row are similar to the second row.

Fig. 12

Original images in column a are MRTA images from three orthogonal viewpoints. Original image in the first, second and third rows is Z-axis, Y-axis and X-axis viewpoints of human head vessels with the skull removed. Columns b–e are the results of TFA, TFAE, SA and TSA, respectively

Two images in Fig. 13 are MRI images from neck and brain. These are borrowed from [47] and provided images with convoluted and occluded vessels. Also, they are low contrast images which make hard the work of the TFA, SA and TFAE techniques. $\varepsilon = 0.001$ and $\varepsilon _1 = 0.1, \varepsilon _2 = 0.001$ are the parameter values for SA and TSA methods. Because of being low contrast and having weak intensities in thin vessels, TFA, SA and TSA methods failed in detection of more thin vessels. However, the yellow boxes on the results of TFA, TFAE, SA show the advantages of SA to TFA, TFAE. The green boxes on the TSA result in the second row show that this result is the best. The prominence of the TSA result in the first row is clear.

Fig. 13

Column a is provided two MRI images of neck and brain. columns b–e contain the results of the TFA, TFAE, SA and TSA methods, respectively

The images in Fig. 14 are catched from different viewpoints in Azar Mehr imaging center Tabriz-Iran. These are similar to the images in Fig. 10, but the difference is that these images have thin vascular structures around the main arteries. The thick carotid vessels at the bottom of the images have brightness levels close to the background where the TFA, TFAE and SA methods failed in detection of them. Against them, TSA somewhat did this task successfully, see the contents of the yellow boxes. $\varepsilon = 0.001$ and $\varepsilon _1 = 0.1, \varepsilon _2 = 0.01$ are the parameter values for SA and TSA methods.

Fig. 14

Column a is provided three carotid vascular system with thin vessels around the main artery vessels. Columns b–e show the results of the TFA, TFAE, SA and TSA methods, respectively

Figure 15 are MRI images from the cerebrovascular system from different angles taken at Azarmahr imaging center Tabriz-Iran. These images have artifacts in the background that are not blood vessels but have similar intensity to the thin vessels in the image, so the thresholding methods cannot handle these images. The second feature of these images is that the parts of the small vessels are so close to the background that the TFA, TFAE and SA methods detect them as a disconnected vessel, see the content of yellow boxes on the results. $\varepsilon = 0.005$ and $\varepsilon _1 = 0.1, \varepsilon _2 = 0.01$ are the parameter values for SA and TSA methods.

Fig. 15

The first row is provided with three brain vascular system with thin disconnected vessels. Rows b–e show the results of the TFA, TFAE, SA and TSA methods, respectively

6 Conclusion and future works

First, we presented three new trigonometric contrast stretching (TCS) functions. Then, based on one of the TCS functions and shearlets frame, we improved TFA as a strong method in the binary vessel segmentation by modifying some main parts of it like its stretching, thresholding and denoising steps and named it as SA method. Based on this modification, we introduced a three-stage algorithm. This method enabled us to detect tubular structures with low intensity and weak edges. Other methods in binary segmentation and edge detection can be improved using the result we provided. It is also possible to localize some of the parameters and perform the method on inhomogeneous images as well. Using this method, it is possible to introduce multiphase segmentation algorithms. It can be suggested to use bendlets [48], which are known as the second generation of shearlets, instead of shearlets to get some better results.