Introduction

The drawdown measured in a pumping water well is the sum of the head losses contributed by the individual components, namely the aquifer, the skin layer, the gravel pack, the screen and, finally, the well interior. The aim of this study is to quantify the individual contribution of the components to total head loss and assess their relative importance. Groundwater flowing to a well experiences a strong velocity increase on its way. In this light, the linear laminar Darcy approach is not applicable everywhere, as inertial and turbulent flow may occur close to and inside the well, respectively. Some of the head losses might be minimized by choosing appropriate designs and materials. Head losses caused by the pump and by installations above the pump are not the topic of this publication. The interested reader is referred to books by Lobanoff and Ross (1992); Karrasik and McGuire (1998); Rishel (2002) and Gülich (2014).

Components of drawdown in a pumping well

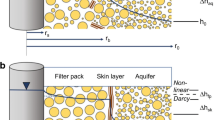
Contributors to head loss in a well-aquifer system

The measured drawdown inside the well is the sum of the head losses contributed by the individual components. The contributors to total head loss of a water well are illustrated in Fig. 1, and can be expressed as s tot = s aq + s sk + s gp + s sc + s up, with s tot = total head loss, measured in the well (L), s aq = aquifer loss (L), s sk = skin layer loss (L), s gp = gravel pack loss (inner and outer), including convergence loss (L), s sc = well screen loss (L), s up = upflow loss in well interior, sum of losses in screen and casing (L); please see the Appendix for term definitions.Head losses caused by partial penetration and the occurrence of a seepage face are not considered here but are discussed in Houben (2015).

Fig. 1
figure 1

Head losses in vertical wells. Upflow losses (s up) not shown (modified after Houben and Treskatis 2007)

Full size image

In wells with dual gravel packs, the inner and outer pack and the interface in between can be treated individually. The interface may be an issue for prepacked screens where the inner pack consists of prepacked gravel material fixed to the screen pipe with a mesh or epoxy resin.

The hydraulic situation at the wellbore may vary from well to well. In a sufficiently developed well, no skin layer should be present and the hydraulic conductivity of the immediately adjacent aquifer zone might even be improved by the removal of fines. With insufficient or no development, a low-permeability skin layer may form (which also hinders the removal of fines from the aquifer and may even accumulate more fines during its service life). The presence of a low-permeability skin layer and a high-permeability development zone is probably mutually exclusive.

Head losses in the aquifer

In unconsolidated porous aquifers, turbulent flow will occur only under the most extreme of circumstances (Houben and Hauschild 2011; Houben 2015). In regular cases, one can assume fully laminar flow up to the wellbore, and calculate the total drawdown in the confined aquifer at steady state by the Thiem (1906) equation, assuming horizontal radially symmetric flow in an isotropic infinite aquifer.

$$ {s}_{\mathrm{aq}}=\frac{Q}{2\cdot \uppi \cdot {K}_{\mathrm{aq}}\cdot B}\cdot \ln \left(\frac{r_0}{r_{\mathrm{b}}}\right) $$
(1)

Calculated aquifer head losses are in the range between a few meters to several tens of meters, depending on the hydraulic conductivity of the formation (Fig. 2). They are, therefore, usually a very important, if not the most important contribution to total head loss. Especially in fractured and karstic aquifers, the assumption of laminar flow may not be valid. Head losses in these cases have to be calculated using the Forchheimer (1901a, b) equation.

Fig. 2
figure 2

Aquifer losses as a function of the hydraulic conductivity of a confined aquifer at steady-state flow conditions, calculated using Eq. (1)

Full size image

The radius of influence r 0, that is the outer limit of the cone of depression (drawdown = zero), can be obtained from pumping tests with several observation wells located at different distances from the well (Cooper and Jacob 1946). The steady-state drawdown in the observation wells can be plotted as a function of distance from the well. In a homogeneous aquifer, these values will plot along a straight line and can be extrapolated to zero drawdown. Alternatively, if the aquifer transmissivity T and storage coefficient S are known, it can be calculated after Cooper and Jacob (1946):

$$ {r}_0=\sqrt{\frac{2.25\cdot T\cdot t}{S}} $$
(2)

Sichardt (1928) introduced an empirical estimate for r 0, valid only for unconfined gravelly aquifers. The unit to be used here for K is m/s to obtain r 0 in meters.

$$ {r}_0=3000\cdot s\cdot \sqrt{K} $$
(3)

Since r 0 occurs in a logarithmic term in Eq. (1), the calculation of aquifer drawdown is relatively insensitive to the value of r 0, so even a roughly estimated value from the dimensionally inconsistent Sichardt (1928) equation will not lead to a significant error.

It can usually be assumed that the hydraulic properties of the aquifer are constant over time. They usually cannot be altered significantly by human intervention, with a few exceptions: Improvements are possible by the removal of fine particles from the near-field during well development. At high pumping rates, fines may also be removed during regular well operation, although at the expense of the pump life. Effects of well development commonly reach only a few centimeters or decimeters into the formation. Wendling et al. (1997) found a maximum effective range of 25 cm. Driscoll (1986) quotes up to 0.6 m. In fractured or karstic aquifers, aquifer conductivity can be stimulated through hydraulic fracturing or acidification. In consolidated formations, the drilling process may lead to the formation of an excavation damage zone with elevated conductivity.

A simple example shall show the potential improvement of aquifer head loss through well development. A fully penetrating well of 20 m screen length L s and 0.5 m borehole diameter pumps Q = 100 m3/h from a confined aquifer with a hydraulic conductivity of K aq = 1 · 10−3 m/s. The radius of influence r 0 is 100 m. According to the Thiem equation (Eq. 1), aquifer head losses would be 1.32 m. Following well development, a zone of 0.25 m around the wellbore now has an improved hydraulic conductivity of an optimistic 2 · 10−3 m/s. This zone contributes 0.08 m head loss and the remaining unaltered aquifer head loss is 1.17 m, according to the Thiem equation. Well development has, thus, decreased head losses by 1.32 m - (1.17 m + 0.08 m) = 0.07 m (around 5 %). The conductivity may decrease if incrustations or fines accumulate in the aquifer (van Beek et al. 2009; Houben and Weihe 2010).

Head losses at the borehole wall: small layer, large effect

As shown in the previous, well development can result in a zone of improved conductivity around the wellbore. More often, however, it is the reverse. At the end of the drilling operation, the borehole wall is often covered by fine material, the so-called filter cake. It may contain remnants of drilling fluid additives (bentonite (swelling clay) or carboxymethylcellulose = CMC) or fines from the aquifer or traversed aquitards, e.g., clay and silt particles. While its presence during the drilling process is useful to minimize drilling fluid losses and assure stability of the borehole, it should be removed prior to operating the well. This can be done before the installation of the screen through mechanical scraping of the borehole wall or, at the latest, during well development. Well development may include chemical destabilisation of the clay aggregates by dissolved polyphosphates or mechanically through intensive, section-wise pumping. Driscoll (1986) or Houben and Treskatis (2007) give detailed descriptions of available techniques and tools.

If the filter cake is not removed, it may significantly disturb the later operation of the well, as its hydraulic conductivity is considerably lower than that of the aquifer or gravel pack. Additional fines may accumulate in front of this filter cake in the course of the operation of the well and further deteriorate the situation. Although most wells are developed somehow after drilling, it commonly happens that during a well rehabilitation, even if performed several years after well completion, bentonite mud still is mobilized, indicating that the initial development was incomplete. In such extreme cases, the resulting well yield after rehabilitation may be even better than that recorded at the initial commissioning of the well (Houben and Treskatis 2007).

Skin layers can also cause significant errors in the analysis of pumping, slug or flowmeter tests, if their head loss is erroneously attributed to the aquifer (van Everdingen 1953; Moench 1984; Yang and Gates 1997; Young 1998; Barrash et al. 2006). In layered aquifers, skin layers can induce additional head losses through flow diversion between layers (Barrash et al. 2006). Assuming an even distribution of the filter cake and laminar flow therein, the head loss can be calculated applying the adapted Thiem (1906) Eq. (4).

$$ {s}_{\mathrm{sk}}=\frac{Q}{2\cdot \uppi \cdot {K}_{\mathrm{sk}}\cdot B}\cdot \ln \frac{r_{\mathrm{sk}-\mathrm{o}}}{r_{\mathrm{sk}-\mathrm{i}}} $$
(4)

In reality, however, the geometry and distribution of hydraulic conductivity in skin layers may be less than homogeneous. They may be discontinuous, eccentric and show spatial variations of conductivity (Obnosov et al. 2010). Figure 3 shows the dramatic effect of the skin layer on the head losses, even if only laminar losses are considered. Clayey skin layers of only a few millimeters thickness can cause head losses ranging from a few meters to several 10s of meters. Thus, losses due to the skin layer are in the same range as losses caused by the aquifer (see the preceding), indicating that the skin is one of the most important contributors to total head loss.

Fig. 3
figure 3

Linear laminar head loss caused by a filter cake (skin layer) at the borehole wall of 1 and 2 mm thickness, in a well at steady-state flow in a confined aquifer, calculated using Eq. (4)

Full size image

The skin effect can also be described by the dimensionless skin factor F s (Earlougher 1977):

$$ {F}_{\mathrm{s}}=\left(\frac{K_{\mathrm{aq}}}{K_{\mathrm{s}\mathrm{k}}}\right) \ln \left(\frac{r_{\mathrm{s}\mathrm{k}}}{r_{\mathrm{b}}}\right) $$
(5)

Alternatively, the dimensionless skin factor F s can be defined as:

$$ {F}_{\mathrm{s}}=\left(\frac{K_{\mathrm{aq}}}{K_{\mathrm{s}\mathrm{k}}}\right)\left(\frac{d_{\mathrm{s}\mathrm{k}}}{r_{\mathrm{b}}}\right) $$
(6)

The skin factor (Eq. 5) can be used to interpret the conductivity around the wellbore (e.g., Kroening et al. 1996). A positive skin factor indicates additional flow resistance near the wellbore, e.g., caused by drilling fluid additives invaded into the aquifer or accumulated fines. A negative skin factor indicates enhanced flow near the wellbore, e.g., caused by the removal of fines during well development or the loosening of a consolidated formation through the drilling process.

A general problem is that both the thickness of the filter cake and its hydraulic conductivity are practically always unknown, since it is difficult to inspect and sample it directly. In most studies its properties are deduced indirectly (e.g., Barrash et al. 2006). Figure 4 shows one of the very few exceptions, where the skin layer of a dewatering well in an open pit mine became accessible when the progressing mine reached the well. Since these dewatering wells, especially the in-field wells, are only short-lived (around 10 years), no well development had been performed. On the other hand, no drilling additives had been used. The filter cake consists of fines taken up from the traversed formations and the material is mostly in the grain size range of silt. The hydraulic conductivities of the aquifer material, the gravel pack and a sample containing aquifer material, gravel pack and the filter cake, were determined using constant head Darcy permeameter tests. The hydraulic conductivities for the aquifer and the gravel pack (affected by iron oxide clogging) were K aq = 5.5 · 10−5 and K gp = 1.4 · 10−3 m/s, respectively. At a measured thickness of 1 mm, the hydraulic conductivity of the filter cake was deduced to be K sk = 1.4 · 10−6 m/s, using Eq. (7).

Fig. 4
figure 4

Sample cylinder (diameter 8 cm) recovered from the annulus of a dewatering well in the open-pit lignite mine Garzweiler, Rhineland, Germany, (plan view) with (from left to right): aquifer (grey), filter cake (dark), gravel pack with iron incrustations. Photo: RWE Power AG, with permission

Full size image

The total hydraulic conductivity of a sequence (“series connection”) of materials can be calculated using Eq. (7), assuming one-dimensional (1D) flow (Domenico and Schwartz 1996):

$$ {K}_{\mathrm{tot}}={b}_{\mathrm{tot}}\cdot \frac{1}{{\displaystyle {\sum}_{i=1}^n}\frac{b_{\mathrm{i}}}{K_{\mathrm{i}}}}=\frac{b_{\mathrm{tot}}}{\left(\frac{b_{\mathrm{gp}}}{K_{\mathrm{gp}}}+\frac{b_{\mathrm{sk}}}{K_{\mathrm{sk}}}+\frac{b_{\mathrm{aq}}}{K_{\mathrm{aq}}}\right)} $$
(7)

For pumping wells, Barrash et al. (2006) obtained average skin hydraulic conductivity values ranging from K sk = 2.5 · 10−5 to 5.0 · 10−6 m/s from analytical modeling of pumping tests.

Studies from the Netherlands show that wells drilled without drilling additives, e.g., by cable tool drilling, display a better hydraulic performance over their life-time compared to rotary drillings which used drilling fluid additives (Timmer et al. 2003, cited in Houben and Treskatis 2007).

Despite its minute thickness, a filter cake can significantly increase entrance losses. Its contribution can match and surpass even that of the aquifer. The filter cake is, thus, one of the most important contributors to well drawdown and one of the few which can be influenced by the driller.

Head losses in the gravel pack

Most aquifers cannot be developed “naturally” but require an artificial gravel pack, also called filter pack. It usually comprises clean, well-rounded quartz grains of uniform grain-size distribution which are backfilled into the annulus between borehole wall and well screen. The gravel pack has to fulfill several conflicting tasks (Saucier 1974)—on one hand, the filter pack must be fine enough to prevent the incursion of sand grains from the aquifer which might lead to pump damage and sedimentation, while on the other hand, it must be coarse and permeable enough to provide a good hydraulic conductivity; thus, minimizing flow velocity and (inertial or turbulent) head loss. A coarse gravel pack is also desirable for an effective development prior to commencement of operation. The same applies to later rehabilitations: a permeable pack allows hydraulic energy applied in the well interior to be transmitted to the borehole wall. Standard procedures of gravel pack design, especially the selection of grain size, are described in detail in, e.g., Blair (1970); Driscoll (1986); Roscoe Moss (1990); ADITCL (1996) and Sterrett (2007).

Drilling companies often tend to be affected by “gravel pack angst” and use finer pack grain sizes than required. This is done to prevent sand intrusion at any cost because their contract usually states that they have to hand over a sand-free well to the client. In most cases, they can get away with this practice. While the well owners can easily retrace whether sand is entering their wells (and hold the driller responsible), the additional energy cost caused by an excessively fine gravel pack in a sand-free well remains invisible.

The effect of the gravel pack arrangement on the hydraulic efficiency of a well was analyzed in detail by Kim (2014), based on step drawdown tests conducted in a sandtank model with variable set-ups, whereby a single filter pack (SFP) and two dual filter packs (DFPs) were compared (Fig. 5). The DFP included one type A (granule-pebble = inner gravel finer than outer) and one type B (pebble-granule = inner gravel coarser than outer). It has to be noted, however, that a DFP of the type A is rather unusual in reality. The hydraulic properties and well efficiencies of these filter packs were evaluated using the Hazen (1911); Eden and Hazel (1973); Jacob (1947) and Labadie and Helweg (1975) methods. The results showed that the hydraulic properties and well efficiency of both DFP types were higher than those of the SFP, and clogging effects and wellhead losses were also lower. The hydraulic conductivity of the DFPs types A and B was about 1.4 and 6.4 times that of the SFP, respectively. In addition, the well efficiency of the DFPs types A and B was about 1.38 and 1.60 times that of the SFP, respectively (Kim 2014). This shows that a conventional DFP with the grain size becoming coarser towards the well screen (type B) is the best option.

Fig. 5
figure 5

Hydraulic conductivity for: a SFP well, b DFP type A well, and c DFP type B well (modified after Kim 2014)

Full size image

In most cases, a DFP cannot be obtained by successive or simultaneous backfilling of two loose materials. The inner gravel pack material is often installed first, either as material pre-glued (pre-coated filter) to the screen or as loose material filled into wire cages attached to the screen, usually during the installation of the screen into the borehole. The remaining outer annulus is then backfilled with loose finer gravel. Installing a DFP has become less and less frequent in the last decades, as it still poses a technical challenge and adds to the total cost. A telling indicator of this development is the fact that the book by Driscoll (1986) still discusses DFP in detail, while its successor by Sterrett (2007) hardly does. Practical experience has shown that both pre-glued gravel packs and wire cages can make later development and rehabilitation difficult (Houben and Treskatis 2007).

Theoretically, a filter pack needs to be only two or three grain layers thick to retain and control migration of fines in an aquifer. Laboratory experiments showed that less than 13 mm of filter pack can be sufficient to control particle migration (Sterrett 2007). In practice, however, such a fine pack is impossible to install. According to Sterrett (2007), thicknesses of 50 mm and below are not practical to install. The maximum thickness should not exceed 127 mm (5 in) to allow an efficient later development, while the optimum filter thickness is given as 76 mm (3 in). Driscoll (1986) recommends a maximum gravel pack thickness of around 200 mm (8 in). Thicker gravel packs are difficult to develop, as the energy applied in the well interior is quickly attenuated in the gravel pack with increasing distance, which leaves little energy reaching the former borehole wall where most of the material that needs to be removed is located (Houben and Treskatis 2007).

A general problem of the assessment of flow in a backfilled artificial gravel pack is that both its porosity and hydraulic conductivity are a priori unknowns. Both will be controlled by processes occurring during its emplacement, e.g., (differential) sedimentation and later compaction.

If flow in the gravel pack is laminar, again an adapted version of the Thiem (1906) equation can be used.

$$ {s}_{\mathrm{gp}}=\frac{Q}{2\cdot \uppi \cdot {K}_{\mathrm{gp}}\cdot B}\cdot \ln \frac{r_{\mathrm{gp}-\mathrm{o}}}{r_{\mathrm{gp}-\mathrm{i}}} $$
(8)

The curves in Fig. 6 show that laminar head losses in the gravel pack down to hydraulic conductivities of K gp = 1 · 10−3 m/s are usually in the range of a few centimeters and are, thus, of relatively low importance for the overall head losses of the well system. Less-permeable gravel packs may cause higher losses but such a pack would miss the fundamental point of filter pack installation.

Fig. 6
figure 6

Linear laminar head loss caused by gravel packs of varying thickness and hydraulic conductivity in a well at steady-state laminar flow (confined aquifer), calculated using Eq. (8). The radius of the screen is constant for all calculations

Full size image

It could be argued that inertial losses should occur in the gravel pack if the critical radius exceeds the well screen radius. In this case, they could contribute to a significant extent to total drawdown. The analytical Engelund (1953) model of Forchheimer (1901b) flow, modified by Barker and Herbert (1992b; Eq. 9) was therefore applied for typical well parameters to assess the relative importance of non-linear laminar flow. The boundary conditions were deliberately chosen to promote turbulence as a worst-case scenario (high hydraulic conductivity of the gravel pack, small borehole diameter, short screen length).

$$ {s}_{\mathrm{gp}}=\frac{Q}{2\cdot \uppi \cdot {K}_{\mathrm{gp}}\cdot B}\cdot \ln \frac{r_{\mathrm{b}}}{r_{\mathrm{s}}}+{\beta}^{\ast}\cdot {\left(\frac{Q}{2\cdot \uppi \cdot {K}_{\mathrm{gp}}\cdot B}\right)}^2\cdot \left(\frac{1}{r_{\mathrm{s}}}-\frac{1}{r_{\mathrm{b}}}\right) $$
(9)

In Fig. 7 the development of drawdown in the gravel pack is plotted as a function of pumping rate. Up to pumping rates of 50 m3/h, this short well hardly shows any influence of non-Darcian (non-linear laminar) flow. The total head loss of the gravel pack remains in the range of centimeters or a few decimeters and, thus, in a similar range as the one from the linear laminar calculations shown in Fig. 6.

Fig. 7
figure 7

Total, linear laminar (viscous) and non-linear laminar (inertial) head losses in the gravel pack of a short-screened well, calculated using Eq. (9)

Full size image

Barker and Herbert (1992b) also found the contributions of non-Darcian flow to total head loss for 17 wells in Bangladesh to be rather small (4 %). For wells in fractured or karstic aquifers, the contribution of non-linear laminar head losses can be more significant.

At the interface between the gravel pack and the screen, the flow paths in the pack have to converge towards the screen slots. Boulton (1947) proposed Eq. (10), unfortunately without showing its derivation, to approximate the extra head loss s cv caused by this convergence, which is valid for screens with long vertical slots spaced evenly along the circumference.

$$ {s}_{\mathrm{c}\mathrm{v}}=\frac{Q}{n_{\mathrm{c}}\cdot {K}_{\mathrm{gp}}\cdot {L}_{\mathrm{s}}}{ \log}_{\mathrm{e}}\left(\frac{2}{1- \cos \delta \cdot \uppi}\right) $$
(10)

The factor δ is the ratio between slot aperture w s and slot distance, the latter defined as the distance between the centers of two neighboring slots. As Fig. 8 shows, convergence losses are generally small for any common number of screen slots, here plotted for the extremes of 10 and 100 slots, but with equal δ. For a coarser and more permeable gravel pack than assumed in Fig. 8, the influence would be even smaller.

Fig. 8
figure 8

Head losses due to convergence of flow paths in the gravel pack to vertical screen slots, calculated using Eq. (10)

Full size image

Head losses in the well screen

The well screen has to fulfill several requirements at the same time: (1) to keep grains from the gravel pack (and the aquifer) from entering the well, (2) to stabilize the borehole against collapse and (3) to minimize entrance losses. For the latter, a large open area (or slot width) would be desirable but this would be in conflict with the first two requirements. Stability might be improved by selecting a sturdy material (e.g., steel instead of PVC), by increasing material thickness or by reducing the open area. A large variety of screen types is available on the market. Standard procedures of screen design, especially the selection of slot size, are described in detail, e.g., in Driscoll (1986); Roscoe Moss (1990); ADITCL (1996) and Sterrett (2007).

The head losses of water flowing through a screen slot are visualized in Fig. 9 and can be expressed using the continuity equation and the Bernoulli equation (Hamill 2001). The head loss at a rectangular constriction (contraction) at the inlet h Lin (Eq. 11) and the outlet (expansion) h Lout (Eq. 12) is (with C c = 0.6):

$$ {s}_{\mathrm{in}}=\frac{{\left(\frac{v_2}{C_{\mathrm{c}}}-{v}_2\right)}^2}{2g}\approx \frac{0.45\cdot {v}_2^2}{2g} $$
(11)
$$ {s}_{\mathrm{out}}=\frac{{\left({v}_3-{v}_4\right)}^2}{2g} $$
(12)
Fig. 9
figure 9

Visualization of water flow through a screen slot: (0) inflow, (1) contraction (vena contracta) at slot inlet, (2) laminar flow in slot, (3) expansion and turbulence at outlet, (4) outflow

Full size image

In more general form, head losses at the transition of tubes of different diameters (d 1 < d 2) can be expressed as (Hamill 2001):

$$ s={\left(1-\frac{d_1^2}{d_2^2}\right)}^2\cdot \frac{v_1^2}{2g}=\psi \cdot \frac{v_1^2}{2g} $$
(13)

Head losses are influenced by the geometry of the constriction. Rounded bell-shaped inlets and outlets have ψ ≈ 0.05 and κ ≈ 0.20, respectively, while sharp-edged inlets and sudden enlargements have ψ ≈ 0.50 and ψ ≈ 1.00, respectively (Hamill 2001).

In theory, differences in material roughness affect the hydraulic performance of screens. On one hand, Barker and Herbert (1992a) found that stainless steel has a higher roughness than plastic or glass-fibre reinforced plastic, while on the other hand, its sturdier characteristic allows for smaller wall thickness, therefore creating a larger internal diameter at the same nominal diameter, an effect that compensates for the higher roughness.

The open area of a screen influences its hydraulic performance. Based on his recommended permissible entrance velocities of 0.6–1.2 m/s (2–4 ft/s) and hydraulic tests on six well screens, Williams (1985) concluded that an open area of 3–5 % is sufficiently large. Corey (1949) found that open areas larger than 15 % provide little or no increase in yield. Some typical open areas of screens are listed in Table 1.

Table 1 Typical open areas of screens (after data from Sterrett 2007)
Full size table

For slotted, bridged and louvered screens the percentage of open area can be calculated using Equation 46 of Sterrett (2007)

$$ {A}_{\mathrm{o}}=\frac{A_{\mathrm{s}\mathrm{l}}}{A_{\mathrm{s}\mathrm{c}}}\cdot 100=\frac{l_{\mathrm{s}\mathrm{l}}\cdot {w}_{\mathrm{s}}\cdot {n}_{\mathrm{s}}}{\uppi \cdot {d}_{\mathrm{s}-\mathrm{o}}\cdot {L}_{\mathrm{s}}}\cdot 100 $$
(14)

For wire-wound screens, Driscoll (1986) presents the following equation to calculate the percentage of open area

$$ {A}_{\mathrm{o}}=\left(\frac{w_{\mathrm{s}}}{\left({w}_{\mathrm{s}}+{w}_{\mathrm{w}}\right)}\right)\cdot 100 $$
(15)

It should be noted that usually 0.15 m at either end for each screen segment are left blank to provide mechanical strength to the section where one pipe is attached to the next one.

As screen slots may be (partially) blocked by grains from the gravel pack, the fractional open area is often approximated by half of the fractional screen slot area or the product of gravel pack porosity and fractional slot area (Barker and Herbert 1992b). Although the hydraulic effect of a large open area is limited, a large screen open area is desirable to allow better development and easier rehabilitation of a well (Driscoll 1986). During development, remnants of the drilling fluid and particles from the aquifer and gravel pack need to be removed and have to pass the screen. During later rehabilitation, mechanical energy, often in the form of flowing water jets, is applied in the interior of the screen but has to take an effect on its outside. For both applications, a large open area provides better access to the annulus (Houben and Treskatis 2007).

Direct measurements of the hydraulic conductivity of a screen are quite a challenge, since the observable head losses are usually very small (s = 0.01 to 1.0 mm at q = 10−2 cm/s; Klotz 1971). The simplest approach to calculate head losses (or the hydraulic conductivity) of screens is to assume linear laminar flow, as done by Klotz (1971, 1990); Barrash et al. (2006); Houben and Hauschild (2011) and Klammler et al. (2014). Klotz (1971) calculated the hydraulic conductivity of well screens by approximating the screen slots as small tubes of limited length (capillaries), which is only valid for linear-laminar flow, with q not exceeding 0.3 to 0.5 cm/s.

$$ {K}_{\mathrm{s}}=\frac{g}{\upsilon}\cdot \frac{A_{\mathrm{p}}\cdot {r}_{\mathrm{h}}^2}{\varOmega_{\mathrm{s}\mathrm{l}}}\cdot \frac{1}{\varOmega_{\mathrm{s}}} $$
(16)

The hydraulic slot radius r h is defined as the ratio of area and circumference of a slot.

$$ {r}_{\mathrm{h}}=\frac{2\cdot {A}_{\mathrm{sl}}}{C_{\mathrm{sl}}} $$
(17)

For a circular slot, r h is simply the radius of the hole. The resistance coefficient of the screen slots Ω sl for rectangular slots is defined as (Klotz 1990):

$$ {\varOmega}_{\mathrm{sl}}=\frac{12\cdot {r}_{\mathrm{h}}^2}{b_{\mathrm{sl}}^2}\cdot {\left[1-\frac{192\cdot {b}_{\mathrm{sl}}}{\uppi^5\cdot {a}_{\mathrm{sl}}}\cdot \left( \tanh \frac{\uppi \cdot {a}_{\mathrm{sl}}}{2\cdot {b}_{\mathrm{sl}}}+\frac{1}{243}\cdot \tanh \frac{3\cdot \pi \cdot {a}_{\mathrm{sl}}}{2\cdot {b}_{\mathrm{sl}}}\right)\right]}^{-1} $$
(18)

whereas for square slots (a sl = b sl), Ω sl ≈ 7, for elongated slots, Ω sl ≈ 12 and for circular slots, Ω sl = 8.

The resistance coefficient of the screen Ω s needs to be determined experimentally, which Klotz (1990) did for 350 different screens, finding that Ω s depends on the screen type. For the same screen type, Ω s increases with increasing screen diameter and increasing hydraulic slot radius, whereas it decreases with increasing wall thickness of the screen.

Barrash et al. (2006) proposed to approximate the well screen as a fractured system of horizontally arranged parallel fractures (= screen slots) between parallel plates. Based on the “cubic law” (Snow 1968) for linear laminar fracture flow, the conductivity of a screen (laminar flow) can then be determined by:

$$ {K}_{\mathrm{s}}={n}_{\mathrm{s}}\cdot \frac{w_{\mathrm{s}}3}{12\cdot {f}_{\mathrm{r}}}\cdot \frac{\rho \cdot g}{\mu } $$
(19)

Despite the assumption of linear laminar flow, Barrash et al. (2006) showed that screen conductivities obtained from laboratory experiments could be recreated reasonably well using Eq. (19), up to rather high flow rates of 12–15 m3/h/m of screen length. At even higher flow rates, non-linear head losses occur, which Eq. (19) does not account for. Even for small slot apertures w s of 0.05 cm, Barrash et al. (2006) found that the hydraulic conductivity of the screen was always higher than that of any other component in their set-up and, thus, plays a minor role for the conductivity of the whole system.

Figure 10, based on Eq. (19) (cubic law), clearly shows that the hydraulic conductivity of the screen is even higher than that of highly permeable aquifers down to slot widths of 0.3 mm, which is usually the smallest slot width commercially available. Therefore, head losses also are negligible above this slot width. A linear laminar numerical model by Houben and Hauschild (2011) showed accordingly that only screens with an unreasonably low hydraulic conductivity (K s < 0.0001 m/s) would contribute significantly to the total well drawdown. Some manufacturers offer screens with slot apertures down to 0.2 mm or even 0.15 mm, but these, additional to their elevated head losses, are difficult to produce and, more importantly, such wells are almost impossible to develop.

Fig. 10
figure 10

Hydraulic conductivity of a screen as a function of slot width calculated using the cubic law (Eq. 19). The obtained conductivities were used to calculate laminar head losses after Thiem (1906; Eq. 1)

Full size image

A second group of authors prefer turbulent approaches to describe flow through screens (e.g., Clark and Turner 1983; Singh and Shakya 1989; Barker and Herbert 1992a, b; Parsons 1994). Clark and Turner (1983) performed laboratory experiments and field tests on the hydraulic performance of different screens with an open area ranging from 5 to 40 %. They were able to fit the experimental results with Eq. (20). The square dependency on velocity indicates non-laminar flow.

$$ {s}_{\mathrm{s}\mathrm{c}}={C}_{\mathrm{CT}}\cdot {v}_{\mathrm{e}}^2={C}_{\mathrm{CT}}\cdot {\left(\frac{Q}{2\cdot \uppi \cdot {r}_{\mathrm{s}}\cdot {L}_{\mathrm{s}}\cdot {A}_{\mathrm{p}}}\right)}^2 $$
(20)

Based on the gradient of the regression line C CT, as indicator of screen performance, they obtained a ranking of the investigated screens. Remarkably, the screen with the highest open area, a wire-wound screen, showed the worst performance (highest C CT). It should be noted, though, that the ranking of screens only became visible at exceptionally high entrance velocities (up to 5 m/s). At more realistic entrance velocities (<0.3 m/s), head losses were small (<5 mm) and similar for all screen types. In a similar approach, Barker and Herbert (1992a) experimentally compared 27 types of well screens with the same nominal diameter and also found differences in head losses to be small.

The orifice law can be used to calculate losses for a screen receiving uniform flow (Barker and Herbert 1992a; Parsons 1994). It is basically a more explicit version of Eq. (20). Commonly used values for the velocity coefficient and slot contraction coefficient are C v = 0.98 and C c = 0.62, respectively.

$$ {s}_{\mathrm{s}\mathrm{c}}=\frac{1}{2g}\cdot {\left(\frac{Q}{2\cdot \uppi \cdot {r}_{\mathrm{s}}\cdot {L}_{\mathrm{s}}\cdot {C}_{\mathrm{v}}\cdot {C}_{\mathrm{c}}\cdot {A}_{\mathrm{p}}}\right)}^2 $$
(21)

Considering the definition of critical entrance velocity (Houben 2015), Eq. (21) reduces to

$$ {s}_{\mathrm{sc}}=\frac{1}{2g}\cdot {\left(\frac{v_{\mathrm{c}\mathrm{rit}}}{C_{\mathrm{v}}\cdot {C}_{\mathrm{c}}}\right)}^2 $$
(22)

Screen head losses calculated using Eq. (21) are, despite the quadratic dependency on flow, rather low (Fig. 11). For “typical” critical entrance velocities of 0.03, 0.1 and 0.5 m/s, corresponding head losses amount to 0.12, 1.4 and 34.5 mm, respectively. Even the worst cases result in head losses in the range of centimeters to a few decimeters only.

Fig. 11
figure 11

Screen head losses as a function of critical entrance velocity, calculated using Eq. (21) (orifice law)

Full size image

Based on work by Garg and Lal (1971) and Cooley and Cunningham (1979); Barker and Herbert (1992a) derived a formula for calculating well screen losses for axial and radial flow. It should be noted, however, that this equation assumes uniform inflow over the whole length of the screen (see the following discussion). They pointed out that screen losses contain both frictional and momentum components. The latter are predominant for screen lengths of 30–40 m for most screen types. Frictional losses become more important with increasing screen length.

$$ {s}_{\mathrm{sc}}={Q}^2\cdot \left(\frac{a_{\mathrm{f}}\cdot {L}_{\mathrm{S}}}{4}+\frac{b_{\mathrm{m}}}{3}\right) $$
(23)

The parameters a f and b m characterize the frictional and momentum head losses, respectively. They are defined after Parsons (1994) as:

$$ {a}_{\mathrm{f}}=\frac{32\cdot {f}_{\mathrm{p}}}{4\cdot \uppi 2\cdot g\cdot {d_{\mathrm{s}}}^5} $$
(24)
$$ {b}_{\mathrm{m}}=\frac{32}{g\cdot \uppi 2\cdot {d_{\mathrm{s}}}^4} $$
(25)

Parsons (1994) used pipe friction factors f p of 0.015, 0.018 and 0.033 for slotted, perforated and for wire-wound screens, respectively.

Singh and Shakya (1989) proposed a non-linear power law that describes head losses across a screen where the exponent y has to be determined experimentally (y ≈ 1.911)

$$ {s}_{\mathrm{s}\mathrm{c}}=\frac{d_{\mathrm{s}\mathrm{w}}}{{\left(2\uppi \cdot {K}_{\mathrm{s}}\cdot {L}_{\mathrm{s}}\right)}^y}\cdot {Q}^y $$
(26)

setting

$$ C=\frac{d_{\mathrm{s}\mathrm{w}}}{{\left(2\uppi \cdot {K}_{\mathrm{s}}\cdot {L}_{\mathrm{s}}\right)}^y} $$
(27)

and y = 2, Eq. (26) reduces to Jacob’s (1947) equation describing well loss (s = C · Q 2)

In good accordance with the other authors, experimental work by Klauder (2010) showed that the screen contributes less than 1 % to the total head losses of a well. Her results show that even the worst screens caused head losses of only 0.5 mm, while the best, wire-wound screens hardly reached 0.1 mm.

Example calculations with the different equations listed in the preceding, experimental studies, field tests and numerical modeling all agree that, at least within typical parameter sets, screen head losses are usually in the range of a few millimeters to a few centimeters and can safely be ignored, when compared to the contributions of other components (e.g., Clark and Turner 1983; Roscoe Moss 1990; Barker and Herbert 1992a; Parsons 1994; Klauder 2010; Houben and Hauschild 2011). It is a little sad to think that the component to which engineers have devoted so many ideas and so much skill in design and manufacture, plays the smallest role.

Annular fill and gravel envelope: seal or hidden water conveyor?

In most countries, regulations require that the remaining annulus above the gravel pack has to be filled with impermeable material, e.g., bentonite or cement grout, to prevent the inflow of oxic and potentially contaminated shallow groundwater. It should be noted that the sealing of the annulus with swelling clays, e.g., bentonite, is only useful in the saturated zone. In the unsaturated zone, there is not enough water available to induce the swelling of the clay minerals. The sealing is especially important in multi-layer aquifers to avoid hydraulic and hydrochemical short-circuits between aquifers.

In the old days, it was common practice to backfill the annulus above the gravel pack with any aquifer material obtained during the drilling operation or even to fill the whole annulus with filter gravel (gravel envelope wells). In layered systems, this often leads to hydraulic and chemical short-circuits between different aquifers, with many undesirable consequences. Although Driscoll (1986) and Roscoe Moss (1990) stated that the volume of water passing through this zone is relatively small, Houben (2006) found severe iron oxide incrustation build-up above the gravel pack in the permeable annular fill of a well, indicating significant influx of oxygenated water. As shallow groundwater is often contaminated by, e.g., pesticides, nitrate or fecal bacteria, it is important to prevent its flow into the well by sealing off the annulus above the screen. Numerical simulations by Horn and Harter (2009) showed that an extended permeable zone above the gravel pack leads to a significantly elongated source area, potentially increasing the vulnerability of the well to near-surface contaminants.

Head losses in a permeable annular fill are difficult to assess, as the hydraulic conductivity is unknown due to the unknown type of material and degree of compaction. Flow might be laminar, non-Darcian and a seepage face might also occur. With the rather small area and an assumed higher conductivity, expected losses are small.

Head losses in the well interior (upflow losses)

As the water moves vertically through the well interior towards the pump, it experiences an energy loss due to friction with the surface of both screen and casing, causing the so-called upflow losses (Parsons 1994). A number of workers have identified ways of quantifying these losses. The most common is probably the Darcy-Weisbach equation (Weisbach 1845) for turbulent flow in pipelines (Eq. 28), e.g., used by Chen and Jiao (1999).

$$ {s}_{\mathrm{up}}={f}_{\mathrm{D}}\cdot \frac{L_{\mathrm{p}}}{d_{\mathrm{p}}}\cdot \frac{v_{\mathrm{f}}^2}{2g}={f}_{\mathrm{D}}\cdot \frac{L_{\mathrm{p}}}{d_{\mathrm{p}}}\cdot \frac{{\left(Q/A\right)}^2}{2g} $$
(28)

with A = π · d p 2/4

The Darcy friction factor f D can be obtained from the Moody (1944) approximation that is valid for values of Re common for most water wells of 4 · 103 < Re < 1 · 107 and for κ/d ≤ 0.01 (Eq. 29). The roughness of the material is described by the parameter κ.

$$ {f}_{\mathrm{D}}=0.0055\cdot \left[1+{\left(20000\cdot \frac{\kappa }{d_{\mathrm{p}}}+\frac{10^6}{\mathrm{Re}}\right)}^{\frac{1}{3}}\right] $$
(29)

A commonly used rule-of-thumb for the permissible maximum upflow velocity is 1.5 m/s (5 ft/s). Considering the losses of 0.5–1.0 cm/m of pipeline at this velocity shown in Fig. 12 and taking into account typical well depths, upflow losses in the range of centimeters to a few decimeters are likely. Only in very deep and small diameter wells, may these contributions become significant.

Fig. 12
figure 12

Head losses per meter of casing for different materials as a function of upflow velocity. Calculated using the Darcy-Weisbach equation (Eq. 28). Friction factors f D used here were obtained using the Moody equation (Eq. 29). Values for equivalent roughness κ were taken from Hamill (2001). The PVC pipe assumes O-ring seals at 6–9 m intervals

Full size image

To address upflow losses, Bakiewicz et al. (1985) used an adaptation of the empirical Manning equation, which is normally used to assess flow in open channels. The specific discharge q here is the flux rate into the screen, Q/L s, which is assumed to be constant over the screen length.

$$ {s}_{\mathrm{up}}=3.428\cdot {q}^2\cdot {\sigma}^2\cdot {L_{\mathrm{S}}}^3\cdot {d_{\mathrm{p}}}^{-16/3} $$
(30)

Similar to the Darcy-Weisbach calculations (Fig. 12), the Manning equation predicts upflow losses in the range of centimeters or decimeters for most well geometries (Fig. 13). Using the same equation and a fixed upflow velocity of 1.5 m/s, Parsons (1994) obtained head losses of 0.2–0.3 m for a wide range of typical well designs.

Fig. 13
figure 13

Head losses for different casing and screen materials as a function of pumping rate. Calculated using Eq. (30) (modified Manning equation). Roughness coefficients σ for smooth pipes, slotted and wire-wound screens of 0.010, 0.013 and 0.018 s2/m2/3 were used (Parsons 1994)

Full size image

Barker and Herbert (1992b) proposed an equation for calculating losses in the unperforated casing above the screen which considers losses not only along the pipes but also the joints, with the latter considered as reducer fittings. An approximate used value for the loss coefficient of a well-designed reducer fitting is ζ rd ≈ 0.2.

$$ {s}_{\mathrm{up}}=\frac{8\cdot {Q}^2}{\uppi^2\cdot g}\cdot \left\{{\displaystyle \sum_{n_{\mathrm{se}}}}\frac{f_{\mathrm{p}}\cdot {L}_{\mathrm{c}}}{d_{\mathrm{p}}^5}+{\displaystyle \sum_{n_{\mathrm{rd}}}}{\zeta}_{\mathrm{rd}}{\left(\frac{1}{d_{\mathrm{rd}1}^2}-\frac{1}{d_{\mathrm{rd}2}^2}\right)}^2-\left(\frac{1}{d_{\mathrm{rd}1}^4}-\frac{1}{d_{\mathrm{rd}2}^4}\right)\right\} $$
(31)

The pressure loss in casing joints may be calculated using Eq. (32) or (33) (Arnold 1993).

$$ \Delta {p}_{\mathrm{j}}={f}_{\mathrm{j}}\cdot \frac{{v_{\mathrm{cs}}}^2\cdot \rho }{2}\cdot {n}_{\mathrm{j}} $$
(32)
$$ \Delta {p}_{\mathrm{j}}={f}_{\mathrm{j}}\cdot \frac{Q^2\cdot \rho }{{d_{\mathrm{p}}}^4}\cdot {n}_{\mathrm{j}}\cdot 0.81 $$
(33)

and

$$ {f}_{\mathrm{j}}={a}_{\mathrm{j}}\cdot {\left[{\left(\frac{d_{\mathrm{p}}}{d_{\mathrm{j}}}\right)}^2-1\right]}^2 $$
(34)

In wells with elevated upflow losses, a convergence of flow may occur in the upper part of the screen. In extreme cases, the lower part of the screen may then be rendered almost completely hydraulically ineffective (Bakiewicz et al. 1985). Such behavior can actually be found in many flowmeter profiles from wells.

Water flowing to the pump has first to flow inside the screen section, then through the casing. As some water enters at the top of the screen, it thus will experience any internal friction with the screen surface. Water entering at the bottom of the screen has to flow past the whole screen length. Assuming an even distribution of inflow over the screen length, the average distance of flow through the screen is equal to half of its length.

The roughness of the screen interior and the casing interior may differ significantly; therefore, upflow has to be considered individually for both parts, using a friction factor for each. Roscoe Moss (1990) concluded that the axial head losses caused by upflow through 2–3 m of blank casing equal head losses of 1 m of screen. For the flow through the riser pipe above the pump, head losses can be calculated using the flow laws 28, 30 and 31.

Pump position: is the current practice based on yet another myth?

Most textbooks on well construction and operation recommend installing the pump in the blank casing section above the screen. Driscoll (1986, p. 596) states that “The intake of a pump should not be placed within the well screen, because distorted flow patterns will occur in the vicinity of the screen…”. This is claimed to limit sand pumping, corrosion, and iron oxide precipitation. Based on physical and numerical models, von Hofe and Helweg (1998); Korom et al. (2003) and Houben and Hauschild (2011) questioned this commonly followed principle. They showed that a pump installed in the screen actually decreases head loss and, thus, improves hydraulic well performance. One explanation for better well performance with a pump installed in the screen is the reduced upflow distance that the water has to cover to get to the pump. Von Hofe and Helweg (1998) concluded that locating the pump intake in the upper 75 % of the screen is more efficient than locating it anywhere in the blank casing above the screen. Locating it in the top 30–45 % of the screen length maximized well efficiencies. Houben and Hauschild (2011) came to similar findings with an optimum pump position at 50 % screen length. They found that head losses could be decreased by several decimeters. These concerns have already found their way into modern textbooks. The book by Sterrett (2007) is already far less dogmatic on this topic as its predecessor by Driscoll (1986). Practical tests have yet to show that improved hydraulics can overcome potential disadvantages of installing the pump in the screen. Von Hofe and Helweg (1998) also investigated the influence of the size of the pump intake and found optimum efficiencies when it was about 60 % of the screen diameter.

Example calculation

Three example scenarios for a vertical, fully penetrating well in a confined aquifer shall show the absolute and relative contribution of the individual components to head loss in the well. Geometry and parameters are based on typical public-water-supply wells. The parameters are listed in Table 2 and calculations follow Eq. (35). The first scenario is a well with standard operational parameters (standard well). The second assumes an elevated specific flux due to a thinner aquifer and fewer but wider screen slots. This set-up shall represent a well which is operated under unfavorable design conditions (stressed well). The third scenario is the same as the second but with slimmer screen and borehole diameters. This is a scenario of a well which violates most common design procedures (slim, stressed well). It should be noted that the numbers of screen slots per circumference used here are very high and very low, respectively and, thus, represent extreme values.

Table 2 Parameters used for example calculations
Full size table

Flow is assumed to be fully Darcian in the aquifer and skin layer and, thus, the Thiem (1906) equation is employed (Eqs. 1 and 4). The skin layer has a thickness of 1 mm. Losses due to inertial flow and convergence are considered for the gravel pack (Eqs. 9 and 10). The inertial coefficient β* was obtained using Eq. (19) by Cox (1977, cited in Barker and Herbert 1992b). Turbulent head losses in the screen and upflow head loss in screen and casing are calculated using the orifice (Eq. 21) and Darcy-Weisbach (1845) equation (Eq. 28), respectively. The aquifer is fully screened with uniform inflow. The pump is located 10 m above the screen top. The average distance of flow to the pump is thus 20 m for the standard well and 15 m for the stressed well. Screen and casing diameters are equal (no telescoping). Both are made of PVC with “O” ring seals. For the sake of simplicity, both have the same roughness. The influence of joints is not considered.

$$ \begin{array}{c}\hfill {s}_{\mathrm{tot}}={s}_{\mathrm{aq}}+{s}_{\mathrm{s}\mathrm{k}}+\left({s}_{\mathrm{gp}}+{s}_{\mathrm{c}\mathrm{v}}\right)+{s}_{\mathrm{s}\mathrm{c}}+{s}_{\mathrm{up}}\hfill \\ {}\hfill =\left[\frac{Q}{2\cdot \uppi \cdot {K}_{\mathrm{aq}}\cdot B}\cdot \ln \left(\frac{r_0}{r_{\mathrm{b}}}\right)\right]+\left[\frac{Q}{2\cdot \uppi \cdot {K}_{\mathrm{s}\mathrm{k}}\cdot B}\cdot ln\left(\frac{r_{\mathrm{s}\mathrm{k}-\mathrm{o}}}{r_{\mathrm{s}\mathrm{k}-\mathrm{i}}}\right)\right]\hfill \\ {}\hfill +\left\{\left[\frac{Q}{2\cdot \uppi \cdot {K}_{\mathrm{gp}}\cdot B}\cdot \ln \left(\frac{r_{\mathrm{b}}}{r_{\mathrm{s}}}\right)+{\beta}^{\ast}\cdot {\left(\frac{Q}{2\cdot \uppi \cdot {K}_{\mathrm{gp}}\cdot B}\right)}^2\cdot \left(\frac{1}{r_{\mathrm{s}}}-\frac{1}{r_{\mathrm{b}}}\right)\right]+\left[\frac{Q}{n_{\mathrm{c}}\cdot {K}_{\mathrm{gp}}\cdot B} \log \left(\frac{2}{1- \cos \delta \cdot \uppi}\right)\right]\right\}\hfill \\ {}\hfill +\left[\frac{1}{2g}\cdot {\left(\frac{Q}{2\cdot \uppi \cdot {r}_{\mathrm{s}}\cdot B\cdot {C}_{\mathrm{v}}\cdot {C}_{\mathrm{c}}\cdot {A}_{\mathrm{p}}}\right)}^2\right]+\left\{{f}_{\mathrm{D}}\cdot \frac{L_{\mathrm{p}}}{d_{\mathrm{p}}}\cdot \frac{\left[Q/\left(\frac{\uppi \cdot {d}_{\mathrm{p}}}{4}\right)\right]2}{2g}\right\}\hfill \end{array} $$
(35)

A spreadsheet (Excel) tool is available as electronic supplementary material (ESM) which includes most of the equations presented here and in Houben (2015).

The results presented in Table 3 and Fig. 14 clarify that, for all scenarios, the aquifer and the skin layer (if present) are the key parameters affecting well loss. All other components can be considered minor contributors. Klauder (2010) came to very similar results. Gravel pack losses are generally small. In the stressed cases, the inertial losses are on par with the viscous head losses (Fig. 15). Convergence losses become noticeable for the second and third scenario since both have a very small number of screen slots (Fig. 15). Calculating head losses to three (or four) decimal places, as done for the screen losses in Table 3, may not be realistic but is needed here to show its diminutive influence. The resulting upflow velocities for the scenarios are Q/A = 0.42, 0.85 and 1.73 m/s, respectively. For scenario 3, this exceeds the recommended upflow velocity of 1.5 m/s and results in noticeable losses (Fig. 14).

Table 3 Results of example calculations
Full size table
Fig. 14
figure 14

Head losses of the individual well components for the six scenarios

Full size image
Fig. 15
figure 15

Head losses in the gravel pack for the six scenarios

Full size image

Cost savings potential

Heads, or head losses, can be translated into the power required to overcome them for a given discharge. This is usually done by using

$$ {P}_{\mathrm{net}}=\rho \cdot g\cdot Q\cdot H $$
(36)

Since pumps do not convert 100 % of the electrical energy into water lift, the pump efficiency η p (0 < η p < 1) or more colloquially, the “wire to water efficiency” has to be taken into account. The gross power needed thus is

$$ {P}_{\mathrm{gros}}=\frac{\rho \cdot g\cdot Q\cdot H}{\eta_{\mathrm{p}}} $$
(37)

When selecting the pump motor, often an additional safety margin of 20 % is added to P gros to avoid overloads and allow for some pump ageing. In some countries, the terms “water horsepower”and “brake horsepower” are used for P net and P gros, respectively.

Using Eq. (37), the gross power needed to lift one cubic meter of water by one meter is thus 4.54 · 10−3 kWh, using an optimistic η p = 0.60. In reality, lower efficiencies may occur. Hübner (2011) found an average efficiency of η p = 0.41 for 2,500 submersible pumps in Germany. Plath et al. (2011) found an average efficiency of η p = 0.48 based on data from 14 German water-supply companies. Both studies found that values as low as η p = 0.20 and sometimes even less are not uncommon.

Knowing the price for one kWh of electricity, the energy demand can easily be converted into monetary units. In Germany, one kWh of electricity costs around € 0.12 for industrial users. Using monetary units allows comparing different design options (e.g., smaller vs. bigger screen diameter) but also whether the additional investment of a well development can redeem itself through lower pumping cost over the time of operation. A lower electricity bill will also reduce the carbon footprint, if non-renewable energy is used. The efficiency of the pump plays a major role here.

If one compares the standard (scenario 1) and the short slim well (scenario 3), both at a pumping rate of 150 m3/h, one sees that the latter produces 6 m more head loss (Table 3). At a pumping rate of 250,000 m3/year, the ill-designed well requires 6,810 kWh (or € 817) more per year than the standard well. Since such wells may run for extended periods of time, say 30 years, this will accumulate to € 24,500 and top the initial savings of a shorter and slimmer well. It should also be noted that hydraulically stressed wells usually experience faster and stronger ageing processes which have to be countered by expensive and repeated rehabilitation measures (Houben and Treskatis 2007).

All scenarios in Tables 2 and 3 consider the presence of a skin layer which causes a significant percentage of the total head loss. For the case of the standard well at Q = 150 m3/h, the skin causes a head loss of 1.47 m. With the same parameters as already given in the preceding, this translates into an extra cost of € 136/year or € 4,090 over 30 years. In this case, a proper development after well completion is well worth the effort (and cost). For dewatering wells for open pit mines, with their commonly shorter time of operation, say 10 years, the break-even point between the cost for a thorough development and the following savings in electricity will probably not be reached during their lifetime.

Conclusions

The absolute and relative importance of the individual components and the geometry on the total head loss of a water well is listed in Table 4. It is valid for common designs and operational parameters of vertical screened drinking-water supply wells in unconsolidated porous media. Significant deviations may occur in very deep wells, or those tapping karstic, volcanic or fractured formations. The term “optimization” used in Table 4 refers to potential design modifications that the well driller may implement.

Table 4 Influence of well components and well geometry on total head loss of a vertical screened water well in unconsolidated porous media (estimation for common well designs and operational parameters)
Full size table

Obviously, the aquifer, commonly the biggest contributor to drawdown, can only be influenced slightly by man through well development. Other components such as the gravel pack, the screen and the casing, can be influenced by choice of material or engineering; nevertheless, their overall contribution is quite small. There is, however, one component that can significantly contribute to head loss and that can actually be influenced by readily available techniques: the borehole wall (skin layer). Instead of wasting money and effort for the optimization of the last per mille of head loss of the screen, much more can be gained from removal of fines from the borehole wall. If the filter cake is not removed, the well will suffer from this inherited negative head start throughout its whole operational life, and energetic and monetary expenses for the well owner will accumulate at the same time. Especially for wells with a long service life, the initial cost for well development are a useful investment, not only because of savings on electricity but also on rehabilitation measures.