1 Introduction

Slope failure caused by earthquakes is one of the most serious geotechnical disasters [1]. The soil elements within a slope are different from that of a level ground because of the existence of initial static shear stress (τs) on the horizontal plane. During earthquake shaking, a cyclic shear stress (τd) will be superimposed on the horizontal plane (see Fig. 1). According to the relative amplitude between τs and τd, Hyodo et al. [2] classified the undrained cyclic behavior within a slope into three types: “stress reversal” (τs < τd), “intermediate” (τs = τd) and “no stress reversal” (τs > τd). For a given slope, the soil elements exhibit “stress reversal” behavior when undergoing relatively large earthquake loadings. As the amplitude of the earthquake loading decreases, the soil elements will experience behaviors from “intermediate” to “no stress reversal”. In view of the fact that large (or strong) earthquakes are rare and small to moderate earthquakes will be frequently encountered in a seismically active area, the “no stress reversal” condition is more common than the “stress reversal” condition in a slope. Moreover, dense sand slopes are more practically meaningful than those of loose sand, as they are usually improved ground to support the embankments, dams or foundations. Thus, the problem of undrained cyclic behavior and liquefaction resistance of saturated dense sand without stress reversals becomes important in engineering practices.

Fig. 1
figure 1

The stresses acting on soil element in a slope subjected to earthquake shaking

Full size image

The cyclic triaxial test on anisotropically consolidated soil samples could be used to study undrained behavior of soil elements within a slope subjected to earthquake loadings. Unlike the case of “stress reversal”, due to the presence of initial static shear stress, the excess pore water pressure in the case of “no reversal” could not build up to the value of initial lateral confining stress. As a result, there will not be a sudden increase in strains during shaking, but the large accumulated residual deformation will also bring the samples to failure without the occurrence of liquefaction [3]. It was also found that the initial static shear stress at some range is beneficial to the cyclic resistance of dense sand in the framework of the triaxial tests [3,4,5,6,7]. However, the underlying mechanism is still unknown. DEM (Discrete Element Method) pioneered by Cundall and Strack [8] offers a promising way to study the macroscopic phenomenon from a microscopic perspective [9,10,11,12,13]. Some microscopic information provided by DEM analysis, such as soil fabric, contact direction, contact forces and number of contacts, could help to better clarify the role of initial static shear stress in affecting cyclic resistance and revealing the mechanism.

In the present study, two-dimensional DEM method is used to simulate a series of stress-controlled undrained cyclic biaxial tests with different combinations of cyclic stress ratio CSR (\(= \tau_{d} /\sigma^{\prime}_{v}\)) and initial static shear stress ratio α (\(= \tau_{s} /\sigma^{\prime}_{v}\)), to investigate the undrained behavior and cyclic resistance of dense granular materials under cyclic loading without stress reversals. The changes of induced microstructure are further examined, including the fabric anisotropy and mechanical coordination number between soil particles, to clarify the role of initial static shear in cyclic resistance and the underlying mechanism.

2 DEM model

2.1 DEM program and particle contact models

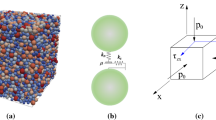
In this paper, a commercial code PFC2D [14] is employed to perform the numerical simulations and the key elements of the DEM could be found in Cundall and Strack [8]. As shown in Fig. 2a, a rectangular packing (85 mm × 40 mm) of circular particles is considered. Inside a rectangular box confined by four rigid frictionless walls, a total number of 4069 particles with diameter ranging from 0.6 mm to 1.2 mm are randomly generated. Figure 2b presents the grain size distribution curve, and the uniform distribution is adopted with mean particle size D50 = 0.90 mm and uniformity coefficient CU = 1.45. According to the method proposed by Yang et al. [15], the maximum void ratio (emax) and the minimum void ratio (emin) of the DEM generated sample are 0.2622 and 0.1961, respectively. In this method, the emax could be estimated by generating samples with particle–particle friction coefficient μpp = 0.5, and the emin could be obtained with μpp = 0, both under a reference confining pressure of 10 kPa. A linear force–displacement contact law for circular disk elements is employed, and the parameters adopted in this study are summarized in Table 1. It should be noted that a trial and error process was conducted to calibrate the parameters used in this study [16], where the laboratory drained shear test is taken as the benchmark and the parameters are tuned until the calculation results are consistent with the mechanical behavior of laboratory test.

Fig. 2
figure 2

The DEM sample: a the configuration, and b the grain size distribution curve

Full size image
Table 1 Input parameters in DEM simulations
Full size table

2.2 Sample generation and loading method

Firstly each assembly is prepared randomly distributed over the two-dimensional space, and then anisotropically consolidated under different sets of major principal stress \(\sigma^{\prime}_{1}\) and minor principal stress \(\sigma^{\prime}_{2}\) to achieve the desired initial static shear stress ratio α. The relationship among them could be expressed as:

$$\alpha = \frac{{\sigma_{1}^{\prime } - \sigma_{2}^{\prime } }}{{\sigma_{1}^{\prime } + \sigma_{2}^{\prime } }}$$
(1)

In order to eliminate the Kσ effect induced by the variation of confining pressures [17], the mean confining stresses after consolidation of all the samples are kept the same, that is, \(p^{\prime}_{0} = (\sigma^{\prime}_{1} + \sigma^{\prime}_{2} )/2 = 200{\text{ kPa}}\). Different coefficients of friction are only employed during consolidation to secure a desired sample while this value was set to 0.5 after consolidation. All samples have identical void ratio (i.e., e = 0.2254–0.2255) with a mean relative density Dr = 56% after consolidation.

Stress-controlled undrained cyclic tests are conducted on the DEM samples. A servo control scheme is adopted, in which the moving velocities of the boundary walls are adjusted in such a way that the volume of sample remains constant while the cyclic deviatoric stress follows a sinusoidal cyclic stress history as follows:

$$q(t) = q_{s} + q_{c} \sin (2\pi ft)$$
(2)

where f is the loading frequency; \(q_{s}\) is the initial static deviatoric stress, defined as \(q_{s} = (\sigma^{\prime}_{1} - \sigma^{\prime}_{2} )\); \(q_{c}\) is the amplitude of the cyclic deviatoric stress, defined as \(q_{c} { = }\sigma_{d} /2\). Here, \(\sigma_{d}\) refers to the amplitude of the vertical cyclic stress in triaxial tests, as shown in Fig. 2a. In view of the sensitivity of the cyclic behavior to the loading frequency in DEM simulation, a parametric study considering various loading frequencies (i.e., f = 0.5‒5000 Hz) reveals that when f is lower than 5 Hz, the rates of generation of excess pore water pressure and strain development stabilize, and the ratio between the maximum unbalanced force and the average contact force is smaller than 0.01 [14], which indicates that the pseudo-static state is satisfied. In addition, the loading frequency of 5 Hz also falls within the recommended frequency range of earthquake ground motions (i.e., 0.5‒5 Hz) [18]. Therefore, a cyclic loading frequency of 5 Hz is used in all DEM simulations in the present study.

2.3 Micromechanical quantities

The mechanical coordination number (MCN) proposed by Thornton [19] is adopted to examine the gross fabric changes during cyclic loading. It is calculated as an average number of inter-particle contacts for each particle, but excludes the particles with only one or zero contact which do not contribute to the stable state of stress. It could be expressed as:

$$MCN = \frac{{2N_{c} - N_{b1} }}{{N_{b} - N_{b0} - N_{b1} }}$$
(3)

where Nb and Nc are total number of particles and contacts, respectively; Nb1 and Nb0 are total number of particles with only one and zero contacts, respectively. In the two-dimensional space, the minimum MCN needed to support a stable load-bearing structure is 3 [20].

The fabric anisotropy could be determined by the fabric tensor, as introduced by Satake [21], which could be expressed as:

$$\phi_{ij} = \frac{1}{{N_{c} }}\sum\limits_{c = 1}^{{N_{c} }} {n_{i}^{c} } n_{j}^{c} { = }\int_{\theta } {f\left( \theta \right)n_{i}^{c} n_{j}^{c} d\theta } \,$$
(4)

where \(n_{i}^{c}\) is the cth unit contact normal vector; \(\phi_{ij}\) is a symmetric tensor with the first trace \(tr(\phi_{ij} ) = 1\); \(\theta\) is the angle between the direction of contact and the horizontal direction; \(f(\theta )\) is the angular distribution of the unit contact normal vector. In the two-dimensional space, it fulfills:

$$\int_{\theta } {f\left( \theta \right)d\theta } { = 1 }$$
(5)

Being expanded by using Fourier series and ignoring the high-order terms [22], \(f(\theta )\) could be written as:

$$f\left( \theta \right) = \frac{1}{2\pi }(1 + a_{ij} n_{i} n_{j} )$$
(6)

where aij is the deviatoric tensor and could be correlated to \(\phi_{ij}\) by:

$$a_{ij} = 4\left( {\phi_{ij} - \frac{1}{2}\delta_{ij} } \right)$$
(7)

where \(\delta_{ij}\) is the Kronecker delta function. The norm of aij is a measure of fabric anisotropy. A larger value of the norm stands for a higher anisotropic level. The norm of aij could be obtained as follows:

$$a = \sqrt {tr(a_{ij}^{2} )} = \frac{\sqrt 2 }{2}\left| {a_{1} - a_{2} } \right|$$
(8)

where a1 and a2 are the two principal components of aij with a1 =  − a2.

3 Calculation results and analyses

3.1 Cyclic behavior

Table 2 lists the details of the cyclic tests simulated with different combinations of cyclic stress ratio CSR and initial static shear stress ratio α. The CSR ranges from 0.125 to 0.200 and the minimum value of CSR is set to 0.125 to secure a time effective calculation. The value of α ranges from 0.150 to 0.225, which corresponds to an infinite slope with angle of 19°‒24° according to Fig. 1. For a given α, a series of CSR smaller than α will be applied to the sample to secure a small to moderate earthquake shaking condition without stress reversals. In order to better investigate the effect of initial static shear stress on the cyclic resistance of saturated dense sand, the test with α = 0 is also conducted as the reference without initial static shear stress.

Table 2 Undrained cyclic biaxial test program
Full size table

Figure 3 shows the undrained cyclic behaviors for tests of e2255_α0.15_c0.125, e2255_α0.225_c0.125 and e2255_α0.225_c0.2. The excess pore water pressure increases during the early stage of loading and then stabilizes at last (Fig. 3a). The terminal excess pore water pressure varies with the combinations of CSR and α. However, the terminal excess pore water pressure of these tests is much less than the initial effective confining pressure 200 kPa, which means that no “initial liquefaction” occurs in the conditions without stress reversal. As shown in Fig. 3b, the plastic axial strain accumulates continuously on the compression side and the accumulation rate essentially keeps constant, and this phenomenon was also found in cyclic triaxial test of saturated Toyoura sand by Yang and Sze [3]. It could also be found that the accumulation rate of plastic strain is dependent on the combination of CSR and α. The stress–strain curves also develop only on the compression side (Fig. 3c). The stress path gradually shifts to the left-hand side and stabilize at last (Fig. 3d). The slopes of hysteresis loops decrease gradually in the beginning and keep constant at the end. No “butterfly” shaped stress path is observed, which is a typical phenomenon in the tests with stress reversal [4, 23, 24]. Note that the stress paths of e2255_α0.15_c0.125 and e2255_α0.225_c0.2 stabilize along the same line eventually, which approaches the critical state line, while the stress path of e2255_α0.225_c0.125 stabilizes along a line different from that of the other two tests.

Fig. 3
figure 3

Undrained cyclic behaviors: a excess pore water pressure, b axial strain, c stress strain curve, and d effective stress path

Full size image

To explore this issue a bit further, the simulations of undrained biaxial tests with three different void ratios are performed. Figure 4 presents the undrained behaviors of these samples. When the axial strain εy > 25%, the deviatoric stress, excess pore water pressure and the mobilized stress ratio tend to stabilize within a narrow band, which suggests that the critical state is achieved. From Fig. 4a and c, we know that the critical state stress ratio M equals 0.8 for the generated DEM samples.

Fig. 4
figure 4

Undrained behaviors of samples with different void ratios: a effective stress path, b deviatoric stress, c stress ratio and d excess pore water pressure

Full size image

3.2 Residual excess pore water pressure

The excess pore water pressure (i.e., EPWP) under cyclic loading contains the transient and the residual parts, and the former reflects the change in total stresses acting on the soil while the latter alters the effective stresses [25]. During the stress-controlled cyclic tests, the residual pore water pressure is defined as the excess pore water pressure at the end of each loading cycle (Fig. 5). Residual pore water pressure is often normalized with respect to the initial mean effective stress, \(r_{u} = \Delta u/p^{\prime}_{0}\). The value of ru varies from 0 to 1. For isotropically consolidated sample, ru could reach 1 (i.e., the criterion of initial liquefaction). However, for the anisotropically consolidated sample under cyclic loading without stress reversal, ru usually stabilizes at a value less than 1 and typical liquefaction behavior could not be observed in this case.

Fig. 5
figure 5

The evolution of EPWP: a EPWP, b residual EPWP, and c transient EPWP

Full size image

Figure 6 shows the evolution of ru under different combinations of CSR and α. It could be seen that all ru stabilize eventually as the cyclic loading proceeds, and the terminal value of ru (i.e., ru_term) seems to be related to the combination of CSR and α. For a given α, the ru_term is positively correlated to the amplitude of CSR. It seems that there is a threshold value of CSR (i.e., CSRth), and when CSR > CSRth, ru_term will approach to the same value regardless of the amplitude of CSR. For example, for the case of α = 0.200 (Fig. 6(c)), ru stabilizes at 0.5 for both CSR = 0.175 and 0.150. However, ru stabilizes at 0.38 instead of 0.50 when CSR is reduced to 0.125. So it seems that there would be a CSRth around 0.150 for a DEM specimen with e = 0.2254, despite the initial static shear stress ratio. The upper bound of ru_term decreases from 0.60 to 0.45 as α increases from 0.150 to 0.225. It implies that ru_term is negatively correlated to α.

Fig. 6
figure 6

The evolution of \({r}_{u}\): a α = 0.150, b α = 0.175, c α = 0.200, and d α = 0.225

Full size image

Figure 7 presents ru_term under different combinations of CSR and α. It is interesting to find out that there is a negatively linear correlation between the upper bound of ru_term (i.e., ru_term,max) and α, which could be expressed as follows:

$$r_{u\_term,\max } = 1 - 2\alpha /M$$
(9)

where M is the critical state stress ratio, and M = 0.8 as mentioned in Sect. 3.1.

Fig. 7
figure 7

The \({r}_{u\_term}\) under different combinations of CSR and α

Full size image

Thus ru_term could be divided into two types according to the relative amplitude of CSR and CSRth. Type 1 with CSR ≥ CSRth: ru_term will approach to 1-2α/M as long as the loading continues; Type 2 with CSR < CSRth: ru_term is less than 1-2α/M regardless the loading cycles, and the larger CSR will result in higher ru_term. The difference between Types 1 and 2 in the stress path is shown in Fig. 8. For Type 1, the stress path stabilizes along the critical state line eventually while the stress path of Type 2 does not go to the critical state line. Similar phenomena were also observed in laboratory tests of saturated sands [2, 7, 26,27,28].

Fig. 8
figure 8

The different stress paths of: a type 1, and b type 2

Full size image

To explore whether the terminal value of ru will belong to Type 1 or Type 2 under different combinations of CSR and α, a parameter defining the degree of stress reversal, D = CSR/α, is introduced. And another parameter U is defined to normalize the term of ru_term, that is, U = ru_term/ru_term,max, which helps distinguishing Type 1 with U = 1 from Type 2 with U < 1. Then the minimum D value making U = 1 is regarded as the threshold degree of stress reversal (i.e., Dth). Figure 9 presents the relationship between D and U. The excess pore water pressure will not develop until D reaches Dmin = 0.42, which essentially corresponds to the minimum CSR required for build-up of excess pore water pressure. After that, U increases almost linearly with D, until it approaches to unity where D equals to 0.75. So, it indicates that Dth is about 0.75 for the DEM samples with e = 0.2255. It should be noted that Dth may vary slightly for different α, and more simulations are needed to identify the function of Dth with relative density and α. Based on the above findings, we know that the degree of stress reversal D is potentially a promising parameter to characterize the cyclic behavior of dense sand in slope. Depending on the ratio between D and Dth, one could readily tell that whether the residual pore water pressure will reach its up limit (i.e., U = 1) or not under a given cyclic loading.

Fig. 9
figure 9

The relationship between D and U

Full size image

3.3 Residual strain

Similar to the treatment of excess pore water pressure, the axial strain εa could also be decomposed into two parts: the reversible component εa,re and the irreversible component εa,ir. The relationship between εa, εa,re and εa,ir could be expressed as:

$$\varepsilon_{a} = \varepsilon_{a,re} + \varepsilon_{a,ir}$$
(10)

As shown in Fig. 10c, the reversible component εa,re fluctuates periodically in each loading cycle, which mainly reflects the non-linear elastic properties of the soil. The irreversible component εa,ir shown in Fig. 10b keeps increasing monotonically with the number of loading cycles, which reflects the plastic damage of the soil fabric.

Fig. 10
figure 10

The evolution of axial strain: a εa, b εa,ir, and c εa,re

Full size image

Figure 11 presents the evolution of residual axial strain εa,ir under different combinations of CSR and α. It could be seen that the strain almost grows at an constant rate with some fluctuations, and the growth rate of εa,ir is CSR- and α-dependent. For a given α, the growth rate of εa,ir increases with the increase of CSR. When CSR remains the same, the sample with larger α shares slower development of residual axial strain. This indicates that the dense sample with larger α has greater resistance to cyclic loading.

Fig. 11
figure 11

The evolution of residual axial strain εa,ir: a CSR = 0.200, b CSR = 0.175, c CSR = 0.150, and d CSR = 0.125

Full size image

In order to quantitatively compare the growth rate of εa,ir between samples with different combinations of CSR and α, the average strain rate \(\dot{\varepsilon }_{{a{\text{,ir}}}}\) is proposed, which is defined as the ratio between the residual axial strain and the number of cycles (i.e., \(\dot{\varepsilon }_{{a{\text{,ir}}}}\) = εa,ir/N). Figure 12 gathers the results of \(\dot{\varepsilon }_{{a{\text{,ir}}}}\) under different combinations of CSR and α, where \(\dot{\varepsilon }_{{a{\text{,ir}}}}\) is negatively correlated to α while positively correlated to CSR, and such phenomenon is consistent with the test results observed by other researchers as mentioned above. The relationship between \(\dot{\varepsilon }_{{a{\text{,ir}}}}\), α and CSR as shown in Fig. 12 could be formulated as follows:

$$\dot{\varepsilon }_{a,ir} = \dot{\varepsilon }_{ref} CSR^{c} \alpha^{d}$$
(11)

where \(\dot{\varepsilon }_{ref}\) is the reference strain rate, equals to 0.027; c and d are empirical parameters, and c = 3.89 and d =  − 3.06, respectively. Note that these values are back calculated from the DEM simulations with conditions listed in Table 2, and further study is needed when different relative densities and confining stresses are considered to describe the development of residual axial strain for saturated dense sand without stress reversals.

Fig. 12
figure 12

The strain rate \(\dot{\varepsilon }_{{a{\text{,ir}}}}\) under different combinations of CSR and α

Full size image

3.4 Cyclic resistance

The cyclic resistance of dense sand or sand containing fines is usually defined as the cyclic stress ratio at the point accompanied by 5% double-amplitude axial strain (εDA), as it could hardly reach the state of "initial liquefaction" with ru = 1.0 [29]. However, in the case of “residual deformation failure” of dense sand, the strain development occurs only in compression side, and 5% εDA may not happen or be difficult to define in this case (see Fig. 10). Yang and Sze [3] proposed that the occurrence of 5% peak axial strain (PS) in compression is regarded as a reasonable criterion in the case of “residual deformation accumulation” behavior. Nevertheless, Pan and Yang [4] argued that the strain development during “residual deformation accumulation” and “cyclic mobility” may be triggered by different mechanisms. And they proposed that, compared with the strain criterion, it is better to use the excess pore pressure criterion to define the cyclic resistance as the CSR at the loading cycle reaching the critical state (i.e., the soil deforms continuously with a constant stress state and void ratio). In this study, reaching a critical state could be equivalent to the stress path touching the critical state line or the ru_term reaching the upper bound. In order to better investigate the effect of initial static shear stress on the cyclic resistance, the test with α = 0 is also conducted. It should be noted that for the tests of α = 0, its undrained cyclic behavior belongs to “stress reversal” type regardless of its CSR value, so 5% εDA is taken as the criterion for liquefaction.

Figure 13 shows the cyclic resistance curves under the abovementioned two sets of criteria. For the pore pressure criterion, only the datasets that reach the critical state (CS) are plotted. It could be seen that similar trends are observed for both sets of curves that the cyclic resistance increases with increasing α, indicating that the presence of initial static shear is beneficial to the cyclic resistance for dense sand. However, the curves with the pore pressure criterion are above those with the strain criterion. This finding echoes the tests mentioned above [3,4,5,6,7]. However, the underlying mechanism is still unknown.

Fig. 13
figure 13

The number of cycles to failure with respect to CSR and α

Full size image

4 Micromechanical mechanism of α effect

In the following section, two micromechanical quantities, including the fabric anisotropy parameter (a) and the mechanical coordination number (MCN), will be introduced to explore the micromechanical mechanism of α effect on cyclic resistance of dense sand.

In the framework of cyclic triaxial tests, anisotropically consolidated method is used to study the initial static shear. The fabric anisotropy parameters (a) of these samples after anisotropically consolidation are plotted against the initial static shear stress ratio (α) in Fig. 14, where a increases from 0.073 to 0.124 as α increases from 0.150 to 0.225. In these samples, the fabric anisotropy evolves due to the concentration of inter-particle contacts along the compression direction. It indicates that the anisotropically consolidated method produces stress-induced initial fabric anisotropy in the samples, and the larger α leads to the higher degree of stress-induced fabric anisotropy. Figure 14 also shows that MCN of these samples decrease slightly from 3.441 to 3.411 with the increase of initial static shear stress ratio α. So it is reasonable to assume that the initial static shear has trivial influence on the density of the particle contacts within the sample.

Fig. 14
figure 14

The relationship between α, a and MCN

Full size image

To depict the change of microstructures of samples during cyclic loading with different initial static shear stress ratio α, the evolution of MCN under different CSR is presented in Fig. 15. The value of MCN decreases sharply in the first cycle regardless of the magnitudes of α, which accounts for about 50% of the reduction. It is interesting to find that the sample with larger α exhibits slower reduction in MCN. When MCN stabilizes, the sample with larger α will share larger residual value of MCN, despite the fact that the initial value of MCN is smaller. Note that all MCN are larger than 3, which means that all samples are stable.

Fig. 15
figure 15

The evolution of MCN under different CSR: a CSR = 0.200, b CSR = 0.175, c CSR = 0.150, and d CSR = 0.125

Full size image

Figure 16 shows the evolution of fabric anisotropy parameter a for different combinations of CSR and α. During cyclic loading, a increases gradually and becomes stable at last. A sudden increase of a is also observed in the first cycle, which corresponds to the sudden drop of MCN. From Fig. 16, we know that the sample with larger α has larger initial fabric anisotropy a. However, as the cyclic loading proceeds, the sample with larger α shares smaller a due to the slower development of fabric anisotropy.

Fig. 16
figure 16

The evolution of \(a\) under different CSR: a CSR = 0.200, b CSR = 0.175, c CSR = 0.150, and d CSR = 0.125

Full size image

Yimsiri and Soga [30] found that the sample becomes stiffer, stronger and more dilative when it is sheared in the major principal direction of fabric anisotropy. It is mainly because the contacts orient more along the shear direction, and then form a structure that could withstand greater forces. However, Wei and Wang [31] states that sample with larger fabric anisotropy may not always have greater cyclic resistance when MCN of the sample with larger α is significantly smaller than that of sample with smaller α. Based on the above knowledge, the combination of a and MCN should be considered when assessing the cyclic resistance from the micromechanical point of view. Before cyclic loading, the MCN values of samples with different α are basically the same while the sample with larger α shares higher degree of stress-induced fabric anisotropy due to anisotropic consolidation. At this time, the fabric anisotropy is the dominated factor affecting the cyclic resistance. Therefore, at the early stage of cyclic loading, the sample with larger α has greater cyclic resistance. This is also consistent with the observation that the sample with larger α exhibits slower reduction in MCN.

As the cyclic loading proceeds, the sample with larger α shares larger residual MCN because of the slower reduction rate in MCN. At this stage, MCN becomes the dominant factor. Taking the cases of α = 0.175 and α = 0.225 as examples, Fig. 17 shows the distribution of number of mechanical contacts when CSR = 0.150. After 20 cycles of cyclic loading, the number of mechanical contacts of both samples decrease significantly. The difference in number of mechanical contacts between N = 0 and N = 20 is 637 for the sample with α = 0.175 while the difference is 392 for that with α = 0.225. The reduction degree in number of mechanical contacts of sample with α = 0.175 is much greater than that of sample with α = 0.225. It should be noted that the reduction zone is mainly in the horizontal direction, and this is also the main reason for the increase of fabric anisotropy. Although the sample with smaller α shares larger a, this comes at the expense of losing more horizontal contacts. The strengthening effect due to the raising of degree of fabric anisotropy could not outweigh the weakening effect due to the lowering of contact density. The above analysis explains why MCN becomes the dominant factor at later loading stage. As a result, the sample with larger α still has greater cyclic resistance although it has lower degree of fabric anisotropy.

Fig. 17
figure 17

The distribution of MCN when N = 0 and N = 20: a α = 0.175, b α = 0.225

Full size image

5 Conclusions

A micromechanical study has been presented to investigate the undrained behavior of dense granular materials under cyclic loading conditions without stress reversals. Based on the DEM simulation results, the induced microstructure changes were further examined, including the mechanical coordination number and the fabric anisotropy. The findings shed light on the effect of initial static shear on cyclic resistance in microscopic point of view. The main findings of the study are summarized as follows:

  1. 1.

    The cyclic behavior of “residual deformation accumulation” was identified from the simulation results, which typical characteristics are: (1) the residual strain only develops on the compression side, and there is no sudden increase in strain because of the excess pore water pressure ratio is less than one; (2) the stress path shifts to the left first and stabilize at last while the stress–strain curve keeps developing.

  2. 2.

    The excess pore water pressure under different combinations of CSR and α will stabilize eventually as the cyclic loading proceeds. The terminal residual pore water pressure ratio could be divided into two types. The main difference between these two types is whether the terminal residual pore water pressure ratio touches the upper bound. In p-q stress space, this difference is expressed in terms of whether the stress path stabilizes along the critical state line. The degree of stress reversal is effective to distinguish between two types.

  3. 3.

    The accumulation rate of residual axial strain is both CSR- and α-dependent. For dense sand, the strain accumulation rate is negatively correlated to α while positively correlated to CSR, and the relationship between the strain accumulation rate, α and CSR could be expressed as a power function.

  4. 4.

    Anisotropically consolidated method produces stress-induced initial fabric anisotropy in the samples, and the sample with larger initial static shear ratio has higher degree of fabric anisotropy. However, the initial static shear stress has almost no influence on the density of particle contacts within the sample. The higher degree of fabric anisotropy at the early stage of cyclic loading and the larger contact density at the subsequent stage of cyclic loading are the main reasons why dense sand with larger α has higher cyclic resistance.

It is important to note that the present study only investigates the “no reversal” condition, which corresponds to the common field condition of a slope subjected to a relatively small earthquake ground motion. Compared with the large earthquake condition with stress reversal, the cyclic behavior and liquefaction resistance of dense sand will exhibit big difference and are worthy of further study.