Fabric evolution of granular soils under multidirectional cyclic loading

Abstract

Cyclic behavior of granular soils under multidirectional shaking is significantly different from that under unidirectional loading. In this study, a series of undrained simple shear simulations were conducted using a discrete-element method (DEM) under unidirectional and multidirectional loading conditions. Although the excess pore water pressure within a sample cannot reach the initial confining pressure, large shear strains of a similar amplitude still develop in samples under multidirectional loading. The simulation results further illustrate that granular soils have vastly different liquefaction resistance under different loading conditions. Evolution of soil fabric is also quantitatively studied in terms of inter-particle contacts and particle-void distribution. The same “stable state” of soil fabric will be reached under different multidirectional loading paths, which corresponds to that of a post-failure hardening state under unidirectional loading. The DEM study provides a new perspective in terms of microstructure evolution of granular soils under a variety of loading conditions.

1 Introduction

Although earthquake loading is multidirectional in nature, most of the laboratory or numerical tests have been performed under a unidirectional cyclic loading condition. Among a few early attempts on multidirectional loading tests, Seed et al. [20] conducted a series of shaking table tests on dry sands and reported that the settlement of sands under multidirectional shaking is greater than that under the shaking in one direction. Ishihara and Yamazaki [9] designed a bidirectional simple shear apparatus and studied the influence of different loading paths, e.g., oval shear stress paths and “alternating cycle” pattern, on the liquefaction resistance of sands. By using a bidirectional simple shear apparatus at UC Berkeley, Boulanger et al. [2] and Boulanger and Seed [1] investigated liquefaction behavior of modified Sacramento river sand under bidirectional monotonic and cyclic simple shear loading conditions. Subsequently, Kammerer et al. [10, 11] carried out a significant number of experimental tests to study the effect of oval and circular loading paths on sand with medium to high relative density and formed in a comprehensive testing database. In addition, Matsuda et al. [12] investigated dynamic behavior of Toyoura sand subjected to rotated oval path, while Sun and Biscontin [23] studied clean Hostun sands under circular paths. All these laboratory investigations reveal that the soil exhibits evidently different pore pressure accumulation, strain development and liquefaction resistance compared with that under unidirectional loading. On the other hand, several constitutive models, such as SANICLAY and SANISAND, have been developed for modeling multidirectional soil responses and validated against experimental data [17, 32].

The fabric of soils refers to the arrangement of particles, particle group and space distribution [13], which has a profound influence on the properties of sands such as peak strength, permeability and liquefaction resistance. Numerical simulation based on DEM provides a convenient and less costly way to directly observe the fabric [3, 4, 6, 14, 16, 18, 24], which has been extensively researched to develop advanced constitutive models [5, 15, 26]. Yet, most of the above micromechanical investigations are based on inter-particle contact force. Although the contact-based fabric tensor is a good indicator of load-bearing structure in response of the applied stress field, it is insufficient for charactering soil liquefaction because it is a state that soil loses nearly all contact points. To overcome this limitation, new void-based fabrics have been recently developed for fully liquefied soils that characterizes internal particle arrangement and void space within a granular packing [25, 27, 28]. Evolution of these fabrics is studied before and after liquefaction through a series of unidirectional cyclic simple shear tests using DEM [29,30,31]. However, characterization of fabric evolution of granular soils under multidirectional loading condition has not yet been available.

In this study, a comprehensive test series are carried out for granular packing subjected to unidirectional and multidirectional loading conditions using DEM simulation. Four different types of cyclic loading tests were performed, including the unidirectional, circular, elliptical and Fig. 8 shear loading conditions. Void-based and contact-based fabric measures are adopted to characterize change in internal particle arrangement and void space within the granular packing. Evolution of the fabric measures is studied in pre- and post-liquefaction stages, providing a quantitative evaluation of the effect of multidirectional loading conditions on soil liquefaction. It is demonstrated that soil samples are evolving toward the same fabric after sufficient loading cycles regardless of loading conditions. For some loading cases, zero mean effective stress cannot be achieved. Yet, large shear strains are still developed without reaching liquefaction. The microscale study aims at providing qualitative results and insights into the mechanism of cyclic soil behaviors under multidirectional loading paths, with an overarching goal to develop micromechanics-based model for engineering applications.

2 Undrained simple shear simulations under multidirectional loading

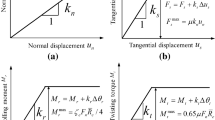
A comprehensive multidirectional test series are conducted using the open-source DEM code Yade [22]. Figure 1a shows a total of 10,000 spherical particles that are randomly generated within a cubic representative volume element (RVE). The simplified Hertz–Mindlin contact model is adopted to describe the inter-particle behavior in the loading and unloading process (Fig. 1b) [33]. The radius of particle ranges from 0.225 to 0.450 mm, and the particle density is 2650 kg/m³. All particles have Young’s modulus of 70 GPa and Poisson’s ratio of 0.3.

Fig. 1

Granular packing in the numerical simulation. a Particle packing of the RVE; b contact model; c stress state of granular packing after consolidation

The normal inter-particle contact force is given by

$$f_{n} = k_{n} \delta^{1.5}$$

(1)

where $k_{n} = \frac{2E}{{3\left( {1 - \nu^{2} } \right)}}\sqrt r$, and $r$ is the equivalent radius determined by the radii of two particles ($r_{A}$ and $r_{B}$) in contact: $r = \frac{{r_{A} r_{B} }}{{r_{A} + r_{B} }}$; $\delta$ is the overlapping of a pair of particles in contact. E and $\nu$ are Young’s modulus and Poisson’s ratio of particles, respectively.

The tangential inter-particle contact force is given by

$$df_{s} = k_{s} dU_{s}$$

(2)

where $k_{s} = \frac{2E\sqrt r }{{\left( {1 + \nu } \right)\left( { 2- \nu } \right)}}\sqrt \delta$, $U_{s}$ is the tangential displacement of the contact. In addition, the tangential force is restricted by a maximum allowable value $f_{s,\hbox{max} }$:

$$f_{s,\hbox{max} } = \mu f_{n}$$

(3)

where $\mu$ is the frictional coefficient of particle. When tangential force reaches the maximum allowable value, contact sliding occurs. During the cyclic loading after sample generation, frictional coefficient of all particles is set to be 0.5.

The granular packing is first isotropically consolidated to have an initial confining pressure p₀ of 100 kPa, followed by an undrained multidirectional simple shear test. In the simulation, the undrained condition is ensured by keeping the volume of the RVE constant. In the meanwhile, a periodic boundary condition is prescribed on the RVE to guarantee a uniform shear strain field.

To quantitatively describe multidirectional loading paths, the shear stress is decomposed into two independent components along orthogonal directions, denoted as $\tau_{zx}$ and $\tau_{zy}$, respectively:

$$\tau_{zx} = \tau_{1} \cos \left( {\omega_{1} t} \right)$$

(4)

$$\tau_{zy} = \tau_{2} \cos \left( {\omega_{2} t + \varphi } \right)$$

(5)

where $\omega_{1}$ and $\tau_{1}$ represent angular loading frequency and amplitude of cyclic shear stress along x direction, $\omega_{2}$ and $\tau_{2}$ denote angular loading frequency and the amplitude of cyclic shear stress along y direction, and $\varphi$ is the phase lag.

As demonstrated in Fig. 2, four different types of cyclic loading tests are performed: (1) the unidirectional loading path, where $\tau_{2}$ is equals zero; (2) the oval loading path, where $\omega_{1} = \omega_{2}$ and $\varphi = - \pi /2$; (3) the circular loading path is a special case of the oval loading where $\tau_{1} = \tau_{2}$; (4) the Figure-8 loading path, where $\omega_{2} = 2\omega_{1}$ and $\varphi = - \pi /2$. Considering variation of shear stresses along two directions, the effective stress tensor $\sigma^{\prime}_{ij}$ of the packing has the following expression:

$$\sigma^{\prime}_{ij} = \left[ {\begin{array}{*{20}c} {p^{\prime}} & 0 & {\tau_{xz} } \\ 0 & {p^{\prime}} & {\tau_{yz} } \\ {\tau_{zx} } & {\tau_{zy} } & {p^{\prime}} \\ \end{array} } \right]$$

(6)

Fig. 2

Plan view of different loading paths

Table 1 summarizes a total of six loading conditions in the test series. The cyclic stress ratio (CSR) is defined as the cyclic shear stress $\tau$ divided by the vertical consolidation stress $\sigma^{\prime}_{v,0} = p_{0} = 100\;{\text{kPa}}$ [7]. In the case of multidirectional loading, the cyclic shear stress ratio is defined as ${\text{CSR}}_{x} = \tau_{1} /\sigma^{\prime}_{v,0}$ and ${\text{CSR}}_{y} = \tau_{2} /\sigma^{\prime}_{v,0}$. The aspect ratio (AR) is defined as the ratio of CSRs along two orthogonal directions (AR = CSR_y/CSR_x) [10]. Specifically, an AR of 1 represents a circular loading path, an AR of 0 indicates a unidirectional loading, while intermediate values denote an oval loading. Throughout the study, we assume cyclic shear stress along x direction is greater than that along y direction (i.e., $\tau_{1} \ge \tau_{2}$), such that CSR_x is greater than CSR_y (i.e., AR is smaller than or equal to 1). We also specify $\tau_{1} { = 25}\,{\text{kPa}}$, CSR_x = 0.25, and $\tau_{2}$ ranges from 0 to 25 kPa.

Table 1 Summary of the loading paths in the numerical simulation

In this study, a servo-controlled approach is adopted to conduct multidirectional loading simulations in DEM while maintain a constant volume of the packing. First, the volume of the packing is kept constant during the cyclic shearing by restricting the normal strains in x/y/z directions to be zero. Displacement boundary conditions are employed to reinforce specified shear stresses on the sample using the following method:

• (1) Measure the current shear stresses ($\tau_{zx}^{\text{mea}}$,$\tau_{zy}^{\text{mea}}$) on the sample;

• (2) If the measured stresses differ from the specified stresses, calculate the stress difference in a vector form: ${\mathbf{\Delta \tau }} = \left( {\Delta \tau_{zx} ,\Delta \tau_{zy} } \right) = \left( {\tau_{zx}^{\text{spe}} - \tau_{zx}^{\text{mea}} ,\tau_{zy}^{\text{spe}} - \tau_{zy}^{\text{mea}} } \right);$

• (3) If the magnitude of the stress difference $\left| {{\mathbf{\Delta \tau }}} \right|$ is greater than a user-specified tolerance $\varepsilon$ (set as 0.3 kPa in the this study), the specimen deforms with a shear strain increment $\left( {\Delta \gamma_{zx} ,\Delta \gamma_{zy} } \right)$ proportional to $\left( {\Delta \tau_{zx} ,\Delta \tau_{zy} } \right)$, under a shear rate of $\dot{\gamma } = 0.01/{\text{s}}$.

Repeat (1)–(3) until the stress difference is less than $\varepsilon$. It should be noted that the servo-controlled approach is accurate under the assumption that the strain increment direction and the stress increment direction are coaxial. However, in the multidirectional shear tests, the strain increment direction may be different from the stress increment direction. Therefore, the specified shear stress needs to be iteratively approached using the servo-controlled approach.

Before the tests, the sample firstly is subjected to a monotonic simple shear test along x direction to reach $\tau_{zx} { = 25}\;{\text{kPa}}$. All the tests start from an initial shear stress state that $\tau_{zx} { = 25}\;{\text{kPa}}$ and $\tau_{zy} { = 0}\;{\text{kPa}}$. Figure 3a and b shows the simulation results of soil specimen subjected to unidirectional loading (i.e., AR = 0). Decrease in effective vertical stress can be observed with increase number of loading cycles, until “zero” effective stress is reached. After liquefaction, the stress path repeatedly forms a pattern of butterfly loops, while the shear strain continues to accumulate to a large strain level (up to 20%) under cyclic loading.

Fig. 3

Cyclic behaviors of the soil specimen during unidirectional loading

The “4-way” plot that comprises evolution of effective stress path, shear strain, shear stress and excess pore water pressure is used to present the macroscale mechanical responses of the soil specimen under multidirectional loading. As shown in Fig. 4, the upper left subplot is the effective stress path (shear stress $\tau = \sqrt {\tau_{zx}^{2} + \tau_{zy}^{2} }$) and bottom left one is the development of excess pore water pressure. It can be observed that as the cycle number increases, effective vertical stress gradually decreases with the increase in excess pore water pressure, and eventually approaches the critical state line (CSL). Two subplots at right-hand side demonstrate plan view of shear stress path and the corresponding shear strain, respectively. Shear strain magnitude increases during cyclic loading under all loading conditions. The simulation results are qualitatively similar to the laboratory tests by [11].

Fig. 4

“4-plot” to demonstrate the simulation results during multidirectional loading

In this study, “initial liquefaction” is defined as the state when single amplitude of shear strain reaches 3%, following criterion by [10, 11]. Accordingly, liquefaction resistance is defined as the number of loading cycles to reach the “initial liquefaction,” as shown in Fig. 5 under different loading conditions. For the oval/circular and unidirectional loading, cycle number decreases with an increase in AR. When AR = 1, the sample reaches “initial liquefaction” within a few loading cycles under Figure-8 loading compared with that under the circular loading path. The simulation results confirm the laboratory observation that sands are more prone to liquefaction if the cyclic shear stress is applied in the second direction. Ishihara and Yamazaki [9] found that CSR causing liquefaction under circular loading was 70% of CSR under unidirectional loading. Seed [19] and Ishihara [8] suggested that liquefaction resistance should be reduced by 10–15% under two-directional cyclic loading tests. In the following section, we will further examine evolution of soil fabric during multidirectional and unidirectional loading, and provide detailed discussion from micromechanical perspectives.

Fig. 5

Liquefaction resistance of granular packing under different loading paths

3 Fabric evolution during multidirectional loading

3.1 Contact-based fabric

Contact-based fabric of granular sample is quantified by statistical analysis of microscale information of the sample in terms of inter-particle contacts. In this study, we first consider the coordination number Z, which is defined as the ratio between twice of total number of inter-particle contacts to the total number of particles (Z = 2 N_c/N_p). The coordination number measures the average number of inter-particle contacts for each particle in the granular packing. Figure 6 shows evolution of the coordination number Z under circular, oval, unidirectional and Figure-8 loading paths.

Fig. 6

Evolution of coordination number Z during different loading paths

Figure 6a shows, under continuous circular loading, effective vertical stress $\sigma^{\prime}_{v}$ reduces from 100 kPa to around 60 kPa, while the coordination number drops from 4.8 to 3.8 within around 13 cycles. Although the packing maintains considerable inter-particle contacts, the stress state approaches the critical state line, and the sample develops large deformation upon failure. It is interesting to notice that Z gradually approaches to a same value of 3.8 (highlighted by a shaded line) for both of circular and oval loading cases. On the other hand, Z could temporarily decrease to zero after initial liquefaction under the unidirectional and Figure-8 loading paths, indicating that load-bearing structure is completely destroyed by losing most of inter-particle contacts in these two cases. With continued shearing, inter-particle contacts will be re-established and form an anisotropic load-bearing structure [25]. Consequently, effective stress $\sigma^{\prime}_{v}$ peaks up again and coordination number increases from zero to the same value of 3.8 as illustrated by the shaded line in Fig. 6.

Another contact-based fabric measure is a second-order tensor constructed by assembling all inter-particle contact normals,

$$\phi_{ij} = \frac{1}{{N_{\text{c}} }}\sum\limits_{k = 1}^{{N_{\text{c}} }} {n_{i}^{\left( k \right)} } n_{j}^{\left( k \right)}$$

(7)

where n denotes the unit vector along the normal direction of inter-particle contact and $N_{\text{c}}$ is the total number of inter-particle contacts. The coordination number and the contact-based fabric tensor are both constructed from the microscale information in terms of inter-particle contacts. Consequently, they can be used to quantify the load-bearing structure of granular packing. The directional distribution of the contact-based fabric tensor $\phi_{ij}$ can be further determined using the following equations [3, 18, 21]:

$$E\left( \varTheta \right) = \frac{1}{4\pi }\left[ {1 + a_{ij} n_{i} n_{j} } \right]$$

(8)

$$a_{ij} = \frac{15}{2}\left( {\phi_{ij} - \frac{1}{3}\delta_{ij} } \right)$$

(9)

where $E\left( \varTheta \right)$ is the directional distribution function of contact normal. If $E\left( \varTheta \right) = 1/4\pi$, it indicates an isotropic fabric; $\delta_{ij}$ is Kronecker delta, and $a_{ij}$ is a second-order tensor that characterizes the fabric anisotropy. If $a_{ij} > 0$, it indicates that the density of contact in the packing is higher than that of an isotropic fabric [21].

In the DEM simulation, the contact-based fabric tensor of the granular packing after consolidation is

$$\phi_{ij,0} = \left[ {\begin{array}{*{20}c} {0.332} & { - \,0.003} & { - \,0.01} \\ { - \,0.003} & {0.334} & {0.001} \\ { - \,0.01} & {0.001} & {0.334} \\ \end{array} } \right]$$

(10)

It can be seen that the contact-based fabric after consolidation is almost isotropic, i.e., the diagonal components $\phi_{xx}$, $\phi_{yy}$ and $\phi_{zz}$ are close to 0.33 and the off-diagonal components ($\phi_{xy}$, $\phi_{xz}$ and $\phi_{yz}$) are close to zero. It is because the isotropic consolidation process and the spherical particles are adopted in this study; therefore, inherent anisotropy in the granular packing can be avoided.

Figure 7 shows the evolution of $\phi_{ij}$ of the sample during circular loading test. The diagonal components $\phi_{xx}$, $\phi_{yy}$ and $\phi_{zz}$ are close to 0.33. In the off-diagonal components, amplitude of $\phi_{zx}$ and $\phi_{zy}$ gradually increases from the initial value of zero to 0.06 after 15 loading cycles. Variation of $\phi_{xy}$ is negligible compared with $\phi_{zx}$ and $\phi_{zy}$, because the shear stress in the test is applied on the x–y plane. Therefore, the contact-based fabric tensor $\phi_{ij}$ during cyclic loading can be approximated as:

$$\phi_{ij} { = }\left[ {\begin{array}{*{20}c} {1/3} & 0 & {\phi_{xz} } \\ 0 & {1/3} & {\phi_{yz} } \\ {\phi_{zx} } & {\phi_{zy} } & {1/3} \\ \end{array} } \right]$$

(11)

in which only two independent variables need to be considered. Using the deviatoric invariants, the anisotropy degree of $\phi_{ij}$ can be quantified:

$$a = \sqrt {\frac{ 3}{ 2}a_{ij} a_{ij} }$$

(12)

where $a_{ij} = 7.5\left( {\phi_{ij} - \frac{1}{3}\delta_{ij} } \right)$, such that:

$$a = 7. 5\sqrt 3\sqrt {\left( {\phi_{zx}^{2} + \phi_{zy}^{2} } \right)}$$

(13)

Fig. 7

Contact-based fabric tensor $\phi_{ij}$ versus cycle number during circular loading test

Figure 8 shows the contact-based fabric component $\phi_{zx}$ versus $\phi_{zy}$ in the circular and oval loading tests (AR = 1.0, 0.8, 0.6, 0.4). With the increase in cycle numbers, the fabric trajectory under the circular loading path starts from a small circle and gradually expands to a big circle (Fig. 8a). For other three oval loading cases, fabric trajectory starts from an oval and gradually expands to a big circle centered in the origin with the increase in the cycle number. It is interesting to note that the fabric trajectory of the big circles is of a similar size (the maximum radius $\sqrt {\phi_{zx}^{2} { + }\phi_{zy}^{2} }$ is around 0.06 in Fig. 8 highlighted by red) regardless of the loading conditions. It also indicates that different loading paths would not influence the ultimate state of the contact-based fabric, as the radial distance of the fabric trajectory is equal to the anisotropy degree of fabric tensor (refer to Eq. 10).

Fig. 8

Fabric trajectory of circular and oval loading paths

The influence of different stress paths to the fabric trajectory of the first loading cycle is demonstrated in Fig. 9. In the first loading cycle, the shape of fabric trajectory is similar to that of the corresponding shear stress path. The expansion of fabric trajectory means that the anisotropy degree of fabric tensor is increasing and fabric re-organization becomes more extensive after the sample reaches “initial liquefaction.”

Fig. 9

a Fabric trajectories of the first loading cycle; b oval/circular loading paths

In the multidirectional loading test, the stress direction rotates with continuous shearing. In order to check the coaxiality between the contact-based fabric and stress during the rotation of stress direction, we compare the major principal direction of fabric tensor in Eq. (11) and effective stress tensor in Eq. (6). In a Cartesian 3D coordination system, the major principal direction can be expressed as follows:

$${\mathbf{n}} = \left( {\sin \alpha \cos \beta ,\sin \alpha \sin \beta ,\cos \alpha } \right)$$

(14)

where $\alpha$ is the angle between the major principal direction ${\mathbf{n}}$ and the vertical direction (z axis). $\beta$ is the angel between x axis and the projection vector of ${\mathbf{n}}$ in the horizontal plane (i.e., xy plane), as shown in Fig. 10. By using the eigenvalue analysis, the major principal direction of effective stress tensor in Eq. (6) and fabric tensor in Eq. (11) can be obtained:

$$\alpha_{\sigma } = \alpha_{\phi } = 45^\circ$$

(15)

$$\tan \beta_{\sigma } = \frac{{\tau_{zy} }}{{\tau_{zx} }}$$

(16.1)

$$\tan \beta_{\phi } = \frac{{\phi_{zy} }}{{\phi_{zx} }}$$

(16.2)

Fig. 10

Major principal direction of effective stress tensor (* indicates $\sigma$) and contact-based fabric tensor (* indicates $\phi$)

Therefore, the major principal direction of effective stress tensor and fabric tensors can be simply represented by $\beta_{\sigma }$ and $\beta_{\phi }$, respectively.

Figure 11 demonstrates the evolution of major principal direction $\beta$ for both effective stress tensor and contact-based fabric tensor during the circular and oval loading tests. The two lines for $\beta_{\sigma }$ and $\beta_{\phi }$ in the figure are almost coincident with each other. It indicates that the stress and contact-based fabric tensors are still coaxial during the stress rotation.

Fig. 11

Major principal direction of the effective stress tensor and contact-based fabric tensor in a circular loading test; b oval loading test with AR = 0.6

3.2 Particle-void fabric

As is discussed before, the contact-based fabric measures describe the load-bearing structure in response to the applied stress field. To further quantify evolution of particle arrangement and particle-void distribution, a particle-void indicator, namely centroid distance (D_c) [25], is adopted to study the cases of multidirectional loading. As shown in Fig. 12a, the Voronoi tessellation can be effectively used to partition the void space around a particle. The vector between centroids of the particle and the Voronoi cell is written as: (refer to Fig. 12b):

$$\varvec{D}_{c}^{(i)} = \frac{{\varvec{P}^{i} - \varvec{O}^{i} }}{{R_{50} }}$$

(17)

in which $R_{50}$ is the mean radii of particles, $\varvec{O}^{i}$ and $\varvec{P}^{i}$ are the mass center of the Voronoi cell and the mass center of the particle, respectively. It should be noted that in 2D case, Voronoi cell is polygon while in 3D case, Voronoi cell is polyhedron. $D_{c}^{(i)}$ is defined to reflect the distribution of the void space surrounding the particles, since particles surrounded by relatively large pores usually have a large value of $D_{c}^{(i)}$. Centroid distance (D_c) associated with the granular packing is further defined as follows:

$$D_{c} = \frac{1}{{N_{\text{p}} }}\sum\limits_{i = 1}^{{N_{\text{p}} }} {\left\| {\varvec{D}_{c}^{(i)} } \right\|}$$

(18)

Fig. 12

Schematic illustration of the centroid distance [25]

While the detailed discussion of D_c is given in [25], it is worth mentioning that evolution of D_c indicates adjustment of the packing structure as well as redistribution of relatively large pores. Due to friction between granular particles or complex particle shape, local arching can be formed during the initial consolidation, which preserves the large pores. Before “initial liquefaction,” the granular packing contains relatively large pores which can be regarded as source of inhomogeneity. However, the arching structure is not cyclically stable and can be destroyed by the cyclic loading. After “initial liquefaction,” large pores diminish and D_c of the packing also decreases.

Figure 13 demonstrates evolution of D_c with the number of loading cycles under different multidirectional loading paths. Note that D_c is computed for a 3D setting. It can be observed that loading patterns significantly influence the number of loading cycles to reach “initial liquefaction.” For the sample under unidirectional loading, 200 loading cycles are required. When sample is loaded under the oval (AR = 0.6), circular (AR = 1.0) and Figure-8 (AR = 0.6) paths, the number of loading cycles to “liquefaction” notably decreases to 46, 13 and 25, respectively. Intuitively, by adding cyclic shearing in the second direction, multidirectional loading causes more disturbance to the particle-void structure per loading cycle and thus needs fewer loading cycles to reach “initial liquefaction” compared with the unidirectional case. Further, it is interesting to cross-examine evolution of particle-void structure in Fig. 13. For circular and oval loading, D_c reduces from an initial value of 0.0595–0.055 (7.5% reduction) at the post-failure state as shown in Fig. 13a and b. On the other hand, for unidirectional loading, D_c decreases from 0.0595 to a minimum value of 0.05 (16% reduction) at the fully liquefied state and then alternatively changes between 0.05 and 0.055 at post-liquefaction state. The variation will remain to be steady upon further unidirectional cyclic loading. For the “Figure-8” loading case, evolution of D_c is similar to that in unidirectional loading, as shown in Fig. 13d. However, in post-liquefaction stage, D_c decreases to 0.053 (11% reduction) and peaks up to 0.055, which is the same as the stabilized value in oval/circular loading. The observation is important as it implies the same particle-void fabric in the post-failure state of circular/oval loading regardless of AR, and interestingly, the same D_c value is achieved in the post-liquefaction hardening state of unidirectional loading shown in Fig. 13c. Note that for all cases, the change in D_c becomes mostly pronounced when the sample is close to and after “initial liquefaction.”

Fig. 13

Evolution of D_c during unidirectional and multidirectional loading tests

Figure 14 shows stabilized D_c evolution patterns in post-liquefaction under oval/circular and unidirectional loading. For unidirectional loading, D_c decreases from 0.055 to 0.05 upon unloading and increases to 0.055 again upon reloading. D_c drops to 0.05 when effective stress is zero. It means that the large size pores are redistributed into small size pores when load-bearing structure is completely destroyed. D_c peaks up at 0.055 when effective vertical stress $\sigma^{\prime}_{v}$ is over 50 kPa. It means that some large size pores are reorganized when the load-bearing structure is fully established. For the oval/circular loading conditions, effective stress $\sigma^{\prime}_{v}$ is always greater than zero and load-bearing structure exists even after “initial liquefaction.” As a consequence, D_c is stabilized around 0.055 which is the same with the peak value of D_c for unidirectional loading.

Fig. 14

Evolution of D_c and $\sigma^{\prime}_{v}$ during a post-liquefaction loading cycle

4 Conclusions

In summary, multidirectional loading behaviors of granular soils were explored using DEM simulations. Compared with unidirectional loading conditions, granular packing is more susceptible to liquefaction under multidirectional loading conditions. The cycle number inducing initial liquefaction (i.e., 3% of shear strain amplitude) decreases with the increase in AR for oval/circular loading conditions. In the unidirectional loading conditions, the maximum excess pore water pressure increases to the initial confining pressure when initial liquefaction occurs. However, for the oval/circular loading condition, the excess pore water pressure is always smaller than the initial confining pressure. It is due to the existence of load-bearing structure even after large deformation.

Evolution of fabric in terms of inter-particle contacts and particle-void distribution during multidirectional loading tests is quantitatively studied. In the unidirectional loading and Figure-8 loading tests, coordination number will decrease to a very small value that is close to zero. It indicates collapse of the load-bearing structure. For oval and circular loading tests in which granular packing will not experience collapse of load-bearing structure, the coordination number decreases from an initial value of 4.8 to a stabilized value of 3.8. Evolution of fabric trajectory ($\phi_{zx}$ and $\phi_{zy}$) starts from a small circle or a small oval, which is similar to the shape of shear stress path. With the increase in cycle number, fabric trajectory gradually expands and finally gets stabilized to form a big circle of a similar size. The ultimate contact-based fabric of the granular packing is almost identical for all oval and circular loading tests.

Centroid distance D_c, indicating the particle-void fabric, shows a decrease in both unidirectional and multidirectional loading tests and the reduction mainly happens after initial liquefaction. It indicates the redistribution of relative large pores during all loading conditions. In the tests when the load-bearing structure of the packing is fully destroyed (e.g., unidirectional and Figure-8 loading tests), D_c will decrease to a smaller value compared with the tests in which the packing will not experience the collapse of load-bearing structure (e.g., circular and oval loading tests). In the unidirectional loading test, the load-bearing structure of a packing collapses upon unloading and re-generates upon loading. When the load-bearing structure is fully established, D_c increases to a same value as in oval/circular loading tests, implying that they have similar microstructures. The DEM study provides a new perspective in terms of fabric evolution in granular soils under a variety of loading conditions.