1 Introduction

Granular materials, e.g., sand, gravels, and rockfill materials, are often used in the construction of large civil engineering structures, such as railways, pilings, embankments and dams. Shear band or strain localization is commonly observed when granular materials are subjected to conventional triaxial compression. This phenomenon is significant for assessing the stability of civil engineering structures. Shear band formation and evolution are examined using true triaxial tests [1, 2], ring shear tests [3], plane strain extension [4], and static and cyclic torsional shear tests [5, 6]. Advanced experimental techniques, such as X-ray computed tomography stereophotogrammetry and particle image velocimetry, are also used to investigate the micro-scale information associated with strain localization [7,8,9,10,11]. These experimental works have revealed that shear band formation is influenced by several factors, including porosity, inherent and stress-induced anisotropy, particle size and shape of the material, and the level of confining stress.

In parallel with the experimental studies, another major contribution to this field comes from discrete element modeling, which provides richer information and deeper insight into the microscopic behavior of granular materials that is not obtained by conventional experiments [12,13,14,15,16,17,18]. The overall response of granular materials has been recognized as the result of various micromechanical processes, namely particle sliding, particle rolling, and particle breakage. Particle breakage was not considered in previously published DEM investigations of shear bands [12,13,14,15,16,17,18]. Additionally, particle shape is generally modeled by bonded discs or spheres [19,20,21] or by employing the rolling resistance model to provide the mechanism of particle anti-rotation [13, 17, 22, 23].

To contribute toward the understanding of shear band formation and its associated microstructural evolution, discrete element modeling of irregularly shaped, crushable particle assembly is presented. The role of particle crushability in the shear banding of granular materials is explored. In depth analyses of the particle scale information inside and outside the shear bands are presented, including the accumulated particle rotation, void ratio distribution, particle breakage behavior, friction mobilization, and force chains. Attempts are made to link shear banding to microstructural evolution.

2 DEM modeling particle shape and particle breakage

2.1 Particle shape

Alonso-Marroquin [24] used Minkowski sum of a polygon with a sphere to generate complex shapes, including non-convex bodies. Wang et al. [25] utilized X-ray tomography imaging to obtain three-dimensional data set of grains and reproduced real particles for DEM simulation. Indraratna et al. [26] imported different elevations of a selected ballast into AutoCAD and converted the group of circles representing a single ballast into a “Block”. Using their subroutines a real ballast was generated in the DEM simulation. Yan et al. [27] created an arbitrary convex polyhedron whose surfaces were extracted as the ballast particle surfaces. Then spheres were filled into the space enclosed by these surfaces with a hexagonal close packing to generate an irregularly shaped ballast. However it is an extremely time-consuming work to prepare the numerical sample by the above method, which need obtain the particle shape information of numerous grains. A time-saving method was proposed by Zhou et al. [28]. They generated convex polyhedral particles from scalene ellipsoids to reflect the complex geometric features of rockfill grains. In this paper, the convex or concave polyhedral particles are generated from circles (see Fig. 1). To ensure that the shapes of the granules are sufficiently random, the vertices of the particles are uniformly distributed over the interval [\(n_{\min }, n_{\max } \)] as follows:

$$\begin{aligned} n=n_{\min } +(n_{\max } -n_{\min } )rand \end{aligned}$$
(1)

where rand is a uniformly distributed random number in the interval [0, 1].

Fig. 1
figure 1

Irregular polyhedral particle

Full size image

The polar coordinate is used to determine the position of each vertex of the polygon as follows:

$$\begin{aligned} \theta _k =2\pi [1+(2rand-1)\delta ]/n \end{aligned}$$
(2)

where \(\theta _k \) is the angle corresponding to the kth edge, and the absolute value of the constant \(\delta \) is less than 1. Because the sum of \(\theta _k \) is not equal to \(2\pi \), \(\theta _k \) should be modified so that the polygons are closed.

$$\begin{aligned} \overline{\theta _k } =\theta _k \left( 2\pi \big /\sum _{j=1}^n {\theta _j } \right) \end{aligned}$$
(3)

The position of the polygon vertex is calculated as:

$$\begin{aligned} \left\{ {\begin{array}{l} x_k =x_0 +r(1+\lambda grand)\cos (\theta _k ^{{\prime }}) \\ y_k =y_0 +r(1+\lambda grand)\sin (\theta _k ^{{\prime }}) \\ \theta _k ^{{\prime }}=\sum \limits _{i=1}^k {\overline{\theta _i } } \\ \end{array}} \right. \end{aligned}$$
(4)

where \(x_0 \), \(y_0 \) are the central coordinates of the circumcircle of polygons. grand is a random number drawn from a normal distribution, with a mean of 0 and a standard deviation of 1.0. The absolute value of the constant \(\lambda \) is less than 1. If \(\lambda \) is equal to 0, a convex polygon is obtained. Otherwise, a concave polygon will be generated.

Fig. 2
figure 2

Particles with different numbers of vertices: a finite element meshes and b DEM clumps

Full size image

There are two ways to generate irregularly shaped grains in DEM modeling: (a) the ‘clump’ composed by overlapping particles is used to model the particle shape [19,20,21, 29,30,31,32], and (b) a hexagonal close packing agglomerate without initial overlap is generated within the surface of the irregularly shaped grain [33,34,35,36]. Representing grains generated by the latter method are composed of bonded disks or spheres, which each bond can be envisioned as a kind of glue joining the two disks or spheres and transmit a force or a moment. In this paper, a novel generation method of irregularly shaped particles is proposed. The random polygons are generated via Eq. (4) and discretized into the finite element mesh. This step is easily realized and the grid size of polygons can be well controlled in the FEM software ANSYS. The information of the polygon including the area and centroid coordinate of every internal grid are obtained by the APDL (ANSYS Parametric Design Language). Finally, each finite element is replaced by a disc with the same area and centroid coordinate and the clump is created by grouping the discs within the same surface of the irregularly shaped grain (see Fig. 2). The clumps consist of rigid bodies of overlapping disks but internal contacts are ignored in the Itasca software (\(\hbox {PFC}^{\mathrm{2D}}\)). The motion of a clump is determined by the resultant force and moment vectors acting upon it. Its motion can be described in terms of the translational motion of a point in the clump and the rotational motion of the entire clump. The numerical problems encountered in the papers of Bagi and Kuhn [37] do not appear here.

2.2 Particle breakage criteria

In the two-dimensional DEM, the stress tensor at an area \(A^{p}\) of a particle is generally defined as [38]:

$$\begin{aligned} \sigma _{ij} =\frac{1}{A^{p}}\sum _{c\subset N_c } {f_j^c } d_i^c \end{aligned}$$
(5)

where \(N_c \) is the total number of contacts, \(f_j^c \) is the contact force, \(d_i^c \) is the branch vector joining the centers of two contacting particles, and \(\sigma _{ij} \) is the stress tensor acting throughout the area. If the particle has more contact points with its neighbors, the induced stress will be lower due to the even distribution of stresses [39].

The stress concentration induced by a large compressive force at the particle contact is the origin of fracture initiation and propagation, which causes surface erosion or bulk fracture [40, 41]. Lobo-Guerrero and Vallejo [42] split a particle with coordination numbers that were less than or equal to 3 if the induced tensile stress exceeded the strength threshold, which is similar to the Brazilian test. Tsoungui et al. [40] deduced that the fracture of a grain that is subject to an arbitrary set of forces may occur when the shearing stress exceeds the critical stress. de Bono and McDowell [20] assumed a particle would break when the octahedral shear stress was greater than or equal to its strength. To capture both the shear fracture modes of the rock aggregate, the Mohr–Coulomb model is used as the particle breakage criteria. The grain is assumed to split along the direction of the largest contact force acting upon it when the stresses calculated by Eqs. (5) and (6) fulfill the fracture criteria, and the generated fragments are treated as new independent grains (see Fig. 3). The breakage mechanism is equivalent to the grain fracture under diametric compression. Fragment spawning is repeated if the fragment stresses satisfy the fracture criteria:

$$\begin{aligned} \left\{ {\begin{array}{l} \tau =\frac{\sigma _{\max } -\sigma _{\min } }{2}\le \tau _f \\ \sigma _{\max ,\min =} \frac{\sigma _{xx} +\sigma _{yy} }{2}\pm \sqrt{\left( \frac{\sigma _{xx} +\sigma _{yy} }{2}\right) ^{2}+\sigma _{xy} \sigma _{yx} } \\ \end{array}} \right. \end{aligned}$$
(6)

where \(\tau _f \) is the shear strength of the particle, which satisfies the Weibull distribution.

Fig. 3
figure 3

Contact forces acting on the grain and the produced fragments after failure

Full size image
Fig. 4
figure 4

Specimen in the DEM simulation and forces applied on flexible boundary. a DEM sample after isotropic compressed and b forces applied on membrane balls

Full size image

In assuming that the shear strength of a particle of size \(d_0 \) is \(\tau _f^0 \), the size effect described by a power function [39] is applied to the particle of size \(d_a \), which leads to:

$$\begin{aligned} \tau _f^a =\tau _f^0 \left( {\frac{d_0 }{d_a }} \right) ^{k} \end{aligned}$$
(7)

where k is the hardening parameter. \(\tau _f^a \) is the characteristic shear strength and a value of the Weibull distribution, such that 37% of random strengths are larger.

3 Numerical sample and input parameters

Table 1 Summary of DEM modeling parameters
Full size table
Fig. 5
figure 5

Stress–dilation–strain behavior of assemblies with different crushability: a deviatoric stress and b volumetric response

Full size image

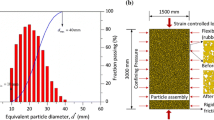
Biaxial tests are performed on a polydisperse assembly of 2918 polygonal particles by a commercial DEM code (Itasca \(\hbox {PFC}^{\mathrm{2D}}\)). Each particle is represented by a clump of balls. The 2918 clumps consist of 44,074 balls, and the vertices of the particles range from 5 to 9 with \(\lambda \) equal to 0. The equivalent particle diameter, \(d^{*}\), ranges from 9 to 21 mm, which gives a mean grain diameter \(d_{50}^*\) of 16 mm, where \(d^{*}\) is defined as the diameter of a circle with an area equal to the irregularly shaped particle. The floppy boundary was realized by connecting the grains on the sides of the packing by line segments in the simulations of Astrom and Herrmann [43] and Alonso-Marroquin and Herrmann [44, 45]. The “side grains” consisted of all the grains on a side of the packing that can be connected by a chain of line segments whose angles to the vertical never exceed some predefined maximum angle. The external pressure was installed by applying the force on the side grains. Gu et al. [19], Jiang et al. [22] and Wang et al. [46] generated frictionless particles in the lateral boundaries of sample. These particles were bonded and could rotate freely at the contact without breakage to simulating the flexible boundary. The membranes of Bono and McDowell [47] and Iwashita and Oda [23] are adopted in this paper. Initially, the polygonal particles are randomly generated in a rectangle of \(600\hbox { mm}\times 1200\hbox { mm}\) with stiff walls. The sample is isotropic compressed until the desired confining pressure is reached. Then the side particle with 1/3 diameter of the smallest sample particle are generated along lateral walls [47]. Two end particles in the linked particles are fixed on the top and bottom boundaries in the vertical direction, but are completely free in the horizontal direction [23]. The contact bond model is installed between the side particles and high strength is assigned, which makes the flexible boundary only transmit a force without break. After the lateral walls deleted, the sample is isotropic compressed again to obtain the desired confining pressure (see Fig. 4a). Finally, the sample is subjected to shearing deformation by applying a constant velocity of 50 mm/s to the top and bottom walls of the sample while maintaining a constant confining stress [38]. Note that the constant stresses on the lateral boundaries are obtained by applying forces to the center of the membrane balls (see Fig. 4b), and the forces are updated step-by-step [19]. The force on the flexible boundary particle can be calculated via Eq. (8). A modified linear contact model is used, and the normal contact stiffness of the particle \(k_n \) varies according to \(k_n =k_0 r\), where \(k_0 =10^{5}\) \(\hbox {KN/m}^{2}\) and r is the radius of the particle [19]. The Weibull distribution and the size-dependent law of particle strengths are based on the sandstone block crushing tests [39]. The input parameters in DEM simulations are listed in Table 1.

$$\begin{aligned} \left\{ {\begin{array}{l} f_x =(r\cos \theta +r\cos \beta )\sigma _3 \\ f_y =(r\sin \theta +r\sin \beta )\sigma _3 \\ \end{array}} \right. \end{aligned}$$
(8)

4 Numerical simulation results

4.1 Effect of crushability on the mechanical behavior of granular materials

Four different biaxial tests under a confining pressure of 1.0 MPa are conducted with different particle strengths to investigate the effect of crushability on the mechanical behaviors of granular materials. The results comprise one simulation with unbreakable particles and three simulations with breakable particles, which possess different characteristic shear strengths \(\tau _f^0 \) of 2.0, 2.5, and 3.0 MPa with \(d_0 =16 \,\hbox {mm}\). Figure 5 shows the macroscopic responses of the numerical biaxial tests in terms of the deviator stress and volumetric strain versus axial strain. The results show that the simulated stress–strain–dilation responses are typical of those observed in laboratory tests. The macroscopic responses of assemblies with lower particle crushability are marked by notable post-peak strain softening and less contraction. By increasing the particle crushability, the strain softening becomes milder and completely disappears in \(\tau _f =2.0\hbox { MPa}\). This behavior is clearly a result of excessive particle breakage, which has an opposing effect on the dilative mechanism and suppresses the mobilization of the assembly dilation [46]. Other 10 samples for each strength are prepared by changing the initial random number of the survival probability of grains. Results with different crushability are presented in Fig. 6. The crosses are the average values. The top and bottom bars represent ± one standard deviation. The results show that the peak deviatoric stress is related to the crushability. The samples with \(\tau _f^0 =2.0\), 2.5 and 3.0 MPa have mean peak deviatoric stresses of 2.49, 3.07 and 3.28 MPa, respectively. Their standard deviations are 0.125, 0.137 and 0.061.

Figure 7 shows the evolution of the accumulated fraction of broken fragments during loading with a characteristic shear strength of 2.5 MPa. Each dark cyan bar is the total number of broken particles that occur in every 0.5% of axial strain. The particle breakage process is synchronized with the development of macroscopic stress. Particle crushing continually occurs during loading. This observation is consistent with previous experimental results [48].

Turcotte [49] found that the fragment size distributions for a wide range of crushed materials satisfy a fractal condition and that the fractal dimension D is approximately 2.5 for materials subjected to pure crushing. A fractal defines a simple power law relation between finer mass and size, which can quantify the variation of particle size distribution after particle breakage [50]. Figure 8 shows the particle size distributions (PSDs) and fractal dimension D for all simulations at 20% axial strain. Figure 9 presents fractal dimension of numerical simulations. The mean fractal dimensions are 2.645, 2.697 and 2.715, and their standard deviations are 0.009, 0.015 and 0.013. As illustrated in Fig. 9, the variation of fractal dimension is related to the particle breakage. As the particle shear strength ranges from 2.0 to 3.0 MPa, the final PSDs yields fractal dimensions between 2.645 and 2.715, while the initial fractal dimension equals to 2.903.

Fig. 6
figure 6

Peak deviatoric stress of numerical simulations

Full size image
Fig. 7
figure 7

Evolution of broken particles with axial strain

Full size image
Fig. 8
figure 8

Particle size distributions at the end of shearing for assemblies with different crushability

Full size image
Fig. 9
figure 9

Fractal dimension of numerical simulations

Full size image
Fig. 10
figure 10

Contours of particle rotations of different crushable assemblies at 15% axial strain

Full size image

4.2 Effect of crushability on shear banding

Of particular interest in the current study is the shear banding of assemblies with different crushability. It has been found that the shear band inclination of angle \(\theta \), with respect to the minor compressive principal stress, varies between the limits \(\theta _R \le \theta \le \theta _C \), where \(\theta _R \) and \(\theta _C \) are given by Roscoe and Coulomb formulae [51]:

$$\begin{aligned} \theta _C =\frac{\pi }{4}+\frac{\varphi }{2} \theta _R =\frac{\pi }{4}+\frac{\psi }{2} \end{aligned}$$
(9)

where \(\varphi \) is the friction angle and \(\psi \) is the dilatancy angle.

Fig. 11
figure 11

Local porosity contours with different crushable assemblies at 15% axial strain

Full size image

Particles within the shear bands have much larger rotation magnitudes compared with the remaining particles in the assembly. Therefore, particle rotation is a good descriptor of the distribution of strain localization. Figure 10 displays the deformed specimen geometries and the contours of particle rotations at 15% axial strain. The dashed blue line denotes the Roscoe inclination angle, and the yellow line represents the Coulomb inclination angle. As indicated by Fig. 10, the inclination angle predicted by the Roscoe formulae is in better agreement with the numerical results. The shear banding pattern is sensitive to the particle crushability. One shear band is clearly visible in the uncrushable assembly, whereas the lateral membrane boundaries deform severely to locally ‘wrap’ around the ends of the shear bands. This result is a clear indication of strong dilation associated with strain localization. However, this phenomenon is substantially reduced or completely absent in the medium to high crushable granular assemblies. With the increase of particle crushability, two major shear bands form an ‘X’ configuration, but these X-shaped shear bands are not symmetrical in most cases. For example, the right shear band is more dominant in the assembly with 3.0 MPa shear strength, but the left and upper shear bands fail to form a connected shear zone.

Fig. 12
figure 12

Fragment distribution with different crushable assemblies at 15% axial strain

Full size image
Fig. 13
figure 13

Evolutions of average friction mobilization of different crushable assemblies. a Uncrushable. b \(\tau _f =2.0\hbox { MPa}\). c \(\tau _f =2.5\hbox { MPa}\). d \(\tau _f =3.0\hbox { MPa}\)

Full size image

Figure 11 displays the local porosity contours of different crushable assemblies at 15% axial strain. The zones near the shear bands have a greater local porosity than the remaining parts of the assembly, which is consistent with the rotation distribution. As shown in Fig. 11, the porosity increases with increasing particle shear strength, which is more obvious inside the shear bands. The greater local porosity inside the shear bands is caused by the rotation of irregularly shaped particles. Figure 12 shows the number of fragments increases with increasing crushability. This finding indicates a strong link between particle breakage and local porosity. The highly crushable particles inside the shear bands are more vulnerable to breakage, and the rotation of small fragments cannot induce strong local dilation. For the assembly with the shear strength of 2.0 MPa, the lateral membrane boundaries deform to shrinkage while the boundaries become bulgy with increasing particle shear strength. Due to massive grains crushing into small fragments, the X-shaped distribution of local porosity becomes less evident and the distribution of larger particle rotation magnitude fails to connect shear zone for the highly crushable assembly. As pointed out by Wang and Yan [46] and Ma et al. [52], the extensive amount of particle breakage prevents the formation of a shear band.

Fig. 14
figure 14

Contours of particle rotations at different strains

Full size image

To quantify particle sliding, the friction mobilization index \(I_{\mathrm{m}} ={\left| {f_{\mathrm{t}}^c } \right| }/{\left( {\mu f_{\mathrm{n}}^c } \right) }\) at each contact is considered, where \(\mu \) is the inter-particle friction coefficient, and \(f_{\mathrm{t}}^c \) and \(f_{\mathrm{n}}^c \) are the normal and tangential forces at contact c, respectively [53]. The average friction mobilization index \(I_{\mathrm{M}} \) is defined as \(\left\langle {{\left| {f_{\mathrm{t}}^c } \right| }/{\left( {\mu f_{\mathrm{n}}^c } \right) }} \right\rangle \), where the average is taken of all the contacts. Figure 13 displays the evolution of the average friction mobilization indices of the contact network inside and outside the shear bands. No obvious difference occurs in the \(I_{\mathrm{M}} \) of subnetworks of the uncrushable assembly, whereas the \(I_{\mathrm{M}} \) of subnetworks outside the shear bands are greater than those inside the shear bands of crushable assemblies. This result indicates that the weakening of friction mobilization outside the shear bands is likely responsible for the macroscopic strain softening [52] and the particle sliding inside the shear bands is less severe due to intensive particle crushing.

Fig. 15
figure 15

Particle breakage density distributions at different strains

Full size image

4.3 Micromechanical analysis of formation of shear bands

Only the assembly with a characteristic shear strength of 2.5 MPa is considered in this section. Particle scale information was investigated to quantify the microstructural evolution inside and outside the shear bands. Figure 14 shows the contours of particle rotations at different strains. The distribution of rotation is slightly uniform at the beginning of shearing. Then, potential shear bands emerge along the diagonals of the specimen. The distribution of particle rotation is localized at two major shear bands, and the X-shaped shear bands are clearly visible at 9% axial strain. With further shearing, part of these localized regions begin disappearing.

Fig. 16
figure 16

Evolutions of the strong force chains

Full size image
Fig. 17
figure 17

Evolutions of average translational velocity and rotational velocity

Full size image

The particle breakage density is defined as the fragment number in a square of size \(d_{50}^*\). The particle breakage density distribution at different strains is presented in Fig. 15. Most particle breakage occurs near the loading walls at the early stage of shearing, and the particle breakage inside the shear bands gradually becomes more severe, which is consistent with the results of Wang et al. [46]. Figure 16 illustrates the evolution of strong force chains. The normal contact force is generally uniform at the start of shearing, but column-like force chains form with increasing shear strain. The columnar force chains, which are initially oriented along the loading direction, gradually collapse and result in the formation of vaulted force chains. The force chains can be divided into four zones when X-shaped shear bands are formed. Most contact forces near the flexible membranes are less than \(f_{\mathrm {mean}} +2f_{\mathrm{0}} \) (\(f_{\mathrm {mean}} \) is the average of the normal force of the assembly and \(f_{\mathrm{0}} \) is equal to \((f_{\mathrm {max}} -f_{\mathrm {mean}} )/10\)), whereas most contact forces near the loading walls are greater than \(f_{\mathrm {mean}} +2f_{\mathrm{0}} \). There is minor branching inside the shear bands, which causes the chain network to become vulnerable to collapse after the shear bands have formed. Particle breakages coinciding with shear band formation are readily comprehensible because of the large induced stress due to poorly-distributed stresses within the shear bands.

It has been demonstrated that there exist constructions of spherical grains that fill a two- or three-dimensional space but which can rotate as a ball bearing without shear stiffness [54, 55]. The simulation of Åström and Timonen [56] shows that ball-bearing grains do not appear if fragmentation is forbidden while such grains are abundant and strongly localized in shear band if breakage is allowed. Figure 17 compares the average translational velocity and rotational velocity of the fragments and all particles. The average translational velocity of crushed particles is less than that of all particles, whereas the fragments have larger rotational magnitudes compared with the remaining particles. This finding indicates that small fragments spawning from parent particles inside the shear bands will lubricate the assembly. As shown in Figs. 14 and 15 the particle breakage also coincides with the formation of shear bands. It can be concluded that the fragments with large rotation will form a microscopic pockets of rotating bearings which significantly promotes the formation of shear bands [56]. While there are extensive particle breakages occurring, the ball-bearing mechanism will weaken whole assembly. This will suppress the shear band formation and reduce the shear resistance of the assembly.

5 Conclusion

Discrete element modeling of irregularly shaped granular materials has been developed. The simulations presented in this paper have demonstrated that it is possible to model the formation of shear bands in crushable and irregularly shaped granular materials. The effects of crushability on the mechanical behavior of granular materials and shear banding are investigated. The micro-mechanism of shear band formation is revealed. The primary findings from this qualitative study are the following:

  1. 1.

    With increasing particle crushability, the peak deviatoric stress decreases and the strain softening becomes milder. Particle crushing continually occurs during shearing and is synchronized with the development of macroscopic stress. The evolution of PSD can be characterized by a fractal dimension. As the particle shear strength ranges from 2.0 to 3.0 MPa, the final PSDs yields fractal dimensions between 2.645 and 2.715, while the initial fractal dimensions equal to 2.903.

  2. 2.

    Particle rotation is used to identify the onset and development of shear bands. The inclination angle of shear bands can be predicted by the Roscoe formulae. The shear banding pattern is sensitive to particle crushability. One shear band is clearly visible in the uncrushable assembly. With increasing particle crushability, two major shear bands form an ‘X’ configuration. The zones of greater porosity are consistent with the rotation distribution. The particles inside the shear bands are more likely to rotate, and particle breakage inside the shear bands is more severe. With high crushability, the particles inside the shear bands are more vulnerable to breakage, and the small fragments prevent large voids from fully developing.

  3. 3.

    The force chains can be divided into four zones by the Roscoe inclination lines after the formation of shear bands. Due to poorly-distributed stresses, the particles inside the shear bands are more vulnerable to breakage. The small fragments with larger rotation magnitudes inside the shear bands form ball-bearing to promote the formation of shear bands. While there are extensive particle breakages occurring, the ball-bearing mechanism will lubricate whole assembly. With the increase of particle crushability the shear band formation is suppressed and the shear resistance of the assembly is reduced.