An analytical framework for evaluating the cohesion effects of coalescence between capillary bridges

Abstract

In this work, we analyse the physical consequences of capillary bridges coalescence between spherical particles agglomerates and more particularly the jump of the capillary force. By referring to Murase et al. (Adv Powder Technol 19(4):349–367, 2008) and Rynhart et al. (Res Lett Inf Math Sci 5:119–127, 2003) about bridges adhered to three particles, we analyse the effects of coalescense between three bridges with two grains and a bridge joining three grains. This monographic synthesis intends to explain analytically and geometrically the significant increase of the inter-particle force, a strengthening cohesion effect, experimentally observed, reported and still largely unelucidated to our knowledge in the literature.

1 Introduction

In a previous work [9], the same authors have proposed a method for parameters identification and resolution of Young–Laplace equations based on an inverse problem approach. Among the results obtained, the classification of capillary bridges associated to an explicit criterion relied on the observation of the contact point, the wetting angle and the gorge radius, lets appear that the only strongly stable case that may be encountered in practice (except in very specific situations) is a portion of nodoid with both positive suction and capillary force. That case will constitute the starting point for describing the evolution and the coalescence of capillary bridges between three spheres and for explaining the strengthening cohesion effect, phenomenon experimentally observed and reported in the literature without substantiated elucidation [1, 4, 6, 8, 12–14, 16, 17, 19, 22]. This matter needs further clarifications by means of quantitative arguments.

The model case that will be considered is the coalescence between three capillary bridges between three spheres centered at the vertices of an equilateral triangle; it corresponds to the experiments performed in [11] (see also Fig. 1). After coalescence, we obtain a three grains capillary bridge whose free surface does not process a global symmetry of revolution anymore. The characteristic data are determined at the coalescence of the three bridges when the meridians inter in contact, under an identical filling of the three bridges. The mechanisms of formation of the micro-bridges leading to the coalescence are not the subject of this study and we may refer to Aarts et al. [1], Decent et al. [4], Eggers et al. [8], Shikhmurzaev [19], Sprittles et Shikhmurzaev [21], M. Wu et al. [22] for these questions. Referring to works of K. Murase et al. [13] and of Rynhart et al. [16], based on the numerical resolution of Young–Laplace equation in spherical and cylindrical coordinates, we propose an explanation of the observed experimental phenomenon [11], according to which the coalescence is the cause of a sudden increase (or a sudden decrease in a drying process), corresponding to a jump, of the vertical capillary force acting on the upper grain (Fig. 1). As a result, we obtain from the analytical expressions that the surface tension (tensile capillary force) only varies a little. Conversely, we observe that the orthogonal projection on an horizontal plane of the new effective surface of the liquid with the upper grain is of quasi-ellipsoidal type and we prove that its area increases strongly. This reinforced cohesive effect, due to the Laplace pressure contribution, is emphasized by an increase of the suction which is quantified in the present work, after the sudden filling of the central part of the capillary bridge after coalescence (cf. Fig. 3). To our knowledge, it is the first time that such an analytical study is proposed. Moreover, some formula existing in the literature are improved or even corrected.

Fig. 1

Evolution of vertical capillary force versus time in a drying process, according to J.P. Gras Ph.D. (Fig. 3.30, p. 103 of [11]). We observe a sudden decrease, corresponding to a jump, of the vertical capillary force acting on the upper grain

2 Motivations of the analysis

Let us recall the experimental setup and main results obtained by Gras [11, pp. 101–103]. We impose simultaneously, by progressive filling until the coalescence, a constant volume of liquid to each double capillary bridge. The resulting capillary force applied to the upper sphere by the capillary bridges is measured by differential weighing. Before the coalescence, it is observed that the increase of the fluid volume of the bridges has only a weak influence of the value on the capillary force: in the experiment presented, a $1.36\,\upmu \hbox {N}$ capillary force is measured for two capillary bridges whose volume is $4.5\,\upmu \hbox {l}$ each, whereas a $1.32\,\upmu \hbox {N}$ capillary force is measured when the volume of each capillary bridge is increased to $9\,\upmu \hbox {l}$ [11]. This observation will be explained, in the context of our study, as follows: during the filling of the capillary bridges, the triple line perimeter and the contact surface area increase, whereas the strictly positive suction s has a tendency to decrease. This antagonistic aspect will be detailed by analytical developments leading to formula (35) which explains the small variations of the suction s during the filling. At the coalescence (exact instant of merging of the capillary bridges), a sudden increase of the capillary force is observed, up to $1.82\,\upmu \hbox {N}$. Conversely, during the drying of a coalesced capillary bridge, the triple bridge splits into three distinct bridges and we observe a sudden decrease of the capillary force from 1.54 to $1.1\,\upmu \hbox {N}$ [11, p. 103, fig. 3.29–3.30]. Fig. 3.30 page 103 of [11] is reproduced above; it represents the evolution of the vertical capillary force versus time in a drying process. The sudden decrease of the vertical capillary force acting on the upper grain is clearly revealed.

Rynhart et al. [16] have confirmed this observation on another triple capillary bridge whose characteristics are $r=39\,\upmu \hbox {m}$, $\gamma =63.1\,\hbox {mNm}^{-1}$, $V=65.6\,\upmu \hbox {l}$. They have measured a $12.51\,\upmu \hbox {N}$ capillary force whereas Simons and Fairbrother [20] have observed, on the same experimental device with two capillary bridges, a maximal capillary force of $8\,\upmu \hbox {N}$ (by optimizing the distance between particles). Many abacuses (monograms) are also provided by Murase et al. [13] for the calculation and the numerical assessment of the static force between three spheres by varying significant factors (see also [14] for similar numerical and experimental data or [6] for the evolution of splitting bridges into multiple bridges between plates; calculations of the capillary force are presented).

The next of the paper is devoted to explain analytically and geometrically this sudden jump of the capillary force between merging bridges, from particular solutions of Young–Laplace equations for three equally sized spherical particles whose centers are located on the vertices of an equilateral triangle (Fig. 3).

3 Solutions of Young–Laplace equation in axisymmetric case

3.1 General solutions and nodoid parameterization

We recall in this section the main results obtained in [9], concerning the solutions of Young–Laplace equation and the properties of the associated capillary bridges. When the capillary bridge is enclosed by a surface of revolution, hydrostatic Young–Laplace equation may be written as (without gravity effects):

$$\begin{aligned} \frac{y^{\prime \prime }}{\left( 1+y^{\prime 2}\right) ^{3/2}}-\frac{1}{y\sqrt{1+y^{\prime 2}}}=-\frac{\Delta p}{\gamma }=:H,\quad H \ne 0 \end{aligned}$$

(1)

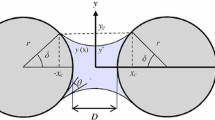
the expression $x \mapsto y(x)$ defining the free meridian equation, with the conditions $y^{\prime \prime }\ge 0, 0<y \le r\sin \delta$ for convex profiles, where $\delta$ denotes the filling angle of the capillary bridge (Fig. 2). For simplification, the two spheres involved have the same radius r and are separated by a distance D. The case $H=0$ is well-known (minimal surface) and does not fall within this framework. The solutions of (1) are then a family of catenoids, limit cases of nodoids at a lower stability.

Fig. 2

Example of static capillary bridge between two grains (axisymmetric surface with convex meridian)

By highlighting a significant invariant with a first integral of Eq. (1), we proved in Res. 1 of [9] that the inter-particle force (or suction force) $F^{cap}$ can be evaluated at any point of the profile as

$$\begin{aligned} F^{cap}= 2\pi \gamma \left( \dfrac{y}{\sqrt{1+y^{\prime 2}}}+\dfrac{Hy^{2}}{2} \right) \text { uniformly in} y\in [y^*,y_c].\nonumber \\ \end{aligned}$$

(2)

It is important to note that this result is only valid for capillary bridges whose free surface is of revolution. In other cases, the resulting capillary force must be evaluated at the triple contact line, as it will be the case after coalescence of the bridges in Sect. 6.1.

After a suitable change of variables and a first integration, Young–Laplace equation (1) may be rewritten as

$$\begin{aligned} 1+y^{\prime 2}=\frac{4y^{2}}{H^{2}\left( y^{2}-\dfrac{2\lambda }{H}\right) ^{2}},\quad \lambda \in {\mathbb {R}}, \quad y=y_{\lambda ,H}, \end{aligned}$$

(3)

whose characteristic expression leads to classical Delaunay’s roulette solutions [5, 7]. Using the principles of calculus of variations, this key relationship also corresponds precisely to the Beltrami identity for the Euler–Lagrange equation associated with the potential energy functional and Lagrange multipliers method. In fact, one gets an additional information: the Lagrange multiplier coincides with the parameter H specifying the mean curvature. Accordingly the constant H can be viewed as a Lagrange multiplier dimensioned to a $\left( length\right) ^{-1}$. Using an original inverse problem method to restore the missing information on the pressure deficiency $\Delta p$, which is often an unknown of the problem, we have revisited the classification of possible existing capillary bridges with respect to given data accessible experimentally (in particular the wetting and filling angles and the gorge radius of the capillary bridge), using for instance a digital camera with macrozoom (see [9] for more details).

Among the results obtained in [9], it appears that the only strongly stable case of capillary bridge that may be encountered in practice, except in very specific situation, is a portion of nodoid with positive suction and capillary force corresponding to $H>0$ and $\lambda >0$. That point can be thoroughly clarified as follows: it is known that for the stability study of a bridge, the fundamental tool is the notion of second variation of the potential energy functional that we can completely explicit for the class of axisymmetric bridges. Without going into very mathematical details (see [10] for more details), indicate that in fact, it is sufficient for testing the bridge stability to know the sign of the first eigenvalue $\lambda _{1}$ (the smallest) of a Dirichlet–Sturm–Liouville problem associated to the meridian equation. When necessary, one must also take into account a Vogel’s stability criterion. That case will be used in the next, as a starting point for describing the evolution and the coalescence of capillary bridges between three spheres and for explaining the strengthening effect of cohesion that occurs. The main characteristics and associated parameterization are detailed in Res. 1 of [9] (Sect. 4.1) when the surface of revolution is a portion of nodoid.

One of the advantages of such an analytical parameterization is that the main characteristic quantities of the capillary bridge (associated volume, free surface area, resulting inter-particle force) may be calculated analytically, from the parameterization of the nodoid meridian.

The total volume of a capillary liquid bridge between two spheres defined by its meridian representation $x\mapsto y(x)$ is classically given by:

$$\begin{aligned} V=\pi {\displaystyle \int _{-x_{c}}^{x_{c}}} y^{2}\left( x\right) dx -2V_c, \end{aligned}$$

where $V_c= \displaystyle { \frac{\pi }{3} r^3(1-\cos \delta )^2 (2+ \cos \delta )}$ denotes the volume of the spherical caps wetted by the liquid. We have in the nodoid case considered here (see [9]):

$$\begin{aligned} V= & {} 2\pi \dfrac{b^{4}}{a} {\displaystyle \int _{0}^{\tau }} \dfrac{e-\cos t}{e+\cos t}\dfrac{\cos t\ dt}{\left( e+\cos t\right) \sqrt{e^{2}-\cos ^{2}t}}\nonumber \\&-\,\frac{2}{3}\pi r^{3}\left( 1-\cos \delta \right) ^{2}\left( 2+\cos \delta \right) \end{aligned}$$

(4)

where $\tau \left( \delta ,r,\theta ,y^{*}\right) =\arccos \left( e~\dfrac{b^{2}-r^{2}\sin ^{2}\delta }{b^{2} +r^{2}\sin ^{2}\delta }\right)$ is solution of $y(\tau )=r\sin \delta$.

Moreover, the free surface area of the liquid bridge is given, for the value $\tau$ of parameter, by:

$$\begin{aligned} \Sigma _{2} (\tau )=2\pi b^{2} {\displaystyle \int _{0}^{\tau }} \dfrac{1}{e+\cos t}\sqrt{\dfrac{e-\cos t}{e+\cos t}}~dt. \end{aligned}$$

(5)

Finally, the inter-particle force may be calculated at the three phase contact line as

$$\begin{aligned} F^{cap}= & {} 2\pi \gamma r\sin \delta \ \sin \left( \delta +\theta \right) \nonumber \\&+\,2\pi \gamma \ \frac{y^{*}-r\sin \delta \ \sin \left( \delta +\theta \right) }{r^{2}\sin ^{2}\delta -y^{*2}}~r^{2}\sin ^{2}\delta \end{aligned}$$

(6)

or, equivalently, according to the gorge method (see [9] for more details):

$$\begin{aligned} F^{cap}=2\pi \gamma y^{*} +2\pi \gamma \ \frac{y^{*}-r\sin \delta \ \sin \left( \delta +\theta \right) }{r^{2}\sin ^{2}\delta -y^{*2}} {{y^{*} }^2} . \end{aligned}$$

(7)

3.2 Key characteristics just before coalescence

The experimental device which is used to illustrate this modeling work consists of three equally sized spherical particles whose centers are located on the vertices of an equilateral triangle (cf. Fig. 3). The spheres of radius r are assumed to have no surface roughness. The main liquid bridge characteristics are obtained by image analysis (gorge radius $y^{*}$, filling angle $\delta$, contact angle $\theta$), that will constitute the boundary conditions before coalescence. A liquid with known surface tension $\gamma$ is simultaneously and uniformly introduced in order to form an assembly between the three grains linked by three separated liquid bridges (“grain-pairs”). The moment of coalescence is obtained when the filling angle is set to $\delta = \frac{\pi }{6}$, the gorge radius then observed being denoted $y_{c}^{*}$ (Fig. 3) for each capillary bridge, using the parameterization of Fig. 2.

Fig. 3

The three liquid bridges just before the coalescence (“sagittal view”)

Realistically we consider here the case of three coalescing nodoids. In this stable case (capillary cohesion due to interstitial liquid [15]), the capillary forces originate from the simultaneously attractive forces caused by the surface tension and pressure deficiency across the liquid interface (unique circumstances that ensure a positive suction). The parameterizations developed in [9] are proven extremely useful for expressing all the key characteristics of the limit state just when the three bridges may coalesce to form a connected bridge between the three grains. Indeed, for each primary bridge, we calculate $\overline{a}$ and $\overline{b}$, the semi-axis of the hyperbola that generates the limit profile (Delaunay hyberbolic roulette) and as a result, the exact mean curvature of the nodoid. According to Res. 1 of [9], we find that:

$$\begin{aligned} \overline{a}= & {} a\left( r,y_{c}^{*},\frac{\pi }{6},\theta \right) =\frac{1}{4}\dfrac{r^{2}-4y_{c}^{*2}}{2y_{c}^{*}-r\ \sin \left( \frac{\pi }{6}+\theta \right) },\quad \dfrac{\Delta p}{\gamma }=-\dfrac{1}{\overline{a}}, \nonumber \\ \overline{b}= & {} \overline{b}\left( r,y_{c}^{*},\frac{\pi }{6} ,\theta \right) =\left( \frac{1}{2}y_{c}^{*}\ r\ \dfrac{r-2y_{c}^{*}\ \sin \left( \frac{\pi }{6}+\theta \right) }{2y_{c}^{*}-r\ \sin \left( \frac{\pi }{6}+\theta \right) }\right) ^{\frac{1}{2}},\nonumber \\ \overline{e}= & {} \sqrt{1+\dfrac{\overline{b}^{2}}{\overline{a}^{2}}}. \end{aligned}$$

(8)

Consequently, the volume of the resulting coalesced bridge with three particles is expressed by adapting (4) as follows

$$\begin{aligned} \overline{V}= & {} 6\pi \dfrac{\overline{b}^{4}}{\overline{a}} {\displaystyle \int _{0}^{\overline{\tau }}} \dfrac{\overline{e}-\cos t}{\overline{e}+\cos t}\dfrac{\cos t\ dt}{\left( \overline{e}+\cos t\right) \sqrt{\overline{e}^{2}-\cos ^{2}t}}~\nonumber \\&-2\pi r^{3}\left( 1-\dfrac{\sqrt{3}}{2}\right) ^{2}\left( 2+\dfrac{\sqrt{3}}{2}\right) \nonumber \\&\hbox {where }\ \ \overline{\tau }=\arccos \left( \overline{e}\ \dfrac{4\overline{b}^{2}-r^{2}}{4\overline{b}^{2}+r^{2}}\right) \end{aligned}$$

(9)

and, by vectorial addition, the resulting inter-particle force immediately before the coalescence is derived from the expressions at the three phase contact line¹ (6)

$$\begin{aligned} \overline{f_{cap}}=\sqrt{3}\pi \gamma r\ \left( \sin \left( \dfrac{\pi }{6}+\theta \right) + r\ \dfrac{2y_{c}^{*}-r\ \sin \left( \frac{\pi }{6}+\theta \right) }{r^{2}-4y_{c}^{*2}}\right) . \end{aligned}$$

(10)

4 Key characteristics just after coalescence

The experimental device that will be used for validation of the modelling is composed of three spheres centered at the summits of an equilateral triangle. The analytical calculation of the capillary bridge properties leads to important complications because the free surface does not process a global symmetry of revolution anymore. In that case, the Young–Laplace equation modelling the problem does not reduce anymore to a nonlinear ODE, but writes as a nonlinear partial differential equation, whose right hand side is constituted of a missing data to be restored (the capillary pressure). The complementary information is given by the boundary conditions on the triple line, which is henceforth a skew curve and by the value of the gorge radius (still considered as a data given by the experiment).

In the general case, the Young–Laplace equation then leads to a divergential problem (a source identification problem which creates a really complicated mathematical situation:

$$\begin{aligned} {\text {div}}_{S}\left( {n} \right) =\frac{\Delta \widetilde{p}}{\gamma } , \quad \Delta \widetilde{p}~\text {unknown to be adjusted} \end{aligned}$$

(11)

where n denotes the unit normal vector to the surface at point m, oriented towards the liquid, ${\text {div}} _{S}$ is the divergence operator applied to the surface, i.e. in an abstract point of view, the trace of the second order tensor ${\text {grad }} n$ [that explains the intrinsic character² of formula (11)]. Note that (11) may be also written on the form:

$$\begin{aligned} {\text {div}}_{S}\left( {n} \right) = -H \end{aligned}$$

(12)

where $H= -\frac{\Delta \widetilde{p}}{\gamma }$ denotes the suction. Equation (11) and the properties of the associated capillary bridge may be specified in the case of three particles device considered here using a judicious choice of the axis associated to cylindrical coordinates. It is the main goal of what follows.

4.1 Recall on theory of parametric surfaces

Let us recall the very basic definition of the geometric properties of a surface S of ${\mathbb {R}}^3$ that will be used in the sequel. Let U be an open set of ${\mathbb {R}}^2$ and

$$\begin{aligned} \displaystyle {\begin{array}{lllll} {f} &{} : &{} {U \subset {\mathbb {R}}^2} &{} \rightarrow &{} {{\mathbb {R}}^3} \\ \; &{} \; &{} {x=(u,v)} &{} \mapsto &{} {m=f(x)} \end{array}} \end{aligned}$$

an embedding. $S=f(U )$ is called a parametric surface of ${\mathbb {R}}^3$ (Fig. 4). In what follows, we assume that f is smooth enough (for instance $C^2 (U)$) in order to introduce the basic elements of differential geometry (see for instance [3, 18]).

Fig. 4

Parametric surface

As f is injective, the vectors $a_1=\frac{\partial f}{\partial u}$ and $a_2=\frac{\partial f}{\partial v}$ are independent and constitute a local basis (the natural basis) of the tangent plane $T_mS$ to S at m. Then the normal vector n to the surface S at m is given by

$$\begin{aligned} N=\frac{a_1\wedge a_2}{\parallel a_1\wedge a_2\parallel } \end{aligned}$$

(13)

The metric tensor (first fundamental form of S) classically stands:

$$\begin{aligned} a_{\alpha \beta } = a_{\alpha }\cdot a_{\beta } \end{aligned}$$

where the dot denotes the usual scalar product of ${\mathbb {R}}^3$. We can also define the dual basis $(a^1,a^2)$ of the tangent map $T_m S$ by

$$\begin{aligned} a^\alpha \cdot a_\beta = \delta ^\alpha _\beta \end{aligned}$$

where $\delta ^\alpha _\beta$ denotes the Kronecker symbol. The contravariant components $(a^{\alpha \beta })$ of the metric tensor are then given by $a^{\alpha \beta }=a^{\alpha } \cdot a^{\beta }$ and satisfy the property $(a^{\alpha \beta })= (a_{\alpha \beta })^{-1}$. Finally, the covariant components $(b_{\alpha \beta })$ of the curvature tensor can be computed as

$$\begin{aligned} b_{\alpha \beta } = n\cdot a_{\alpha ,\beta }. \end{aligned}$$

(14)

4.2 Young–Laplace equation in cylindrical coordinates

Using a judicious choice of the axis [16], the study may be limited to 1 / 12 of the capillary bridge, with a choice of the representation of the height z using cylindrical coordinates

$$\begin{aligned} z=z\left( \rho ,\varphi \right) ,\quad z~\text {is }\frac{\pi }{2}-\text {periodic with respect to }\varphi , \end{aligned}$$

where $\rho$ axis is vertical and the origin coincides with the center of the upper sphere (Fig. 5).

The regular transformation between Cartesian and cylindrical coordinate systems classically matches

$$\begin{aligned} {\mathbf {U}}\left( \rho ,\varphi \right)= & {} \left( \begin{matrix} X \\ X \\ Z \\ \end{matrix} \right) \text { where } X=\rho ,\ Y=z\left( \rho ,\varphi \right) \cos \varphi ,\ \nonumber \\ Z= & {} z\left( \rho ,\varphi \right) \sin \varphi . \end{aligned}$$

(15)

Once the normal n being calculated on the surface S using definition (13), the divergential problem (11) enables to determine $H=-\frac{\Delta \widetilde{p}}{\gamma }$.

Fig. 5

Cylindrical coordinates used for the parameterization of the capillary bridge just after coalescence

The divergence operator on the surface S may be computed using the intrinsic definition

$$\begin{aligned} \text {div}_S (n) = Tr (\text {grad}_S n) \end{aligned}$$

(16)

where Tr denotes the trace operator. The gradient on the surface S may be defined by

$$\begin{aligned} \text {grad}_S = a^\rho \frac{\partial }{\partial \rho } + a^\varphi \frac{\partial }{\partial \varphi } \end{aligned}$$

(17)

where $a^\rho$ and $a^\varphi$ are the vectors of the contravariant basis at point M on the surface S. They are determined using the definitions of Sect. 4.1 and the parameterization (15) based on cylindrical coordinates. We get:

$$\begin{aligned} a_\rho= & {} \displaystyle \frac{\partial {{\mathbf {U}}}}{\partial {\rho } } = \left( \begin{matrix} 1 \\ z_\rho \cos \varphi \\ z_\rho \sin \varphi \\ \end{matrix} \right) , \nonumber \\ a_\varphi= & {} \displaystyle \frac{\partial {{\mathbf {U}}}}{\partial {\varphi } } = \left( \begin{matrix} 0 \\ -z \sin \varphi + z_\varphi \cos \varphi \\ z \cos \varphi + z_\varphi \sin \varphi \\ \end{matrix} \right) \end{aligned}$$

(18)

and

$$\begin{aligned} n =\frac{1}{\sqrt{z^2(1 + z_\rho ^2) + z_\varphi ^2}} \left( \begin{matrix} z z_\rho \\ - z_\varphi \sin \varphi - z \cos \varphi \\ z_\varphi \cos \varphi - z \sin \varphi \\ \end{matrix} \right) \end{aligned}$$

(19)

with the notations $z_\rho = \frac{\partial z}{\partial \varphi }$ and $z_\varphi = \frac{\partial z}{\partial \varphi }$. The associated metric tensors are then given by

$$\begin{aligned} (a_{\alpha \beta })= & {} \left( \begin{matrix} 1 + z_\rho ^2 &{} z_\rho z_\varphi &{} \\ z_\rho z_\varphi &{} z^2 + z_\varphi ^2 \\ \end{matrix} \right) , \nonumber \\ (a^{\alpha \beta })= & {} \frac{1}{z^2(1 + z_\rho ^2) + z_\varphi ^2 }\left( \begin{matrix} z^2 + z_\varphi ^2 &{} - z_\rho z_\varphi &{} \\ - z_\rho z_\varphi &{} 1 + z_\rho ^2 \\ \end{matrix} \right) \end{aligned}$$

(20)

leading to the contravariant base vectors:

$$\begin{aligned} a^\rho= & {} \frac{1}{z^2(1 + z_\rho ^2) + z_\varphi ^2 } \left( \begin{matrix} z^2 + z_\varphi ^2 \\ z^2 z_\rho \cos \varphi + z z_\rho z_\varphi \sin \varphi \\ z^2 z_\rho \sin \varphi - z z_\rho z_\varphi \cos \varphi \\ \end{matrix} \right) , \nonumber \\ a^\varphi= & {} \frac{1}{z^2(1 + z_\rho ^2) + z_\varphi ^2 } \left( \begin{matrix} - z_\rho z_\varphi \\ z_\varphi \cos \varphi - (1 + z_\rho ^2 ) z \sin \varphi \\ z_\varphi \sin \varphi + (1 + z_\rho ^2 ) z \cos \varphi \\ \end{matrix} \right) \end{aligned}$$

(21)

Finally, applying definitions (16) and (17), Young–Laplace equation may be expressed in terms of z and the partial derivatives of z. It leads to the nonlinear elliptic partial differential equation

$$\begin{aligned}&\dfrac{z^{2}-zz_{\varphi \varphi }+2z_{\varphi }^{2}-z^{2}z_{\rho }^{2} -zz_{\varphi \varphi }z_{\rho }^{2}+2zz_{\rho \varphi }z_{\rho }z_{\varphi } -z_{\rho \rho }z^{3}-zz_{\rho \rho }z_{\varphi }^{2}}{\left( z_{\varphi }^{2} +z^{2}\left( 1+z_{\rho }^{2}\right) \right) ^{3/2}}\nonumber \\&\quad = \frac{\Delta \widetilde{p}}{\gamma } = -H \end{aligned}$$

(22)

with the notations $z_{\varphi \varphi } = \frac{\partial ^2 z}{\partial \varphi ^2}$, $z_{\rho \rho } = \frac{\partial ^2 z}{\partial \varphi ^2}$ and $z_{\rho \varphi } = \frac{\partial ^2 z}{\partial \rho \varphi }$. Note that we find a similar expression as Eq. (2.58) of [16] with a slightly different definition of H.

5 Outline of the bridge properties just after coalescence

5.1 The numerical strategies of resolution of Young–Laplace equation existing in literature

In order to determine the capillary bride properties just after coalescence, a first strategy would be to solve numerically Young–Laplace equation (22) for given constant mean curvature, contact angle and inter-particle separation distance, introducing an $n\times m$ mesh and using a robust nonlinear equation solver. By varying $\Delta \widetilde{p}$, as a parameter, we can a family of liquid bridges with different volumes. Notably, the binding force $F_{cap}$ between the particles can be calculated (in $\mu N)$ at the three phase contact line and plotted as a function of liquid bridge volume V (in $\mu m^{3}$) according to a monotonic relationship available in practice (cf. Fig. 58, p. 126 in [16]).

An alternative numerical and conceptual approach is due to Murase et al. [13]: the three-dimensional bridge profile is acquired by grid generation for the simulation in spherical coordinates, using Galerkin finite element method, in a quarter of the region, i.e. $\rho =f\left( \varphi ,\psi \right)$, $0\le \varphi \le \frac{\pi }{2}, -\frac{\pi }{2}\le \psi \le \frac{\pi }{2}$, the integral domain being divided into isoparametric elements. The formulation of the static shape of the bridge adhered to three spheres is based on an optimization problem: the minimization of the potential energy with respect to the constraint of a given constant bridge volume. According to classical calculus of variations, the constrained minimal problem with fixed boundaries introduces a Lagrange multiplier $\lambda$ in order to express the total energy. Again according to Murase et al. [13], the surface area $\Sigma _{3}$ and the volume $V_{3}$ are formulated as

$$\begin{aligned} \Sigma _{3}= & {} 4 {\displaystyle \int _{-\frac{\pi }{2}}^{\frac{\pi }{2}}} {\displaystyle \int _{0}^{\frac{\pi }{2}}} f\sqrt{\left( f^{2}+f_{\psi }^{2}\right) \cos ^{2}\psi +f_{\varphi }^{2} }\ d\varphi d\psi ,\nonumber \\&\Sigma _{3}=\Sigma _{3}\left( f\right) , \end{aligned}$$

(23)

$$\begin{aligned} V_{3}= & {} 4 {\displaystyle \int _{-\frac{\pi }{2}}^{\frac{\pi }{2}}} {\displaystyle \int _{0}^{\frac{\pi }{2}}} \frac{f^{3}\cos \psi }{3}\ d\varphi d\psi ,\quad V_{3}=V_{3}\left( f\right) . \end{aligned}$$

(24)

In this context, the formulation of the bridge shape for a constant bridge volume V is based on the minimization of the Lagrangian

$$\begin{aligned} \Lambda _{V}\left( f\right)= & {} \Sigma _{3}\left( f\right) +\lambda \left( V-V_{3}\left( f\right) \right) \quad for \quad f=\mathbf f\left( \varphi ,\psi \right) , 0\\\le & {} \varphi \le \frac{\pi }{2},\ -\frac{\pi }{2}\le \psi \le \frac{\pi }{2} \end{aligned}$$

by searching ${\arg }_{f}\min$ $\Lambda _{V}\left( f\right)$, with f real-valued function smooth enough.

This approach is particularly well suited for our study because the volume V is a parameter known precisely at the coalescence from formula (9) adapted for fine numerical calculations. However, to simplify the problem, Murase et al. [13] made some geometric simplifying assumptions on the geometry of the contact lines: the contact lines on higher and lower spheres where approximated by circles through contact points based on the three different filling angles experimentally determined by digital images [16, p. 358]). As the determination of the binding force is performed on the contact line, the approximation performed may alter the results and the conclusions. The reader may find in [13] numerical estimations of the strength of a liquid bridge adhered to three spheres.

The numerical resolution of Young–Laplace equation is not an easy task; it depends strongly on the boundary conditions on the contact line. For this reason, we will focus in the next of this paper on the geometric and analytical accurate determination of the triple line profile and of the associated capillary force. The analytical formula that will be established will enable a comparison of the value of the resultant capillary force before and after coalescence. To our knowledge, such results do not exist in the literature. They enable to explain accurately the strong increasing of the capillary force observed experimentally just after the coalescence and may constitute a starting point for numerical resolution of Young–Laplace equation of coalesced capillary bridges, that is not the subject of the present work.

5.2 Remark on least energy solutions subject to frictional dissipation mechanism

We consider the more general case of the liquid bridge formed between three equally sized spherical particles, optionally made up of different materials.

The contact angles values $\delta _{i}$, $i=1,2,3$, related to the different surface tensions, are presumed strongly imposed in an option involving a free boundary problem since the contact curves are obviously free to move; these values are assumed to be constant at all possible contact points while ignoring all of realistic hysteresis phenomena. In fact, the contact lines are subject to a frictional force [2] generating a dissipation mechanism; hence $\left| \Sigma \right|$ the area of the free surface and $\left| \Lambda _{i}\right| _{i=1,2,3}$ the area of the wetted region on solid $S_{i}$ are the unknown of the constrained problem.

In the absence of gravity effects or other disrupting external potentials, the shape of the free surface then arises from minimizing the following capillary energy functional at prescribed volume and taking into account the free boundaries contribution to transcribe a physically relevant formulation:

$$\begin{aligned}&{\mathcal {E}}=\gamma \left( \left| \Sigma \right| -\cos \delta _{1}\ \left| \Lambda _{1}\right| -\cos \delta _{2}\ \left| \Lambda _{2}\right| -\cos \delta _{3}\ \left| \Lambda _{3}\right| \right) ,\\&\quad \delta _{i}\in \left[ 0,\pi \right] . \end{aligned}$$

Because contact angles are fixed and by compliance with this requirement, Fourier–Robin boundary conditions are imposed on the variation.

It is well known in the calculus of variations that the first order conditions from the corresponding minimization confirm that the mean curvature must be constant and that the normals to $\Sigma$ and $\Lambda _{i}$ at fixed i form a constant angle along the curve $\partial \Sigma \cap \partial \Lambda _{i}$. The second variation introduces then a quadratic form related to stability at a given critical point.

In the context of this paper (solid balls made of the same material), by $\dfrac{2\pi }{3}$-rotational symmetry (gravitational effects are not taken into account), one has

$$\begin{aligned} \delta = \delta _{i},\quad \left| \Lambda \right| =\left| \Lambda _{i}\right| ,\quad i=1,2,3, \end{aligned}$$

and the energy ${\mathcal {E}}^{-}$ at the instant immediately before coalescence is exactly known by previous analytical expressions for three disjoint bridges.

Accordingly, the energy ${\mathcal {E}}^{+}$ at the instant immediately after coalescence has to verify:

$$\begin{aligned} {\mathcal {E}}^{+}=\gamma \left( \left| \Sigma ^{+}\right| -3\cos \delta \ \left| \Lambda ^{+}\right| \right) \le {\mathcal {E}}^{-}. \end{aligned}$$

5.3 Analytical and geometrical determination of the bridge properties after coalescence

The analytical expressions of capillary bridges properties just after coalescence established here will be used in Sect. 6 for explaining the jump of the capillary force that occurs at coalescence.

The free surface area of the liquid bridge is given via the norm of the fluid surface normal vector $\left\| a_{\rho }\times a_{\varphi }\right\|$ by the formulation

$$\begin{aligned} \Sigma _{3}=12 {\int _{0}^{\frac{\pi }{2}}} {\displaystyle \int _{\rho _{s}\left( \varphi \right) }^{\rho _{p}\left( \varphi \right) }} \sqrt{z^{2}\left( 1+z_{\rho }^{2}\right) +z_{\varphi }^{2}}\ \ d\rho d\varphi \end{aligned}$$

For each $\varphi$ $\in \left[ 0,\frac{\pi }{2}\right]$, the point $\rho _{p}=\rho _{p}\left( \varphi \right)$ on the $\rho$ axis corresponds to the intersection between the fluid free surface and the so-called “symmetry contour” bisecting the liquid bridge between adjacent particles and $\rho _{s}=$ $\rho _{s}\left( \varphi \right)$ is the $\rho -$coordinate of the fluid -sphere intersection point (Fig. 6).

Fig. 6

Region where the problem is solved

According to formulas (3.69) and (3.72) of [16], the total volume of the liquid bridge is given by

$$\begin{aligned} V= & {} 12 {\displaystyle \int _{0}^{\frac{\pi }{2}}} {\displaystyle \int _{\rho _{s}\left( \varphi \right) }^{\rho _{p}\left( \varphi \right) }} {\displaystyle \int _{0}^{z}} zdzd\rho d\varphi \nonumber \\&- {\displaystyle \int _{0}^{\frac{\pi }{2}}} \left( 4r^{3}-6r^{2}\rho _{s}\left( \varphi \right) +2\left( \rho _{s}\left( \varphi \right) \right) ^{3}\right) d\varphi \nonumber \\&+\,2 {\displaystyle \int _{0}^{\frac{\pi }{2}}} z^{2}\left( \rho _{p}\left( \varphi \right) ,\varphi \right) \left( \rho _{0}-\rho _{p}\left( \varphi \right) \right) d\varphi . \end{aligned}$$

(25)

We point out that the inter-particle force acting on the upper sphere must be calculated at the three phase contact line (a skew curve) according to the boundary method and consequently its value is expressed as

$$\begin{aligned} F_{cap}&=4\gamma {\displaystyle \int _{0}^{\frac{\pi }{2}}} \sqrt{z^{2}\left( \rho _{s}\left( \varphi \right) ,\varphi \right) +\left( \frac{d\rho _{s}\left( \varphi \right) }{d\varphi }\right) ^{2}}\ \sin \left( \delta \left( \varphi \right) +\widetilde{\theta }\right) d\varphi \nonumber \\&\qquad -2\Delta \widetilde{p} {\displaystyle \int _{0}^{\frac{\pi }{2}}} z^{2}\left( \rho _{s}\left( \varphi \right) ,\varphi \right) d\varphi \end{aligned}$$

(26)

where $\widetilde{\theta }$ denotes the contact angle, a physical property of the fluid and

$$\begin{aligned} \delta \left( \varphi \right) =\arccos \dfrac{\rho _{s}\left( \varphi \right) }{r} \end{aligned}$$

with r the particle radius. It is important to note that Rynhart et al. [16] set out the following simplified formula [p. 124, (3.74)] for the inter-particle force where the torsion term $\dfrac{d\rho _{s}\left( \varphi \right) }{d\varphi }$ is neglected:

$$\begin{aligned} \widetilde{F}_{cap}&=4\gamma {\displaystyle \int _{0}^{\frac{\pi }{2}}} z\left( \rho _{s}\left( \varphi \right) ,\varphi \right) \sin \left( \delta \left( \varphi \right) +\widetilde{\theta }\right) d\varphi \nonumber \\&\quad -4\Delta \widetilde{p} {\displaystyle \int _{0}^{\frac{\pi }{2}}} {\displaystyle \int _{0}^{z\left( \rho _{s}\left( \varphi \right) ,\varphi \right) }} zdzd\varphi . \end{aligned}$$

(27)

Thus, expression (26) constitutes an improvement of the existing formulas in the literature to compute accurately the inter-particles cohesion forces.

In order to establish further comparisons, we note that the exact perimeter of contact at the interface boundary is obtained by calculating

$$\begin{aligned} \Pi _{3}=4 {\displaystyle \int _{0}^{\frac{\pi }{2}}} \sqrt{z^{2}\left( \rho _{s}\left( \varphi \right) ,\varphi \right) +\left( \frac{d\rho _{s}\left( \varphi \right) }{d\varphi }\right) ^{2}} \ d\varphi . \end{aligned}$$

(28)

In view of further developments, suitable assumptions of continuity being fulfilled, we observe that the first mean value theorem for integration states that there exists $\varphi _{0}\in \left] 0,\frac{\pi }{2}\right[$ such that

$$\begin{aligned} \Pi _{3}=2\pi \sqrt{z^{2}\left( \rho _{s}\left( \varphi _{0}\right) ,\varphi _{0}\right) +\left( \frac{d\rho _{s}\left( \varphi _{0}\right) }{d\varphi }\right) ^{2}} \end{aligned}$$

(29)

and $\varphi _{1}\in \left] 0,\frac{\pi }{2}\right[$ such that the vertical component of the surface tension force (first term of expression (27) of the total capillary force) is expressed by

$$\begin{aligned}&F_{tension}\nonumber \\&\quad =2\pi \gamma \sqrt{z^{2}\left( \rho _{s}\left( \varphi _{1}\right) ,\varphi _{1}\right) +\left( \frac{d\rho _{s}\left( \varphi _{1}\right) }{d\varphi }\right) ^{2}}\ \sin \left( \delta \left( \varphi _{1}\right) +\widetilde{\theta }\right) . \nonumber \\ \end{aligned}$$

(30)

Fig. 7

Top view scheme showing: (i) Contact line with the upper sphere in case of three just coalesced nodoids. (ii) Resulting quasi-ellipsoidal cross-section used to evaluate the contribution of the Laplace pressure to the cohesive strengthening

6 Analysis of the capillary force jump at coalescence

In this section, using only the mathematical modeling, we analyze the causes of the quantitative jump of the capillary force at the coalescence. The variations of the superficial tensile force of the liquid, of the suction and of the effective surface area measured (or calculated) at the triple line, that occur at the coalescence, will be analyzed separately.

We dispose of exact analytical formulas which express the physical characteristics of the three capillary bridges immediately before the coalescence. For example, formula (9) gives exactly the liquid volume $\overline{V}$ of the three double capillary bridges before the coalescence. The latter can be evaluated with an accurate numerical integration formula (a composite Simpson’s rule to avoid the overestimating trapezium rule because of the convexity of the meniscus). From (5) and (9), the total free surface area is given by $3\Sigma _2(\tau )$.

Immediately after the coalescence, according to the studies of Rynhart et al. [16], p. 126, the binding force between the particles may be calculated at the three phase contact line and plotted as a function of liquid bridge volume via the available law

$$\begin{aligned} \overline{F}_{cap}=f_{r},_{\gamma },_{\widetilde{\theta }}\ \left( \overline{V}\right) \end{aligned}$$

leading to a strictly monotonic relationship available in practice (cf. Fig. 58, p. 126 in [16]).

Once the new value of the capillary force known with such kinds of abacus, it may be compared with the vertical resulting capillary force applied on the upper sphere before the coalescence through formula (10). The jump of the capillary force observed experimentally may be calculated analytically by this way. Let us quote that these deterministic formulas do not take into account the complex hysteresis effects during a wetting-drying cycle, and a fortiori the sensitivity due to the impurities and roughness that affect the wetting angle $\theta$.

6.1 Contribution of the surface tension of the liquid

Before the coalescence, the length of the total triple line on the upper sphere is $2\pi r$, which corresponds to the perimeter at the equator of the sphere.³ However, to take into account the composition rule of the forces, the effective length to be considered is $\sqrt{3}\pi r$, according to formula (10). Otherwise, after coalescence, the triple line is a skew curve plotted on the boundary of the lower spherical cap of the upper grain, whose base is the horizontal disk of radius $\frac{\sqrt{3}}{2}r$ (corresponding to the radius of the spherical cap joining the upper extremities of the triple line), centered on the vertical axis (Fig. 7). Its perimeter is given exactly by the abstract formula (28).

Even expression (28) is not easy to use in practice, the first mean value theorem for integration implies that the perimeter may be calculated as the perimeter of a circle of radius $z_0$ given by

$$\begin{aligned}&z_{0}=z\left( \rho _{s}\left( \varphi _{0}\right) ,\varphi _{0}\right) \sqrt{1+\dfrac{\left( \dfrac{d\rho _{s}\left( \varphi _{0}\right) }{d\varphi }\right) ^{2}}{z^{2}\left( \rho _{s}\left( \varphi _{0}\right) ,\varphi _{0}\right) }}\nonumber \\&\quad \text {where}\quad \varphi _{0}\in \left] 0,\frac{\pi }{2}\right[. \end{aligned}$$

(31)

Moreover, we have $z\left( \rho _{s}\left( \varphi _{0}\right) ,\varphi _{0}\right) <\frac{\sqrt{3}}{2}r$ as we have after coalescence, a small decrease of the filling angle, due to the sudden filling of the central void of the equilateral triangle (cf. Fig. 3). A graphic evaluation of $z\left( \rho _{s}\left( \varphi _{0}\right) ,\varphi _{0}\right)$ leads to an indicative value close to $\frac{\sqrt{2}}{2}r$. As a consequence, the multiplicative coefficient resulting form accounting for the torsion does not have a significant influence on the new length of the triple line, in the sense of the remarked quantitative jump for the cohesion effect.

However, the effect of the whole triple line length is not the only one involved in the sudden variation of the capillary force. In order to fix ideas, we assume that the fluid used is glycerol whose contact angle on glass ballotini is measured to be $50^{\circ }$ as in [16]. According to formulas (10) and (30), using a similar argument, we may establish that the vertical component of the surface tension force cannot increase very suddenly, but presents a very low increase. To do this, let us compute the ratio of the vertical components of the surface tension force after and before coalescence, i.e.:

$$\begin{aligned}&\dfrac{2z\left( \rho _{s}\left( \varphi _{1}\right) ,\varphi _{1}\right) }{\sqrt{3}r}\ \ \ \ \sqrt{1+\dfrac{\left( \dfrac{d\rho _{s}\left( \varphi _{1}\right) }{d\varphi }\right) ^{2}}{z^{2}\left( \rho _{s}\left( \varphi _{1}\right) ,\varphi _{1}\right) }}\nonumber \\&\qquad \times \dfrac{\sin \left( \delta \left( \varphi _{1}\right) +\widetilde{\theta }\right) }{\sin \left( \dfrac{\pi }{6}+\theta \right) },\quad \varphi _{1}\in \left] 0,\frac{\pi }{2}\right[ \end{aligned}$$

(32)

The three following observations must be done.

• (i) The wetting angles $\theta$ and $\widetilde{\theta }$ concern the same liquid and are a priori equal.

• (ii) According to relation (30), the inequality $z\left( \rho _{s}\left( \varphi _{1}\right) ,\varphi _{1}\right) <\frac{\sqrt{3}}{2}r$ is still valid, so that the first factor is lower than 1 (probably close to $\frac{\sqrt{2}}{\sqrt{3}}$, using graphic considerations). However, we must take into account the amplification factor

  $$\begin{aligned} \sqrt{1+\dfrac{\left( \dfrac{d\rho _{s}\left( \varphi _{1}\right) }{d\varphi }\right) ^{2}}{z^{2}\left( \rho _{s}\left( \varphi _{1}\right) ,\varphi _{1}\right) }} \end{aligned}$$

  (33)

  due to the torsion of the new triple line.

• (iii) The angle $\delta \left( \varphi _{1}\right) +$ $\widetilde{\theta }$ resulting from the first mean value theorem for integration is, in the frame of Rynhart et al. [16], certainly bounded by the values $80^{\circ }$ and $105^{\circ }$, with a value close to the center of this interval. It is comprised in an interval whose range is linked to the torsion of the triple line. This value must be compared with the $80^{\circ }$ angle involved in the formula (10) corresponding to the instant just before the coalescence. So that this third factor implied in formula (32) has a very low amplification effect. Therefore, it appears that the evolution of the surface tension to an increase play a minor role in the observed phenomenon; this is the key point to note.

Let us now perform another analysis of the evolution of the surface tension force at the coalescence, that will highlight point (ii), henceforth decisive to explain the sudden increase of the whole capillary force. As already noticed, just after the coalescence, the maximum value of the filling angle on the spheres decreases very slightly. So that, let $\frac{\pi }{3}-\varepsilon$ be the new maximum value of the filling angle of the upper particle,⁴ $\varepsilon >0$ being expressed in radians (see Fig. 7). This corresponds to a decrease of the liquid level on the upper sphere whose value is $\frac{\sqrt{3}}{2}\varepsilon r$ at the first order, if $\varepsilon$ is small. This decrease of the liquid level should mainly contribute to increase the suction value s and therefore to create an attractive effect through the modification of the mean curvature, after a relaxation time. The accurate calculus of the relative suction $\dfrac{\Delta s}{s}$ by shrinking turns out to be difficult.

However, we can prove that a positive gradient of the suction occurs and estimate its value. Indeed, let us consider the variation of the suction resulting from a retraction as in a drying process of a nodoid bridge between two spheres, at the coalescence instant, when the filling angle decreases of $\varepsilon$. Referring to formula (22) of [9] where $y_{\delta }^{*}$ denotes the gorge radius observed for a filling angle $\delta$ considered as the varying parameter, we have (Fig. 8):

$$\begin{aligned} s\left( \delta \right) =2\gamma \ \frac{y_{\delta }^{*}-r\sin \delta \ \sin \left( \delta +\theta \right) }{r^{2}\sin ^{2}\delta -y_{\delta }^{*2} }. \end{aligned}$$

(34)

In the sequel, we assume that the denominator is locally almost constant for $s>0$. That corresponds to the effective non degenerate nodoid case, before the limit case of the catenary,⁵ i.e. provided the following conditions are satisfied:

$$\begin{aligned} y_{\delta }^{*}-r\sin \delta \ \sin \left( \delta +\theta \right) >0\quad and\quad \ r\sin \delta -y_{\delta }^{*}>0. \end{aligned}$$

Fig. 8

Schematic description of the triple contact line on the upper sphere after coalescence (rough perspective view). C and $C'$ are the highest points. Just before the coalescence, the triple line consists in the two tangent circles of diameter AB and $AB'$. The circular arcs BC and $BC'$ represent the slight fall in the liquid level, causing the strengthening of the suction

In a neighboring of $\delta$, we obtain by differentiation:

$$\begin{aligned}&\dfrac{\Delta s}{s}\left( \delta \right) =\frac{\Delta y_{\delta }^{*}-r\sin \left( 2\delta +\theta \right) }{y_{\delta }^{*}-r\sin \delta \ \sin \left( \delta +\theta \right) }\,\Delta \delta \quad \text {with}\nonumber \\&\quad \Delta y_{\delta }^{*}\cong \frac{1}{2}\frac{r^{2}\sin 2\delta }{y_{\delta }^{*}}~\Delta \delta , \end{aligned}$$

(35)

In particular, for $\delta =\dfrac{\pi }{6}$ and $\Delta \delta =-\varepsilon$, we get the strictly positive value:

$$\begin{aligned} \dfrac{\Delta s}{s}\left( \dfrac{\pi }{6}\right) =\frac{r}{y_{\frac{\pi }{6} }^{*}}\ \frac{2y_{\frac{\pi }{6}}^{*}\sin \left( \dfrac{\pi }{3} +\theta \right) -r\dfrac{\sqrt{3}}{2}}{2y_{\frac{\pi }{6}}^{*}-r\sin \left( \dfrac{\pi }{6}+\theta \right) }\ \varepsilon . \end{aligned}$$

(36)

From numerical and graphical results of Murase et al. [13], p. 358, we notice that the orthogonal projection, on an horizontal plane, of the part of the capillary bridge stuck to the upper sphere has a quasi-ellipsoidal form denotes $\Xi$. This observation will be useful in the next for the calculus of Laplace pressure contribution in the vertical attractive force applied to the upper sphere. It will induce some remarks on the length of the triple line, without the mathematical precision of the last developments (mean value theorem for integration applied to the exact theoretical integral formula).

First, let us quote that the length of the triple line, which is a skew curve (this point is confirmed by the experiments of [11, 13, 16]), may be approached, in first approximation underestimating the solution, by the boundary of the projection $\Xi$ using an oval of basket-handle type, whose semi-major axis is $a=r\sin \left( \frac{\pi }{3}-\varepsilon \right)$ and semi-minor axis⁶ $b=a\frac{4-\sqrt{3}}{3}$. Therefore its perimeter is equal to $2\times \frac{8}{9}\pi r\sin \left( \frac{\pi }{3}-\varepsilon \right)$.

The difference between the perimeters of the effective triple lines (before and after coalescence), after correction to take into account the force composition, then reduces to:

$$\begin{aligned}&\pi r\left( \sqrt{3}-\frac{16}{9}\sin \left( \dfrac{\pi }{3}-\varepsilon \right) \right) \\&\quad \cong \pi r\left( \sqrt{3}-\frac{16}{9}\left( \dfrac{\sqrt{3}}{2}-\frac{\varepsilon }{2}\right) \right) \ \text {if } \varepsilon \text { is small}. \end{aligned}$$

This positive quantity, really overestimated because of the real torsion of the new triple line (an amplification factor similar to (33) should be introduced), would lead in first approximation to a decreasing of the surface tension. However, a torsion corrective factor of the order of value 1.13 would reverse the trend to opt for a greater perimeter of contact.

Anyway, this point cannot explain the sudden visible increase of the cohesive force measured on the upper sphere. In addition, the multiplicative parameter $\sin \left( \delta +\theta \right)$ linked to the solid–liquid interaction does not vary strongly. Finally, without modifying the conclusion, an approximate formula of the perimeter of an ellipse, by default or by excess, of Kepler ou Euler’s type, may be used:

$$\begin{aligned}&\pi r\sin \left( \dfrac{\pi }{3}-\varepsilon \right) \left( 1+\frac{4-\sqrt{3}}{3}\right) ,\\&\pi r\sqrt{2\sin ^{2}\left( \dfrac{\pi }{3}-\varepsilon \right) +2\left( \frac{4-\sqrt{3}}{3}\right) ^{2}}. \end{aligned}$$

As a consequence, although the surface tension force may present a small increase, only the hydrostatic force (linked to the capillary force) have a priori a significant influence on the phenomenon, as already noted in a previous different approach.

6.2 Contribution of the increase of contact surface area and suction force

According to the notations introduced previously, $\Xi$ denotes the orthogonal projection on a horizontal plane of the part of the capillary bridge stuck to the upper sphere. The quasi-ellipsoidal surface area implied in the calculus of the hydrostatic force (cf. Fig. 7), that may be considered as the effective section at the triple line, can be calculated using the exact formula of the area of an ellipse. We obtain:

$$\begin{aligned} \pi \dfrac{4-\sqrt{3}}{3}r^{2}\sin ^{2}\left( \dfrac{\pi }{3}-\varepsilon \right) . \end{aligned}$$

Let us recall that the inter-particle force of a liquid bridge (in this case adhered to three spheres) must be defined only at the contact line with a sphere. Nonetheless specifically for the two particles problem concerning axisymmetric liquid bridges, the “gorge method” and the contact line method (so-called “boundary method”) or the evaluation on any cross-section are equivalent according to the invariance property (see [9] for more explanations).

On the other hand, just before the coalescence, the effective surface involved corresponds to $\frac{\sqrt{3}}{4}\pi r^{2}$ and results from the composition of two concurring forces acting on the two inclined disks of radius $\frac{r}{2}$. Therefore, just after the coalescence, the increase of the surface area $\Delta {\mathcal {A}}$ stands as:

$$\begin{aligned} \Delta {\mathcal {A}}= & {} \pi r^{2}\left( \dfrac{4-\sqrt{3}}{3}\sin ^{2}\left( \dfrac{\pi }{3}-\varepsilon \right) -\dfrac{\sqrt{3}}{4}\right) \nonumber \\\cong & {} \pi r^{2}\left( 1-\dfrac{\sqrt{3}}{2}-\varepsilon \dfrac{\sqrt{3}}{6}\left( 4-\sqrt{3}\right) \right) . \end{aligned}$$

(37)

It is materialized by the difference of areas between the connected ellipsoidal form and the two tangent ellipses of semi-major and semi-minor axis $(r/2, r \sqrt{3} /4)$ (Fig. 7).

The increase of surface area $\Delta {\mathcal {A}}$ corresponds to the new contribution of the lower part of the upper sphere which is now in contact with the liquid, around the vertical axis (cf. Fig. 7). Numerically, at zero order in $\varepsilon$, we have

$$\begin{aligned} \dfrac{\Delta {\mathcal {A}}}{{\mathcal {A}}}=\dfrac{4\sqrt{3}}{3}-2\simeq \dfrac{30.9}{100} \end{aligned}$$

(38)

That corresponds to an increase of about $30\,\%$ compared to the effective surface area whose value is $\frac{\sqrt{3}}{4}\pi r^{2}$ (resulting from the composition of two concurring forces acting on the two inclined disks of radius $\frac{r}{2}$ just before the coalescence). Besides, this increase is amplified by the expected increase of the suction according to (36) as

$$\begin{aligned} \dfrac{\Delta {\mathcal {F}}_{suc}}{{\mathcal {F}}_{suc}}=\dfrac{\Delta {\mathcal {A}}}{{\mathcal {A}}}+\dfrac{\Delta s}{s}. \end{aligned}$$

(39)

This result must be compared to the increase of the order of $38\,\%$ of the capillary force observed experimentally at Sect. 2.

Conversely, the same considerations are valid to explain and measure the weakening by drying of a coalesced capillary bridge between three spheres. At the rupture, the surface tension force is weakly decreased by the evolution of the perimeter of the contact line involved in the composition of the concurring forces. Anyway, this effect is of low amplitude in comparison with the large decrease of the contact surface area and the decrease of the suction. According to Gras [11, pp. 102–103], a ratio of 0.7 is measured between the capillary force before and after the coalescence.

In summary, before the coalescence of the three nodoids, the filling has a little impact on the vertical cohesive force on the upper sphere. We have an antagonist aspect: the active contact area and the triple contact line length increase, whereas the suction decreases, leading to a relatively weak increase of the whole capillary force acting on the upper sphere. After coalescence, the observed jump results mainly from the effect of Laplace pressure: the suction and the active contact area increase. The evolution of the properties before and after the coalescence of three nodoids during the filling is summarized in Table 1.

Table 1 Evolution of the properties before and after the coalescence of three nodoids during the filling

Finally, it is well known by dimensional analysis that surface tension $\gamma$ has the dimension of force per unit length or of energy per unit area; consequently this parameter can be also measured in SI system as joules per square meter. So, $\gamma$ being constant at constant temperature, the free surface area of a capillary bridge is proportional to an energy, somehow stored as potential energy. Since the mechanical system evolves towards a state of minimum potential energy at fixed volume, the modified surface area of the resulting coalesced bridge, that leads to the change in energy, is necessarily less than the free surface area of the three disjoint bridges at coalescence time. The actual determination of this issue would require sophisticated numerical calculations and remains a delicate matter. The explicit calculation of the nodoids free area, namely $3\Sigma _{2} (\tau )$ with the notations (5) and (9), is obtained in practice by a numerical integration formula from a Hermite interpolation of the convex meridian via the differential element $y\left( x\right) \sqrt{1+y^{\prime 2}\left( x\right) }dx$.

7 Conclusions

The criteria for identifying quickly the nature of the meridian and providing exact parametric equations in order to calculate all the physical characteristics of bridges between two grains has been revisited in [9]. On the basis of the results obtained, we have considered the coalescence of three capillary bridges constituted of portions of nodoid with positive suction and attractive capillary force, as the only strongly stable case that may be encountered in practice (except in very specific situations). We have clearly demonstrated the origin of the sudden jump of the capillary force at the coalescence of three bridges between two grains, phenomenon experimentally observed and reported in the literature without elucidation. The additional strength in three particles agglomerate is due to both the significant increase for the area of the projection on a horizontal plane of the contact surface with the upper sphere and the greater suction while a slight increasing variation is expected in the surface tension force. In summary, the observed jump is essentially the result of the double effects of the Laplace pressure: greater suction acting on larger areas. Theoretical results are in good agreement with experimental data available in the literature.