Improved Delay-Dependent Approach to Passivity Analysis for Uncertain Neural Networks with Discrete Interval and Distributed Time-Varying Delays

Abstract

This paper is considered with the delay-dependent passivity analysis issue for uncertain neural networks with discrete interval and distributed time-varying delays. By constructing an augmented Lyapunov functional and combining integral inequality with approach to estimate the derivative of the Lyapunov–Krasovskii functional, which estimated some integral terms by Wirtinger’s inequality, sufficient conditions are established to ensure the passivity of the considered neural networks. Some useful information on the neuron activation function ignored in the existing literature is taken into account. Finally, numerical examples are given to illustrate the effectiveness of the proposed theoretical results.

1 Introduction

The dynamics of neural networks have been extensively considered in the past two decades because of their great significance for both practical and theoretical purposes, for examples bidirectional associative memories, optimization and signal processing, image processing, pattern recognition problems, and so on [3–5]. However, considerable effort has been devoted to analyzing the stability of neural networks without a time delay. In recent years, the stability of delayed neural networks has also received attention [6, 17, 18] since time delay is frequently encountered in neural networks. Moreover, it is often a source of instability and oscillation in a system. In [19], the authors considered the problem of global asymptotic stability for a class of generalized neural networks with interval time-varying delays. Delay-dependent stability criteria of uncertain Markovian jump neural networks with discrete interval and distributed time-varying delays have been presented in [13]. Delay neural networks can be classified into two categories: delay-independent and delay-dependent. Delay-independent criteria do not employ any information on the size of the delay, while delay-dependent criteria make use of such information at different levels. The problem of delay-dependent in neural networks has been extensively studied for the sake of theoretical interest as well as applicable considerations [12, 20]. In [20], the authors considered the problem of global asymptotic stability analysis for delayed neural networks. By using a matrix-based quadratic convex approach to derive a sufficient condition, the positive definiteness of chosen LKF can be ensured. As a result, the constraint P > 0 in both Kim (2011) and Zhang et al. (2013) is removed.

On the other hand, the passivity theory has also received a great deal of attention, see [7–9, 14, 21, 23, 24]. Passivity theory is closely related to the circuit analysis method. The main scope of passivity theory is that the passive properties of system can keep the system internally stable. The passication problem is also called as the passive control problem. The objective of passive control problem designs for a controller so that the resulting closed-loop system is passive. Because of this feature, the passivity and passication problems have been an active area of research in the past decades. Considering neural networks with time-varying delays, passivity conditions has been presented in [15]. The authors considered the problem of delay-dependent passivity conditions for uncertain neural networks with discrete and distributed time-varying delays, which improved the passivity conditions in [1, 2, 24]. Improved conditions for passivity of neural networks with a time-varying delay are proposed in [16, 25], which construct a delay-interval-dependent Lyapunov–Krasovskii functional (LKF). In [10], the authors considered passivity criteria for continuous-time neural networks with mixed time-varying delays. However, it is worth pointing out that there still exist some points waiting for the improvement. In most of the works above [12, 20, 25], the augmented Lyapunov matrix P must be positive definite. In our work, we will remove this restriction by assuming that P are only real matrices. By utilizing a new type, LKF and some estimating are assumed in [20]. Moreover, we consider passivity analysis for neural networks that provides a powerful tool for analyzing the stability of system, which obtained distributed delay such that the system is more applicable for solving the general problem of recognized patterns in a time-dependent signal.

Motivated by above discussing, this paper investigates the delay-dependent approach to passivity analysis for uncertain neural networks with discrete interval and distributed time-varying delays. Based on delay partitioning, a LKF is constructed to obtain several improved delay-dependent passivity conditions which guarantee the passivity of uncertain neural networks. We consider the additional useful terms with the distributed delays and estimate some integral terms by Wirtinger’s inequality provided a tighter lower bound than Jensen’s inequality, so integral inequalities derived by Jensen’s inequality lead to less conservative results and some techniques in [20]. These conditions are expressed in terms of linear matrix inequalities (LMIs), which can be solved numerically and efficiently by resorting to numerical algorithms. The effectiveness is verified by two illustrating examples.

Notation

$\mathcal {R}^{n}$ is the n-dimensional Euclidean space; $\mathcal {R}^{m\times n}$ denotes the set of m×n real matrices; I _n represents the n-dimensional identity matrix; λ(A) denotes the set of all eigenvalues of A; λ _max(A)= max{Re λ;λ∈λ(A)}; $C([0, t],\mathcal {R}^{n})$ denotes the set of all $\mathcal {R}^{n}$-valued continuous functions on [0,t]; $L_{2}([0, t],\mathcal {R}^{m})$ denotes the set of all the $\mathcal {R}^{m}$-valued square integrable functions on [0,t]. The notation X≥0 (respectively, X > 0) means that X is positive semidefinite (respectively, positive definite); diag(⋯ ) denotes a block diagonal matrix; $\left [ {\begin {array}{*{20}c} X & Y \\ \ast & Z \end {array}} \right ]$ stands for $\left [ {\begin {array}{*{20}c} X & Y \\ Y^{T} & Z \end {array}} \right ]$. Matrix dimensions, not explicitly stated, are assumed to be compatible for algebraic operations.

2 Preliminaries

Consider the following neural networks with discrete interval and distributed time-varying delays:

$$ \left\{ \begin{array}{l} \dot{x}(t)=-Ax(t)+Wg(x(t))+W_{1}g(x(t-\tau(t)))+W_{2}{\int}_{t-k(t)}^{t}g(x(s))\,ds + u(t),\\ y(t)=g(x(t)),\\ x(t)=\phi(t), \quad t\in[-\tau_{\max},0], \quad \tau_{\max}=\max\{\tau_{2},k\}, \end{array} \right. $$

(1)

where $x(t)=[x_{1}(t),x_{2}(t),\dots ,x_{n}(t)] \in \mathcal {R}^{n}$ is the state of the neural, A = diag(a ₁, a ₂,…,a _n ) > 0 represents the self-feedback term, W, W ₁ and W ₂ represent the connection weight matrices, g(⋅) = (g ₁(⋅), g ₂(⋅),…,g _n (⋅))^T represents the activation functions, u(t) and y(t) represent the input and output vectors, respectively; ϕ(t) is an initial condition. The variables τ(t) and k(t) are the discrete and distributed delays and satisfy the following conditions:

$$ 0\leq\tau_{1}\leq\tau(t)\leq\tau_{2},\quad 0\leq\dot\tau(t)\leq\mu<\infty,\quad 0\leq k(t)\leq k\quad \forall t\geq0, $$

(2)

where τ ₁, τ ₂, μ and k are constants. The neural activation functions g _k (⋅), k = 1,2,…,n satisfy g _k (0)=0 and for $s_{1}, s_{2} \in \mathcal {R}$, s ₁≠s ₂,

$$ l_{k}^{-} \le \frac{g_{k}(s_{1}) - g_{k}(s_{2})}{s_{1}-s_{2}} \le l_{k}^{+}, $$

(3)

where $l_{k}^{-}$, $l_{k}^{+}$ are known real scalars. Moreover, we denote $L^{+} = \text {diag}(l_{1}^{+},l_{2}^{+},\dots ,l_{n}^{+})$, $L^{-} = \text {diag}\left (l_{1}^{-}, l_{2}^{-},\dots , l_{n}^{-}\right )$.

Definition 1

[8] The neural network (1) is said to be passive if there exists a scalar γ such that for all t _f ≥ 0

$$2{\int}_{0}^{t_{f}}y(s)^{T}u(s)ds\geq-\gamma{\int}_{0}^{t_{f}}u(s)^{T}u(s)ds, $$

and for all solutions of (1) with x(0) = 0.

Lemma 1

Let $f_{1}, f_{2},\dots , f_{N}\in \mathcal {R}^{{m}}\rightarrow \mathcal {R}$ have positive values in an open subset $\mathcal {D}$ of $\mathcal {R}^{\mathrm {m}}$ . Then, the reciprocally convex combination of f _i over $\mathcal {D}$ satisfies

$$\min_{\{\alpha_{i} | \alpha_{i} > 0,{\sum}_{i} \alpha_{i} = 1\}} \sum\limits_{i} \frac{1}{\alpha_{i}}f_{i}(t) = \sum\limits_{i} f_{i}(t) + \max_{g_{i,j}(t)} \sum\limits_{i \ne j} g_{i,j}(t) $$

subject to

$$\left\{g_{i,j}(t): \mathcal{R}^{m} \to \mathcal{R}, g_{i,j} \buildrel {\Delta} \over = g_{i,j}(t), \left[\begin{array}{*{20}{c}} f_{i}(t)&g_{i,j}(t)\\ g_{i,j}(t)&f_{j}(t) \end{array} \right] \ge 0 \right\}. $$

Lemma 2

[6] For any symmetric positive definite matrix M > 0, a scalar γ > 0 and a vector function $x:[0,\gamma ]\rightarrow \mathcal {R}^{n}$ such that the integrations concerned are well defined, the following inequality holds:

$$\left( {\int}_{0}^{\gamma} x(s)ds\right)^{T}M\left( {\int}_{0}^{\gamma} x(s)ds\right) \leq \gamma\left( {\int}_{0}^{\gamma} x^{T}(s)Mx(s)ds\right). $$

Lemma 3

[12] For a given matrix R > 0, the following inequality holds for any continuously differentiable function $x:[a,b]\rightarrow \mathcal {R}^{n}$ ,

$${{{\int}_{a}^{b}}}\dot{x}^{T}(s)R\dot{x}(s)ds \geq\frac{1}{b-a}\left( {{{\Gamma}_{1}^{T}}} R{\Gamma}_{1}+3{{{\Gamma}_{2}^{T}}}R{\Gamma}_{2}\right), $$

where

$$\begin{array}{@{}rcl@{}} {\Gamma}_{1}&=&x(b)-x(a),\\ {\Gamma}_{2}&=&x(b)+x(a)-\frac{2}{b-a}{{{\int}_{a}^{b}}}x(s)ds. \end{array} $$

Lemma 4

[20] Let τ(t) be a continuous function satisfying 0 ≤ τ ₁ ≤ τ(t) ≤ τ ₂. For any n × n real matrix R ₁ > 0 and a vector $\dot {x}:[-\tau _{2},0]\rightarrow \mathcal {R}^{n}$ such that the integration concerned below is well defined, the following inequality holds for any 2n × 2n real matrices D satisfying $\left [ \begin {array}{cc} \bar {R}_{1} &D\\ \ast &\bar {R}_{1} \end {array}\right ]\geq 0$, and

$$-(\tau_{2}-\tau_{1}){\int}_{t-\tau_{2}}^{t-\tau_{1}}\dot{x}^{T}(s)R_{1}\dot{x}(s)ds \leq2\varphi_{11}^{T}D\varphi_{21}-\varphi_{11}^{T}\bar{R}_{1}\varphi_{11}-\varphi_{21}^{T}\bar{R}_{1}\varphi_{21}, $$

where $\bar {R_{1}}=\text {diag}\{R_{1},3R_{1}\}$ and

$$\begin{array}{@{}rcl@{}} \varphi_{11}&=&\left[\begin{array}{cc} x(t-\tau(t))-x(t-\tau_{2})\\ x(t-\tau(t))+x(t-\tau_{2})-\frac{2}{\tau_{2}-\tau(t)}{\int}_{t-\tau_{2}}^{t-\tau(t)}x(s)ds \end{array}\right],\\ \varphi_{21}&=&\left[\begin{array}{cc} x(t-\tau_{1})-x(t-\tau(t))\\ x(t-\tau_{1})+x(t-\tau(t))-\frac{2}{\tau(t)-\tau_{1}}{\int}_{t-\tau(t)}^{t-\tau_{1}}x(s)ds \end{array}\right]. \end{array} $$

Lemma 5

[20] Let τ(t) be a continuous function satisfying 0 ≤ τ ₁ ≤ τ(t) ≤ τ ₂. For any n × n real matrix R ₂ > 0 and a vector $\dot {x}:[-\tau _{2},0]\rightarrow \mathcal {R}^{n}$ such that the integration concerned below is well defined, the following inequality holds for any $\phi _{i1}\in \mathcal {R}^{q}$ and real matrices $Z_{i}\in \mathcal {R}^{q\times q}$, $B_{i}\in \mathcal {R}^{q\times n}$ satisfying $\left [ \begin {array}{cc} Z_{i} &B_{i}\\ \ast &R_{2} \end {array}\right ]\geq 0 \ (i=1,2)$ and

$$\begin{array}{@{}rcl@{}} -{\int}_{t-\tau_{2}}^{t-\tau_{1}}(\tau_{2}-t+s)\dot{x}^{T}(s)R_{2}\dot{x}(s)ds &\leq&\frac{1}{2}(\tau_{2}-\tau(t))^{2}\phi_{11}^{T}Z_{1}\phi_{11}+2(\tau_{2}-\tau(t))\phi_{11}^{T}B_{1}\phi_{12}\\ &&+\frac{1}{2}[(\tau_{2}-\tau_{1})^{2}-(\tau_{2}-\tau(t))^{2}]\phi_{21}^{T}Z_{2}\phi_{21}\\ &&+2\phi_{21}^{T}B_{2}[(\tau_{2}-\tau(t)\phi_{22}+(\tau(t)-\tau_{1})\phi_{23}], \end{array} $$

where

$$\begin{array}{@{}rcl@{}} \phi_{12}&=&x(t-\tau(t))-\frac{1}{\tau_{2}-\tau(t)}{\int}_{t-\tau_{2}}^{t-\tau(t)}x(s)ds,\\ \phi_{22}&=&x(t-\tau_{1})-x(t-\tau(t)),\\ \phi_{23}&=&x(t-\tau_{1})-\frac{1}{\tau(t)-\tau_{1}}{\int}_{t-\tau(t)}^{t-\tau_{1}}x(s)ds. \end{array} $$

Lemma 6

[20] Let $\mathcal {P}_{0}$, $\mathcal {P}_{1}$, and $\mathcal {P}_{2}$ be m × m real symmetric matrices and a scalar continuous function τ satisfy τ ₁ ≤ τ ≤ τ ₂ where τ ₁ and τ ₂ are constants satisfying 0 ≤ τ ₁ ≤ τ ₂. If $\mathcal {P}_{0} \geq 0$, then

$$\begin{array}{@{}rcl@{}} \tau^{2}\mathcal{P}_{0}+\tau\mathcal{P}_{1}+\mathcal{P}_{2}<0 (\leq 0) \forall\tau\in [\tau_{1},\tau_{2}] &\Longleftrightarrow& {{\tau_{i}^{2}}}\mathcal{P}_{0}+\tau_{i}\mathcal{P}_{1}+\mathcal{P}_{2}<0 (\leq 0), i=1,2,\\ \tau^{2}\mathcal{P}_{0}+\tau\mathcal{P}_{1}+\mathcal{P}_{2}>0 (\geq 0) \forall\tau\in [\tau_{1},\tau_{2}] &\Longleftrightarrow&{{\tau_{i}^{2}}}\mathcal{P}_{0}+\tau_{i}\mathcal{P}_{1}+\mathcal{P}_{2}>0 (\geq 0), i=1,2. \end{array} $$

Lemma 7

[6] Let H,E and F(t) be real matrices of appropriate dimensions with F(t) satisfying F ^T (t)F(t) < I. Then, for any scalar > 0,

$$HF(t)E+(HF(t)E)^{T}\leq\epsilon^{-1}HH^{T}+\epsilon E^{T}E. $$

Lemma 8

[6] (Schur complement) Given constant symmetric matrices X, Y, Z with appropriate dimensions satisfying X = X ^T, Y = Y ^T > 0. Then X + Z ^T Y ⁻¹ Z < 0 if and only if

$$\begin{pmatrix} X&Z^{T} \\ Z&-Y \end{pmatrix} <0 \quad\text{ or} \quad \begin{pmatrix} -Y&Z \\ Z^{T}&X \end{pmatrix} <0. $$

3 Main Results

In this section, we consider robust passivity of the neural networks (1) with interval time-varying delays. For the sake of simplicity, we consider the LKF as

$$ V(x_{t})=V_{1}(x_{t})+V_{2}(x_{t})+V_{3}(x_{t})+V_{4}(x_{t})+V_{5}(x_{t}), $$

(4)

where

$$\begin{array}{@{}rcl@{}} V_{1}(x_{t})&=&\eta^{T}(t)P\eta(t)+{\int}_{t-\tau_{1}}^{t}\dot{x}^{T}(s)Q_{0}\dot{x}(s)ds\\ &&+2\sum\limits_{k=1}^{n} \rho_{k} {\int}_{0}^{x(t)}[g_{k}(s)-l_{k}^{-}s]ds + 2\sum\limits_{k=1}^{n} \sigma_{k} {\int}_{0}^{x(t)}[l_{k}^{+}s-g_{k}(s)]ds,\\ V_{2}(x_{t})&=&{\int}_{t-\tau_{1}}^{t}\left\{x^{T}(s) Q_{1}{x}(s) + g^{T}(x(s)) S_{1}g(x(s))\right\} ds \\ &&+{\int}_{t-\tau(t)}^{t-\tau_{1}}\left\{x^{T}(s) Q_{2}{x}(s) + g^{T}(x(s)) S_{2} g(x(s))\right\} ds \\ &&+{\int}_{t-\tau_{2}}^{t-\tau(t)}\left\{x^{T}(s) Q_{3}x(s) + g^{T}(x(s)) S_{3} g(x(s)) \right\} ds, \\ V_{3}(x_{t})&=&{\int}_{t-\tau_{1}}^{t}\left\{\tau_{1}(\tau_{1}-t+s) \dot{x}^{T}(s) Y_{1}\dot{x}(s) + (\tau_{1}-t+s )^{2}\dot{x}^{T}(s) Y_{2}\dot{x}(s)\right\} ds, \\ V_{4}(x_{t})&=&{\int}_{t-\tau_{2}}^{t-\tau_{1}} \left\{\tau_{21}(\tau_{2}-t+s )\dot{x}^{T}(s) R_{1}\dot{x}(s) + (\tau_{2}-t+s)^{2}\dot{x}^{T}(s)R_{2}\dot{x}(s)\right\}ds,\\ V_{5}(x_{t})&=&k{\int}_{-k}^{0}{\int}_{t+\theta}^{t}g^{T}(x(s)) S_{0} g(x(s))ds d\theta, \end{array} $$

where $\eta (t)=\text {col}\{x(t), x(t-\tau _{1}),{\int }_{t-\tau _{1}}^{t}x(s)ds, {\int }_{t-\tau (t)}^{t-\tau _{1}}x(s)ds, {\int }_{t-\tau _{2}}^{t-\tau (t)}x(s)ds\}$, Q _i > 0, S _i > 0, Y ₁ > 0, Y ₂ > 0, R ₁ > 0, R ₂ > 0, (i = 0, 1, 2, 3), U ₁ = diag{ρ ₁, ρ ₂,…,ρ _n } ≥ 0, U ₂ = diag{σ ₁, σ ₂,…,σ _n } ≥ 0 are to be determined, a real matrix P with appropriate dimension, τ ₂₁ = τ ₂−τ ₁ and let

$$\begin{array}{@{}rcl@{}} x(t)&=&G_{1}\upsilon(t), \\ g(x(t))&=&G_{2}\upsilon(t), \end{array} $$

where υ(t)=col{x(t),g(x(t))}, G ₁ = [I,0] and G ₂ = [0,I].

For the sake of simplicity on matrix representation, e _i (i = 1,2,…,11) are defined as block-row vectors of the 11n×11n identity matrix (For example, e ₃ = [0 0 I 0 0 0 0 0 0 0 0]) and v(t) = e ₁ ζ(t), $v(t-\tau (t))=e_{2}\zeta (t),\dots ,\dot {x}(t-\tau _{1})=e_{11}\zeta (t)$ such that the notations of several matrices are defined as:

$$\begin{array}{@{}rcl@{}} \zeta(t)&=&\text{col}\left\{v(t),v(t-\tau(t)),v(t-\!\tau_{1}),v(t-\tau_{2}),\frac{1}{\tau_{1}}{\int}_{t-\tau_{1}}^{t}\!\!\!\!x(s)ds, \frac{1}{\tau(t)-\tau_{1}}{\int}_{t-\tau(t)}^{t-\tau_{1}}\!\!\!\!x(s)ds,\right.\\ &&\qquad\left.\frac{1}{\tau_{2}-\tau(t)}{\int}_{t-\tau_{2}}^{t-\tau(t)}x(s)ds,{\int}_{t-k}^{t}g(x(s))ds, u(t),\dot{x}(t), \dot{x}(t-\tau_{1})\right\}. \end{array} $$

We apply a matrix-based quadratic convex approach combined with some improved boundary techniques for integral terms such as Wirtinger-based integral inequality; as a result, we obtain inequality encompassing the Jensen’s inequality and also go to tractable LMIs criteria to further reduce the conservatism over the existing results to derive a sufficient condition.

Remark 1

It is shown that using Lemmas 3, 4, 5 one can obtain some less conservative results than the other results [16, 25] that show the effectiveness in Table 1. However, these lemmas contain many free-weighting matrices which may lead to higher computational complexity than them.

Table 1 Allowable upper bounds of τ ₂ for μ

Remark 2

Those of [9, 24], previous works only focused on some augment vectors but our work includes not only x(t), ${\int }_{t-\tau _{1}}^{t}x(s)ds$ but also x(t), x(t−τ ₁), ${\int }_{t-\tau _{1}}^{t}x(s)ds$, ${\int }_{t-\tau (t)}^{t-\tau _{1}}x(s)ds$, ${\int }_{t-\tau _{2}}^{t-\tau (t)}x(s)ds$. We can see that the adaptation of new augmented variables, cross terms of variables and more multiple integral terms may lead to reduce to the conservatism.

Proposition 1

[20] For the Lyapunov–Krasovskii functional (4), and prescribed scalars τ ₂ ≥ τ ₁ > 0, there exist scalars 𝜖 ₁ > 0 and 𝜖 ₂ > 0 such that

$$ \epsilon_{1}\|x\|^{2}\leq V(t,x_{t},\dot x_{t})\leq \epsilon_{2}\|x_{t}\|_{W}^{2}, $$

(5)

if there exist real matrices M ₁ and N ₁ with appropriate dimensions such that

$$ \left\{\begin{array}{c} \left[\begin{array}{cc} M_{1} & N_{1}\\ {{N_{1}^{T}}}&Y_{1} \end{array}\right]\geq0,\quad {\Omega}_{0}\geq0,\quad \tilde{e}_{1}P\tilde{e}_{1}^{T}>0, \\ {{\tau_{1}^{2}}}{\Omega}_{0}+\tau_{1}{\Omega}_{1}+{\Omega}_{2}\geq0, \quad {{\tau_{2}^{2}}}{\Omega}_{0}+\tau_{2}{\Omega}_{1}+{\Omega}_{2}\geq0, \end{array}\right. $$

(6)

where

$$\begin{array}{@{}rcl@{}} {\Omega}_{0}&=&\mathcal{D}_{2}^{T}P\mathcal{D}_{2},\\ {\Omega}_{1}&=&\mathcal{D}_{1}^{T}P\mathcal{D}_{2}+\mathcal{D}_{2}^{T}P\mathcal{D}_{1}+\mathcal{C}_{4}-\mathcal{C}_{5},\\ {\Omega}_{2}&=&{\Omega}_{3}+{\Omega}_{4}+\mathcal{C}_{3}-\tau_{1}\mathcal{C}_{4}+\tau_{2}\mathcal{C}_{5}+\mathcal{D}_{1}^{T}P\mathcal{D}_{1}-\tilde{e}_{1}^{T}\tilde{e}_{1}P\tilde{e}_{1}^{T}\tilde{e}_{1}, \end{array} $$

with

$$\begin{array}{@{}rcl@{}} \mathcal{D}_{1}&=&\text{col}\{\tilde{e}_{1}, \tilde{e}_{2}, \tau_{1}\tilde{e}_{3}, -\tau_{1}\tilde{e}_{4}, \tau_{2}\tilde{e}_{5}\},\\ \mathcal{D}_{1}&=&\text{col}\{0,0,0, \tilde{e}_{4}, -\tilde{e}_{5}\},\\ {\Omega}_{3}&=&\left( \mathcal{C}_{1}^{T}U\mathcal{C}_{1}+3\mathcal{C}_{2}^{T}U\mathcal{C}_{2}\right)/\tau_{1},\\ {\Omega}_{4}&=&\tau_{1}(\tilde{e}_{1}-\tilde{e}_{3})^{T} Y_{2} (\tilde{e}_{1}-\tilde{e}_{3})-\left( {{\tau_{1}^{3}}}/2\right)\mathcal{C}_{6}^{T} M_{1}\mathcal{C}_{6} - {{\tau_{1}^{2}}}(\tilde{e}_{1}-\tilde{e}_{3})^{T}{{N_{1}^{T}}}\\ &&-{{\tau_{1}^{2}}}\mathcal{C}_{6}^{T}N_{1}(\tilde{e}_{1}-\tilde{e}_{3})\mathcal{C}_{6},\\ \mathcal{C}_{1}&=&\tilde{e}_{1}-\tilde{e}_{2}, \quad \mathcal{C}_{2}=\tilde{e}_{1}+\tilde{e}_{2}-2\tilde{e}_{3},\\ \mathcal{C}_{3}&=&\tau_{1}\left[\tilde{e}_{1}^{T} \tilde{e}_{4}^{T}\right]Q_{1}\left[\tilde{e}_{1}^{T} \tilde{e}_{4}^{T}\right]^{T},\quad \mathcal{C}_{4}=\left[\tilde{e}_{1}^{T} \tilde{e}_{4}^{T}]Q_{2}[\tilde{e}_{1}^{T} \tilde{e}_{4}^{T}\right]^{T},\\ \mathcal{C}_{5}&=&\left[\tilde{e}_{1}^{T} \tilde{e}_{5}^{T}\right]Q_{3}\left[\tilde{e}_{1}^{T} \tilde{e}_{5}^{T}\right]^{T},\quad \mathcal{C}_{6}=\text{col}\{\tilde{e}_{1}, \tilde{e}_{2}, \tilde{e}_{2} \}. \end{array} $$

Proof

By [20] and $V_{5}(x_{t})\leq k^{2}\max \{\lambda _{s_{0}}\}\|x_{t}\|_{W}^{2}$. □

Remark 3

The constraint P > 0 is removed from Proposition 1. Thus, we can see that the introduction of the vector ζ(t) plays a key role in deriving a quadratic convex combination Σ(τ(t)). So, a matrix-based quadratic convex technique can be used to design an LMI-based sufficient condition.

Then, we have the following result.

Theorem 1

Given scalars τ ₁, τ ₂ and k, the system (1) with (3) is passive for any delays τ(t) and k(t) satisfying (2) if there exist real matrices Q _i > 0, S _i > 0, Y ₁ > 0, Y ₂ > 0, R ₁ > 0, R ₂ >0 (i = 0, 1, 2, 3), real positive diagonal matrices U ₁, U ₂, T _s , T _ab (s = 1, 2, 3, 4; a = 1, 2, 3; b = 2, 3, 4; a < b), real matrices M ₂, N ₂, Z ₁, Z ₂, B ₁, B ₂, D, X ₁, X ₂ and P with appropriate dimensions, and a scalar γ > 0 such that the following linear matrix inequalities hold:

$$\begin{array}{@{}rcl@{}} &&\left\{ \begin{array}{l} \boldsymbol{\Sigma}(\tau(t),\dot\tau(t)) <0|_{\tau(t)=\tau_{1}, \dot\tau(t)=0},\\ \boldsymbol{\Sigma}(\tau(t),\dot\tau(t)) <0|_{\tau(t)=\tau_{1}, \dot\tau(t)=\mu},\\ \boldsymbol{\Sigma}(\tau(t),\dot\tau(t)) <0|_{\tau(t)=\tau_{2}, \dot\tau(t)=0},\\ \boldsymbol{\Sigma}(\tau(t),\dot\tau(t)) <0|_{\tau(t)=\tau_{2}, \dot\tau(t)=\mu}, \end{array} \right. \end{array} $$

(7)

$$\begin{array}{@{}rcl@{}} &&\left\{ \begin{array}{l} \left[\begin{array}{cc} M_{2} & N_{2}\\ \star&Y_{2} \end{array}\right]>0, \quad \left[\begin{array}{cc} \bar{R}_{1} &D\\ \star &\bar{R}_{1} \end{array}\right]>0, \quad Z_{1}>Z_{2},\\ \left[\begin{array}{cc} Z_{1} & B_{1}\\ \star& {R}_{2} \end{array}\right]>0, \quad \left[\begin{array}{cc} Z_{2} &B_{2}\\ \star&R_{2} \end{array}\right]>0, \end{array} \right. \end{array} $$

(8)

where $\bar {R_{1}} = \text {diag}\{R_{1},3R_{1}\}$ and

$$\begin{array}{@{}rcl@{}} \boldsymbol{\Sigma}(\tau(t),\dot\tau(t))&=&{\Sigma}_{11}+{\Sigma}_{12}+{\Sigma}_{2}+{\Sigma}_{3}+{\Sigma}_{4}+{\Sigma}_{5}+{\Sigma}_{6}+{\Sigma}_{7}\\ &&-{{e_{9}^{T}}}G_{2}e_{1}-{{e_{1}^{T}}}{{G_{2}^{T}}}e_{9}-\gamma {{e_{9}^{T}}}e_{9}, \end{array} $$

(9)

$$\begin{array}{@{}rcl@{}} {\Sigma}_{11}&=& ({\Theta}_{1}+\tau(t){\Theta}_{2})^{T}P({\Theta}_{3}+\dot\tau(t){\Theta}_{4})+({\Theta}_{3}+\dot\tau(t){\Theta}_{4})^{T}P({\Theta}_{1}+\tau(t){\Theta}_{2})\\ && +e_{10}^{T}Q_{0} e_{10}-e_{11}^{T}Q_{0} e_{11}, \end{array} $$

(10)

$$\begin{array}{@{}rcl@{}} {\Sigma}_{12}&=&({\Pi}_{1}+{\Pi}_{2})^{T}+{\Pi}_{1}+{\Pi}_{2}, \end{array} $$

(11)

$$\begin{array}{@{}rcl@{}} {\Sigma}_{2}&=& (1-\dot\tau(t)){\Pi}_{3}+{\Pi}_{4}, \end{array} $$

(12)

$$\begin{array}{@{}rcl@{}} {\Sigma}_{3}&=& e_{10}^{T}({{\tau_{1}^{2}}}Y_{1}+{{\tau_{1}^{2}}}Y_{2})e_{10} -{{\phi_{1}^{T}}} \text{diag}\{Y_{1},3Y_{1}\}\phi_{1} \\ && +2\tau_{1}[N_{2}(G_{1}e_{1}-e_{5})+(G_{1}e_{1}-e_{5})^{T}{{N_{2}^{T}}}] + {{\tau_{1}^{2}}}M_{2}, \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}} {\Sigma}_{4}&=& (\tau_{2}-\tau(t))^{2}(Z_{1}-Z_{2})+(\tau_{2}-\tau(t)){\Pi}_{5} +(\tau(t)-\tau_{1}){\Pi}_{6}+{\Pi}_{7}, \end{array} $$

(14)

$$\begin{array}{@{}rcl@{}} {\Sigma}_{5}&=& {{e_{1}^{T}}}{{G_{2}^{T}}}S_{0}G_{2}e_{1}-{{e_{8}^{T}}}S_{0}e_{8}, \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}} {\Sigma}_{6}&=& {{{\Pi}_{8}^{T}}}{\Pi}_{9}+{{{\Pi}_{9}^{T}}}{\Pi}_{8}, \end{array} $$

(16)

$$\begin{array}{@{}rcl@{}} {\Sigma}_{7}&=&\sum\limits_{a=1}^{3}\sum\limits_{b=2,b>a}^{4}(e_{a}-e_{b})^{T} {\Pi}^{T}_{10} T_{ab} {\Pi}_{11}(e_{a}-e_{b}) \\ && + \sum\limits_{a=1}^{3}\sum\limits_{b=2,b>a}^{4}(e_{a}-e_{b})^{T} {\Pi}^{T}_{11} T_{ab} {\Pi}_{10}(e_{a}-e_{b}) \\ && + \sum\limits_{s=1}^{4} \left( {{e_{s}^{T}}}{\Pi}^{T}_{10} T_{s} {\Pi}_{11}e_{s} + {{e_{s}^{T}}} {\Pi}^{T}_{11} T_{s} {\Pi}_{10}e_{s}\right), \end{array} $$

(17)

with

$$\begin{array}{@{}rcl@{}} {\Theta}_{1}&=& \text{col}\{G_{1}e_{1}, G_{1}e_{3}, \tau_{1}e_{5}, -\tau_{1}e_{6}, \tau_{2}e_{7}\},\\ {\Theta}_{2}&=& \text{col}\{0, 0, 0, e_{6}, -e_{7}\},\\ {\Theta}_{3}&=& \text{col}\{e_{10}, e_{11}, G_{1}(e_{1}-e_{3}), G_{1}(e_{3}-e_{2}),G_{1}(e_{2}-e_{4})\},\\ {\Theta}_{4}&=& \text{col}\{0, 0, 0, G_{1}e_{2}, -G_{1}e_{2}\}, \end{array} $$

$$\begin{array}{@{}rcl@{}} {\Pi}_{1} &=& {{e_{1}^{T}}}{{G_{2}^{T}}}(U_{1}-U_{2})e_{10},\\ {\Pi}_{2} &=& {{e_{1}^{T}}}{{G_{1}^{T}}}(L^{+}U_{2}-L^{-}U_{1})e_{10},\\ {\Pi}_{3} &=& (G_{1}e_{2})^{T}(Q_{3}-Q_{2})(e_{1}G_{2})^{T}+(G_{2}e_{2})^{T}(S_{3}-S_{2})(G_{2}e_{2}),\\ {\Pi}_{4} &=& (G_{1}e_{1})^{T}Q_{1}(G_{1}e_{1})-(G_{1}e_{4})^{T}Q_{3}(G_{1}e_{4})+(G_{1}e_{3})^{T}(Q_{2}-Q_{1})(G_{1}e_{3})\\ && +(G_{2}e_{1})^{T}S_{1}(G_{2}e_{1})-(G_{2}e_{4})^{T}S_{3}(G_{2}e_{4})+(G_{2}e_{3})^{T}(S_{2}-S_{1})(G_{2}e_{3}),\\ {\Pi}_{5} &=& 2B_{1}(G_{1}e_{2}-e_{7})+2(G_{1}e_{2}-e_{7})^{T}{{B_{1}^{T}}}+2B_{2}G_{1}(e_{3}-e_{2})+2(e_{3}-e_{2})^{T}{{G_{1}^{T}}}{{B_{2}^{T}}},\\ {\Pi}_{6} &=& 2B_{2}(G_{1}e_{3}-e_{6})+2(G_{1}e_{3}-e_{6})^{T}{{B_{2}^{T}}},\\ {\Pi}_{7} &=& e_{11}^{T}\left( \tau_{21}^{2}R_{1}+\tau_{21}^{2}R_{2}\right)e_{11}+\tau_{21}^{2}Z_{2}+{{\phi_{2}^{T}}}D\phi_{3} + {{\phi_{3}^{T}}}D\phi_{2}+{{\phi_{2}^{T}}}\bar{R}_{1}\phi_{2}+{{\phi_{3}^{T}}}\bar{R}_{1}\phi_{3},\\ {\Pi}_{8} &=& {{e_{1}^{T}}}{{G_{1}^{T}}} X_{1}+e_{10}^{T} X_{2},\\ {\Pi}_{9} &=& -AG_{1}e_{1}+WG_{2}e_{1}+W_{1}G_{2}e_{2}+W_{2}e_{8}+e_{9}-e_{10},\\ {\Pi}_{10}&=& G_{2}-L^{-}G_{1},\\ {\Pi}_{11}&=& L^{+}G_{1}-G_{2}. \end{array} $$

Proof

Differentiating V(x _t ) along the solution of (1), we get

$$\begin{array}{@{}rcl@{}} \dot{V}_{1}(x_{t})&=& \eta^{T}(t) P\dot{\eta}(t)+\dot{\eta}^{T}(t) P\eta(t)+\dot{x}^{T}(t) Q_{0}\dot{x}(t) - \dot{x}^{T}(t-\tau_{1}) Q_{0}\dot{x}(t-\tau_{1})\\ &&+2\sum\limits_{k=1}^{n}\left\{\rho_{k} \dot{x}(t)[g_{k}(x(t))-l_{k}^{-}]+\sigma_{k} \dot{x}(t)[l_{k}^{+}-g_{k}(x(t))]\right\}\\ &=&\zeta^{T}(t)[({\Theta}_{1}+\tau(t){\Theta}_{2})^{T}P({\Theta}_{3}+\dot\tau(t){\Theta}_{4})+({\Theta}_{3}+\dot\tau(t){\Theta}_{4})^{T}P({\Theta}_{1}+\tau(t){\Theta}_{2})\\ &&+e_{10}^{T}Q_{0} e_{10}-e_{11}^{T}Q_{0} e_{11}+({\Pi}_{1}+{\Pi}_{2})^{T}+{\Pi}_{1}+{\Pi}_{2}] \zeta(t), \\ &=&\zeta^{T}(t) ({\Sigma}_{11}+{\Sigma}_{12}) \zeta(t), \end{array} $$

(18)

$$\begin{array}{@{}rcl@{}} \dot{V}_{2}(x_{t})&=&x^{T}(t)Q_{1}x(t)+g^{T}(x(t)) S_{1}g(x(t))-x^{T}(t)(t-\tau_{2}) Q_{3}x(t-\tau_{2})\\ &&-g^{T}(x(t-\tau_{2}))S_{3}g(x(t-\tau_{2}))+x^{T}(t-\tau_{1}) (Q_{2}-Q_{1})x(t-\tau_{1})\\ &&+g^{T}(x(t-\tau_{1}))(S_{2}-S_{1})g(x(t-\tau_{1}))+(1-\dot\tau(t))\left\{x^{T}(t-\tau(t))\right.\\ &&\left.\times(Q_{3}-Q_{2})x(t-\tau(t))+g^{T}(x(t-\tau(t)))(S_{3}-S_{2})g(x(t-\tau(t)))\right\},\\ &=&\zeta^{T}(t) {\Sigma}_{2} \zeta(t), \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}} \dot{V_{3}}(x_{t})&=&{{\tau_{1}^{2}}}\dot{x}^{T}(t)(Y_{1}+Y_{2})\dot{x}(t)-{\int}_{t-\tau_{1}}^{t}\tau_{1}\dot{x}^{T}(s)Y_{1}\dot{x}(s)ds \\ &&- {\int}_{t-\tau_{1}}^{t}2(\tau_{1}-t+s) \dot{x}^{T}(s) Y_{2}\dot{x}(s)ds, \end{array} $$

(20)

$$\begin{array}{@{}rcl@{}} \dot{V_{4}}(x_{t})&=&\tau_{21}^{2}\dot{x}^{T}(t-\tau_{1})(R_{1}+R_{2})\dot{x}(t-\tau_{1})-{\int}_{t-\tau_{2}}^{t-\tau_{1}}\tau_{21}\dot{x}^{T}(s) R_{1}\dot{x}(s)ds \\ &&- {\int}_{t-\tau_{2}}^{t-\tau_{1}}2(\tau_{2}-t+s) \dot{x}^{T}(s)R_{2}\dot{{x}}(s)ds, \end{array} $$

(21)

$$\begin{array}{@{}rcl@{}} \dot{V}_{5}(x_{t})&=&k^{2}g^{T}(x(t)) S_{0} g(x(t))-k{\int}_{t-k}^{t}g^{T}(x(s)) S_{0} g(x(s)) ds, \\ &\leq& k^{2}g^{T}(x(t)) S_{0} g(x(t))-k(t){\int}_{t-k(t)}^{t}g^{T}(x(s)) S_{0} g(x(s)) ds, \end{array} $$

(22)

where Σ₁₁, Σ₁₂, and Σ₂ are defined in (10), (11), and (12) respectively. Applying Lemmas 3–5, it can be shown that

$$\begin{array}{@{}rcl@{}} &&-{\int}_{t-\tau_{1}}^{t} \tau_{1}\dot{x}^{T}(s) Y_{1}\dot{x}(s)ds \leq -\zeta^{T}(t){{\phi^{T}_{1}}}\text{diag}\{Y_{1},3Y_{1}\}\phi_{1}\zeta(t), \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} &&-{\int}_{t-\tau_{1}}^{t}2(\tau_{1}-t+s) \dot{x}^{T}(s) Y_{2}\dot{x}(s)ds \leq-\zeta^{T}(t)\left[{{\tau_{1}^{2}}}M_{2}+4\tau_{1}N_{2}(G_{1}e_{1}-e_{5})\right]\zeta(t),\qquad \end{array} $$

(24)

$$\begin{array}{@{}rcl@{}} &&-{\int}_{t-\tau_{2}}^{t-\tau_{1}} \tau_{21}\dot{x}^{T}(s)R_{1}\dot{x}(s)ds\\ && \leq-\zeta^{T}(t)\left[\phi^{T}_{2}D\phi_{3}+{{\phi^{T}_{3}}}D\phi_{2}-{{\phi^{T}_{2}}}\bar{R}_{1}\phi_{2}-{{\phi^{T}_{3}}} \bar{R}_{1}\phi_{3}\right]\zeta(t), \end{array} $$

(25)

$$\begin{array}{@{}rcl@{}} &&-{\int}_{t-\tau_{2}}^{t-\tau_{1}}2(\tau_{2}-t+s) \dot{x}^{T}(s)R_{2}\dot{x}(s)ds\\ && \leq-\zeta^{T}(t)\left\{(\tau_{2}-\tau(t))^{2}Z_{1}+4(\tau_{2}-\tau(t))B_{1}(G_{1}e_{2}-e_{7})+\left[\tau_{21}^{2}-(\tau_{2}-\tau(t))^{2}\right] \right.\\ &&\left. \times Z_{2}+4B_{2}[(\tau_{2}-\tau(t))G_{1}(e_{3}-e_{2})+(\tau(t)-\tau_{1})(G_{1}e_{3}-e_{6})]\right\}\zeta(t), \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} &&-k(t){\int}_{t-k(t)}^{t}g^{T}(x(s)) S_{0} g(x(s)) ds\leq \zeta^{T}(t) {{e_{8}^{T}}} S_{0} e_{8} \zeta(t), \end{array} $$

(27)

where $\bar {R}_{1}=\text {diag}\{R_{1},3R_{1}\}$, (8) and

$$ \left\{ \begin{array}{l} \phi_{1}=\text{col}\{G_{1}(e_{1}-e_{3}), G_{1}(e_{1}+e_{3})-2e_{5} \},\\ \phi_{2}=\text{col}\{G_{1}(e_{2}-e_{4}), G_{1}(e_{2}+e_{4})-2e_{7} \},\\ \phi_{3}=\text{col}\{G_{1}(e_{3}-e_{2}), G_{1}(e_{3}+e_{2})-2e_{6} \}. \end{array} \right. $$

(28)

From (20)–(27), we obtain

$$\begin{array}{@{}rcl@{}} \dot{V}_{3}(x_{t})&\leq&\zeta^{T}(t) {\Sigma}_{3} \zeta(t), \end{array} $$

(29)

$$\begin{array}{@{}rcl@{}} \dot{V}_{4}(x_{t})&\leq&\zeta^{T}(t) {\Sigma}_{4} \zeta(t), \end{array} $$

(30)

$$\begin{array}{@{}rcl@{}} \dot{V}_{5}(x_{t})&\leq&\zeta^{T}(t) {\Sigma}_{5} \zeta(t), \end{array} $$

(31)

where Σ₃, Σ₄, and Σ₅ are defined in (13)–(15), respectively.

On the other hand, for any matrices X ₁ and X ₂ with appropriate dimensions, it is true that

$$\begin{array}{@{}rcl@{}} 0&=& 2[x^{T}(t)X_{1}+\dot x^{T}(t)X_{2}][-Ax(t)+Wg(x(t))+W_{1}g(x(t-\tau(t))) \\ &&+W_{2}{\int}_{t-k(t)}^{t}g(x(s))ds+u(t)-\dot{x}(t)],\\ &=& \zeta^{T}(t) {\Sigma}_{6} \zeta(t), \end{array} $$

(32)

where Σ₆ is defined in (16).

From (3), the nonlinear function g _k (x _k ) satisfies

$$l_{k}^{-} \le \frac{g_{k}(x_{k})}{x_{k}} \le l_{k}^{+},\quad k=1,2,\dots,n, x_{k}\neq 0. $$

Thus, for any t _k > 0,(k = 1,2,…,n), we have

$$2t_{k}[{{g^{T}_{k}}}(x(\theta))-l_{k}^{-} x(\theta)] [l_{k}^{+} x(\theta)-g_{k}(x(\theta))]\geq0, $$

which implies

$$2[g^{T}(x(\theta))-x^{T}(\theta)L^{-}]^{T} T[L^{+} x(\theta)-g(x(\theta))]\geq0, $$

where T = diag{t ₁, t ₂,…,t _n }. Let 𝜃 be t, t−τ(t), t−τ ₁, and t−τ ₂, and replace T by T _s (s = 1,2,3,4), then we have

$$ 2\zeta^{T}(t){{e^{T}_{s}}} {\Pi}^{T}_{10} T_{s} {\Pi}_{11}e_{s}\zeta(t)\geq 0, $$

(33)

where s = 1,2,3,4 and

$$ \left\{ \begin{array}{l} {\Pi}_{10} =G_{2}-L^{-}G_{1}, \\ {\Pi}_{11} =L^{+}G_{1}-G_{2}. \end{array} \right. $$

(34)

As another observation from (3), we have

$$l_{k}^{-} \le \frac{g_{k}(x(\theta_{1}))-g_{k}(x(\theta_{2}))}{x(\theta_{1})-x(\theta_{2})} \le l_{k}^{+}, \quad k=1,2,\dots,n. $$

Thus, for any t _k > 0(k = 1,2,…,n) and Λ = g _k (x(𝜃 ₁))−g _k (x(𝜃 ₂)), we have

$$2t_{k}[{\Lambda}-l_{k}^{-} (x(\theta_{1})-x(\theta_{2}))]\left[l_{k}^{+} (x(\theta_{1})-x(\theta_{2}))-{\Lambda}\right]\geq0, $$

which implies

$$2[{\Lambda}-L^{-}(x(\theta_{1})-x(\theta_{2}))]^{T} T [L^{+}(x(\theta_{1})-x(\theta_{2}))-{\Lambda}]\geq0, $$

where Λ=col{Λ₁,Λ₂,…,Λ _n }.

Let 𝜃 ₁ and 𝜃 ₂ take values in t, t−τ(t), t−τ ₁ and t−τ ₂, and replace T by T _{a b} (a = 1,2,3;b = 2,3,4;b > a), then we have

$$ 2\zeta^{T}(t)(e_{a}-e_{b})^{T} {\Pi}^{T}_{10} T_{ab}{\Pi}_{11}(e_{a}-e_{b})\zeta(t)\geq 0, $$

(35)

where a = 1,2,3, b = 2,3,4, b > a.

From (33) and (35), it can be shown that

$$ \zeta^{T}(t) {\Sigma}_{7} \zeta(t)\geq 0, $$

(36)

where Σ₇ is defined in (17).

Next, to show the passivity of system (1), we set

$$J(t_{f})={\int}_{0}^{t_{f}}[-\gamma u(t)^{T}u(t)-2y(t)^{T}u(t)]dt. $$

where t _f ≥ 0. Noting the zero initial condition, we have

$$\begin{array}{@{}rcl@{}} J(t_{f})&=&{\int}_{0}^{t_{f}}[\dot V(x_{t})-\gamma u(t)^{T}u(t)-2y(t)^{T}u(t)]dt-V(x_{t_{f}})\\ &\leq&{\int}_{0}^{t_{f}}[\dot V(x_{t})-\gamma u(t)^{T}u(t)-2y(t)^{T}u(t)]dt. \end{array} $$

(37)

From (18), (19), (29)–(32), and (36), we obtain

$$\dot V(x_{t})-\gamma u(t)^{T}u(t)-2y(t)^{T}u(t)\leq \zeta^{T}(t) \boldsymbol{\Sigma}(\tau(t),\dot\tau(t)) \zeta(t), $$

where $\boldsymbol {\Sigma }(\tau (t),\dot \tau (t))$ is defined in (9). It is clear to see that $\boldsymbol {\Sigma }(\tau (t),\dot \tau (t))$ is a quadratic convex combination of matrices on τ(t)∈[τ ₁, τ ₂] and $\boldsymbol {\Sigma }(\tau (t),\dot \tau (t))$ is also a convex combination of matrices on $\dot \tau (t)\in [0,\mu ]$.

If we have $\boldsymbol {\Sigma }(\tau (t),\dot \tau (t))<0$, then $\dot V(t,x_{t})-\gamma u(t)^{T}u(t)-2y(t)^{T}u(t)< 0$ for any ζ(t) ≠ 0. By (37), we have

$$J(t_{f})<0 $$

for any t _f ≥ 0, when (3) is satisfied. Thus, neural network (1) is passive. This completes the proof. □

Remark 4

Theorem 1 presents estimating of the integral terms in (23), (24), (25), and (26) by Wirtinger’s inequality and [20], which provided a tighter lower bound than Jensen’s inequality [24].

In the following, it is interesting to consider passivity condition of passivity analysis for uncertain neural networks with discrete interval and distributed time-varying delays:

$$ \left\{ \begin{array}{l} \dot{x}(t)=-(A+\triangle A(t))x(t)+(W+\triangle W(t))g(x(t))+(W_{1}+\triangle W_{1}(t))\\ \qquad \times g(x(t-\tau(t)))+(W_{2}+\triangle W_{2}(t)){\int}_{t-k(t)}^{t} g(x(s))\,ds+u(t), \\ y(t)=g(x(t)),\\ x(t)=\phi(t), \quad t\in[-\tau_{\max},0], \quad \tau_{\max}=\max\{\tau_{2},k\}, \end{array} \right. $$

(38)

where △A(t), △W(t), △W ₁(t), and △W ₂(t) represent the time-varying parameter uncertainties that are assumed to satisfy the following conditions:

$$ [\triangle A(t)\ \triangle W(t)\ \triangle W_{1}(t)\ \triangle W_{2}(t)] = HF(t)[E_{1} E_{2} E_{3} E_{4}], $$

(39)

where H, E ₁, E ₂, E _3, and E ₄ are known real constant matrices, and F(⋅) is an unknown time-varying matrix function satisfying

$$F^{T}(t)F(t)\leq I. $$

Then, we have the following result.

Theorem 2

Given scalars τ ₁, τ ₂ and k, the uncertain system (38) with (3) is robust passive for any delays τ(t) and k(t) satisfying (2) if there exist real matrices Q _i > 0, S _i > 0, Y ₁ > 0, Y ₂ > 0, R ₁ > 0, R ₂ > 0(i = 0, 1, 2, 3), real positive diagonal matrices U ₁, U ₂, T _s , T _ab (s = 1, 2, 3, 4; a = 1, 2, 3; b = 2, 3, 4; a < b), real matrices M ₂, N ₂, Z ₁, Z ₂, B ₁, B ₂, D, X ₁, X ₂ and P with appropriate dimensions, and scalars γ > 0 and 𝜖> 0 such that the following linear matrix inequalities hold:

$$ \left[ \begin{array}{cc} \boldsymbol{\Sigma}+\epsilon\mathcal{M}_{2}^{T}\mathcal{M}_{2} & \mathcal{M}_{1}^{T}\\ \mathcal{M}_{1} & -\epsilon I \end{array}\right]<0, $$

(40)

$$ \left\{ \begin{array}{l} \left[\begin{array}{cc} M_{2} &N_{2}\\ \star&Y_{2} \end{array}\right]>0, \quad \left[ \begin{array}{cc} \bar{R}_{1} &D\\ \star & \bar{R}_{1} \end{array}\right]>0, \quad Z_{1}>Z_{2}, \\\\ \left[ \begin{array}{cc} Z_{1} &B_{1}\\ \star& {R}_{2} \end{array}\right]>0, \quad \left[ \begin{array}{cc} Z_{2} &B_{2}\\ \star&R_{2} \end{array}\right]>0, \end{array} \right. $$

(41)

where

$$\begin{array}{@{}rcl@{}} \mathcal{M}_{1}&=& {{e_{1}^{T}}}{{G_{1}^{T}}} X_{1}H+e_{10}^{T} X_{2}H,\\ \mathcal{M}_{2}&=& -E_{1}G_{1}e_{1}+E_{2}G_{2}e_{1}+E_{3}G_{2}e_{2}+E_{4}e_{8}, \end{array} $$

Σ and (41) are defined in Theorem 1.

Proof

Replacing A, W, W _1, and W ₂ in (7) with A + H F(t)E ₁, W + H F(t)E ₂, W ₁ + H F(t)E ₃, and W ₂ + H F(t)E ₄ respectively, so we have

$$\boldsymbol{\Sigma}+\mathcal{M}_{1}^{T}F(t)\mathcal{M}_{2}+\mathcal{M}_{2}^{T}F(t)\mathcal{M}_{1}<0. $$

By Lemma 7, it can be deduced that 𝜖 > 0 and

$$\boldsymbol{\Sigma}+\epsilon^{-1}\mathcal{M}_{1}^{T}\mathcal{M}_{1}+\epsilon\mathcal{M}_{2}^{T}\mathcal{M}_{2}<0 $$

is equivalent to (40) in the sense of the Schur complements Lemma 8. The proof is complete. □

4 Numerical Examples

In this section, we present examples to illustrate the effectiveness and the reduced conservatism of our results.

Example 1

Revisit nominal neural network with (1) with the following parameters:

$$A=\left[\begin{array}{cc} 2.2 & 0 \\ 0 & 1.8 \end{array}\right],\quad W=\left[\begin{array}{cc} 1.2 & 1\\ -0.2 & 0.3 \end{array}\right],\quad W_{1}=\left[\begin{array}{cc} 0.8& 0.4 \\ -0.2 & 0.1 \end{array}\right],\quad W_{2}=\left[\begin{array}{cc} 0 & 0\\ 0 & 0 \end{array}\right]. $$

The neural activation functions are assumed to be g _i (x _i (t)) = 0.5(|x _i + 1| − |x _i − 1|),i = 1, 2. It is easy to see

$$L^{-}=\left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right],\quad L^{+}=\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]. $$

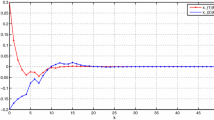
According to Theorem 1, we get the upper bounds of the time-varying delay τ(t) for various μ, and summarize them in Table 1 for comparison with the results obtained in [16, 25]. It is concluded that our results have improvements at the amount of 109.86%, 89.00%, and 92.64% for μ = 0.5,0.9 and μ ≥ 1 respectively, compared with the recent work [25]. Figure 1 gives the state trajectory of the neural network (1) under zero input, 0.3 ≤ τ(t) ≤ 2.8193 and the initial condition [x ₁(t),x ₂(t)]^T = [0.3,−0.2]^T, which shows that the neural network is stable.

Fig. 1

State trajectory of neural network in Example 1

Remark 5

Our obtained results have been shown to be the less conservative than some existing results, but still have some comments because Wirtinger-based integral inequality approach still requires less decision variables to manipulate of Lyapunov–Krasovskii functional candidates. Recently, a new class of integral inequalities for quadratic functions via some intermediate terms called auxiliary functions, are recent bounding techniques because these inequalities turn into the existing inequality, such as the Jensen inequality, the Wirtinger based integral inequality and the Bessel–Legendre (B-L) inequality by appropriately choosing the auxiliary functions.

Example 2

Consider the uncertain neural networks (38) with the following parameters:

$$\begin{array}{@{}rcl@{}} A&=&\left[\begin{array}{cc} 2.1 & 0 \\ 0 & 2.3 \end{array}\right],\quad W=\left[\begin{array}{cc} -0.2 & 0.1\\ -0.2 & 0.1 \end{array}\right],\ W_{1}=\left[\begin{array}{cc} 0.7& 0.5 \\ 0.5 & 0.4 \end{array}\right],\\ W_{2}&=&\left[\begin{array}{cc} 0.5 & -0.3\\ 0.2 & 1.2 \end{array}\right],\quad L^{-}=\left[\begin{array}{cc} -0.5 & 0 \\ 0 & -1 \end{array}\right],\quad L^{+}=\left[\begin{array}{cc} 0.5 & 0\\ 0 & 1 \end{array}\right],\\ H&=&\left[\begin{array}{cc} 0.4 & 0\\ 0 & 0.4 \end{array}\right],\quad E_{1}=E_{2}=E_{3}=E_{4}=\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]. \end{array} $$

According to Theorem 2, we get the upper bounds of the interval time-varying delay τ(t) for various μ, and summarize them in Table 2 for comparison with the results obtained in [10]. On the other hand, the eigenvalues of P for 0.3 ≤ τ(t) ≤ 1.5714 and μ = 0.7 are 0.1813, −0.0284, −0.0206, −0.0000, 0.0001, 0.0121, 0.0418, 0.0556, 0.1581, 0.5081, and 0.5081. So, P is not a positive matrix.

Table 2 Allowable upper bounds of τ ₂ for μ

Example 3

Consider the uncertain neural networks (38) with the following parameters:

$$\begin{array}{@{}rcl@{}} A&=&\left[\begin{array}{cc} 2 & 0 \\ 0 & 1.5 \end{array}\right],\quad W=\left[\begin{array}{cc} -1 & 1\\ 0.5 & -1 \end{array}\right],\quad W_{1}=\left[\begin{array}{cc} -0.5& 0.6 \\ 0.7 & 0.8 \end{array}\right],\quad W_{2}=\left[\begin{array}{cc} 0 & 0\\ 0 & 0 \end{array}\right],\\ L^{-}&=&\left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right],\quad L^{+}=\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right],\quad H=I,\\ E_{1}&=&\left[\begin{array}{cc} 0.4 & 0\\ 0 & 0.4 \end{array}\right],\quad E_{2}=\left[\begin{array}{cc} 0.3 & 0\\ 0 & 0.3 \end{array}\right],\quad E_{3}=\left[\begin{array}{cc} 0.2 & 0\\ 0 & 0.2 \end{array}\right],\quad E_{4}=\left[\begin{array}{cc} 0 & 0\\ 0 & 0 \end{array}\right]. \end{array} $$

By Theorem 2, we get the upper bounds of the interval time-varying delay τ(t) for various μ, and summarize them in Table 3 for comparison with the results obtained in [11, 22].

Table 3 Allowable upper bounds of τ ₂ for μ

5 Conclusions

In this paper, the delay-dependent passivity analysis issue for uncertain neural networks with discrete interval and distributed time-varying delays was studied by the Lyapunov–Krasovskii functional method, via an LMIs approach. The delay-dependent passivity conditions have been considered for two types of time-varying delays. To estimate the derivative of the Lyapunov–Krasovskii functional, we applied Wirtinger’s inequality to provide a tighter lower bound than Jensen’s inequality, which established less conservative results. Numerical examples are given to illustrate the effectiveness of our theoretical results.