1 Introduction

With the increasing maturity of 3D laser scanning technology and widespread use of 3D digital model, skeleton, as an effective and simplified manifestation of 3D model shape, has been widely adopted in many fields, for example, geometric modeling, computer animation, virtual navigation, component split, and shape matching. Digital 3D modeling field has paid more and more attention to skeleton. The major reasons are not only that the skeleton of the model can well maintain the topological connectivity and its form of the original model, but also that its 1D curve form is easier to operate and accurately guide the reconstruction of 3D model to solve the incomplete data in the modeling process.

Trees are an important component in the natural environment and constructing its 3D model has always been a long-term research hotspot in botany, computer graphics, and architecture. Current traditional skeleton extraction methods can be classified into two types, body method and geometric method. Body method uses internal information of the application model for skeleton extraction operation. Common body methods mainly include refining and distance field transformation. Ge Yaorong, Palagyi, and Gong et al. provided a rapid refining method and then the refined skeleton is settled and smoothed to make results conform to skeletons better [1,2,3,4]. Che Wujun and Yang Linian put forward an improved refinement algorithm [5]. Firstly, traditional refining methods are used to connect skeletons; then, snake model is introduced to adjust the positions of skeletons so as to solve the inaccuracy. di Baja and Svensson, Tran and Shih, Sundary, Niblack, and Gibbon et al. proposed distance field-based skeleton extraction algorithm [6,7,8,9]. Because voxel model-based data volume is huge, the whole process is time-consuming. With 3D model surface information, skeleton extraction based on geometric method can directly extract the model skeleton from polygon mesh or point cloud model can greatly reduce the to-be-handled data volume. Dey, Ogniewicz, Reddy, and Turkiyyah et al. proposed to utilize Voronoi graph to extract skeletons [10,11,12]. A Voronoi graph owns a very huge calculation quantity and it is very sensitive to boundary noise, which may lead to an overly dense Voronoi graph. It may need extra cutting treatments, so this method has no widespread use. Cao et al. extracted the curve skeleton of the point cloud model with hole on the basis of the Laplace operator point cloud shrinkage method [13]. George Reeb put forward the concept of the Reeb graph [14]. This kind of method shows good performance in topological structure maintenance of the model while it still needs improvements in maintaining tiny characteristics.

Tree branches own typical axial creep features, namely, shapes which are mostly generalized cylinder and which show a symmetric distribution along the axis of branches. At the same time, tree point cloud model obtains the measuring point data on the branch surface, so the point cloud distribution is directly related to the branch geometrical morphology. This kind of geometric correlation and axial symmetry of tree branches can be taken as geometric constraint conditions of skeleton extraction-based tree model. According to the symmetry of measuring point normal vector and centrality of skeleton nodes, the skeleton of the tree model is extracted through branch segmentation.

2 Tree skeleton extractions based on geometric features and point cloud properties

On the basis of branch geometric features and point cloud properties, for example, neighbor domain, normal vector, and curvature, the key to model skeleton extraction is seeking for an optimal model skeleton node. First of all, local least square plane fitting is utilized to estimate the normal vector of each measuring point. Then, point cloud is segmented into different branches on the basis of the Mahalanobis distance. Later, axial symmetry of branch point cloud is utilized to estimate the optimal positions of skeleton nodes. Finally, single-source shortest path is used to construct the linear skeleton of the model. The whole flow is shown as Fig. 1.

Fig. 1
figure 1

Skeleton extraction flowchart

Full size image

2.1 Estimation and adjustment of point cloud normal vector

Normal vector is a concept in space analytic geometry and it is a vector vertical to a tangent line of one curve or a tangent plane of one curved surface. The tree point cloud in this study is obtained by ground 3D laser scanning system. The data volume is extremely huge, so this paper adopts local surface fitting-based method [15]. The estimation from literature is mainly about the eigenvalue calculation of the scattered point cloud. Because point cloud is scattered and disordered, relevant eigenvalues are only the optimal fitting solutions under relevant constraint conditions, instead of refined calculation in mathematics. Through the normal vector estimation and direction adjustment, the optimal normal vectors of all points can be obtained. Figure 2 shows the normal vector estimation graph of point cloud data of one tree. Red parts represent the tree point cloud data and blue lines represent the normal vector pointing after the point cloud adjustment.

Fig. 2
figure 2

Normal vector of point cloud

Full size image

2.2 Branch segmentation

Tree point cloud data from laser scanning describe tree geometrical morphology in details. Specific to the complex tree morphology, tree point cloud model is divided into different component units by component segmentation. Based on the similarity of branch local geometric property, for example, spatial orientation and branch radius, this paper divides branches into different small segments.

For any point, pi in the point cloud model, it is constituted of point position xi and the corresponding surface normal vector ni, noted as pi = (xi, ni) ∈ R3 × S2. Meanwhile, the Mahalanobis distance between any other point pj and point pi in the model is defined as:

$$ \mathrm{Dist}\left({p}_i,{p}_j\right)=\left\Vert {x}_j-{x}_i+{F}_{\mathrm{squash}}\left\langle {x}_j-{x}_i\cdot {n}_i\right\rangle {n}_i\right\Vert $$
(1)

where Fsquash represents a regulation constant. Here, based on spatial positions of points and their corresponding normal vectors, Euclidean distance and spatial direction information are utilized to calculate space the Mahalanobis distance of point cloud with normal vector [16,17,18,19]. Dist(⋅) is defined as ellipsoid formed by the contour surface of surrounding point pi. Its axle and normal vector ni are in one line, with variation coefficient of1/(1 + Fsquash). This means that the more deviant pj to the tangent plane of pi is, the faster the distance increases.

Base on the defined Mahalanobis distance and selected approximate threshold εD, a graph of point model is constructed. However, connectivity of a graph is determined by the distance between points, namely, if and only if Dist(pi, pj) < εD, a side can be constructed between pi and pj, or a side cannot be constructed. Based on the constructed graph, breadth-first search is implemented from the root node of the point cloud model, dividing branch point cloud into different sub-segments. As shown in Fig. 3, for tree point cloud model, the above defined segmentation rules are used to divide branches into different sub-segments and each sub-segment is rendered with different colors to distinguish the branch segmentation.

Fig. 3
figure 3

Branch segmentation

Full size image

2.3 Skeleton node estimation

Tree branches own typical generalized cylindrical features. Namely, under the condition of neglecting tiny difference, branches approximately present cylindrical or circular table structures. As shown in Fig. 4, the point cloud of one tangent plane vertical to the axial direction is cut. It can be seen from the direction of its normal vector that branch point cloud is symmetrically distributed corresponding to the axis. Therefore, the optimal skeleton node of tree branches is the point set constituted of the axis. These points not only own a good axis but also it can accurately recover the true form of the model (Fig. 5).

Fig. 4
figure 4

The branch form. a Branch point cloud. b Section with normal vector

Full size image
Fig. 5
figure 5

Skeleton node estimation. a Normal vector estimation. b Node estimation

Full size image

On the basis of the above branch segmentation sets, skeleton nodes of each branch section are solved one by one. For trees with complete point cloud data, the center of mass of point sets can be taken as the nodes of skeleton according to generalized cylinder feature of branches. However, in the actual data, due to the influences of various factors, for example, branch shade and instrument precision, the collected tree point cloud have certain incomplete data. However, only depending on the center of mass will lead to the deviation of the axis. Thus, the spatial position of point cloud and direction of normal vector are utilized to estimate the optimal node position [20]. For one segmentation subset Qi, suppose it is constituted of N measuring points pj = (mj, nj), (j = 1,…, N), where mj = (xj, yj, zj) represents space 3D coordinate pj and nj represents the normal vector of pj. Plane S is made by passing one point pj in point cloud subset Qi, with normal vector of \( {\overline{v}}_i \). At the same time, to better utilize the symmetry characteristics of point cloud, the normal vector of cylinder surface shall be symmetrically distributed along the skeleton node, and the direction of normal vector, \( {\overline{v}}_i \), shall be consistent with the axis. Therefore, the included angle between the normal vector \( {\overline{v}}_i \) of plane S and the normal vector nj of a point is utilized. Iteration is used to optimize \( {\overline{v}}_i \) and the initial direction is selected to be the same as the main direction vertical to pj.

$$ {\overline{v}}_i^{t+1}=\underset{{\overline{v}}_i\in {\mathrm{\mathbb{R}}}^3,\left\Vert {\overline{v}}_i\right\Vert =1}{\arg \min}\kern0.5em \operatorname{var}\left\{\left\langle {\overline{v}}_i,{n}_j\right\rangle :{p}_j\in {N}_i^{(t)}\right\},\kern0.5em t\ge 0 $$
(2)

where \( {N}_i^{(t)} \) represents the neighbor domain of the tangent plane at iteration t, and nj represents the normal vector of pj. Formula (2) can be converted to solve the minimum of quadratic form, \( {{\overline{v}}_j}^TM{\overline{v}}_j \), where \( \left\Vert {\overline{v}}_j\right\Vert =1 \).

$$ M=\left[\begin{array}{ccc}\overline{x^2}-{\overline{x}}^2& 2\overline{xy}-2\overline{x}\overline{y}& 2\overline{xz}-2\overline{x}\overline{z}\\ {}2\overline{xy}-2\overline{x}\overline{y}& \overline{y^2}-{\overline{y}}^2& 2\overline{yz}-2\overline{y}\overline{z}\\ {}2\overline{xz}-2\overline{x}\overline{z}& 2\overline{yz}-2\overline{y}\overline{z}& \overline{z^2}-{\overline{z}}^2\end{array}\right] $$
(3)

x, y, and z in M respectively represent a random variable of components, x, y, and z in point’s normal vectors of the neighbor domain \( {N}_i^{(t)} \), and \( \overline{x} \), \( \overline{y} \), and \( \overline{z} \) respectively represent the mean components of the neighbor set \( {N}_i^{(t)} \). Meanwhile, this quadratic problem can be solved by singular value decomposition.

After the optimal normal vector, \( {\overline{v}}_i \), is estimated, plane S is made by passing point pj. Point cloud and normal vector of segmentation set Qi are projected on plane S to calculate the point with the shortest distance to the negative direction of the normal vector of point cloud, namely,

$$ {O}_i=\underset{Oe{0}^3}{\arg \min}\sum \limits_{j-1}^N{\left\Vert \left(O-{p}_j\right){xn}_j\right\Vert}^2 $$
(4)

Formula (4) is a typical quadratic minimization problem and the closed solution can be obtained by direct differentiation.

2.4 Construction of the initial skeleton

In the extracted node set of discrete skeleton, the connectivity between nodes is uncertain, especially at branch bifurcation. Based on the graph theory, single-source shortest path is used to solve, namely, constructing a graph on the basis of skeleton node set. In this weighed directed graph, tree skeleton is reconstructed. First of all, all the extracted skeleton nodes are selected as the vertex of the graph and vertex set, V = {1, 2, …, n}, of a graph is established. Then, starting from root nodes of the tree model, each vertex in set V is connected to the vertex in its neighboring threshold range by overall traversal. Meanwhile, the distance between two points is assigned to the corresponding side as weight. This is constructing a weighted directed graphG = (V, E), where Erepresents the side set constituted of vertexes in set V. Later, vertex set V in graph G is divided into two groups. The first group is vertex set S with the shortest path; the second group is vertex set U with uncertain short path. Root node O of the tree is selected as the source point of the graph. Through loop traversal, the shortest path of the graph is determined. The solving process is as follows.

  1. 1)

    At first, S only includes source point O, namely S = {1}. U contains other vertexes except point O. In U, the distance of each vertex u in U is the weight of the corresponding side.

  2. 2)

    In U, vertex k with the shortest path to point O is selected and then it is added in S (the selected distance is the shortest path from k to source point O).

  3. 3)

    Taking k as the new intermediate point, the distance of each vertex in U is modified. If the distance (passing through vertex k) from source point O to vertex u (u ∈ U) is shorter than the original distance (not passing through vertex k), the distance of vertex u is modified. The modified distance is the distance of vertex k plus the weight of side.

  4. 4)

    Repeat step 2 and step 3 until set U is null, namely, all the vertexes are included in set S.

Through the above loop iteration operation, the minimum spanning tree of the shortest path sets from all nodes to root node of graph G = (V, E) is formed. It not only extracts the tree logic model but also eliminates the ambiguity of node connection, for example, loop caused by fault connection between skeleton points, as shown in Fig. 6b. Finally, other nodes, except root node, all have their father nodes. Along the shortest path of root node, it is easy to determine skeletons of different tree branches by loop traversal. The overall construction process of initial skeletons is shown in Fig. 6. It is a 2D skeleton construction, and at the same time, proper hypothesis is made on the distance between nodes. If nodes are adjacent, the distance is 3; if nodes are opposite, the distance is 4.

Fig. 6
figure 6

The initial skeleton construction. a Scattered point cloud. b Formed graph. c Path search. d Branch segmentation

Full size image

2.5 Curve skeleton optimization

The tree initial skeletons are constituted of skeleton nodes that are connected by line but they are a little stiff. Especially, the abrupt bending variation at branch bifurcation differs from true tree morphology, as shown in Fig. 7a. Thus, it is necessary to make moderate optimization on the constructed initial skeleton to ensure its geometrical morphology can better conform to true tree morphology on the basis of guaranteeing unchanged topological structure. According to the angle of branch bifurcation, the cubic Hermite curves are utilized for moderate smooth fitting. First of all, the fitted cubic Hermite curve is supposed as P(t), t ∈ [t0, t1] (where t0, t1 ∈ R and t0 < t1). Besides, point A and point C are taken as end points and \( \overset{\rightharpoonup }{AO} \) and \( \overset{\rightharpoonup }{OC} \) are the corresponding directions of tangential vector. Then,

Fig. 7
figure 7

Skeleton optimization. a The initial skeleton. b Optimization skeleton

Full size image
$$ P\left({t}_0\right)=A,P\left({t}_1\right)=C,{P}^{\hbox{'}}\left({t}_0\right)=\overline{AO},{P}^{\hbox{'}}\left({t}_1\right)=\overline{OB} $$
(5)

From the above formula, the expression formula of the cubic Hermite curve can be

$$ P(t)={F}_0A+{F}_1C+{G}_0\left({t}_1-{t}_0\right)\overline{AO}+{G}_1\left({t}_1-{t}_0\right)\overline{OC}\kern1em t\in \left[{t}_0,{t}_1\right] $$
(6)

where F0, F1, G0, and G1 are the cubic linear functions of t. End point and tangent vector of end point are utilized to generate the coordinates of other points in the range of t ∈ [t0, t1]and the values of coordinates are only related to parameter t. Among them, F0 and F1 are in specialized control of the influences of end point’s function value on curves, irrelevant to the tangent vector value of end point. G0 and G1 are in specialized control of the influences of end point’s tangent vector value on curve shape, irrelevant to the tangent vector value of end point. After the smoothing fit of the cubic Hermite curve on AOC, as shown in Fig. 7b, six nodes are inserted to realize excessive smoothing. Similarly, smoothing repair also is made on AOB. Starting from tree root node, loop traversal is used to search for nodes with greater branching angle. The cubic Hermite curve is adopted to make moderate smooth optimization on the corresponding skeleton line to make it conform to the true tree morphology better.

3 Experimental test and analysis

To test the skeleton extraction method (GC) of the above tree model, samples of three common trees are selected for experimental analysis and this method is compared with the voxel switch (VS)- and point cloud contraction (PCC)-based skeleton extraction method in literature. The algorithm test is based on MATLAB 7.13 platform and the computer configuration is Windows 7 system, with CPU of Intel Core 3.10 GHz and internal storage of 4.0 G.

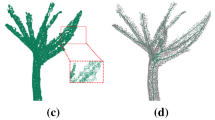
From the test results of samples by methods in Figs. 8, 9, and 10, it can be seen that these three methods can realize 1D linear skeleton extraction of the tree model. However, they differ in detail treatment. VS method generates refined skeleton iteratively by voxel on the basis of space 3D topological operation. Because it is sensitive to edge noise, it is easy to generate redundancy branch. Thus, the extracted tree skeleton by VS method is just an approximation of the true skeleton. In the topological structure, there is no accurate fidelity in central symmetry and other aspects. PCC method generates refined skeletons iteratively by point cloud contraction switch. It shows good performance in maintaining the topological structure of the model. However, it also has a problem, namely, the top skeleton of each branch may contract inwards, and after times of switch, the overly subtle branches may be switched into a point. Therefore, in the practical application, the selection of reasonable contraction weight and attractive contraction weight and the setting of end conditions directly influence the skeleton quality of the model. By aid of local attribute of point cloud and tree growth characteristic, GC method owns an optimal estimation foundation in branch segmentation and skeleton node extraction. Thus, the skeleton extracted by this method is relatively complete and accurate. This method displays strong anti-interference and high-precision characteristics at branch bifurcation and crossed ending part of fine tree branches. All these can be seen from the amplification parts of details in each figure. At the same time, the extracted curve skeleton is inserted into the internal tree model and the proposed curve skeleton satisfies the requirements of centrality, refinement, component separability, and other correlation properties. It can satisfy the practical application demands.

Fig. 8
figure 8

Skeleton extraction of sample 1. a Point cloud. b VS skeleton. c PCC skeleton. d GC skeleton

Full size image
Fig. 9
figure 9

Skeleton extraction of sample 2. a Point cloud. b VS skeleton. c PCC skeleton. d GC skeleton

Full size image
Fig. 10
figure 10

Skeleton extraction of sample 3. a Point cloud. b VS skeleton. c PCC skeleton. d GC skeleton

Full size image

The above test analyzes the processing capacity of skeleton extraction methods. To make more comprehensive performance tests on each method, this paper makes statistics on the skeleton extraction time and center deviation of different objects by each method. The operation time is the total time of each method to extract skeletons, with unit of second (s). Center deviation makes vertical tangent plane of different axial directions on branch point cloud and the deviation between the fitting center and skeleton points on each plane is compared. Then, the mean deviations of all tangent planes are solved, with unit of millimeter (mm). The statistical results of each index are shown in Table 1.

Table 1 The processing capacity of skeleton extraction methods
Full size table

It can be seen from the statistical results in Table 1 that different methods differ a lot in computational efficiency and skeleton extraction quality. VS method is seriously lagged behind the other two methods in computational efficiency. The reason for this is that in detail process, the judgment of each simple point needs testing the surrounding adjacent relationship. Thus, loop judgment test greatly limits the execution efficiency of the algorithm. The operation efficiencies of PCC method and GC method are improved by over four times compared with VS method. At the same time, PCC method has faster execution efficiency than that of GC method. This may be that after five times of iterations, PCC method can be basically contracted into the discrete form of skeletons, while GC method needs to make more calculation on the geometric attribute of point cloud, which may influence its execution speed. Specific to the statistics of center deviation, VS method also has certain defects. For example, it has over three times of deviation compared with the other two methods. GC method owns the minimum center deviation, because it fully utilizes the branch geometrical features and internal characteristics of point cloud, which improves the accuracy of the skeleton construction. From the comparison in operation efficiency and the central deviation in Figs. 11 and 12, it can be obviously seen that each algorithm owns different performances in different indexes.

Fig. 11
figure 11

Operation time

Full size image
Fig. 12
figure 12

Center deviation

Full size image

4 Conclusion

Based on branch axial creep geometric features and local properties of point cloud, the Mahalanobis distance is utilized to segment point cloud into different branch parts and the axial symmetry of branch point cloud is utilized to estimate the optimal position of skeleton nodes. According to the graph theory, single-source shortest path is used to accurately reconstruct the curve skeleton of the model. By aid of local attributes of point cloud and tree growth characteristic, GC method owns optimal estimation foundation in branch segmentation and skeleton node extraction. The extracted skeleton based on this method is relatively complete and accurate and the constructed skeleton can better conform to true tree morphology. The method proposed in this paper directly applies point cloud to extract skeletons and it can achieve effective curve skeletons. Voxel switch may decrease the skeleton extraction quality. Therefore, these experimental tests not only analyze the effectiveness of various algorithms but also provide much guidance for the design of future algorithms.