Keywords

1 Introduction

Skeleton extraction has been studied for a long time and can be applied to various areas [4, 8, 11, 13, 21, 24, 26, 37, 43], such as computer graphics, computer vision and image processing. We are interested in the contraction based methods [7, 17, 22, 35, 36, 39, 44] which gradually shrink the clouds to obtain the skeleton.

In particular, we are interested in the Locally Optimal Projection (LOP) [25] based methods [17, 23, 32] among the contraction oriented ideas. LOP was originally for computing the geometry surfaces of raw scans, which projects each point to its nearby local center according to a support radius. It was recruited by Hang et al. [17] to compute \(L_1\)-medial skeletons of 3D point clouds. However, this method is not stable because it does not consider the local geometrical structure when doing the contraction. In addition, its contraction can be very inefficient without discriminating the surface variations of the local shapes.

Existing improvements [23, 32] either rely on an additional local medial surface for effective contraction [23] or take a mixture model for fast computation [32]. However, their performances are still limited. The local distribution of points reflects the shape of the object and thus plays an important role in the skeleton estimation during the contraction process However, it is not explicitly considered in these methods.

Therefore, this paper takes the local geometrical distribution as the starting point and revises LOP from two aspects for better skeleton estimation. One is a bilateral filter [3, 38] based idea adopted in the contraction process so that the geometrical similarity in curvature is additionally considered for better shape consensus. The other is an eigenvalue based radius estimation so that adaptive radii reflecting the variations of the local surface can be used for effcient contraction of different object parts. These two combine together so that an improved LOP algorithm incorporating local geometrical distributions are proposed.

2 Related Work

Skeleton extraction has been studied for a long time [11, 37]. One popular type of methods for curve extraction is the contraction based method [1] which, however, cannot ensure a central skeleton because of the varying contraction speeds [7, 36, 39]. Therefore, some studies [17, 22] focus on generating the centered curves, which is interesting to us. Especially Huang et al. [17] adopted locally optimal projection (LOP) [25] for extracting the skeletons from raw scanned data. They adopted L1-medians locally for 1D based \(L_1\)-medial skeletons, which is also used by [35, 44] through iteratively contracting sample points while gradually increasing their neighborhood sizes.

There are also variants of LOP [16, 23, 32]. Huang et al. [16] extended LOP to cope with non-uniform distributions by a weighted locally optimal projection operator, which was later improved by Preiner et al. [32] with a Gaussian mixture model for fast computation. Wang [23] extended LOP for 3D curve skeletons by two ideas, constraining the LOP operator applied on the medial surface and adaptively computing variable support radii, and fulfilled fast computation and accurate localization without interference.

There have been other non-contraction based methods, such as image based [27], medial surface based [10, 40], graph based [2, 9, 28] and geodesic distance based methods [18, 19, 41]. Qin et al. [33] took the mass transport view and estimated the skeleton with the minimization of Wasserstein distance between mass distributions of point clouds and curve skeletons. Jiang et al. [20] even combined the contraction and graph based ideas together and proposed a graph contraction method, including a contraction term in graph geodesic distances and a topology-preserving term by the local principal direction. Similar compound way is taken by Fu et al. [14]. However our focus here is on the contraction based methods, especially on LOP and its variants.

Deep learning based methods [12, 15, 29,30,31, 42] become popular nowadays. For example, Panichev et al. [31] took an U-Net based approach for direct skeleton extraction; Luo et al. [29] included an encoder-decoder network to fulfill hierarchical skeleton extraction. Deep learning techniques are attractive, however, they generally require skillful training with large data for high performance.

Some studies also extend skeleton extraction to structure or outline estimation from point sets [8, 34], whose foci are on fitting outer structure lines but not the skeletons.

3 The Improved LOP

This section introduces the proposed LOP method, where the general idea of LOP and its two proposed local geometry based improvements are presented in succession.

3.1 Overview

Generally, LOP is to find the set I representing the \(L_1\)-medial skeleton point set \(X=\{\boldsymbol{x}_{i_{i\in {I}}}\}\) of an unorganized and unoriented set J of points \(P=\{\boldsymbol{p}_{j_{j\in J}}\}\subset \mathbb {R}^3\).

$$\begin{aligned} \arg \min _{X} G(X) + R(X), \end{aligned}$$
(1)

where G(X) keeps the geometry of J in I and R(X) lets points in I evenly distributed.

$$\begin{aligned} G(X)=\sum _{i \in I} \sum _{j\in J} \Vert \boldsymbol{x}_i -\boldsymbol{p}_j\Vert \theta (\Vert \boldsymbol{x}_i - \boldsymbol{p}_j \Vert ), \end{aligned}$$
(2)

where

$$\begin{aligned} \theta (r)=e^{-r^2/(h/4)^2} \end{aligned}$$
(3)

is a fast-decreasing smooth weighting function with the compact support radius h defining the size of the influence radius [25].

$$\begin{aligned} R(X) = \sum _{i\in I} \lambda _{i} \sum _{i'\in {I \setminus {i}}} \eta (\Vert \boldsymbol{x}_{i} - \boldsymbol{x}_{i'} \Vert ) \theta (\Vert \boldsymbol{x}_{i} - \boldsymbol{x}_{i'} \Vert ), \end{aligned}$$
(4)

where: \(\lambda _{i} \) represents the balancing term; and \(\eta (r)\) is another decreasing function penalizing \(\boldsymbol{x}_{i}\) too close to each other, which is generally set to be \(1/3r^3\), or \(-r\) for slow decreasing of large contraction radii.

Accordingly, I is generated as follows. First the input cloud is down sampled to obtain the sampling points evenly. These sampled points are the future source points of the estimated skeleton. Then the displacement of each sampling point \(\boldsymbol{x}_i\) is estimated recursively till convergence, which is based on the eigen decomposition with the neighboring points. Here, weighted principal components analysis (PCA) is used to compute the eigenvalues in decreasing order \(\lambda _i^m(m\in {\{0,1,2\}})\) and their corresponding eigenvectors \(\boldsymbol{v}_i^m\) from the covariance matrix \(C_i\),

$$\begin{aligned} C_i = \sum _{i'\in {I \setminus {i}}} \theta (\Vert \boldsymbol{x}_i-\boldsymbol{x}_{i'}\Vert )(\boldsymbol{x}_i-\boldsymbol{x}_{i'})^T(\boldsymbol{x}_i-\boldsymbol{x}_{i'}). \end{aligned}$$
(5)

These values will guide the update of \(\boldsymbol{x}_i\) according to Eq. 1 [17, 25].

As can be seen, the contraction process relies heavily on the distances of points between I and J. However, it only considers the spatial distances, which can mislead the process to wrong positions without considering the local geometrical relationships. In addition, the decay weight relies on a fixed radius for contraction which also omits the differences of local shapes of the cloud object, i.e., a wide and flat shape can have a big radius for robust contraction and vice versa. Apparently, local geometrical distributions should be considered when doing the contraction. Therefore, two geometry based improvements are proposed to update the optimization process for more robust contraction, which will be discussed in details in the following.

3.2 Bilateral Filter Based Weighting

The weighting function (Eq. 3) computes the weights by the spatial distance only, which may overlooks the importance of the geometrical similarities. Therefore, local geometrical similarities should also be considered in weighting the contributions. Therefore, the bilateral filter [38] based weighting scheme which takes these two properties together is proposed.

Traditional, the bilateral filter aims at replacing the intensity of the central pixel, \(\boldsymbol{u}_c\), at c with a weighted average of the intensities of the neighboring pixels \(\{\boldsymbol{u}_{c_1}, \boldsymbol{u}_{c_2}, \ldots , \boldsymbol{u}_{c_N}\}\), \(\hat{\boldsymbol{u}}_c\). These weights are estimated by both Euclidean distances and radiometric differences between the central pixel and its neighbors.

$$\begin{aligned} \hat{\boldsymbol{u}}_c = \frac{1}{W_c} \sum _{i=1}^{N} f_g(\Vert \boldsymbol{u}_c- \boldsymbol{u}_{c_i}\Vert )f_r(c-c_i)\boldsymbol{u}_{c_i}. \end{aligned}$$
(6)

Here, \(W_c\) is a normalization term, and \(f_g\) and \(f_r\) are the spatial and range weighting kernels for the Euclidean and radiometric distances respectively.

For the skeleton estimation of 3D clouds, the Euclidean distance for the spatial difference measurement is kept. But the radiometric difference can be substituted with geometrical similarity, where curve distance of two points is adopted. Consequently, a bilateral filter based on the spatial and geometrical distances can be superimposed to the neighboring points by the following equation:

$$\begin{aligned} \rho (\boldsymbol{x}_i,\boldsymbol{p}_j)= \omega _s(\hat{s}(\boldsymbol{x}_i, \boldsymbol{p}_j)) \omega _g(\hat{g}(\boldsymbol{x}_i, \boldsymbol{p}_j) h(\boldsymbol{x}_i, \boldsymbol{p}_j), \end{aligned}$$
(7)

where standard Gaussian filters represent \(\omega _s(x)\) and \(\omega _g(t)\) respectively, i.e., \(\omega _s(x)=e^{-x^2/2\sigma _s^2}\) and \(\omega _g(t)=e^{-t^2/2\sigma _g^2}\) with \(\sigma _s\) and \(\sigma _g\) being the variances. Here \(\hat{s}\) and \(\hat{g}\) targets at spatial and geometrical distances and measure the Euclidean distances and the curvature distances between \(x_i\) and \(p_j\) respectively:

$$\begin{aligned} \hat{s}(\boldsymbol{x}_i, \boldsymbol{p}_j)= \Vert \boldsymbol{x}_i - \boldsymbol{p}_j\Vert \end{aligned}$$
(8)

and

$$\begin{aligned} \hat{g}(\boldsymbol{x}_i, \boldsymbol{p}_j) = \Vert \delta (\boldsymbol{x}_i)-\delta (\boldsymbol{p}_j)\Vert , \end{aligned}$$
(9)

where \(\delta (\cdot )\) computes the curvatures. Note that in Eq. 7, to effectively capture the local geometrical variance, the weights are superimposed on the sample points according to their distanaces projected to the tangent plane, i.e.,

$$\begin{aligned} h(\boldsymbol{x}_i, \boldsymbol{p}_j)=<\boldsymbol{n}_i, \boldsymbol{x}_i-\boldsymbol{p}_j>. \end{aligned}$$
(10)

To constraint the contraction process, \(\sigma _s\) is chosen according to the standard deviation among neighboring points and \(\sigma _g\) is defined to be the radius of the neighboring set, i.e., \(\sigma _g=\Vert \boldsymbol{x}_i- \boldsymbol{m}_i\Vert \) with \(\boldsymbol{m}_i\) being the fartherest point in the neighbors of \(\boldsymbol{x}_i\). Consequently, the following updated version for the contraction (Eq. 2) is obtained based on Eq. 7,

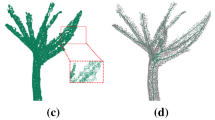
$$\begin{aligned} G(X)=\sum _{i \in I} \sum _{j\in J} \Vert \boldsymbol{x}_i -\boldsymbol{p}_j\Vert \rho (\boldsymbol{x}_i, \boldsymbol{p}_j) \end{aligned}$$
(11)

Figure 1 shows the effects before (Fig. 1b) and after (Fig. 1c) applying the bilateral filter based weights. There are more stray samples shown in the traditional LOP than the proposed method. This experiment shows that the additionally bilateral filter based weighting scheme makes the samples distributed more conformal and consistent with the object shape than the original LOP.

Fig. 1.
figure 1

Color figure onlinetracted samples by LOP or the bilateral filtering updated LOP. The sample points are shown in red. (a) Source cloud; (b): samples contracted by LOP; and (c): samples contracted by the bilateral filter based LOP. (Color figure online)

Full size image

3.3 Adaptive Radius

The contraction radius is also very important because it decides the contraction scale and affects the areas to be contracted. Intuitively, the wide and flat area can have a bigger contraction scale while the narrow area should be with a smaller one. Figure 2a demonstrates this observation, where the belly should have a bigger radius than the arm for an efficient contraction. However the traditional one is fixed and thus cannot cope with the contraction efficiently and may lead to wrong estimation. Therefore, an adaptive radius is expected, where the local geometrical property can be taken as the clue to the solution.

Fig. 2.
figure 2

Illustration of the adaptive contraction radius and its working examples. The dashed circus show the sizes of radii for the principle (a), and the sample contraction in the intermediate (b) and 5 more iteration steps (c) during the optimization.

Full size image

However, it is difficult to directly capture the relationship between the local geometry and radius. Luckily, the covariance matrix points a way out. A covariance matrix of a point cloud captures the distribution or spread of the cloud, e.g., the direction of the largest variance represents the largest dimension of the data. In addition, these directions can be computed as the eignevectors by decomposing the covariance matrix of the cloud through PCA (Fig. 3). Accordingly, the eigenvalues can be adopted to measure the extensions of clouds in all directions and, therefore, taken as a measurement of the local shape variation.

To capture the local shape variation, the eigenvalues of the covariance matrix of the local neighbors (Eq. 5) which reflects the local geometrical distributions are adopted to define a gradually increasing contraction radius. First, the directionality degree [17] defining the shape spreading feature of \(\boldsymbol{x}_i\), \(d_i\), is adopted

$$\begin{aligned} d_i=\frac{\lambda _i^{2}}{\sum _{m=0}^2\lambda _i^{m}}. \end{aligned}$$
(12)

It can be seen that the shape turns narrow as \(d_i\) approaches 1. Clearly, it is expected that the radius used in the narrow part to be also small for an effective contraction. Therefore, the following adaptive radius \(h(i)^{(t)}\) for t-th iteration of \(\boldsymbol{x}_i\) can be obtained.

$$\begin{aligned} h(i)^{(t)} = h(i)^{(t-1)} + e^{\frac{1}{d_i}}, \end{aligned}$$
(13)

where \(h(i)^{(0)}=0\). Accordingly, the contraction radius h in Eq. 3 is replaced with Eq. 13 during the iterations.

Fig. 3.
figure 3

Illustration of the directions of a point cloud estimated by PCA with the covariance matrix of a 2D cloud. The red and blue arrows represent the major and minor directions respectively. (Color figure online)

Full size image

The contraction happens first in narrow parts such as arms and legs with small radii and then gradually find the correct position with big radii for the wide parts, such as torso. Figure 2 gives the example of the adaptive radii during the contraction process. It can be seen that the narrow parts are contracted significantly first with smaller radii (Fig. 2b) and then gradually the wide parts are contracted apparently with bigger radii (Fig. 2c). These varying radii can help obtain a geometrically consistent skeleton.

The geometrically updated contraction weights and radii are incorporated into the traditional LOP algorithm and then an improved method is resulted. For more details on how to iteratively implement the algorithm, please check  [17, 25].

4 Experimental Results

Experiments are undertaken with two human and animal mesh datasets: TOSCA [6] and FAUST [5]. Two related improvements of LOP are considered for performance comparison: the \(L_1\) medial skeleton based method [17] (L1) and the KNN based method [44] (KNN).

Figure 4 shows the results of our method on four clouds consisting of different object shapes. They show that our method can contract the sample points successfully to be the central skeleton points.

Fig. 4.
figure 4

Example results of our method

Full size image

Figure 5 shows the experimental results on TOSCA. Here performance comparisons with L1 and CNN are taken. There are apparent unconnected and uncontracted samples for L1 and KNN, with L1 being generally worse. Ours, on the other hand, obtains the best performances among all methods, even though there are a few unconnected joints between some skeleton parts.

Figure 6 shows the performance comparisons on FAUST. The same observations about the three methods can be found, where ours still achieves the best performaces among all methods.

Statistical evaluation of the proposed method are also undertaken. Generally all skeleton points should be close to the neutral axis of the skeleton for a compact skeleton generation. However, the true neutral axis may not be easy to localize for each mesh. Here the max distance among all skeleton points to the center axis of the skeleton bounding box is taken as the metric. The smaller the distance, the better accuracy is. Figure 7 visualizes the max distances of different methods for 14 meshes from the two sets. Our method almost always the best one for all meshes among all methods, which further demonstrates the merits of our method.

Fig. 5.
figure 5

Skeleton estimation by different methods for TOSCA.

Full size image
Fig. 6.
figure 6

Skeleton estimation by different methods for FAUST.

Full size image
Fig. 7.
figure 7

Statistical comparisons of the max distance of each estimated skeleton for 14 meshes by different methods.

Full size image

5 Conclusions

This paper proposed an improved LOP algorithm for skeleton extraction. Building on closely capturing the local geometrical variations, we update the traditional LOP algorithm from two aspects: One is a bilateral filter based weighting scheme where additional local geometrical similarities are used to make the contraction consensus to the mesh surface; and the other is an eigenvalue based varying radius scheme where the local geometrical distributions are used produce efficient contraction radii according to the shapes of different object parts. Experimental results demonstrate the merits of the proposed method.

The estimated skeleton in the contraction oriented methods may be difficult to converge to a skeleton keypoint connecting different skeleton segments, as the experiments have shown. The density of the clouds is often different in different part, which can lead to different contraction speed and, therefore, the common joint is sometimes difficult to get. In addition, more samples will improve the accuracy of skeleton estimation experimentally, however, this also incurs high computation load. Those two shortcomings will be the focus of our future work for more robust skeleton extraction.