Model of uncertainty for the variability of water microbiological enumeration in a proficiency testing scheme

Abstract

Data processing of microbial enumeration expressed as colony counts requires the use of specific statistical approaches due to the particular aspect of the analyte and the consideration of the variability related to the growth of microorganisms. A challenging matter in the organization of proficiency testing (PT) schemes for water microbiology is to provide representative, homogeneous and stable enough samples with the aim of assessing participants’ performance but also characterizing the accuracy of measurement. As a consequence, the proficiency testing design may help to make clear distinction between the different sources of variation and facilitate the subsequent error analysis associated with the analytical procedures of the participants. Besides, the statistical tools may be selected to provide explicit outcomes which enable the participants to interpret the data in line with other existing indicators such as those arising from validation studies or measurement uncertainty procedures in the laboratory quality assurance system. In this paper, the suitability of a Poisson–Gamma hierarchical generalized linear model is tested in order to evaluate the interlaboratory error, the batch homogeneity and the repeatability error from water microbiology PT. A probabilistic approach deriving from the negative binomial distribution is proposed for assessing the participating laboratories performance in terms of generalized z-score.

Introduction

In water microbiology, the mathematical modeling of uncertainty components started in the early 2000s [1]. The decomposition of the analytical procedure into different steps that are evaluated individually is considered as a concrete component approach (GUM approach) for the assessment of the measurement uncertainty associated with water microbiological determinations [2].

For the external quality control (EQC) of routine laboratories, a thorough design of PT (proficiency testing) schemes can be developed as an experimental approach. The statistical distinction between the sources of variability can be established using traditional analysis of variance when laboratory analysis results follow approximately a Gaussian distribution [3, 4]. However, microbial enumeration in water, expressed as colony counts, does not follow a Gaussian distribution. The particulate nature of microorganisms and their random distribution even in perfectly mixed waters lead to specific statistical considerations and inexorably limit the enumeration precision.

In this paper, the implementation of a hierarchical generalized linear model (HGLM) for fitting microbial count data from a PT and the reliability of the outcomes are discussed. A generalized z-score is proposed to assess the analytical performance of laboratories. It is based on a specific probabilistic approach to the distribution of colony count results on Petri dishes.

Model of measurement uncertainty for water microbiological determinations

The Poisson distribution is commonly used as a basic statistical model for the characterization of the random distribution of microorganisms in a suspension [5]. If additional variability corresponding to operational uncertainty is detected, the over-dispersion can be expressed using the model of variance from the negative binomial distribution such as:

$$s^{2}=\bar{x} + u_{0}^{2} \bar{x}^{2}$$

(1)

where $\bar{x}$ is the mean number of colonies counted and u₀ is the over-dispersion, the relative operational standard deviation.

The first part of the variance is due to the Poisson process, and the rest is due to the combined effect of all the random over-dispersion factors [6]. Figure 1 illustrates the variance-to-mean ratio in different cases of over-dispersion.

Fig. 1

Graphical representation of the over-dispersion in the model of variance derived from the negative binomial distribution. Dividing both sides of formula (1) by the mean number of colonies, $\bar{x}$ yields an equation of a line. Its slope represents the relative operational variance $u_{0}^{2}$. The solid line corresponds to the case where no over-dispersion is observed, $u_{0}^{2} = 0$. The property of the Poisson distribution is verified, and the variance is equal to the mean. The dashed line, the dotted line and the dash-dotted line correspond to examples of increasing over-dispersion. In these cases, the variance becomes larger than the mean due to the technical over-dispersion

The relative variance $u_{0}^{2}$ is then the most appropriate expression of uncertainty in water microbiology. This over-dispersion constant is explicitly used by microbiologists to quantify the significant components of measurement errors. In a global approach of MU (measurement uncertainty), the relative variance is considered, as a whole, the combination of all the uncertainties associated with technical steps of the analytical procedure [7]. The final expression of uncertainty can be defined as follows:

$$u_{\text{c, rel}} \left( y \right) = \sqrt {u_{{ 0 , {\text{rel}}}}^{2} + u_{\text{d,rel}}^{2} }$$

(2)

where $u_{\text{c,rel}} \left( y \right)$ is the combined relative standard uncertainty, $u_{{ 0 , {\text{rel}}}}^{2}$ is the relative operational uncertainty and $u_{\text{d, rel}}^{2}$ is the relative distribution uncertainty (generally Poisson distribution).

In a bottom-up approach of MU (GUM), the combined operational relative variance is obtained as the sum of the relative variances of the technical components of the method [2]:

$$u_{{ 0 , {\text{rel}}}}^{2} = u_{\text{rel,M}}^{2} + u_{\text{rel,F}}^{2} + u_{\text{rel,V}}^{2} + u_{\text{rel,I}}^{2} + u_{\text{rel,L}}^{2}$$

(3)

where $u_{\text{rel,M}}^{2}$ is the matrix component, $u_{\text{rel,F}}^{2}$ is the dilution factor component, $u_{\text{rel,V}}^{2}$ is the test portion volume component, $u_{\text{rel,I}}^{2}$ is the incubation effects component and $u_{\text{rel,L}}^{2}$ is the uncertainty of counting component.

The use of the negative binomial distribution as a suitable model for over-dispersed microbial counts has been widely demonstrated [8, 9].

The negative binomial distribution (NB) is generalized as a Poisson–Gamma mixture: Poisson (λ) distribution, where λ follows a Gamma distribution [10, 11]. The parameters of the different probability distribution functions used are summarized in Table 1.

Table 1 Parameters and parameterizations of the different probability distribution functions used

Experimental design and statistical model for water microbiology PT

The objective of the PT planning in water microbiology can be multiple: to assess accuracy, including trueness and precision, but also to produce estimates of uncertainty that can be used by the profession [12]. Furthermore, specific accreditation guidelines require that samples sent to laboratories be homogeneous [13]. Sample stability is another parameter that must be sufficiently controlled to avoid any interference with the EQC.

To this end, the analysis in duplicate by each participant of several contaminated water samples from the same batch in a recommended short period of time to begin processing the samples (24 h to 48 h depending on the analytical parameter) can be an optimal PT design.

One of the data analysis methods that is generally cited for quantitative microbiological counts in PT scheme is the Poisson distribution, and therefore, the evaluation interval may be determined using a Poisson probabilities table, based on the average count for participants [14].

From a technical point of view, the Poisson distribution can only cover the case where the only source of variability of the PT is the randomness of the microorganisms in the samples. This model does not take into account any additional dispersion due to the technical steps when implementing the analysis of the test samples by participants.

Another generally recommended statistical method is the use of the logarithmic normal distribution including a logarithmic transformation of the counts as a first step in data processing [15].

The use of logarithmic transformation is expected to take into consideration the random effect of the microorganisms in suspension as well as the components of additional variability. However, the use of such a transformation leads to expression of variance in log unit that is not always explicit for environmental biologists in general [16] and for water microbiologists in particular who often treat slightly contaminated samples. In addition, for test samples where low counts are sought and technical over-dispersion is observed, the logarithmic normal distribution does not always properly fit the low and high tail-end statistical distribution of the counts.

A statistical model that takes into consideration the over-dispersion compared to the Poisson model and is capable of including the random effects of the chosen PT design is a Poisson–Gamma hierarchical generalized linear model. The Poisson–Gamma HGLM model, applied to quality control in microbiology, has been first introduced in [17] from a mathematical perspective. An example of applying the model to a theoretical distribution based on the product of independent generalized Gamma distributions is presented in this paper. However, the advantage of the Poisson–Gamma HGLM model for common use in the statistical processing of microbiological data is plural. The Poisson distribution included in the model as a base distribution is valid when no other component of variability is significant in the PT design. It corresponds to the suitable model necessary to characterize the PT dispersion when no over-dispersion is observed. (No laboratory effect, no sample effect and no replicate effect are detected.) The use of a hierarchical model is appropriate for the selected PT design which is based on three nested factors: dispersion between replicates, dispersion between samples and dispersion between laboratories. Besides, when significant in the model, the effect of each factor can be assessed individually by using the Gamma distribution.

For y_ijk, the result of the count performed on replicate k of sample j by the laboratory i, the following model is used:

$$\log \lambda_{ijk} = \mu + \alpha_{i} + \beta_{ij} + \gamma_{ijk}$$

(4)

It is assumed that conditionally to the random effects $e^{{\alpha_{i} }} ,e^{{\beta_{ij} }}$ and $e^{{_{ijk} }} , \gamma_{ijk}$ follows a Poisson distribution with parameter λ_ijk. It is considered that $e^{{\alpha_{i} }} ,e^{{\beta_{ij} }}$ and $e^{{\gamma_{ijk} }}$ follow Gamma distributions with respective shape parameters $\frac{1}{{u_{1}^{2} }},\frac{1}{{u_{2}^{2} }}$ and $\frac{1}{{u_{3}^{2} }}$ and expected value 1:

• $e^{{\alpha_{i} }} \sim \varGamma\left( {\frac{1}{{u_{1}^{2} }},\frac{1}{{u_{1}^{2} }}} \right)$ represents the effect of laboratory i,

• $e^{{\beta_{ij} }} \sim \varGamma\left( {\frac{1}{{u_{2}^{2} }},\frac{1}{{u_{2}^{2} }}} \right)$ represents the effect of sample j of laboratory i, and

• $e^{{_{ijk} }} \sim \varGamma\left( {\frac{1}{{u_{3}^{2} }},\frac{1}{{u_{3}^{2} }}} \right)$ represents the measurement error between the replicates k of one sample.

The assigned value of the measurand is directly obtained from an estimate $\hat{\mu } = e^{\mu }$, used as a consensus value.

The scale parameters of the random variables $e^{{\alpha_{i} }} ,e^{{\beta_{ij} }}$ and $e^{{\gamma_{ijk} }}$ correspond, respectively, to the dispersion induced by the laboratory ($u_{1}^{2}$), the sample ($u_{2}^{2}$) and the replicate ($u_{3}^{2}$). These parameters are unequivocal for the data user as they are expressed in the same metric as that used for the expression of MU for microbiological determinations.

It should be noted that the use of random effects in the model allows the assessments of $u_{1}^{2} ,u_{2}^{2}$ and $u_{3}^{2}$ to be considered as generalizable and therefore applicable to the analysis of a given microorganism for the profession (including other laboratories than participants who took part in a given PT for example). This property of the model allows the use of the assessments according to the guidelines of the French technical reports on the expression of MU, based on external quality control data, for “general information on the profession” [7, 12].

Harmonization of the MU expression with EQC tools

From microbiological and technical points of view, the interlaboratory error $e^{{\alpha_{i} }}$ is due to:

• the definition of the measurand based on the viability of the analyte: a living microorganism that is defined taxonomically or, in some cases, by a less precise group designation than taxonomic definitions (e.g., coliforms);

• the method used by the different laboratories: type, productivity and selectivity of the culture medium used;

• the experience and competence of the operator to detect and select the presumptive colonies before confirmation;

• the recovery of the whole detection set used (plate, set of plates, membrane filtration …); and

• the nature of the samples used: microorganisms occurring in many different physiological states depending on the matrix (disinfectant stress in chlorinated water, nutrient depletion in oligotrophic waters…).

The homogeneity of the prepared batch of samples expressed in $e^{{\beta_{ij} }}$ in the model is under control depending on:

• the nature of the microorganisms used and the tendency of microbial populations to form clumped distributions;

• the batch homogenization procedure when preparing test samples by the PT provider; and

• the ability to ensure randomness of replicate sample bottle during filling from a batch of test material.

The measurement error in a laboratory $e^{{\gamma_{ijk} }}$ may be due to:

• a non-ideal mixing of the sample by the laboratory before inoculation;

• inappropriate repetition of the samples inoculations (test portion volume, water filtration system…);

• spatial heterogeneity of temperature during incubation (metrological control of the incubator, stacks of plates…).

The intensity of each parameter $\left( {u_{1}^{2} } \right),\left( {u_{2}^{2} } \right)$ and $\left( {u_{3}^{2} } \right)$ can be interpreted as indicators of PT variability in the same way that relative variance characterizes the operational uncertainty for every standard microbiological method.

Suitability assessment of the Poisson–Gamma HGLM by numerical simulation

A numerical simulation was used to study the Poisson–Gamma HGLM (hierarchical generalized linear model)  suitability in the range of the most common situations encountered in routine water microbiology PT. For a fixed number of samples j = 2 and a fixed number of replicates k = 2, 2100, simulations were computed considering the following cases:

• number of participants (p): {20; 50; 150};

• assigned value (µ) for the number of observed colonies: {5; 10; 15; 20; 30; 150};

• laboratory effect ($u_{1}^{2}$): {0.00; 0.05; 0.10; 0.15; 0.20; 0.25; 0.40};

• sample effect ($u_{2}^{2}$): {0.00; 0.01; 0.02; 0.05; 0.10}; and

• replicate effect ($u_{3}^{2}$): {0.00; 0.01; 0.02; 0.05; 0.10}.

A complete factorial design including all combinations of µ, $u_{1}^{2} ,u_{2}^{2}$ and $u_{3}^{2}$ was computed for p = 150 participants, which led to the first 1050 simulations. Secondly, 525 additional simulations were performed for each case where p = 20 and p = 50 participants, using the three assigned values µ = 10, µ = 20 and µ = 30 and all other combinations of $u_{1}^{2} ,u_{2}^{2}$ and $u_{3}^{2}$.

The ratio $\frac{{\hat{\mu }}}{\mu }$ is expected to be equal to one when the outcome of the assigned value $\hat{\mu }$ from Poisson–Gamma HGLM is precisely the same as the simulation hypothesis. Similarly, the ratios $\frac{{\widehat{{u_{1}^{2} }}}}{{u_{1}^{2} }},\frac{{\widehat{{u_{2}^{2} }}}}{{u_{2}^{2} }}$ and $\frac{{\widehat{{u_{3}^{2} }}}}{{u_{3}^{2} }}$ are expected to be equal to one for the laboratory effect, the between-sample effect and the replicate effect, respectively.

The simulation study results summarized in Table 2 show that a statistically significant bias is detected for the ratio $\frac{{\hat{\mu }}}{\mu }$, as neither the 95 % confidence interval nor the 99 % confidence interval includes the “reference” value of one. The order of magnitude of the bias was studied for different values of u² using a linear regression approach (see Fig. 2). Table 3 shows that the intercept of the linear regression is not significantly different from the value of one. However, the slope is significantly different from the zero value, which shows that the larger the expression of u², the greater the deviation of $\hat{\mu }$ from the simulation hypothesis µ.

Table 2 Simulation study results for the different parameters of the Poisson–Gamma HGLM

Fig. 2

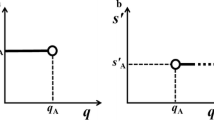
Quality of the estimate $\hat{\mu }$ from the Poisson–Gamma HGLM depending on the u². Each cross corresponds to a simulation point of the simulation plan. In the range u² ∈ [0; 0.4], which corresponds to the most common over-dispersion range, the minimum deviation is about 0.2 %, when no over-dispersion is detected (u² = 0.0000). The maximum deviation from the simulation hypothesis is observed for u² = 0.4000 with a corresponding value of 4.4 %

Table 3 Linear regression coefficients and confidence intervals for the quality of the estimate $\hat{\mu }$

Although this deviation appears statistically significant, it can be considered quantitatively acceptable from a practical point of view, particularly with regard to the rounding of estimated assigned values that is generally applied when using the scale change from logarithmic to natural scale in routine microbiological PT schemes [15].

With respect to the dispersion parameters ($u_{1}^{2}$), ($u_{2}^{2}$) and ($u_{3}^{2}$), the simulation study (Table 2) showed an unbiased estimate from Poisson–Gamma HGLM and a satisfactory assessment of the corresponding ratios.

Laboratory performance evaluation and scoring

The bias assessment for each laboratory participating in a PT is generally expressed in terms of z-score. Applied to the specific discrete distribution of microbial counts, the standardized position of each laboratory result can be derived from the quantiles of the negative binomial probability distribution.

Using the following re-parameterization: $\varGamma^{{\prime }} \left( {\lambda ,u^{2} } \right) = \lambda \cdot \varGamma \left( {\frac{1}{{u^{2} }},\frac{1}{{u^{2} }}} \right)$

Assume a PT including p laboratories that perform n repeated measurements for q samples. (y_ijk is the result of the count performed on replicate k of sample j by the laboratory i.)

Following the Gamma distribution properties, the distribution of the sums of the n repeated measurements per sample in one laboratory can be written as follows:

$$\mathop \sum \limits_{k = 1}^{n} y_{ijk} \sim{\mathcal{P}}\left( {n \cdot \lambda \cdot \varGamma^{{\prime }} \left( {1,\frac{{u_{3}^{2} }}{n}} \right) \cdot \varGamma^{{\prime }} \left( {1,u_{2}^{2} } \right) \cdot \varGamma^{{\prime }} \left( {1,u_{1}^{2} } \right)} \right)$$

(5)

Similarly, for the sums of the n repeated measurements obtained for the q samples in one laboratory:

$$\mathop \sum \limits_{j = 1}^{q} \mathop \sum \limits_{k = 1}^{n} y_{ijk} \approx {\mathcal{P}}\left( {n \cdot q \cdot \lambda \cdot \varGamma^{{\prime }} \left( {1,\frac{{\frac{{u_{3}^{2} }}{n} + u_{2}^{2} }}{q}} \right) \cdot \varGamma^{{\prime }} \left( {1,u_{1}^{2} } \right)} \right)$$

(6)

The implementation of the near-exact distribution for the product of independent generalized Gamma random variables [17] may be applied to the sum of counts. From a practical point of view, the approximation error induced in Eq. 6 (product of two Gamma distributions considered as a Gamma distribution) does not represent more than 0.02 in terms of cumulative probability derived from the distribution function for the sum $\sum\nolimits_{j = 1}^{q} {\sum\nolimits_{k = 1}^{n} {y_{ijk} } }$.Then, the total number of colonies observed by one laboratory approximately follows a NB distribution:

$$\mathop \sum \limits_{j = 1}^{q} \mathop \sum \limits_{k = 1}^{n} y_{ijk} \approx NB\left( {n \cdot q \cdot \lambda ,\frac{{u_{3}^{2} }}{n \cdot q} + \frac{{u_{2}^{2} }}{q} + u_{1}^{2} } \right)$$

(7)

We defined the generalized z-score as the normalized position of the sum of the counts of each laboratory, based on the corresponding cumulative probability of the NB distribution. As the NB cumulative distribution function provides the probability related to the sum of the counts of each laboratory, each calculated probability can finally be transformed into a standard normal distribution probability used to derive the generalized z-score (see Fig. 3). The generalized z-score can be interpreted conventionally using the limits of ± 2.0 and ± 3.0 as a warning and action signal, respectively.

Fig. 3

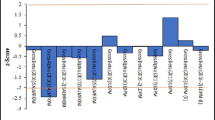
Calculation example of generalized z-score derivation using NB distribution. For a total number of 249 colonies observed by the laboratory code 26 (dashed circle) in Table 4, the corresponding probability from the NB distribution is 0.61 (a). The vertical and horizontal arrow dashed line corresponds to the probability “shift” from the NB distribution toward the standard normal distribution. The generalized z-score (solid circle) calculated for the given laboratory is then + 0.29 (b)

Table 4 provides an example of generalized z-score calculation for a data set on aerobic flora culturable at 36 °C of routine PT on indicator germs in bacteriologically controlled waters. This type of external quality assessment is intended for hospital and environmental laboratories that use an enumeration method of counting all the colonies present after filtering a volume of 100 ml on a 0.45-µm pore size membrane and depositing the filter on a non-selective culture medium such as “Plate Count Agar—PCA.” For this PT, taking into account the assigned value (λ = 58.43) and the estimated dispersion parameters $\left( {u_{1}^{2} } \right),\left( {u_{2}^{2} } \right)$ and $\left( {u_{3}^{2} } \right)$, a recommendation of performance to be monitored due to a possible underestimation of the bacterial load would be referred to laboratories coded 3 and 22 whose results appear statistically questionable (generalized z-score < −2).

Table 4 Generalized z-score calculated for a data set obtained for culturable microorganisms at 36 °C by membrane filtration method

Conclusion

The statistical model tested, based on the methodological principles of microbial enumeration in terms of distribution of microorganisms in suspension and extra-analytical variations observed in PT, showed satisfactory performance with regard to the reliability of the estimation of the various parameters.

The model provides estimates of parameters that are directly usable to express the measurement uncertainty, under interlaboratory conditions, for the needs of the profession. This uncertainty, capitalized on successive PTs, can be used by health authorities who would like to evaluate the maximum variability around a result of analysis of a regulatory microbiological parameter. The expression of the estimated parameters u² can also be considered as concrete EQC indicators in relation to method characterization and measurement uncertainty ISO standards.

The derivation of a generalized z-score from corresponding NB probability distribution gives the advantage of relying on dispersion which reflects the colony growth of bacteria while at the same time using common interpretation of the laboratory performance. The approach could make the bias estimate more reliable, especially in the detection of a significant underestimation or overestimation of the bacterial load.