Introduction

The evaluation of measurement uncertainty aims at estimating the impact of all analytical steps and effects that contribute to the measurement error (i.e. the difference between the measured and the reference quantity values [1]) in order to produce an interval that should encompass the conventional true value of the measurand with a known probability. The effects contributing to the measurement uncertainty can be divided into random and systematic effects.

The generic term ‘quantity’ is used when concepts are applicable to various specific quantities such as mass, concentration, mass concentration, mass fraction, pH and conductivity.

Different approaches have been developed to estimate the measurement uncertainty that use different types of information specific to the implementation of the measurement procedure in the laboratory or applicable to several laboratories [2,3,4]. For most analytical applications, the selected approach for the evaluation of the measurement uncertainty is the simplest one to apply that guarantees that the reported uncertainty is smaller than the target (i.e. maximum admissible) uncertainty [1, 5, 6].

The more pragmatic approach for the evaluation of the measurement uncertainty based on the specific performance of a laboratory, collected during the in-house validation of the measurement procedure, divides uncertainty components into precision, trueness and other components. Some authors designate the trueness component as the bias component. This approach is designated ‘supra-analytical’ [3], ‘single-laboratory validation’ [4] or ‘top-down based on in-house validation data’. The trueness uncertainty component is also relevant for more detailed models of the measurement uncertainty such as the ones produced by the differential approach [7,8,9].

The precision and trueness uncertainty components are usually dominated by random and systematic effects, respectively. For instance, the standard deviation of the intermediate precision used to quantify the precision component reflects the randomisation of systematic effects attributed to the daily run of analysis. The trueness component is also not a ‘pure’ representation of systematic effects since it is not possible to perform an infinite number of replicate measurements that would produce a mean not affected by random effects.

The trueness measurement uncertainty can be estimated from results of the analysis of internal and/or external reference materials. External reference materials, such as certified reference materials or proficiency test materials, are ideal references if the analyte speciation or bonding in the matrix of the reference materials is analytically similar to the analyte speciation or bonding in the matrix of the samples to be analysed. The reference value should be traceable to an adequate reference, typically an SI unit, and have an uncertainty smaller than one-fifth of the target uncertainty to make it easier to produce measurements with an uncertainty smaller than the target value.

If no external reference material is available, the analysis of spiked materials can allow the assessment of the systematic effects. The spiking can be performed on items with or without native quantity. A native quantity is a quantity present in the analysed item, i.e. not artificially added/spiked to the analysed item in the laboratory. The native analyte is typically present from the natural cycle of analyte occurrence (e.g. the contamination process of heavy metals in river water). The spiking of materials without detectable levels of the native quantity in the material allows for the assessment of measurement performance with a smaller uncertainty since the additional uncertainty component associated with the quantification of the native quantity is eliminated. However, in some fields it is not possible to have ‘real’ materials free from the quantity of interest, such as oranges without ascorbic acid or urban wastewaters without nitrates. The analysis of spiked samples has the advantage of testing performance in laboratory samples, and these materials are cheaper than external references. However, if the analyte speciation and/or bonding to the matrix is critical for measurement performance, the spiking reference and methodology must be carefully selected. In many cases, the spiking reference is a stock solution of the analyte from which a portion is taken to be added to an aliquot of the studied matrix. The spiking methodology describes how the reference is added to the matrix including procedures that try to promote the interaction of the spike with the matrix such as a delay of some hours between spiking and analysis to allow some interaction between added quantity and the matrix. For instance, in the analysis of total mercury in fish tissue, sample preparation can volatilise the naturally occurring methylmercury more easily than spiked inorganic mercury. Therefore, fish tissue should be spiked with methylmercury instead of mercury(II) nitrate reference solution.

Since the magnitude of systematic effects is frequently proportional to the quantity of interest, their value is monitored by the value of the ratio of the estimated and the reference quantity value of the reference material known as ‘recovery’. The reference value should be adequate for the studied measurement; e.g. if the aqua regia extractable mass fraction of chromium in a soil is measured, the reference mass fraction of total chromium in soil is inadequate if only a fraction of total chromium is extracted by the aqua regia.

The statistical and metrological quality of the estimated recovery increases if the mean of various recovery values (i.e. the mean recovery) is estimated from the analysis of the same or difference reference materials. A mean recovery close to 1 or 100 % suggests that the estimated values are not affected by recovery. The mean recovery is less affected by random effects as the number of estimated recoveries increases [10]. If at least 25 recovery tests are performed, the random effects affecting mean recovery estimation are at least five times less than the ones affecting single measurements, making it negligible in the measurement uncertainty evaluation for a single measurement result. (The standard deviation, \( s\left( {\bar{x}} \right) \), of a mean of 25 results is \( \sqrt {25} = 5 \) times smaller than the standard deviation, s, of a single measurement: \( s\left( {\bar{x}} \right) = s/\sqrt {25} \) [10].) Regardless of mean recovery uncertainty relevance, the mean recovery should be used to correct results affected by large or low mean recovery values, if necessary.

The systematic effects can also be quantified by the mean relative error (i.e. the mean of ratios between measurement error and the reference value). The mean relative error can be estimated by subtracting the mean recovery by one.

After the mean recovery has been estimated, it is necessary to assess whether any deviation to the ideal 100 % recovery is relevant.

Some authors proposed combining the mean error [11] or the mean squared error [12] with the expanded or squared standard uncertainty of results not corrected for recovery, respectively, to avoid the need to assess recovery magnitude. These combinations are suggested for operationally defined measurands/measurement procedures or for cases where estimated mean error has a chance of not being representative of performance in ‘real’ sample measurements. For clarity, two examples of the described scenarios are presented:

Example 1

In an operationally defined procedure, such as the determination of malathion in oranges using extraction procedure A, the combination of the mean error with other uncertainty components is expected to produce confidence intervals overlapping the ones for the analysis of the same sample using extraction procedure B, even if the extraction procedures have significantly different efficiencies.

Example 2

If measurement procedure performance is dominated by the liquid/liquid extraction of the analyte, analyte losses are expected due to its partition in the two phases producing analyte recoveries below 100 %. However, if observed mean analyte recovery is above 100 %, the results of unknown samples should not be corrected for recovery since the positive error observed in reference material analysis has the chance of not occurring in the analysis of unknown samples. In this case, mean error is combined with other uncertainty components of measurements not corrected for the mean error.

The decision to correct or not to correct the measurement error or recovery that was observed in the analysis of a reference material, in the analysis results for the unknown materials, has an impact on measurement traceability that must be considered. Only if systematic effects observed in the analysis of a reference material are corrected in the measurement results of the unknown item, the results are traceable to the value embodied in the reference material. da Silva and Camões [13] discussed that taking the mean recovery in the uncertainty budget or to correct measurement results for observed recovery does not guarantee equivalent compliance decisions from the same measurement.

This work discusses the management of systematic effects by determining the recovery from the analysis of adequate reference materials and by correcting recovery if it is significantly different from 100 % taking the uncertainty of estimated recovery into account.

Barwick and Ellison [14, 15] developed strategies for evaluating mean recovery from the analysis of a certified reference material, samples without native analyte spiked at the same level, the same sample with native analyte spiked at the same or different levels, or a sample characterised by a reference procedure. However, these authors did not discuss how to assess mean recovery if at least two of these reference materials are used (e.g. recovery estimated from the analysis of two certified reference materials and ten samples with different levels of native analyte and spiked at different levels).

The Nordtest report for the evaluation of the measurement uncertainty [12] presents approximate algorithms for estimating trueness uncertainty from different reference materials, assuming some uncertainty components are negligible and the combination of measurement errors on different mathematical expressions allows for an approximate quantification of the impact of systematic effects on the measurement results. However, Nordtest approximations can be too optimistic or pessimistic depending on the relevant details of the trueness tests, such as the covered quantity levels and diversity of reference value uncertainties, suggesting the need for alternative approaches.

This work presents a methodology to assess mean recovery from the analysis of independent reference materials of different types. The method is based on the propagation of uncertainty components for models where the measurements precision varies with the quantity of interest and also considers the metrological significance of the mean measurement error. This methodology is applicable to cases where measurements of the native and of the spiked quantities are affected by relevant and significantly different uncertainties. This work extends methodologies proposed by Barwick and Ellison [14, 15] for evaluating the uncertainty associated with the observed mean recovery, to the determination of recovery from the analysis of a larger diversity of materials.

This methodology was successfully applied to the determination of metals in natural water by ICP-OES.

Theory

The theory is divided into two parts, i.e. the art of recovery evaluation and in the description of a novel methodology to assess mean recovery from a large diversity of reference materials. The impact of recovery test precision conditions on the assessment of systematic effects is discussed in detail.

Recovery estimation from one reference material

Barwick and Ellison [14, 15] proposed general algorithms for estimating mean recovery, \( \bar{R} \), and the respective recovery uncertainty, \( u_{{\bar{R}}} \), from the analysis of a reference material from two reference material types, i.e. a reference material external to the measurement procedure and a reference material internal to the measurement procedure.

Reference material external to the measurement procedure

If the reference material is prepared independently of measurements performed by the assessed measurement procedure, Eq. (1) is used to estimate \( u_{{\bar{R}}} \):

$$ u_{{\bar{R}}} = \bar{R}\sqrt {\left( {\frac{{s_{R} }}{{\bar{R}\sqrt n }}} \right)^{2} + \left( {\frac{{u_{Q} }}{Q}} \right)^{2} } $$
(1)

where \( \bar{R} \) is the mean recovery (\( \bar{R} = {{\bar{q}} \mathord{\left/ {\vphantom {{\bar{q}} Q}} \right. \kern-0pt} Q} \); \( \bar{q} \) and Q are the estimated mean and reference quantity values, respectively), \( s_{R} \) the standard deviation of estimated n recovery values and \( u_{Q} \) the standard uncertainty of Q. Usually, \( s_{R} \) is estimated under intermediate precision conditions to allow that \( u_{{\bar{R}}} \) will be applicable to tests performed in subsequent days. This equation is applicable to recovery estimated from the analysis of a certified reference material, materials with negligible native quantity spiked at the same level of the quantity of interest and a material characterised by a reference procedure. In these cases, Q is the certified value, spiked value or value estimated by the reference procedure, respectively. This equation combines the standard uncertainty of \( \bar{q} \) and Q using the law of propagation of uncertainty, where the relative standard uncertainty of \( \bar{q} \) is equivalent to the relative standard deviation of the mean recovery (\( {{s_{R} } \mathord{\left/ {\vphantom {{s_{R} } {\left( {\bar{R}\sqrt n } \right)}}} \right. \kern-0pt} {\left( {\bar{R}\sqrt n } \right)}} \)).

All systematic effects affecting measurements, such as the ones resulting from the sample preparation, instrument calibration and matrix effects are combined in the estimated recovery. Equation 1 does not take into account the impact of measurement precision, typically the intermediate precision, in the measurement uncertainty since this component is to be accounted for by the measurement precision component.

Reference material internal to the measurement procedure

If the recovery is estimated from the analysis of a material with native quantity before and after spiking at a specific level of the quantity of interest, making recovery estimation dependent of native quantity determination, Eqs. (2) and (3) can be used to estimate mean recovery, \( \bar{R} \), and the respective recovery standard uncertainty, \( u_{{\bar{R}}} \).

$$ \bar{R} = \frac{{\bar{q} - \bar{q}_{0} }}{{q_{ + } }} $$
(2)

where \( \bar{q} \) and \( \bar{q}_{0} \) are the calculated mean values of the quantity of interest after and before spiking, respectively, and \( q_{ + } \) is the spiked quantity.

$$ u_{{\bar{R}}} = \bar{R}\sqrt {\left( {\frac{{\frac{{s^{2} \left( q \right)}}{n} + \frac{{s^{2} \left( {q_{0} } \right)}}{m}}}{{\left( {\bar{q} - \bar{q}_{0} } \right)^{2} }}} \right) + \left( {\frac{{u\left( {q_{ + } } \right)}}{{q_{ + } }}} \right)^{2} } $$
(3)

where \( s\left( q \right) \) and \( s\left( {q_{0} } \right) \) are the standard deviations of estimated n and m replicate results of material analysis after and before spiking, and \( u\left( {q_{ + } } \right) \) the standard uncertainty of \( q_{ + } \).

In most cases, each pair of estimated quantities in the material after, \( q_{i} \), and before, \( q_{0i} \), spiking is determined under repeatability conditions (i.e. in a short period of time and using the same analyst and equipment combination), and \( s\left( q \right) \) and \( s\left( {q_{0} } \right) \) are the repeatability standard deviations. Equation (3) represents the combination of the uncertainty components of the variables in Eq. (2). In these cases, systematic effects quantification is affected by random effects observed under repeatability conditions. The assessed systematic effects can be divided into components that are constant and specific for the daily measurement runs, the laboratory and, if relevant, the measurement procedure. In operationally defined measurement procedures, the systematic effects attributed to the measurement procedure are, by definition, null [2]. The components of systematic effects attributed to the daily measurement run and to the laboratory are not cancelled in operationally defined measurements.

If the estimated quantities \( q_{i} \) and \( q_{0i} \) are determined on different days, the \( s\left( q \right) \) and \( s\left( {q_{0} } \right) \) are the intermediate precision standard deviations that quantify random effects responsible for the difference between \( \bar{q} \) and \( \bar{q}_{0} \). In these cases, the mean recovery assesses in particular the combination of systematic effects associated with the laboratory and, if relevant, the measurement procedure.

After \( \bar{R} \) and \( u_{{\bar{R}}} \) are estimated, it is tested whether \( \bar{R} \) is significantly different from the ideal value of 1 by testing the following condition:

$$ \frac{{\left| {1 - \bar{R}} \right|}}{{u_{{\bar{R}}} }} \le t_{\nu }^{95\,\% } $$
(4)

where \( t_{\nu }^{95\,\% } \) is the two-tailed Student’s t for the degrees of freedom, ν, of \( u_{{\bar{R}}} \) and a 95 % confidence level. If the condition in Eq. (4) is true, the \( \bar{R} \) is metrologically equivalent to 1 and no recovery correction of the original measurement results is required. If the condition in Eq. (4) is not true, a correction of the original measured quantity values of the unknown samples should be considered by multiplying the measured results by the reverse of the mean recovery (\( {1 \mathord{\left/ {\vphantom {1 {\bar{R}}}} \right. \kern-0pt} {\bar{R}}} \)).

Barwick and Ellison [14, 15] also discussed how to estimate an additional uncertainty component for when recovery estimated for one quantity level/matrix combination is used to estimate measurement trueness for another quantity value/matrix combination. This approach relies on assessing measurement trueness from an adequate diversity of relevant effects affecting systematic effects, such as different matrixes of the measurement scope. If systematic effects vary significantly with the analysed matrix, the standard deviation of the mean of recovery estimated for different matrices should be considered as an additional uncertainty component for trueness.

Recovery estimation from various reference materials

This section describes the algorithms developed and applied in this work.

Reference material external to the measurement procedure

If recovery is estimated from the analysis of N reference materials prepared independently of measurements performed by the assessed procedure and each reference material is analysed n i times, the \( \bar{R} \) is estimated by Eq. (5).

$$ \bar{R} = {{\sum\limits_{i = 1}^{N} {\left( {\frac{{\bar{q}_{i} }}{{Q_{i} }}} \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{N} {\left( {\frac{{\bar{q}_{i} }}{{Q_{i} }}} \right)} } N}} \right. \kern-0pt} N} $$
(5)

where \( \bar{q}_{i} \) and \( Q_{i} \) are the estimated mean (\( \bar{q}_{i} = {{\sum {q_{ij} } } \mathord{\left/ {\vphantom {{\sum {q_{ij} } } {n_{i} }}} \right. \kern-0pt} {n_{i} }} \), where \( q_{ij} \) is the jth replicate of reference material i analysis; j = 1 to n i ) and reference values of reference material i, respectively.

If the replicate analysis of the reference materials is performed on different days, since the procedure is to be used over an extended period of time, \( u_{{\bar{R}}} \), is estimated by Eq. (6).

$$ u_{{\bar{R}}} = {{\sqrt {\sum\limits_{i = 1}^{N} {\left\{ {\left( {\frac{{\bar{q}_{i} }}{{Q_{i} }}} \right)^{2} \left[ {\left( {\frac{{s\left( {q_{{i}} } \right)}}{{\bar{q}_{i} \sqrt {n_{i} } }}} \right)^{2} + \left( {\frac{{u\left( {Q_{i} } \right)}}{{Q_{i} }}} \right)^{2} } \right]} \right\}} } } \mathord{\left/ {\vphantom {{\sqrt {\sum\limits_{i = 1}^{N} {\left\{ {\left( {\frac{{\bar{q}_{i} }}{{Q_{i} }}} \right)^{2} \left[ {\left( {\frac{{s\left( {q_{{i}} } \right)}}{{\bar{q}_{i} \sqrt {n_{i} } }}} \right)^{2} + \left( {\frac{{u\left( {Q_{i} } \right)}}{{Q_{i} }}} \right)^{2} } \right]} \right\}} } } N}} \right. \kern-0pt} N} $$
(6)

where \( s\left( {q_{i} } \right) \) is the intermediate precision standard deviation of \( q_{ij} \) values and \( u\left( {Q_{i} } \right) \) the standard uncertainty of \( Q_{i} \). If the reference materials have equivalent \( Q_{i} \), the same \( s\left( {q_{i} } \right) \) (e.g. a pooled intermediate precision standard deviation) can be considered. Models of intermediate precision variation with the quantity value can also be used to estimate \( s\left( {q_{i} } \right) \), in particular if \( Q_{i} \) are significantly different [5, 6]. The estimated \( \bar{R} \) is not focused on the quantification of systematic effects attributed to the daily run since it varies between runs. The intermediate precision standard deviation quantifies the combination of pure random effects with the variation of between run systematic effects. The repeatability standard deviation quantifies pure random effects.

If the reference materials are analysed under repeatability conditions, for instance when the measurement procedure is to be validated and used in a single day due to a request for urgent sample analysis, the \( s\left( {q_{i} } \right) \) is the repeatability standard deviation and \( \bar{R} \) assesses all possible systematic effects including the one attributed to the specific daily run.

Replicate analysis of the reference material should be performed in the same precision conditions (i.e. repeatability or intermediate precision conditions).

If each studied reference material is analysed once (i.e. n i  = 1), Eq. (6) is not converted into Eq. (1) since \( Q_{i} \) are assumed to be independent. Equation (6) is converted into Eq. (1) when only one reference material is analysed making N = 1.

Reference material internal to the procedure

If N materials with independent, different or equivalent, native quantity levels are spiked at independent levels, and materials are quantified n i and m i times after and before spiking, respectively (i = 1 to N), the mean recovery is estimated by Eq. (7).

$$ \bar{R} = {{\sum\limits_{i = 1}^{N} {\frac{{\bar{q}_{i} - \bar{q}_{0i} }}{{q_{ + i} }}} } \mathord{\left/ {\vphantom {{\sum\limits_{i = 1}^{N} {\frac{{\bar{q}_{i} - \bar{q}_{0i} }}{{q_{ + i} }}} } N}} \right. \kern-0pt} N} $$
(7)

where \( \bar{q}_{i} \) and \( \bar{q}_{0i} \) are the estimated mean quantities of material i after and before spiking, respectively, and \( q_{ + i} \) the spiked quantity of material i (\( \bar{q}_{i} = {{\sum {q_{ij} } } \mathord{\left/ {\vphantom {{\sum {q_{ij} } } {n_{i} }}} \right. \kern-0pt} {n_{i} }} \), where \( q_{ij} \) is the jth replicate result of the analysis of material i after spiking (j = 1 to n i ) and \( \bar{q}_{0i} = {{\sum {q_{0ik} } } \mathord{\left/ {\vphantom {{\sum {q_{0ik} } } {m_{i} }}} \right. \kern-0pt} {m_{i} }} \), where \( q_{0ik} \) is the kth replicate result of the analysis of material i before spiking (k = 1 to m i )). If materials, before and after spiking, are analysed under repeatability conditions, the standard uncertainty, \( u_{{\bar{R}}} \), of the mean recovery (Eq. (7)) is estimated by Eq. (8).

$$ u_{{\bar{R}}} = {{\sqrt {\sum\limits_{i = 1}^{N} {\left\{ {\left( {\frac{{\bar{q}_{i} - \bar{q}_{0i} }}{{q_{ + i} }}} \right)^{2} \left[ {\frac{{\frac{{s^{2} \left( {q_{i} } \right)}}{{n_{i} }} + \frac{{s^{2} \left( {q_{0i} } \right)}}{{m_{i} }}}}{{\left( {\bar{q}_{i} - \bar{q}_{0i} } \right)^{2} }} + \left( {\frac{{u\left( {q_{ + i} } \right)}}{{q_{ + i} }}} \right)^{2} } \right]} \right\}} } } \mathord{\left/ {\vphantom {{\sqrt {\sum\limits_{i = 1}^{N} {\left\{ {\left( {\frac{{\bar{q}_{i} - \bar{q}_{0i} }}{{q_{ + i} }}} \right)^{2} \left[ {\frac{{\frac{{s^{2} \left( {q_{i} } \right)}}{{n_{i} }} + \frac{{s^{2} \left( {q_{0i} } \right)}}{{m_{i} }}}}{{\left( {\bar{q}_{i} - \bar{q}_{0i} } \right)^{2} }} + \left( {\frac{{u\left( {q_{ + i} } \right)}}{{q_{ + i} }}} \right)^{2} } \right]} \right\}} } } N}} \right. \kern-0pt} N} $$
(8)

where \( s\left( {q_{i} } \right) \) and \( s\left( {q_{ 0i} } \right) \) are the repeatability standard deviations of \( q_{ij} \) and \( q_{0ik} \) replicate results, respectively, and \( u\left( {q_{ + i} } \right) \) the standard uncertainty of \( q_{ + i} \). If n i and m i are smaller than 10, the \( s\left( {q_{i} } \right) \) and \( s\left( {q_{ 0i} } \right) \) can be estimated from previously developed models of the variation of the standard deviation of the repeatability with the measured quantity associated with a larger number of degrees of freedom [5, 6]. Since precision conditions considered in Eq. (8) are repeatability conditions, the systematic effects assessed from estimated \( \bar{R} \) and \( u_{{\bar{R}}} \) are the ones observed within a run, in the laboratory and, for rational measurements, attributed to measurement procedure principles.

In the uncommon situations where materials after and before spiking are analysed on different days (i.e. under intermediate precision conditions), the \( s\left( {q_{i} } \right) \) and \( s\left( {q_{ 0i} } \right) \) are intermediate precision standard deviations.

Equation (8) is not applicable to data collected under different precision conditions.

If each material after and before spiking is analysed once, Eq. (8) is simplified to Eq. (9):

$$ u_{{\bar{R}}} = {{\sqrt {\sum\limits_{i = 1}^{N} {\left\{ {\left( {\frac{{q_{i} - q_{0i} }}{{q_{ + i} }}} \right)^{2} \left[ {\frac{{s^{2} \left( {q_{i} } \right) + s^{2} \left( {q_{0i} } \right)}}{{\left( {q_{i} - q_{0i} } \right)^{2} }} + \left( {\frac{{u\left( {q_{ + i} } \right)}}{{q_{ + i} }}} \right)^{2} } \right]} \right\}} } } \mathord{\left/ {\vphantom {{\sqrt {\sum\limits_{i = 1}^{N} {\left\{ {\left( {\frac{{q_{i} - q_{0i} }}{{q_{ + i} }}} \right)^{2} \left[ {\frac{{s^{2} \left( {q_{i} } \right) + s^{2} \left( {q_{0i} } \right)}}{{\left( {q_{i} - q_{0i} } \right)^{2} }} + \left( {\frac{{u\left( {q_{ + i} } \right)}}{{q_{ + i} }}} \right)^{2} } \right]} \right\}} } } N}} \right. \kern-0pt} N} $$
(9)

Reference material internal to the procedure: liquid reference materials internal to the procedure

In the analysis of liquid samples spiked with a standard solution volume, native quantity is diluted and, if relevant, this dilution should be taken into account in recovery assessment.

The most convenient way to perform these spikes is by taking a volumetric flask with volume, V A, adding spiked volume, V 1, of the standard solution and filling up the flask with the sample solution. In this case, the spiked mass concentration of solution i, \( \gamma_{ + i} \), is [\( \gamma_{ + i} = \gamma_{{{\text{S}}i}} \left( {{{V_{1i} } \mathord{\left/ {\vphantom {{V_{1i} } {V_{{{\text{A}}i}} }}} \right. \kern-0pt} {V_{{{\text{A}}i}} }}} \right) \)] where \( \gamma_{{{\text{S}}i}} \) is the mass concentration of the standard solution. (The notation \( q \) is changed to \( \gamma \) since the gamma is the notation indicated for mass concentrations.) The native quantity in spiked sample i, \( \gamma_{{0 ( {\text{d)}}i}} \), is \( \gamma_{{0 ( {\text{d)}}i}} = \gamma_{0i} \left[ {{{(V_{{{\text{A}}i}} - V_{1i} )} \mathord{\left/ {\vphantom {{(V_{{{\text{A}}i}} - V_{1i} )} {V_{{{\text{A}}i}} }}} \right. \kern-0pt} {V_{{{\text{A}}i}} }}} \right] \), where \( \gamma_{0i} \) is the native mass concentration. The native sample dilution factor in spiked samples (i.e. \( \left[ {{{(V_{{{\text{A}}i}} - V_{1i} )} \mathord{\left/ {\vphantom {{(V_{{{\text{A}}i}} - V_{1i} )} {V_{{{\text{A}}i}} }}} \right. \kern-0pt} {V_{{{\text{A}}i}} }}} \right] \)) should not be smaller than 80 % to guarantee that the recovery in the diluted matrix will be representative of the recovery observed in undiluted samples. Even if strong matrix effects affect measurements, the dilution of about 20 % of the matrix should not produce matrix effects significantly different from those observed in undiluted matrices.

If N pairs of samples before and after spiking are analysed, the \( \bar{R} \) is estimated by Eq. (10):

$$ \bar{R} = \sum\limits_{i = 1}^{N} {\frac{{\bar{\gamma }_{i} - \bar{\gamma }_{0i} \cdot \left[ {\left( {V_{{{\text{A}}i}} - V_{1i} } \right)/V_{{{\text{A}}i}} } \right]}}{{N \cdot \gamma_{{{\text{S}}i}} \left( {{{V_{1i} } \mathord{\left/ {\vphantom {{V_{1i} } {V_{{{\text{A}}i}} }}} \right. \kern-0pt} {V_{{{\text{A}}i}} }}} \right)}}} = \sum\limits_{i = 1}^{N} {\frac{{\bar{\gamma }_{i} \cdot V_{{{\text{A}}i}} - \bar{\gamma }_{0i} \cdot \left( {V_{{{\text{A}}i}} - V_{1i} } \right)}}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }}} $$
(10)

where \( \bar{\gamma }_{i} \) and \( \bar{\gamma }_{0i} \) are the estimated mean mass concentrations of sample i after and before spiking.

The \( u_{{\bar{R}}} \) is estimated by Eq. (11), which consists of the application of the law of propagation of uncertainty to combine standard uncertainties of Eq. (10) variables:

$$ \begin{aligned} u_{{\bar{R}}} & = \sqrt {\sum\limits_{i = 1}^{N} {\left\{ \begin{aligned} \left( {\frac{{\partial \bar{R}}}{{\partial \bar{\gamma }_{i} }} \cdot u\left( {\bar{\gamma }_{i} } \right)} \right)^{2} + \left( {\frac{{\partial \bar{R}}}{{\partial \bar{\gamma }_{0i} }} \cdot u\left( {\bar{\gamma }_{0i} } \right)} \right)^{2} + \left( {\frac{{\partial \bar{R}}}{{\partial V_{{{\text{A}}i}} }} \cdot u\left( {V_{{{\text{A}}i}} } \right)} \right)^{2} + \hfill \\ \left( {\frac{{\partial \bar{R}}}{{\partial V_{1i} }} \cdot u\left( {V_{1i} } \right)} \right)^{2} + \left( {\frac{{\partial \bar{R}}}{{\partial \gamma_{{{\text{S}}i}} }} \cdot u\left( {\gamma_{{{\text{S}}i}} } \right)} \right)^{2} \hfill \\ \end{aligned} \right\}} } &\\ = \sqrt {\sum\limits_{i = 1}^{N} {\left\{ \begin{aligned} \left( {\frac{{V_{{{\text{A}}i}} }}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }} \cdot \frac{{s\left( {\gamma_{i} } \right)}}{{\sqrt {n_{i} } }}} \right)^{2} + \left( {\frac{{V_{1i} - V_{{{\text{A}}i}} }}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }} \cdot \frac{{s\left( {\gamma_{0i} } \right)}}{{\sqrt {m_{i} } }}} \right)^{2} + \left( {\frac{{\bar{\gamma }_{{_{i} }} - \bar{\gamma }_{{0i}} }}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }} \cdot u\left( {V_{{{\text{A}}i}} } \right)} \right)^{2} + \hfill \\ \left( {\frac{{\bar{\gamma }_{{0i}} - \left( {\gamma_{{{\text{S}}{i}}} \cdot \bar{R}_{i} } \right)}}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }} \cdot u\left( {V_{1i} } \right)} \right)^{2} + \left( { - \frac{{\bar{R}_{i} }}{{N \cdot \gamma_{{{\text{S}}i}} }} \cdot u\left( {\gamma_{{{\text{S}}i}} } \right)} \right)^{2} \hfill \\ \end{aligned} \right\}} } \\ \end{aligned} $$
(11)

where \( s\left( {\gamma_{i} } \right) \) and \( s\left( {\gamma_{0i} } \right) \) are the repeatability standard deviations of \( \gamma_{ij} \) (j = 1 to n i ) and \( \gamma_{0ik} \) (k = 1 to m i ) measurements if, for each recovery test i, measurements are performed under repeatability conditions and \( \bar{R}_{i} \) is the mean recovery estimated from test i. The independent recovery tests (e.g. recovery tests i = 1 and i = 2) can be performed on the same or different days since this is irrelevant for Eq. (11).

If a volume, V 1i , of the stock solution of the quantity of interest (stock solution mass concentration \( \gamma_{{{\text{S}}i}} \)) is not the only one added to the flask (flask volume V Ai ) where the sample will be diluted, but (p − 1) additional volumes \( V_{2i} \) to \( V_{pi} \) of other solutions of the same solvent are being added with no relevant levels of the quantity of interest, recovery is estimated by Eq. (12). The additional solutions can be spikes of other analytes.

$$ \bar{R} = \sum\limits_{i = 1}^{N} {\frac{{\bar{\gamma }_{i} - \bar{\gamma }_{0i} \cdot \left[ {\left( {V_{{{\text{A}}i}} - V_{1i} - V_{{{\text{B}}i}} } \right)/V_{{{\text{A}}i}} } \right]}}{{N \cdot \gamma_{{{\text{S}}i}} \left( {{{V_{1i} } \mathord{\left/ {\vphantom {{V_{1i} } {V_{{{\text{A}}i}} }}} \right. \kern-0pt} {V_{{{\text{A}}i}} }}} \right)}}} = \sum\limits_{i = 1}^{N} {\frac{{\bar{\gamma }_{i} \cdot V_{{{\text{A}}i}} - \bar{\gamma }_{0i} \cdot \left( {V_{{{\text{A}}i}} - V_{1i} - V_{{{\text{B}}i}} } \right)}}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }}} $$
(12)

where V Bi is the sum of solution volumes, other than \( V_{1i} \), added to diluted sample flask (i.e. \( V_{{{\text{B}}i}} = \sum\limits_{i = 2}^{p} {V_{pi} } \)). The standard uncertainty of \( \bar{R} \), determined by Eq. (12), is estimated by Eq. (13):

$$ \begin{aligned} u_{{\bar{R}}} &= \sqrt {\sum\limits_{i = 1}^{N} {\left\{ \begin{aligned} \left( {\frac{{\partial \bar{R}}}{{\partial \bar{\gamma }_{i} }} \cdot u\left( {\bar{\gamma }_{i} } \right)} \right)^{2} + \left( {\frac{{\partial \bar{R}}}{{\partial \bar{\gamma }_{0i} }} \cdot u\left( {\bar{\gamma }_{0i} } \right)} \right)^{2} + \left( {\frac{{\partial \bar{R}}}{{\partial V_{{{\text{A}}i}} }} \cdot u\left( {V_{{{\text{A}}i}} } \right)} \right)^{2} + \hfill \\ \left( {\frac{{\partial \bar{R}}}{{\partial V_{1i} }} \cdot u\left( {V_{1i} } \right)} \right)^{2} + \left( {\frac{{\partial \bar{R}}}{{\partial \gamma_{{{\text{S}}i}} }} \cdot u\left( {\gamma_{{{\text{S}}i}} } \right)} \right)^{2} + \left( {\frac{{\partial \bar{R}}}{{\partial V_{{{\text{B}}i}} }} \cdot u\left( {V_{{{\text{B}}i}} } \right)} \right)^{2} \hfill \\ \end{aligned} \right\}} } \\ &= \sqrt {\sum\limits_{i = 1}^{N} {\left\{ \begin{aligned} \left( {\frac{{V_{{{\text{A}}i}} }}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }} \cdot \frac{{s\left( {\gamma_{i} } \right)}}{{\sqrt {n_{i} } }}} \right)^{2} + \left( {\frac{{V_{1i} - V_{{{\text{A}}i}} }}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }} \cdot \frac{{s\left( {\gamma_{0i} } \right)}}{{\sqrt {m_{i} } }}} \right)^{2} + \left( {\frac{{\bar{\gamma }_{{_{i} }} - \bar{\gamma }_{{0i }} }}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }} \cdot u\left( {V_{{{\text{A}}i}} } \right)} \right)^{2} + \hfill \\ \left( {\frac{{\bar{\gamma }_{{0i}} - \left( {\gamma_{{{\text{S}}{i} }} \cdot \bar{R}_{i} } \right)}}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }} \cdot u\left( {V_{1i} } \right)} \right)^{2} + \left( { - \frac{{\bar{R}_{i} }}{{N \cdot \gamma_{{{\text{S}}i}} }} \cdot u\left( {\gamma_{{{\text{S}}i}} } \right)} \right)^{2} + \left( {\frac{{\bar{\gamma }_{{0i}} }}{{N \cdot \gamma_{{{\text{S}}i}} \cdot V_{1i} }} \cdot u\left( {V_{{{\text{B}}i}} } \right)} \right)^{2} \hfill \\ \end{aligned} \right\}} } \\ \end{aligned} $$
(13)

Estimation of the precision of the recovery tests

Depending on the precision conditions affecting the estimated recovery, the mean recovery standard uncertainty can be determined using repeatability or intermediate precision standard deviations. The precision conditions affecting mean recovery will also determine which systematic effects are assessed from the mean recovery as discussed previously.

For the trueness test, reference materials external or internal to the measurement procedure can be analysed. For the case where these reference materials are analysed once or from a small number of tests, it is convenient to use prior models of precision variation with the quantity of interest build from an adequately large number of experimental data. For most analytical applications, precision estimation is adequate if it is associated with at least 14 degrees of freedom [16].

Ideally, the models of precision variation with the quantity should be based on information collected at several quantity levels. However, the information from a single level can be used to model precision in a wide range if some general trends in measurement precision are considered.

In most classical and instrumental measurements, precision standard deviation is approximately constant in a narrow range and tends to increase as the quantity increases in a wider range. On the other hand, the precision relative standard deviation tends to decrease in an abrupt way from the Limit of Detection to two times the Limit of Quantification (2q LoQ), decreasing slightly after this level [5, 6]. Therefore, regardless of the level of the quantity of interest at which precision was estimated, it can be assumed, by approximation, that the observed precision standard deviation overestimates precision below the studied level and the precision relative standard deviation overestimates precision above the studied level (Fig. 1a, b) [5, 6]. If precision is estimated at various levels, adequate step models can be built. Figures 2a, b and 3a, b present examples where precision models are defined from precision estimated at two or three levels positioned below and above 2q LoQ. If more levels are studied, more complex models, such as a linear relation between the precision standard deviation and the quantity of interest, can be built [9, 17, 18].

Fig. 1
figure 1

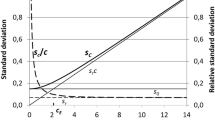
Model of measurement precision variation with the quantity of interest built from precision estimated at one quantity, \( q_{\text{A}} \). a The precision standard deviation, \( s_{\text{A}} \), estimated at a specific quantity, \( q_{\text{A}} \), overestimates precision below \( q_{\text{A}} \); b the precision relative standard deviation, \( s_{\text{A}}^{\prime } \) (\( s_{\text{A}}^{\prime } = {{s_{\text{A}} } \mathord{\left/ {\vphantom {{s_{\text{A}} } {q_{\text{A}} }}} \right. \kern-0pt} {q_{\text{A}} }} \)), estimated at \( q_{\text{A}} \), overestimates precision above \( q_{\text{A}} \)

Full size image
Fig. 2
figure 2

Model of measurement precision variation with the quantity of interest (thicker line) built from precision estimated at quantities \( q_{\text{A}} \) and \( q_{\text{B}} \) positioned below and above two times the Limit of Quantification (\( 2\gamma_{\text{LoQ}} \)), respectively. The \( s_{\text{A}} \) and \( s_{\text{B}}^{\prime } \) represent the absolute and relative precision standard deviations associated with \( q_{\text{A}} \) and \( q_{\text{B}} \), respectively

Full size image
Fig. 3
figure 3

Model of measurement precision variation with the quantity of interest built from precision estimated at quantities \( q_{\text{A}} \), \( q_{\text{B}} \) and \( q_{\text{C}} \). \( q_{\text{A}} \) is smaller than two times the Limit of Quantification (\( 2\gamma_{\text{LoQ}} \)), and \( q_{\text{B}} \) and \( q_{\text{C}} \) are larger than \( 2\gamma_{\text{LoQ}} \). The \( s_{\text{A}} \), \( s_{\text{B}}^{\prime } \) and \( s_{\text{C}}^{\prime } \) represent the absolute and relative precision standard deviations associated with \( q_{\text{A}} \), \( q_{\text{B}} \) and \( q_{\text{C}} \), respectively (the apostrophes identify relative quantities)

Full size image

Experimental

The developed methodology for mean recovery assessment, particularly the presented algorithms to estimate recovery from the analysis of different liquid samples with native quantity before and after spiking, was applied to the determination of dissolved metals in natural waters by inductively coupled plasma atomic emission spectrometry (ICP-OES). Samples were analysed after filtration with a 0.45 μm pore cellulose acetate filter. The top-down approach based on in-house validation data was used to estimate measurement uncertainty by combining two major uncertainty components: recovery/trueness and precision components. No relevant additional uncertainty components were identified.

Material

The volumetric operations were performed using class A volumetric glassware subject to an adequate washing procedure. The 0.45 μm pore cellulose acetate filter was purchased from Pall Corporation (New York, USA). A Thermo Scientific (Waltham, MA, USA) iCAP 7400 ICP-OES Duo spectrometer was used in quantifications.

Chemicals

Purified chemicals adequate for performed analysis and checked with blank tests were used. Single-element stock solutions purchased from Merck (Darmstadt, Germany) with a reference value of (1000 ± 10) mg L−1 (coverage factor of 2) of the metal were used. Different lots of Merck solutions were used to prepare calibrators and to spike samples to guarantee deviation in stock solution values do not cancel in recovery tests. Merck solutions have metal contents traceable to the unit mg L−1 of the International System of Units (SI) checked through the analysis of the corresponding Standard Reference Materials (NIST SRM®) produced by the National Institute of Standards and Technology of the USA. Suprapur grade nitric acid purchased from Merck (Darmstadt, Germany) was used.

Analysed samples

Samples of surface natural waters, collected in rivers and bayous, were spiked and analysed to estimate recovery.

Proficiency test

The developed methodology was assessed through the participation in two proficiency tests: (1) Aquacheck 1S, Round 485, May 2015—Soft water—Major Inorganic Components [19]; (2) RELACRE EAA, 1st Round, June 2015, Drinking water [20].

Measurement procedure

The measurement procedure involves sample filtration and acidification to 0.2 % nitric acid with a negligible volume and, if relevant, dilution before collecting ICP-OES signals. The spectrometer is subject to an analytical calibration before samples analysis. Table 1 lists the studied elements, the wavelength of emission lines, the plasma view configurations and the calibration range. For some elements, instrument response was calibrated in a low and a high mass concentration range to allow direct measurement of samples with higher concentrations. The details of calibrators preparation are omitted for simplicity. Calibrations were performed at six levels, including blank, with approximately equidistant mass concentrations.

Table 1 List of elements analysed in natural water by ICP-OES, relevant instrument details and studied calibration ranges
Full size table

Results and discussion

Measurement performance assessment

The following sections describe how different performance parameters were determined and the maximum values for these parameters. Since the decision about measurement procedure fitness for the intended use is based in the comparison of the Limit of Quantification, \( \gamma_{\text{LoQ}} \), and uncertainty with the Maximum Limit of Quantification, \( \gamma_{\text{LoQ}}^{\text{Max}} \), and the target uncertainty, respectively, the maximum values for measurements repeatability and intermediate precision are only indicative [6]. The \( \gamma_{\text{LoQ}} \) is also relevant to set models of the variation of measurement precision throughout the calibration range (see sections “Results and discussion—Measurement performance assessment—Measurement repeatability” and “Measurement intermediate precision”).

The linearity of the variation of the ICP-OES emission with the mass concentration of the studied element in analysed solution was assessed, and a linear regression model was used to build the calibration curve. Relevant deviations from linearity can make the analyte recovery observed by interpolating signal in one portion of the calibration curve not applicable to interpolations performed in another segment of the calibration curve.

Limit of Quantification

The assessment of measurement procedure performance started with \( \gamma_{\text{LoQ}} \) determination (\( \gamma_{\text{LoQ}} = 10s\left( {\gamma_{\text{CS}} } \right) \)), by taking ten times the standard deviation, \( s\left( {\gamma_{\text{CS}} } \right) \), of at least ten (n ≥ 10) measurement results, \( \gamma_{{{\text{CS}}i}} \) (i = 1 to n), obtained on different days, of a control standard with a quantity level, \( \varGamma_{\text{CS}} \), equivalent to the expected \( \gamma_{\text{LoQ}} \). If the estimated \( \gamma_{\text{LoQ}} \) is more than five times different from \( \varGamma_{\text{CS}} \) (i.e. if \( \left( {{{\bar{\gamma }_{\text{CS}} } \mathord{\left/ {\vphantom {{\bar{\gamma }_{\text{CS}} } {\varGamma_{\text{CS}} }}} \right. \kern-0pt} {\varGamma_{\text{CS}} }}} \right) < 0.2 \) or \( \left( {{{\bar{\gamma }_{\text{CS}} } \mathord{\left/ {\vphantom {{\bar{\gamma }_{\text{CS}} } {\varGamma_{\text{CS}} }}} \right. \kern-0pt} {\varGamma_{\text{CS}} }}} \right) > 5 \)), a control standard with a different concentration should be prepared and analysed on different days to guarantee \( s\left( {\gamma_{\text{CS}} } \right) \) adequately estimates the precision at the \( \gamma_{\text{LoQ}} \). The trueness of control standard measurements was assessed, in a pragmatic way, by checking whether the absolute value of the difference (\( \bar{\gamma }_{\text{CS}} - \varGamma_{\text{CS}} \)) is smaller than the standard deviation, \( s\left( {\bar{\gamma }_{\text{CS}} } \right) \), of \( \bar{\gamma }_{\text{CS}} \) times the Student’s t for (n − 1) degrees of freedom and 99 % confidence level, t \( \left(\left| {\bar{\gamma }_{\text{CS}} - \varGamma_{\text{CS}} } \right| \le t \cdot {{s\left( {\gamma_{{{\text{CS}}i}} } \right)} \mathord{\left/ {\vphantom {{s\left( {\gamma_{{{\text{CS}}i}} } \right)} {\sqrt n }}} \right. \kern-0pt} {\sqrt n }}\right) \), where \( \bar{\gamma }_{\text{CS}} \) is the mean of \( \gamma_{{{\text{CS}}i}} \) values, \( \bar{\gamma }_{\text{CS}} = \sum {{{\gamma_{{{\text{CS}}i}} } \mathord{\left/ {\vphantom {{\gamma_{{{\text{CS}}i}} } n}} \right. \kern-0pt} n}} \), and \( \left. s\left( {\bar{\gamma }_{\text{CS}} } \right) = {{s\left( {\gamma_{{{\text{CS}}i}} } \right)} \mathord{\left/ {\vphantom {{s\left( {\gamma_{{{\text{CS}}i}} } \right)} {\sqrt n }}} \right. \kern-0pt} {\sqrt n }} \right.\). If this condition is valid, no relevant systematic effects affect quantifications at the \( \gamma_{\text{LoQ}} \). This condition is not adequate to compare \( \bar{\gamma }_{\text{CS}} \) with \( \varGamma_{\text{CS}} \) if \( \varGamma_{\text{CS}} \) is associated with a relevant uncertainty.

The \( \gamma_{\text{LoQ}}^{\text{Max}} \) is 30 % of the ‘environmental quality standard’ value set by the national regulator for water status monitoring as defined in Directive 2009/90/EC [21]. If no reference for the environmental monitoring is set, the \( \gamma_{\text{LoQ}}^{\text{Max}} \) is defined from the maximum Limit of Detection, \( \gamma_{\text{LoD}}^{\text{Max}} \), set for the analysis of drinking water in Council Directive 98/83/EC [22], assuming that the \( \gamma_{\text{LoQ}}^{\text{Max}} \) is 10/3 larger than the \( \gamma_{\text{LoD}}^{\text{Max}} \). For elements with no limits set due to its low toxicological relevance, the \( \gamma_{\text{LoQ}} \) should be smaller than analysed sample concentrations.

Table 2 presents the defined \( \gamma_{\text{LoQ}}^{\text{Max}} \) and the estimated \( \gamma_{\text{LoQ}} \). Since quantifications of \( \varGamma_{\text{CS}} \) are not affected by relevant systematic effects and \( \gamma_{\text{LoQ}} \) is not significantly larger than \( \gamma_{\text{LoQ}}^{\text{Max}} \), measurement procedure \( \gamma_{\text{LoQ}} \) is fit for the intended use. For measurements of the mass concentration of Cu, the estimated \( \gamma_{\text{LoQ}} \) (i.e. 0.0029 mg L−1) is not significantly larger than the \( \gamma_{\text{LoQ}}^{\text{Max}} \) set from ‘environmental quality standards’ (i.e. 0.0023 mg L−1) taking the expected variability of precision estimates [5, 6]. The calibration ranges for which no \( \gamma_{\text{LoQ}}^{\text{Max}} \) is set, have a \( \gamma_{\text{LoQ}} \) or lower calibration level, excluding the blank, smaller than levels in studied samples.

Table 2 Calibration range, and target and observed performance parameters
Full size table

Instrument signal linearity

The linearity of instrument response variation with the analyte mass concentration was tested with the ANOVA lack-of-fit test (ANOVA-LOF) [24] or the Chi-squared lack-of-fit test (χ 2-test) [25] applicable to calibration ranges where signal variances are constant or vary with the quantity of interest, respectively. The homogeneity of signal variance was tested with Levene’s test [24]. If instrument signal varies linearly with the concentration, the least squares regression model, LSRM, is adequate to estimate the intercept and the slope of the calibration curve regardless of the homogeneity or heterogeneity of signal’s variance [10]. da Silva [26] presented experimental evidences of the statistical equivalence of results estimated by the linear unweighted (i.e. the LSRM) or the linear weighted regression model even if signal variance varies in the calibration range.

The instrument signal varies linearly in the studied mass concentration ranges of the various elements.

Measurement repeatability

The measurement repeatability was estimated from duplicate measurements, obtained under repeatability conditions, of different real samples. The range (the range is the absolute value of the difference), A j , of duplicate results of N samples (j = 1 to N) with a mean value between the \( \gamma_{\text{LoQ}} \) and \( 2\gamma_{\text{LoQ}} \) inclusive, designated interval I, were combined in the same mean range, \( \bar{A} \) (\( \bar{A} = {{\sum {A_{j} } } \mathord{\left/ {\vphantom {{\sum {A_{j} } } N}} \right. \kern-0pt} N} \)) to estimate the repeatability standard deviation, \( s_{r{\rm{(I)}}} \), in this concentration interval: \( s_{r{\rm(I)}} = {{\bar{A}} \mathord{\left/ {\vphantom {{\bar{A}} {1.128}}} \right. \kern-0pt} {1.128}} \) [27]. For sample concentrations larger than the two times the \( \gamma_{\text{LoQ}} \) (i.e. in interval II), duplicate results relative ranges, \( A_{j}^{\prime } \) (i.e. the range divided by the mean value), are combined in the same mean relative range, \( \bar{A}^{\prime } \), to estimate the relative repeatability standard deviation, \( s^{\prime }_{r{\rm(II)}} \), in interval II: \( s_{r{\rm(II)}}^{\prime } = {{\bar{A}^{\prime } } \mathord{\left/ {\vphantom {{\bar{A}^{\prime } } {1.128}}} \right. \kern-0pt} {1.128}} \). Table 2 presents estimated \( s_{r{\rm(I)}} \) and \( s_{r{\rm(II)}}^{\prime } \). For the cases where less than six samples were analysed in ‘interval I’, the \( s_{r{\rm(I)}}\) is estimated indirectly using the \( s_{r{\rm(II)}}^{\prime } \) (\( s_{r{\rm(I)}} = s_{r{\rm(II)}}^{\prime } \cdot 2 \cdot \gamma_{\text{LoQ}} \)).

The measurements repeatability was assumed to be fit for the intended use if the repeatability relative standard deviation is not larger than 5 % in interval I and not larger than 2.5 % in interval II. The \( s_{r{\rm(I)}} \) is compared with the target value after dividing it by the \( \gamma_{\text{LoQ}} \) to estimate the largest relative standard deviation in interval I. The (\( {{s_{r{\rm(I)}} } \mathord{\left/ {\vphantom {{s_{r(I)} } {\gamma_{\text{LoQ}} }}} \right. \kern-0pt} {\gamma_{\text{LoQ}} }} \)) and \( s_{r{\rm(II)}}^{\prime } \) are not significantly larger than 5 % and 2.5 %, respectively, proving repeatability is fit for the intended use. In K measurements between 0.4 mg L−1 and 2 mg L−1, the (\( {{s_{r{\rm(I)}} } \mathord{\left/ {\vphantom {{s_{r(I)} } {\gamma_{\text{LoQ}} }}} \right. \kern-0pt} {\gamma_{\text{LoQ}} }} \)) is only slightly larger than 5 % (i.e. 5.2 %).

Measurement intermediate precision

Intermediate precision of the measurements was estimated at two concentration levels from the analysis of control standards with values equivalent to the \( \gamma_{\text{LoQ}} \) and above \( 2\gamma_{\text{LoQ}} \) (approximately in the middle of the calibration range). The intermediate precision standard deviation, \( s_{\rm{IP(I)}} \), estimated at the \( \gamma_{\text{LoQ}} \), is used to determine precision in concentration interval I (i.e. between \( \gamma_{\text{LoQ}} \) and \( 2\gamma_{\text{LoQ}} \), inclusive) and the relative standard deviation of the second control standard results, \(s_{\rm{IP(II)}}^{\prime}\), used to estimate the relative precision in interval II (i.e. above \( 2\gamma_{\text{LoQ}} \)). Control standards are prepared independently of calibrators. Table 2 presents the estimated \( s_{\rm{IP(I)}} \) and \(s_{\rm{IP(II)}}^{\prime}\). Intermediate precision of the measurements is considered fit for the intended use since (\( {{s_{\rm{IP(I)}}} \mathord{\left/ {\vphantom {{s_{\rm{IP(I)}} } {\gamma_{\text{LoQ}} }}} \right. \kern-0pt} {\gamma_{\text{LoQ}} }} \)) and \( s_{\rm{IP(II)}}^{\prime } \) are not significantly larger than 10 % and 5 %, respectively. The \( {{s_{\rm{IP(I)}}} \mathord{\left/ {\vphantom {{s_{\rm{IP(I)}} } {\gamma_{\text{LoQ}} }}} \right. \kern-0pt} {\gamma_{\text{LoQ}} }} \) is exactly 10 % since \( s_{\rm{IP(I)}}\) is used to estimate the \( \gamma_{\text{LoQ}} \) (\( \gamma_{\text{LoQ}} = 10s_{\rm{IP(I)}}\)). In the first calibration range of the determination of the mass concentration of K, the \( s_{\rm{IP(II)}}^{\prime } \) is slightly above 5 % (i.e. \( s_{\rm{IP(II)}}^{\prime } = 5.2\,\,\% \)).

Measurement recovery

The measurement recovery was assessed from the analysis of real samples before and after spiking. The \( \bar{R} \) and \( u_{{\bar{R}}} \) were estimated as described previously in section “Reference material internal to the procedure: Liquid reference materials internal to the procedure” for all the calibration ranges. No target values for this uncertainty component alone are defined. Table 2 presents the estimated recovery and respective uncertainty. In all studied calibration ranges, except for the determination of Cr and Mg, and in the larger calibration range for Fe determination, estimated mean recovery is metrologically equivalent to 1 for a confidence level of 95 %. For the three specified cases, recovery becomes equivalent to 1 if a 99 % confidence level is considered. The estimated \( u_{{\bar{R}}} \) are associated with a large number of degrees of freedom since more than 14 recovery tests were pooled. Therefore, it was decided not to correct results for recovery in all cases.

Measurement uncertainty

The precision and trueness uncertainty components were combined as relative standard uncertainties to estimate a combined standard uncertainty, \( u_{\text{c}} \). The \( u_{\text{c}} \) was multiplied by a coverage factor of 2 to estimate the expanded uncertainty \( U_{\text{c}} \) for a confidence level of approximately 95 %. The large number of data used to estimate both uncertainty components guaranteed that this coverage factor is adequate. The degrees of freedom of the precision component are the degrees of freedom of the standard deviation of the intermediate precision. The degrees of freedom of the trueness component can be estimated by the Welch–Satterthwaite equation but should not be smaller than the degrees of freedom of the standard deviation of estimated recoveries [28, 29]. When two uncertainty components with equivalent impact on the model equation are combined and components are associated with a similar number of degrees of freedom, the combined uncertainty has a number of degrees of freedom equivalent to the components’ one.

Although the Commission Directive 2009/90/EC [21] for monitoring water status sets a maximum relative expanded uncertainty of 50 %, it was decided to apply some stricter performance criteria set for drinking water monitoring [22] for elements where a maximum permissible value is set for drinking water. The Directive 98/83/EC [22] defines maximum values for the intermediate precision standard deviation and for the mean error that were converted in a target uncertainty using the algorithm proposed in section 5.1.3 of the Eurachem/CITAC guide for setting the target measurement uncertainty [6]. The defined target uncertainties are smaller or equal to the proposed in Commission Directive 2009/90/EC [21].

Table 2 presents the expanded relative uncertainty of measurements performed in the various calibration ranges applicable to the analysis of samples requiring no dilution or a dilution with a negligible uncertainty. If the sample is diluted once, where the initial volume is not smaller than 0.5 mL and the final volume is not smaller than 5 mL measured using class A volumetric glassware, the dilution factor relative standard uncertainty is not larger than 1.2 % [26]. This dilution factor uncertainty is negligible if ICP-OES quantifications are associated with an expanded relative uncertainty not smaller than 7.2 % (7.2 % = 1.2 %·3·2, where factor 3 is used to increase the uncertainty to a significantly larger value and 2 to expand the standard uncertainty to a 95 % confidence level).

In all the quantifications performed in the studied ranges, except in two cases, the estimated uncertainty is smaller than the target uncertainty presented in Table 2. The determination of Mn in the calibration range with larger concentrations has an expanded uncertainty smaller than the target values below 0.096 mg L−1. However, the maximum permissible manganese mass concentration in drinking water (i.e. 0.05 mg L−1) suggests that the defined target uncertainty for the second half of the calibration range is too low. Similarly, the determination of Fe in the calibration range with lower concentrations is only associated with an expanded uncertainty smaller than the target uncertainty for quantified concentrations below 0.475 mg L−1, where the maximum permissible mass concentration of iron in drinking water (i.e. 0.2 mg L−1) is positioned. Therefore, the deviation to the initially defined target uncertainties is not critical in both these cases.

Figures 4, 5 and 6 present the developed models of relative expanded uncertainty variation with analyte concentration in the calibration curve. The figures also present the target measurement uncertainty. The axes of Figs. 4, 5 and 6 are logarithmic to allow representing significantly different ranges in the same graph. The logarithmic scale is rather convenient since many lines become straight lines.

Fig. 4
figure 4

Variation of estimated (U′; Na: ; Ca: =) and target (U′tg; Na: - -;Ca: = =) relative expanded uncertainty, reported in percentage, with the measured mass concentrations of Na and Ca in water, γ (mg L−1), in two calibration ranges. Continuous and dashed lines represent the estimated and target uncertainty, respectively. Calibration ranges with larger concentrations are represented by a thicker line. Both U′ and γ values are presented on a logarithmic scale

Full size image
Fig. 5
figure 5

Variation of estimated (U′; K: ; Mg: =) and target (U′tg; K: - -;Mg: = =) relative expanded uncertainty, reported in percentage, with the measured mass concentrations of K and Mg in water, γ (mg L−1), in one or two calibrations ranges. Continuous and dashed lines represent the estimated and target uncertainty, respectively. The calibration range for the determination of K with larger concentrations is represented by a thicker line. Both U′ and γ values are presented on a logarithmic scale

Full size image
Fig. 6
figure 6

Variation of estimated (U′; Cr: ; Fe: ≡ ; Mn: =, Cu: ) and target (U′tg; Cr: - -; Fe: ≡ ≡ ; Mn: = = , Cu: ) relative expanded uncertainty, reported in percentage, with the measured mass concentrations of Cr, Fe, Mn and Cu in water, γ (mg L−1), in one (Cr and Cu) or two (Fe and Mn) calibrations ranges. Continuous and dashed lines represent the estimated and target uncertainty, respectively. The calibration ranges for the determinations of Fe and Mn with larger concentrations are represented by a thicker line. Both U′ and γ values are presented on a logarithmic scale

Full size image

Measurement traceability

Since quantifications are supported in calibrators prepared from Merck stock solutions using volumetric equipment that measure volume traceable to the SI unit metre, and no relevant lack of linearity or selectivity of ICP-OES response was observed, it can be concluded that the produced measurement results of unknown samples are directly traceable to the value embodied in the Merck stock solution and indirectly to the SI unit mg L−1.

Proficiency test results

The developed measurement models were applied to the analysis of metals in water samples from two proficiency tests.

Table 3 presents the reference and estimated mass concentrations of metals in proficiency test samples and respective scores, namely the z-score and the E n number [30]. The z-score is the ratio between the measurement error and half the maximum admissible error defined by the proficient test provider, being satisfactory between − 2 and 2. The E n number is the ratio between the measurement error and the expanded uncertainty of the error assuming the reference and estimated values’ uncertainties were expanded to a 95 % confidence level using a coverage factor of 2. Therefore, E n numbers are satisfactory if have a value between − 1 and 1.

Table 3 Results and scores of the participation in Aquacheck and RELACRE proficiency tests
Full size table

The results of Table 3 prove that the measurement error is within the acceptable range defined by the proficiency test providers and that the measurement uncertainty adequately predicts the measurement error. The reported expanded uncertainties are smaller than the target measurement uncertainty presented in Table 2.

The diversity of elements, calibration ranges and experimental data used in the uncertainty evaluations suggest that the developed algorithms and models are adequate to estimate measurement uncertainty. Although in some cases, the reported uncertainty is smaller than the one associated with the reference value, the detailed uncertainty models adequately described the quality of the measurements.

Conclusions

The developed methodology for estimating the mean recovery and respective standard uncertainty from the analysis of independent reference materials successfully pooled the recovery and uncertainty of various recovery tests into a single performance parameter. The estimated mean recovery and respective uncertainty allowed for the assessment of deviations from the ideal recovery relevant to ensure that the measurement results are traceable to the SI unit mg L−1. The adequate identification of precision conditions affecting the estimated recovery allowed for the reliable estimation of the recovery uncertainty. For the analysis of samples with native analyte, before and after spiking, in the same run, measurement repeatability affects recovery estimation. For the analysis of certified reference materials or spiked samples with negligible native quantity, the intermediate precision should be considered for the estimation of the recovery uncertainty. The precision conditions affecting recovery estimation also influence the systematic effects assessed in the mean recovery. If the recovery estimation is affected by the measurement repeatability, the recovery reflects the combined effect of all systematic effects occurring in the measurement results. On the other hand, if the recovery estimation is affected by the intermediate precision, all the systematic effects, except the within-run systematic effect, are assessed by the mean recovery.

The developed methodology was successfully applied to the analysis of Na, K, Mg, Ca, Cr, Mn, Fe and Cu in waters of Aquacheck and RELACRE proficiency tests by ICP-OES.