Relaxation in Pulsed EPR: Thermal Fluctuation of Spin-Hamiltonian Parameters of an Electron-Nuclear Spin-Coupled System in a Malonic Acid Single Crystal in a Strong Harmonic-Oscillator Restoring Potential

Abstract

Random fluctuations in the $\tilde{g}$ and $\tilde{A}$ matrices of a spin system due to thermal motion of a molecule are specifically considered to calculate the relaxation matrix for the four-level electron-nuclear spin-coupled system ($S = 1/2$; $I = 1/2$) in a malonic acid crystal, using the formalism outlined by Lee et al. (J Chem Phys 98:3665–3689, 1993). The correlation time, τ_c, and the value of the parameter λ, characterizing the harmonic-oscillator restoring potential of the small-amplitude fluctuation of the director of the malonic-acid molecule due to thermal motion are estimated from the knowledge of the experimental values of (τ_c, λ). The four electronic, $T_{2e} ,$ and the two nuclear, $T_{{2{\text{n}}}}$, spin relaxation times are calculated to be functions of (τ_c, λ) governing the fluctuations. The values of (τ_c, λ), evaluated with these expressions, when fitted to the experimental values of $T_{2e}$ and $T_{2n}$, assuming the molecule to be in the ground state (n = 0) in the harmonic-oscillator potential, a rather narrow region of (τ_c, λ) values about τ_c = 0.081 μs and $\lambda = 4.4$ is found. These values are then used to calculate the time-dependent echo-ELDOR signal by the relevant Liouville von-Neumann (LVN) equation. The resulting Fourier transform is found to be in excellent agreement with the experimental data. The (τ_c, λ) values for the excited states described by $n = 1,2$ have also been calculated, although these states are unlikely to be populated at room temperature.

1 Introduction

The dynamics of spin probes embedded in diamagnetic systems can be exploited in detail by pulsed electron paramagnetic resonance (EPR). In particular, one can use echo-ELDOR (electron–electron double resonance) signal, which is sensitive to the details of the relaxation of spin systems. In order to consider relaxation rigorously, one needs to solve Liouville von Neumann (LVN) equation, which is an exact quantum–mechanical equation of motion for the density matrix.

In the experimental study by Lee et al. [1] on a γ-irradiated single crystal of malonic acid, the theory of two-dimensional (2D)-EPR with nuclear modulation, as described by Gamliel and Freed [2], was extended to treat the combined effect of nuclear modulation and spin relaxation to calculate SECSY (spin echo correlation spectroscopy) and echo-ELDOR signals, defining the elements of the relaxation matrix in a phenomenological manner, fitting to the relative intensities of the experimental peaks.

It is the purpose of this paper to treat relaxation due to thermal fluctuation of the spin-Hamiltonian parameters (SHP), i.e., the elements of $\tilde{g}$ and $\tilde{A}$-matrices, for the coupled electron-nuclear spin system with electron spin $S = 1/2$ and nuclear spin $I = 1/2$ in a γ-irradiated malonic acid crystal more quantitatively. Here the stochastic fluctuating parts of the spin Hamiltonian are defined explicitly in terms of the time-dependent interaction constants, $\delta \left( {{\text{SHP}}} \right)$ s, i.e., $\delta g$, $\delta a$, etc., following the outline given in [1] in (Table IV). To this end, the fluctuations of $\delta$(SHP) due to thermal motion, governed by a restoring harmonic-oscillator potential, are considered. On the average, the fluctuations of the tip of the director axis of the malonic acid then take place within a cone about the symmetry axis. Knowing the experimental values of the electronic and nuclear spin-relaxation times, T_2e and T_2n, respectively, one can estimate the values of the motional correlation time, τ_c, as well as the strength of the restoring potential, λ. It is noted that information on correlation time of a given system is important to calculate time averages of physical quantities. The memory of a system to retain a certain property is dependent on the value of its correlation time, e.g., the magnetization due to a microwave pulse, as produced in a pulsed EPR experiment, such as SECSY, echo-ELDOR. The longer is the correlation time the longer is the physical property retained by the system.

The organization of this paper is as follows: Section 2 deals with the calculation of the changes in the diagonal elements of $\tilde{\varvec{g}}$ and $\tilde{\varvec{A}}$ matrices due to thermal fluctuations. These are then used to calculate the various terms in the consequent time-dependent spin Hamiltonian, which are listed in Table IV of [1]. The matrix elements of the relaxation matrix are explicitly calculated in this section as outlined in Appendix B of [1], which depend on the relevant auto-correlation functions. These, in turn, are found to depend on the average value of the square of the angular spread of the cone, governed by the restoring harmonic potential, as described in Sect. 3. Estimations of the values of the correlation time (τ_c) and the strength of the restoring potential, λ, by exploiting the experimental values of the nuclear and electronic spin-relaxation times, T_2e and T_2n, respectively, are carried out in Sect. 4. The details of calculation of the average parameters of fluctuation in the presence of a strong restoring potential are given in Sect. 5. The concluding remarks are made in Sect. 6. In Appendix A, the static Hamiltonian and the eigenvalue basis used to calculate the relaxation matrix are included. The procedure to exploit Liouville von-Neumann equation to calculate echo-ELDOR signal is briefly explained in Appendix B.

2 Spin Hamiltonian Due to Thermal Fluctuation

The time-dependent matrix elements for the four-level $S = 1/2; I = 1/2$ spin system of the Hamiltonian, $\hat{H}_{1} \left( t \right)$, causing relaxation, can be written in general form, in the eigenvalue basis, as follows [1]:

$$\hat{H}_{1} \left( t \right)_{\gamma \delta } = \mathop \sum \limits_{p} F^{p} \left( t \right)A^{p}_{\gamma \delta } ; \gamma ,\delta = a,b,c,d;p = 1,10,$$

(1)

where a, b, c, d refer to the four energy levels of the spin system, as described in Appendix A, $A^{p}$ are the spin operators in the laboratory frame that appear in the spin Hamiltonian, which are orientation dependent and are listed in Table 4 of [1], and $F^{p} \left( t \right)$ are functions of spatial variables, which are, in fact, the time-dependent fluctuating parts of the spin-Hamiltonian,$\delta \left( {{\text{SHP}}} \right)$, as listed below for the various $F^{p} \left( t \right)$ terms in the spin Hamiltonian Eq. (1):

$$\begin{aligned} F^{1} \left( t \right) & = \frac{{\beta_{e} B_{0} }}{\hbar }\delta g; \\ F^{2} \left( t \right) & = \delta F\frac{1}{2}\left( {3\cos^{2} \beta - 1} \right) + \delta F^{\left( 2 \right)} \sin^{2} \beta \cos \left( {2\gamma } \right); \\ F^{3} \left( t \right) & = \delta F\frac{3}{8}\sin \left( {2\beta } \right) - \delta F^{\left( 2 \right)} \frac{1}{4}\sin \left( {2\beta } \right)\cos \left( {2\gamma } \right); \\ F^{4} \left( t \right) & = - \frac{{\gamma_{e} }}{\hbar }\delta a; \\ F^{6} \left( t \right) & = \delta D\frac{1}{2}\left( {3\cos^{2} \beta - 1} \right) + \delta D^{\left( 2 \right)} \sin^{2} \beta \cos \left( {2\gamma } \right); \\ F^{8} \left( t \right) & = \delta D\frac{3}{8}\sin \left( {2\beta } \right) - \delta D^{\left( 2 \right)} \frac{1}{4}\sin \left( {2\beta } \right)\cos \left( {2\gamma } \right); \\ F^{10} \left( t \right) & = \delta D\frac{3}{8}\sin^{2} - \delta D^{\left( 2 \right)} \frac{1}{4}\left( {1 + \cos^{2} \beta } \right)\cos \left( {2\gamma } \right); \\ F^{5} \left( t \right) & = F^{7} \left( t \right) = F^{9} \left( t \right) = 0. \\ \end{aligned}$$

(2)

It is noted that in the above expressions the interaction constants (δg, δa, δF, δD, δF⁽²⁾, δD⁽²⁾) are time dependent, representing the deviations from the respective average values, e.g., δg = g(t) − $\overline{g}$.

The diagonal elements of the T₂-type relaxation in Liouville space are expressed as [1]follows:

$$\left( {T_{2}^{ - 1} } \right)_{\alpha \beta } = - R_{\alpha \beta \alpha \beta } = \mathop \int \limits_{0}^{\infty } {\text{d}}\tau \overline{{\omega_{\alpha \beta } \left( t \right)\omega_{\alpha \beta } \left( {t + \tau } \right)}} + \frac{1}{2}\left( {\mathop \sum \limits_{\gamma \ne \alpha } W_{\alpha \gamma } + \mathop \sum \limits_{\gamma \ne \beta } W_{\beta \gamma } } \right),$$

(3)

where the time-dependent values of $\omega_{\alpha \beta } \left( t \right)$ = $H_{1} \left( t \right)_{\alpha \alpha }$ − $H_{1} \left( t \right)_{\beta \beta }$, are stochastic, and thus only their time-correlation values can be estimated, as shown below. The relaxation matrix elements, $R_{\alpha \beta \gamma \delta }$, are defined by the Redfield equation. They are valid for fast relaxation, given as follows [1, 3]:

$$\frac{{{\text{d}}\chi_{\alpha \alpha ^{\prime}} }}{{{\text{d}}t}} = - i \omega_{\alpha \alpha ^{\prime}} \chi_{\alpha \alpha ^{\prime}} + \mathop \sum \limits_{\beta \beta ^{\prime}} R_{\alpha \alpha ^{\prime}\beta \beta ^{\prime}} .$$

(4)

The procedure to solve the above equation is outlined in Appendix B. The integral and the transition probabilities $W_{\alpha \gamma }$ in Eq. (3) are [1] the following:

$$\mathop \int \limits_{0}^{\infty } {\text{d}}\tau \overline{{\omega_{\alpha \beta } \left( t \right)\omega_{\alpha \beta } \left( {t + \tau } \right)}} = \mathop \sum \limits_{q,r} (A_{\alpha \alpha }^{q} - A_{\beta \beta }^{q} )\left( {A_{\alpha \alpha }^{r} - A_{\beta \beta }^{r} } \right) \times \mathop \int \limits_{ - \infty }^{\infty } {\text{d}}\tau \overline{{F^{q} \left( t \right)F^{r*} \left( {t + \tau } \right)}} ,$$

(5)

$$W_{\alpha \gamma } = R_{\alpha \alpha ,\gamma \gamma } = \mathop \sum \limits_{q,r} A_{\alpha \gamma }^{q} A_{\gamma \alpha }^{r} \times \mathop \int \limits_{ - \infty }^{\infty } {\text{d}}\tau \overline{{F^{q} \left( t \right)F^{r*} \left( {t + \tau } \right)}} e^{{ - i \omega_{\alpha \gamma } \tau }} .$$

(6)

Calculation of the non-zero elements of the relaxation matrix, $R_{\alpha \beta \alpha \beta } ,$ in Eq. (3) due to the fluctuating perturbation can be carried out by considering the auto-correlation function, $\overline{{F^{q} \left( t \right)F^{r*} \left( {t + \tau } \right)}}$, between the fluctuating parts of the spin Hamiltonian at times t = 0 and t = $\tau .$ According to Eq. (2), all required autocorrelation functions can be expressed in terms of the $\delta \left( {{\text{SHP}}} \right)$s: δg, δA, δD. δD⁽²⁾, δF. δF⁽²⁾, which are calculated here using the conical model of fluctuation, wherein one considers small thermal fluctuations of the director of the malonic-acid molecule in the plane transverse to the average director axis as shown in Fig. 1. The procedure to calculate $\delta \left( {{\text{SHP}}} \right)$ is described in Sect. 3 below.

Fig. 1

Figure to show the fluctuations of the ensemble-average director of the molecules. The tip of the director indicated by the arrow fluctuates within the circular periphery of the cone. Here x axis represents the symmetry axis of malonic molecule

3 Conical Fluctuation: Symmetry of Molecules in Malonic Acid Crystal

The principal values of the g-matrix show that it possesses axial symmetry ($g_{yy} \approx g_{zz} > g_{xx}$; $g_{xx}$ = 2.0026, $g_{yy}$ = 2.0035, $g_{zz}$ = 2.0033 within the experimental error of 0.0001). Thus, in the absence of any thermal fluctuations, the directors of the molecules in the crystal are oriented along the $x$ axis, their symmetry axis, as shown in Fig. 1. One can then assume that that the spatial fluctuation due to thermal vibrations of the malonic acid molecules in the crystal exhibit axial symmetry about their x-axes. In the presence of a restoring potential, as assumed in this work, and described in detail in Ref. [6], the molecules tend to return to their equilibrium positions, to become oriented along their symmetry axis. The thermal fluctuations, which change the instantaneous orientations of the molecules on the one hand, and the presence of a restoring potential, on the other hand, lead to motions of the directors of malonic acid molecules within a cone about their symmetry axes as shown in Fig. 1.

In our earlier publication, exploiting cylindrical fluctuations [5] of the director, the restoring potential was assumed to operate only in the plane perpendicular to the symmetry axis, i.e., the yz plane, without considering any specific restoring potential. The resulting model possessed cylindrical symmetry, wherein the tip of the director moved in the yz plane. In the conical fluctuation model, on the other hand, the restoring potential is assumed to restore the director along the x-axis, the axis of symmetry, subsequent to its fluctuation by an angle $\alpha$ (Fig. 1) about the $x$ axis, so that random fluctuations will cause the director to execute the surface of a cone with the semi conical angle $\alpha$. It is noted that the conical model of fluctuation is more sophisticated than the cylindrical model in that it is based on a realistic potential well, amenable to quantum mechanical treatment [6], as described here in Sect. 4 below.

3.1 Fluctuation of SHP Due to Thermal Motion

To calculate the effect of thermal vibrations, the problem can be treated in a statistical manner as an ensemble of a large number of malonic-acid molecules. Of these, consider a molecule representing the average of all the molecules in the ensemble undergoing the low amplitude orientational motion about its equilibrium position due to thermal fluctuations. The resulting changes in the SHP due to the fluctuations, δ (SHP), caused by thermal motion, cause relaxation. This is taken into account as follows:

In the magnetic frame, the average of $\tilde{g}$ and $\tilde{A}$ matrices, assumed to have the same principal axes, is

$$\tilde{\varvec{\sigma }} = \left( {\begin{array}{*{20}c} {\sigma_{xx} } & 0 & 0 \\ 0 & {\sigma_{yy} } & 0 \\ 0 & 0 & {\sigma_{zz} } \\ \end{array} } \right),$$

(7)

where $\tilde{\sigma }$ stands for $\tilde{g}$, or $\tilde{A}.$ Due to thermal motion of the molecule, its director executes infinitesimal random fluctuations about the symmetry axis of the molecule, assumed to be along the $x$ axis, as shown in Fig. 1. These fluctuations can be seen to be equivalent to infinitesimal rotations of the director of malonic acid molecules by angles α, about axes randomly distributed in the yz plane. Now the matrix for rotation by angle α about an axis in the yz plane, oriented at an angle θ from the y axis, is

$$L = \left( {\begin{array}{*{20}c} {\cos \;\alpha } & { - \sin \alpha \sin \theta } & {\cos \theta \sin \alpha } \\ {\sin \alpha \sin \theta } & {\cos^{2} \theta + \cos \;\alpha \sin^{2} \theta } & {\left( {1 - \cos \;\alpha } \right)\cos \theta \sin \theta } \\ { - \cos \theta \sin \alpha } & {\left( {1 - \cos \;\alpha } \right)\cos \theta \sin \theta } & {\sin^{2} \theta + \cos \;\alpha \cos^{2} \theta } \\ \end{array} } \right).$$

(8)

Using Mathematica, the diagonal elements of the transformed $\tilde{\sigma }$ matrix, for either $\tilde{g}$, or $\tilde{A}$ matrices: $\tilde{\sigma }^{^{\prime}} = L \cdot \tilde{\sigma } \cdot L^{ - 1}$ are calculated to be

$$\begin{aligned} \sigma^{\prime}_{xx} & = \sigma_{xx} {\text{Cos}}^{2} \alpha + {\text{Sin}}^{2} \alpha \left( {\sigma_{zz} {\text{Cos}}^{2} \theta + \sigma_{yy} {\text{Sin}}^{2} \theta } \right) \\ \sigma^{\prime}_{yy} & = \sigma_{yy} \left( {{\text{Cos}}^{2} \theta + {\text{Cos}} \alpha {\text{Sin}}^{2} \theta } \right)^{2} \\ & \quad + \sigma_{zz} \left( {1 - {\text{Cos}} \alpha } \right)^{2} {\text{Cos}}^{2} \theta {\text{Sin}}^{2} \theta + \sigma_{xx} {\text{Sin}}^{2} \alpha {\text{Sin}}^{2} \theta \\ \sigma^{\prime}_{zz} & = \sigma_{zz} \left( {{\text{Cos}} \alpha {\text{Cos}}^{2} \theta + {\text{Sin}}^{2} \theta } \right)^{2} + \sigma_{xx} {\text{Cos}}^{2} \theta {\text{Sin}}^{2} \alpha \\ & \quad + \sigma_{yy} \left( {1 - {\text{Cos}} \alpha } \right)^{2} {\text{Cos}}^{2} \theta {\text{Sin}}^{2} \theta . \\ \end{aligned}$$

(9)

The random fluctuations of the director are now taken into account by considering all possible values of $\theta$ in the yz plane. Although a crystal contains molecules with random orientations of their directors due to random thermal fluctuations with respect to the symmetry axis, the director in Fig. 1 represents the ensemble average of motion of all molecules in the crystal, confined to a cone, with the tails of all the directors made coincident. To calculate the average of all possible orientations of the director, one needs to integrate Eq. (9) over $\theta$ from 0 to $2\pi ,$ and then dividing it by $2\pi$. The average diagonal elements of the resulting $(\sigma ^{\prime})_{{{\text{avg}}}}$ are as follows:

$$\begin{aligned} (\sigma^{\prime}_{avg} )_{xx} & = \sigma_{xx} {\text{Cos}}^{2} \alpha + \frac{1}{2}\left( {\sigma_{yy} + \sigma_{zz} } \right){\text{Sin}}^{2} \alpha \\ (\sigma^{^{\prime}}_{avg} )_{yy} & = \frac{1}{16}\sigma_{yy} \left( {9 + 4 {\text{Cos }}\alpha + 3 {\text{Cos}}\left( {2\alpha } \right)} \right) + \frac{1}{4}\sigma_{xx} \left( {1 - {\text{Cos}}\left( {2\alpha } \right)} \right) \\ & \quad + \frac{1}{16}\sigma_{zz} \left( {3 - 4 {\text{Cos }}\alpha + {\text{Cos}}\left( {2\alpha } \right)} \right) \\ (\sigma^{^{\prime}}_{avg} )_{zz} & = \frac{1}{16}\sigma_{zz} \left( {9 + 4 {\text{Cos }}\alpha + 3 {\text{Cos}}\left( {2\alpha } \right)} \right) + \frac{1}{4}\sigma_{xx} \left( {1 - {\text{Cos}}\left( {2\alpha } \right)} \right) \\ & \quad + \frac{1}{16}\sigma_{yy} \left( {3 - 4 {\text{Cos }}\alpha + {\text{Cos}}\left( {2\alpha } \right)} \right). \\ \end{aligned}$$

(10)

Since $\alpha$ is infinitesimal, the above expressions can be expanded in a series in $\alpha$. Keeping only the lowest order terms in $\alpha$, one obtains

$$\begin{gathered} (\sigma ^{\prime}_{{{\text{avg}}}} )_{xx} = \sigma_{xx} + \frac{1}{2}\left( { - 2\sigma_{xx} + \sigma_{yy} + \sigma_{zz} } \right)\alpha^{2} ; \hfill \\ (\sigma ^{\prime}_{{{\text{avg}}}} )_{yy} = \sigma_{yy} + \frac{1}{2}\left( {\sigma_{xx} - \sigma_{yy} } \right)\alpha^{2} ; \hfill \\ (\sigma ^{\prime}_{{{\text{avg}}}} )_{zz} = \sigma_{zz} + \frac{1}{2}\left( {\sigma_{xx} - \sigma_{zz} } \right)\alpha^{2} . \hfill \\ \end{gathered}$$

(11)

The changes in the diagonal elements of $\stackrel{\sim }{\sigma }$, i.e. those of $\stackrel{\sim }{g}$ and $\stackrel{\sim }{A}$ matrices, due to thermal motion of the director, $\updelta \stackrel{\sim }{\sigma }={\stackrel{\sim }{\sigma }}^{^{\prime}}-\stackrel{\sim }{\sigma }$, are as follows:

$$\updelta {\sigma }_{xx}=\frac{1}{2}\left(-2{\sigma }_{xx}+{\sigma }_{yy}+{\sigma }_{zz}\right){\alpha }^{2 };\updelta {\sigma }_{yy}=\frac{1}{2}\left({\sigma }_{xx}-{\sigma }_{yy}\right){\alpha }^{2};\updelta {\sigma }_{zz}=\frac{1}{2}\left({\sigma }_{xx}-{\sigma }_{zz}\right){\alpha }^{2}.$$

(12)

The above expressions are consistent with the results obtained in [4, 5]. δ(SHP) are then calculated to be, in terms of the fluctuating diagonal elements of the $\tilde{g}$ and $\tilde{A}$ matrices, as follows:

$$\begin{gathered} \delta g = \frac{1}{3} \left( {\delta g_{xx} + \delta g_{yy} + \delta g_{zz} } \right);\; \delta a = \frac{1}{3} \left( {\delta A_{xx} + \delta A_{yy} + \delta A_{zz} } \right); \hfill \\ \delta F = \frac{2}{3}\left( {\delta g_{zz} - \frac{1}{2}\left( {\delta g_{xx} + \delta g_{yy} } \right)} \right);\; \delta D = \frac{2}{3}\left( {\delta A_{zz} - \frac{1}{2}\left( {\delta A_{xx} + \delta A_{yy} } \right)} \right); \hfill \\ \delta F^{\left( 2 \right)} = \frac{1}{2} \left( {\delta g_{xx} - \delta g_{yy} } \right); \delta D^{\left( 2 \right)} = \frac{1}{2}\left( {\delta A_{xx} - \delta A_{yy} } \right). \hfill \\ \end{gathered}$$

(13)

Substituting the above expressions in Eq. (2), the auto-correlation functions $\overline{{F^{q} \left( t \right)F^{r*} \left( {t + \tau } \right)}}$ can be calculated. They are needed to obtain the relaxation matrix elements given by Eq. (3). Since all δ(SHP)s in Eq. (13) are linear in $\delta \sigma ,$ which are proportional to $\alpha^{2} \left( t \right)$, according to Eq. (12), the correlation functions $\overline{{F^{q} \left( t \right)F^{r*} \left( {t + \tau } \right)}}$ can be expressed in terms of $\alpha^{2}$ as follows:

$$\overline{{ F^{q} \left( 0 \right)F^{r*} \left( \tau \right)}} = f^{q} f^{r*} \left\langle {\overline{{\alpha^{2} \left( 0 \right)\alpha^{2} \left( \tau \right)}} } \right\rangle = f^{q} f^{r*} h e^{{ - \left| \tau \right|/\tau_{{\text{c}}} }} .$$

(14)

Here $f^{i}$ represents the amplitude of fluctuation of $F^{i} \left( t \right)$, and $h( = \overline{{\alpha^{4} }}$) is the parameter that represents the average fluctuation of the director in the transverse (yz) plane. The procedure of how to calculate $h$ is described in Sect. 4 below.

4 Calculation of the Average of the Fluctuation Angle in a Strong Restoring Potential

As the malonic acid molecule fluctuates around its symmetry axis, it is brought back to its equilibrium position by the restoring potential acting on it. This can be treated by a quantum mechanical equation for the spherical top as described in [6]. Assuming that the malonic acid molecule in the crystal experiences a strong harmonic-oscillator restoring potential, for which the wave function is [6]

$$\psi_{K,M}^{n} \left( {\vartheta ,\alpha ,\xi } \right) = \exp \left( {iK\vartheta } \right)y_{n} \left( \alpha \right) \exp \left( {iM\xi } \right),$$

(15)

where $\left( {\vartheta ,\alpha ,\xi } \right)$ are the Euler angles that relate the orientation of the director to the magnetic frame, with $\alpha$ assumed to be a small deviation from the equilibrium position of the molecule, as shown in Fig. 1, and K, M, n are the quantum numbers that characterize the harmonic-oscillator wave functions in a restoring potential [6]. Here the function $y_{n} \left( \alpha \right)$ is the following:

$$y_{n} \left( \alpha \right) = N_{n} \exp \left( { - \left| \lambda \right|\frac{{\alpha^{2} }}{2}} \right)H_{n} \left( {\left| \lambda \right|^{1/2} \alpha } \right).$$

(16)

In the above, $\lambda = - \frac{{\upchi }}{{k_{{\text{B}}} T}}$, is the dimensionless parameter of the restoring potential, with $\chi$ being the strength of the restoring potential, $k_{{\text{B}}}$ is Boltzmann’s constant; $H_{n}$ in Eq. (16) are Hermite polynomials and $N_{n}$ are the normalization coefficients:

$$N_{n} = \left( {\frac{\sqrt \lambda }{{\sqrt \pi 2^{n} n!}}} \right)^{1/2} .$$

(17)

The average fluctuation of the director axis, $h = \overline{{\alpha^{4} }} ,{ }$ appearing in Eq. (14), needed to calculate the relaxation matrix elements in Eq. (3), can be estimated, using the wave function of the spherical top in a strong restoring potential, as follows:

$$\overline{{\alpha^{4} }} = \mathop \int \limits_{{}}^{{}} \psi_{K,M}^{n} \left( {\vartheta ,\alpha ,\xi } \right)^{*} \alpha^{4} \psi_{K,M}^{n} \left( {\vartheta ,\alpha ,\xi } \right) {\text{d}}\vartheta {\text{d}}\alpha {\text{ d}}\xi = \mathop \int \limits_{ - \infty }^{\infty } y_{n}^{*} \alpha^{4} y_{n} {\text{d}}\alpha .$$

(18)

Note that the choice of the limits of the above integral from $- \infty$ to $+ \infty$ instead of $\left( { - \frac{\pi }{2},\frac{\pi }{2}} \right)$ is justified in the case when $\lambda \gg 1$. With $h = \overline{{\alpha^{4} }}$ calculated above and using Eqs. (12)–(14), one can calculate the elements of the relaxation matrix expressed by Eq. (3).

5 Estimation of the Correlation Time (τ _c) and the Strength of the Restoring Potential (λ)

Exploiting the procedure described in Sects. 3 and 4 above, the elements of the relaxation matrix, $R_{\alpha \beta \alpha \beta } \left( {\tau_{{\text{c}}} ,{\uplambda }} \right)$, can be calculated in the eigenvalue basis, denoted by a, b, c, d (also denoted equivalently hereafter as 1,2,3,4) as functions of the correlation time, τ_c, and the strength of the restoring potential λ$.$ According to Eq. (3), T₂-type relaxation elements for the various electron and nuclear spin transitions are related to the relaxation matrix elements as follows: $(T_{2} )_{ac}$ = $\frac{1}{{R_{1313} }},$ $(T_{2} )_{bd}$ = $\frac{1}{{ R_{2424} }}, (T_{2} )_{ad}$ = $\frac{1}{{ R_{1414} }}, (T_{2} )_{bc}$ =$\frac{1}{{ R_{2323} }},$ $(T_{2} )_{ab}$ =$\frac{1}{{R_{1212} }},$ $(T_{2} )_{cd}$ = $\frac{1}{{ R_{3434} }}$, where the energy levels a, b, c, d are defined in appendix B below. Having the experimental values of electron spin-relaxation times $(T_{2e} )_{{{\text{exp}}}}$ and nuclear spin-relaxation times $(T_{2n} )_{{{\text{exp}}}}$ available from [1], one can now solve for $(\tau_{{\text{c}}} ,{\uplambda })$ by assuming the four calculated $T_{2e\alpha \beta } \left( {\tau_{{\text{c}}} ,\lambda } \right) = (T_{2e} )_{\exp } ,$ and the two calculated $T_{2n\alpha \beta } \left( {\tau_{{\text{c}}} ,{\uplambda }} \right) = (T_{2n} )_{{{\text{exp}}}} ;$ for $\alpha ,\beta = a,b,c,d$. Note that from [1], only two experimental values, $T_{2e}$ and $T_{2n}$, were estimated, so it is assumed here that $(T_{2} )_{ac}$ = $(T_{2} )_{bd}$ = $(T_{2} )_{ad} =$ $(T_{2} )_{bc} =$ $T_{2e}$ and $(T_{2} )_{cd}$ = $(T_{2} )_{ab} = T_{2n}$ In fact, these relaxation times are slightly different from each other as shown in Fig. 2. If an experiment is performed in which only one transition between the four levels is involved, e.g., a → c, then one can measure the electronic relaxation time $\left( {T_{2e} } \right)_{ac}$ for that specific transition. However, when the experiment is not sensitive to individual transitions, one can replace the relaxation times for the various transitions by a single, average, relaxation time.

Fig. 2

Contour plots of (T₂)_ac, (T₂)_bd, (T₂)_ad, (T₂)_bc for the experimental value T_2e = 900 ns and those for (T₂)_ab, (T₂)_cd for the experimental value T_2n = 22 μs as a function of the correlation time τ_c and λ for the ground state (a), first excited state (b) and second excited state (c) of the harmonic oscillator. The red circle in the overlapping region represents the average of (τ_c, λ) values used for simulation of the echo-ELDOR signal representing the best average which are found to be a (8.1 $\times 10^{ - 8}$ s, 4.43), b (8.$0 \times 10^{ - 8}$ s, 9.93) and c (7.9 $\times 10^{ - 8}$ s, 15.85)

In Fig. 2, all values of $(T_{2} )_{\alpha \beta } ;\alpha \ne \beta$ corresponding to the four different electron spin transitions ($(T_{2} )_{ac}$, $(T_{2} )_{bd}$, $(T_{2} )_{ad} ,$ $(T_{2} )_{bc} )$ and two different nuclear spin transitions ($(T_{2} )_{cd}$,$(T_{2} )_{ab} )$ are plotted for the first three lowest energy states (n = 0, 1, 2) of the malonic acid molecule as functions of $\tau_{{\text{c}}} ,\lambda$, using the experimental values, reported in [1]: $T_{2e} = 900\;{\text{ns}}$ and $T_{2n} = 22\;\mu {\text{s}}$. For each energy state, n, of the harmonic oscillator one then obtains six lines as shown in Fig. 2 in the (τ_c,$\lambda$) plane. The average values of (τ_c,$\lambda$), i.e., those lying at the center of this area are then chosen to calculate the elements of the relaxation-matrix. The values of $\left( {\tau_{{\text{c}}} ,\lambda } \right)$ that correspond best to the experimental values of T_2e and T_2n are found to be (τ_c = 8.1 × 10^–8 s and $\lambda$ = 4.43), (τ_c = 8.0 × 10^–8 s and $\lambda$ = 9.93) and (τ_c = 7.9 × 10^–8 s and $\lambda$ = 15.85) for the molecule in the ground state (n = 0), first excited state (n = 1) and second excited state (n = 2), respectively. (For comparison, it is noted that the value of the parameter $\lambda$, in NO crystal was $\left| \lambda \right| = 7.5$ [6]). It is further noted that at the temperature ($T$) the experiment was performed [1] (T ~ 77 K), the molecule is predominantly in the ground state, since the vibrational energy level differences due to the restoring potential are presumably much higher than k_BT, where k_B is Boltzmann’s constant and $T$ is 77 K. The relaxation matrix, consistent with the ground state, is then used to simulate the time-domain echo-ELDOR signal and its Fourier transform (FT), as shown in Fig. 3, using the procedure outlined in Appendix B. Comparing the calculated and experimental FTs, as reported in [1], an excellent agreement is found.

Fig. 3

Fourier transform of the simulated echo-ELDOR spectrum for a second excited state (n = 2), b first excited state (n = 1), c ground state (n = 0), and d the experimental Fourier transforms of the echo-ELDOR signal. The simulations are done for the orientation of the external magnetic field $\left( {\alpha ,\beta ,\gamma } \right) = \left( {0, - 30^{ \circ } ,0} \right)$, with the mixing times T_m = 40 μs. The same best fit values of the correlation time $\tau_{{\text{c}}}$ and λ, as determined in Fig. 2 are used in these simulations. An inhomogeneous Gaussian broadening along the f₂ axis with the width $\Delta$ = 5 MHz is used in the simulations. All simulated figures, drawn using the best fit values, show excellent agreements with the experiment (d), but (c), the one for n = 0 (ground state), represents the most populated state at room temperature. The experimental (d) is reproduced with the permission of the authors of [1]

5.1 Expected Temperature Variation of Relaxation Times

The most likely process that affects the electronic spin $S = 1/2$ system in malonic acid in the temperature region around 77 K, for which the experimental data are being interpreted in this paper, is the direct process of relaxation [7, 8]. This arises due to spin-phonon modulation, whose temperature dependence for non-Kramers ions is described by 1/$T_{1} \propto \omega_{0}^{3} \coth \left( {\hbar \omega_{0} /2k_{{\text{B}}} T} \right),$ which, at higher temperatures ($T \gg \hbar \omega_{0} /k_{{\text{B}}} )$ is proportional to $B^{2 } T$, i.e. linear in temperature, where $\hbar \omega_{0} = g\mu_{{\text{B}}} B$ so that at resonance the spin system exchanges its energy of the Zeeman splitting, $g\mu_{{\text{B}}} B$, with the phonon vibrations of energy $\hbar \omega_{0} .$ (Here $\mu_{{\text{B}}}$ is the Bohr magneton, $\hbar$ is Planck’s constant (h) divided by 2$\pi$, B is the intensity of the external magnetic field, and g ~ 2.0 is the average electronic g factor for the spins.) As for the spin–spin relaxation times, $T_{2e} ,T_{{{\text{2n}}}}$, they are assumed not to change significantly over the temperature range about liquid-nitrogen temperature considered here.

6 Conclusions

The salient features of the present work dealing with the calculation of the matrix elements of the relaxation matrix due to fluctuation of spin-Hamiltonian parameters caused by thermal motion in a γ-irradiated malonic acid crystal of an electron-nuclear spin-coupled system ($S = 1/2$; $I = 1/2$) are as follows:

• i. A model is presented of how to calculate, under a restoring harmonic-oscillator potential, the relaxation matrix due to changes in the spin-Hamiltonian parameters, characterizing an electron-nuclear spin-coupled system of a malonic-acid molecule, due to thermal fluctuations of the director axes of the molecules in the transverse plane to the symmetry axis.

• ii. The correlation time (τ_c) and the strength of the restoring potential, λ, have been estimated, using the experimental values of the electronic and nuclear spin relaxation times T_2e and T_2n, respectively, considering the ensemble average of the fluctuations of the director axis of the molecule to be within an infinitesimal cone about the symmetry axis of the molecule.

• iii. When the four calculated T_2e and the two calculated T_2n (Sect. 4) are plotted as functions of the correlation time (τ_c) and the strength of the restoring potential (λ) (Fig. 2), the values of $\left( {\tau_{{\text{c}}} ,\lambda } \right)$ that correspond best to the experimental values of T_2e and T_2n are found to be (τ_c = 8.1 × 10^–8 s and $\lambda$ = 4.43) for the molecule in the ground state (n = 0) of the restoring harmonic-oscillator potential. With the elements of the relaxation matrix calculated, using these values, the Fourier transform of the simulated echo-ELDOR signal using the LVN equation turns out to be in excellent agreement with the experimental echo-ELDOR signal [1] as seen from Fig. 3.

Appendices

Appendix A: Spin Hamiltonian

For the specific case of a single nucleus ($I = 1/2$) interacting with an unpaired electron ($S = 1/2$) by hyperfine (HF) interaction, where the HF matrix has the same principal axes as those of the g matrix, the total Hamiltonian is

$$\hat{H} = \hat{H}_{0} + \hat{H}_{1} ,$$

(19)

where

$$\hat{H}_{0} = CS_{z} - \omega_{n} I_{z} + AS_{z} I_{z} + \frac{1}{2}BS_{z} I_{ + } + \frac{1}{2}B^{*} S_{z} I_{ - } .$$

(20)

In Eq. (20) the coefficients are expressed as follows:

$$\begin{gathered} C = \frac{{\beta_{e} B_{0} }}{h}\left[ {\overline{g} + F\frac{1}{2}\left( {3\cos^{2} \beta - 1} \right) + F^{\left( 2 \right)} \sin^{2} \beta \cos \left( {2\gamma } \right)} \right] \hfill \\ A = - 2\pi \left[ {\overline{a} + D\frac{1}{2}\left( {3\cos^{2} \beta - 1} \right) + D^{\left( 2 \right)} \sin^{2} \beta \cos \left( {2\gamma } \right)} \right] \hfill \\ B = - 4\pi \left\{ {D\frac{3}{4}\sin \beta \cos \beta - D^{\left( 2 \right)} \frac{1}{2}\sin \beta \left[ {\cos \beta \cos \left( {2\gamma } \right) - i\sin \left( {2\gamma } \right)} \right]} \right\}, \hfill \\ \end{gathered}$$

(21)

where

$$\begin{gathered} \overline{g} = \frac{1}{3}\left( {g_{xx} + g_{yy} + g_{zz} } \right);\; \overline{a} = \frac{1}{3}\left( {A_{xx} + A_{yy} + A_{zz} } \right); F = \frac{2}{3}\left( {g_{zz} - \frac{1}{2}\left( {g_{xx} + g_{yy} } \right)} \right); \hfill \\ D = \frac{2}{3}\left( {A_{zz} - \frac{1}{2}\left( {A_{xx} + A_{yy} } \right)} \right);\; F^{\left( 2 \right)} = \frac{1}{2}\left( {g_{xx} - g_{yy} } \right); D^{\left( 2 \right)} = \frac{1}{2}\left( {A_{xx} - A_{yy} } \right). \hfill \\ \end{gathered}$$

(22)

Here ${\Omega }\left( {\eta ,\beta ,\gamma } \right) = \left( {0, - {\Theta },0} \right)$ are the Euler angles, which describe the orientation of the $\tilde{g}$ and $\tilde{A}$ matrices with respect to the static magnetic field, with $\Theta$ being the angle between the z axis of the magnetic frame and the Z-axis of the laboratory fixed frame.

The eigenvalues of the Hamiltonian, $\hat{H}_{0}$, as given by Eq. (20) are [1]

$$E_{a} = \frac{C}{2} + \frac{1}{2}\omega_{\alpha } ;\;E_{b} = \frac{C}{2} - \frac{1}{2}\omega_{\alpha } ;\;E_{c} = - \frac{C}{2} - \frac{1}{2}\omega_{\beta } ;\;E_{d} = - \frac{C}{2} + \frac{1}{2}\omega_{\beta } ,$$

(23)

where $\omega_{\alpha }$, $\omega_{\beta }$ are

$$\omega_{\alpha } = \left[ {\left( {\omega_{n} - \frac{A}{2}} \right)^{2} + \left( \frac{B}{2} \right)^{2} } \right]^{1/2} ;\;\omega_{\beta } = \left[ {\left( {\omega_{n} + \frac{A}{2}} \right)^{2} + \left( \frac{B}{2} \right)^{2} } \right]^{1/2} .$$

(24)

The eigenvectors are

$$\begin{gathered} \left| a \right. = \left[ {\begin{array}{*{20}c} {c_{1} } & { - c_{2} } & 0 & 0 \\ \end{array} } \right]^{{\text{T}}} ; |b = \left[ {\begin{array}{*{20}c} {c_{2} } & {c_{1} } & 0 & 0 \\ \end{array} } \right]^{{\text{T}}} \hfill \\ \left| c \right. = \left[ {\begin{array}{*{20}c} 0 & 0 & {c_{3} } & { - c_{4} } \\ \end{array} } \right]^{{\text{T}}} ; \left| d \right. = \left[ {\begin{array}{*{20}c} 0 & 0 & {c_{4} } & {c_{3} } \\ \end{array} } \right]^{{\text{T}}} , \hfill \\ \end{gathered}$$

(25)

where the superscript T denotes the transpose. The coefficient $c_{i} , i = 1, \ldots ,4$, in the above expressions are

$$\begin{gathered} c_{1} = \frac{1}{\sqrt 2 }\left[ {1 \pm \frac{{\left( {A/2} \right) - \omega_{n} }}{{\omega_{\alpha } }}} \right]^{1/2} ;c_{2} = - \frac{1}{\sqrt 2 }\left[ {1 \mp \frac{{\left( {A/2} \right) - \omega_{n} }}{{\omega_{\alpha } }}} \right]^{1/2} ; \hfill \\ c_{3} = \frac{1}{\sqrt 2 }\left[ {1 + \frac{{\left( {A/2} \right) + \omega_{n} }}{{\omega_{\beta } }}} \right]^{1/2} ;c_{4} = - \frac{1}{\sqrt 2 }\left[ {1 - \frac{{\left( {A/2} \right) + \omega_{n} }}{{\omega_{\beta } }}} \right]^{1/2} . \hfill \\ \end{gathered}$$

(26)

Here $\omega_{n}$ is the nuclear Larmor frequency.

Appendix B: Solution of Liouville von Neumann (LVN) equation

The equation of motion of the reduced density matrix, $\chi \left( t \right) = \rho \left( t \right) - \rho 0$, applicable during free evolution, i.e. in the absence of any time-dependent part in the Hamiltonian, is expressed as Liouville von Neumann (LVN) equation in Liouville space as follows [9,10,11,12,13,14,15].

$$\frac{{{\text{d}}\widehat{{\hat{\chi }}}}}{{{\text{d}}t}} = - i\widehat{{\hat{L}}}\widehat{{\hat{\chi }}} - \widehat{{\hat{R}}}\widehat{{\hat{\chi }}} = - \widehat{{\hat{L}}}^{\prime}\widehat{{\hat{\chi }}},$$

(27)

where $\widehat{{\hat{\chi }}}$ is the column vector in Liouville space corresponding to $\chi \left( t \right)$ in Hilbert space as defined above, $\widehat{{\hat{R}}}$ is the relaxation superoperator and $\widehat{{\hat{L}}}^{\prime}$ is the Liouvillian, which is defined as

$$\widehat{{\hat{L}}}^{^{\prime}} \equiv i\left[ {I_{4} \otimes \hat{H}_{0} - \left( {\hat{H}_{0} } \right)^{T} \otimes I_{4} } \right] + \widehat{{\hat{R}}},$$

(28)

with $\hat{H}_{0}$ being the spin Hamiltonian in Hilbert space and $I_{n}$ is a 4 $\times$ 4 identity matrix. The formal solution of Eq. (27) for $\widehat{{\hat{\chi }}}\left( t \right)$ after time t is expressed as

$$\widehat{{\hat{\chi }}}\left( t \right) = {\text{e}}^{{ - \left( {t - t_{0} } \right)\widehat{{\hat{L}}}^{^{\prime}} }} \widehat{{\hat{\chi }}}\left( {t_{0} } \right),$$

(29)

with the initial time being $t_{0}$.During the application of a pulse, the relaxation is neglected since the duration of the pulses, $t_{p}$, is much smaller than the relaxation times $T_{2e}$ and $T_{{{\text{2n}}}}$. The solution of the LVN equation after a pulse of duration $t_{p}$ is given by

$$\rho \left( {t_{0} + t_{p} } \right) = {\text{e}}^{{ - I\left( {\hat{H}_{0} + \hat{\varepsilon }} \right)t_{p} }} \rho \left( {t_{0} } \right){\text{e}}^{{I\left( {\hat{H}_{0} + \hat{\varepsilon }} \right)t_{p} }} ,$$

(30)

where the pulse, $\hat{\varepsilon }$, is expressed, in the rotating frame, as

$$\hat{\varepsilon } = B_{1} \gamma_{e} \left( {S_{x} \cos \phi + S_{y} \sin \phi } \right).$$

(31)

In Eq. (31) $\gamma_{e}$, $\phi$ and $B_{1}$ are the gyromagnetic ratio of the electron, the phase angle and amplitude of the pulse magnetic field, respectively,

The two-dimensional (2D) time-domain signal is calculated from $\rho_{{\text{f}}}$ as follows:

$$S\left( {t_{1} ,t_{2} } \right) = {\text{Tr}}(S_{ + } \rho_{{\text{f}}} ) = {\text{Tr}}\left( {\left( {S_{x} + iS_{y} } \right)\rho_{{\text{f}}} } \right).$$

(32)

The Fourier transform (FT) of the time domain signal $S\left( {t_{1} ,t_{2} } \right)$ is the corresponding 2D-FT signal, $S\left( {\omega_{1} ,\omega_{2} } \right)$.

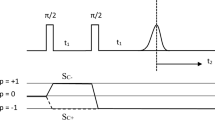
Both during a pulse and free evolution the calculations are carried in the rotating frame. At resonance, so that the effective magnetic field $B_{{{\text{eff}}}} = \left( {B - \frac{\hbar \omega }{{g\mu_{{\text{B}}} }}} \right)$ becomes zero. The echo-ELDOR calculations are made for the pulse sequences shown in Fig. 

Fig. 4

(Top) Figure to show the pulse sequence used for echo-ELDOR experiment. Here T_m is the mixing time, t₁ is the time between the first two pulses and the t₂ is stepped from the echo. (Bottom) Coherence pathways used in the echo-ELDOR experiment. Here $p$ represents the transverse magnetization, corresponding to spins rotating in a plan perpendicular to the external field [1]

4 for the coherent pathway $S_{c - }$ in accordance with that used in [1]. There are used two times, t₁ and t₂, which are stepped in the experiment (Fig. 4) for time-domain signals.

The signal is calculated over the coherent pathway $S_{c - }$ The values of the Spin-Hamiltonian parameters and the external magnetic field $\left( {B_{0} } \right)$ used are as follows [1]: the $\pi /2$ pulse is of duration $\sim 5\;{\text{ns}}$ [1];$\omega_{n} = 14.5\;{\text{MHz}}$; $\tilde{g} = \left( {g_{xx} , g_{yy} , g_{zz} } \right) = \left( {2.0026, 2.0035, 2.0033} \right)$; $\tilde{A} = \left( {A_{xx} , A_{yy} , A_{zz} } \right) = \left( { - 61.0\;{\text{MHz}}, - 91.0\;{\text{MHz}}, - 29.0\;{\text{MHz}}} \right)$. The Gaussian inhomogeneous broadening effect in the frequency domain along the axis $\omega_{2}$ $\left( { = 2\pi \nu } \right)$, corresponding to the step time $t_{2}$, as depicted in Fig. 3, is considered [1] by multiplying the time-domain signal with ${\text{e}}^{{ - 2\left( {\pi \Delta t_{2} } \right)^{2} }}$.

Full details of how to solve the LVN equation in the present case are described in [9, 10].