A mixed duopoly input market: uniform pricing versus spatial price discrimination

Abstract

We uniquely model an upstream mixed duopoly engaging in either uniform pricing or spatial price discrimination when facing a continuum of downstream firms. Uniform pricing generates higher welfare with a fully public firm. Uniform pricing generates greater optimal partial privatization except when the cost disadvantage of the public firm is large and downstream cost convexity is large. Similarly, welfare under optimal partial privatization is larger under uniform pricing except when the cost disadvantage of the public firm is relatively large and downstream cost convexity is large. Thus, the implications of the pricing scheme depend critically on the upstream and downstream cost structure and the ownership structure.

1 Introduction

Understanding the welfare implications of spatial pricing methods remains a fundamental area of inquiry. While the literature often focuses on only a final goods market (for example, Anderson et al. 1989), there exists a separate focus on the pricing consequences within a vertical chain. Within this focus, several papers compare spatial pricing methods of an upstream monopoly facing a continuum of downstream firms (Holahan 1975; Chen and Hwang 2014) but none do so in the context of a mixed oligopoly upstream. We uniquely compare uniform pricing and spatial price discrimination when a mixed upstream duopoly faces a continuum of downstream firms with elastic demand.

To the best of our knowledge the only paper to consider an upstream mixed duopoly facing a continuum of downstream firms is Heywood et al. (2023). They assume spatial price discrimination and do not compare pricing methods, the focus of so many previous papers. We show that the presence of the upstream public firm fundamentally changes the insights of earlier work. Neither pricing method is routinely welfare superior. When the cost advantage of the public firm is large and the cost convexity downstream is large, optimal partial privatization will make discriminatory pricing welfare superior.

The relevance of this demonstration is illustrated by the cigarette industry in China which produces more than 40 percent of the world’s cigarettes. Keeler et al. (1996) show that cigarette producers in the United States spatially price discriminate across distributors and retailers (largely by state). China’s cigarette industry differs in two relevant ways.¹ First, the upstream input market for cigarettes has traditionally been a mixed oligopoly with both public and private firms. Second, the input price faced by retailers of cigarettes is strictly regulated by the law and prohibits upstream spatial price discrimination. These characteristics raise exactly the issues we examine: the justification of the pricing prohibition and the extent to which partial privatization upstream should be pursued.

A similar example is provided by the pharmaceutical industry.² Ballreich (2017) examines pricing policy in the US confirming price discrimination across regions for cancer drugs. In China, the pharmaceutical industry consists of both public and private firms. Government policy again influences pricing policy as a national unified online platform increases price transparency and access to reduce spatial price discrimination in the procurement of drugs.³

In what follows, the next section places our contribution in the context of past literature and further describes its practical importance. Section 3 presents the model and derives the equilibria for uniform and then discriminatory pricing. Section 4 compares the equilibria for exogenously given partial privatization. It then compares the optimal degree of partial privatization across pricing schemes and finally compares the resulting welfare demonstrating the critical role of the cost structure both upstream and down.

2 Placing our contribution in the literature

Our value added is comparing uniform mill pricing and spatial price discrimination for two rival input producers. We do so in a model in which one rival is a mixed ownership firm and we examine the optimal extent of privatization of that firm. We compare welfare, market size (both boundary and output) and the optimal extent of privatization across the two pricing schemes.

This differs in several respects from earlier examinations. It does share the focus of comparing welfare across spatial pricing methods with Norman (1981), DeCanio (1984), Hobbs (1986), Hwang and Mai (1990), Yang and Muñoz-García (2018) and many others,⁴ Unlike those papers, it examines an input market rather than a final market. Thus, we retain the double marginalization that is a key component of vertical structure and the resulting welfare judgment (Spengler 1950).⁵ The current paper shares both the focus on comparing welfare across pricing schemes and the vertical structure with Holahan (1975) and Chen and Hwang (2014). Yet, unlike those contributions, it does not assume a private monopoly upstream.

In place of a monopoly upstream we imagine a mixed duopoly (DeFraja and Delbono 1989). Others have been concerned with the consequences of a mixed duopoly in a vertical chain and on spatial pricing comparisons but not simultaneously. Thus, Kawasaki (2022) imagines a mixed duopoly in which firms produce imperfect complements. The extent of partial privatization and the degree of complementarity determine whether the public firm should discriminate between two markets or offer a uniform price. The discrimination can only be by the public firm. The only discrimination is across the two markets and only a final goods market is considered. Relatedly, Kawasaki (2023) considers a mixed duopoly competing on price in two markets where the partially privatized firm can access only one of the two markets. Full nationalization is socially preferable under uniform pricing and there exists optimal partial privatization under discriminatory pricing. A different constant return to technology makes discriminatory pricing socially preferable.

Others introduce the vertical chain and pricing comparisons but not spatial pricing. Choi and Lim (2023) show that the choice of price discrimination or uniform pricing influences the endogenous competition strategy downstream and that the equilibrium depends on the cost difference among retailers. Building from Vetter (2017), Han and Zeng (2023) consider a vertical mixed oligopoly with a partially privatized upstream firm and endogenous downstream entry. They find that uniform pricing reduces social welfare when the upstream firm is highly nationalized. Our examination of spatial pricing will yield a different result.

Earlier work imagines a mixed oligopoly in a vertical chain and spatial pricing but makes no pricing comparisons. Heywood et al. (2020) model a private monopoly selling inputs to a mixed duopoly downstream that spatially discriminates. The presence of the public firm reduces the incentive of the downstream firms to locate inefficiently to gain concessions from the upstream monopoly (Gupta et al 1994). Heywood et al. (2021a) model a mixed duopoly upstream selling to a downstream private duopoly that spatially discriminates. The upstream public firm reduces the extent of double marginalization but produces at a higher cost. In both models, the spatial price discrimination remains downstream and pricing methods are never compared.

Heywood et al. (2023) adopted the vertical structure of Holahan (1975) and Chen and Hwang (2014) with upstream producers facing a continuum of downstream markets. Instead of a monopoly upstream producer, they imagined a mixed duopoly and showed that a fully public firm that is not too inefficient improves social welfare relative to a monopoly or a private duopoly. They also confirmed the existence of an optimal degree of partial privatization that better aligns the trade-off between production costs and pricing distortions. Spatial price discrimination was taken for granted and never compared to uniform pricing.

Research on mixed oligopolies often examines the optimal extent to privatize a public firm. A partially privatized firm can be socially optimal by reducing production costs relative to the fully public firm while still maintaining a focus on welfare (Matsumura 1998). In addition to providing output more cheaply, changing the ownership structure can also influence investment behavior (Feldman et al. 2021) and the provision of public goods (Schmitz 2021). Under the usual assumption, a partially privatized firm maximizes a weighted average of social welfare and own profit with the weights reflecting relative public and private ownership. In the current paper we both compare pricing policies and identify their interaction with the optimal degree of privatization.

The implications of this focus are important. The presence of a public firm can improve welfare by reducing the extent of double marginalization. Partial privatization may further enhance welfare by reducing the cost disadvantage of an entirely public firm. Thus, in Chinese industries such as mining and oil (with geographically differentiated markets) or tea (with a differentiated product), the government partially privatized upstream public firms that often competed with private firms. This “double-hundred action” which took place in 2018–2020 was explicitly designed to improve firm efficiency. Indeed, Liu and Zhao (2023) confirm empirically that the resulting partial privatization improved efficiency and innovation.

We combine a focus on vertical structure with the presence of a mixed duopoly upstream. For the first time we use this combination to explicitly compare uniform mill pricing and spatial price discrimination following a long line of literature. We further add the relevant policy issue of partial privatization to this comparison.

3 Model formulation and initial results

Mixed ownership firm 1, with private ownership share $\lambda \in [0,1]$, competes with private firm 2 in an upstream market selling a homogeneous good to downstream firms. Production costs upstream are zero for private firm 2 and $c > 0$ per unit for the mixed ownership firm 1. This formulation assumes that production costs are greater with public ownership (see among others Pal 1998; Wang and Mukherjee 2012 and Gelves and Heywood 2013).⁶

The downstream market is a line segment with consumers uniformly distributed and each having the inverse demand $P_{x} = 1 - q_{x}$, where ${p}_{x}$ and $q_{x}$ are the price and the quantity for consumers at $x\ge 0$ the distance from $0$. We fix the locations of both upstream firms at x = 0.⁷ Thus, the inputs could be raw materials that are site-specific at a mining, forest, or farm region. As in Holahan (1975), Chen and Hwang (2014) and Heywood et al. (2023), we assume that there is only one downstream firm in each final good market $x$ that charges the monopoly price and does not sell into other markets. Each downstream firm incurs transport cost $tx$ per input and produces one final good from one input. In addition to the transport cost and input cost, the downstream firm has quadratic cost $vq_{x}^{2} /2$ for producing and retailing final goods.⁸

The objectives of the mixed ownership firm 1 and the private firm 2 in the upstream market are as follows:

$$\begin{gathered} Firm \, 1: \, \max \, G = \lambda \pi_{1} + (1 - \lambda )SW \hfill \\ Firm \, 2: \, \max \, \pi_{2} \hfill \\ \end{gathered}$$

(1)

where $\pi_{1}$ and $\pi_{2}$ are defined as the upstream firm profits and SW is social welfare defined as follows:

$$SW = \pi_{1} + \pi_{2} + \Omega + CS$$

(2)

where $\Omega$ and CS are respectively the sum of all downstream profits and consumer surplus:

$$\Omega = \int\limits_{0}^{{x_{{limit}} }} {\Omega _{x} dx} ,CS = \int\limits_{0}^{{x_{{limit}} }} {\frac{{q_{x}^{2} }}{2}dx}$$

(3)

Here $x_{limit}$ represents the boundary of the entire downstream market. We require that the mixed ownership firm be able to earn a profit (is not excluded from the market because of its elevated cost) and so assume that $0 < c < \frac{1}{3}$. In addition, we assume that in pursuing increased welfare, the mixed ownership firm cannot violate a zero-profit constraint (there is no subsidy for the mixed ownership firm).

The game has three stages. In stage 1, the government chooses the partial privatization degree for social welfare maximization, λ. In stage 2, the upstream firms simultaneously choose the quantity. In stage 3, the downstream firms choose quantities for profit maximization. This game is solved by backward induction with the right-hand side market boundary determined endogenously as in Chen and Hwang (2014).

We examine the game separately on the assumptions of uniform pricing and spatial price discrimination. Under uniform pricing the upstream firms play a quantity game for the entire downstream market and set the resulting price which does not vary by location. Under spatial price discrimination, the upstream firms play a quantity game within each downstream market and allow prices that do vary by location.

Under either pricing assumption the equilibrium in the third stage of the game is the same. Each downstream firm maximizes profit:

$$\mathop {\max }\limits_{{q_{x} }} \, \Omega_{x} = \left( {1 - q_{x} - \omega_{x} - tx} \right)q_{x} - vq_{x}^{2} /2$$

(4)

where $\Omega_{x}$ is the profit of the downstream firm at market $x$, and $\omega_{x}$ is the price of the inputs charged by the upstream firm. Differentiating $\Omega_{x}$ with respect to $q_{x}$ yields the optimal output in market $x$:

$$q_{x} (\omega_{x} ) = \frac{{1 - \omega_{x} - tx}}{2 + v}$$

(5)

As in Chen and Hwang (2014), the market boundary is the location just sufficiently far away that the equilibrium output becomes zero. Setting (5) equal to 0 yields the market boundary:

$$x_{limit} = \frac{{1 - \omega_{x} }}{t}$$

(6)

It is the conditions in (5) and (6) that the upstream firms see in setting their quantities under either pricing assumption.

3.1 Uniform pricing upstream (U)

The upstream firms charge a fixed input price to downstream firms across all markets. This yields upstream profits $\pi_{i}$:

$$\pi_{1}^{u} = \left( {\omega^{u} - c} \right)q_{1} , \, \pi_{2}^{u} = \omega^{u} q_{2}$$

(7)

where $i = 1,2$ and $\omega^{u}$ is the uniform input price. The quantities $q_{1}$ and $q_{2}$ are those supplied by the relevant upstream firms. Let $x_{limit}^{u}$ be the market boundary associated with the uniform pricing as in (6).

In equilibrium, the upstream supply equals downstream demand, $q_{1} + q_{2} = \int\limits_{0}^{{x_{\lim it}^{u} }} {q_{x} (\omega )dx} = \frac{{\left( {1 - \omega^{u} } \right)^{2} }}{{2{\kern 1pt} t\left( {2 + v} \right)}}$ and thus:

$$\omega^{u} = 1 - \sqrt {2t\left( {2 + v} \right)\left( {q_{1}^{u} + q_{2}^{u} } \right)}$$

(8)

Substituting (8) into (1) yields the objective of the upstream mixed ownership firm:

$$\begin{aligned} G^{u} = & \lambda \pi _{1}^{u} + \left( {1 - \lambda } \right)SW^{u} \\ = & \lambda \left( {\omega ^{u} - c} \right)q_{1} + \left( {1 - \lambda } \right)\left[ {\left( {\omega ^{u} - c} \right)q_{1} + \omega ^{u} q_{2} } \right] + \left( {1 - \lambda } \right)\int\limits_{0}^{{x_{{limit}}^{u} }} {\frac{{q_{x}^{2} (\omega ^{u} )}}{2}dx} \\ + & \left( {1 - \lambda } \right)\int\limits_{0}^{{x_{{limit}}^{u} }} {\left( {1 - q_{x} (\omega ^{u} ) - \omega ^{u} - tx} \right)q_{x} (\omega ^{u} ) - \frac{{vq_{x}^{2} (\omega ^{u} )}}{2}dx} \\ \end{aligned}$$

(9)

Jointly solving $\frac{{\partial G^{u} }}{{\partial q_{1} }} = 0$ and $\frac{{\partial \pi_{2}^{u} }}{{\partial q_{2} }} = 0$, yields equilibrium output:

$$\begin{gathered} q_{1}^{u} = {\kern 1pt} \frac{{2\left( {1 - c + \lambda } \right)\left( {3 - 6{\kern 1pt} c - \lambda + v - 3{\kern 1pt} cv} \right)}}{{t\left( {3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda + 2{\kern 1pt} v + 3} \right)^{2} }} \hfill \\ q_{2}^{u} = {\kern 1pt} \frac{{2\left( {1 - c + \lambda } \right)\left( {2{\kern 1pt} cv + \lambda {\kern 1pt} v + 4{\kern 1pt} c + 3{\kern 1pt} \lambda - 1} \right)}}{{t\left( {3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda + 2{\kern 1pt} v + 3} \right)^{2} }} \hfill \\ \end{gathered}$$

(10)

The output of the upstream private firm will be positive, $q_{2}^{u} > 0$, given our assumptions that $0 < c < \frac{1}{3}$ and $\lambda \in [0,1]$. The resulting equilibrium uniform input price is:

$$\omega^{u} = \frac{{\left( {v + 3} \right)\lambda + 2{\kern 1pt} cv + 4{\kern 1pt} c - 1}}{{\left( {3{\kern 1pt} v + 7} \right)\lambda + 2{\kern 1pt} v + 3}}$$

(11)

If (11) implies that $\omega^{u} \ge c$, the zero-profit constraint does not bind and we refer to it as “unconstrained equilibrium.”

If the input price in (11) implies that $\omega^{u} < c$, then the zero-profit constraint binds, the “constrained equilibrium”. The mixed firm produces the output such that $\omega^{u} = c$. Jointly solving the best response function of the private firm and this constraint yields equilibrium outputs. The following lemma summarizes how privatization affects the equilibrium output.

Lemma 1

Recognizing that $\hat{\lambda }^{u} = \frac{1 - c}{{3 - 7c + v\left( {1 - 3c} \right)}} \in (0,1)$ divides the constrained and unconstrained equilibria, it is the case that (i) with a more privatized mixed firm ($\hat{\lambda }^{u} < \lambda \le 1$), the firm outputs are in (10), the input price in (11), output in market $x$ is $q_{x}^{u} = \frac{{2{\kern 1pt} \left( {1 + \lambda - c} \right)}}{{\left( {3{\kern 1pt} v + 7} \right)\lambda + 2{\kern 1pt} v + 3}} - \frac{tx}{{2 + v}}$ and the market boundary is $x_{limit}^{u} = {\kern 1pt} \frac{{2\left( {2 + v} \right)\left( {1 - c + \lambda } \right)}}{{\left[ {\left( {3{\kern 1pt} v + 7} \right)\lambda + 2{\kern 1pt} v + 3} \right]t}}$; and (ii) with a less privatized public firm ($0 \le \lambda \le \hat{\lambda }^{u}$), $\omega^{u} = c$, firm outputs are $q_{1}^{u} = \frac{{\left( {3{\kern 1pt} c - 1} \right)\left( {c - 1} \right)}}{{2\left( {2 + v} \right){\kern 1pt} t}}$ and $q_{2}^{u} = \frac{{c\left( {1 - c} \right)}}{{\left( {2 + v} \right)t}}$, output in market $x$ is $q_{x}^{u} = \frac{1 - tx - c}{{2 + v}}$ and the market boundary is $x_{limit}^{u} = {\kern 1pt} \frac{1 - c}{t}$.⁹

Proof

In the appendix.

Lemma 1 shows that changes in privatization influence the market boundary only when it is large ($\lambda > \hat{\lambda }^{u}$). The zero-profit constraint applies when privatization is low as the mixed firm produces higher quantities, decreasing the input price. Consequently, privatization will be more likely to play a role when the mixed ownership firm is not too inefficient (as $\frac{{\partial \hat{\lambda }^{u} }}{\partial c} > 0$). This yields the following proposition.

Proposition 1

Under uniform pricing, when $\hat{\lambda }^{u} < \lambda \le 1$, increasing privatization decreases the market boundary and the total output.

Proof

In the appendix.

The result is intuitive and follows from (i) of the Lemma’s proof. Privatization increases the weight on profit, decreases total output, raises the market price, and so decreases the market boundary.¹⁰

While privatization decreases the market size and the total output, it also reduces the market share of the mixed ownership firm reducing total production cost. This trade-off allows us to move to the initial stage of the game and explore the government’s choice of the optimal degree of partial privatization. Substituting the unconstrained results into $SW^{u}$ and solving $\frac{{\partial SW^{u} }}{\partial \lambda } = 0$, we have the unconstrained optimal partial privatization degree $\lambda^{u}$ under uniform pricing:

$$\lambda^{u} = c - 1 + \frac{{\left( {3cv + 7c - v - 4} \right)c}}{{\sqrt {\left( {2 + v} \right)\left[ {\left( {9c^{2} + 1 - 3c} \right)\left( {2 + v} \right) + cv} \right]} - \left( {c + v + 2} \right)}}$$

(12)

This yields the following proposition:

Proposition 2

Under uniform pricing, optimal partial privatization is anywhere in the range $0 \le \lambda \le \hat{\lambda }^{u}$ if $v < \frac{{\left( {3{\kern 1pt} c - 1} \right)^{2} }}{{2{\kern 1pt} c\left( {1 - 2{\kern 1pt} c} \right)}}$. The optimal partial privatization is 1 if $v > {\kern 1pt} \frac{{2\left( {1 - 3{\kern 1pt} c} \right)\left( {9{\kern 1pt} c - 8} \right)}}{{26{\kern 1pt} c^{2} - 29{\kern 1pt} c + 4}}$ and $\frac{{29 - 5{\kern 1pt} \sqrt {17} }}{52} < c < \frac{1}{3}$. In other cases, the optimal partial privatization is $\lambda^{u}$.

Proof

In the appendix.

This differs drastically from the model of substitute goods of Kawaski (2023) in which partial privatization never improved welfare under uniform pricing. Our difference is generated by the setting of an endogenous market boundary and the focus on a vertical market structure. Proposition 2 shows that when c is small, there always exists an optimal partial privatization less than 1. This reflects that the cost asymmetry upstream is sufficiently small that the extra output of the mixed ownership firm increases welfare by reducing the double-marginalization problem. For large c, this reverses, and full privatization is optimal. Note, however, that the extra output upstream from a mixed ownership firm comes not only with a higher upstream cost but that it interacts with the extent of convexity downstream. With increased v, the threshold value of c for full privatization decreases. With larger convexity downstream, the extra output upstream increases the downstream marginal cost by more. Increased privatization will be socially preferable for a given c when v is high. Thus, when both c and v are large, full privatization is optimal as the increased production costs at both levels outweigh the advantages of reducing double marginalization.

Figure 1 illustrates this proposition under the assumption that $t = 1$ and c = 0.2. It shows that when downstream cost convexity is small or moderate, v = 1 or v = 2, there exists an internal optimal degree of partial privatization. Some privatization reduces the cost of production sufficiently to outweigh the reduced output and decreased market boundary associated with worsened double-marginalization. Further privatization worsens double marginalization enough to lower social welfare. Hence, a partially privatized mixed firm is socially preferable.

Fig. 1

Social welfare and privatization under uniform pricing. Note: These assume $t = 1$ and $c = 0.2$

3.2 Spatial price discrimination upstream (D)

We now assume the upstream firms engage in spatial price discrimination. We start by determining the upstream quantities when each downstream market $x$ has a unique input price $\omega_{x}^{d}$. The profit of the upstream firm in a given market is

$$\pi_{1x}^{d} = \left( {\omega_{x}^{d} - c} \right)q_{1x} , \, \pi_{2x}^{d} = \omega_{x}^{d} q_{2x}$$

(13)

where $q_{ix}$ is the quantity supplied by the upstream firm $i$, $i = 1,2$. At equilibrium, the upstream supply equals the downstream demand in each market $x$, $q_{1x} + q_{2x} = q_{x} (\omega_{x}^{D} ) = \frac{{1 - \omega_{x}^{d} - tx}}{2 + v}$ and thus we have the inverse demand function:

$$\omega_{x}^{d} = 1 - tx - \left( {2 + v} \right)\left( {q_{1x} + q_{2x} } \right)$$

(14)

Since the upstream firms have linear costs, maximizing total profit implies maximizing profit in each downstream market. Substituting (14) into (1) yields the objective function of the upstream mixed ownership firm:

$$\begin{aligned} G_{x}^{d} = & \lambda \pi _{{1x}}^{d} + \left( {1 - \lambda } \right)SW_{x}^{d} \\ = & \lambda \left( {\omega _{x}^{d} - c} \right)q_{{1x}} + \left( {1 - \lambda } \right)\left[ {\left( {\omega _{x}^{d} - c} \right)q_{{1x}} + \omega _{x}^{d} q_{{2x}} + \frac{{\left( {q_{{1x}} + q_{{2x}} } \right)^{2} }}{2}} \right] \\ + & \left( {1 - \lambda } \right)\left[ {\left( {1 - q_{{1x}} - q_{{2x}} - \omega _{x}^{d} - tx} \right)\left( {q_{{1x}} + q_{{2x}} } \right) - \frac{{v\left( {q_{{1x}} + q_{{2x}} } \right)^{2} }}{2}} \right] \\ \end{aligned}$$

(15)

Jointly solving $\frac{{\partial G_{x}^{d} }}{{\partial q_{1x} }} = 0$ and $\frac{{\partial \pi_{2x}^{d} }}{{\partial q_{2x} }} = 0$, yields the unconstrained outputs:

$$\begin{gathered} q_{1x}^{d} = {\kern 1pt} \frac{{\left( {1 - tx} \right)\left( {1 - \lambda } \right) + \left( {2 + v} \right)\left( {1 - 2c - tx} \right)}}{{\left( {2 + v} \right)\left( {2\lambda v + 5{\kern 1pt} \lambda + v + 1} \right)}} \hfill \\ q_{2x}^{d} = {\kern 1pt} \frac{{\left( {2 + v} \right)\left[ {c + \lambda \left( {1 - tx} \right)} \right] - \left( {1 - tx} \right)\left( {1 - \lambda } \right)}}{{\left( {2 + v} \right)\left( {2\lambda v + 5{\kern 1pt} \lambda + v + 1} \right)}} \hfill \\ \end{gathered}$$

(16)

Notice that the upstream private firm serves market $x$ only when $q_{2x}^{d} > 0$. The upstream mixed ownership firm serves market $x$ without the zero-profit constraint only when $\omega_{x}^{d} \ge c$.

Recognizing that $\hat{\lambda }^{d} = \frac{1 - c}{{3 + v - 2cv - 5c}} \in (0,1)$ now divides the constrained and unconstrainted equilibria, the following lemma shows how privatization affects the equilibrium output strategy.

Lemma 2

There are three types of equilibria with a more privatized mixed firm, $\hat{\lambda }^{d} < \lambda \le 1$: (i) in markets $0 \le x < \hat{x}_{1} = \frac{{c\left( {1 - \lambda } \right)}}{{t\left( {1 - 3{\kern 1pt} \lambda - \lambda v} \right)}} + \frac{{1 - 2{\kern 1pt} c}}{t}$, the outputs are those in (16); (ii) in markets $\hat{x}_{1} \le x < \overline{x}_{1} = \frac{{1 - 2{\kern 1pt} c}}{t}$, the equilibrium is constrained and $q_{1x}^{d} = \frac{1 - 2c - tx}{{2 + v}}$, $q_{2x}^{d} = \frac{c}{2 + v}$ and (iii) in markets $\overline{x}_{1} \le x \le x_{limit}^{d} = \frac{1}{t}$, $q_{1x}^{d} = 0$, $q_{2x}^{d} = \frac{1 - tx}{{2\left( {2 + v} \right)}}$, a monopoly equilibrium. With a less privatized mixed firm, $0 \le \lambda < \hat{\lambda }^{d}$, there are only 2 types of equilibria: (i) the constrained equilibrium when $0 \le x < \overline{x}_{1}$ and (ii) the monopoly equilibrium when $\overline{x}_{1} \le x \le x_{limit}^{d}$.

Proof

See appendix.

Figure 2 summarizes the types of equilibria described in Lemma 2. In the case of the more privatized public firm, for close downstream markets, the unconstrained equilibrium persists. For those at an intermediate distance, the higher transport cost means that the resulting demand leads to a constrained equilibrium. At the greatest distance, the transport cost means that demand (combined with the zero-profit constraint) requires the mixed firm to drop out. When the mixed firm is mostly public, the zero-profit constraint immediately binds as shown in the second panel.

Fig. 2

Types of equilibria with spatial price discrimination. Note: $\hat{\lambda }^{d} = \frac{1 - c}{{3 + v - 2cv - 5c}} \in (0,1)$

The spatial segmentation of the equilibrium is generated by the cost asymmetry of the upstream firms. With its higher production costs, the mixed firm faces a zero-profit constraint producing less output than does the private firm. Thus, there will be markets that are far enough away that the mixed firm does not enter and in which the private firm becomes a monopoly. A more privatized mixed firm has greater incentives to reduce output from the point where profit is zero (the constraint is less likely to bind). Having a mixed firm facing fewer zero-profit constraints results in a larger set of markets having an unconstrained equilibrium.

The influence of privatization on the market boundary differs under discriminatory pricing from that under uniform pricing.

Proposition 3

Under discriminatory pricing, the market boundary is independent of the degree of privatization. Privatization does, however, increase the locations with the unconstrained equilibrium.

Proof

By Lemma 2.

Under price discrimination, the market boundary for the entire market is set by the private firm $x_{limit}^{d} = \frac{1}{t}$ and is independent of privatization. However, the market boundary for the mixed ownership firm is $\overline{x}_{1} = \frac{{1 - 2{\kern 1pt} c}}{t}$, which is determined by the upstream marginal costs. This contrasts with uniform pricing in which the boundary is determined by the upstream cost c. Privatization reduces the average production cost by reallocating the market share between the two firms which retain fixed but different marginal costs.¹¹ Even though privatization does not change the entire market boundary under discriminatory pricing, a more privatized mixed firm generates a larger set of markets for the unconstrained equilibrium. Privatization increases the profit of the mixed ownership firm, moving it away from the zero-profit constraint and from pricing equal to marginal cost.

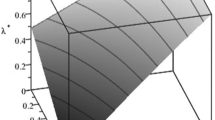
Figure 3 illustrates the influence of privatization on quantities and welfare. Note that the output of the mixed firm is larger than that of the private firm with small degrees of privatization but smaller than that of the private firm with large degrees of privatization. Greater privatization has offsetting influences. It can harm welfare by reducing total output in the region with the unconstrained equilibrium. However, it can improve welfare by moving market share from the mixed firm to the private firm. When $\hat{\lambda }^{d} < \lambda \le 1$ and $0 \le x < \hat{x}_{1}$, greater privatization increases the equilibrium output of the relatively efficient private firm ($\frac{{\partial q_{2x}^{d} }}{\partial \lambda } = - \frac{{tvx + 2{\kern 1pt} cv + 4{\kern 1pt} tx + 5{\kern 1pt} c - v - 4}}{{\left( {2{\kern 1pt} v\lambda + 5{\kern 1pt} \lambda + v + 1} \right)^{2} }} > 0$) but decreases that of the relatively inefficient mixed firm ($\frac{{\partial q_{1x}^{d} }}{\partial \lambda } = \frac{{2\left( {tvx + 2{\kern 1pt} cv + 4{\kern 1pt} tx + 5{\kern 1pt} c - v - 4} \right)}}{{\left( {2{\kern 1pt} v\lambda + 5{\kern 1pt} \lambda + v + 1} \right)^{2} }} < 0$). Therefore, greater privatization decreases welfare near the origin but raises welfare away from it as shown in the second panel.¹²

Fig. 3

Social welfare and quantity under discriminatory pricing ($c = 0.2$, $t = 1$, $v = 2$, $\hat{\lambda }^{d} = 0.25$). Note: The left panel shows outputs across locations. The red line is the quantity of the mixed ownership firm and the blue line is that of the private firm. The solid line is when $\lambda = 0.4$ and the dashed line is when $\lambda = 0.6$. The right panel shows the effect of privatization on the social welfare at each location $\Delta SW_{x}^{d} = SW_{x}^{d} \left( {\lambda = 0.6} \right) - SW_{x}^{d} \left( {\lambda = 0.4} \right)$

Greater privatization brings additional double-marginalization and reduced output compared with the constrained equilibrium, the size effect. Greater privatization also reduces the output of the mixed firm and so the average production cost, the cost effect. The influence on total welfare depends on the strength of the two effects. The optimal privatization $\lambda^{d}$ is that associated with $\frac{{\partial SW^{d} }}{\partial \lambda } = 0$.

Although we cannot obtain an analytic result, Fig. 4 illustrates the existence of optimal partial privatization under discriminatory pricing.

Fig. 4

Social welfare and privatization under discriminatory pricing. Notes: The influence of privatization, λ, on welfare assuming $t = 1$, $c = 0.2$ and $v = 2$

We summarize this pattern in a lemma that applies to all cases, not just that illustrated.

Lemma 3

When the convexity of the downstream market is large enough (e.g. $v > \frac{1 - 3c}{c}$), optimal privatization is in the unconstrained region ($\lambda \in (\hat{\lambda }^{d} ,1]$).

Proof

In the Appendix.

Lemma 3 reflects the interaction of c and v to identify the production cost increase associated with the mixed firm increasing output. As c is larger, that cost increases. The extra output also has additional costs downstream, as those firms move up their marginal cost curve. Thus, as before, this indicates that the higher cost of the public firm interacts with the convex downstream cost structure to increase the extent of optimal privatization. We now turn to a more complete comparison of the pricing methods.

4 Comparing uniform and discriminatory pricing

In this section we compare outcomes between the two pricing schemes. To show the effect of the two schemes, we fix the privatization degree and compare the boundary, output and welfare. We then compare the optimal extent of privatization and the associated welfare at these endogenized levels.

We use the first two lemmas to compare equilibrium output and the market boundary. We recognize that while there is a single market boundary with both firms serving the entire market under uniform pricing, the market boundary of the two firms can differ under spatial price discrimination. With spatial price discrimination there can be markets that only the private firm serves. This is summarized in the following proposition:

Proposition 4

(i) The market boundary of the private firm is larger with discriminatory pricing. The market boundary of the mixed ownership firm is larger with discriminatory pricing only when cost differences are small ($0 < c < \frac{1}{8}$) and privatization is large ($\frac{{2{\kern 1pt} c\left( {v + 1} \right) + 1}}{{3 - 14c + v(1 - 6{\kern 1pt} c)}} < \lambda \le 1$). Otherwise, discriminatory pricing decreases the market boundary of the mixed ownership firm. (ii) When $0 < \lambda \le \hat{\lambda }^{d}$, discriminatory pricing has a larger output; when $\hat{\lambda }^{d} \le \lambda \le \hat{\lambda }^{u}$, discriminatory pricing has a larger output for large cost differences but smaller output for small cost differences; when $\hat{\lambda }^{u} < \lambda \le 1$, discriminatory pricing has a larger output for small cost differences but smaller output for large cost differences.

Proof

In the Appendix.

The presence of a mixed ownership firm does not change the conclusion that there is a larger market boundary under discriminatory pricing (Chen and Hwang 2014).¹³ It does, however, introduce an important nuance as the market boundary for the mixed firm need not increase with discriminatory pricing. A mixed firm tends to let the efficient private firm take more market share to reduce the average production cost. The decrease in the market boundary of the mixed firm can be generated by the two forces. First, the mixed firm reduces the market share in each market. Greater privatization increases the output of the private firm ($\frac{{\partial q_{2x}^{d} }}{\partial \lambda } = - \frac{{tvx + 2{\kern 1pt} cv + 4{\kern 1pt} tx + 5{\kern 1pt} c - v - 4}}{{\left( {2{\kern 1pt} v\lambda + 5{\kern 1pt} \lambda + v + 1} \right)^{2} }} > 0$) but decreases that of the mixed firm ($\frac{{\partial q_{1x}^{d} }}{\partial \lambda } = \frac{{2\left( {tvx + 2{\kern 1pt} cv + 4{\kern 1pt} tx + 5{\kern 1pt} c - v - 4} \right)}}{{\left( {2{\kern 1pt} v\lambda + 5{\kern 1pt} \lambda + v + 1} \right)^{2} }} < 0$). Second, the mixed firm reduces its market boundary. The mixed firm uses both methods to increase the market share of the private firm. Thus, its boundary will often be smaller under discriminatory pricing.

The exception is when the mixed firm is not too inefficient ($0 < c < \frac{1}{8}$). Here discriminatory pricing increases its boundary when privatization is large. Consequently, the boundary for the mixed firm with high privatization and little inefficiency exceeds that under uniform pricing.

Unlike the case of an upstream monopolist (Chen and Hwang 2014), discriminatory pricing need not have a larger output. The total output depends on the output in each market and the total market size. This gives rise to three regions.

When privatization is small such that ($0 < \lambda \le \hat{\lambda }^{d}$), the constrained equilibrium exists under both pricing schemes. In the constrained equilibrium, increased privatization does not influence the within-market output only the market size. In this case, the larger market boundary generated by discriminatory pricing leads to more output ($x_{limit}^{d} = \frac{1}{t} > x_{limit}^{u} = \frac{1 - c}{t}$).

When privatization is of medium value ($\hat{\lambda }^{d} \le \lambda \le \hat{\lambda }^{u}$), increased privatization reduces the within-market output under the unconstrained discriminatory pricing equilibrium but does not affect that of the uniform pricing ($Q_{x}^{u} = \frac{1 - tx - c}{{v + 2}}$). This offsets the larger market boundary. Here, discriminatory pricing produces more only when c is large enough such that the market size under the uniform pricing is small enough ($\frac{{\partial x_{limit}^{u} }}{\partial c} = - \frac{1}{t} < 0$) while it does not affect that under the discriminatory pricing ($x_{limit}^{d} = \frac{1}{t}$).

When privatization is large ($\hat{\lambda }^{u} < \lambda \le 1$), increased privatization decreases the within-market output under the two unconstrained equilibria. However, with increased privatization a larger c tends to generate a smaller loss in the market size under uniform pricing ($x_{limit}^{u} = \frac{{2\left( {v + 2} \right)\left( {1 - c + \lambda } \right)}}{{\left( {3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda + 2{\kern 1pt} v + 3} \right)t}}$, $\frac{{\partial x_{limit}^{u} }}{\partial c} = - {\kern 1pt} \frac{{2\left( {v + 2} \right)}}{{\left( {3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda + 2{\kern 1pt} v + 3} \right)t}} < 0$, $\frac{{\partial^{2} x_{limit}^{u} }}{\partial c\partial \lambda } = \frac{{2\left( {v + 2} \right)\left( {3{\kern 1pt} v + 7} \right)}}{{\left( {3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda + 2{\kern 1pt} v + 3} \right)^{2} t}} > 0$). Moreover, for discriminatory pricing a larger c reduces the market size of the unconstrained equilibrium ($\frac{{\partial \hat{x}_{1} }}{\partial c} = - \frac{{2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda - 1}}{{t\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right)}} < 0$) but increases the market size of the private monopoly ($\frac{{\partial \left( {1 - \overline{x}_{1} } \right)}}{\partial c} = \frac{{2{\kern 1pt} }}{t} > 0$). Therefore, when c is large enough, the output under the discriminatory pricing decreases more and uniform pricing generates more output.

Figure 5 illustrates the influence of the pricing method on total output. In the illustration $t = 1,v = 1,\lambda = 0.28$ and the cases of moderate and large privatization are examined. For the moderate case in panel 1, $\hat{\lambda }^{d} \le \lambda \le \hat{\lambda }^{u}$ implies that $\frac{{\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1}}{{3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda - 1}} \le c \le \frac{{\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1}}{{2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda - 1}} \Leftrightarrow c \in (0.067,0.125)$. The plot shows greater output with discriminatory pricing when $c > 0.073$ but smaller output for $c < 0.073$. For the greater privatization case in panel 2, $\hat{\lambda }^{d} < \hat{\lambda }^{u} < \lambda \le 1$ implies that $0 < c \le \frac{{\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1}}{{3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda - 1}} \Leftrightarrow c \in (0,0.067)$. It shows the reverse pattern with greater output with discriminatory pricing when $c < 0.020$ but smaller output when $c > 0.020$. This illustrates the general result of Proposition 4(ii).

Fig. 5

Illustrating the output difference between discriminatory and uniform pricing. Notes:$\Delta Q = Q^{d} - Q^{u} = \left( {q_{1}^{d} + q_{2}^{d} } \right) - \left( {q_{1}^{u} + q_{2}^{u} } \right)$ and parameters are $t = 1,v = 1,\lambda = 0.28$

Now we turn to the welfare comparison given exogenous privatization.

Proposition 5

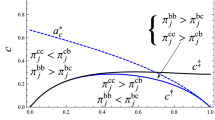
For a given degree of privatization, spatial price discrimination implies higher social welfare only when: (i) the cost disadvantage is moderate ($0.125 < c < 0.308$); (ii) cost convexity is extremely large; (iii) privatization is large.

Proof

See appendix.

While these are sufficient conditions, they isolate the interaction of the cost parameters upstream and down and they imply two additional points. First, there exist conditions under which discriminatory pricing is superior. Second, those conditions are limiting, suggesting that uniform pricing will often be superior. Figure 6 illustrates both these points by comparing social welfare given the extent of privatization and adopting a moderate cost disadvantage of c = 0.2. The first panel presents cost convexity v = 2 and the second panel presents cost convexity v = 4. Throughout the range of all possible privatization, uniform pricing is welfare superior for both cases. The final panel presents cost convexity v = 10. With this extremely high convexity and only with privatization above 0.78, spatial price discrimination becomes welfare superior.

Fig. 6

The comparison between the social welfare under SPD and under UP ($t = 1$)

Spatial price discrimination is preferable as higher privatization reduces the average production cost in each market by reallocating market share to the more efficient firm.¹⁴ This, in turn, improves the welfare gain from serving new markets. Yet, for this to dominate the fact that uniform pricing can significantly prevent double marginalization requires a very large degree of privatization. Thus, the relevant policy combinations emerge as low privatization and uniform pricing or high privatization and discriminatory pricing.

Next, we compare the optimal partial privatization across pricing schemes.

Proposition 6

In the “more privatized” region where $\hat{\lambda }^{d} < \lambda \le 1$ and for large c > 0.13, discriminatory pricing generates smaller optimal partial privatization when downstream cost convexity is small but larger optimal privatization when convexity is large. For $c < 0.13$, discriminatory pricing generates smaller optimal privatization for any downstream cost convexity.

Proof

See appendix.

Proposition 6 demonstrates how the cost structure influences optimal privatization. Discriminatory pricing extends the market boundary increasing the concern with the double-marginalization problem. With a small cost disadvantage, the additional output of a more public firm can alleviate this concern. Thus, the optimal extent of privatization is less under discriminatory pricing for smaller cost parameters.

When the cost disadvantage of the public firm is large, optimal privatization is determined by costs downstream. With less convexity (v is small), the additional output of the public firm can continue to control the double-marginalization problem made worse by discriminatory pricing resulting in lower degrees of privatization. Yet, given both a larger cost disadvantage upstream and high convexity downstream, the additional output of the public firm comes at too great a total cost. In this case, the public firm should be more privatized under discriminatory pricing. The optimal degree of privatization always trades off alleviating double marginalization and the cost effect.¹⁵

Finally, we are interested in the social welfare comparison with optimal privatization for each pricing scheme.

Proposition 7

Under optimal privatization, discriminatory pricing could be welfare superior only in the “more privatized” region. It can happen only when the downstream cost convexity is large, and the upstream cost difference is large but not extreme ($0.130 < c < 0.308$). Otherwise, uniform pricing is welfare superior.

Proof

See appendix.

Consistent with the analysis in Proposition 4, spatial price discrimination extends the market size but increases the loss from double marginalization. This yields different cases. Given the constrained equilibrium for both pricing schemes, the upstream cost differential and downstream cost convexity are relatively small. Discriminatory pricing generates greater loss from double marginalization making uniform pricing socially preferable. This persists with the unconstrained equilibrium for uniform pricing but a constrained equilibrium for discriminatory pricing. Even though the production cost difference generates a greater output reduction with uniform pricing, optimal partial privatization improves welfare enough so that double marginalization still generates more inefficiency and uniform pricing is preferred.

With the increase of the upstream and downstream costs, the importance of production efficiency increases. With the unconstrained equilibrium for both pricing schemes, optimal partial privatization reduces production costs under both schemes. Importantly, discriminatory pricing becomes preferred as it decreases the market size of the inefficient firm without the shrinking of the market boundary.

But when c is very large, full privatization is chosen under either pricing scheme. Complete privatization reduces production inefficiency but not enough to offset the increased double marginalization associated with price discrimination. Compared with uniform pricing, discriminatory pricing generates greater double-marginalization both because of the larger region for the private monopoly under full privatization and because of the greater market power in each market with an unconstrained equilibrium. As these losses outweigh the efficiency gain, uniform pricing results in greater welfare.

5 Conclusion

We examine a vertical chain in which an upstream mixed duopoly faces a continuum of downstream firms each with downward-sloping demand. In this framework we compare uniform pricing and spatial price discrimination. Uniform pricing generates higher welfare with a fully public firm. Yet, a fully public firm is typically not optimal.

Uniform pricing generates greater optimal partial privatization except when the cost disadvantage of the public firm is large and downstream cost convexity is large. Similarly, welfare under optimal partial privatization is larger under uniform pricing except when the cost disadvantage of the public firm is larger (moderate) and downstream cost convexity is large. Thus, the implications of the pricing scheme depend critically on the upstream and downstream cost structure and the ownership structure. Once optimal partial privatization is considered spatial price discrimination can be welfare superior.

Future work might examine a variety of extensions or variations. First, the private firm in the duopoly might be foreign-owned. In such cases the relevant policy objective could be domestic welfare which would exclude the profit of the foreign firm (Corneo and Jeanne 1994; Fjell and Pal 1996; Inoue et al. 2009). This could drastically change the extent of optimal privatization and the resulting comparison of the pricing schemes. Second, we placed both firms in the left corner. While attempts to endogenize location proved intractable, varying this location could be instructive. Third, our assumption of a monopoly in each downstream market could be modified.

Despite these possible extensions, our results isolate the importance of partial privatization to improve welfare. Moreover, once this is recognized, discriminatory pricing can be welfare superior depending on the cost structure both upstream and down. This argues against a blanket prohibition on such pricing by input suppliers.

Appendix

Proof of Lemma 1.

(i) When $\hat{\lambda }^{u} < \lambda \le 1$, we have $\omega^{u} > c$. Substituting (11) into Eqs. (5) and (6) directly derives the results. (ii) When $0 \le \lambda \le \hat{\lambda }^{u}$, we $\omega^{u} = c$ and so by (8) $c = 1 - \sqrt {2t\left( {2 + v} \right)\left( {q_{1}^{u} + q_{2}^{u} } \right)}$. Jointly solving with the response function of the private firm,$q_{u2} = \frac{{1 - 6t\left( {2 + v} \right)q_{u1} + \sqrt {1 + 6t\left( {2 + v} \right)q_{u1} } }}{{9{\kern 1pt} t\left( {2 + v} \right)}}$, derives the equilibrium results.

Proof of Proposition 1

$\frac{{\partial x_{limit}^{u} }}{\partial \lambda } = {\kern 1pt} {\kern 1pt} \frac{{2\left( {v + 2} \right)\left( {3{\kern 1pt} cv + 7{\kern 1pt} c - v - 4} \right)}}{{\left( {3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda + 2{\kern 1pt} v + 3} \right)^{2} t}} < 0$ $\frac{{\partial \left( {q_{1}^{u} + q_{2}^{u} } \right)}}{\partial \lambda } = {\kern 1pt} \frac{{4\left( {2 + v} \right)\left( {1 + \lambda - c} \right)\left( {3{\kern 1pt} cv + 7{\kern 1pt} c - v - 4} \right)}}{{\left( {3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda + 2{\kern 1pt} v + 3} \right)^{3} t}} < 0$.

Proof of Proposition 2

When $0 \le \lambda \le \hat{\lambda }^{u}$, $SW^{u,c} = \frac{{\left( {1 - c} \right)\left( {7{\kern 1pt} c^{2} v + 15{\kern 1pt} c^{2} - 2{\kern 1pt} cv - 6{\kern 1pt} c + v + 3} \right)}}{{6{\kern 1pt} \left( {v + 2} \right)^{2} t}}$. When $\hat{\lambda }^{u} < \lambda \le 1$, the social welfare is denoted as $SW^{u,uc}$. It is easy to derive that $SW_{{\lambda = \hat{\lambda }^{u} }}^{u,uc} = SW^{u,c}$. In the “unconstrained equilibrium” the monotonicity of social welfare with privatization depends on a quadratic function: $sign\left\{ {\frac{{\partial SW^{u,uc} }}{\partial \lambda }} \right\} = sign\left\{ {\Phi_{0} \lambda^{2} + \Phi_{1} \lambda + \Phi_{2} } \right\}$, where

$$\Phi_{0} = 9{\kern 1pt} cv^{2} + 36{\kern 1pt} cv - 2{\kern 1pt} v^{2} + 35{\kern 1pt} c - 12{\kern 1pt} v - 16$$

$$\Phi_{1} = - 2{\kern 1pt} \left( {9{\kern 1pt} c^{2} v^{2} + 39{\kern 1pt} c^{2} v - 8{\kern 1pt} cv^{2} + 42{\kern 1pt} c^{2} - 36{\kern 1pt} cv + v^{2} - 41{\kern 1pt} c + 6{\kern 1pt} v + 8} \right)$$

$$\Phi_{2} = - c\left( {2{\kern 1pt} v + 3} \right)\left( {4{\kern 1pt} cv + 8{\kern 1pt} c - 2{\kern 1pt} v - 5} \right)$$

At $\lambda = 0$, $\frac{{\partial SW^{u,uc} }}{\partial \lambda } > 0$. If $\frac{{\partial SW^{u,uc} }}{\partial \lambda }|_{{\lambda = \hat{\lambda }^{u} }} > 0$, then when $\hat{\lambda }^{u} < \lambda \le 1$, the optimal privatization can only be at $\lambda = \min \left\{ {\lambda^{u} ,1} \right\}$. If $\frac{{\partial SW^{u,uc} }}{\partial \lambda }|_{{\lambda = \hat{\lambda }^{u} }} < 0$, then there is $v < \frac{{\left( {3{\kern 1pt} c - 1} \right)^{2} }}{{2{\kern 1pt} c\left( {1 - 2{\kern 1pt} c} \right)}}$. Given the constraint, it is easy to derive that $\frac{{\partial SW^{u,uc} }}{\partial \lambda }|_{\lambda = 1} < 0$, which means $\frac{{\partial SW^{u,uc} }}{\partial \lambda } < 0$ for $\hat{\lambda }^{u} < \lambda \le 1$ and thus the optimal privatization is in the range $0 \le \lambda \le \hat{\lambda }^{u}$. By computing $\lambda^{u} = 1$, we can derive the condition for whether the optimal privatization equals to $\lambda^{u}$ or 1.

Proof of Lemma 2

(i) When $\hat{\lambda }^{d} < \lambda \le 1$, we have the unconstrained equilibrium in Eq. (16) where both $q_{1x}^{d}$ and $q_{2x}^{d}$ are non-negative if $0 \le x < \hat{x}_{1} = \frac{{c\left( {1 - \lambda } \right)}}{{t\left( {1 - 3{\kern 1pt} \lambda - \lambda v} \right)}} + \frac{{1 - 2{\kern 1pt} c}}{t}$. If $\hat{x}_{1} \le x < \overline{x}_{1} = \frac{{1 - 2{\kern 1pt} c}}{t}$, $q_{1x}^{d}$ in Eq. (16) would be negative. But for the profit maximization the private firm would choose the output such that $\omega_{x}^{d} = c$, which makes the mixed firm not exit the market. By jointly solving $\omega_{x}^{d} = 1 - tx - \left( {2 + v} \right)\left( {q_{1x} + q_{2x} } \right) = c$ and $\frac{{\partial \pi_{2x}^{d} }}{{\partial q_{2x} }} = 0$, we have the constrained equilibrium $q_{1x}^{d} = \frac{1 - 2c - tx}{{2 + v}}$ and $q_{2x}^{d} = \frac{c}{2 + v}$. If $\overline{x}_{1} \le x \le x_{limit}^{d} = \frac{1}{t}$, under the constrained equilibrium $q_{1x}^{d} = \frac{1 - 2c - tx}{{2 + v}} < 0$, the mixed firm exists the market and it turns to a monopoly equilibrium. By solving $q_{1x}^{d} = 0$ and $\frac{{\partial \pi_{2x}^{d} }}{{\partial q_{2x} }} = 0$, the equilibrium output becomes $q_{1x}^{d} = 0$ and $q_{2x}^{d} = \frac{1 - tx}{{2\left( {2 + v} \right)}}$.

(ii)When $0 \le \lambda < \hat{\lambda }^{d}$, the unconstrained equilibrium in (i) does not exist because of $q_{1x}^{d} < 0$. Therefore, there are only 2 types of equilibria: the constrained equilibrium when $0 \le x < \overline{x}_{1}$ and the monopoly equilibrium when $\overline{x}_{1} \le x \le x_{limit}^{d}$.

Proof of Lemma 3

At $\lambda \to \hat{\lambda }^{d}$, $sign\left\{ {\frac{{\partial SW^{d} }}{\partial \lambda }} \right\} = sign\left\{ { - \frac{{6c^{2} \left( {v + 2} \right)^{2} \left( {cv + 3{\kern 1pt} c - 1} \right)\left( {2{\kern 1pt} cv + 5{\kern 1pt} c - v - 4} \right)^{2} }}{{\left( {2{\kern 1pt} cv + 5{\kern 1pt} c - v - 3} \right)^{3} }}} \right\}$. Therefore, when $v > \frac{1 - 3c}{c}$, the optimal partial privatization must locate in the unconstrained region, $\lambda \in (\hat{\lambda }^{d} ,1]$.

Proof of Proposition 4

(i) By Proposition 1 and Lemma 1, for $\lambda \in [0,1]$, $\max x_{limit}^{u} = \frac{1 - c}{t}$. Thus, $x_{limit}^{d} - x_{limit}^{u} = \frac{c}{t} > 0$. By Lemma 2, the market boundary for the mixed firm is $\overline{x}_{1} = \frac{{1 - 2{\kern 1pt} c}}{t}$ under spatial price discrimination.

If $0 < \lambda \le \hat{\lambda }^{u}$, $\overline{x}_{1} - x_{limit}^{u} = - \frac{c}{t} < 0$.

If $\hat{\lambda }^{u} < \lambda \le 1$, $\overline{x}_{1} - x_{limit}^{u} = \frac{{2{\kern 1pt} c\left( {v + 2} \right) + \lambda \left( {v + 3} \right){\kern 1pt} - 1}}{{\left( {3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda + 2{\kern 1pt} v + 3} \right)t}} - \frac{2c}{t}$. In this case, if $c > \frac{1}{8}$, then $\overline{x}_{1} < x_{limit}^{u}$; if $c < \frac{1}{8}$, then $\overline{x}_{1} < x_{limit}^{u}$ when $\lambda < \frac{{2{\kern 1pt} c\left( {v + 1} \right) + 1}}{{3 - 14c + v(1 - 6{\kern 1pt} c)}}$ while $\overline{x}_{1} > x_{limit}^{u}$ when $\lambda > \frac{{2{\kern 1pt} c\left( {v + 1} \right) + 1}}{{3 - 14c + v(1 - 6{\kern 1pt} c)}}$.

(ii) Define $\Delta Q = Q^{d} - Q^{u} = \left( {q_{1}^{d} + q_{2}^{d} } \right) - \left( {q_{1}^{u} + q_{2}^{u} } \right)$.

If $0 < \lambda \le \hat{\lambda }^{d}$, $\Delta Q = \frac{{c^{2} }}{{2t\left( {v + 2} \right)}} > 0$.

If $\hat{\lambda }^{d} \le \lambda \le \hat{\lambda }^{u}$,$\Delta Q = \frac{1}{{2{\kern 1pt} t(v + 2)}}\left[ {c^{2} - \frac{{\left( {2cv + 5c - v - 3} \right)^{2} \left( {\lambda - \hat{\lambda }^{d} } \right)^{2} }}{{\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right)\left( {2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda + v + 1} \right)}}} \right]$. As $\hat{\lambda }^{d} = \frac{1 - c}{{3 + v - 2cv - 5c}} > \frac{1}{3 + v}$, $\Delta Q > 0$ when $c > \overline{c}_{1} = \frac{{\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1}}{{\sqrt {\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right)\left( {2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda + v + 1} \right)} + 2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda - 1}}$. Note that $\hat{\lambda }^{d} \le \lambda \le \hat{\lambda }^{u}$ implies that $\frac{{\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1}}{{3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda - 1}} \le c \le \frac{{\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1}}{{2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda - 1}}$. By comparing the lower boundary $\frac{{\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1}}{{3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda - 1}}$ with the critical value, we have that: when $\lambda \le \frac{{\left( {v + 2} \right)\left( {\sqrt {v^{2} + 4{\kern 1pt} v + 12} - v} \right) + 2}}{{2\left( {v^{2} + 7{\kern 1pt} v + 11} \right)}}$, $\Delta Q > 0$ if $c > \overline{c}_{1}$ and $\Delta Q < 0$ if $c < \overline{c}_{1}$; when $\lambda > \frac{{\left( {v + 2} \right)\left( {\sqrt {v^{2} + 4{\kern 1pt} v + 12} - v} \right) + 2}}{{2\left( {v^{2} + 7{\kern 1pt} v + 11} \right)}}$, $\Delta Q > 0$.

When $\hat{\lambda }^{u} < \lambda \le 1$, it is that $\Delta Q = \frac{1}{{2t\left( {\lambda + 1} \right)}}\left[ {\frac{{\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right)^{2} \left( {c - \lambda - 1} \right)^{2} }}{{\left( {3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda + 2{\kern 1pt} v + 3} \right)^{2} \left( {2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda + v + 1} \right)}} + \frac{{\left( {\lambda^{2} + \lambda {\kern 1pt} v + 2{\kern 1pt} \lambda - 1} \right)c^{2} }}{{\left( {v + 2} \right)\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right)}}} \right]$. Notice that $\hat{\lambda }^{u} = \frac{1 - c}{{3 - 7c + v\left( {1 - 3c} \right)}}$. If $\lambda \ge \frac{{\sqrt {v^{2} + 4{\kern 1pt} v + 8} - \left( {2 + v} \right)}}{2}$, $\Delta Q > 0$. If $\lambda < \frac{{\sqrt {v^{2} + 4{\kern 1pt} v + 8} - \left( {2 + v} \right)}}{2}$, we have that $\Delta Q > 0$ as long as $c < \overline{c}_{2} = \frac{{\sqrt {\left( {v + 2} \right)\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right)^{3} } \left( {\lambda + 1} \right)}}{{\sqrt {\left( {1 - \lambda^{2} - 2{\kern 1pt} \lambda - \lambda {\kern 1pt} v} \right)\left( {3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda + 2{\kern 1pt} v + 3} \right)^{2} \left( {2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda + v + 1} \right)} + \sqrt {\left( {v + 2} \right)\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right)^{3} } }}$. Notice that $\hat{\lambda }^{d} < \hat{\lambda }^{u} \le \lambda \le 1$ means $c \le \frac{{\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1}}{{3{\kern 1pt} \lambda {\kern 1pt} v + 7{\kern 1pt} \lambda - 1}}$. By comparing the lower bound with the critical value, we have that $\Delta Q < 0$ if $c > \overline{c}_{2}$.

Proof of Proposition 5

Given the exogenous privatization degree $\lambda$, we define $\Delta SW = SW^{d} - SW^{u}$. Even though the welfare function is complicated, it is sufficient to focus on $\lambda = 1$ which yields

$$\Delta SW|_{\lambda = 1} = SW^{d} |_{\lambda = 1} - SW^{u} |_{\lambda = 1} = \frac{{\left( {1 - 8{\kern 1pt} c} \right)\left( {253{\kern 1pt} c^{2} - 52{\kern 1pt} c - 8} \right)v - 3476{\kern 1pt} c^{3} + 1281{\kern 1pt} c^{2} + 138{\kern 1pt} c - 92}}{{6750{\kern 1pt} t\left( {v + 2} \right)^{2} }}$$

When $\frac{1}{8} < c < \frac{26 + 30\sqrt 3 }{{253}}$, the numerator increases with $v$. Hence, when $v$ is large enough, $\Delta SW|_{\lambda = 1} > 0$.

Proof of Proposition 6:

Since $\hat{\lambda }^{u} > \hat{\lambda }^{d}$, the “more privatized” region implies $\hat{\lambda }^{u} \le \lambda \le 1$. By Proposition 2,$v > \frac{{\left( {3{\kern 1pt} c - 1} \right)^{2} }}{{2{\kern 1pt} c\left( {1 - 2{\kern 1pt} c} \right)}}$. Optimal partial privatization in the “more privatized” region under uniform pricing is $\lambda^{u}$ from (12). Optimal partial privatization under discriminatory pricing follows from $\frac{{\partial SW^{d} }}{\partial \lambda } = 0$. This sign is determined by a cubic function $g(\lambda ) = \phi_{0} \lambda^{3} + \phi_{1} \lambda^{2} + \phi_{2} \lambda + \phi_{3}$ where:

$$\phi_{0} = - \left( {5{\kern 1pt} v^{2} + 25{\kern 1pt} v + 32} \right)\left( {2{\kern 1pt} v + 5} \right)^{2} c^{2} + \left( {v + 4} \right)\left( {v + 3} \right)\left( {7{\kern 1pt} v + 19} \right)\left( {2{\kern 1pt} v + 5} \right)c - 2{\kern 1pt} \left( {v + 4} \right)^{2} \left( {v + 3} \right)^{2}$$

$$\phi_{1} = - \left( {2{\kern 1pt} v + 5} \right)\left( {3{\kern 1pt} v^{3} - 7{\kern 1pt} v^{2} - 83{\kern 1pt} v - 118} \right)c^{2} + \left( {v + 4} \right)\left( {3{\kern 1pt} v^{3} - 9{\kern 1pt} v^{2} - 113{\kern 1pt} v - 179} \right)c + 4{\kern 1pt} \left( {v + 4} \right)^{2} \left( {v + 3} \right)$$

$$\phi_{2} = \left( {15{\kern 1pt} v^{3} + 55{\kern 1pt} v^{2} + 17{\kern 1pt} v - 68} \right)c^{2} - \left( {v + 4} \right)\left( {6{\kern 1pt} v^{2} + 8{\kern 1pt} v - 19} \right)c - 2{\kern 1pt} \left( {v + 4} \right)^{2}$$

$$\phi_{3} = - 3{\kern 1pt} c\left( {v + 1} \right)\left( {3{\kern 1pt} cv + 6{\kern 1pt} c - v - 4} \right) > 0$$

If $c < {\kern 1pt} \frac{{2\left( {v + 4} \right)\left( {v + 2} \right)}}{{\left( {3{\kern 1pt} v + 7} \right)\left( {3{\kern 1pt} v + 5} \right)}}$, then $sign\left\{ {\frac{{\partial SW^{d} }}{\partial \lambda }} \right\} = sign\left\{ { - g(\lambda )} \right\}$; if $c > {\kern 1pt} \frac{{2\left( {v + 4} \right)\left( {v + 2} \right)}}{{\left( {3{\kern 1pt} v + 7} \right)\left( {3{\kern 1pt} v + 5} \right)}}$, then $sign\left\{ {\frac{{\partial SW^{d} }}{\partial \lambda }} \right\} = sign\left\{ {g(\lambda )} \right\}$.

Given that $0 < c < \frac{1}{3}$ and $v > \frac{{\left( {3{\kern 1pt} c - 1} \right)^{2} }}{{2{\kern 1pt} c\left( {1 - 2{\kern 1pt} c} \right)}}$, we have $\phi_{1} > 0$ and $\phi_{2} < 0$. Moreover, we can derive the following when $\hat{\lambda }^{u} \le \lambda \le 1$: (1) if $\phi_{0} > 0$, then $g^{\prime}(\lambda ) > 0$ and $g(\hat{\lambda }^{u} ) > 0$; (2) if $\phi_{0} < 0$ and $g^{\prime}(\hat{\lambda }^{u} ) < 0$, then $g(\lambda ) < 0$; (3) if $\phi_{0} < 0$ and $g^{\prime}(\hat{\lambda }^{u} ) > 0$, then $g(\lambda )$ could be monotonically increasing with $\lambda$ or first increasing and then decreasing with $\lambda$.

By computation, under $\hat{\lambda }^{u} \le \lambda \le 1$, with the increase of v there are 4 cases: (1) when v is small $g(\lambda )$ is always non-positive; (2) when v gets larger $g(\lambda )$ is first non-positive and then non-negative and finally non-positive; (3) when v is large $g(\lambda )$ is first non-negative and then non-positive; (4) when v is large enough $g(\lambda )$ is always non-negative. Given $\hat{\lambda }^{u} \le \lambda \le 1$ and under discriminatory pricing, case (1) means $\lambda^{d} \le \lambda^{u}$. For case (2), $\lambda^{d} = \hat{\lambda }^{u} \le \lambda^{u}$ or $\lambda^{d} > \hat{\lambda }^{u}$ and $g(\lambda^{d} ) = 0$. For case (3), $g(\lambda^{d} ) = 0$. For case (4), $\lambda^{d} = 1$.

By solving $\lambda^{u} = 1$, $v < \frac{{2\left( {1 - 3{\kern 1pt} c} \right)\left( {9{\kern 1pt} c - 8} \right)}}{{26{\kern 1pt} c^{2} - 29{\kern 1pt} c + 4}}$ (when $c > 0.16$) and $v > \frac{{2\left( {1 - 3{\kern 1pt} c} \right)\left( {9{\kern 1pt} c - 8} \right)}}{{26{\kern 1pt} c^{2} - 29{\kern 1pt} c + 4}}$ (when $c < 0.16$) ensuring that $\lambda^{u} < 1$.

We identify the sign of $g(\lambda^{u} )$ under different values of c and v with the restrictions above and summarize in the following figure:

The feasible areas under the constraints are I and II. The solid line represents $g(\lambda^{u} ) = 0$. The dashed line represents $v = \frac{{2\left( {1 - 3{\kern 1pt} c} \right)\left( {9{\kern 1pt} c - 8} \right)}}{{26{\kern 1pt} c^{2} - 29{\kern 1pt} c + 4}}$. The dotted line represents $v = \frac{{\left( {3{\kern 1pt} c - 1} \right)^{2} }}{{2{\kern 1pt} c\left( {1 - 2{\kern 1pt} c} \right)}}$. Notice that when $c > 0.16$, under the constraint that $v < \frac{{2\left( {1 - 3{\kern 1pt} c} \right)\left( {9{\kern 1pt} c - 8} \right)}}{{26{\kern 1pt} c^{2} - 29{\kern 1pt} c + 4}}$ there is always $c < {\kern 1pt} \frac{{2\left( {v + 4} \right)\left( {v + 2} \right)}}{{\left( {3{\kern 1pt} v + 7} \right)\left( {3{\kern 1pt} v + 5} \right)}}$. Therefore, in area I $g(\lambda^{u} ) < 0$ and $\lambda^{d} < \lambda^{u}$. In area II $g(\lambda^{u} ) > 0$ and $\lambda^{d} > \lambda^{u}$. By solving $\mathop {\lim }\limits_{v \to + \infty } g(\lambda^{u} ;v,c) = 0$, we have the root $\underline {c} \approx 0.13$, which means that when $c < \underline {c}$, all pairs (c,v) are located in area I and thus $\lambda^{d} < \lambda^{u}$. When $c > \underline {c}$, (c,v) are located in area I when $v$ is small ($\lambda^{d} < \lambda^{u}$) but in area II when $v$ is large enough ($\lambda^{d} > \lambda^{u}$).

Proof of Proposition 7

When optimal privatization is in the “less privatized” region for both schemes, $\lambda^{u} \le \hat{\lambda }^{d}$ and $\lambda^{d} \le \hat{\lambda }^{d}$, then $\Delta SW_{1} = SW^{u,c} - SW^{d,c} = \frac{{c^{3} \left( {v + 1} \right)}}{{6{\kern 1pt} \left( {v + 2} \right)^{2} t}} > 0$.

When the optimal partial privatization is in the “more privatized” region under discriminatory pricing but in the “less privatized” region under uniform pricing,$\hat{\lambda }^{d} \le \lambda^{u} < \hat{\lambda }^{u}$ and $\hat{\lambda }^{d} \le \lambda^{d} < \hat{\lambda }^{u}$, uniform pricing is socially preferable. To see this,

define $\Delta SW_{2} = SW^{d,uc} - SW^{d,c} = \frac{{\left( {2{\kern 1pt} c\lambda {\kern 1pt} v + 5{\kern 1pt} c\lambda - \lambda {\kern 1pt} v - c - 3{\kern 1pt} \lambda + 1} \right)^{2} }}{{6{\kern 1pt} t\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right)^{2} \left( {v + 2} \right)^{2} \left( {2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda + v + 1} \right)^{2} }} \cdot \psi_{1}$.$\psi_{1} = \left( \begin{gathered} 8{\kern 1pt} \lambda^{2} v^{3} + 60{\kern 1pt} \lambda^{2} v^{2} + 3{\kern 1pt} \lambda {\kern 1pt} v^{3} + 150{\kern 1pt} \lambda^{2} v + 10{\kern 1pt} \lambda {\kern 1pt} v^{2} \hfill \\ + 125{\kern 1pt} \lambda^{2} - 4{\kern 1pt} \lambda {\kern 1pt} v - 3{\kern 1pt} v^{2} - 26{\kern 1pt} \lambda - 10{\kern 1pt} v - 7 \hfill \\ \end{gathered} \right)c - \left( {\lambda {\kern 1pt} v^{2} + 8{\kern 1pt} \lambda {\kern 1pt} v + 13{\kern 1pt} \lambda + v + 1} \right)\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right)$ Note that: $c\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right) - \left( {2{\kern 1pt} c\lambda {\kern 1pt} v + 5{\kern 1pt} c\lambda - \lambda {\kern 1pt} v - c - 3{\kern 1pt} \lambda + 1} \right) = - 1 - \left( {cv + 2{\kern 1pt} c - v - 3} \right)\lambda$. At $\lambda = \hat{\lambda }^{d}$, it equals $- \frac{{c^{2} \left( {v + 2} \right)}}{{2{\kern 1pt} cv + 5{\kern 1pt} c - v - 3}} > 0$. Hence when $\hat{\lambda }^{d} \le \lambda < \hat{\lambda }^{u}$, $c\left( {\lambda {\kern 1pt} v + 3{\kern 1pt} \lambda - 1} \right) > \left( {2{\kern 1pt} c\lambda {\kern 1pt} v + 5{\kern 1pt} c\lambda - \lambda {\kern 1pt} v - c - 3{\kern 1pt} \lambda + 1} \right)$.

Since $\psi_{1} - c\left( {v + 1} \right)\left( {2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda + v + 1} \right)^{2}$ is still a linear function with c, we can specify the sign by computing the value at $c = 0$ and $c = 1/3$. Both are negative and thus $\psi_{1} < c\left( {v + 1} \right)\left( {2{\kern 1pt} \lambda {\kern 1pt} v + 5{\kern 1pt} \lambda + v + 1} \right)^{2}$.

Therefore, when $\hat{\lambda }^{d} \le \lambda < \hat{\lambda }^{u}$, $\Delta SW_{1} > \Delta SW_{2} \Rightarrow SW^{u,c} > SW^{d,uc}$.

When optimal privatization is in the “more privatized” region for both schemes, $\lambda^{u} \ge \hat{\lambda }^{u}$ and $\lambda^{d} \ge \hat{\lambda }^{u}$, we compute $\Delta SW_{3} = SW_{opt}^{u,uc} - SW_{opt}^{d,uc}$, where the footnote “opt” means “optimized results”. We can derive a closed form $\lambda^{u}$ as in the paper but a much more complicated closed form $\lambda^{d}$ by solving a cubic equation.

Under both pricing policies, optimal privatization, increases with upstream cost $c$ and downstream cost convexity $v$. Therefore, letting v go to infinity, there are two cases: (i) full privatization is optimal; (ii) partial privatization is optimal.

In the first case when both are fully privatized, the result is.

$\Delta SW_{3} = SW_{\lambda = 1}^{u,uc} - SW_{\lambda = 1}^{d,uc} = \frac{{\left( {8{\kern 1pt} c - 1} \right)\left( {253{\kern 1pt} c^{2} - 52{\kern 1pt} c - 8} \right)v + 3476{\kern 1pt} c^{3} - 1281{\kern 1pt} c^{2} - 138{\kern 1pt} c + 92}}{{6750{\kern 1pt} \left( {v + 2} \right)^{2} t}}$.

When $0 < c < 1/3$, $3476{\kern 1pt} c^{3} - 1281{\kern 1pt} c^{2} - 138{\kern 1pt} c + 92 > 0$. Therefore, $\Delta SW_{3} < 0$ when $\frac{1}{8} < c < \frac{26 + 30\sqrt 3 }{{253}} \approx 0.308$ and v is large enough.

When privatization is partial under both pricing schemes,$\mathop {\lim }\limits_{v \to + \infty } \lambda^{u} = \frac{{9{\kern 1pt} c^{2} - \sqrt {\left( {9{\kern 1pt} c^{2} - 2{\kern 1pt} c + 1} \right)\left( {3{\kern 1pt} c - 1} \right)^{2} } - 8{\kern 1pt} c + 1}}{{9{\kern 1pt} c - 2}}$ and $\mathop {\lim }\limits_{v \to + \infty } \lambda^{d} = \frac{{3{\kern 1pt} c}}{{2 - 10{\kern 1pt} c}}$. $0 < \mathop {\lim }\limits_{v \to + \infty } \lambda^{u} < 1$ when $0 < c < \frac{{29 - 5{\kern 1pt} \sqrt {17} }}{52} \approx 0.161$ and $0 < \mathop {\lim }\limits_{v \to + \infty } \lambda^{d} < 1$ when $0 < c < \frac{2}{13} \approx 0.154$. In this case, when v goes to positive infinity, we have:

$$\begin{gathered} sign\left\{ {\Delta SW_{3} } \right\} = sign\left\{ {SW_{{\lambda = \lambda^{u} }}^{u,uc} - SW_{{\lambda = \lambda^{d} }}^{d,uc} } \right\} \\ = sign\left\{ {\frac{1}{2 - 9c}\left[ \begin{gathered} \left( {12150{\kern 1pt} c^{5} - 9585{\kern 1pt} c^{4} + 3123{\kern 1pt} c^{3} - 657{\kern 1pt} c^{2} + 80{\kern 1pt} c - 4} \right)\sqrt {9{\kern 1pt} c^{2} - 2{\kern 1pt} c + 1} \hfill \\ + 36450{\kern 1pt} c^{6} - 32805{\kern 1pt} c^{5} + 14364{\kern 1pt} c^{4} - 4348{\kern 1pt} c^{3} + 801{\kern 1pt} c^{2} - 84{\kern 1pt} c + 4 \hfill \\ \end{gathered} \right]} \right\} \\ \end{gathered}$$

Hence, when v goes to positive infinity $0 < c < 0.130$ means $SW_{{\lambda = \lambda^{u} }}^{u,uc} > SW_{{\lambda = \lambda^{d} }}^{d,uc}$ and $0.130 < c < 0.154$ means $SW_{{\lambda = \lambda^{u} }}^{u,uc} < SW_{{\lambda = \lambda^{d} }}^{d,uc}$.

When $0.130 < c < 0.308$, if v is small (e.g. $v \to \frac{{\left( {3{\kern 1pt} c - 1} \right)^{2} }}{{2{\kern 1pt} c\left( {1 - 2{\kern 1pt} c} \right)}}$), $\Delta SW_{3} = SW_{\lambda = \lambda }^{u,uc} - SW_{\lambda = \lambda }^{d,uc} > 0$ for any $\lambda \in (0,1)$ and $0 < c < 1/3$. By simulating $\Delta SW_{3} = SW_{opt}^{u,uc} - SW_{opt}^{d,uc}$ we have that $\Delta SW_{3} = SW_{opt}^{u,uc} - SW_{opt}^{d,uc} < 0$ only when v is large but $\Delta SW_{3} = SW_{opt}^{u,uc} - SW_{opt}^{d,uc} > 0$ when v is small.