Alternative forms of buyer power in a vertical duopoly: implications for profits, welfare, and cost pass-through

Abstract

We examine the implications of different ways in which downstream firms can exercise buyer power over their upstream suppliers. We derive several variations of a model in which two upstream firms supply a differentiated product under exclusive contracts to two downstream firms which compete in prices in the retail market. We begin with a benchmark model (upstream first-mover pricing), and then compare its outcomes with those of models that feature different modes of exercising buyer power: downstream first-mover pricing; Nash Bargaining with linear and two-part tariffs; and vertical integration. We rank these five regimes in terms of wholesale and retail prices, social welfare, the pass-through rates of changes in upstream costs, and downstream firms’ profits. We show under what conditions more powerful downstream firms benefit consumers by exercising ‘countervailing power’ against upstream suppliers. We also show that the lump-sum component of the two-part tariff can go in either direction (a slotting allowance or a franchise fee), depending in a very precise way only on parameters representing bargaining power and the degree of product differentiation. Exactly the same configuration of these parameters is shown to determine the ranking of wholesale and retail prices, pass-through rates, and downstream profits, as between the Nash Bargaining regimes with linear and two-part tariffs. Finally, we show that downstream firms which possess buyer power always prefer vertical arrangements that are socially sub-optimal.

1 Introduction

In the theory of industrial organization, models of vertical structure traditionally emphasized the power of large upstream producers over small downstream retailers. More recently, however, the focus has shifted to buyer power in vertical relations. With large retailers, there is a change in the structure of power in a supply chain. Such firms may exercise monopsony power in input markets as well as monopoly power in output markets.¹ They can depress the prices of the products supplied to them by upstream firms, but they may not pass on these lower prices to consumers.

In this paper, we explore the consequences of buyer power in a model of bilateral duopoly with exclusive trading within each vertical pair of firms. We first obtain the equilibrium values of output, prices, and upstream and downstream profits when upstream sellers are first movers in setting prices. Treating this as a benchmark, we then derive the corresponding results for four types of vertical arrangements representing different modes of exploiting buyer power in the same setting: downstream first-mover pricing; Nash Bargaining between upstream and downstream firms, alternatively with linear and two-part tariffs; and vertical integration. These results enable us to obtain a complete ranking of wholesale and retail prices, consumer surplus, social welfare, and the pass-through rates of changes in upstream input costs into downstream prices, over these five vertical arrangements. We thus contribute to the literature on the circumstances under which the “countervailing power” of powerful downstream retailers can benefit consumers.²

We also derive a result which shows how the direction of the lump-sum component of the two-part tariff depends in a simple and intuitively appealing way only on parameters representing the relative bargaining power of upstream and downstream firms and the degree of product differentiation. Quite remarkably, it turns out that exactly the same condition determines the ranking of wholesale and retail prices, pass-through rates, and downstream profits as between the linear and two-part tariff regimes. For four of our five regimes, we also derive a clear ranking of downstream firms’ profits which is conditional on the same two parameters. We show that downstream firms always prefer vertical arrangements that are inferior in terms of welfare. To the best of our knowledge, no earlier contribution has compared these vertical arrangements from these multiple perspectives. One further contribution of our paper is to draw attention to similar results that have appeared in economics and management journals, which seldom cite each other. Some of these results emerge as special cases of our model.

In relation to earlier literature, our benchmark case is similar to that of McGuire and Staelin (1983), who studied the effect of product substitutability on Nash equilibrium distribution structures, when upstream manufacturers are first movers. Like our model, they also assumed a bilateral duopoly in which each manufacturer sells its good through a single exclusive retailer, with price competition and linear demand. They found that when products are highly differentiated, each manufacturer distributes through its own company store, i.e. it is vertically integrated. But when products are very similar, they prefer franchised outlets (a decentralized or vertically separated structure). In the economics literature, this idea was developed independently by Bonanno and Vickers (1988) and Lin (1990), using different specifications of demand for differentiated products, in a similar setting of rival supply chains.

These early papers showed that both manufacturers are better off with vertical separation. This is because a vertically integrated firm will maximize profits with respect to its upstream marginal costs, whereas separation induces manufacturers to set their wholesale prices above marginal costs. This makes it credible for their retailers to set higher prices that enable them to exploit the strategic complementarity of prices under Bertrand competition in the final goods market. That is, manufacturers strategically delegate pricing authority to their retailers in order to commit to a ‘puppy dog’ strategy (Fudenberg and Tirole 1984). In our study, we compare the outcomes of this regime with four others in which downstream firms use different methods of exploiting buyer power.

The first such regime we model is when downstream firms exercise first-mover advantage by committing to their retail markups, anticipating the optimal reactions of the upstream firms. In a similar setting, but using different specifications of demand, Zhang et al (2012) compare only upstream vs downstream first-movers, while Wang et al (2016) compare fixed vs percentage markups. Using a demand specification that is standardly used in the economics literature, we compare the outcomes of upstream and downstream first-mover advantage with three other modes of exercising buyer power.

Upstream first-mover models assume that firms exploit their first-mover advantage to impose “take it or leave it” offers on the weaker downstream firms. Some authors (e.g., Bonanno and Vickers 1988; Gal-Or 1991) additionally assumed that the upstream firms can extract the entire producer surplus of the downstream firms through a fixed franchise fee, by auctioning exclusive franchises to one out of many competing potential distributors. This two-part tariff maximizes the profits of the entire vertical chain by aligning the incentives of the upstream and downstream firms. Shaffer (1991) inverted this insight in a model in which differentiated retailers can extract the entire upstream profit by auctioning scarce retail space to many competing upstream firms who produce a homogenous product. Again, the entire channel profit is appropriated by the more powerful party.

A Nash Bargaining (NB) solution to the contractual terms between upstream and downstream firms in a vertical chain is more general because it allows for different degrees of bargaining power, with “take it or leave it” offers as special cases when all bargaining power is upstream or downstream. Horn and Wolinsky (1988) were the first to apply NB to the determination of a linear wholesale price in this context. The more recent literature has extended it to bargaining between agents on both wholesale price and franchise fee, but it is concerned with issues such as incentives for investment (Wang et al 2010; Chen 2019; Alipranti and Petrakis 2022), horizontal mergers (Milliou and Petrakis 2007; Symeonidis 2010; Gaudin 2018), the degree of downstream collusion (Buccella and Fanti 2022), or the comparison between price and quantity competition between downstream firms (Basak and Wang 2016; Alipranti and Petrakis 2020; Wang and Li 2020; Din and Sun 2023). We also use NB to determine the pricing contract between upstream and downstream firms, but we are focusing on how different degrees of buyer power can alter profit allocation and consumer welfare. We contrast the results when upstream and downstream firms bargain over both the wholesale price and a lump-sum transfer (a two-part tariff), or just the wholesale price (a linear tariff).

Finally, we derive outcomes when the upstream and downstream firms in each supply chain merge into a vertically integrated unit. This is a standard single-tier duopoly model. However, instead of assuming that the entire channel profit accrues to the formerly upstream firms, as in the foundational papers cited above, we enable comparison of outcomes under vertical integration with those of our earlier models by assuming that the profits of an integrated firm are distributed to the shareholders of its erstwhile upstream and downstream constituents according to the same bargaining power parameter as in our NB models.

The paper proceeds as follows. In Sect. 2, we first motivate the vertical structure and the assumptions regarding costs and demand which we maintain throughout the paper. This is followed by an exposition and derivation of the equilibrium outcomes of the benchmark model and the four regimes with buyer power. Section 3 ranks these outcomes in respect of wholesale and retail prices, social welfare, pass-through rates of upstream costs into retail prices, and downstream profits. Section 4 summarizes and concludes the paper.

2 The model

2.1 Model structure and assumptions

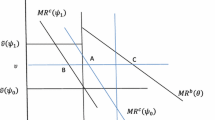
We assume two identical upstream agents selling a differentiated product to two identical downstream firms under exclusive bilateral contracts of different types, so there is no market for this product. This structure is illustrated in Fig. 1. By suitable choice of units, we assume that each downstream firm uses one unit supplied by an upstream agent to produce one unit of the final good. Downstream firms sell these horizontally differentiated products to consumers, but do not provide any retailing services (for example, demonstration of the product). This allows us to assume that downstream costs are zero. It also abstracts from the problem of horizontal and vertical externalities arising from retailers’ sales efforts, allowing us to focus on comparing the effects of buyer power in different kinds of relationships between upstream and downstream firms.³

Fig. 1

Bilateral duopoly with exclusive trading

This market structure is quite common in the literature, and has been motivated in different ways. One formulation treats the upstream agents as plant-specific labor unions whose objective function is to maximize their members’ wage bill (e.g. Horn and Wolinsky 1988; Symeonidis 2010). Workers at one plant cannot work at the other, due to the distance between plants, relationship-specific investments, or an agreement with the employing firm that no non-union member can be employed. However, our analysis includes two-part tariffs and vertical integration, which are not compatible with the interpretation of upstream agents as unions. A more reasonable justification for the structure is to interpret the upstream firms as manufacturers and downstream firms as retailers with scarce shelf space. Each retailer can stock the product of at most one upstream manufacturer. Scarce space can be allotted to the manufacturer who pays the highest ‘slotting allowance’ (Shaffer 1991). Alternatively, according to Lin (1990), a retailer who is selling the product of one upstream firm will not want to switch to the other supplier, because then it will be competing against the other retailer for the same product (intra-brand competition), which will result in the Bertrand Paradox with zero profits.

A different explanation of bilateral duopoly, in which downstream firms are manufacturers rather than retailers, is as follows. Each upstream manufacturer produces a different specialized intermediate input which is further processed or assembled by a particular downstream manufacturer that sells directly to consumers. Each vertical pair may specialize its technology or product with relationship-specific investments, so an upstream or downstream firm cannot switch to another buyer or supplier, respectively. Even if the downstream firm provides the upstream firm with equipment and raw materials to produce a good that is not relationship-specific, the downstream firm would not like its supplier to sell it to a rival. It may then impose an exclusive supply contract.

Whatever the underlying justification for assuming bilateral duopoly, we denote the upstream manufacturers as U₁ and U₂, and the downstream duopolists (which may be manufacturers or retailers) as D₁ and D₂. We assume that the terms of a contract involving the i^th supply chain will specify w_i, the wholesale price. In our Nash Bargaining regime with a two-part tariff, we have a contract of type (w_i, S_i) where S_i is the slotting allowance, a fixed amount independent of number of units sold. It can be regarded as the mirror image of a franchise fee paid by the downstream firm to the upstream firm.⁴ We assume that the contract of each vertical pair cannot be renegotiated and is observable by the rival pair.⁵ Finally, downstream firms compete by simultaneously setting prices, i.e. as a Bertrand duopoly in differentiated products. The i^th downstream firm will sell its product to final consumers at a price of p_i. Cost and demand functions are common knowledge.

Consumers’ demand for the final good is linear, as in Singh and Vives (1994) with a slight change in notation (Wang et al 2016):

$${q}_{i}=a-{p}_{i}+\gamma {p}_{j} \quad {\text{i}},\mathrm{ j }=\mathrm{ 1,2}; \, {\text{a}}>0$$

(1)

Here, q_i is the quantity of good i sold by downstream firm i at price p_i, while p_j is the price of the good sold by downstream firm j. The coefficient of p_i is negative, confirming the inverse relationship between price of good i and quantity of good i. The coefficient of p_j is positive, indicating that the goods are demand substitutes. In Appendix 1 we have shown how the above direct demand function can be obtained from an inverse demand function, which is in turn derived from a standard quasi-linear utility function. Appendix 1 also shows how the following interpretations and assumptions in regard to our direct demand specification correspond to the inverse demand functions.

Product differentiation and inter-brand substitutability are captured by parameter γ in the direct demand function, with $\gamma \in [0, 1)$. When γ approaches 1, products are close to perfect substitutes.⁶ When γ = 0, the demand function reduces to ${q}_{i}=a-{p}_{i}$, which shows that products are demand independent.

Each upstream manufacturer is assumed to have constant and identical marginal costs $c$∊ (0, a). We assume it to be strictly positive to prevent the price of the goods from falling to zero, which would lead to the same result as the case of demand independence in Eq. (1) if ${p}_{j}=0$.

2.2 Benchmark model

The stages of the game in our benchmark case are as follows: In stage 1, each upstream firm contracts with a downstream firm over a wholesale price w. In stage 2, downstream firms simultaneously set their strategic variable (retail price) after having observed the wholesale prices faced by their competitors. We solve this model by backward induction, starting with stage 2. Since firms at each level of the supply chain are identical, we work out all solutions from the perspective of representative chain 1. We first write downstream firm 1’s profit function as:

$${\uppi }^{{\text{D}}1}= \left({{p}_{1}-w}_{1}\right){q}_{1}$$

When we differentiate this firm’s profit function with respect to p₁, we get the following first order condition

$$\frac{\partial {\pi }^{D1}}{\partial {p}_{1}}={q}_{1}+\left({{p}_{1}-w}_{1}\right)\left(-1\right)=0$$

On solving this we get the best response function

$$\frac{a+\gamma {p}_{2}{+w}_{1}}{2}={p}_{1}$$

(2)

A similar expression holds for firm 2. Solving simultaneously, we get

$$\frac{a(2+\gamma ){+(2w}_{1}+\gamma {w}_{2})}{4-{\gamma }^{2}}={p}_{1}$$

(3)

In stage 1, we maximize the related upstream firm’s profit function given the prices and quantities from the above equations:

$$\pi^{U1} = \left( {w_{1} - c} \right)q_{1}$$

$$\begin{aligned} \frac{{\partial \pi^{U1} }}{{\partial {\text{w}}_{1} }} & = { }\frac{{\partial {\text{q}}_{1} }}{{\partial {\text{w}}_{1} }}\left( {w_{1} - c} \right) + {\text{q}}_{1} = 0 \\ & = \frac{{\partial q_{1} }}{{\partial p_{1} }}*\frac{{\partial p_{1} }}{{\partial w_{1} }}\left( {w_{1} - c} \right) + q_{1} \\ \end{aligned}$$

$$\frac{{\partial \pi^{U1} }}{{\partial w_{1} }} = \frac{{\left( {{\upgamma }^{2} - 2} \right)\left( {w_{1} - c} \right)}}{{4 - {\upgamma }^{2} }} + \frac{{2a + a{\upgamma } - 2w_{1} + {\upgamma }^{2} {\text{w}}_{1} + {\gamma w}_{2} }}{{4 - {\upgamma }^{2} }} = 0$$

$$w_{1} = \frac{{a\left( {2 + {\upgamma }} \right) + {\gamma w}_{2} + c\left( {2 - {\upgamma }^{2} } \right)}}{{4 - 2{\upgamma }^{2} }}$$

(4)

A similar expression holds for firm 2.⁷ Solving these best response functions simultaneously gives us

$$w_{1}^{*} = \frac{{a\left( {2 + {\upgamma }} \right) + c\left( {2 - {\upgamma }^{2} } \right)}}{{4 - 2{\upgamma }^{2} - {\upgamma }}};\;w_{2}^{*} = \frac{{a\left( {2 + {\upgamma }} \right) + c\left( {2 - {\upgamma }^{2} } \right)}}{{4 - 2{\upgamma }^{2} - {\upgamma }}}$$

When we substitute these wholesale prices into the demand functions,we get the equilibrium prices, quantities and profits as given in Table 1.

Table 1 Comparison of equilibrium outcomes

2.3 Alternative vertical regimes with buyer power

2.3.1 Downstream firms’ first-mover pricing model

In this model we have two sequential steps, reversing the order of moves of the benchmark model. Now the downstream firms are leaders while the upstream firms are followers. In stage 1, both downstream firms simultaneously announce that the retail price p_i will be a markup m_i over whatever wholesale price w_i the upstream firm might subsequently charge, so ${p}_{i}={w}_{i}+{m}_{i}$. Each downstream firm sets its markup in stage 1 and remains committed to it after it receives goods from its upstream supplier in stage 2, because it is not profitable to deviate to any other retail price which maximizes its profits. In stage 2, anticipating the retail price p_i, each upstream firm determines its optimal wholesale price w_i. We find the equilibrium solution by using backward induction.

Profit functions of the upstream and downstream firms are as follows:

$${\uppi }_{{\text{i}}}^{{{\text{D}}}^{*} }= \left({{p}_{i}-w}_{i}\right){q}_{i} \quad {\text{i}}=\mathrm{1,2}$$

(5)

$${\uppi }_{{\text{i}}}^{{{\text{U}}}^{*} }= \left({w}_{i} -c\right){q}_{i} \quad {\text{i}}=\mathrm{1,2}$$

(6)

Using backward induction, beginning with stage 2 of the game we first maximize upstream firm 1’s profit with respect to wholesale price and get the following first order condition:

$$\begin{aligned} \frac{{\partial \pi^{U1} }}{{\partial w_{1} }} & = { }\frac{{\partial q_{1} }}{{\partial w_{1} }}\left( {w_{1} - c} \right) + q_{1} = 0 \\ & = \frac{{\partial q_{1} }}{{\partial p_{1} }}*\frac{{\partial p_{1} }}{{\partial w_{1} }}\left( {w_{1} - c} \right) + q_{1} \\ & = a - p_{1} + \gamma p_{2} - \left( {w_{1} - c} \right) = 0 \\ \end{aligned}$$

(since ${p}_{1}={w}_{1}+{m}_{1}$ and ${q}_{1}=a-{p}_{1}+\gamma {p}_{2}$). Rearranging terms and using symmetry,

$$w_{i} = \frac{{a - m_{i} + \gamma \left( {m_{j} + w_{j} } \right) + c}}{2}$$

Solving simultaneously gives us optimal wholesale prices for given downstream markups:

$${w}_{i}=\frac{\left(a+c\right)\left(2+\gamma \right)-{m}_{i}(2-{\gamma }^{2})+{m}_{j}\gamma }{4-{\gamma }^{2}}$$

(7)

Now, since $q_{i} = a - p_{i} + \gamma p_{j}$ and $p_{i} = m_{i} + w_{i}$, we can redefine quantity as a function of markups for firm 1: ${q}_{1}=a-{w}_{1}-{m}_{1}+\gamma {w}_{2}+\gamma {m}_{2}$. Substituting ${w}_{1}$ from Eq. (7) and simplifying,

$${q}_{1}= \frac{\left(2+\gamma \right)\left[a-\left(1-\gamma \right)c\right]-(2-{\gamma }^{2}){m}_{1}+\gamma {m}_{2} }{4-{\gamma }^{2}}$$

(8)

We now move to stage 1 of the game. Differentiating firm 1’s downstream profits from (5) with respect to m₁ gives the first order condition:

$$\frac{\partial {\pi }^{D1}}{\partial {m}_{1}}={m}_{1}\frac{\partial {q}_{1}}{\partial {m}_{1}}{+ q}_{1}=0$$

(9)

From Eq. (8), we get,

$$\frac{\partial {q}_{1}}{\partial {m}_{1}}=\frac{{\gamma }^{2}-2}{4-{\gamma }^{2}}$$

(10)

Substituting Eqs. (8) and (10) into Eq. (9) gives us

$$\frac{\partial {\pi }^{D1}}{\partial {m}_{1}}={m}_{1} \frac{{\gamma }^{2}-2}{4-{\gamma }^{2}}+ \frac{\left(2+\gamma \right)\left[a-\left(1-\gamma \right)c\right]-(2-{\gamma }^{2}){m}_{1}+\gamma {m}_{2} }{4-{\gamma }^{2}} =0$$

Solving this for ${m}_{1}$ and using symmetry finally gives us the equilibrium downstream markups:

$${m}_{i}^{*}= \frac{\left(2+\gamma \right)[a-\left(1-\gamma \right)c]}{(4-2{\gamma }^{2}-\gamma )} \, {\text{i}}=\mathrm{1,2}$$

Substituting these into the expressions for prices, quantities and profits gives the equilibrium values in Table 1. It is interesting to note that equilibrium prices and quantities of final goods in this regime and in the benchmark model are same, while upstream firms’ equilibrium wholesale prices are different. This means that the difference in the two models’ equilibrium values is due to difference in margins. Comparison between the two regimes shows that margins are higher for downstream firms if they are first movers. The following simple Lemma will be used to prove this result, and repeatedly thereafter⁸:

Lemma 1

$\left({{a}}-\left(1-\gamma \right){{c}}\right)>0$

Proof

We must have $a>c$ for production to be viable. Since by assumption 0 $\le\upgamma <1 ,$ $0<\left(1-\upgamma \right)\le 1$. Therefore, $\left(a-\left(1-\upgamma \right)c\right)>0.$ Hence proved.

We henceforth denote the benchmark and downstream first-mover models by B and FM, respectively.

Lemma 2

${{{w}}}_{\rm{i},\rm{B}}^{{*}}>{{{w}}}_{\rm{i},\rm{F}\rm{M}}^{{*}}$

Proof

${w}_{{\text{i}},{\text{B}}}^{*} - {w}_{{\text{i}},{\text{FM}}}^{*}=\frac{2\left(a-\left(1-\upgamma \right)c\right)}{\left(4-2{\upgamma }^{2}-\upgamma \right)\left(2-\gamma \right)}>0$

The denominator of this expression is positive, as $\left(2-\upgamma \right)>0 \,\text {and} \,\left({4-2\upgamma }^{2}-\upgamma \right)>0\, \mathrm{ for} \,\gamma <1$. In the numerator, $\left(a-\left(1-\upgamma \right)c\right)>0$ by Lemma 1. Hence proved.

Since the equilibrium retail prices are the same in the two regimes, the reverse must hold for the margins of the downstream firms, i.e., ${m}_{i,FM}^{{D}^{*}}>{m}_{i,B}^{{D}^{*}}$. Thus, the reversal in order of moves only changes the division of a given level of profits between the upstream and downstream firms, without affecting consumers. The firms that are first movers make higher profits (see the last row of Table 1). In this setting, buyer power for downstream firms does not countervail seller power of upstream firms as far as consumers are concerned.

2.3.2 Nash bargaining models

2.3.2.1 Linear tariffs

Extensive form: In stage 1, each upstream firm contracts with a downstream firm through simultaneous bilateral bargains where upstream and downstream firm i bargain over wholesale price w. Relative bargaining power of upstream firms is μ $\in [0, 1]$ and downstream firms is 1-μ. In stage 2, downstream firms simultaneously set their strategic variable (retail price) after having observed the wholesale prices faced by their competitors.⁹

We begin with stage 2 in which downstream firms simultaneously set retail prices using consumers’ final demand, which was already worked out in the benchmark case. From their optimization problem we get retail prices as functions of wholesale prices which leads us to stage 1 of the game, where the equilibrium of bargaining between upstream firm 1 and downstream firm 1 over wholesale price w₁ is given by the following maximization problem:

$$\underset{{w}_{1}}{{\text{argmax}}}({\pi }_{1}^{U}-{{\pi }_{0}^{U})}^{\mu } ({\pi }_{1}^{D}-{{\pi }_{0}^{D})}^{1- \mu }$$

(11)

For simplicity, we assume disagreement payoffs ${\pi }_{0}$ of both upstream and downstream firms equal to zero, which is reasonable given our vertical structure in which neither has an alternative trading partner. First order conditions on maximizing (11) for w₁ gives:

$$\frac{{\frac{{\partial \pi_{1}^{D} }}{{\partial w_{1} }}}}{{\frac{{\partial \pi_{1}^{U} }}{{\partial w_{1} }}}} = \frac{{\mu \left( {p_{1} - w_{1} } \right)}}{{\left( {\mu - 1} \right)\left( {w_{1} - c} \right)}}$$

On simplifying we get,

$$\begin{gathered} \frac{{2\left( {\frac{{\partial p_{1} }}{{\partial w_{1} }} - 1} \right)}}{{\left( {p_{1} - w_{1} } \right) + \left( {w_{1} - c} \right)\left( {\frac{{\partial p_{1} }}{{\partial w_{1} }} - 1} \right)}} = \frac{\upmu }{{\left( {\upmu - 1} \right)\left( {w_{1} - c} \right)}} \hfill \\ w_{1} = \frac{{a\upmu \left( {2 + \gamma } \right) + \upmu \gamma w_{2} + c\left( {\gamma ^{2} - 2} \right)\left( {\upmu + 2} \right)}}{{2\left( {\gamma ^{2} - 2} \right)}} \hfill \\ w_{2} = \frac{{a\upmu \left( {2 + \gamma } \right) + \upmu \gamma w_{1} + c\left( {\gamma ^{2} - 2} \right)\left( {\upmu + 2} \right)}}{{2\left( {\gamma ^{2} - 2} \right)}} \hfill \\ \end{gathered}$$

On substituting ${w}_{2}$ in ${w}_{1}$, and further into the expressions for prices and quantities, we get the equilibrium values of the endogenous variables reported in Table 1.

In (11), if we take $\mu =$ 1, the expression reduces to $\mathop {{\text{argmax}}}\limits_{w1 } (\pi_{1}^{U} - \pi_{0}^{U} )$, which is the same as the maximization problem of an upstream firm under the benchmark regime, and the resulting equilibrium prices and quantities are also the same. This confirms that the benchmark model corresponds to the NB model with a linear tariff when all bargaining power is with the upstream firm. At the other extreme, when all bargaining power is with the downstream firm $(\mu =0)$, it enforces marginal cost pricing (w* = c) on its supplier to extract the entire channel profit. The equilibrium price will be same as for vertical integration, as in Shaffer (1991, Proposition 1). This amounts to a contract of ‘wholesale price maintenance’, which is the mirror image of the familiar retail price maintenance imposed by powerful upstream firms on powerless retailers.

We henceforth use NB1 for the Nash Bargaining case with a linear tariff, to distinguish it from the case with a two-part tariff which we shall derive below and denote as NB2. On differentiating the ${p}_{1,NB1}^{*}$ derived above with respect to $\mu$ we get a positive relationship:

$$\frac{\partial {p}_{1,NB1}^*}{\partial \mu }= \frac{2\left(2+\gamma \right)\left(a-c(1-\gamma )\right)\left(2-{\gamma }^{2}\right)}{(2-\gamma ){(2{\gamma }^{2}+\gamma \mu -4)}^{2}}>0$$

This implies that, starting with the benchmark case with $\mu =1$, retail prices vary inversely with downstream bargaining power, decreasing to the level of upstream costs when $\mu =0$. This confirms the existence of countervailing power exercised by downstream firms in the NB1 regime.

2.3.2.2 Non-linear (Two-part) tariffs

Extensive form: Now in stage 1, each upstream firm simultaneously bargains with a downstream firm to arrive at a contract which specifies a wholesale price w and slotting allowance S. As before, relative bargaining power of an upstream firm is μ and downstream firm is 1-μ. In stage 2, downstream firms simultaneously set their strategic variable (retail price) after having observed the wholesale prices faced by their competitors. Stage 2 is solved exactly as in the linear tariff case, yielding retail prices as a function of wholesale prices. This leads us to stage 1 of the game, where bargaining between upstream firm 1 and downstream firm 1 is over the wholesale price w₁ and slotting allowance S₁. The equilibrium is given by the following maximization problem:

$$\mathop {argmax }\limits_{{w_{1} ,S_{1} }} \left( {\pi_{1}^{U} - \pi_{0}^{U} } \right)^{\mu } \left( {\pi_{1}^{D} - \pi_{0}^{D} } \right)^{1 - \mu }$$

(12)

In this case also, we take disagreement payoffs of both upstream firm and downstream firm equal to zero. First order conditions on maximizing (12) for w₁ and S₁ give (see Appendix 2 for proofs):

$$\frac{{\partial \pi_{1}^{D} }}{{\partial w_{1} }} + \frac{{\partial \pi_{1}^{U} }}{{\partial w_{1} }} = 0$$

(13)

$$S_{1} = \left( {1 - \mu } \right)\pi^{Ua} - \mu \pi^{Da}$$

(14)

where $\pi^{Ua}$ is profit of an upstream firm excluding slotting allowance, and similarly $\pi^{Da}$ is downstream firm’s profit excluding slotting allowance. $\pi^{Ua} - S$ gives us $\pi_{1}^{U}$, the upstream firm’s total profit, and $\pi^{Da} + S$ gives $\pi_{1}^{D}$, the downstream firm’s total profit. Thus,

$$\pi^{Ua} = \left( {w - c} \right)q;{ }\pi^{Da} = \left( {p - w} \right)q$$

$$\pi_{i}^{D} = \left( {p_{i} - w_{i} } \right)q_{i} + S_{i} ; \pi_{i}^{U} = \left( {w_{i} - c} \right)q_{i} - S_{i} \quad {\text{i = 1,2}}$$

When we solve these first order conditions for the optimal wholesale price, we get

$$w_{i}^{*} = \frac{{a\gamma^{2} + c\left( {2 - \gamma^{2} )(2 - \gamma } \right)}}{{\left( {4 - 2\gamma - \gamma^{2} } \right)}}$$

On substituting this into the expressions for prices and quantities, we get the equilibrium values reported in Table 1. As is usual in models with two-part tariffs, prices are independent of the bargaining parameter μ, which affects the redistribution of maximized profits only via S_i*. So greater buyer power in the NB2 model does not translate into greater countervailing power on behalf of consumers. We shall show in Proposition 2 below that this regime gives lower consumer prices than the benchmark and downstream first-mover regimes, so it creates countervailing power relative to those regimes. However, we shall also show that it may give higher or lower prices compared to the NB1 regime, depending on relative bargaining power and the degree of product differentiation.

Further, when γ = 0 we again get marginal cost pricing of the upstream product (w* = c), but now the reason is different. When the downstream products are demand independent, the strategic motive for raising retail prices is absent. The channel partners’ interest is to maximize their joint profits by setting wholesale price equal to marginal cost to avoid double marginalization, as in the vertically integrated solution for independent monopolists. However, here they remain vertically separated and share the profits via the lump-sum transfer.

We now determine conditions under which the sign of the transfer S* is positive or negative. Substituting the equilibrium values of profits into Eq. (14) gives

$$S_{i}^{*} = \frac{{\left( {\gamma^{2} - 2\mu } \right)\left( {2 - \gamma^{2} } \right)\left( {a - c\left( {1 - \gamma } \right)} \right)^{2} }}{{\left( {4 - \gamma^{2} - 2\gamma } \right)^{2} }}$$

The denominator in this expression is a squared term which will always be positive. In the numerator, $(a-c{\left(1-\gamma )\right)}^{2}>0$ and ${(2-\gamma }^{2})>0$. Therefore,

Proposition 1

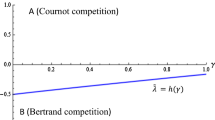
For all values of $\gamma , \mu$∈ [0, 1), S_i* ⋛ 0 as $\left({\gamma }^{2}\gtreqless2\mu \right)$

This inequality is graphed in ($\mu ,$ γ) space in Fig. 2. We shall show that the same Figure depicts the relative magnitudes of four other outcome variables when we compare Nash Bargaining regimes with linear and two-part tariffs. These results, summarized as (ii)–(v) in the caption of Fig. 2, can be ignored for the present.

Fig. 2

Values of $\upgamma$ and $\mu$ for which (i) S* > 0; (ii) ${p}_{{\text{i}},{\text{NB}}2}^{*}> {p}_{{\text{i}},{\text{NB}}1}^{*}$; (iii) ${w}_{{\text{i}},{\text{NB}}2}^{*}> {w}_{{\text{i}},{\text{NB}}1}^{*}$; (iv)$\frac{\partial {p}_{i,NB2}^{*}}{\partial c}<\frac{\partial {p}_{i,NB1}^{*}}{\partial c}$; (v) ${\pi }_{iNB2}^{{D}^{*}}>{\pi }_{iNB1}^{{D}^{*}}$

The area of parameter space compatible with positive slotting allowances corresponds to combinations of higher downstream bargaining power (lower μ) and lower product differentiation (higher γ). We can show that this condition $\left({\gamma }^{2}>2\gamma \right)$ implies that bargaining power lies in the range 0 ≤ μ < 0.5.

Lemma 3

$\gamma^{2} > 2\mu \Rightarrow 0 \le \mu < 0.5$.

Proof

By assumption, $0 \le \gamma < 1$. This implies that $0 \le {\upgamma }^{2} < {\upgamma }$. Along with our condition $2\mu < \gamma^{2}$, this gives $0 \le 2\mu < \gamma^{2} < \gamma < 1 \Rightarrow 0 \le \mu < 0.5$. Hence proved.

Hence, slotting allowance ${S}_{i}^{*}$ will be positive only if $\mu < 0.5$, as shown in Fig. 2. That is, a slotting allowance is observed only if the balance of bargaining power is in favour of the downstream firms. However, this condition is not sufficient. We can have negative values of ${S}_{i}^{*}$, i.e. a franchise fee payable to the upstream firms, even if the latter have low bargaining power $\mu .$ With higher product differentiation (lower $\gamma$) by upstream firms, we enter the unshaded region where even an upstream firm with low bargaining power can extract a franchise fee rather than pay a slotting allowance. Product differentiation can thus offset lower upstream bargaining power.

On differentiating ${S}_{i}^{*}$ with respect to μ, we find that as μ falls ${S}_{i}^{*}$ rises.

$$\frac{{\partial S_{i}^{*} }}{\partial \mu } = \frac{{ - 2\left( {2 - \gamma^{2} } \right)\left( {a - c\left( {1 - \gamma } \right)} \right)^{2} }}{{\left( {\gamma^{2} + 2\gamma - 4} \right)^{2} }} < 0$$

This shows that, as expected, greater bargaining power with downstream firms monotonically reduces the franchise fee and turns it into a slotting allowance. In contrast, ${S}_{i}^{*}$ behaves non-monotonically with respect to $\gamma$. The switch from negative to positive ${S}_{i}^{*}$ as $\gamma$ increases is well defined as in Fig. 2, but we can show that ${S}_{i}^{*}$ again approaches zero as $\gamma \to 1$ (i.e. as products become almost homogenous).

The wholesale price component of the two-part tariff maximizes total channel profit. Our analysis shows how its lump-sum component is used to redistribute it between upstream and downstream firms, either as a slotting allowance or as a franchise fee, on the basis of relative bargaining power and the degree of product differentiation. Further intuition will emerge from our similar results on the ranking of retail and wholesale prices below.

A special case of our Nash Bargaining results under two-part tariffs was derived by Gal-Or (1991), where upstream firms can extract all the profits of downstream firms in the form of franchise fee. Her results can be shown to be the special case of our model when $\mu$ = 1. Similarly, Shaffer (1991) showed that when downstream firms have all the bargaining power, they extract all the profits of upstream firms in the form of slotting allowance, like we showed for $\mu$ = 0. Our paper allows for intermediate degrees of bargaining power between these two extremes. It also differs from their papers because they compare two-part tariffs in these special cases with resale price maintenance, while we compare much more general two-part tariffs against four other regimes.

2.3.3 Vertical integration

In vertical integration (denoted VI), upstream and downstream firms in each supply chain integrate to form a single entity. The profit function of a vertically integrated firm is as below:

$$\pi_{1} = \left( {p_{1} - c} \right)q_{1}$$

(15)

Differentiating the profit function with respect to price, for firm 1,

$$\begin{aligned} \frac{{\partial \pi_{1,VI} }}{{\partial p_{1} }} & = \left( {p_{1} - c} \right)\frac{{\partial q_{1} }}{{\partial p_{1} }} + q_{1} = 0 \\ & = \left( {p_{1} - c} \right)\left( { - 1} \right) + a - p_{1} + \gamma p_{2} = 0 \\ \end{aligned}$$

Solving sequentially for prices, quantities and profits, we get the equilibrium outcomes in Table 1, where we assume that profits in the VI case are allocated to upstream and downstream firms according to the Nash Bargaining parameter μ. The logic is that the terms of any merger are worked out so as to compensate their shareholders accordingly, either by a cash buyout or via the swap ratio for shares in the merged firm. Buyer power in this case manifests itself through a greater share of the integrated firm’s profits, rather than in the terms of a contract between vertically separated firms.

From Table 1, the following results can be derived for all five vertical regimes (results available on request): (1) Equilibrium prices and profits are always non-negative; (2) Partial derivatives of the downstream profits and prices with respect to exogenous variables c, γ, and μ are of the expected signs;¹⁰ (3) As products become more homogenous (γ$\to 1$), the wholesale and retail prices fall to marginal cost, and the slotting allowance S* and profits of upstream and downstream firms tend to zero, confirming the existence of the Bertrand paradox in the model. For the four vertically separated regimes, we can also prove that upstream firms’ wholesale prices exceed their marginal costs (w* > c). This is unlike the case of vertical integration of both chains, or a single vertical chain of successive monopolies, for which the optimal two-part tariff eliminates double marginalization and thereby maximizes channel profits by setting w* = c. Instead, with Bertrand duopoly in the final goods market, profit maximization for each vertically separated channel involves w* > c, in order to induce the downstream firms to exploit strategic complementarity of prices.¹¹ We now proceed to compare these equilibrium values of the endogenous variables across the vertical regimes.

3 Comparisons across vertical regimes

Let π_i,j^k* represent equilibrium profit for firms denoted by k which can be U (upstream firm) or D (downstream firm). ‘i’ can be equal to 1 referring to firm 1, or 2 for firm 2. ‘j’ defines regime type, which can be B (Benchmark model), NB1 (Nash Bargaining with linear tariff), NB2 (Nash Bargaining with two-part tariff), FM (downstream First-Mover pricing model) or VI (Vertical Integration model).

3.1 Comparing retail prices, consumer surplus, and welfare

We can obtain the following proposition (proof in Appendix 3):

Proposition 2

For all values of $\gamma ,\mu$∈ (0, 1),

$${p}_{i,VI}^{*}<{p}_{i,NB2}^{*}\lesseqgtr{p}_{i,NB1}^{*}<{p}_{i,FM}^{*}={p}_{i,B}^{*} \, {\text{as}} \, {\gamma }^{2}\lesseqgtr2\mu$$

In a model with a similar structure of bilateral duopoly, Gal-Or (1991) showed that ${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}> {{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*}$ when the upstream firms make ‘take it or leave it’ offers to their retailers. This corresponds to our benchmark case, or to the limiting value of our NB1 case with $\mu$ = 1, which would lie along the right-hand border of Fig. 2. Her result is thus a special case of ours. It does not hold for combinations of high buyer power and substitutability between goods, corresponding to the shaded region of Fig. 2, which is determined by exactly the same function as the one that distinguished positive from negative slotting allowances. Our ranking of wholesale prices, presented later, will provide further intuition.

With symmetric firms whose products enter symmetrically into consumer demand, prices are inversely related to consumer surplus and social welfare, so Proposition 2 enables us to rank the latter as well. As is well known, vertical integration is welfare enhancing in this setting because it eliminates double marginalization in the vertical structure. If integration is not feasible, we have shown that some kind of buyer power is weakly better for welfare, and it is strictly better if it is exercised in the form of Nash Bargaining between upstream and downstream firms, rather than downstream first-mover advantage. As between the two Nash Bargaining regimes, a linear (two-part) tariff is better for consumers and welfare when product differentiation is low (high) relative to upstream bargaining power, in a very precise sense given by ${\gamma }^{2}\lesseqgtr2\mu$.

3.2 Comparing wholesale prices

Binary comparisons presented in Appendix 4 rule out all except the following three possible orderings of wholesale prices across the five regimes:

• 1. ${w}_{i,VI}^{*}<{w}_{i,NB1}^{*}<{w}_{i,NB2}^{*}<{w}_{i,FM}^{*}<{w}_{i,B}^{*}$

• 2. ${w}_{i,VI}^{*}<{w}_{i,NB2}^{*}<{w}_{i,NB1}^{*}<{w}_{i,FM}^{*}<{w}_{i,B}^{*}$

• 3. ${w}_{i,VI}^{*}<{w}_{i,NB2}^{*}<{w}_{i,FM}^{*}{<w}_{i,NB1}^{*}<{w}_{i,B}^{*}$

These cases hold in the respective shaded regions in Fig. 3.

Fig. 3

Values of $\gamma$ and $\mu$ consistent with different rankings of wholesale prices

Zones 1 and 2 correspond to the different rankings of wholesale prices which emerge from Nash Bargaining outcomes with linear and two-part tariffs. In Zone 3, ${w}_{i,NB1}^{*}>{w}_{i,NB2}^{*}$ as in Zone 2, the only difference being that the ranking of ${w}_{i,NB1}^{*}$ and ${w}_{i,FM}^{*}$ is reversed.¹² The reasoning is as follows. As we showed in Sect. 2.3.2.1, for a given level of product differentiation, higher upstream bargaining power is associated with increasing equilibrium wholesale prices in the NB1 regime, from c (as in the VI regime) when μ = 0 to the same level as in the benchmark regime when μ = 1. Wholesale prices remain independent of μ in all other regimes. Correspondingly, in Fig. 3, increasing μ takes us from Zone 1 to 2 and then 3.

Our focus is on buyer power (μ < 0.5). Suppose we exclude Zone 3 as well as the small unshaded area where none of the inequalities hold, by constraining μ below 0.47 (depicted by the vertical black line) instead of 0.5. The difference between equilibrium wholesale prices in the two NB regimes is given by:

$${w}_{i,NB2}^{*}-{w}_{i,NB1}^{*}=\frac{2(2-{\gamma }^{2})({\gamma }^{2}-2\mu )(a+c(-1+\gamma ))}{(4-2\gamma -{\gamma }^{2})(4-2{\gamma }^{2}-\gamma \mu )}$$

All the terms in this expression are strictly positive except for ${(\gamma }^{2}-2\mu )$, which can take either sign. This is exactly the same condition which determined the sign of the slotting allowance S* in Proposition 1 and the ranking of retail prices in Proposition 2, so the boundary between Zones 1 and 2 in Fig. 3 corresponds to the boundary between the shaded and unshaded regions in Fig. 2. We can state the following:

Proposition 3

For all values of $\gamma$∈ (0, 1), $\mu$∈ (0, 0.47),

$${w}_{i,VI}^{*}<{w}_{i,NB2}^{*}\lesseqgtr{w}_{i,NB1}^{*}<{w}_{i,FM}^{*}<{w}_{i,B}^{*} \, {\text{as}} \, {\gamma }^{2}\lesseqgtr2\mu$$

The conjunction of the three Propositions provides the intuition for the difference between the NB1 and NB2 cases. As noted earlier, an optimal two-part tariff sets the wholesale price so as to induce a retail price which maximizes the total profits of each vertical chain. These prices remain independent of relative bargaining power, which only determines the redistribution of profits through the lump-sum transfer S*. With a linear tariff, the wholesale price carries the burden of both maximizing and distributing channel profits. Wholesale and retail prices in this case are both monotonically increasing in $\mu$. An increase in buyer power (i.e., lower $\mu$) can be visualized as a horizontal leftward movement across Figs. 2 and 3 for any given level of product differentiation ($\gamma$), ultimately reversing the ranking of wholesale and retail prices as between the NB1 and NB2 regimes, since prices remain invariant with respect to $\mu$ in the latter. Combined with Proposition 1, these results also show that the switch from franchise fee to slotting fee as $\mu$ decreases or $\gamma$ increases occurs at the parameter values that reverse the ranking of wholesale and retail prices.

3.3 Comparing pass-through of upstream costs into retail prices

A recent emerging literature examines how vertical separation influences the pass-through of common shocks to upstream firms’ costs into downstream firms’ prices. This has implications for understanding the effects of changes in minimum wages, import tariffs, and exchange rates on the prices of final goods. Most of this literature explores the role of varying degrees of competition, demand curvature, and bargaining power on the pass-through rate (Gaudin 2016; Adachi 2020). Our contribution, while keeping the linear demand specification and duopolistic structure unchanged, is to compare pass-through rates under the five modes of exercising buyer power, allowing for varying degrees of bargaining power and demand substitutability. From the expressions for equilibrium prices in Table 1, we can obtain the partial derivatives in Table 2. From these, given the symmetry of the two supply chains, the following Proposition can be derived straightforwardly:

Table 2 Partial derivatives of retail prices with respect to upstream cost

Proposition 4

For all values of $\upgamma ,\upmu$∈(0, 1),

• (i) $0<\frac{\partial {p}_{i,B}^{*}}{\partial c}=\frac{\partial {p}_{i,FM}^{*}}{\partial c} <\frac{\partial {p}_{i,NB1}^{*}}{\partial c}\lesseqgtr\frac{\partial {p}_{i,NB2}^{*}}{\partial c}<\frac{\partial {p}_{i,,VI}^{*}}{\partial c}<1 \,$as ${\gamma }^{2}\lesseqgtr2\mu$

• (ii) $\frac{{\partial }^{2}{p}_{i,j}^{*}}{\partial c\partial \gamma } \& \frac{{\partial }^{3}{p}_{i,j}^{*}}{\partial c\partial {\gamma }^{2}}>0 \,$for i = 1, 2 and all regimes j.

Result (i) shows that all the vertical arrangements are cost-absorbing (i.e., they exhibit incomplete pass-through, as we would expect with linear demand); vertically separated arrangements dampen the pass-through compared to vertical integration; and that the ranking of pass-through rates is the reverse of the ranking of equilibrium prices, with the ranking of the NB1 and NB2 regimes getting reversed for exactly the same range of parameter values. Along with Proposition 2, these results imply that the differences in retail prices as between the different regimes become smaller as upstream cost levels increase. From result (ii), we can unambiguously conclude that in all regimes, the pass-through rates are increasing and convex in the degree of product substitutability.¹³

3.4 Comparing downstream profits under different regimes

Our ranking of wholesale and retail prices was built up from pair-wise comparisons between vertical regimes. In comparing downstream profits, however, such comparisons often turn out to be parameter-dependent, and no clear ranking over all five regimes can be obtained. Therefore, we present two results for subsets of the regimes for which rankings are possible.¹⁴ First, we show that downstream profits under the NB1 and NB2 regimes are ranked by the same condition derived above for the other outcome variables. Then, we drop the NB1 contract type and rank the remaining four regimes, with Nash Bargaining outcomes represented only by NB2. Since firms are symmetric at both levels, and we assume that both supply chains adopt the same kind of vertical regime, we can compare profits for a representative downstream firm.

For our first result, we take the difference

$${\uppi }_{{\text{i}},{\text{NB}}2}^{{{\text{D}}}^{*} }- {\uppi }_{{\text{i}},{\text{NB}}1}^{{{\text{D}}}^{*} }=\frac{{\left(a-c+c\gamma \right)}^{2}\left(2-{\gamma }^{2}\right)\left({\gamma }^{2}-2\mu \right)({\gamma }^{4}({\mu }^{2}-12\mu +12)+{\gamma }^{3}(24\mu -16-4{\mu }^{2})+{\gamma }^{2}(4{\mu }^{2}+16\mu -24)+\gamma (32-48\mu )+16\mu )}{{(\gamma -2)}^{2}{({\gamma }^{2}+2\gamma -4)}^{2}{(2{\gamma }^{2}+\gamma \mu -4)}^{2}}$$

The denominator of this complicated expression is clearly positive, and so are the first two terms in the numerator. A plot of the last term in the numerator confirms that it is positive for all permissible values of $\gamma$ and μ. Hence, the sign of the entire expression once again depends only on the term ${(\gamma }^{2}-2\mu )$, as illustrated by Fig. 2. This result can be stated as:

Proposition 5

For all values of γ$,{{\upmu}}$∈(0, 1), ${{{\pi}}}_{{{i}},{{N}}{{B}}2}^{{{{D}}}^{{*}}{ }}\gtreqless{{{\pi}}}_{{{i}},{{N}}{{B}}1}^{{{{D}}}^{{*}}}$ as ${{{\gamma}}}^{2}{ }\gtreqless{ }2{{\mu}}$

The rationale for this reversal is as follows. We know that the NB2 regime maximizes channel profits. Prices remain unchanged as downstream bargaining power increases, but downstream profits increase because the franchise fee declines and becomes a slotting allowance, which continues to increase until the entire channel profit accrues to the downstream firm. On the other hand, in the NB1 regime, both wholesale and retail prices decline as downstream bargaining power increases, and therefore the quantity sold must rise. Each of these will have a different effect on downstream profits. But we can derive the net effect unambiguously:

$$\frac{\partial {\pi }_{i,NB1}^{{D}^{*} }}{\partial \mu }=\frac{4{\left(a+c\left(\gamma -1\right)\right)}^{2}{\left({\gamma }^{2}-2\right)}^{2}({\gamma }^{2}+\gamma -2)(\mu -2)}{{(\gamma -2)}^{2}{(2{\gamma }^{2}+\gamma \mu -4)}^{3}}<0$$

In the denominator, $\left(2{\gamma }^{2}+\gamma \mu -4\right)$ can be shown by numerical simulation to be negative for all relevant values of μ and γ. In the numerator, the expressions $\left(\mu -2\right)$ and $\left({\gamma }^{2}+\gamma -2\right)$ are both strictly negative. Thus, we can conclude that as downstream bargaining power increases, downstream profits increase monotonically in both the NB1 and NB2 regimes. This is not surprising. However, it is surprising, given the very different roles played by prices in the two regimes, resulting in different aggregate channel profits, that the ranking of downstream profits reverses at exactly the same parameter combinations as for the other endogenous variables $({S}_{i}^{*}, {w}_{i}^{*}, {p}_{i}^{*})$, as shown in Proposition 5. Propositions 2 and 5 together allow us to state the following:

Corollary

As between Nash Bargaining contracts with linear and two-part tariffs, for any combination of γ and μ ${(\gamma }^{2}\ne 2\mu )$, downstream firms would always prefer the one that is worse for consumers and welfare. For ${\gamma }^{2}=2\mu$, the two contracts are equivalent from the perspective of both downstream profits and welfare.

For our second result, in which we drop the NB1 regime, we analyze the six possible binary comparisons of downstream profits among the remaining four regimes:

• 1. (π_1,NB2^D*, π_2,NB2^D*) > (π_1,VI^D*, π_2,VI^D*)

• 2. (π_1,FM^D*, π_2,FM^D*) > (π_1,B^D*, π_2,B^D*)

• 3. (π_1,NB2^D*, π_2,NB2^D*) > (π_1,B^D*, π_2,B^D*)

• 4. (π_1,VI^D*, π_2,VI^D*) > (π_1,FM^D*, π_2,FM^D*)

• 5. (π_1,NB2^D*, π_2,NB2^D*) > (π_1,FM^D*, π_2,FM^D*)

• 6. (π_1,VI^D*, π_2,VI^D*) > (π_1,B^D*, π_2,B^D*)

In results 1–3 of Appendix 5, we show that the first three inequalities hold unconditionally (for μ > 0), while the others are conditional on $\mu$ and γ values. Bonanno and Vickers (1988) showed that upstream firms which can extract the entire downstream profits through a franchise fee get higher profits as compared to VI, because the upstream firms set w > c, which raises the prices charged by retailers. This commitment to higher prices exploits the strategic complementarity in prices and softens competition between the chains. The proof of the first inequality shows that the same holds for downstream firms with any positive bargaining power when a lump-sum transfer is possible, and for even slightly substitutable products.

Out of the 4! = 24 possible orderings of profits under the four regimes, 19 can be ruled out because they violate the unconditional inequalities 1–3. This leaves the following possible rankings for downstream profits under the four regimes:

• 1. ZONE 1: (π_1,NB2^D*, π_2,NB2^D*) > (π_1,VI^D*, π_2,VI^D*) > (π_1,FM^D*, π_2,FM^D*) > (π_1,B^D*, π_2,B^D*)

• 2. ZONE 2: (π_1,NB2^D*, π_2,NB2^D*) > (π_1,FM^D*, π_2,FM^D*) > (π_1,VI^D*, π_2,VI^D*) > (π_1,B^D*, π_2,B^D*)

• 3. ZONE 3:(π_1,NB2^D*, π_2,NB2^D*) > (π_1,FM^D*, π_2,FM^D*) > (π_1,B^D*, π_2,B^D*) > (π_1,VI^D*, π_2,VI^D*)

• 4. ZONE 4: (π_1,FM^D*, π_2,FM^D*) > (π_1,NB2^D*, π_2,NB2^D*) > (π_1,VI^D*, π_2,VI^D*) > (π_1,B^D*, π_2,B^D*)

• 5. ZONE 5: (π_1,FM^D*, π_2,FM^D*) > (π_1,NB2^D*, π_2,NB2^D*) > (π_1,B^D*, π_2,B^D*) > (π_1,VI^D*, π_2,VI^D)

For case 3 there is no common region of the parameter space for which the inequalities hold true. The remaining cases hold in the respective shaded regions in Fig. 4, which is based on results 4–6 in Appendix 5 and the associated Figures.

Fig. 4

Zones for different values of $\upgamma$ and $\mu$ consistent with different rankings of downstream profits under the four vertical regimes

From the graph it is clear that Zones 1 and 2, with Nash Bargaining, are the best for downstream firms when they have more bargaining power and products are more differentiated. When downstream firms have less bargaining power and/or products are more similar, they prefer first-mover pricing (Zones 4 and 5). These two regimes are always better for them than vertical integration, which does not allow them to exploit strategic complementarity of prices, and the benchmark case, in which downstream firms have no buyer power. Once again, the interests of powerful downstream firms are opposed to that of consumers.

4 Conclusions

For this study we set up a model of two competing supply chains producing and selling differentiated products. We compared a standard benchmark case, in which upstream firms are first movers, against four alternative vertical regimes representing different modes of exercising buyer power: downstream first movers, Nash Bargaining with linear and two-part tariffs, and vertical integration. We found that reversing the order of moves only affects the firms’ margins in favour of the downstream firms, without affecting the price of the final good. Greater buyer power in the Nash Bargaining solution to a linear wholesale pricing contract does depress the retail price. But if bargaining takes place over the components of a two-part tariff contract, greater bargaining power with downstream firms leaves prices unaffected and only reduces the franchise fee that they would pay, turning it into a slotting allowance that they can extract from suppliers. However, for sufficiently differentiated products, even high downstream bargaining power can yield a franchise fee in equilibrium. Standard results from earlier literature emerged as special cases of our model when all bargaining power is assumed to reside either upstream or downstream. We also derived the effect of changes in bargaining power between these two extremes on the endogenous variables of our model (the lump-sum transfer component of the two-part tariff, wholesale and retail prices).

We then ranked the equilibrium values of the endogenous variables across the different vertical regimes. From the perspective of consumer surplus or social welfare, vertical integration is the best, while Nash Bargaining is ranked second. The benchmark regime is (weakly) the least desirable. Buyer power in some form is therefore beneficial not only for the downstream firms, but also (weakly) for social welfare. It is strictly better if it is exercised in the form of Nash Bargaining between upstream and downstream firms, rather than downstream firms exercising first-mover advantage. These findings support the downstream countervailing power hypothesis in a wider range of situations than was analyzed in earlier literature. We also found that the ranking of the pass-through rates of upstream costs into downstream prices is exactly the reverse of the ranking of equilibrium prices across the five regimes. Pass-through is invariably incomplete, and dampened in all vertically separated arrangements as compared to integration. The dispersion of retail prices across the different regimes becomes smaller as upstream cost levels increase

For the two Nash Bargaining regimes with linear and two-part tariffs, we showed that the sign of the inequalities that give the ranking of equilibrium wholesale and retail prices, pass-through rates, and downstream profits, as well as the direction of the lump-sum transfer, is determined by the same simple function of the parameters representing relative bargaining power and the degree of product differentiation. Finally, dropping the Nash Bargaining regime with linear tariff, we derived clearly-demarcated zones of the parameter space in which downstream firms do better under either Nash Bargaining with a two-part tariff or first-mover pricing, depending on their bargaining power and the degree of product differentiation. One or both of these vertically separated arrangements always dominates vertical integration for downstream firms, while the benchmark regime without buyer power obviously gives them the worst outcomes.

In terms of policy implications, vertical integration is obviously first-best for social welfare in our setting, while firms prefer separation. As between the two Nash Bargaining regimes, we showed that the firms always prefer the one that is inferior for consumers and welfare. When we compared the four regimes excluding Nash Bargaining with a linear tariff, we found that the firms may even prefer first-mover pricing over the second-best two-part tariff contract. Competition (antitrust) policy can block welfare-decreasing mergers, but it can neither enforce welfare-increasing ones, nor impose the optimal second-best Nash Bargaining contracts between separated firms. It can penalize firms for colluding on prices, quantities, and market allocation, but probably not on their choice of non-exclusionary vertical contracts.

One limitation of this study was that we could not work out the endogenous choice of vertical arrangement, because simultaneous choice from among our five vertical regimes would give us a 5x5 payoff matrix for the downstream firms alone. Determining the Nash equilibria would be prohibitively complicated. However, in ongoing work we endogenize the decision to integrate, by posing it pairwise as an alternative to each of our vertically separated structures which involve buyer power.¹⁵ The objective would be to find out whether unilateral, simultaneous, or sequential vertical integration are Nash equilibrium outcomes. We find that unilateral integration of a single channel is always welfare-improving, regardless of the contract between separated firms in the rival channel. In the case in which channels can independently choose between vertical integration versus vertical separation with a two-part tariff, Gupta (2022) shows that the latter is a dominant strategy. Therefore, whether firms decide simultaneously or sequentially, separation is the Nash equilibrium, while integration would have been better for social welfare.

Appendices

Appendix 1: Derivation of the demand function

Following Singh and Vives (1994), we assume a representative consumer’s utility function as:

$$U\left( {q_{0} ,q_{1} ,q_{2} } \right) = \alpha q_{1} + \alpha q_{2} - \frac{{\beta q_{1}^{2} + \beta q_{2}^{2} + 2\lambda q_{1} q_{2} }}{2} + q_{0}$$

Here q_i is quantity produced by upstream firm i. ${q}_{0}$ is a Hicksian composite commodity consisting of all other goods outside the market of interest. Since we are working with real prices we are normalizing price one unit of this basket equal to 1. We assume $\alpha >0, \beta >0.$ To derive the demand function we maximize this utility function for q₀, q₁ and q₂:

$$\mathop {{\text{max}}}\limits_{{q_{0} ,~q_{1} ,q_{2} }} \left\{ {U\left( {q_{1} ,q_{2} } \right) = \alpha q_{1} + \alpha q_{2} - \frac{{\beta q_{1}^{2} + \beta q_{2}^{2} + 2\lambda q_{1} q_{2} }}{2} + q_{0} } \right\}$$

Subject to the budget constraint:$Y={q}_{0}+{p}_{1}{q}_{1}+{p}_{2}{q}_{2}$

On maximization we get the following inverse demand function

$$p_{1} = \alpha - \beta q_{1} + \lambda q_{2}$$

$$p_{2} = \alpha - \beta q_{2} + \lambda q_{1}$$

On rearranging terms we get direct demand functions as

$${q}_{1}=a-b{p}_{1}+\upgamma {{\text{p}}}_{2}$$

where,

$$a = \alpha \left( {\beta - \lambda } \right)/\delta$$

$$b = \beta /\delta$$

$$\mathrm{\gamma }=\frac{\lambda }{\delta }$$

where $\delta \equiv (\beta ^{2} - \lambda ^{2} )$

• When γ/b approaches 1 it implies $\frac{\gamma }{b} = \frac{{{\uplambda }/{\updelta }}}{{{\upbeta }/{\updelta }}} = \frac{{\uplambda }}{{\upbeta }} \to 1$, which implies that δ$\to 0$, where the demands are undefined. Therefore, we assume γ < b. We have adapted this restriction for the case where b = 1, which is used to derive the results. b = 1 implies $\frac{\beta }{\delta }=1$.

• Most papers in economics journals follow Singh and Vives (1994) by substituting the parameters of the inverse demand function into the a, b and γ parameters of the direct demand function before proceeding with the firms’ profit-maximization exercise. The direct demand specification without substitution was used in the early papers on vertical relationships with downstream competition in prices, e.g. Lin (1990) and O’Brien and Shaffer (1993). It was actually first used by McGuire and Staelin (1983), and continues to be used extensively in the literature on marketing and operations research (although it is not derived from maximizing a utility function). See Wang et al (2016), Li et al (2020) and many other papers cited there. However, it creates a problem of discontinuity as γ/b approaches 1.

• Another problem with using the direct demand specification, which does not seem to have been noticed by earlier authors, is that it gives the same 'monopoly' results when either γ = 0 (signifying independent demands and no competition), or p_j = 0 (signifying intense competition). This can be averted by bounding prices above zero by assuming positive marginal costs, with $\alpha \ge c$, and the upstream firm assumed to have constant marginal cost of production equal to c.

Appendix 2: First order conditions for the Nash Bargaining model with two-part tariff

An upstream firm’s profit can be written as

$${\uppi }_{U1}=\left({w}_{1}-c\right){q}_{1}-{S}_{1}$$

where,

${w}_{1}$: wholesale price.

${S}_{1}$: slotting allowance

Downstream firm’s profit can be written as

$${\uppi }_{D1}=\left({{p}_{1}-w}_{1}\right){q}_{1}+{S}_{1}$$

(16)

Define the Nash product of upstream and downstream profits as:

$$N={\uppi }_{D1}^{ 1-\mu } {\uppi }_{U1}^{ \mu }$$

(17)

On differentiating with respect to S₁, we get

$$\frac{\partial N}{\partial {S}_{1}}=\left(1-\mu \right){\uppi }_{D1}^{ -\mu } {\uppi }_{U1}^{ \mu }+{\left(-\mu \right)\uppi }_{D1}^{ 1-\mu } {\uppi }_{U1}^{ \mu -1}=0$$

(18)

When we solve the above first order condition for ${\uppi }_{D1}$ we get

$$=>\frac{\left(1-\upmu \right){\uppi }_{U1} }{\upmu }={\uppi }_{D1}$$

(19)

When we substitute into equation A4 above the profit function of the upstream and downstream firms, we get below equation

$$\frac{\left(1-\upmu \right) }{\upmu }\left[\left({w}_{1}-c\right){q}_{1}-{S}_{1}\right]=\left({p}_{1}-{w}_{1}\right){q}_{1}+{S}_{1}$$

On rearranging the terms on both sides, we get:

$${{S}}_{1}^{{*}} = \left( {1 - {{\mu}}} \right)\left[ {\left( {{{w}}_{1} - {{c}}} \right){{q}}_{1} } \right] - {{\mu}}\left[ {\left( {{{p}}_{1} - {{w}}_{1} } \right){{q}}_{1} } \right]$$

On differentiating N with respect to wholesale price w, we get

$$\frac{\partial N}{\partial {w}_{1}}=\left(1-\mu \right){\uppi }_{D1}^{ -\mu } {\uppi }_{U1}^{ \mu }\frac{\partial {\uppi }_{D1}}{\partial {w}_{1}}+{\left(\mu \right)\uppi }_{D1}^{ 1-\mu } {\uppi }_{U1}^{ \mu -1}\frac{\partial {\uppi }_{U1}}{\partial {w}_{1}}=0$$

$$=>\frac{\left(1-\upmu \right){\uppi }_{U1} }{\upmu }\frac{\partial {\pi }_{D1}}{\partial {w}_{1}}={-\uppi }_{D1}\frac{\partial {\pi }_{U1}}{\partial {w}_{1}}$$

Substituting equation A4 into the above equation we get

$$\frac{\partial {\pi }_{D1}}{\partial {w}_{1}}+ \frac{\partial {\pi }_{U1}}{\partial {w}_{1}}=0$$

Appendix 3: Proof of Proposition 2

$${p}_{i,VI}^{*}<{p}_{i,NB2}^{*}\lesseqgtr{p}_{i,NB1}^{*}<{p}_{i,FM}^{*}={p}_{i,B}^{*} \, {\text{as}} \, {\gamma }^{2}\lesseqgtr2\mu$$

We have already shown above that prices are the same in the FM and benchmark cases. Now we prove the inequalities successively.

• 1. ${{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}\le {{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}$

  $${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}=\frac{a(2\left(2+\mu \right)-2{\gamma }^{2})-c(2-{\gamma }^{2})(\mu -2)}{(2-\gamma )(4-2{\gamma }^{2}-\gamma \mu )}, {{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}=\frac{a+{\text{c}}}{(2-\upgamma )}$$
  $${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}-{{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}=\frac{a\left(2\left(2+\mu \right)-2{\gamma }^{2}\right)-c\left(2-{\gamma }^{2}\right)\left(\mu -2\right)}{\left(2-\gamma \right)\left(4-2{\gamma }^{2}-\gamma \mu \right)}- \frac{a+{\text{c}}}{(2-\upgamma )}$$
  $$=\frac{(a+c(-1+\gamma ))(2+\gamma )\mu }{(2-\gamma )(4-2{\gamma }^{2}-\gamma \mu )}\ge 0, \, \mathrm{with equality for} \, \mu =0$$

In the above expression, in the numerator $\left(a+c\left(-1+\gamma \right)\right)>0$ by Lemma 1, and ($2+\gamma )>0$. So, the numerator is positive. In the denominator, $\left(2-\gamma \right)>0$ and $\left(4-2{\gamma }^{2}-\gamma \mu \right)>0$ for all values of $\gamma {\text{and}} \mu$ in the given ranges. Thus, ${{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}\le {{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}$, with the vertically integrated outcome emerging when downstream firms have all bargaining power, as explained in the text.

• 2. ${{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}\le {{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*}$

  $${\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} = \frac{{2a + c\left( {2 - \gamma^{2} } \right)}}{{\left( {4 - 2\gamma - \gamma^{2} } \right) }}, {\text{p}}_{{{\text{i}},{\text{VI}}}}^{*} = \frac{a + c}{{\left( {2 - \gamma } \right)}}$$
  $${\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} - {\text{p}}_{{{\text{i}},{\text{VI}}}}^{*} = \frac{{2a + c\left( {2 - \gamma^{2} } \right)}}{{\left( {4 - 2\gamma - \gamma^{2} } \right) }} - \frac{a + c}{{\left( {2 - \gamma } \right)}}$$

  $= \frac{{\gamma^{2} \left( {a - \left( {1 - \gamma } \right)c} \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma - \gamma^{2} } \right) }} \ge 0$, with equality for $\gamma <0$

The denominator here is positive, as $\left(2-\upgamma \right)>0, \left(4{-2\upgamma }^{2}-\upgamma \right)>0$. In the numerator, $\left(a-\left(1-\upgamma \right)c\right)>0$ and ${\upgamma }^{2}\ge 0$ for all values of γ between 0 and 1. This shows that ${{\text{p}}}_{{\text{i}},{\text{VI}}}^{*}$≤${{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*}$ holds true for all relevant values of $\upgamma$ and c. Once again, the vertical integration outcome emerges when goods are independent.

• 3. ${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}\lesseqgtr{{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*} \, {\text{as}} \, 2\mu \lesseqgtr{\gamma }^{2}$

  $${\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} = \frac{{2a - c\left( {\gamma^{2} - 2} \right)}}{{\left( {4 - 2\gamma - \gamma^{2} } \right) }}, {\text{p}}_{{{\text{i}},{\text{NB}}1}}^{*} = \frac{{a\left( {2\left( {2 + \mu } \right) - 2\gamma^{2} } \right) + c\left( {2 - \gamma^{2} } \right)\left( {2 - \mu } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma^{2} - \gamma \mu } \right)}}$$
  $$\begin{gathered} {\text{p}}_{{{\text{i}},{\text{NB}}1}}^{*} - {\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} = \frac{{a\left( {2\left( {2 + \mu } \right) - 2\gamma^{2} } \right) + c\left( {2 - \gamma^{2} } \right)\left( {2 - \mu } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma^{2} - \gamma \mu } \right)}} - \frac{{2a + c\left( {2 - \gamma^{2} } \right)}}{{\left( {4 - 2\gamma - \gamma^{2} } \right)}} \hfill \\ = \frac{{2\left( {a + c\left( { - 1 + \gamma } \right)} \right)\left( {2 - \gamma^{2} } \right)\left( {\gamma^{2} - 2\mu } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma - \gamma^{2} } \right)\left( { - 4 + 2\gamma^{2} + \gamma \mu } \right)}} \hfill \\ \end{gathered}$$

Note that $\left(a+c\left(-1+\gamma \right)\right)>0$ by Lemma 1; the second term in the numerator and the first two terms in the denominator are also positive; but the last term in the denominator is strictly negative. So the sign of the entire expression will be the opposite of the sign of ${(\gamma }^{2}-2\mu )$, which determined the sign of S* in Proposition 1. Not surprisingly, therefore, when $\frac{(2-{\gamma }^{2})({\gamma }^{2}-2\mu )}{(2-\gamma )(4-2\gamma -{\gamma }^{2})(-4+2{\gamma }^{2}+\gamma \mu )}$ is plotted in Mathematica software, the region for which ${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}>{{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*}$ turns out to be identical to the zone consistent with a franchise fee (unshaded region) in Fig. 2.

• 4. ${p}_{i,NB1}^{*}\le {p}_{i,FM}^{*}$, with equality for $\mu$=1.

  $${{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}=\frac{a\left(2\left(2+\mu \right)-2{\gamma }^{2}\right)+c\left(2-{\gamma }^{2}\right)\left(2-\mu \right)}{\left(2-\gamma \right)\left(4-2{\gamma }^{2}-\gamma \mu \right)}$$
  $${{\text{p}}}_{{\text{i}},{\text{FM}}}^{*}= \frac{6a-2a{\upgamma }^{2}+c({2-\upgamma }^{2})}{(4-2{\upgamma }^{2}-\upgamma )(2-\upgamma )}$$
  $$\begin{aligned} {\text{p}}_{{{\text{i}},{\text{FM}}}}^{*} - {\text{p}}_{{{\text{i}},{\text{NB}}1}}^{*} & = \frac{{6a - 2a\gamma ^{2} + c\left( {2 - \gamma ^{2} } \right)}}{{\left( {4 - 2\gamma ^{2} - \gamma } \right)\left( {2 - \gamma } \right)}} \\ & \quad - \frac{{a\left( {2\left( {2 + \mu } \right) - 2\gamma ^{2} } \right) + c\left( {2 - \gamma ^{2} } \right)\left( {2 - \mu } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma ^{2} - \gamma \mu } \right)}} \\ & = \frac{{2\left( {a - \left( {1 - \gamma } \right)c} \right)\left( {2 + \gamma } \right)\left( {2 - \gamma ^{2} } \right)\left( {1 - \mu } \right)}}{{\left( {2 - \gamma } \right)\left( {2\gamma ^{2} + \gamma - 4} \right)\left( {2\gamma ^{2} + \gamma \mu - 4} \right)}} \\ \end{aligned}$$

In the numerator $\left(a-\left(1-\gamma \right)c\right)>0$ by Lemma 1, $\left(1-\mu \right)\ge 0$, $\left({2-\gamma }^{2}\right)>0$. So, the numerator is positive. In the denominator, $\left(2-\gamma \right)>0$, $\left(2{\gamma }^{2}+\gamma -4\right)<0$ and $\left(2{\gamma }^{2}+\gamma \mu -4\right)<0$ for all values of $\gamma$ and μ in the relevant ranges (the last two expressions are non-factorizable and checked in Mathematica for the direction of their signs). Thus, ${{\text{p}}}_{{\text{i}},{\text{FM}}}^{*}\ge {{\text{p}}}_{{\text{i}},{\text{NB}}1}^{*}.$

• 5. ${{\text{p}}}_{{\text{i}},{\text{NB}}2}^{*}<{{\text{p}}}_{{\text{i}},{\text{FM}}}^{*}$

  $${\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} = \frac{{2a + c\left( {2 - \gamma^{2} } \right) }}{{\left( {4 - 2\gamma - \gamma^{2} } \right) }};\quad {\text{p}}_{{{\text{i}},{\text{FM}}}}^{*} = \frac{{6a - 2a\gamma^{2} + c\left( {2 - \gamma^{2} } \right)}}{{\left( {4 - 2\gamma^{2} - \gamma } \right)\left( {2 - \gamma } \right)}}$$
  $$\begin{aligned} {\text{p}}_{{{\text{i}},{\text{FM}}}}^{*} - {\text{p}}_{{{\text{i}},{\text{NB}}2}}^{*} &= \frac{{6a - 2a\gamma^{2} + c\left( {2 - \gamma^{2} } \right)}}{{\left( {4 - 2\gamma^{2} - \gamma } \right)\left( {2 - \gamma } \right)}} - \frac{{2a + c\left( {2 - \gamma^{2} } \right) }}{{\left( {4 - 2\gamma - \gamma^{2} } \right)}} \hfill \\ &= \frac{{2\left( {2 - \gamma^{2} } \right)^{2} \left( {a - \left( {1 - \gamma } \right)c} \right)}}{{\left( {4 - 2\gamma^{2} - \gamma } \right)\left( {2 - \gamma } \right)\left( {4 - 2\gamma - \gamma^{2} } \right)}} > 0 \hfill \\ \end{aligned}$$

All three terms in both the numerator and denominator are strictly positive for all values of γ between 0 and 1.

Combining results 1–5 and excluding the polar cases for μ and γ proves Proposition 2, which gives us a ranking of retail prices across the five regimes.

Appendix 4: Binary comparisons of wholesale prices

• 1. ${{w}_{i,B}^{*}\ge w}_{i,NB1}^{*}$, with equality for $\mu$ = 1.

  $$\begin{aligned} w_{i,B}^{*} - w_{i,NB1}^{*} & = \frac{{a\left( {2 + \gamma } \right) - c\left( {\gamma^{2} - 2} \right)}}{{4 - 2\gamma^{2} - \gamma }} - \frac{{a\left( {2 + \gamma } \right)\mu + c\left( {\gamma^{2} - 2} \right)\left( {\mu - 2} \right)}}{{2\left( {2 - \gamma^{2} } \right) - \gamma \mu }} \\ & = \frac{{2\left( {a + c\left( { - 1 + \gamma } \right)} \right)\left( {2 + \gamma } \right)\left( {2 - \gamma^{2} } \right)\left( {1 - \mu } \right)}}{{\left( {4 - \gamma - 2\gamma^{2} } \right)\left( {4 - 2\gamma^{2} - \gamma \mu } \right)}} \\ \end{aligned}$$

For $0\le \mu$ < 1, all terms in the numerator and denominator are positive; while for $\mu =1$ the numerator is zero. Hence proved.

• 2. ${w}_{i,FM}^{*}>{w}_{i,NB2}^{*}$

  $${w}_{i,FM}^{*}-{w}_{i,NB2}^{*}=\frac{a\left(2-{\gamma }^{2}\right)+c(6-4\gamma -2{\gamma }^{2}+{\gamma }^{3})}{(2-\gamma )(4-2{\gamma }^{2}-\gamma )}-\frac{{a\gamma }^{2}+c\left(({2-\gamma }^{2})(2-\gamma )\right)}{\left(4-2\gamma -{\gamma }^{2}\right)}$$
  $${w}_{i,FM}^{*}-{w}_{i,NB2}^{*}=\frac{2\left(4-2\gamma -7{\gamma }^{2}+4{\gamma }^{3}+2{\gamma }^{4}-{\gamma }^{5}\right)\left(a-\left(1-\gamma \right)c\right)}{(2-\gamma )(4-2{\gamma }^{2}-\gamma )\left(4-2\gamma -{\gamma }^{2}\right)}$$

All three terms in the denominator of the above expression are positive for $\gamma <1$. In the numerator, $\left(a-\left(1-\upgamma \right)c\right)>0$ (Lemma 1), and the expression $4-2\upgamma -7{\upgamma }^{2}+4{\upgamma }^{3}+2{\upgamma }^{4}-{\upgamma }^{5}$ can be factorized to $(1-\upgamma )(4+2\upgamma -5{\upgamma }^{2}-{\upgamma }^{3}+{\upgamma }^{4})$ which is positive for all values of $\gamma$ between 0 and 1. Hence proved.

Finally, amongst the five vertical regimes, it is obvious that wholesale price will be lowest for vertical integration, as firms maximize their integrated profit behaving as single entity, setting wholesale price equal to the upstream marginal costs. From Table 1 and our earlier discussion, the NB1 regime gives the same outcome when μ = 0, corresponding to what we described as “wholesale price maintenance” when the downstream firm has all the bargaining power and can extract the entire channel profit. Along with Lemma 2, and excluding the polar cases for μ and γ, these results rule out all except the three orderings in the text, on the basis of which we proved Proposition 3.

Appendix 5: Binary comparisons of downstream profits

• 1. Comparing downstream profits from Vertical integration and Nash Bargaining contract with two-part tariff:

  $$\begin{aligned} \pi_{{{1},{\text{NB2}}}}^{{{\text{D}}*}} - \pi_{{{1},{\text{VI}}}}^{{{\text{D}}*}} & = \frac{{2(1 - \gamma )(2 - \gamma^{2} )(a - c(1 - \gamma ))^{2} }}{{(4 - \gamma^{2} - 2\gamma )^{2} }} - \frac{{(1 - \gamma )(a - c + \gamma c)^{2} }}{{(2 - \gamma )^{2} }} \\ & = \frac{{\gamma^{3} \left( {1 - \mu } \right)\left( {4 - 3\gamma } \right)\left( {a - c\left( {1 - \gamma } \right)} \right)^{2} }}{{\left( {4 - \gamma^{2} - 2\gamma } \right)^{2} \left( {2 - \gamma } \right)^{2} }} \ge 0,\;{\text{with}}\;{\text{equality}}\;{\text{for}}\;\gamma \;{\text{or}}\;\mu \, = \,{1} \\ \end{aligned}$$

For μ < 1 and γ strictly between 0 and 1, both the numerator and denominator of the above expression are positive.

• 2. Comparing profits from First-mover pricing model and Linear Pricing (benchmark) model

This result was already implied by our earlier finding that the only difference between the two regimes is that wholesale prices are lower, and therefore downstream margins are higher, in the FM case. However, this can be confirmed explicitly by comparing the profit expressions as follows:

$$\begin{aligned} \pi_{{{1},{\text{FM}}}}^{{{\text{D}}*}} - \pi_{{{1},{\text{B}}}}^{{{\text{D}}*}} &= \frac{{\left( {a - c + c\gamma } \right)^{2} \left( {2 - {\upgamma }^{2} } \right)\left( {2 + {\upgamma }} \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} }} - \frac{{\left( {2 - {\upgamma }^{2} } \right)^{2} \left( {a + \left( {{\upgamma } - 1} \right)c} \right)^{2} }}{{\left( {\left( {4 - 2{\upgamma }^{2} - {\upgamma }} \right)\left( {2 - {\upgamma }} \right)} \right)^{2} }} \hfill \\ &= \frac{{2\left( {2 - {\upgamma }^{2} } \right)\left( {{\text{a}} - c\left( {1 - {\upgamma }} \right)} \right)^{2} }}{{\left( {4 - 2{\upgamma }^{2} - {\upgamma }} \right)^{2} \left( {2 - {\upgamma }} \right)^{2} }} > 0 \hfill \\ \end{aligned}$$

All the terms in both the numerator and denominator of this expression are positive for all values of $\upgamma$ between 0 and 1.

• 3. Comparing profits from Nash Bargaining with two-part tariff and Linear Pricing (benchmark),

  $$\begin{aligned} \pi_{{{1},{\text{NB2}}}}^{{^{{{\text{D}}*}} }} &= \frac{{2\left( {1 - } \right)\left( {2 -^{2} } \right)\left( {a - c\left( {1 - } \right)} \right)^{2} }}{{\left( {4 -^{2} - 2} \right)^{2} }} - \frac{{\left( {2 -^{2} } \right)^{2} \left( {a + \left( { - 1} \right)c} \right)^{2} }}{{\left( {\left( {4 - 2^{2} - } \right)\left( {2 - } \right)} \right)^{2} }} \hfill \\ &= \frac{{\left( {^{2} - 2} \right)\left( {a - c\left( {1 - } \right)} \right)^{2} \left( {2\left( { - 1} \right)\left( {\left( {4 - 2^{2} - } \right)\left( {2 - } \right)} \right)^{2} - \left( {^{2} - 2} \right)\left( {4 -^{2} - 2} \right)^{2} } \right)}}{{\left( {4 - 2^{2} - } \right)^{2} \left( {2 - } \right)^{2} \left( {4 -^{2} - 2} \right)^{2} }} > 0 \hfill \\ \end{aligned}$$

The denominator of the above expression is positive as all the terms are squared. In the numerator, $\left(a-\left(1-\upgamma \right)c\right)>0 ;\left({\upgamma }^{2}-2\right)<0$ for all values of $\gamma$ between 0 and 1. The expression $\left(2\left(\upmu -1\right){\left(\left(4-2{\upgamma }^{2}-\upgamma \right)\left(2-\upgamma \right)\right)}^{2}-\left({\upgamma }^{2}-2\right){\left(4-{\upgamma }^{2}-2\upgamma \right)}^{2}\right)$ can be shown by numerical simulation to be negative for all relevant values of $\mu$ and $\gamma .$ This shows that π_1,NB2^D* > π_1,B^D* holds true for all relevant values of $\gamma , \mu$ and c.¹⁶ The two-part tariff enables each chain to maximize its combined profit, and downstream firms with more bargaining power benefit from this.

• 4. Comparing profits from vertical integration and downstream first-mover model:

  $$\begin{aligned} \pi_{{{1},{\text{VI}}}}^{{{\text{D}}*}} - \pi_{{{1},{\text{FM}}}}^{{{\text{D}}*}} & = \frac{{\left( {1 - \mu } \right)\left( {a - c + \gamma c} \right)^{2} }}{{\left( { - 2 + \gamma } \right)^{2} }} - \frac{{\left( {a - c + c\gamma } \right)^{2} \left( {2 - \gamma^{2} } \right)\left( {2 + \gamma } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} }} \\ & = \frac{{\left( {a - c + \gamma c} \right)^{2} }}{{\left( {2 - \gamma } \right)^{2} \left( {4 - 2\gamma^{2} - \gamma } \right)^{2} }}\left[ {\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} \left( {1 - {\upmu }} \right) - \left( {2 - {\upgamma }^{2} } \right)\left( {4 - {\upgamma }^{2} } \right)} \right] \\ \end{aligned}$$

All the expressions are squared, except the one in square brackets. If we plot this expression $[\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} \left( {1 - {\upmu }} \right) - \left( {2 - {\upgamma }^{2} } \right)\left( {4 - {\upgamma }^{2} } \right)]$ in (μ, γ) space we get Fig. 5. 

Fig. 5

Values of $\gamma$ and $\mu$ for which (π_1,VI^D*, π_2,VI^D*) > (π_1,FM^D*, π_2,FM^D*)

• 5. Comparing profits from downstream first-mover contract and Nash Bargaining contract with a two-part tariff, i.e.,

  $$\begin{aligned} {\uppi }_{{1,{\text{NB}}2}}^{{\text{D*}}} - {\uppi }_{{1,{\text{FM}}}}^{{\text{D*}}} & = \frac{{2\left( {1 - \mu } \right)\left( {2 - \gamma^{2} } \right)\left( {a - c\left( {1 - \gamma } \right)} \right)^{2} }}{{\left( {4 - \gamma^{2} - 2\gamma } \right)^{2} }} \\ & \quad - \frac{{\left( {a - c + c\gamma } \right)^{2} \left( {2 - \gamma^{2} } \right)\left( {2 + \gamma } \right)}}{{\left( {2 - \gamma } \right)\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} }} \\ & = \left( {2 - {\upgamma }^{2} } \right)\left( {a - c\left( {1 - {\upgamma }} \right)} \right)^{2} \left( {\frac{{2\left( {1 - {\upmu }} \right)}}{{\left( {4 - {\upgamma }^{2} - 2{\upgamma }} \right)^{2} }} - \frac{{\left( {2 + {\upgamma }} \right)}}{{\left( {2 - {\upgamma }} \right)\left( {4 - 2{\upgamma }^{2} - {\upgamma }} \right)^{2} }}} \right) \\ \end{aligned}$$

We can plot $\left(\frac{2(1-\upmu )}{{\left(4-{\upgamma }^{2}-2\upgamma \right)}^{2}}-\frac{\left(2+\upgamma \right)}{\left(2-\gamma \right){\left(4-2{\gamma }^{2}-\gamma \right)}^{2}}\right)$ in $(\mu , \gamma )$ space to get Fig. 6. 

Fig. 6

Values of $\gamma$ and $\mu$ for which (π_1,FM^D*, π_2,FM^D*) < (π_1,NB2^D*, π_2,NB2^D*)

• 6. Comparing profits from Vertical Integration and Benchmark models i.e.,

  $$\begin{aligned} {\uppi }_{{1,{\text{VI}}}}^{{\text{D*}}} - {\uppi }_{{1,{\text{B}}}}^{{\text{D*}}} & = \frac{{\left( {1 - \mu } \right)\left( {a - c + \gamma c} \right)^{2} }}{{\left( {2 - \gamma } \right)^{2} }} - \frac{{\left( {2 - \gamma^{2} } \right)^{2} \left( {a + \left( {\gamma - 1} \right)c} \right)^{2} }}{{\left( {\left( {4 - 2\gamma^{2} - \gamma } \right)\left( {2 - \gamma } \right)} \right)^{2} }} \\ & = \frac{{\left( {a + \left( {\gamma - 1} \right)c} \right)^{2} \left( {\left( {1 - \mu } \right)\left( {4 - 2\gamma^{2} - \gamma } \right)^{2} - \left( {2 - \gamma^{2} } \right)^{2} } \right)}}{{\left( {\left( {4 - 2\gamma^{2} - \gamma } \right)\left( {2 - \gamma } \right)} \right)^{2} }} \\ \end{aligned}$$

If we plot $\left((1-\upmu \right){\left(4-2{\upgamma }^{2}-\upgamma \right)}^{2}-{\left(2-{\upgamma }^{2}\right)}^{2})$ in (μ, γ) space we get Fig. 7. 

Fig. 7

Values of $\upgamma$ and $\mu$ for which (π_1,VI^D*, π_2,VI^D*) > (π_1,B^D*, π_2,B^D*)