1 Introduction

The shielding of cracks owing to the presence of nearby dislocations has been discussed by many investigators (see, for example, [1,2,3,4,5,6,7,8,9,10]). The dislocation–crack interaction problem becomes considerably challenging when the tip of the crack is lodged inside an elastic inhomogeneity. In this case, the dislocation interacts not only with the crack, but also with the elastic inhomogeneity.

In this paper, we investigate the interaction between a screw dislocation and a semi-infinite crack partially penetrating a parabolic elastic inhomogeneity under far-field anti-plane mechanical loading. The crack passes through the vertex of the parabolic interface and has its tip located at the focus of the parabolic interface. Under this assumption, analytical solutions are derived for two specific cases: (i) when the screw dislocation is located in the matrix; (ii) when the screw dislocation is located inside the parabolic elastic inhomogeneity. In addition, the local mode III stress intensity factor at the crack tip and the image force acting on the screw dislocation are obtained. The shielding effect of the screw dislocation on the local mode III stress intensity factor is illustrated for typical locations of the screw dislocation. The condition for dislocation emission from the crack is established.

2 General solution

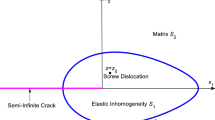
As shown in Fig. 1, we consider a semi-infinite crack with its cleavage plane on the negative \(x_{1} \)-axis partially penetrating a parabolic elastic inhomogeneity. Let \(S_{1} ,S_{2} \), and \(S_{3} \) denote, respectively, the upper half matrix, the inhomogeneity, and the lower half matrix, all of which are perfectly bonded through the parabolic interface L described by

$$\begin{aligned} L: x_{1} =-H+\frac{x_{2}^{2} }{4H}, H>0. \end{aligned}$$
(1)

The crack passes through the vertex of the parabolic interface at \(z=-H\), and the crack tip is located at the focus of the parabola L. In addition, a screw dislocation with Burgers vector b is applied at \(z=z_{0} =r\exp (\hbox {i}\theta )\) with r and \(\theta \) being the polar coordinates of \(z_{0} \) either in the upper half matrix \(S_{1} \) or in the inhomogeneity \(S_{2} \). Throughout the paper, the subscripts 1, 2, and 3 are used to identify the respective quantities in \(S_{1} ,S_{2} \), and \(S_{3} \).

Fig. 1
figure 1

A screw dislocation interacting with a semi-infinite crack partially penetrating a parabolic elastic inhomogeneity

Full size image

For the anti-plane shear deformations of an isotropic elastic material, the two anti-plane shear stress components \(\sigma _{31} \) and \(\sigma _{32} \), the out-of-plane displacement \(u_{3} \), and the single stress function \(\phi \) can be expressed in terms of a single analytic function f(z) of the complex variable \(z=x_{1} +\hbox {i}x_{2} \) as [11]

$$\begin{aligned} \sigma _{32} +\hbox {i}\sigma _{31} =\mu {f}'(z),\phi +\hbox {i}\mu u_{3} =\mu f(z), \end{aligned}$$
(2)

where \(\mu \) is the shear modulus. In addition, the two anti-plane stress components can be expressed in terms of the single stress function by [11]

$$\begin{aligned} \sigma _{32} =\phi _{,1} ,\sigma _{31} =-\phi _{,2}. \end{aligned}$$
(3)

We introduce the following conformal mapping function:

$$\begin{aligned} z=\omega (\xi )=\xi ^{2},\xi =\omega ^{-1}(z)=\sqrt{z} ,\hbox {Re}\left\{ \xi \right\} \ge 0. \end{aligned}$$
(4)
Fig. 2
figure 2

The image \(\xi \)-plane

Full size image

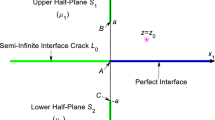
As shown in Fig. 2, using the mapping function in Eq. (4), the z-plane containing the semi-infinite crack is mapped onto the right half-plane: \(\hbox {Re}\left\{ \xi \right\} \ge 0\); the upper half matrix \(S_{1} \) is mapped onto the upper and right quarter-plane \({S}'_{1} :\left\{ {h\le \hbox {Im}\left\{ \xi \right\} <+\infty ,\hbox {Re}\left\{ \xi \right\} \ge 0} \right\} \) with \(h=\sqrt{H} \); the parabolic inhomogeneity \(S_{2} \) is mapped onto the middle semi-infinite strip \({S}'_{2} :\left\{ {-h\le \hbox {Im}\left\{ \xi \right\} \le h, \hbox {Re}\left\{ \xi \right\} \ge 0} \right\} \); the lower half matrix \(S_{3} \) is mapped onto the lower and right quarter-plane \({S}'_{3} :\left\{ {-\infty <\hbox {Im}\left\{ \xi \right\} \le -h, \hbox {Re}\left\{ \xi \right\} \ge 0} \right\} \); the crack surfaces are mapped onto the vertical straight line: \(\left\{ {\hbox {Re}\left\{ \xi \right\} =0,-\infty<\hbox {Im}\left\{ \xi \right\} <+\infty } \right\} \); the location of the screw dislocation at \(z=z_{0} \) is mapped onto the point \(\xi =\xi _{0} \) with \(\xi _{0} =\sqrt{z_{0} } \).

By imposing the continuity conditions of traction and displacement across the perfect parabolic interface L, all three analytic functions \(f_{i} (\xi )=f_{i} (\omega (\xi )),i=1,2,3\) can be expressed in terms of a single analytic function \(g(\xi )\) as follows:

$$\begin{aligned} f_{3} (\xi )= & {} g(\xi ), \nonumber \\ \quad f_{2} (\xi )= & {} \frac{\Gamma +1}{2}g(\xi )+\frac{\Gamma -1}{2}\bar{{g}}(\xi +2\hbox {i}h), \nonumber \\&f_{1} (\xi )=\frac{(\Gamma +1)^{2}}{4\Gamma }g(\xi )-\frac{(\Gamma -1)^{2}}{4\Gamma }g(\xi -4\hbox {i}h)\nonumber \\&+\frac{\Gamma ^{2}-1}{4\Gamma }\bar{{g}}(\xi +2\hbox {i}h)-\frac{\Gamma ^{2}-1}{4\Gamma }\bar{{g}}(\xi -2\hbox {i}h), \end{aligned}$$
(5)

where

$$\begin{aligned} \Gamma =\frac{\mu _{1} }{\mu _{2} }. \end{aligned}$$
(6)

It remains to determine the specific expression for \(g(\xi )\). Once \(g(\xi )\) is known, the three analytic functions \(f_{1} (\xi ),f_{2} (\xi )\), and \(f_{3} (\xi )\) can be conveniently determined using Eq. (5).

3 Screw dislocation in \(S_{1} \)

When the screw dislocation is located in the upper half matrix \(S_{1} \), the analytic function \(g(\xi )\) is given by

$$\begin{aligned} g(\xi )=\sqrt{\frac{2}{\pi }} \frac{K_{\hbox {III}} }{\mu _{1} }\xi +\frac{2b\Gamma }{\pi (\Gamma +1)^{2}}\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi -\xi _{0} -4nh\hbox {i})} -\frac{2b\Gamma }{\pi (\Gamma +1)^{2}}\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi +\bar{{\xi }}_{0} -4nh\hbox {i})} , \end{aligned}$$
(7)

where \(K_{\hbox {III}} \) is the mode III intensity factor characterizing the far-field loading, and

$$\begin{aligned} M=\frac{\Gamma -1}{\Gamma +1},\quad \left| M \right| <1. \end{aligned}$$
(8)

Substitution of Eq. (7) into Eq. (5) yields the following explicit expressions for\(f_{1} (\xi ),f_{2} (\xi )\), and \(f_{3} (\xi )\):

$$\begin{aligned} f_{3} (\xi )= & {} \sqrt{{\frac{2}{\pi }}} \frac{K_{\hbox {III}} }{\mu _{1} }\xi +\frac{2b\Gamma }{\pi (\Gamma +1)^{2}}\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi -\xi _{0} -4nh \hbox {i})} \nonumber \\&\quad -\frac{2b\Gamma }{\pi (\Gamma +1)^{2}}\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi +\bar{{\xi }}_{0} -4nh\hbox {i})} , \end{aligned}$$
(9.1)
$$\begin{aligned} f_{2} (\xi )= & {} \sqrt{{\frac{2}{\pi }}} \frac{K_{\hbox {III}} }{\mu _{2} }\xi +\frac{b\Gamma }{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi -\xi _{0} -4nh\hbox {i})} \nonumber \\&\quad -\frac{b\Gamma }{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi +\bar{{\xi }}_{0} -4nh\hbox {i})} \nonumber \\&\quad +\frac{b\Gamma }{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi -\bar{{\xi }}_{0} +2(2n+1)h\hbox {i}]} \nonumber \\&\quad -\frac{b\Gamma }{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi +\xi _{0} +2(2n+1)h\hbox {i}]} , \nonumber \\ \end{aligned}$$
(9.2)
$$\begin{aligned}&f_{1} (\xi )=\sqrt{{\frac{2}{\pi }}} \frac{K_{\hbox {III}} }{\mu _{1} }\xi \nonumber \\&\quad +\frac{b}{2\pi }\ln (\xi -\xi _{0} )-\frac{b}{2\pi }\ln (\xi +\bar{{\xi }}_{0} ) \nonumber \\&\quad +\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi -\bar{{\xi }}_{0} +2(2n+1)h\hbox {i}]} -\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi +\xi _{0} +2(2n+1)h\hbox {i}]} \nonumber \\&\quad -\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi -\bar{{\xi }}_{0} +2(2n-1)h\hbox {i}]} +\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi +\xi _{0} +2(2n-1)h\hbox {i}]} . \end{aligned}$$
(9.3)

The local mode III stress intensity factor, denoted here by \(k_{\hbox {III}} \), can be derived from \(f_{2} (\xi )\) in Eq. (9.2) as follows:

$$\begin{aligned} k_{\hbox {III}} =K_{\hbox {III}} -\sqrt{\frac{2}{\pi }} \frac{b\mu _{1} }{\Gamma +1}\sqrt{r} \cos \frac{\theta }{2}\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{r+4n\sqrt{Hr} \sin \frac{\theta }{2}+4n^{2}H}} . \end{aligned}$$
(10)

Using \(f_{1} (\xi )\) in Eq. (9.3) and the Peach–Koehler formula [12], the image force acting on the screw dislocation is then

$$\begin{aligned}&F_{1} -\hbox {i}F_{2} =\frac{K_{\hbox {III}} b}{\sqrt{2\pi } \xi _{0} }-\frac{\mu _{1} b^{2}}{8\pi \xi _{0}^{2} }-\frac{\mu _{1} b^{2}}{4\pi \xi _{0} }\left( {\frac{1}{\xi _{0} +\bar{{\xi }}_{0} }+\frac{M}{\xi _{0} -\bar{{\xi }}_{0} -2h\hbox {i}}-\frac{M}{2\xi _{0} -2h\hbox {i}}} \right) \nonumber \\&+\frac{\mu _{1} b^{2}(1-M^{2})(\xi _{0} +\bar{{\xi }}_{0} )}{8\pi \xi _{0} }\sum \limits _{n=0}^{+\infty } {\frac{M^{2n+1}}{\left[ {\xi _{0} +(2n+1)h\hbox {i}} \right] \left[ {\xi _{0} -\bar{{\xi }}_{0} +2(2n+1)h\hbox {i}} \right] }} , \end{aligned}$$
(11)

where \(F_{1} \) and \(F_{2} \) are, respectively, the force components along the \(x_{1} \) and \(x_{2} \) directions. It can be easily verified that when \(M=0\), Eqs. (10) and (11) simply reduce to the classical solution by Majumdar and Burns [1].

4 Screw dislocation in \(S_{2} \)

When the screw dislocation is located within the parabolic inhomogeneity \(S_{2} \), the analytic function \(g(\xi )\) is given by

$$\begin{aligned}&g(\xi )=\sqrt{\frac{2}{\pi }} \frac{K_{\hbox {III}} }{\mu _{1} }\xi +\frac{b}{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi -\xi _{0} -4nh\hbox {i})} \nonumber \\&+\frac{b}{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi -\bar{{\xi }}_{0} -2(2n+1\hbox {)}h\hbox {i}]} \nonumber \\&\quad -\frac{b}{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi +\bar{{\xi }}_{0} -4nh\hbox {i})} -\frac{b}{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi +\xi _{0} -2(2n+1\hbox {)}h\hbox {i}]} . \end{aligned}$$
(12)

Substitution of Eq. (12) into Eq. (5) yields the following explicit expressions for \(f_{1} (\xi ),f_{2} (\xi )\), and \(f_{3} (\xi )\):

$$\begin{aligned}&f_{3} (\xi )=\sqrt{\frac{2}{\pi }} \frac{K_{\hbox {III}} }{\mu _{1} }\xi +\frac{b}{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi -\xi _{0} -4nh\hbox {i})}\nonumber \\&\quad +\frac{b}{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi -\bar{{\xi }}_{0} -2(2n+1\hbox {)}h\hbox {i}]} \nonumber \\&\quad -\frac{b}{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi +\bar{{\xi }}_{0} -4nh\hbox {i})} -\frac{b}{\pi (\Gamma +1)}\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi +\xi _{0} -2(2n+1\hbox {)}h\hbox {i}]} , \end{aligned}$$
(13.1)
$$\begin{aligned}&f_{2} (\xi )=\sqrt{\frac{2}{\pi }} \frac{K_{\hbox {III}} }{\mu _{2} }\xi +\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi -\xi _{0} -4nh\hbox {i})} +\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi -\bar{{\xi }}_{0} -2(2n+1\hbox {)}h\hbox {i}]} \nonumber \\&\quad -\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n}\ln (\xi +\bar{{\xi }}_{0} -4nh\hbox {i})} -\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi +\xi _{0} -2(2n+1\hbox {)}h\hbox {i}]} \nonumber \\&\quad +\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi -\bar{{\xi }}_{0} +2(2n+1)h\hbox {i}]} +\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n+2}\ln [\xi -\xi _{0} +4(n+1\hbox {)}h\hbox {i}]} \nonumber \\&\quad -\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln (\xi +\xi _{0} +2(2n+1)h\hbox {i})} -\frac{b}{2\pi }\sum \limits _{n=0}^{+\infty } {M^{2n+2}\ln [\xi +\bar{{\xi }}_{0} +4(n+1)h\hbox {i}]} , \end{aligned}$$
(13.2)
$$\begin{aligned}&f_{1} (\xi )=\sqrt{\frac{2}{\pi }} \frac{K_{\hbox {III}} }{\mu _{1} }\xi +\frac{b(\Gamma +1)}{4\pi \Gamma }\ln (\xi -\xi _{0} )-\frac{b(\Gamma +1)}{4\pi \Gamma }\ln (\xi +\bar{{\xi }}_{0} ) \nonumber \\&\quad +\frac{b(\Gamma -1)}{4\pi \Gamma }\sum \limits _{n=0}^{+\infty } {M^{2n}\ln [\xi -\bar{{\xi }}_{0} +2(2n+1)h\hbox {i}]} +\frac{b(\Gamma -1)}{4\pi \Gamma }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi -\xi _{0} +4\hbox {i}h(n+1\hbox {)}]} \nonumber \\&\quad -\frac{b(\Gamma -1)}{4\pi \Gamma }\sum \limits _{n=0}^{+\infty } {M^{2n}\ln [\xi +\xi _{0} +2(2n+1)h\hbox {i}]} -\frac{b(\Gamma -1)}{4\pi \Gamma }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln [\xi +\bar{{\xi }}_{0} +4\hbox {i}h(n+1\hbox {)}]} \nonumber \\&\quad -\frac{b(\Gamma -1)}{4\pi \Gamma }\sum \limits _{n=1}^{+\infty } {M^{2n}\ln [\xi -\bar{{\xi }}_{0} +2(2n-1)h\hbox {i}]} -\frac{b(\Gamma -1)}{4\pi \Gamma }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln (\xi -\xi _{0} +4nh\hbox {i})} \nonumber \\&\quad +\frac{b(\Gamma -1)}{4\pi \Gamma }\sum \limits _{n=1}^{+\infty } {M^{2n}\ln [\xi +\xi _{0} +2(2n-1)h\hbox {i}]} +\frac{b(\Gamma -1)}{4\pi \Gamma }\sum \limits _{n=0}^{+\infty } {M^{2n+1}\ln (\xi +\bar{{\xi }}_{0} +4nh\hbox {i)}} . \end{aligned}$$
(13.3)

The local mode III stress intensity factor can be derived from \(f_{2} (\xi )\) in Eq. (13.2) as follows:

$$\begin{aligned} k_{\hbox {III}} =K_{\hbox {III}} -\frac{\mu _{2} b}{\sqrt{2\pi } }\sqrt{r} \cos \frac{\theta }{2}\left( {\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{r+4n\sqrt{Hr} \sin \frac{\theta }{2}+4n^{2}H}} +\sum \limits _{n=1}^{+\infty } {\frac{M^{n}}{r-4n\sqrt{Hr} \sin \frac{\theta }{2}+4n^{2}H}} } \right) , \end{aligned}$$
(14)

Using \(f_{2} (\xi )\) in Eq. (13.2) and the Peach–Koehler formula, the image force acting on the screw dislocation is given by

$$\begin{aligned}&F_{1} -\hbox {i}F_{2} =\frac{K_{\hbox {III}} b}{\sqrt{2\pi } \xi _{0} }-\frac{\mu _{2} b^{2}}{8\pi \xi _{0}^{2} }-\frac{\mu _{2} b^{2}}{4\pi \xi _{0} (\xi _{0} +\bar{{\xi }}_{0} )}-\frac{\mu _{2} b^{2}(\xi _{0} +\bar{{\xi }}_{0} )}{2\pi \xi _{0} }\sum \limits _{n=1}^{+\infty } {\frac{M^{2n}}{(\xi _{0} +\bar{{\xi }}_{0} )^{2}+16n^{2}h^{2}}} \nonumber \\&\quad +\frac{\mu _{2} b^{2}(\xi _{0} -\bar{{\xi }}_{0} )}{2\pi \xi _{0} }\sum \limits _{n=0}^{+\infty } {\frac{M^{2n+1}}{(\xi _{0} -\bar{{\xi }}_{0} )^{2}+4(2n+1\hbox {)}^{2}h^{2}}} -\frac{\mu _{2} b^{2}}{4\pi }\sum \limits _{n=0}^{+\infty } {\frac{M^{2n+1}}{\xi _{0}^{2} +(2n+1\hbox {)}^{2}h^{2}}} . \end{aligned}$$
(15)

It is again not difficult to verify that when \(M=0\), Eqs. (14) and (15) simply reduce to the classical solution by Majumdar and Burns [1].

5 Discussion

In this section, several typical cases will be discussed in detail to demonstrate the analytical solutions obtained in the previous two sections and to establish a dislocation emission criterion from the crack.

5.1 The screw dislocation is absent

In the absence of the screw dislocation with \(b=0\), it is seen from Eqs. (9.1–3) and (13.1–3) that

$$\begin{aligned}&f_{1} (z)=f_{3} (z)=\sqrt{\frac{2}{\pi }} \frac{K_{\hbox {III}} }{\mu _{1} }\sqrt{z} ,\ z\in S_{1} \cup S_{3} ; \nonumber \\&f_{2} (z)=\sqrt{\frac{2}{\pi }} \frac{K_{\hbox {III}} }{\mu _{2} }\sqrt{z} ,\ z\in S_{2} , \end{aligned}$$
(16)

which indicates that the stress field in the two-phase composite: \(\sigma _{32} +\hbox {i}\sigma _{31} ={K_{\hbox {III}} } / {\sqrt{{2\pi z}}},z\in S_{1} \cup S_{2} \cup S_{3} \) is identical to that near the tip of a mode III crack. In this case, \(k_{\hbox {III}} \equiv K_{\hbox {III}} \), which is in sharp contrast to the analogous result for a semi-infinite crack partially penetrating a circular elastic inhomogeneity [13].

5.2 A screw dislocation far from the crack tip

When the screw dislocation is located far from the crack tip (i.e., \(r\rightarrow \infty )\), both Eqs. (10) and (14) reveal that

$$\begin{aligned} k_{\hbox {III}} \cong K_{\hbox {III}} -\frac{\mu _{1} b}{\sqrt{2\pi r} }\cos \frac{\theta }{2}, r\rightarrow \infty , \end{aligned}$$
(17)

and Eq. (11) for a screw dislocation in the upper half matrix becomes

$$\begin{aligned} F_{1} -\hbox {i}F_{2} \cong \frac{K_{\hbox {III}} b}{\sqrt{2\pi } \xi _{0} }-\frac{\mu _{1} b^{2}}{8\pi \xi _{0}^{2} }-\frac{\mu _{1} b^{2}}{4\pi \xi _{0} (\xi _{0} +\bar{{\xi }}_{0} )},\ r\rightarrow \infty , \end{aligned}$$
(18)

and Eq. (15) for a screw dislocation inside the parabolic inhomogeneity becomes

$$\begin{aligned} F_{1} -\hbox {i}F_{2} \cong \frac{K_{\hbox {III}} b}{\sqrt{2\pi r} }-\frac{b^{2}(\mu _{1} +\mu _{2} )}{8\pi r},\ r\rightarrow \infty \hbox { and }\theta \rightarrow 0. \end{aligned}$$
(19)

Equations (17) and (18) are the corresponding equations for a screw dislocation near a semi-infinite crack in a homogeneously elastic plane with shear modulus \(\mu _{1} \) [1]. The result in Eqs. (17) and (18) implies that when the screw dislocation in the matrix is located far from the crack tip, the interaction problem can be treated equivalently to the case when the z-plane is elastically homogeneous with shear modulus \(\mu _{1} \).

5.3 A screw dislocation on the parabola L

When the screw dislocation is located on the parabola L, the following relationship is established: \(\sqrt{r} \sin \frac{\theta }{2}=\sqrt{H} \). In this case, it follows from either Eq. (10) or Eq. (14) that

$$\begin{aligned} k_{\hbox {III}} =K_{\hbox {III}} -\frac{\mu _{1} bY(r)}{\sqrt{2\pi r} }\cos \frac{\theta }{2}, \end{aligned}$$
(20)

where the function Y(r) is defined as

$$\begin{aligned} Y(r)=r(1-M)\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{r+4Hn(n+1)}} >0, r\ge H, \end{aligned}$$
(21)
Fig. 3
figure 3

Variation of the function Y(r) defined by Eq. (21) for different values of M

Full size image

which is illustrated in Fig. 3 for different values of M. It is seen from Fig. 3 that: \(0<Y(r)<1\) when \(M>0\); \(Y(r)\equiv 1\) when \(M=0\); \(Y(r)>1\) when \(M<0\). The shielding effect of the screw dislocation on the local mode III stress intensity factor can be clearly observed from Fig. 3.

5.4 A screw dislocation on the positive \(x_{1} \)-axis inside the parabolic inhomogeneity

When the screw dislocation lies on the positive \(x_{1} \)-axis inside the parabolic inhomogeneity, Eq. (14) becomes

$$\begin{aligned} k_{\hbox {III}} =K_{\hbox {III}} -\frac{\mu _{1} bQ(r)}{\sqrt{2\pi r} }, \end{aligned}$$
(22)

where the function Q(r) is defined as

$$\begin{aligned} Q(r)=\frac{1-M}{1+M}\left( {2r\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{r+4n^{2}H}} -1} \right) >0,r\ge 0, \end{aligned}$$
(23)
Fig. 4
figure 4

Variation of the function Q(r) defined by Eq. (23) for different values of M

Full size image
Fig. 5
figure 5

Variation of \(\lambda _{c} \) defined by Eq. (26) as a function of M for different values of \(\tilde{{H}}\)

Full size image

which is illustrated in Fig. 4 for different values of M. It is seen from Fig. 4 that the behavior of the function Q(r) is quite similar to that of Y(r) shown in Fig. 3. The shielding effect of the screw dislocation on the local mode III stress intensity factor is again clearly observed this time from Fig. 4.

In addition, when the screw dislocation lies on the positive \(x_{1} \)-axis inside the parabolic inhomogeneity, Eq. (15) becomes

$$\begin{aligned} F_{1} =\frac{K_{\hbox {III}} b}{\sqrt{2\pi r} }-\frac{\mu _{2} b^{2}}{4\pi }\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{r+n^{2}H}} ,\ F_{2} =0. \end{aligned}$$
(24)

Thus, according to Rice and Thomson [14], the dislocation emission criterion from the crack can be established as follows:

$$\begin{aligned} K_{\hbox {III}} >K_{c} =\frac{\mu _{2} b}{2\sqrt{{2\pi r_{c} }} }\sum \limits _{n=0}^{+\infty } {\frac{M^{n}}{n^{2}\tilde{{H}}+1}} , \end{aligned}$$
(25)

where \(\tilde{{H}}=H / {r_{c} }\) in which \(r_{c} \) denotes the core radius of the screw dislocation and \(K_{c} \) is the critical stress intensity factor for dislocation emission. Illustrated in Fig. 5 is the normalized critical stress intensity factor defined by

$$\begin{aligned} \lambda _{c} =\frac{2\sqrt{{{2\pi r_{c}} }} }{\mu _{2} b}K_{c} , \end{aligned}$$
(26)

as a function of the parameter M for different values of \(\tilde{{H}}\). It is seen from Fig. 5 that: (i) \(0<\lambda _{c} <1\) when the inhomogeneity is harder than the matrix with \(M<0\), \(\lambda _{c} >1\) when the inhomogeneity is softer than the matrix with \(M>0\); (ii) \(\lambda _{c} \) is an increasing function of M, an increasing function of \(\tilde{{H}}\) for \(M<0\), and a decreasing function of \(\tilde{{H}}\) for \(M>0\).

6 Conclusions

We have analytically solved the anti-plane problem associated with a screw dislocation near a semi-infinite crack partially penetrating a parabolic elastic inhomogeneity. The general solution in terms of the single analytic function \(g(\xi )\) is derived in Eq. (5). When the screw dislocation is located in the upper half matrix, the three analytic functions are given explicitly by Eqs. (9.1–3), and the local mode III stress intensity factor and the image force are, respectively, presented in Eqs. (10) and (11). When the screw dislocation lies inside the parabolic inhomogeneity, the three analytic functions are given explicitly by Eqs. (13.1–3), and the local mode III stress intensity factor and the image force are presented in Eqs. (14) and (15), respectively.