1 Introduction

The existence of the defects such as inclusions, holes, dislocations, and cracks is inevitable and exhibits a significant influence on the mechanical behaviors of the piezoelectric material when the size of these defects reduces to nanometer. By regarding the surface layer as an elastic membrane without thickness but different mechanical properties from the bonded bulk materials, Gurtin and Murdoch [7] firstly proposed a continuum mechanics model of the surface elasticity to capture the surface/interface effects. During the past few decades, the continuum mechanics model attracted much attention on the analysis of the structures with the nanoinhomogeneities [1, 3, 4, 13, 15, 22,23,24], the nanohole problems [5, 11, 26, 27] and the fracture problems [10, 29, 30]. For optimizing the nanodesign, Nanthakumar et al. [20] developed a computational method to capture the surface stress and surface elastic effects, and the boundary value problem was solved via the extended finite element method.

Based on the existing experimental observations to define the surface stresses to be linearly to the electric field, Huang and Yu [9] extended the Gurtin and Murdoch model to the surface piezoelectric analysis and applied the model to the investigation of the effects of the surface piezoelectricity on the electric displacements and the stresses when the size of the piezoelectric ring was reduced to the nanometer level. This coupling surface piezoelectric model was applied in the investigations of the nanostructures with the surface piezoelectricity. For example, Nan and Wang [17, 18] obtained the solution for the problem of a nanocrack in piezoelectric materials with the effects of residual surface stress. Wang and Fan [31] studied the influence of the surface piezoelectricity on the screw dislocation interacting with the interface between the hexagonal piezoelectric materials. Zhang et al. [35] investigated the effects of the surface piezoelectricity on the wave propagation in an infinite plate with nanothickness

During the past years, the issues of the interaction between the dislocation and the anti-plane nanocrack incorporating the surface piezoelectricity were addressed. By using the conformal mapping method, Xiao et al. [33] proposed a rigorous solution for the nanoelliptical holes with surface piezoelectricity under infinite in-plane electric field and anti-plane shear load, the solution was extended to the crack problem. Later, Xiao et al. [34] developed a close-form solution for a nanoscale cracked equilateral triangle hole under infinite in-plane electric load and anti-plane load. By applying the singular integral method, Nan and Wang [19] studied the crack with surface elasticity and piezoelectricity in the piezoelectric materials under anti-plane load. Gao and Li (2018) derived the exact solutions for the intensity factors of the anti-plane crack with surface piezoelectricity under electrically permeable and impermeable boundary conditions via the technique of conformal mapping. By simplifying the problem to the coupled Cauchy singular integrodifferential equations and using the collocation method, Wang and Xu [31] studied the problem of a piezoelectric crystal with a screw dislocation and a finite crack and established the complete solution for the problem. The hexagonal piezoelectric solid with a crack incorporating the surface piezoelectricity under anti-plane deformation was studied by Wang and Zhou [32]

In general, the finite-form solution is essential for the exact evaluation of the stress and displacement fields. The solutions in all the literature proposed by others so far were, however, derived by assuming previously one or more functions in infinite series and then truncating finite terms for the following analysis or calculation, and therefore their results were approximate near the crack tip.

In this paper, the conformal mapping technique was used to find the finite-form solution for the interaction between an anti-plane nanocrack with the surface piezoelectricity and a screw dislocation. By integrating the boundary equations and applying the conformal mapping technique as well as the Cauchy’s integral formula, the problem was transformed into a first-order differential equation in image plane. The finite-form solution for the problem was then obtained via the inverse mapping. The results by the present solution and the singularities of the stresses and electric displacements at the crack tip were discussed.

2 Problem and formulation

In the Cartesian coordinate system O-xyz, consider the piezoelectric material (bulk) that is polarized in the z-axis direction and the isotropic plane is in xy plane. In the anti-plane deformation, the equilibrium equations in the absence of the body forces and the constitutive relations read [6]

$$\begin{aligned} \tau _{jz,j}= & {} 0,\quad D_{j,j} =0 \end{aligned}$$
(1)
$$\begin{aligned} \gamma _{jz}= & {} w_{,j} ,\quad E_{j} =-\varphi _{,j} \end{aligned}$$
(2)
$$\begin{aligned} \tau _{jz}= & {} c_{44} w_{,j} +e_{15} \varphi _{\,,j} ,\quad D_{j} =e_{15} w_{,j} -d_{11} \varphi _{\,,j} \end{aligned}$$
(3)

in which \(j = 1, 2\) corresponding to the Cartesian coordinate x and y, w denotes the anti-plane displacement, \(\gamma _{jz}\) and \(\tau _{jz}\) represent the anti-plane shear strains and shear stresses, respectively, \(\varphi \) is the in-plane electric potential, \(E_{j}\) and \(D_{j}\) are the in-plane electric fields and electric displacements, respectively, \(c_{\mathrm {44}}\) represents the shear modulus for the stable electric field, \(d_{\mathrm {11}}\) stands for the dielectric modulus at the stable stress field and\( e_{\mathrm {15}}\) denotes the piezoelectric modulus.

The equilibrium equations from the Gurtin and Murdoch [7] continuum mechanics model read

$$\begin{aligned} \left\| { \sigma _{j\alpha } n_{j} } \right\| +\sigma _{\beta \alpha ,\beta }^{s} =0,\quad \left\| { \sigma _{ji} n_{i} n_{j} } \right\| =\sigma _{\alpha \beta }^{s} k_{\alpha \beta } \end{aligned}$$
(4)

where the superscript s denotes the surface, \(\sigma _{\alpha \beta }^{s} \) is the surface stress tensor, \(k_{\alpha \beta } \) stands for the surface curvature tensor, and \(\left\| { *} \right\| \) represents the jump across the surface.

The surface electric displacement \(D_{j}^{s} \) and the surface stress \(\tau _{jz}^{s} \) in the coupling surface piezoelectric model read [2, 9]

$$\begin{aligned} \tau _{jz}^{s} =c_{44}^{s} w_{\,,j} +e_{15}^{s} \varphi _{,j} ,D_{j}^{s} =e_{15}^{s} w_{,j} -d_{11}^{s} \varphi _{,j} \end{aligned}$$
(5)

in which \(c_{44}^{s} \) is the surface shear modulus for the stable electric field, \(d_{11}^{s} \) denotes the surface dielectric modulus at the stable stress field and \(e_{15}^{s} \) represents the surface piezoelectric modulus.

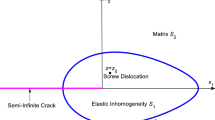
Now consider a piezoelectric body (z-plane) subjected to the in-plane electric displacements \(D_{\mathrm {1}}\), \(D_{\mathrm {2}}\) and the anti-plane shear stresses \(\tau _{\mathrm {1}}\), \(\tau _{\mathrm {2}}\) at infinity, there is a nanocrack of length 2a and a screw dislocation (Burgers vector \({\mathbf{b}}=[b_{z} \;\;b_{\varphi } ]^{\text{ T }})\) locating at any point \(z_{\mathrm {0}}\) as shown in Fig. 1. Substituting (3) into (1) yields

$$\begin{aligned} {\mathbf{M}}\nabla ^{2}{\mathbf{U}}={\mathbf{0}} \end{aligned}$$
(6)

where

$$\begin{aligned} {\mathbf{M}}=\left[ {{\begin{array}{cc} {c_{44} } &{}\quad {e_{15} } \\ {e_{15} } &{}\quad {-\,d_{11} } \\ \end{array} }} \right] ,\quad {\mathbf{U}}=\left[ {{\begin{array}{c} w \\ \varphi \\ \end{array} }} \right] \end{aligned}$$
(7)

and \(\nabla ^{2}={\partial ^{2}} / {\partial x^{2}}+{\partial ^{2}} / {\partial y^{2}}\)denotes the 2D Laplace operator.

The equilibrium Eq. (6) can be reduced to a harmonic equation\(\nabla ^{2}{\mathbf{U}}=0\) and the general solution can be expressed in a complex potential vector \({\mathbf{f}}(z)\) as [14]

$$\begin{aligned} {\mathbf{U}}(z)={\text {Re}}[{\mathbf{f}}(z)] \end{aligned}$$
(8)

in which \({\mathbf{f}}(z)=[f_{w} (z)\;\;f_{\varphi } (z)]^{\text{ T }}\)and \(z=x+\text{ i }y\) represents the complex variable. From (3), (7) and (8), we have

$$\begin{aligned} {\mathbf{\Sigma }}_{x} =\left[ {{\begin{array}{*{20}c} {\tau _{xz} } \\ {D_{x} } \\ \end{array} }} \right] =\frac{{\mathbf{M}}}{2}[{\mathbf{{f}'}}(z)+\overline{{\mathbf{{f}'}}(z)} ],\quad {\mathbf{\Sigma }}_{y} =\left[ {{\begin{array}{*{20}c} {\tau _{yz} } \\ {D_{y} } \\ \end{array} }} \right] =\frac{\text{ i }{\mathbf{M}}}{2}[{\mathbf{{f}'}}(z)-\overline{{\mathbf{{f}'}}(z)} ] \end{aligned}$$
(9)
Fig. 1
figure 1

The screw dislocation and the linear nanocrack

Full size image

The boundary conditions for the two crack faces can be expressed as [32]

$$\begin{aligned}&(\tau _{xz,x}^{s} )^{+}+(\tau _{yz} )^{+}=0,\ (D_{x,x}^{s} )^{+}+(D_{y} )^{+}=0 \end{aligned}$$
(10)
$$\begin{aligned}&(\tau _{xz,x}^{s} )^{-}-(\tau _{yz} )^{-}=0,\quad (D_{x,x}^{s} )^{-}-(D_{y} )^{-}=0 \end{aligned}$$
(11)

where the symbols “\(+\)” and “−” in (10) and (11) represent the upper crack face (\(y>0)\) and the lower crack face (\(y<0)\) as shown in Fig. 1. Substituting (5) into (10) and (11), the boundary conditions are written as

$$\begin{aligned}&(\tau _{yz} )^{+}=-c_{44}^{s} w_{,xx}^{+} -e_{15}^{s} \varphi _{,xx}^{+} ,\quad (D_{y} )^{+}=-e_{15}^{s} w_{,xx}^{+} +d_{11}^{s} \varphi _{,xx}^{+} \end{aligned}$$
(12)
$$\begin{aligned}&(\tau _{yz} )^{-}=c_{44}^{s} w_{,xx}^{-} +e_{15}^{s} \varphi _{,xx}^{-} ,\quad (D_{y} )^{-}=e_{15}^{s} w_{'xx}^{-} -d_{11}^{s} \varphi _{'xx}^{-} \end{aligned}$$
(13)

On the crack faces, \({\mathbf{U}}_{,xx} ={\mathbf{{U}''}}(z)={[{\mathbf{{f}''}}(z)+\overline{{\mathbf{{f}''}}(z)} ]}/ 2 \), the boundary conditions (12) and (13) are then expressed equivalently in the form as

$$\begin{aligned}&\left[ {{\begin{array}{*{20}c} {\tau _{yz} } \\ {D_{y} } \\ \end{array} }} \right] ^{+}=-{\mathbf{M}}^{s}\left[ {{\begin{array}{*{20}c} {w_{,xx} } \\ {\varphi _{,xx} } \\ \end{array} }} \right] ^{+}=-{\mathbf{M}}^{s}{\mathbf{U}}_{,xx}^{+} =-\frac{1}{2}{\mathbf{M}}^{s}[{\mathbf{{f}''}}(z)+\overline{{\mathbf{{f}''}}(z)} ]^{+} \end{aligned}$$
(14a)
$$\begin{aligned}&\left[ {{\begin{array}{*{20}c} {\tau _{yz} } \\ {D_{y} } \\ \end{array} }} \right] ^{-}={\mathbf{M}}^{s}\left[ {{\begin{array}{*{20}c} {w_{,xx} } \\ {\varphi _{,xx} } \\ \end{array} }} \right] ^{-}={\mathbf{M}}^{s}{\mathbf{U}}_{,xx}^{-} =\frac{1}{2}{\mathbf{M}}^{s}[{\mathbf{{f}''}}(z)+\overline{{\mathbf{{f}''}}(z)} ]^{-} \end{aligned}$$
(14b)

where \({\mathbf{M}}^{s}\) denotes the stiffness matrix of the crack faces in stable electric field

$$\begin{aligned} {\mathbf{M}}^{s}=\left[ {{\begin{array}{*{20}c} {c_{44}^{s} } &{}\quad {e_{15}^{s} } \\ {e_{15}^{s} } &{}\quad {-\,d_{11}^{s} } \\ \end{array} }} \right] \end{aligned}$$
(15)

With inserting of (9) into (14), the boundary conditions become

$$\begin{aligned}&\text{ i }{\mathbf{M}}[{\mathbf{{f}'}}(z)-\overline{{\mathbf{{f}'}}(z)} ]^{+}=-{\mathbf{M}}^{s}[{\mathbf{{f}''}}(z)+\overline{{\mathbf{{f}''}}(z)} ]^{+} \end{aligned}$$
(16a)
$$\begin{aligned}&\text{ i }{\mathbf{M}}[{\mathbf{{f}'}}(z)-\overline{{\mathbf{{f}'}}(z)} ]^{-}={\mathbf{M}}^{s}[{\mathbf{{f}''}}(z)+\overline{{\mathbf{{f}''}}(z)} ]^{-} \end{aligned}$$
(16b)

Two boundary Eqs. (16a) and (16b) can be reduced to one via the loop integration [12] as follows: the upper segment of the loop integration begins at the left end and finishes at the right end of the crack while the lower segment of the loop integration begins at the right end and finishes at the left end of the crack, we thus have

$$\begin{aligned} \frac{1}{\text{ i }}{\mathbf{M}}[{\mathbf{f}}(z)-\overline{{\mathbf{f}}(z)} ]=-{\mathbf{M}}^{s}[{\mathbf{{f}'}}(z)+\overline{{\mathbf{{f}'}}(z)} ]\quad z\in L \end{aligned}$$
(17)

The following mapping functions are employed to map the z-plane onto the \(\zeta \)-plane

$$\begin{aligned} z=\omega (\zeta )=\frac{a}{2}\left( {\zeta +\frac{1}{\zeta }} \right) ,\quad \zeta =\omega ^{-1}(z)=\frac{z}{a}\left[ {1+\sqrt{1-\left( {\frac{a}{z}} \right) ^{2}} } \right] \end{aligned}$$
(18)

where \(\zeta =\xi +\text{ i }\eta \) represents the complex variable in \(\zeta \)-plane.

The mapping function pair (18) transforms the physical region (z-plane) into the image region (\(\zeta \)-plane) and the straight line nanocrack (Fig. 1) is mapped onto a circle with unit radius (Fig. 2). After transformation, the boundary Eq. (17) becomes

$$\begin{aligned} \frac{1}{\text{ i }}{\mathbf{M}}[{\mathbf{f}}_{1} (\zeta )-\overline{{\mathbf{f}}_{1} (\zeta )} ]=-{\mathbf{M}}^{s}\left[ {\frac{{\mathbf{{f}'}}_{1} (\zeta )}{{\omega }'(\zeta )}+\frac{\overline{{\mathbf{{f}'}}_{1} (\zeta )} }{\overline{{\omega }'(\zeta )} }} \right] \quad \zeta \in \gamma \end{aligned}$$
(19)
Fig. 2
figure 2

The transformed \(.\zeta \)-plane

Full size image

3 Solution

Consider an infinity plane (z-plane), which contains a piezoelectric screw dislocation (Burgers vector \({\mathbf{b}}=[b_{z} \;\;b_{\varphi } ]^{\text{ T }})\) and a nanocrack, is subjected to the in-plane electric displacements \(D_{\mathrm {1}}\), \(D_{\mathrm {2}}\) and the anti-plane loads \(\tau _{\mathrm {1}}\), \(\tau _{\mathrm {2}}\) at infinity. For piezoelectric solid, the complex potential function can be expressed as

$$\begin{aligned} {\mathbf{f}}(z)={{\Gamma }}z+\frac{1}{2\text{ i }\pi }{\mathbf{b}}\ln (z-z_{0} )+{\mathbf{f}}_{0} (z) \end{aligned}$$
(20)

where \({\mathbf{f}}_{0} (z)\) is the analytic part in \(S^{\mathrm {+}}\) (Fig. 1), and

$$\begin{aligned} {{\Gamma }}={\mathbf{M}}^{-1}\left[ {{\begin{array}{*{20}c} {\tau _{1} -\text{ i }\tau _{2} } \\ {D_{1} -\text{ i }D_{2} } \\ \end{array} }} \right] \end{aligned}$$
(21)

in which the superscript “−1" represents the inverse of the matrix. The boundary conditions \(\tau _{xz} =\tau _{1} \), \(\tau _{yz} =\tau _{2} \) and \(D_{x} =D_{1} \), \(D_{y} =D_{2} \) at infinity require that \({\mathbf{f}}_{0} (\infty )=0\).

The following integration and conformal mapping techniques are used to find the unknown function \({\mathbf{f}}_{0} (z)\). In \(\zeta \)-plane, (20) becomes

$$\begin{aligned} {\mathbf{f}}_{1} (\zeta )=\frac{a}{2}{{\Gamma }}\zeta +\frac{1}{2\text{ i }\pi }{\mathbf{b}}\ln (\zeta -\zeta _{0} )+{\mathbf{f}}_{10} (\zeta ) \end{aligned}$$
(22)

in which \({\mathbf{f}}_{10} (\zeta )\) is the analytic part in \(s+\) (Fig. 2). Substituting (22) into (19), we arrive at

$$\begin{aligned}&\frac{1}{\text{ i }}{\mathbf{M}}[{\mathbf{f}}_{10} (\sigma )-\overline{{\mathbf{f}}_{10} (\sigma )} ]+{\mathbf{M}}^{s}\left[ {\frac{{\mathbf{{f}'}}_{10} (\sigma )}{{\omega }'(\sigma )}+\frac{\overline{{\mathbf{{f}'}}_{10} (\sigma )} }{\overline{{\omega }'(\sigma )} }} \right] \nonumber \\&\quad =-\frac{1}{\text{ i }}{\mathbf{M}}\left[ {\frac{a}{2}{{\Gamma }}\sigma +\frac{1}{2\text{ i }\pi }{\mathbf{b}}\ln (\sigma -\zeta _{0} )-\frac{a}{2\sigma }{{\bar{\Gamma }}}+\frac{1}{2\text{ i }\pi }{\mathbf{b}}\ln \left( {\frac{1}{\sigma }-\bar{{\zeta }}_{0} } \right) } \right] \nonumber \\&\qquad -\,{\mathbf{M}}^{s}\left[ {\frac{\frac{a}{2}{{\Gamma }}+\frac{1}{2\text{ i }\pi }{\mathbf{b}}\frac{1}{\sigma -\zeta _{0} }}{{\omega }'(\sigma )}+\frac{\frac{a}{2}{{\bar{\Gamma }}}-\frac{1}{2\text{ i }\pi }{\mathbf{b}}\frac{1}{\sigma ^{-1}-\bar{{\zeta }}_{0} }}{\overline{{\omega }'(\sigma )} }} \right] \quad (\sigma \in \gamma ) \end{aligned}$$
(23)

In order to find the analytic function \({\mathbf{f}}_{10} (\zeta )\) which satisfies (23) and the boundary condition at infinity, the integration for both sides of (23) is performed on the boundary of the unit orifice (Fig. 2) and then the application of the following Cauchy’s integral formula

$$\begin{aligned} \frac{1}{2\text{ i }\pi }\oint \limits _\gamma {\frac{f(\sigma )}{\sigma -\zeta }\text{ d }\sigma } =-f(\zeta )+f(\infty ) \end{aligned}$$
(24)

This operation transforms the boundary Eq. (23) into a first-order differential equation as follows:

$$\begin{aligned}&\frac{1}{\text{ i }}{\mathbf{Mf}}_{10} (\zeta )+\frac{1}{{\omega }'(\zeta )}{\mathbf{M}}^{s}{\mathbf{{f}'}}_{10} (\zeta )=\frac{a}{2\text{ i }\zeta }{\mathbf{M}}{{\bar{\Gamma }}} +\frac{1}{1-\zeta ^{2}}{\mathbf{M}}^{s}{{\Gamma }}-\frac{1}{2\pi }{\mathbf{Mb}}\ln \left( {\frac{\zeta }{\zeta -1 / {\bar{{\zeta }}_{0} }}} \right) \nonumber \\&\quad +\frac{1}{\text{ i }\pi a}{\mathbf{M}}^{s}{\mathbf{b}}\left[ {\frac{\zeta +\zeta _{0} }{(\zeta ^{2}-1)(\zeta _{0}^{2} -1)}-\frac{1}{(\zeta -1 / {\bar{{\zeta }}_{0} )(\bar{{\zeta }}_{0}^{2} -1)}}} \right] \end{aligned}$$
(25)

The solution of (25) can be derived as ([8], Chapter 5, Eq. (5.17))

$$\begin{aligned} {\mathbf{f}}_{10} (\zeta )=\exp \left\{ {-\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (\zeta )} \right\} \int _\infty ^\zeta {\exp \left\{ {\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (s)} \right\} \cdot {\mathbf{J}}(s)\text{ d }s} \end{aligned}$$
(26)

in which

$$\begin{aligned}&{\mathbf{J}}(s)=\frac{a}{4\text{ i }}[{\mathbf{M}}^{s}]^{-1}{} \mathbf{M}{\bar{\Gamma }} \frac{1}{s}\left( {1-\frac{1}{s^{2}}} \right) -\frac{a}{2}{\mathbf{\Gamma }}\frac{1}{s^{2}}-\frac{a}{4\pi }[{\mathbf{M}}^{s}]^{-1}{\mathbf{Mb}}\left( {1-\frac{1}{s^{2}}} \right) \ln \left( {\frac{s}{s-1 / {\bar{{\zeta }}_{0} }}} \right) \nonumber \\&\quad +\frac{1}{2\text{ i }\pi }{\mathbf{b}}\left( {1-\frac{1}{s^{2}}} \right) \left[ {\frac{s+\zeta _{0} }{(s^{2}-1)(\zeta _{0}^{2} -1)}-\frac{1}{(s-1 / {\bar{{\zeta }}_{0} )(\bar{{\zeta }}_{0}^{2} -1)}}}\right] \end{aligned}$$
(27)

The unknown function \({\mathbf{f}}_{0} (z)\) in (20) is then given by

$$\begin{aligned} {\mathbf{f}}_{0} (z)={\mathbf{f}}_{10} [\omega ^{-1}(z)] \end{aligned}$$
(28)

It can be verified that the value of \({\mathbf{f}}_{10} (\zeta )\) in (26) vanishes as \(\zeta \rightarrow \infty \) and thus the boundary condition \({\mathbf{f}}_{0} (\infty )=0\) is satisfied.

When the effects of the surface piezoelectricity are neglected, \({\mathbf{M}}^{s}=0\), the boundary Eqs. (17) and (19) reduce to, respectively

$$\begin{aligned}&{\mathbf{f}}^{*}(z)-\overline{{\mathbf{f}}^{*}(z)} =0\quad z\in L \end{aligned}$$
(29)
$$\begin{aligned}&{\mathbf{f}}_{1}^{*} (\zeta )-\overline{{\mathbf{f}}_{1}^{*} (\zeta )} =0\quad \zeta \in \gamma \end{aligned}$$
(30)

where the superscript “*” denotes the complex potential functions in the cases where the effects of the surface piezoelectricity are not incorporated. After similar derivation, the complex potential function is obtained as

$$\begin{aligned} {\mathbf{f}}_{1}^{*} (\zeta )=\frac{a}{2}{{\Gamma }}\zeta +\frac{a}{2\zeta }{{\bar{\Gamma }}}+\frac{1}{2\text{ i }\pi }{\mathbf{b}}[\ln (\zeta -\zeta _{0} )-\ln (\zeta -1 / {\bar{{\zeta }}_{0} })+\ln \zeta ] \end{aligned}$$
(31)

The solution (31) is the same as that in Muskhelishvili [16].

4 Stresses and electrical displacements

From (9), the electric displacement and the stress fields can be written as

$$\begin{aligned} {\mathbf{\Sigma }}_{x} -\text{ i }{\mathbf{\Sigma }}_{y} ={\mathbf{M{f}'}}(z) \end{aligned}$$
(32)

When the effects of the surface piezoelectricity are incorporated, substituting (26), (28), (20) and (18) into (32) yields

$$\begin{aligned}&{\mathbf{\Sigma }}_{x} -\text{ i }{\mathbf{\Sigma }}_{y} =-\frac{1}{\text{ i }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\exp \left\{ {-\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (\zeta )} \right\} \int _\infty ^\zeta {\exp \left\{ {\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (s)} \right\} \cdot {\mathbf{J}}(s)\text{ d }s} \nonumber \\&\quad +\,\frac{a}{2\text{ i }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{} \mathbf{M}{\bar{\Gamma }} \frac{1}{\zeta }-\frac{1}{2\pi }{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{Mb}}\ln \left( {\frac{\zeta }{\zeta -1 / {\bar{{\zeta }}_{0} }}} \right) \nonumber \\&\quad +\,\frac{1}{\text{ i }\pi a}{\mathbf{Mb}}\left[ {\frac{\zeta _{0}^{2} }{(\zeta _{0}^{2} -1)(\zeta -\zeta _{0} )}-\frac{1}{(\zeta -1 / {\bar{{\zeta }}_{0} })(\bar{{\zeta }}_{0}^{2} -1)}} \right] +{\mathbf{M }\Gamma } \end{aligned}$$
(33)

In the case where the effects of the surface piezoelectricity are excluded, substituting (31) and (18) into (32), we have

$$\begin{aligned} {\mathbf{\Sigma }}_{x}^{*} -\text{ i }{\mathbf{\Sigma }}_{y}^{*} ={\mathbf{M}}\left[ {\frac{\zeta ^{2}{{ \Gamma }}-{{\bar{\Gamma }}}}{\zeta ^{2}-1}+\frac{1}{2\text{ i }\pi {\omega }'(\zeta )}{\mathbf{b}}\left( {\frac{1}{\zeta -\zeta _{0} }-\frac{1}{\zeta -1 / {\bar{{\zeta }}_{0} }}+\frac{1}{\zeta }} \right) } \right] \end{aligned}$$
(34)

It can be verified that the stresses and the electric displacements represented by (33) exhibit the finite values at the crack tip (as shown in Sect. 6) while those expressed by (34) tend to be infinity.

The intensity factors of the electric displacements and stresses are different from those of the classical solution when the effects of the surface piezoelectricity are incorporated. Xiao et al. [33] developed a rigorous solution of the piezoelectric materials with elliptic cavity under anti-plane deformation and extended the solution to the crack problem, and later, Xiao et al. [34] proposed a closed-form solution for a cracked equilateral triangle hole under in-plane electric load and anti-plane load. In their work, however, the potential function was expanded in infinite Laurent series and then finite terms of the series were truncated for following derivation. Their results showed that the intensity factors are size dependent but non-trivial at the crack tip. Similar results can be found in Guo and Li [6] where the forms of the potential functions were taken in finite terms previously.

Wang and Xu [31] investigated the screw dislocation interacting with the finite crack incorporating the surface piezoelectricity in anti-plane shear deformation, and Wang and Zhou [32] studied the anti-plane problem of a hexagonal piezoelectric solid containing a crack with the surface piezoelectricity. In their analysis, the stresses and the electric displacements were presented in infinite series and then the finite terms were truncated for following calculation. Their results indicated that the singularities of the electric displacements and stresses at the two crack tips are the strong square root and the weak logarithmic.

Walton [25] investigated the influence of the deformed crack-surface curvature and the stretching on the stress singularity for mixed mode fracture problems when the surface elasticity was included, and concluded that the stress at the crack tip was bounded (finite) for the straight line crack in mode-III deformation.

In present method, the problem is transformed into a first-order differential equation by the boundary integration and the Cauchy’s integral formula, the differential equation is solved in image region and then the solution in physical region is established via the inverse mapping. In this method, it is unnecessary in derivation process to preset some functions in the infinite series and the solution is derived in nature. The derived solution (33) shows that the electric displacements and the stresses at the crack tip are finite, and as a result, the singularities at the crack tip are eliminated.

5 Dislocation forces

The perturbed stresses and electric displacements, which can be regarded as the increment of the stresses from an operation that the crack is engendered in an infinite body with a stable dislocation and then the loads are applied at infinity, are obtained by subtracting the stresses corresponding to an uncracked infinite elastic body with a screw dislocation from (33) and (34) respectively, and then taking the limitation of \(z\rightarrow z_{0}\)

$$\begin{aligned} {\tilde{\varvec{\Sigma }}}_{x} (z_{0} )-\text{ i }{\tilde{\varvec{\Sigma }}} _{y} (z_{0} )=\lim \limits _{z\rightarrow z_{0} } \left( {{\varvec{\Sigma }}_{x} -\text{ i }{{\varvec{\Sigma }}}_{y} -\frac{1}{2\text{ i }\pi }{\mathbf{Mb}}\frac{1}{z-z_{0} }} \right) \end{aligned}$$
(35)

where

$$\begin{aligned} \widetilde{{\mathbf{\Sigma }}}_{x1} (z_{0} )-\text{ i }\widetilde{{\mathbf{\Sigma }}}_{y1} (z_{0} )=\mathbf{M}{\Gamma }+\frac{1}{\text{ i }}{\mathbf{M}} \ [{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\cdot e^{\frac{a}{\text{2i }}\ [{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\left( {\zeta _{0} +\frac{1}{\zeta _{0} }} \right) }\int _\infty ^{\zeta _{0} } {e^{-\frac{a}{\text{2i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\left( {\zeta +\frac{1}{\zeta }} \right) }\cdot {\mathbf{J}}(s)} \text{ d }s \end{aligned}$$
(36)

With inserting of (33) and (34) into (35), respectively, the perturbed stresses and electric displacements become

With surface piezoelectricity

$$\begin{aligned}&{\tilde{\varvec{\Sigma }}}_{x} (z_{0} )-\text{ i }{\tilde{\varvec{\Sigma }}}_{y} (z_{0} ) =-\frac{1}{\text{ i }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\exp \left\{ {-\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (\zeta _{0} )} \right\} \int _\infty ^{\zeta _{0} } {\exp \left\{ {\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (s)} \right\} \cdot {\mathbf{J}}(s)\text{ d }s} \nonumber \\&\quad +\,\frac{a}{2\text{ i }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\varvec{M{\bar{\Gamma }}}} \frac{1}{\zeta _{0} }-\frac{1}{2\pi }{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{Mb}}\ln \left( {\frac{\zeta _{0} }{\zeta _{0} -1/ {\bar{{\zeta }}_{0} }}} \right) \nonumber \\&\quad +\,\frac{1}{\text{ i }\pi a}{\mathbf{Mb}}\left[ {\frac{\zeta _{0} }{(\zeta _{0}^{2} -1)^{2}}-\frac{1}{(\zeta _{0} -1 / {\bar{{\zeta }}_{0} })(\bar{{\zeta }}_{0}^{2} -1)}} \right] +{\mathbf{M }\Gamma } \end{aligned}$$
(37)

Without surface piezoelectricity

$$\begin{aligned} {\tilde{\varvec{\Sigma }}}_{x}^{*} (z_{0} )-\text{ i }{\tilde{\varvec{\Sigma }}}_{y}^{*} (z_{0} )={\mathbf{M}}\frac{{{\Gamma }}\zeta _{0}^{2} -{{\bar{\Gamma }}}}{\zeta _{0}^{2} -1}-\frac{1}{\text{ i }\pi a}{\mathbf{Mb}}\left[ {\frac{\zeta _{0} }{(\zeta _{0}^{2} -1)(\zeta _{0} \bar{{\zeta }}_{0} -1)}+\frac{\zeta _{0} }{(\zeta _{0}^{2} -1)^{2}}} \right] \end{aligned}$$
(38)

The dislocation forces from the Peach Koehler formula in [21] are expressed as

$$\begin{aligned} f_{x} -\text{ i }f_{y} =\text{ i }{\mathbf{b}}^{\text{ T }}[{\tilde{\varvec{\Sigma }}} _{x} (z_{0} )-\text{ i }{\tilde{\varvec{\Sigma }}}_{y} (z_{0} )] \end{aligned}$$
(39)

Substituting (37) and (38) into (39), respectively, the dislocation forces for both cases are

With surface piezoelectricity

$$\begin{aligned} f_{x} -\text{ i }f_{y}= & {} -{\mathbf{b}}^{\text{ T }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\exp \left\{ {-\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (\zeta _{0} )} \right\} \int _\infty ^{\zeta _{0} } {\exp \left\{ {\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (s)} \right\} \cdot {\mathbf{J}}(s)\text{ d }s} \nonumber \\&+\,\frac{a}{2}{\mathbf{b}}^{\text{ T }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{{M{\bar{\Gamma }}}} \frac{1}{\zeta _{0} }-\frac{\text{ i }}{2\pi }{\mathbf{b}}^{\text{ T }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{Mb}}\ln \left( {\frac{\zeta _{0} }{\zeta _{0} -1 / {\bar{{\zeta }}_{0} }}} \right) \nonumber \\&+\,\frac{1}{\pi a}{\mathbf{b}}^{\text{ T }}{\mathbf{Mb}}\left[ {\frac{\zeta _{0} }{(\zeta _{0}^{2} -1)^{2}}-\frac{1}{(\zeta _{0} -1 / {\bar{{\zeta }}_{0} })(\bar{{\zeta }}_{0}^{2} -1)}} \right] +\text{ i }{\mathbf{b}}^{\text{ T }}{\mathbf{M }\Gamma } \end{aligned}$$
(40)

Without surface piezoelectricity

$$\begin{aligned} f_{x}^{*} -\text{ i }f_{y}^{*} =\text{ i }{\mathbf{b}}^{\text{ T }}{\mathbf{M}}\frac{{{\Gamma }}\zeta _{0}^{2} -{{\bar{\Gamma }}}}{\zeta _{0}^{2} -1}-\frac{1}{\pi a}{\mathbf{b}}^{\text{ T }}{\mathbf{Mb}}\left[ {\frac{\zeta _{0} }{(\zeta _{0}^{2} -1)(\zeta _{0} \bar{{\zeta }}_{0} -1)}+\frac{\zeta _{0} }{(\zeta _{0}^{2} -1)^{2}}} \right] \end{aligned}$$
(41)

For the case where the screw dislocation in z-plane is located on the x-axis and \(z_{0}=x{0}>a\), in \(\zeta \)-plane, we have

$$\begin{aligned} {\mathbf{F}}_{x1} -\text{ i }{\mathbf{F}}_{y1} =\text{ i }{\mathbf{b}}^{T}{\mathbf{M }\Gamma }+{\mathbf{b}}^{T}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\cdot e^{\frac{a}{\text{2i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\left( {\xi _{0} +\frac{1}{\xi _{0} }} \right) }\int _\infty ^{\xi _{0} } {e^{-\frac{a}{\text{2i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\left( {\zeta +\frac{1}{\zeta }} \right) }\cdot {\mathbf{J}}(s)} \text{ d }s \end{aligned}$$
(42)

In this case, the dislocation forces (40) and (41) reduce to, respectively

$$\begin{aligned} f_{x} -\text{ i }f_{y}= & {} -{\mathbf{b}}^{\text{ T }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\exp \left\{ {-\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (\xi _{0} )} \right\} \int _\infty ^{\xi _{0} } {\exp \left\{ {\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (s)} \right\} \cdot {\mathbf{J}}(s)\text{ d }s} \nonumber \\&+\,\frac{a}{2}{\mathbf{b}}^{\text{ T }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{} \mathbf{M}{\bar{\Gamma }} \frac{1}{\xi _{0} }-\frac{\text{ i }}{2\pi }{\mathbf{b}}^{\text{ T }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{Mb}}\ln \left( {\frac{\xi _{0}^{2} }{\xi _{0}^{2} -1}} \right) +\text{ i }{\mathbf{b}}^{\text{ T }}{\mathbf{M }\Gamma } \end{aligned}$$
(43)

and

$$\begin{aligned} f_{x}^{*} -\text{ i }f_{y}^{*} =\text{ i }{\mathbf{b}}^{\text{ T }}{\mathbf{M}}\frac{{{ \Gamma }}\xi _{0}^{2} -{{\bar{\Gamma }}}}{\xi _{0}^{2} -1}-\frac{2}{\pi a}{\mathbf{b}}^{\text{ T }}{\mathbf{Mb}}\frac{\xi _{0} }{(\xi _{0}^{2} -1)^{2}} \end{aligned}$$
(44)

6 Numerical analysis and discussion

In this section, the effects of the surface piezoelectricity on the stresses, the electric displacements and the piezoelectric dislocation forces are analyzed and discussed, respectively. The material parameters suggested by Xiao et al. (2015) for PZT-5H piezoelectric ceramic material are as follows:

$$\begin{aligned} c_{44} =3.53\times 10^{10}\ {\text{ N }} / {\text{ m}^{\text{2 }}},\quad e_{15} =17.0\ {\text{ C }} / {\text{ m}^{2}},\quad d_{11} =1.51\times 10^{-8}\ {\text{ C}^{2}} / {\text{ Nm}^{2}} \end{aligned}$$

and the stiffness matrix of the crack faces reads [4, 9]

$$\begin{aligned} {\mathbf{M}}^{s}=\left[ {{\begin{array}{cc} {7.56\ {\text{ N }}/ {\text{ m }}} &{}\quad {3\times 10^{-8}\ {\text{ C }} / {\text{ m }}} \\ {3\times 10^{-8}\ {\text{ C }} / {\text{ m }}} &{}\quad 0 \\ \end{array} }} \right] \end{aligned}$$
(45)

6.1 Effects of the surface piezoelectricity on stresses and electric displacements

In the case without screw dislocation but the anti-plane shear stresses \(\tau _{\mathrm {1}}\), \(\tau _{\mathrm {2}}\) and electric displacements \(D_{\mathrm {1}}\), \(D_{\mathrm {2}}\) at infinity, (33) and (34) reduce to, respectively

$$\begin{aligned} {\mathbf{\Sigma }}_{x} -\text{ i }{\mathbf{\Sigma }}_{y}= & {} {\mathbf{M }\Gamma }-\frac{1}{\text{ i }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\exp \left\{ {-\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (\zeta )} \right\} \int _\infty ^\zeta {\exp \left\{ {\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (s)} \right\} \cdot {\mathbf{J}}(s)\text{ d }s} \nonumber \\&+\,\frac{a}{2\text{ i }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{} \mathbf{M}{\bar{\Gamma }} \frac{1}{\zeta } \end{aligned}$$
(46)

and

$$\begin{aligned} {\mathbf{\Sigma }}_{x}^{*} -\text{ i }{\mathbf{\Sigma }}_{y}^{*} ={\mathbf{M}}\frac{\zeta ^{2}{{\Gamma }}-{{\bar{\Gamma }}}}{\zeta ^{2}-1} \end{aligned}$$
(47)

in which \({\mathbf{J}}(s)\) reduces to

$$\begin{aligned} {\mathbf{J}}(s)=\frac{a}{4\text{ i }}[{\mathbf{M}}^{s}]^{-1}{} \mathbf{{M}}{\bar{\Gamma }} \frac{1}{s}\left( {1-\frac{1}{s^{2}}} \right) -\frac{a}{2}{{\Gamma }}\frac{1}{s^{2}} \end{aligned}$$
(48)

The dimensionless stress \(\tau _{yz} \text{/ }\tau _{2} \) versus the ratio \(x\text{/ }a\) in the case of \(\tau _{1} =\tau _{2} \) and \(D_{1} =D_{2} =0\) is shown in Fig. 3a and the variation of the dimensionless electric displacement \({D_{y} } / {D_{2} }\) near the crack tip for \(D_{1} =D_{2} \) and \(\tau _{1} =\tau _{2} =0\) is shown in Fig. 3b The results of the classical solution are also shown for comparison.

It is seen that the dimensionless electric displacement and dimensionless stress decrease as the ratio x/a increases, and the results from the classical solution are always higher than those with the surface piezoelectricity.

Fig. 3
figure 3

a the dimensionless stress \(\tau _{yz} \text{/ }\tau _{2} \) versus \(x\text{/ }a\) for \(\tau _{1} =\tau _{2} \) and \(D_{1} =D_{2} =0\); b the dimensionless electric displacement \({D_{y} } / {D_{2} }\) versus \(x\text{/ }a\) for \(D_{1} =D_{2} \) and \(\tau _{1} =\tau _{2} =0\)

Full size image

The significant difference can be observed near the crack tip (\(x / a=1)\) where the effects of the surface piezoelectricity decrease as the crack length a increases. The shear stress and the electric displacement by the present solution with surface piezoelectricity are finite, which is against that of the classical solution where both of them tend to be infinity at the crack tip.

Fig. 4
figure 4

a The dimensionless stress \(\tau _{yz} /\tau _{1} \) versus the ratio \(x\text{/ }a\) for \(a = 5\) nm and \(D_{1} =D_{2} =0\); b the dimensionless electric displacement \({D_{y} } / {D_{1} }\) versus \(x\text{/ }a\) for \(a= 5\) nm and \(\tau _{1} =\tau _{2} =0\)

Full size image

When the crack length is fixed as \(a = 5\) nm, the variation of the dimensionless stress \(\tau _{yz} /\tau _{1} \) versus the ratio \(x\text{/ }a\) for \(D_{1} =D_{2} =0\) is shown in Fig. 4a while the dimensionless electric displacement \({D_{y} } / {D_{1} }\) versus the ratio \(x\text{/ }a\) for \(\tau _{1} =\tau _{2} =0\) is plotted in Fig. 4b. It is similar to that observed in Fig. 3, i.e., at the crack tip, both the stresses and the electric displacements for all cases are finite. It is also seen that the values of the stress and the electric displacement increase with an increasing of the ratios \(\tau _{2} /\tau _{1} \) and \({D_{2} } / {D_{1} }\), respectively.

6.2 Effects of the surface piezoelectricity on dislocation forces

When the shear stresses \(\tau _{\mathrm {1}}\), \(\tau _{\mathrm {2}}\) and the electric displacements \(D_{\mathrm {1}}\), \(D_{\mathrm {2}}\) at infinity vanish in the piezoelectric material, and the electric potential dislocation \(b_{\varphi } =0\), the position of the screw dislocation is \(x_0(z_{0}=\bar{z}_{0}=x_{0}>a)\) on the x-axis, (43) and (44) reduce to, respectively

$$\begin{aligned} f_{x} -\text{ i }f_{y}= & {} -{\mathbf{b}}^{\text{ T }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\exp \left\{ {-\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (\xi _{0} )} \right\} \int _\infty ^{\xi _{0} } {\exp \left\{ {\frac{1}{\text{ i }}[{\mathbf{M}}^{s}]^{-1}{\mathbf{M}}\omega (s)} \right\} \cdot {\mathbf{J}}(s)\text{ d }s} \nonumber \\&-\,\frac{\text{ i }}{2\pi }{\mathbf{b}}^{\text{ T }}{\mathbf{M}}[{\mathbf{M}}^{s}]^{-1}{\mathbf{Mb}}\ln \left( {\frac{\xi _{0}^{2} }{\xi _{0}^{2} -1}} \right) \end{aligned}$$
(49)

and

$$\begin{aligned} f_{x}^{*} -\text{ i }f_{y}^{*} =-\frac{2}{\pi a}{\mathbf{b}}^{\text{ T }}{\mathbf{Mb}}\frac{\xi _{0} }{(\xi _{0}^{2} -1)^{2}} \end{aligned}$$
(50)

in which \({\mathbf{J}}(s)\) reduces to

$$\begin{aligned} {\mathbf{J}}(s)= & {} -\frac{a}{4\pi }[{\mathbf{M}}^{s}]^{-1}{\mathbf{Mb}}\left( {1-\frac{1}{s^{2}}} \right) \ln \left( {\frac{s}{s-1 / {\bar{{\zeta }}_{0} }}} \right) \nonumber \\&+\,\frac{1}{2\text{ i }\pi }{\mathbf{b}}\left( {1-\frac{1}{s^{2}}} \right) \left[ {\frac{s+\zeta _{0} }{(s^{2}-1)(\zeta _{0}^{2} -1)}-\frac{1}{(s-1 / {\bar{{\zeta }}_{0} )(\bar{{\zeta }}_{0}^{2} -1)}}} \right] \end{aligned}$$
(51)

The dimensionless dislocation force \({f_{x} \pi a} / {2c_{44} b_{z}^{2} }\) versus the ratio \({x_{0} } / a \) (the relative position) is shown in Fig. 5. It is seen that the magnitudes of the dislocation forces with the surface piezoelectricity are always less than that from the classical theory and the effects of the surface piezoelectricity on the dislocation force are localized, i.e., the dislocation force \({f_{x} \pi a} / {2c_{44} b_{z}^{2} }\) approaches to zero as the ratio \({x_{0} } / a\) increases. The dislocation forces are negative for all cases (thus the dislocation is always attracted by the crack), and their magnitudes decrease with the reduction in the crack length.

Fig. 5
figure 5

The dimensionless dislocation force \({f_{x} \pi a} / {2c_{44} b_{z}^{2} }\) versus the ratio \({x_{0} } / a \)

Full size image

7 Oblique crack problem

Certainly, oblique problems can also be solved by employing the same method as being used in the above analysis on the horizontal crack problem. As shown in Fig. 6, the rotation of the crack can be replaced by the rotation of the element or the coordinate system.

Fig. 6
figure 6

Element rotation replace crack rotation. a horizontal crack; b oblique crack

Full size image

By virtue of the identical stress state element from (a) to (b), referring to Fig. 6, the relation between the old element (a) to the new element (b) reads

$$\begin{aligned} \left\{ {{\begin{array}{ll} {{\tau }'_{1} =-\tau _{1} \sin \alpha +\tau _{2} \cos \alpha } \\ {{\tau }'_{2} =\tau _{1} \cos \alpha +\tau _{2} \sin \alpha } \\ \end{array} }} \right. \end{aligned}$$
(52)

and

$$\begin{aligned} \left\{ {{\begin{array}{ll} {{D}'_{1} =D_{1} \cos ^{2}\alpha +D_{2} \sin ^{2}\alpha } \\ {{D}'_{2} =D_{1} \sin ^{2}\alpha +D_{2} \cos ^{2}\alpha } \\ \end{array} }} \right. \end{aligned}$$
(53)

Therefore, the solution for the problem of the oblique crack with clockwise angle can be directly obtained by replacing the loads \(\left\{ {\tau _{1} ,\tau _{2} ;D_{1} ,D_{2} } \right\} \)in equations of the horizontal crack with the associating forms of the loads \(\left\{ {{\tau }'_{1} ,{\tau }'_{2} ;{D}'_{1} ,{D}'_{2} } \right\} \).

8 Conclusions

A solution for the screw dislocation interacting with the nanocrack incorporating the surface piezoelectricity under anti-plane loads was developed. The problem was reduced to a first-order differential equation by the mapping function, the boundary integration and the Cauchy integral formula. The solution in physical region was then established via the inverse mapping.

Compared to the solutions reported in the literature, the present solution was derived without pre-settings and expressed in finite form. This is different from the solutions by others in which some functions were assumed to be in the infinite series and then finite terms were truncated for following analysis and calculation. The results by the present solution presented that the stresses and the electric displacements are finite at the crack tip when the effects of the surface piezoelectricity are incorporated and, as a result, the intensity factors of the stresses and electric displacements are zero.

In the case of incorporating the effects of the surface piezoelectricity, the numerical results indicated that the stresses, the electric displacements and the dislocation forces are size dependent and their magnitudes are always less than those by the classical solution. With an increasing in the crack length, the effects of the surface piezoelectricity weaken and the electric displacements, the stresses, and the dislocation forces from the present solution approach to those by the classical solution.