1 Introduction

The analysis on the propagation of surface waves is an interesting topic for researchers and scientists in the field of geophysics, civil engineering, and earthquake engineering. The propagation of SH-waves though the surface irregularity may lead to the scattering of surface waves (Love type waves and SH-waves), which may further affect the stability of engineering structures. The generation of surface waves takes place after the occurrence of earthquake. There are different types of orthotropic materials like carbon fiber, prepreg, wood, biological tissues, polymers such as Low-Density Polyethylene (LDPE), Polyethylene Terephthalate (PET), and so on that can be found in the real-world scenarios. Materials properties of orthotropic material totally depends along the coordinate axes. There are different kinds of orthotropic materials like carbon fiber, prepreg, wood, biological tissues which are orthotropic in nature. Material properties of orthotropic materials totally depend along the coordinate axes. There exist some sorts of materials that are also viscoelastic in nature. The materials that respond elastically under the influence of small transient forces but behaves viscously under the impact of long durational forces are called viscoelastic materials [5]. In the viscoelastic structures, stress does not depend only on strain but also on strain-rate. There exist different types of viscoelastic materials viz. carbon fiber, prepreg, bitumen materials, etc., can be used in the construction of engineering structures.

The investigation on orthotropic viscoelastic modeling of polymeric battery separator has been accomplished by Yan et al. [16]. Several researchers put significant efforts to deal with the linear orthotropic viscoelastic structures. Cansız et al. [1] studied orthotropic viscoelastic material model for passive myocardium: theory and algorithmic treatment. There are different kinds of rock structures that can be found on the earth’s crust. The upper surface of these materials is not smooth. There may exist some kinds of irregularity on the upper surface of these structures. Surface irregularity occurs in the upper surface of some medium due to different natural phenomena viz. weathering, erosion, and external impacts, etc. Due to SH-waves propagation through the surface irregularity of medium, scattering phenomena take place. Reflection phenomena occurs due to scattering of SH-waves through the surface irregularity. Therefore, induced reflection wave field may damage the shape of surface irregularity of the medium. Therefore, it is important to investigate the scattering nature and propagation phenomena of SH-waves through the surface irregularity in the medium.

Wolf [15] studied the propagation of Love waves through the surface irregularity in a layered isotropic elastic structure. The phenomena of the scattering of Love waves through the irregularity boundary of an elastic layer overlying an elastic half-space has been investigated by Slavin and Wolf [12]. Fung and Eom [4] discussed the bistatic wave scattering and reflection characteristics due to the irregular interface of the inhomogeneous layered elastic structure. Chattopadhyay et al. [2] studied the scattering characteristics of SH-waves due to the interaction of Love waves and irregular surface of a layered isotropic viscoelastic structure. Negi and Singh [7] studied the propagation and scattering characteristics of Love waves through the irregular surface of a transversely isotropic piezoelectric composite structure. Singh and Kumari [11] analyzed the scattering behavior of plane SH-waves propagating in a layered piezomagnetic structure containing surface irregularity. Singh et al. [10] investigated on the scattering phenomena of Love waves passing through the upper irregular surface of a layered porous-piezoelectric structure. Chattopadhyay [3] investigated the propagation of SH-waves in a layered and irregular viscoelastic structure. Singh et al. [9] studied the impact of irregularity on SH-type wave propagation in micropolar elastic composite structure.

It has been found from the existing literatures that many researchers have done the investigation of propagation and scattering characteristics of SH-wave and Love waves interacting through the surface irregularity in the isotropic elastic, isotropic viscoelastic, piezoelectric, and piezomagnetic layered structure. But, to the best of author’s knowledge, the study on the scattering and reflection characteristics of SH-waves in a layered orthotropic viscoelastic composite structure with surface irregularity has not been accomplished till date. These facts motivated the authors to investigate the scattering and reflection characteristics of SH-waves passing through the surface irregularity in the layered orthotropic viscoelastic composite structure. In this paper, scattering and reflection characteristics of SH-waves propagating through the surface irregularity in the orthotropic viscoelastic composite structure have been investigated. Analytical expressions of dispersion and damping relations of scattered SH-waves have been obtained. The expressions of displacement components due to scattering of SH-waves for different type of surface irregularity have been derived. Impact of anisotropy parameter (related to shear modulus) of upper layer on the phase velocity and attenuation coefficient has also been discussed. The effects of vertical irregularity parameter and anisotropy parameter of upper layer on the reflected displacement fields have been observed for three distinct surface irregularity viz. parabolic, triangular notch, and rectangular, respectively. A comparative observation for the reflected displacement can be done for three types of surface irregularity.

2 Formulation of the problem

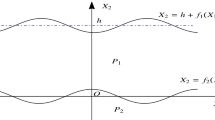
In the present study, a model of linear orthotropic viscoelastic layer of thickness \(H\) overlying orthotropic viscoelastic half-space has been considered. A rectangular coordinate system has been selected in such a way that SH-waves (horizontally polarized shear waves) propagate along the direction of \(y\)-axis. In this model, x-axis is considered along the downwards direction, and z-axis is considered along the oscillations of SH-waves. The origin is denoted by \(x = 0\) which is situated between the layer and half-space of this medium.

The equation of the upper free surface containing surface irregularity can be expressed as

$$ x = x_{B} = - H + bh(y), $$
(1)

in which, the term \(h(y)\) can be written as

$$ h(y) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{for}}\,\,\,\,y \le - \frac{s}{2}\,\,\,{\text{and}}\,\,\,y \ge \frac{s}{2}} \hfill \\ {h_{0} (y),} \hfill & {{\text{for}}\,\,\,\, - \frac{s}{2} \le y \le \frac{s}{2}} \hfill \\ \end{array} } \right.. $$
(2)

where \(s\) indicates the span of the surface irregularity;\(H\) denotes the thickness of the upper layer;\(b\,\,( \ll 1)\) denotes the amplitude of the surface irregularity, and \(h_{0} (y)\) associated with the shape of the surface irregularity of the upper layer. The geometry of the present model is depicted in Fig. 1.

Fig. 1
figure 1

Geometry of the problem

Full size image

The displacement components during the propagation of SH-waves can be written as

$$ u_{1} = v_{1} = 0,\,\,\,w_{1} = w_{1} (x,\,\,y,\,\,t),\,\,\,u_{2} = v_{2} = 0,\,\,w_{2} = w_{2} (x,\,\,y,\,\,t), $$
(3)

where \((u_{p} ,v_{p} ,w_{p} )\) are the components of displacement along x, y and z-axis direction, respectively; p = 1 corresponds to the upper layer while p = 2 associated with the lower half-space.

The equations of motion in absence of external forces can be expressed as

$$ \sigma_{ij,j} = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }},\quad (i,j = 1,2,3) $$
(4)

where \(\sigma_{ij}\) are components of stress tensor; \(u_{i}\) is the displacement components; \(\rho\) is the density of the medium.

Stress–strain relations in orthotropic medium can be written as

$$ \left[ {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ {\sigma_{33} } \\ {\sigma_{23} } \\ {\sigma_{13} } \\ {\sigma_{12} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {c_{11} } &\quad {c_{12} } &\quad {c_{13} } &\quad 0 &\quad 0 &\quad 0 \\ {c_{12} } & {c_{22} } & {c_{23} } & 0 & 0 & 0 \\ {c_{13} } & {c_{23} } & {c_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {c_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {c_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {c_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{11} } \\ {\varepsilon_{22} } \\ {\varepsilon_{33} } \\ {\varepsilon_{23} } \\ {\varepsilon_{13} } \\ {\varepsilon_{12} } \\ \end{array} } \right], $$
(5)

where \( \, c_{ij} \left( {i,j = 1,2,...6} \right)\), \(\varepsilon_{ij} \left( {i,j = 1,2,3} \right)\) are the components of elastic constants and strain, respectively.

Due to viscoelasticity in the considered medium, the elastic constants of the orthotropic medium can be expressed as [13, 14]

$$ \left\{ \begin{gathered} c_{11} = c_{11}^{R} + c_{11}^{I} \frac{\partial }{\partial t},\,\,c_{12} = c_{12}^{R} + c_{12}^{I} \frac{\partial }{\partial t},\,\,c_{13} = c_{13}^{R} + c_{13}^{I} \frac{\partial }{\partial t},\,\,c_{33} = c_{33}^{R} + c_{33}^{I} \frac{\partial }{\partial t}, \hfill \\ c_{44} = c_{44}^{R} + c_{44}^{I} \frac{\partial }{\partial t},\,\,c_{55} = c_{55}^{R} + c_{55}^{I} \frac{\partial }{\partial t},\,\,c_{66} = c_{66}^{R} + c_{66}^{I} \frac{\partial }{\partial t}, \hfill \\ \end{gathered} \right\}, $$
(6)

where \(c_{11}^{R} ,\,\,c_{12}^{R} ,\,\,c_{13}^{R} ,\,\,c_{33}^{R} ,\,\,c_{44}^{R} ,\,\,c_{55}^{R} ,\,\,c_{66}^{R} ,\,\,c_{11}^{I} ,\,\,c_{12}^{I} ,\,\,c_{13}^{I} ,\,\,c_{33}^{I} ,\,\,c_{44}^{I} ,\,\,c_{55}^{I} \,\,{\text{and}}\,\,c_{66}^{I} \,\) are the real and imaginary part of elastic coefficients, respectively.

Strain components and displacement components can be related as

$$ \varepsilon_{11} = \frac{\partial u}{{\partial x}},\varepsilon_{22} = \frac{\partial v}{{\partial y}},\varepsilon_{33} = \frac{\partial w}{{\partial z}},\varepsilon_{23} = \frac{1}{2}\left( {\frac{\partial w}{{\partial y}} + \frac{\partial v}{{\partial z}}} \right),\varepsilon_{13} = \frac{1}{2}\left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}}} \right),\varepsilon_{12} = \frac{1}{2}\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right). $$
(7)

Using Eqs. (3), (5), (6), and (7) in Eq. (4), we obtain

$$ \left( {c_{55}^{pR} + c_{55}^{pI} \frac{\partial }{\partial t}} \right)\frac{{\partial^{2} w_{p} }}{{\partial x^{2} }} + \left( {c_{44}^{pR} + c_{44}^{pI} \frac{\partial }{\partial t}} \right)\frac{{\partial^{2} w_{p} }}{{\partial y^{2} }} = \rho_{p} \frac{{\partial^{2} w_{p} }}{{\partial t^{2} }}, $$
(8)

where \(p = 1,\,\,2.\) Here, subscript 1 is related with the linear orthotropic viscoelastic layer and subscript 2 corresponds to the linear orthotropic viscoelastic half-space.

Equation (8) can be rewritten as

$$ \frac{{\partial^{2} w_{p} }}{{\partial y^{2} }} + \frac{1}{{\overline{\lambda }_{p}^{2} }}\frac{{\partial^{2} w_{p} }}{{\partial x^{2} }} = \frac{1}{{\overline{\beta }_{p}^{2} }}\frac{{\partial^{2} w_{p} }}{{\partial t^{2} }}, $$
(9)

where \(\frac{1}{{\overline{\lambda }_{p} }}\) and \(\frac{1}{{\overline{\beta }_{p} }}\) can be expressed as \(\begin{aligned} & \frac{1}{{\overline{\lambda }_{p} }} = \sqrt {\frac{{\overline{c}^{p}_{55} }}{{\overline{c}^{p}_{44} }}\,} \,\, = \sqrt {\frac{{c_{55}^{pR} \left( {1 + i\omega \frac{{c_{55}^{pI} }}{{c_{55}^{pR} }}} \right)}}{{c_{44}^{pR} \left( {1 + i\omega \frac{{c_{44}^{pI} }}{{c_{44}^{pR} }}} \right)}}} = \sqrt {\frac{{c_{55}^{pR} \left( {1 + i\omega \kappa_{2} } \right)\left( {1 + i\omega \kappa_{1} } \right)^{ - 1} }}{{c_{44}^{pR} }}} = \sqrt {\frac{{c_{55}^{pR} }}{{c_{44}^{pR} }}\left( {1 + i\omega (\kappa_{1} - \kappa_{2} ) + \omega^{2} \kappa_{1} \kappa_{2} + - - } \right)} , \\ & \frac{1}{{\overline{\beta }_{p} }} = \sqrt {\frac{{\rho_{p} }}{{\overline{c}^{p}_{44} }}} = \sqrt {\frac{{\rho_{p} }}{{c_{44}^{pR} \left( {1 + i\omega \frac{{c_{44}^{pI} }}{{c_{44}^{pR} }}} \right)}}} = \sqrt {\frac{{\rho_{p} }}{{c_{44}^{pR} \left( {1 + i\omega \kappa_{1} } \right)}}} = \sqrt {\frac{{\rho_{p} \left( {1 + i\omega \kappa_{1} } \right)^{ - 1} }}{{c_{44}^{pR} }}} = \sqrt {\frac{{\rho_{p} }}{{c_{44}^{pR} }}\left( {1 - i\omega \kappa_{1} - \omega^{2} \kappa_{1}^{2} + - - } \right)} . \\ \end{aligned}\)

Since, \(\kappa_{1} = \frac{{c_{44}^{pI} }}{{c_{44}^{pR} }} < < < 1\) and \(\kappa_{2} = \frac{{c_{55}^{pI} }}{{c_{55}^{pR} }} < < < 1\) are very small quantity in aforesaid medium, so the above expression can be written in the following way

$$ \frac{1}{{\overline{\lambda }_{p} }} \approx \sqrt {\frac{{c_{55}^{pR} }}{{c_{44}^{pR} }}} \quad {\text{and}}\quad \frac{1}{{\overline{\beta }_{p} }} \approx \sqrt {\frac{{\rho_{p} }}{{c_{44}^{pR} }}} . $$

Let us consider the following transformation for the displacement components

$$ w_{p} \left( {x,\,\,y,\,\,t} \right) = \,W_{p} (x,\,\,y)e^{i\omega t} , $$
(10)

where \(\omega\) represents the angular frequency;\(p = 1\) corresponds to the upper layer, and \(p = 2\) is associated with the lower half-space.

Using Eq. (10) in Eq. (8), we obtain

$$ \frac{{\partial^{2} w_{1} }}{{\partial y^{2} }} + \frac{1}{{\overline{\lambda }_{1}^{2} }}\frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} + \overline{M}_{1}^{2} w_{1} = 0, $$
(11a)
$$ \frac{{\partial^{2} w_{2} }}{{\partial y^{2} }} + \frac{1}{{\overline{\lambda }_{2}^{2} }}\frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} + \overline{M}_{2}^{2} w_{2} = 0, $$
(11b)

where \(\overline{\lambda }_{1}^{2} ,\overline{\lambda }_{2}^{2} ,\overline{M}_{1}^{2} ,\) and \(\overline{M}_{2}^{2}\) are given in the Appendix.

3 Boundary conditions

For the mathematical model used in the present problem (depicted by Fig. 1), the following boundary conditions are used.

The traction free condition at upper boundary, i.e., at \(x = - H + bh(y)\) is

$$ \sigma_{31}^{1} - \overline{\lambda }_{1}^{2} bh^{\prime}\sigma_{32}^{1} = 0. $$
(12)

where \(h^{\prime} = \frac{{{\text{d}}h}}{{{\text{d}}x}}\).

The continuity conditions for stress and displacement at the interface, i.e., at \(x = 0\) are

$$ w_{1} = w_{2} , $$
(13)
$$ \sigma_{13}^{1} = \sigma_{32}^{2} . $$
(14)

4 Solution of the problem

In view of Eqs. (11a–11b), the solution of the incident wave field for the propagation of SH-waves can be expressed as [2, 15]

$$ w_{1,in} = A\cos \overline{\lambda }_{1} \overline{s}_{1} (x + H)e^{ - i\eta y} , $$
(15)
$$ w_{2,in} = Be^{{ - \overline{\lambda }_{2} \overline{s}_{2} x}} e^{ - i\eta y} , $$
(16)

where \(\overline{s}_{1}^{2} = \overline{M}_{1}^{2} - \eta^{2}\), \(\overline{s}_{2}^{2} = \overline{M}_{2}^{2} - \eta^{2}\); \(\eta = \frac{\omega }{{c_{ph} }}\) is the angular wave number; \(c_{ph}\) represents the phase velocity of shear waves; \(A\) and \(B\) indicate the coefficients of displacement.

Similarly, in view of Eqs. (11a–11b), the solution of the reflected wave field for the propagation of SH-waves can be written as [2, 15]

$$ w_{1,scatt} = \int\limits_{c} {\left\{ {C(\upsilon )e^{{ - i\overline{\lambda }_{1} \overline{\xi }_{1} x}} + D(\upsilon )e^{{i\overline{\lambda }_{1} \overline{\xi }_{1} x}} } \right\}} e^{ - i\upsilon y} {\text{d}}\upsilon , $$
(17)
$$ w_{2,scatt} = \int\limits_{c} {E(\upsilon )} e^{{ - \overline{\lambda }_{2} \overline{\xi }_{2} x}} e^{ - i\upsilon y} {\text{d}}\upsilon , $$
(18)

where \(\overline{\xi }_{1}^{2} = \overline{M}_{1}^{2} - \upsilon^{2} ,\,\,\overline{\xi }_{2}^{2} = \upsilon^{2} - \overline{M}_{2}^{2}\); \(\upsilon = \frac{\omega }{{c_{ph} }}\); \(C(\upsilon ),\,\,D(\upsilon )\) and \(E(\upsilon )\) represent the arbitrary coefficients in the expression of scattered displacements in \(\upsilon\)-plane.

The contour integral of scattered wave field in the \(\upsilon\)-plane can be represented through Fig. 2 as [6, 15]

Fig. 2
figure 2

Contour integral in \(\upsilon\)-plane with branch cut

Full size image

In view of Eqs. (15–16) and (17–18), the total displacement field for SH-waves in the aforesaid medium can be obtained as

$$ w_{1} = w_{1,in} + w_{1,scatt} = A\cos \overline{\lambda }_{1} \overline{s}_{1} (x + H)e^{ - i\eta y} + \int\limits_{c} {\left\{ {C(\upsilon )e^{{ - i\overline{\lambda }_{1} \overline{\xi }_{1} x}} + D(\upsilon )e^{{i\overline{\lambda }_{1} \overline{\xi }_{1} x}} } \right\}} e^{ - i\upsilon y} d\upsilon , $$
(19)
$$ w_{2} = w_{2,in} + w_{2,scatt} = Be^{{ - \overline{\lambda }_{2} \overline{s}_{2} x}} e^{ - i\eta y} + \int\limits_{c} {E(\upsilon )} e^{{ - \overline{\lambda }_{2} \overline{\xi }_{2} x}} e^{ - i\upsilon y} {\text{d}}\upsilon . $$
(20)

Using Eqs. (19–20) in the boundary condition (13), we get

$$ A\cos \overline{\lambda }_{1} \overline{s}_{1} H = B, $$
(21)
$$ C\left( \upsilon \right) + D\left( \upsilon \right) = E\left( \upsilon \right). $$
(22)

Using Eq. (21) in Eq. (20), we have

$$ w_{2} = A\cos \overline{\lambda }_{1} \overline{s}_{1} He^{{ - \overline{\lambda }_{2} \overline{s}_{2} x}} e^{ - i\eta y} + \int\limits_{c} {E(\upsilon )} e^{{ - \overline{\lambda }_{2} \overline{\xi }_{2} x}} e^{ - i\upsilon y} {\text{d}}\upsilon . $$
(23)

Using Eqs. (19) and (23) in the boundary condition (14), we get

$$ C\left( \upsilon \right) - D\left( \upsilon \right) = \frac{1}{\gamma }E\left( \upsilon \right), $$
(24)

where \(\gamma = \frac{{i\overline{\lambda }_{1} \overline{\xi }_{1} \overline{c}_{55}^{1} }}{{\overline{\lambda }_{2} \overline{\xi }_{2} \overline{c}_{55}^{2} }}\).

On solving Eqs. (22) and (24), we obtain

$$ E\left( \upsilon \right) = C\left( \upsilon \right)\left( {\frac{2\gamma }{{\gamma + 1}}} \right)\quad {\text{and}} \quad D\left( \upsilon \right) = C\left( \upsilon \right)\left( {\frac{\gamma - 1}{{\gamma + 1}}} \right). $$
(25)

Using Eq. (25) in Eqs. (19) and (23), we have

$$ w_{1} = A\cos \overline{\lambda }_{1} \overline{s}_{1} (x + H)e^{ - i\eta y} + \int\limits_{c} {\frac{2C}{{1 + \gamma }}\left\{ {\gamma \cos \overline{\lambda }_{1} \overline{\xi }_{1} x - i\sin \overline{\lambda }_{1} \overline{\xi }_{1} x} \right\}} e^{ - i\upsilon y} {\text{d}}\upsilon , $$
(26)
$$ w_{2} = A\cos \overline{\lambda }_{1} \overline{s}_{1} He^{{ - \overline{\lambda }_{2} \overline{s}_{2} x}} e^{ - i\eta y} + \int\limits_{c} {\frac{2C}{{1 + \gamma }}} \left\{ {\gamma e^{{ - \overline{\lambda }_{2} \overline{\xi }_{2} x}} } \right\}e^{ - i\upsilon y} {\text{d}}\upsilon . $$
(27)

Due to upper irregular surface of the stratum, perturbation technique on \(C(\upsilon )\) provides

$$ C(\upsilon ) = bC_{1} (\upsilon ) + b^{2} C_{1} (\upsilon ) + b^{3} C_{1} (\upsilon ) + b^{4} C_{1} (\upsilon ) + \cdots $$
(28a)

Since, the irregularity in the upper surface is very small in the considered orthotropic viscoelastic layer, i.e., \(b < < 1\), therefore, we have

$$ C(\upsilon ) = bC_{1} (\upsilon )\,,\,\,sin\eta_{1} bh \cong \eta_{1} bh\,,\,\,\cos \eta_{1} bh \cong 1\,(b < < 1). $$
(28b)

Using Eqs. (26–27) and Eqs. (28a–28b), the boundary condition (12) yields

$$ A\left[ { - i\overline{\lambda }_{1} \eta h^{\prime} + \overline{\lambda }_{1} \overline{s}_{1}^{2} h} \right]e^{ - i\eta y} + \int\limits_{c} {\left( {\frac{2}{1 + \gamma }} \right)C_{1} (\upsilon )(i\cos \overline{\lambda }_{1} \overline{\xi }_{1} H - \gamma \sin \overline{\lambda }_{1} \overline{\xi }_{1} H)\overline{\xi }_{1} } e^{ - iy\upsilon } {\text{d}}\upsilon = 0. $$
(29)

On inverting Eq. (29), we have

$$ C_{1} (\upsilon ) = \frac{A(\gamma + 1)}{{4\pi (i\cos \overline{\lambda }_{1} \overline{\xi }_{1} H - \gamma \sin \overline{\lambda }_{1} \overline{\xi }_{1} H)\overline{\xi }_{1} }}\int\limits_{ - \infty }^{\infty } {\left[ {i\overline{\lambda }_{1} \eta h^{\prime} - \overline{\lambda }_{1} \overline{s}_{1}^{2} h} \right]} e^{iz(\upsilon - \eta )} {\text{d}}z. $$
(30)

With the help of Eq. (30), Eqs. (26–27) provide

$$ \begin{aligned} w_{1} & = A\cos \overline{\lambda }_{1} \overline{s}_{1} (x + H)e^{ - i\eta y} \\ & \quad + b\int\limits_{ - \infty }^{\infty } {\frac{A}{2\pi }\left[ {i\overline{\lambda }_{1} \eta h^{\prime} - \overline{\lambda }_{1} \overline{s}_{1}^{2} h} \right]e^{ - i\eta z} } \times \int\limits_{c} {\frac{{\left\{ {\gamma \cos \overline{\lambda }_{1} \overline{\xi }_{1} x - i\sin \overline{\lambda }_{1} \overline{\xi }_{1} x} \right\}e^{i\upsilon y - i\upsilon z} }}{{(i\cos \overline{\lambda }_{1} \overline{\xi }_{1} H - \gamma \sin \overline{\lambda }_{1} \overline{\xi }_{1} H)\overline{\xi }_{1} }}} {\text{d}}\upsilon {\text{d}}z, \\ \end{aligned} $$
(31)
$$ \begin{aligned} w_{2} & = A\cos \overline{\lambda }_{1} \overline{s}_{1} He^{ - i\eta y} e^{{ - \overline{\lambda }_{2} \overline{\xi }_{2} x}} \\ & \quad + b\int\limits_{ - \infty }^{\infty } {\frac{A}{2\pi }\left[ {i\overline{\lambda }_{1} \eta h^{\prime} - \overline{\lambda }_{1} \overline{s}_{1}^{2} h} \right]e^{ - i\eta z} } \times \int\limits_{c} {\frac{{\gamma e^{{ - \overline{\lambda }_{2} \overline{\xi }_{2} x}} e^{i\upsilon y - i\upsilon z} }}{{(i\cos \overline{\lambda }_{1} \overline{\xi }_{1} H - \gamma \sin \overline{\lambda }_{1} \overline{\xi }_{1} H)\overline{\xi }_{1} }}} {\text{d}}\upsilon {\text{d}}z. \\ \end{aligned} $$
(32)

Equations (31–32) can be rewritten as

$$ w_{1} = A\cos \overline{\lambda }_{1} \overline{s}_{1} (x + H)e^{ - i\eta y} + \frac{Ab}{{2\pi }}\int\limits_{ - \infty }^{\infty } {\left[ {i\overline{\lambda }_{1} \eta h^{\prime} - \overline{\lambda }_{1} \overline{s}_{1}^{2} h_{0} } \right]} e^{ - i\eta z} dz\,\, \times \int\limits_{c} {\Psi_{0} (\upsilon )} {\text{d}}\upsilon , $$
(33)
$$ w_{2} = A\cos \overline{\lambda }_{1} \overline{s}_{1} He^{{ - \overline{\gamma }_{2} \overline{\xi }_{2} x}} e^{ - i\eta y} + \frac{Ab}{{2\pi }}\int\limits_{ - \infty }^{\infty } {\left[ {i\overline{\lambda }_{1} \eta h^{\prime} - \overline{\lambda }_{1} \overline{s}_{1}^{2} h} \right]} e^{ - i\eta z} dz\,\, \times \int\limits_{c} {\Psi_{00} (\upsilon )} {\text{d}}\upsilon . $$
(34)

where \(\Psi_{0} (\upsilon )\) and \(\Psi_{00} (\upsilon )\) are given in the Appendix.

The singularities of the contour integrals in Eqs. (31–32) can be obtained as

$$ (i\cos \overline{\lambda }_{1} \overline{\xi }_{1} H - \gamma \sin \overline{\lambda }_{1} \overline{\xi }_{1} H)\overline{\xi }_{1} = 0. $$
(35)

Equation (35) can be further simplified as

$$ \tan \left( {\frac{{\sqrt {\overline{c}_{44}^{1} } }}{{\sqrt {\overline{c}_{55}^{1} } }}\sqrt {(\overline{M}_{1}^{2} - \upsilon^{2} )} } \right)H = \frac{{\frac{{\sqrt {\overline{c}_{44}^{2} } }}{{\sqrt {\overline{c}_{55}^{2} } }}\overline{c}_{55}^{2} \sqrt {(\upsilon^{2} - \overline{M}_{2}^{2} )} }}{{\frac{{\sqrt {\overline{c}_{44}^{1} } }}{{\sqrt {\overline{c}_{55}^{1} } }}\overline{c}_{55}^{1} \sqrt {(\overline{M}_{1}^{2} - \upsilon^{2} )} }}. $$
(36)

Equation (36) represents the dispersion relation for the scattered SH-waves propagating in the orthotropic viscoelastic structure. Equation (36) contains \(\upsilon_{m}\) roots in the \(\upsilon\) plane satisfying the relation \(- \overline{M}_{1} \le \upsilon_{m} \le - \overline{M}_{2}\) described in Fig. 2. From Fig. 2, it is also cleared that there are \(N\) roots of Eq. (36), where \(N\) is the integral part of \(\left[ {\left\{ {(\overline{M}_{1}^{2} - \overline{M}_{2}^{2} )\frac{H}{\pi }} \right\} + 1} \right]\)[15].

Due to the viscoelasticity in the considered medium, \(\upsilon\) can be expressed as \(\upsilon = \upsilon_{r} - i\upsilon_{i} = \upsilon_{r} \left( {1 - i\delta } \right)\) where \(\delta = \frac{{\upsilon_{i} }}{{\upsilon_{r} }}\) is defined as attenuation parameter of the medium. Using \(\upsilon = \upsilon_{r} - i\upsilon_{i}\),\(\overline{c}_{ij} = c_{ij}^{R} + i\omega c_{ij}^{I}\), and \(\overline{M}_{p}^{2} = \frac{{\omega^{2} }}{{\overline{\beta }_{p}^{2} }}\) (p = 1 for the layer and p = 2 for the half-space) in Eq. (36), we get

$$ \frac{{\tan \upsilon_{r} H\lambda_{1} \Gamma_{3} \left( { - \tanh^{2} \upsilon_{r} H\lambda_{1} \Gamma_{4} + 1} \right)}}{{1 + \tan^{2} \upsilon_{r} H\lambda_{1} \Gamma_{3} \tanh^{2} \upsilon_{r} H\lambda_{1} \Gamma_{00} }} = \frac{{\lambda_{2} \Gamma_{11} \Gamma_{0} }}{{\lambda_{1} }}, $$
(37)
$$ \frac{{\tanh \upsilon_{r} H\lambda_{1} \Gamma_{3} \left( {\tan^{2} \upsilon_{r} H\lambda_{1} \Gamma_{4} + 1} \right)}}{{1 + \tan^{2} \upsilon_{r} H\lambda_{1} \Gamma_{3} \tanh^{2} \upsilon_{r} H\lambda_{1} \Gamma_{00} }} = \frac{{\lambda_{2} \Gamma_{11} \Gamma_{00} }}{{\lambda_{1} }}, $$
(38)

where \(\Gamma_{3} ,\Gamma_{4} ,\Gamma_{0} ,\Gamma_{00} ,\lambda_{1} ,\lambda_{2}\) and \(R_{12}\) are provided in the Appendix.

Equation (37) represents the dispersion relation while Eq. (38) provides the damping relation for the scattered SH-waves in the considered irregular orthotropic viscoelastic composite structure.

Using the concept of contour integration and Fig. 2, the contour integrals \(\int\nolimits_{c} {\Psi_{0} (\upsilon )} {\text{d}}\upsilon\) and \(\int\nolimits_{c} {\Psi_{00} (\upsilon )} {\text{d}}\upsilon\) can be expressed as

$$ \int\limits_{c} {\Psi_{0} (\upsilon ){\text{d}}\upsilon = 2\pi i\sum {{\text{Res}}\,\Psi_{0} (\upsilon ) - \int\limits_{\begin{subarray}{l} {\text{Branch}}\, \\ {\text{line}} \end{subarray} } {\Psi_{0} (\upsilon ){\text{d}}\upsilon } - } } \int\limits_{{c_{\infty } }} {\Psi_{0} (\upsilon ){\text{d}}\upsilon ,} $$
(39)
$$ \int\limits_{c} {\Psi_{00} (\upsilon ){\text{d}}\upsilon = 2\pi i\sum {{\text{Res}}\,\Psi_{00} (\upsilon ) - \int\limits_{\begin{subarray}{l} {\text{Branch}}\, \\ {\text{line}} \end{subarray} } {\Psi_{00} (\upsilon ){\text{d}}\upsilon } - } } \int\limits_{{c_{\infty } }} {\Psi_{00} (\upsilon ){\text{d}}\upsilon } . $$
(40)

The residues of contour integrals \(\int\nolimits_{c} {\Psi_{0} (\upsilon )} {\text{d}}\upsilon\) and \(\int\nolimits_{c} {\Psi_{00} (\upsilon )} {\text{d}}\upsilon\) at the poles \(\upsilon_{m}\) can be written as

$$ {\text{Res}} \left( {\Psi_{0} (\upsilon_{m} )} \right) = \frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{1m} \left( {x + H} \right)e^{{i\upsilon_{m} \left( { - y + z} \right)}} }}{{\overline{\lambda }_{1} \upsilon_{m} H}}, $$
(41)
$$ {\text{Res}} \left( {\Psi_{00} (\upsilon_{m} )} \right) = \frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{1m} He^{{ - \overline{\lambda }_{1} \overline{\xi }_{2m} x}} e^{{i\upsilon_{m} \left( { - y + z} \right)}} }}{{\overline{\lambda }_{1} \upsilon_{m} H}}, $$
(42)

where \(\overline{\xi }_{1m}\) and \(\overline{\xi }_{2m}\) are defined at \(\upsilon_{m}\).

Equations (39–40) can be evaluated by the method by Sezawa [8]. For this purpose, a contour with branch cuts \(\overline{M}_{1} ,\,\,\overline{M}_{2}\) containing real axis and an infinite radius semi-circle in the upper half- plane have been taken into account. In this study, the impact of propagation of SH-waves is considered near the upper surface of the aforesaid structure. Due to the contribution of the term \(1/x^{3/2}\) in the Eqs. (39–40), the value of branch integrals becomes negligible. So, we move away from the irregular region in the upper layer of said orthotropic viscoelastic structure. Due to higher values of x and y, the integrals over the arc at infinity in the upper layer becomes zero in the Eqs. (39–40).

With the help of the Eqs. (41–42) and using the concept for \(z > x\,\,{\text{and Re}} \left( {\upsilon_{m} } \right) < 0\) in the Eqs. (41–42), we get

$$ \int\limits_{c} {\Psi_{0} (\upsilon )} {\text{d}}\upsilon = 2\pi i\sum\limits_{m = 1}^{N} {\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{1m} \left( {x + H} \right)e^{{i\upsilon_{m} \left( { - y + z} \right)}} }}{{\overline{\lambda }_{1} \upsilon_{m} H}}} , $$
(43)
$$ \int\limits_{c} {\Psi_{00} (\upsilon )} {\text{d}}\upsilon = 2\pi i\sum\limits_{m = 1}^{N} {\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{1m} He^{{ - \overline{\lambda }_{2} \overline{\xi }_{2m} x}} e^{{i\upsilon_{m} \left( { - y + z} \right)}} }}{{\overline{\lambda }_{1} \upsilon_{m} H}}} . $$
(44)

Similarly, for \(z < x\) and \({\text{Re}} \left( {\upsilon_{m} } \right) > 0,\) we have

$$ \int\limits_{c} {\Psi_{0} (\upsilon )} {\text{d}}\upsilon = - 2\pi i\sum\limits_{m = 1}^{N} {\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{1m} \left( {x + H} \right)e^{{i\upsilon_{m} \left( { - y + z} \right)}} }}{{\overline{\lambda }_{1} \upsilon_{m} H}}} , $$
(45)
$$ \int\limits_{c} {\Psi_{00} (\upsilon )} {\text{d}}\upsilon = - 2\pi i\sum\limits_{m = 1}^{N} {\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{1m} He^{{ - \overline{\lambda }_{2} \overline{\xi }_{2m} x}} e^{{i\upsilon_{m} \left( { - y + z} \right)}} }}{{\overline{\lambda }_{1} \upsilon_{m} H}}} , $$
(46)

where N represents the number of roots.

Using Eqs. (43–46) in the Eqs. (33–34), we obtain

$$ \begin{aligned} w_{1} & = A\cos \overline{\lambda }_{1} \overline{s}_{1} (x + H)e^{ - i\eta y} - iAb\sum\limits_{m = 1}^{N} {\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{1m} \left( {x + H} \right)}}{{\upsilon_{m} H}}} \\ & \quad \times \left\{ {e^{{ - i\upsilon_{m} y}} \int\limits_{ - \infty }^{y} {\left( {i\eta h^{\prime} - \overline{s}_{1}^{2} h} \right)} \times e^{{i\left( {\upsilon_{m} - \eta } \right)z}} {\text{d}}z + e^{{i\upsilon_{m} y}} \int\limits_{y}^{\infty } {\left( {i\eta h^{\prime} - \overline{s}_{1}^{2} h} \right)} e^{{ - i\left( {\upsilon_{m} + \eta } \right)z}} {\text{d}}z} \right\}, \\ \end{aligned} $$
(47)
$$ \begin{aligned} w_{2} & = A\cos \overline{\lambda }_{1} \overline{s}_{1} He^{{ - \overline{\lambda }_{2} \overline{s}_{2} x}} e^{ - i\eta y} - iAb\sum\limits_{m = 1}^{N} {\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{1m} He^{{ - \overline{\gamma }_{2} \overline{s}_{2} x}} }}{{\upsilon_{m} H}}} \\ & \quad \times \left\{ {e^{{ - i\upsilon_{m} y}} \int\limits_{ - \infty }^{y} {\left( {i\eta h^{\prime} - \overline{s}_{1}^{2} h} \right)} e^{{i\left( {\upsilon_{m} - \eta } \right)z}} {\text{d}}z + e^{{i\upsilon_{m} y}} \int\limits_{y}^{\infty } {\left( {i\theta h^{\prime} - \overline{s}_{1}^{2} h} \right)} e^{{ - i\left( {\upsilon_{m} + \eta } \right)z}} {\text{d}}z} \right\}, \\ \end{aligned} $$
(48)

with \({\text{Re}} \left( {\upsilon_{m} } \right) > 0\).

Using Eq. (2) in the expressions in Eqs. (47–48), we obtain

$$ w_{1} = A\cos \overline{\lambda }_{1} \overline{s}_{1} (x + H)e^{ - i\eta y} + iAb\sum\limits_{m = 1}^{N} {\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{1m} \left( {x + H} \right)}}{{\upsilon_{m} H}}} e^{{i\upsilon_{m} x}} \times \left\{ {\left( {\eta \upsilon_{m} + \eta^{2} + \overline{s}_{1}^{2} } \right)\int\limits_{{ - \frac{s}{2}}}^{\frac{s}{2}} {he^{{ - i\left( {\upsilon_{m} + \eta } \right)z}} {\text{d}}z} } \right\}, $$
(49)
$$ w_{2} = A\cos \overline{\lambda }_{1} \overline{s}_{1} He^{{ - \overline{\lambda }_{2} \overline{s}_{2} x}} e^{ - i\eta y} + iAb\sum\limits_{m = 1}^{N} {\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{1m} He^{{ - \overline{\lambda }_{2} \overline{s}_{2} x}} }}{{\upsilon_{m} H}}} \left\{ {e^{{i\upsilon_{m} y}} \left( {\eta \upsilon_{m} + \eta^{2} + \overline{s}_{1}^{2} } \right)\int\limits_{{ - \frac{s}{2}}}^{\frac{s}{2}} {he^{{ - i\left( {\upsilon_{m} + \eta } \right)z}} {\text{d}}z} } \right\}. $$
(50)

Equations (49–50) represents the total displacement component of SH-waves in linear orthotropic viscoelastic structure.

5 Some special cases

The obtained analytical results can be applicable in three different physical scenarios of surface irregularity viz. (1) parabolic type surface irregularity (2) triangular notch type surface irregularity and (3) rectangular type of surface irregularity in the considered orthotropic viscoelastic structure.

5.1 Case I: Parabolic type of surface irregularity

Surface irregularity of parabolic type in the upper surface of considered orthotropic viscoelastic structure (as depicted in Fig. 3) can be expressed as

$$ h_{0} (y) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {y > \frac{s}{2},\,\,{\text{and}}\,\,y < \frac{ - s}{2}} \hfill \\ {\left( {1 - \frac{{4y^{2} }}{{s^{2} }}} \right),} \hfill & {\frac{ - s}{2} \le y \le \frac{s}{2}} \hfill \\ \end{array} } \right. $$
(51)
Fig. 3
figure 3

Parabolic type surface irregularity

Full size image

Due to irregular boundary in the upper surface, we can take only the first mode of SH-wave in upper layer can propagate which also satisfied Eq. (36). Now, putting \(\eta = \upsilon_{1} = \upsilon_{r} - i\upsilon_{i} ,\,\,\overline{s}_{1} = \overline{\xi }_{11}\); \(m = 1\) (for first mode) in Eq. (49) and using Eq. (51), we get

$$ \begin{aligned} \frac{{w_{1,ref}^{P} }}{A} & = ib\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{11} \left( {x + H} \right)}}{{\upsilon_{1} H}}e^{{i\upsilon_{1} y}} (2\upsilon_{1}^{2} + \overline{\xi }_{11}^{2} )\left( {\frac{{2\sin \upsilon_{1} s}}{{s^{2} \upsilon_{1}^{3} }} - \,\frac{{2\cos \upsilon_{1} s}}{{s\upsilon_{1}^{2} }}} \right), \\ & = - \frac{b}{H}\Upsilon_{00}^{P} + i\frac{b}{H}\Upsilon_{0}^{P} , \\ \end{aligned} $$
(52)

where \(\Upsilon_{0}^{P}\) and \(\Upsilon_{00}^{P}\) are given in the Appendix.

Equation (52) provides the expression of reflected displacement component due to scattered SH-waves when the upper surface contains parabolic type surface irregularity. In the above expression, superscript P represents the case of parabolic type surface irregularity.

5.2 Case II: Triangular notch type surface irregularity

The triangular notch type surface irregularity (displayed in Fig. 4) can be expressed as

$$ h_{0} (y) = \left\{ \begin{gathered} 0\,\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y > \frac{s}{2},\,y < \,\,\frac{ - s}{2} \hfill \\ \,1 + \frac{2y}{s},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{ - s}{2}\,\,\, \le y \le 0 \hfill \\ 1 - \frac{2y}{s},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\,\,\, \le y \le \frac{s}{2} \hfill \\ \end{gathered} \right. $$
(53)
Fig. 4
figure 4

Triangular notch type surface irregularity

Full size image

Similarly, the propagation of first mode of SH-waves has been considered in the upper layer in such a way that it satisfies Eq. (36). With the help of Eq. (53) and putting \(\theta = \upsilon_{1} = \upsilon_{r} - i\upsilon_{i} ,\,\,\overline{s}_{1} = \overline{\xi }_{11}\); \(m = 1\) (for first mode) in Eq. (49), the reflected displacement component can be expressed as

$$ \begin{aligned} \frac{{w_{1,ref}^{T} }}{A} & = ib\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{11} \left( {x + H} \right)}}{{\upsilon_{1} H}}e^{{i\upsilon_{1} y}} (2\upsilon_{1}^{2} + \overline{\xi }_{11}^{2} )\left( {\frac{{2\sin^{2} \frac{{\upsilon_{1} s}}{2}}}{{s\upsilon_{1}^{2} }}} \right), \\ & = - \frac{b}{H}\Upsilon_{00}^{T} + i\frac{b}{H}\Upsilon_{0}^{T} , \\ \end{aligned} $$
(54)

where \(\Upsilon_{0}^{T}\) and \(\Upsilon_{00}^{T}\) are given in the Appendix. The superscript “T” is associated with the triangular notch type surface irregularity.

5.3 Case III: Rectangular type surface irregularity

The rectangular type surface irregularity (depicted in Fig. 5) can be expressed as

$$ h_{0} (x) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {y > \frac{s}{2},\,\,\,y < \frac{ - s}{2}} \hfill \\ {1,} \hfill & {\frac{ - s}{2} \le y \le \frac{s}{2}} \hfill \\ \end{array} } \right. $$
(55)
Fig. 5
figure 5

Surface irregularity of rectangular shape

Full size image

Similarly, using Eq. (55) and putting \(\theta = \upsilon_{1} = \upsilon_{r} - i\upsilon_{i} ,\,\,\overline{s}_{1} = \overline{\xi }_{11}\); \(m = 1\) (for first mode) in Eq. (49), the reflected displacement component can be written as

$$ \begin{aligned} \frac{{w_{1,ref}^{R} }}{A} & = ib\frac{{\cos \overline{\lambda }_{1} \overline{\xi }_{11} \left( {x + H} \right)}}{{\upsilon_{1} H}}e^{{i\upsilon_{1} y}} (2\upsilon_{1}^{2} + \overline{\xi }_{11}^{2} )\left( {\frac{{\sin \upsilon_{1} s}}{{\upsilon_{1} }}} \right), \\ & = - \frac{b}{H}\Upsilon_{00}^{R} + i\frac{b}{H}\Upsilon_{0}^{R} , \\ \end{aligned} $$
(56)

where \(\Upsilon_{0}^{R}\) and \(\Upsilon_{00}^{R}\) are given in the Appendix. The superscript “R” is associated with the rectangular type surface irregularity.

6 Validation

6.1 Validation of dispersion relation

If \(c_{44}^{1R} = c_{55}^{1R} = \mu_{1}\), \(c_{44}^{2R} = c_{55}^{2R} = \mu_{2}\), \(\upsilon_{r} = \upsilon ,\) and \(\upsilon_{i} = 0,\) then, the dispersion Eq. (37) reduces to

$$ \tan \sqrt {\left( {\frac{{c_{ph}^{2} }}{{\beta_{1}^{2} }} - 1} \right)} \upsilon H = \frac{{\mu_{2} \sqrt {\left( {1 - \frac{{c_{ph}^{2} }}{{\beta_{2}^{2} }}} \right)} }}{{\mu_{1} \sqrt {\left( {\frac{{c_{ph}^{2} }}{{\beta_{1}^{2} }} - 1} \right)} }}, $$
(57)

and the damping Eq. (38) vanishes completely. In the above expression (57), \(\mu_{1}\) and \(\mu_{2}\) are the rigidity of the isotropic layer and isotropic substrate, respectively. Equation (57) validates exactly with the classical Love wave equation [6].

6.2 Reflected mechanical displacement for the parabolic type surface irregularity

If \(c_{44}^{1R} = c_{55}^{1R} = 1\,\, i.e., \,\,\overline{\lambda }_{1} = \sqrt {\frac{{c_{44}^{1R} }}{{c_{55}^{1R} }}} = 1,\) \(\overline{\xi }_{11} = \xi_{11}\), \(\upsilon_{r} = \upsilon ,\) and \(\upsilon_{i} = 0\), Eq. (52) transforms to

$$ \frac{{w_{1,ref}^{P} }}{A} = ib\frac{{\cos \xi_{11} \left( {x + H} \right)}}{\upsilon H}e^{i\upsilon y} (2\upsilon^{2} + \xi_{11}^{2} )\left( {\frac{2\sin \upsilon s}{{s^{2} \upsilon^{3} }} - \,\frac{2\cos \upsilon s}{{s\upsilon^{2} }}} \right). $$
(58)

Equation (58) represents the reflected displacement for the propagation of SH-waves in isotropic elastic composite structure. Equation (58) is matched with the pre-established result given by Chattopadhyay et al. [2] by reducing viscoelastic case of isotropic case \(\left( {\mu^{\prime}_{1} \to 0\,\,{\text{and}}\,\mu^{\prime}_{2} \to 0} \right)\,\) and Wolf [15] for the isotropic structure containing parabolic type surface irregularity.

6.3 Reflected mechanical displacement for triangular notch type surface irregularity

In a similar manner, on putting the values \(\overline{\lambda }_{1} = \sqrt {\frac{{c_{44}^{1R} }}{{c_{55}^{1R} }}} = 1,\overline{\xi }_{11} = \xi_{11}\), and \(\upsilon_{r} = \upsilon ,\)\(\upsilon_{i} = 0\) in Eq. (54), we have

$$ \frac{{w_{1,ref}^{T} }}{A} = ib\frac{{\cos \xi_{11} (x + H)}}{\upsilon H} \times e^{i\upsilon y} (2\upsilon^{2} + \xi_{11}^{2} )\left( {\frac{{2\sin^{2} \frac{\upsilon s}{2}}}{{s\upsilon^{2} }}} \right). $$
(59)

Similarly, Eq. (59) gives the expression of reflected mechanical displacement for the propagation of SH-waves for isotropic elastic structure containing triangular notch type surface irregularity. Equation (59) is found to be well in agreement with the result obtained by Chattopadhyay et al. [2] by reducing viscoelastic case of isotropic case \(\left( {\mu^{\prime}_{1} \to 0\,\,{\text{and}}\,\mu^{\prime}_{2} \to 0} \right)\,\) and Wolf [15] for the isotropic structure containing triangular notch type surface irregularity.

7 Numerical results and discussion

For the numerical computation and graphical demonstrations, the following physical properties of the orthotropic viscoelastic materials (viz. carbon fiber for layer and prepreg for half-space) have been considered:

For orthotropic viscoelastic upper layer, Yu et al. [17]

$$ c_{55}^{R(1)} = 6.15\,{\text{Gpa}},\,\,\,c_{44}^{R(1)} = 6.15\,\,{\text{Gpa}},\,\,\rho_{1} = 1.5\,\,{\text{g/cm}}^{3} . $$

For orthotropic viscoelastic lower half-space, Yu et al. [17]

$$ c_{55}^{R(2)} = 7.8\,\,{\text{Gpa}},\,\,\,c_{44}^{R(2)} = 7.8\,\,{\text{Gpa}},\,\,\rho_{2} = 1.595\,\,{\text{g/cm}}^{{3}} . $$

Unless otherwise stated:

$$ \left( {y + H} \right)/H = 10,\,\,\,x/H = 10,\,\,\,\,s/H = 0.01,\,\,\,b/H = 0.001. $$

The graphical manifestation of the dimensionless phase velocity, attenuation coefficient, and reflected displacement component due to the scattering of SH-waves propagating through surface irregularity in the orthotropic viscoelastic composite structure has been represented through Figs. 6a, 7, 8, 9.

Fig. 6
figure 6

Variation of dimensionless phase velocity \(\left( {{{c_{ph} } / {\beta_{1} }}} \right)\) and attenuation coefficient \(\left( {\log \delta } \right)\) against dimensionless wave number \(\left( {\upsilon_{1} H} \right)\) for the different values of anisotropy parameter \(\left( {\lambda_{1} = \sqrt {{{c_{55}^{1R} } /{c_{44}^{1R} }}} } \right)\) of the considered orthotropic viscoelastic structure

Full size image

Figure 6a displays the impact of anisotropy parameter of upper layer on the phase velocity of SH-waves in the considered orthotropic viscoelastic composite structure. It has been observed from Fig. 6a that the phase velocity of scattered SH-waves decreases with the increase in the anisotropy parameter of the upper layer.

Figure 6b depicts the effect of anisotropy parameter on the attenuation coefficient, which is related to damping phenomena of scattered SH-waves in the said orthotropic viscoelastic structure. It has been observed from Fig. 6b that the anisotropic parameter has a favorable effect on the attenuation coefficient associated with the damping of the scattered SH-waves in the considered orthotropic viscoelastic structure.

The impact of anisotropy parameter on the reflected displacement for different type of surface irregularities, i.e., parabolic type surface irregularity, triangular notch type surface irregularity, and rectangular type surface irregularity has been demonstrated through Fig. 7a–c, respectively. From Fig. 7a–c, it is observed that the reflected displacement for all three cases diminishes with the increase in anisotropic parameter (associated with the ratio of shear modulus) of upper layer in the considered orthotropic viscoelastic composite structure. It is examined that as the anisotropy prevails in the medium, some energy of the SH-waves may entrap in the medium, which may further cause decrease in the reflected displacement.

Fig. 7
figure 7

Variation of dimensionless reflected displacement against dimensionless vertical width \(\left( {\upsilon_{1} s} \right)\) for the distinct values of anisotropy parameter \(\left( {\lambda_{1} = \sqrt {{{c_{55}^{1R} } / {c_{44}^{1R} }}} } \right)\) for the case of a parabolic type surface irregularity \(\left[ {{\text{Re}} \left( {w_{1,\,\,ref\,}^{P} /A} \right)} \right]\); b triangular notch type surface irregularity \(\left[ {{\text{Re}} \left( {w_{1,\,ref\,}^{T} /A} \right)} \right]\); and c rectangular type surface irregularity \(\left[ {{\text{Re}} \left( {w_{1,\,ref}^{R} /A} \right)} \right]\) in the considered orthotropic viscoelastic composite structure

Full size image

Figure 8a–c demonstrated the influence of vertical irregularity parameter on the reflected displacement in aforesaid medium for the parabolic type surface irregularity, triangular notch type surface irregularity, and rectangular type surface irregularity, respectively. It is observed from these figures that the reflected displacement increases with the increase in the vertical irregularity parameter. The vertical irregularity parameter is associated with the ratio of vertical depth of surface irregularity to thickness of the layer. The increase in vertical irregularity parameter causes the increase in vertical irregularity depth as compared to layer thickness. In this situation, more wave components strike through the irregularity wall; therefore, reflected displacement increases accordingly.

Fig. 8
figure 8

Variation of dimensionless reflected displacement \(\left[ {{\text{Re}} \left( {v_{1,\,\text{ref}\,}^{P} /A} \right)} \right]\) against dimensionless vertical width \(\left( {\upsilon_{1} s} \right)\) for the distinct values of vertical irregularity parameter \(\left( {b/H} \right)\) for the case of a parabolic type surface irregularity \(\left[ {{\text{Re}} \left( {w_{{1,\,\,{\text{ref}}\,}}^{P} /A} \right)} \right]\); b triangular notch type surface irregularity \(\left[ {{\text{Re}} \left( {w_{1,\,\text{ref}\,}^{T} /A} \right)} \right]\); and c rectangular type surface irregularity \(\left[ {{\text{Re}} \left( {w_{1,\,\text{ref}}^{R} /A} \right)} \right]\) in the said orthotropic viscoelastic composite structure

Full size image

A comparative exploration of induced reflected displacement among three types of surface irregularity has been observed through Fig. 9. It has been noticed from this figure that the reflected displacement for the case of rectangular type surface irregularity is maximum while it is minimum for the case of parabolic type surface irregularity in the considered orthotropic viscoelastic structure. Further, the reflected displacement for the triangular notch type surface irregularity lies between the former two cases.

Fig. 9
figure 9

Variation of dimensionless displacement field \(\left[ {{\text{Re}} \left( {w_{{1,\,\,{\text{ref}}}} /A} \right)} \right]\) against dimensionless vertical width \(\left( {\upsilon_{1} s} \right)\) for distinct types of surface irregularity viz. parabolic type surface irregularity (PTSI), triangular notch type surface irregularity (TTTSI), and rectangular type surface irregularity (RTSI)

Full size image

8 Conclusions

This paper deals with the scattering phenomena of SH-waves on an irregular surface of the layered orthotropic viscoelastic structure. The dispersion relation between the phase velocity and wave number has been obtained for the propagation of SH-waves. The impact of anisotropy parameter of the upper orthotropic viscoelastic layer on the phase velocity and attenuation coefficient associated with the damping of scattered SH-waves has also been examined. The exact expression of reflected displacement field due to scattering phenomena is also obtained by contour residue theorem. The expression of reflected displacement component for different types of surface irregularity viz. parabolic, triangular notch, and rectangular has also been derived. The effect of different influencing parameters viz. anisotropy parameter (associated with shear modulus), vertical irregularity parameter on the reflected displacement component has been observed for all three types of surface irregularity (i.e., PTSI, TTTSI, and RTSI). Moreover, the major outcomes of the present study can be considered as follow:

  1. 1.

    The phase velocity of scattered SH-waves decreases when the anisotropy prevails in orthotropic viscoelastic composite material structure.

  2. 2.

    The attenuation coefficient (association with damping of scattered SH-waves) escalates with the rise in the anisotropy parameter in the aforesaid medium.

  3. 3.

    The anisotropy parameter has an amplifying impact on reflected displacement component for the propagation of SH-waves for all types of surface irregularity viz. parabolic, triangular notch, and rectangular, respectively.

  4. 4.

    The vertical irregularity parameter favors the induced reflected displacement component for all types of surface irregularity viz. parabolic, triangular notch, and rectangular, respectively.

  5. 5.

    The induced reflected displacement in the case of rectangular type surface irregularity is observed maximum, while it is found minimum for the case of parabolic type surface irregularity.

9 Engineering applications

The present study can have some significant applications to examine the stability of engineering structures made by orthotropic viscoelastic structures in the earthquake prone area. The various orthotropic viscoelastic materials like carbon fiber and prepreg materials are used in the construction of highways and bridges. SH-waves are destructive in nature, and the propagation of SH-waves occurs during the earthquake event. As the SH-waves propagate through the irregular surface of the structure, the phenomena of scattering of SH-waves may occur in that place. Due to scattering phenomena of SH- waves, the amplitude of reflected displacement can become higher which can damage the engineering structure. The outcomes of the present study provide the knowledge about the parameters through which the damaging effect can be reduced. It is examined from the present analysis that the materials having higher values of anisotropic parameter (associated with the ratio of shear modulus) may reduce the velocity of SH-wave and may generate the reflected displacement of lesser amplitude. It is also analyzed from the present investigation that the upper layer containing rectangular type surface irregularity is more dangerous because it can generate higher reflected displacement, while the upper surface containing the parabolic type of surface irregularity of same depth and span can generate lower reflected displacement.

Moreover, the present analysis also provides that the material having larger vertical irregularity parameter (ratio of maximum irregularity depth to the thickness of layer) can generate higher reflected displacement and can be avoided for the construction purpose. By obtaining this crucial information, the special attention can be taken for the selection of materials used in the engineering structures such as highways and bridges in the earthquake prone area. Therefore, the present investigation can be useful in the field of civil and earthquake engineering.