1 Introduction

Insects possess exceptional aerial capabilities despite their small size, making them a natural source of inspiration for the design of flapping wing microair vehicles (FWMAVs). The military and civilian potential of FWMAVs for tasks such as intelligence gathering, fixed-point patrolling and disaster relief has attracted considerable research interest. In particular, insect-based hovering FWMAVs offer several advantages such as low cost, low noise, high stealth and flexibility [1,2,3,4,5].

The motion of insect wings is quite complicated [6] and influenced by numerous parameters, including pitch amplitude, deviation, stroke, flapping frequency, etc. [7, 8]. Most theoretical and experimental studies [7, 9,10,11,12,13,14,15,16,17] have focused on rigid wings where the aeroelastic coupling of solid and fluid was ignored. The experimental study conducted by Sane and Dickinson [7] using a fruitfly-like rigid flapping wing planform at Reynolds number of about 100 revealed that lift was maximum when the pitch amplitudes and stroke were 45◦ and 180◦, respectively. Bhat et al. [18] proposed that the flapping motion profile influenced the overall change in the lift coefficient of the rigid flapping wing, while the pitching motion profile only affected the lift at stroke reversal. The above researches only focus on the influence of motion parameters on rigid flapping wings; it is important to note that these results may not be generalizable to flexible flapping wings.

The structural deformation can significantly change the flow behavior around the wing and consequently have an essential effect on its aerodynamic performance [19,20,21,22]. Nakata et al. [23] conducted an integrated study on the aerodynamics of a FWMAV by combining wind tunnel experiments and in-house computational fluid dynamic approach. They found that, compared with a rigid wing, the clap and fling of a flexible wing can adjust the feathering angle near the wing tip at stroke reversal so as to avoid some unfavorable phase delay during wing rotation. Kim et al. [24] proposed a coupling method to analyze the fluid–structural interaction (FSI) of a flexible flapping wing. They revealed that the passive or active deformation of the flexible flapping wing contributed to generate appropriate aerodynamic performances according to the various flight modes. Yin and Luo [25] investigated wing inertia on aerodynamic performance by simulating the FSI of a flapping wing during hovering flight in a 2D numerical study. They found that both inertial-induced and flow-induced deformations can result in lift enhancement, and the latter can also lead to higher efficiency. The combined influence of aspect ratio (AR), deflection and pitch angle on flexible flapping wing aerodynamics during hovering was investigated experimentally by Akoto et al. [26]. Again, the study revealed that as the AR increased, the flexible wings mostly outperformed the rigid ones in aerodynamic performance. A theoretical model was proposed by Chen et al. [27] to quickly estimate the passive deformation and aerodynamic performance of flexible flapping wings. They found that the flexibility of insect wings and model wings in FWMAVs was crucial to guarantee an economic flight. Wang et al. [28] recently investigated highly simplified bio-inspired models (either mathematical or mechanical) in an effort to elucidate the flow physics associated with FSI. A unanimous conclusion was obtained that some degree of flexibility (both chordwise and spanwise) can be beneficial for improving propulsive performance (in terms of thrust, cruising speed and efficiency). Reade and Jankauski [29] developed a simplified 2D model for a flapping wing, by employing unsteady vortex lattice method and the assumed mode method to model the fluid and structural dynamics, respectively. They found that for hovering flight, the optimized flexible wing produced 20% more lift and required 15% less power compared to a rigid wing. Zhao et al. [30] developed four different airfoils to study how camber influences aerodynamic forces. They found that certain camber of airfoil could improve the aerodynamic characteristics of flapping wing and the flapping wing with a 20-mm camber was optimal.

Insect wings do not contain any muscle [31] and are actuated and controlled by insect thoracic muscles. As these muscles contract, they deform the thorax, which indirectly causes the wings of insects to flap [32, 33]. Jankauski [34] confirmed that the thorax behaved as a nonlinear hardening spring via static force–displacement testing. Casey et al.[35] used a tethered flight experiment to quantify the thorax deformation and the aerodynamic/inertial forces operating on the thorax generated by the flapping wing, and the results demonstrated that thoracic muscle elasticity contributed significantly to the wing motion. Recent studies have imagined the thorax as an elastically distributed system [36], and mathematical models have shown the significance of elastic components in flight energetics [37]. Based on the actuation inside the thorax of insects, the actuation muscles are further classified into two categories: synchronous flight muscle and asynchronous flight muscle [38, 39]. Actuation by synchronous flight muscles is synchronized with the neuro-controlled signals. These muscles can control each wing directly and cause direct flight [40], whereas actuation by asynchronous flight muscles is not synchronized with the neuro-controlled signals. These muscles expand and contract the thorax to actuate the wing. This indirect flight actuation is the simplest technique for flapping wings among all the flyers, which are available in nature [33].

Despite the potential importance of thoracic muscle effect on flexible flapping wing aerodynamic performance, limited research has been conducted on this topic. Thus, we aim to evaluate the effect of thoracic muscles on passive deformations and aerodynamic performance in a hovering flexible flapping wing. This research is focused on the indirect flight actuation. We simplify the insect's asynchronous thoracic muscles as torsional spring attached to the base of the wings. The twisting and untwisting of the torsional spring represent the contraction and relaxation of the thoracic muscles, respectively, and also the energy storage and release during wing movement, respectively. The intention for simplifying insect thorax muscles into torsional springs is rooted in the desire to capture the essential aspects of the wing motion while minimizing complexity. Another intention is to help optimize the design of FWMAVs. Our research shows that adding torsional springs to FWMAVs can enhance the efficiency of lift production. Section 2 presents a flexible flapping wing model, containing the structural model, the quasi-steady (QS) aerodynamic model and the motion equations derivation. The proposed model is validated in Sect. 3, and a benchmark case analysis is followed in Sect. 4.1. The effect of thoracic muscle is discussed in details in Sect. 4.2. Finally, Sect. 5 presents the conclusions.

2 FSI flapping wing model

2.1 Morphology and kinematics

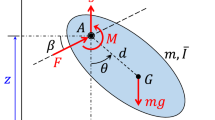
Figure 1 shows the morphology and kinematics of an insect flapping wing. The isotropic flexible rectangular plate is a simplification of the flexible flapping wing with elastic modulus E Poisson’s ratio ν, thickness h and density ρw. c and R correspond to the flapping wing's mean chord length and wingspan, respectively (along the span, c is constant). The aspect ratio is defined as AR = R/c. The distance between the flapping rotation center and the wing root is r0. The thorax is considered as an elastic system consisting of two parts: a rigid body, representing the flight muscles that provides active drive, and a chordwise torsional spring, which simulates the influence of thoracic muscle deformation [35, 36, 41]. As shown in Fig. 1b, the rigid body with angular velocity \(\dot{\varphi }\) drives the wing flapping by the chordwise torsional spring with stiffness kφ, located at the wing root. The leading edge of the wing is where the pitching axis is located. A spanwise wing-root torsional spring of stiffness kα (in Fig. 1c, along the pitching axis) produces the pitching motion of the wing (i.e., the passive rotation). The two torsional springs' neutral positions are situated with the plate exactly perpendicular to the plane of stroke.

Fig. 1
figure 1

Schematics of kinematics and morphology of a flexible flapping wing: a real insect, b flapping frame, c pitching frame, d co-rotating frame and twisting along the span, e bending along the span, f sectional view of the local twisting angle η at the kth strip and g axonometric plot of the local bending angle ς at the kth strip

Full size image

The flexible flapping wing's kinematics in a hovering state are broken down into four motions: reciprocating rotating motion relative to the vertical axis, pitching motion about the pitching axis, as well as elastic bending and twisting across its span. Since the deviation motion from the stroke plane in hovering can be considered negligible, it is not included in this study [42, 43]. The wing's kinematics and deformation are proposed to be described, respectively, by four rigid-body rotating frames as well as another two elastic frames. The flapping angle (φw) is obtained from revolving the inertial frame xiyizi around yi axis, resulting in the flapping frame xφyφzφ (Fig. 1b). Figure 1c illustrates that through rotating the flapping frame xφyφzφ further about the xφ axis, the pitching frame xαyαzα and the corresponding pitching angle α are determined. Since the root of the wing is not connected to the common rotation center of the inertial, flapping and pitching frames, a co-rotating frame (xcyczc) is established by relocating the pitching frame to the wing root (Fig. 1d and e). Our definition of rotation matrices yields the following [44],

$${\mathbf{R}}_{\varphi } = \left[ {\begin{array}{*{20}c} {\cos \varphi_{{\text{w}}} } & \quad 0 & \quad {\sin \varphi_{{\text{w}}} } \\ 0 & \quad 1 & \quad 0 \\ { - \sin \varphi_{{\text{w}}} } & \quad 0 & \quad {\cos \varphi_{{\text{w}}} } \\ \end{array} } \right]{\text{ and }}{\mathbf{R}}_{\alpha } = \left[ {\begin{array}{*{20}c} 1 & \quad 0 & \quad 0 \\ 0 & \quad {\cos \alpha } & \quad { - \sin \alpha } \\ 0 & \quad {\sin \alpha } & \quad {\cos \alpha } \\ \end{array} } \right]$$
(1)

The elastic frames (xηyηzη and xζyζzζ) are attached to the wing’s kth strip, whose twisting and bending along the span are approximated as a further rotation about the respective axes (Fig. 1f and g). \({\varvec{r}}_{i} = \left[ {x_{i} ,y_{i} ,z_{i} } \right]^{T}\) and \({\varvec{r}}_{c} = \left[ {x_{c} ,y_{c} ,z_{c} } \right]^{T}\), respectively, can be used to describe the position vector for a generic point P (xc0, yc0, 0) placed in the inertial and co-rotating frames. Additionally, rc can be divided into two parts, \({\varvec{r}}^{ela} = \left[ {u_{c} ,v_{c} ,w_{c} } \right]^{T}\)and \({\varvec{r}}_{c}^{0} = \left[ {x_{c0} ,y_{c0} ,0} \right]^{T}\), which stand by the elastic displacement and the position vector for P without deformation, respectively. The wing strips are supposed to remain straight and unstretched after elastic deformation, as shown in Fig. 1f and g, but their relative positions alter. Whereas no chordwise stretching is involved, the spanwise stretching along the span increases progressively. Then, uc, vc and wc can be expressed by

$${\mathbf{r}}_{{}}^{{{\text{ela}}}} = \left[ {\begin{array}{*{20}c} {u_{c} } \\ {v_{c} } \\ {w_{c} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {u_{{\text{c}}}^{\max } x_{{{\text{c0}}}} /R} \right)\cos \zeta + y_{c0} \sin \eta \sin \zeta } \\ {y_{c0} \left( {\cos \eta - 1} \right)} \\ {\left( {u_{{\text{c}}}^{\max } x_{{{\text{c0}}}} /R} \right)\sin \zeta - y_{c0} \sin \eta \cos \zeta } \\ \end{array} } \right]$$
(2)

Here, u maxc represents the maximal rootward displacement at the wingtip [45]; ζ and η are the local bending angle and twisting angle, respectively.

The flexible flapping wing’s angular velocity and acceleration can be estimated by

$${{\varvec{\upomega}}}_{c} = \left[ {\begin{array}{*{20}c} {\omega_{xc} } \\ {\omega_{yc} } \\ {\omega_{zc} } \\ \end{array} } \right] = \left( {{\mathbf{R}}_{\varphi } {\mathbf{R}}_{\alpha } {\mathbf{R}}_{\eta } {\mathbf{R}}_{\zeta } } \right)^{{\text{T}}} \left[ {\begin{array}{*{20}c} 0 \\ {\dot{\varphi }{}_{{\text{w}}}} \\ 0 \\ \end{array} } \right] + {\mathbf{R}}_{\zeta }^{{\text{T}}} \left[ {\begin{array}{*{20}c} {\dot{\eta } + \dot{\alpha }} \\ 0 \\ 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ {\dot{\zeta }} \\ 0 \\ \end{array} } \right]$$
(3)

and

$${{\varvec{\upalpha}}}_{c} = \left[ {\begin{array}{*{20}c} {\alpha_{xc} } \\ {\alpha_{yc} } \\ {\alpha_{zc} } \\ \end{array} } \right] = \left( {{\mathbf{R}}_{\varphi } {\mathbf{R}}_{\alpha } {\mathbf{R}}_{\eta } {\mathbf{R}}_{\zeta } } \right)^{{\text{T}}} \left[ {\begin{array}{*{20}c} 0 \\ {\ddot{\varphi }_{{\text{w}}} } \\ 0 \\ \end{array} } \right] + {\mathbf{R}}_{\zeta }^{{\text{T}}} \left[ {\begin{array}{*{20}c} {\ddot{\eta } + \ddot{\alpha }} \\ 0 \\ 0 \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ {\ddot{\zeta }} \\ 0 \\ \end{array} } \right]$$
(4)

Here, Rζ is the rotation matrices caused by the local bending angle in the co-rotating frame, while Rη is induced by the local twisting angle.

The flexible flapping wing’s translational velocity and acceleration of the can be calculated by

$${\mathbf{v}}_{c} = \left[ {\begin{array}{*{20}c} {v_{xc} } \\ {v_{yc} } \\ {v_{zc} } \\ \end{array} } \right] = {{\varvec{\upomega}}}_{c} \times {\mathbf{r}}$$
(5)

and

$${\mathbf{a}}_{c} = \left[ {\begin{array}{*{20}c} {a_{xc} } \\ {a_{yc} } \\ {a_{zc} } \\ \end{array} } \right] = {{\varvec{\upalpha}}}_{c} \times {\mathbf{r}}_{c} + {{\varvec{\upomega}}}_{c} \times {\mathbf{v}}_{c}$$
(6)

Polynomial functions define the spanwise distributions of η and ζ, i.e., [44],

$$\eta \left( {x_{c} } \right) = a_{{1}} x_{c0}^{{}} { + }a_{{2}} x_{c0}^{{2}} { 0} \le x_{c0}^{{}} \le R$$
(7)

and

$$\zeta \left( {x_{c} } \right) = b_{{1}} x_{c0}^{{}} { + }b_{{2}} x_{c0}^{{2}} { 0} \le x_{c0}^{{}} \le R$$
(8)

The twisting and bending angles at xc0 = 0.5R and R determine the coefficients ai and bi (i = 1,2) in Eqs. (7), (8). \(q_{1,i}^{{{\text{ela}}}}\) and \(q_{2,i}^{{{\text{ela}}}}\) (i = 1, 2) represent the correspondent twisting and bending angles, respectively.

2.2 Unsteady aerodynamic force modeling

The improved QS model is employed to calculate the unsteady aerodynamic force of the flexible flapping wing [46], with consideration given to both the coupling effect of rotational and translation motion. The aerodynamic forces in the QS model are presumed to be related only to the transient kinematic performance of the flexible flapping wing, namely, accelerations, velocities and attack angle, while disregarding the flow history effect. Due to the fact that the kinematic performance of a general point on the flexible flapping wing is affected by the local radius, the blade element method allows for the division of the flexible flapping wing into multiple chordwise strips, where the interval dx is taken to be infinitesimal. The flexible wing’s chordwise strips all remain flat, and the force element (dFaero) is presumed perpendicular to the local strip. The dFaero can be expressed as

$${\text{d}}{\mathbf{F}}_{{{\text{aero}}}} = \left( {F_{{\text{n}}}^{{{\text{tran}}}} + F_{{\text{n}}}^{{{\text{rot}}}} + F_{{\text{n}}}^{{{\text{coup}}}} + F_{{\text{n}}}^{{{\text{am}}}} } \right){\mathbf{e}}_{{\text{n}}} {\text{d}}x$$
(9)

where the dFaero is divided into four components based on the QS model, known as, \(F_{{\text{n}}}^{{{\text{coup}}}} ,F_{{\text{n}}}^{{{\text{rot}}}} , \, F_{{\text{n}}}^{{{\text{am}}}} {\text{ and }}F_{{\text{n}}}^{{{\text{tran}}}}\). They stand by the translation-rotation coupling, rotation (about the pitching axis), added-mass effect and translation components, respectively. Wang et al. [46] provide various detailed components derivations, and the following is a summary,

$$F_{{\text{n}}}^{{{\text{tran}}}} = - {\text{sgn}} \left( {v_{zc} } \right)\frac{1}{2}\rho_{f} \left( {v_{yc}^{2} + v_{zc}^{2} } \right)C_{{{\text{tran}}}} c_{{1}}^{{}}$$
(10)
$$F_{{\text{n}}}^{{{\text{rot}}}} = {\text{sgn}} \left( {\omega_{xc} } \right)\int_{{ - c_{{1}} }}^{0} {{\text{sgn}} \left( {y_{c} } \right)\frac{1}{2}\rho_{f} \omega_{xc}^{2} y_{c}^{2} C_{{{\text{rot}}}} {\text{d}}y_{c} }$$
(11)
$$F_{{\text{n}}}^{{{\text{coup}}}} = - \frac{3\pi }{4}\rho_{f} c_{{1}}^{2} \omega_{xc} v_{yc} - \frac{\pi }{4}\rho_{f} c_{{1}}^{2} \omega_{xc} v_{yc} = - \pi \rho_{f} c_{{1}}^{2} \omega_{xc} v_{yc}$$
(12)
$$F_{{\text{n}}}^{{{\text{am}}}} = - \frac{\pi }{4}\rho_{f} c_{{1}}^{2} a_{zc} - \frac{\pi }{8}\rho_{f} c_{{1}}^{{3}} a_{xc}$$
(13)

Here, Ctran (\(C_{{{\text{trans}}}} = 2\pi AR\sin \alpha_{e} (2+\sqrt {AR^{2} + 4} )^{ - 1}\) ) indicates the coefficient of translational force, while Crot is the coefficient of rotational force. Crot equals Ctran when the strip’s effective attack angle αe is π/2. Moreover, when αe is less than π/2, only can the translation-rotation coupling effect be considered. In Eqs. (10)–(13), the symbol c1 represents a local strip’s chord length (even though c1 is equal to the mean value c because of its rectangular shape). According to Eqs. (10)–(13), the four aerodynamic force components are estimated nonlinearly with respect to the wing kinematics. Furthermore, the pressure centers \(\tilde{d}_{{{\text{cp}}}}^{*}\) of these force components of each strip are expressed by Eqs. (14)–(17), where the superscript “*” denotes different force components.

$$\tilde{d}_{{{\text{cp}}}}^{{{\text{trans}}}} = {{\left| {\alpha_{e} } \right|} \mathord{\left/ {\vphantom {{\left| {\alpha_{e} } \right|} \pi }} \right. \kern-0pt} \pi }$$
(14)
$$\tilde{d}_{{{\text{cp}}}}^{{{\text{rot}}}} = {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}$$
(15)
$$\tilde{d}_{{{\text{cp}}}}^{{{\text{coup}}}} = \frac{1}{4}{\text{ and }}\frac{3}{4}$$
(16)
$$\tilde{d}_{{{\text{cp}}}}^{{{\text{am}}}} = \frac{1}{2}{\text{ and }}\frac{9}{16}$$
(17)

2.3 Motion equations and kinematic constraints

The generalized coordinates are used to describe the hovering flexible flapping wing’s kinematics,

$${\mathbf{q}} = \left[ {\begin{array}{*{20}c} {\left[ {{\mathbf{q}}^{{{\text{rot}}}} } \right]^{{\text{T}}} } & {\left[ {{\mathbf{q}}_{{1}}^{{{\text{ela}}}} } \right]^{{\text{T}}} } & {\left[ {{\mathbf{q}}_{2}^{{{\text{ela}}}} } \right]^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}}$$
(18)

in which \({\mathbf{q}}^{{{\text{rot}}}} = \left[ {\begin{array}{*{20}c} \varphi & {\varphi_{{\text{w}}} } & \alpha \\ \end{array} } \right]^{{\text{T}}}\), \({\left[ {{{q}}_1^{{\text{ela}}}{{ = q}}_{1,1}^{{\text{ela}}}{{,q}}_{1,2}^{{\text{ela}}}{{,u}}_c^{\max }} \right]^T}{\text{ and }}q_2^{{\text{ela}}}{{ = }}{\left[ {{{q}}_{2,1}^{{\text{ela}}}{{,q}}_{2,2}^{{\text{ela}}}} \right]^T}.\)

The motion equation of the flexible flapping wing is carried out by Lagrange’s equation,

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{\partial E_{{\text{k}}} }}{{\partial {\dot{\mathbf{q}}}}}} \right) - \frac{{\partial E_{{\text{k}}} }}{{\partial {\mathbf{q}}}} + \frac{{\partial E_{{\text{P}}} }}{{\partial {\mathbf{q}}}} = {\mathbf{Q}}$$
(19)

where Ek and Ep stand by the kinetic and potential energy, respectively. Aerodynamic loads and driving torque are included in the generalized external forces Q.

Ek can be derived by

$$E_{{\text{k}}}^{{}} = \frac{1}{2}\iint {h\rho_{{\text{w}}} {\dot{\mathbf{r}}}_{i}^{{\text{T}}} {\dot{\mathbf{r}}}_{i}^{{}} {\text{d}}s} + \frac{{1}}{{2}}m_{{\text{r}}} l^{2} \dot{\varphi }^{2} = \frac{1}{2}{\dot{\mathbf{q}}}^{{\text{T}}} {\mathbf{M}}_{{\text{w}}} {\dot{\mathbf{q}}} + \frac{{1}}{{2}}m_{{\text{r}}} l^{2} \dot{\varphi }^{2}$$
(20)
$${\mathbf{M}}_{{\text{w}}} = \frac{1}{2}\iint {\rho_{{\text{w}}} h{\mathbf{L}}^{{\text{T}}} {\mathbf{L}}{\text{d}}s}$$
(21)

and

$${\mathbf{L}} = \frac{{\partial {\mathbf{r}}_{i} }}{{\partial {\mathbf{q}}_{i} }}$$
(22)

in which Mw is the flexible flapping wing’s mass matrix, mr respects the muscle mass driving the insect flapping, and l denotes the vertical distance between the rigid body and the flexible flapping wing’s leading edge.

The potential energy Ep is broken down into contributions from its wing-root torsion (because of the torsional springs), bending and twisting of the flexible flapping wing. Hence, EP can be given by

$$E_{{\text{P}}} = E_{{\text{P}}}^{{{\text{rot}}}} + E_{{\text{P}}}^{{{\text{ela}}}}$$
(23)

According to the linear elastic assumption, \(E_{{\text{P}}}^{{{\text{rot}}}}\) can be formulated as,

$$E_{{\text{P}}}^{{{\text{rot}}}} = \frac{1}{2}\left[ {k_{\alpha } \alpha^{2} { + }k_{\varphi } \left( {\varphi_{{\text{w}}} - \varphi } \right)^{{2}} } \right]$$
(24)

\(E_{{\text{P}}}^{{{\text{ela}}}}\) is derived as follows,

$$E_{{\text{P}}}^{{{\text{ela}}}} = \frac{1}{2}\iiint {{{\varvec{\upvarepsilon}}}^{{\text{T}}} {\mathbf{C\varepsilon }}{\text{d}}V}$$
(25)

Based on the von Kármán nonlinear plate theory [35], the strain ε is

$${{\varvec{\upvarepsilon}}} = \left[ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\partial u_{c} }}{{\partial x_{c} }} + \frac{1}{2}\left( {\frac{{\partial w_{c} }}{{\partial x_{c} }}} \right)^{2} - z_{c} \frac{{\partial^{2} w_{c} }}{{\partial x_{c}^{2} }}} \\ {\frac{{\partial v_{c} }}{{\partial y_{c} }} + \frac{1}{2}\left( {\frac{{\partial w_{c} }}{{\partial y_{c} }}} \right)^{2} - z_{c} \frac{{\partial^{2} w_{c} }}{{\partial y_{c}^{2} }}} \\ {\frac{{\partial v_{c} }}{{\partial x_{c} }} + \frac{{\partial u_{c} }}{{\partial y_{c} }} + \frac{{\partial w_{c} }}{{\partial x_{c} }}\frac{{\partial w_{c} }}{{\partial y_{c} }} - 2z_{c} \frac{{\partial^{2} w_{c} }}{{\partial x_{c} \partial y_{c} }}} \\ \end{array} } \right]$$
(26)

and the constitutive matrix C can be presented by

$${\mathbf{C}} = \frac{E}{{1 - \nu^{2} }}\left[ {\begin{array}{*{20}c} 1 & \quad \nu &\quad 0 \\ \nu &\quad 1 &\quad 0 \\ 0 &\quad 0 &\quad {{{\left( {1 - \nu } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \nu } \right)} 2}} \right. \kern-0pt} 2}} \\ \end{array} } \right]$$
(27)

The generalized Coriolis and centrifugal forces (QV) as well as the elastic force (Qela) are calculated by

$${\mathbf{Q}}_{{\text{V}}} = {\dot{\mathbf{M}}}_{{\text{w}}} {\dot{\mathbf{q}}} - \left[ {\frac{\partial }{{\partial {\mathbf{q}}}}\left( {\frac{1}{2}{\dot{\mathbf{q}}}^{{\text{T}}} {\mathbf{M}}_{{\text{w}}} {\dot{\mathbf{q}}}} \right)} \right]^{{\text{T}}} + \left[ {\begin{array}{*{20}c} {m_{{\text{r}}} l^{2} \dot{\varphi }} & 0 & \cdots & 0 \\ \end{array} } \right]_{{{8} \times {1}}}^{{\text{T}}}$$
(28)
$$\begin{aligned}{\mathbf{Q}}_{{{\text{ela}}}} = &\frac{{\partial E_{{\text{p}}}}}{{\partial {\mathbf{q}}}} = \left[ {\begin{array}{*{20}c} { -k_{\varphi } \left( {\varphi_{{\text{w}}} - \varphi } \right) \,k_{\varphi } \left( {\varphi_{{\text{w}}} - \varphi } \right) \,k_{\alpha } \alpha } & {\frac{{\partial E_{{\text{p}}}^{{{\text{ela}}}} }}{{\partial {\mathbf{q}}_{1}^{{{\text{ela}}}} }}} & {\frac{{\partial E_{{\text{p}}}^{{{\text{ela}}}} }}{{\partial {\mathbf{q}}_{2}^{{{\text{ela}}}} }}} & {\frac{{\partial E_{{\text{p}}}^{{{\text{ela}}}} }}{{\partial q_{3}^{{{\text{ela}}}}}}} \\\end{array} } \right]^{{\text{T}}} \\ =& \left[ {\begin{array}{*{20}c} { - k_{\varphi } \left( {\varphi_{{\text{w}}} - \varphi } \right)} & {{\tilde{\mathbf{Q}}}_{{{\text{ela}}}} } \\ \end{array} } \right]^{{\text{T}}} \\ \end{aligned}$$
(29)

To achieve the prescribed flapping motion,Q in Eq. (19) also comprises the driving torque and aerodynamic components, namely, Qφ and Qaero. Qaero can be broken into four subsections as

$$\begin{aligned}{\mathbf{Q}}_{{{\text{aero}}}} = &\int_{0}^{R} {\left\{{F_{{\text{n}}}^{{{\text{tran}}}} \left[ {\frac{{\partial {\mathbf{r}}_{{\text{i,cp}}}^{{{\text{tran}}}} }}{{\partial {\mathbf{q}}}}} \right]^{{\text{T}}} +F_{{\text{n}}}^{{{\text{rot}}}} \left[ {\frac{{\partial {\mathbf{r}}_{{\text{i,cp}}}^{{{\text{rot}}}} }}{{\partial {\mathbf{q}}}}} \right]^{{\text{T}}} +F_{{\text{n}}}^{{{\text{coup}}}} \left[ {\frac{{\partial {\mathbf{r}}_{{\text{i,cp}}}^{{{\text{coup}}}} }}{{\partial {\mathbf{q}}}}} \right]^{{\text{T}}} } \right.} \\ &\left. { +F_{{\text{n}}}^{{{\text{am}}}} \left[ {\frac{{\partial {\mathbf{r}}_{{\text{i,cp}}}^{{{\text{am}}}} }}{{\partial {\mathbf{q}}}}} \right]^{{\text{T}}} } \right\}\left({{\mathbf{R}}_{\varphi } {\mathbf{R}}_{\alpha } {\mathbf{R}}_{\eta }{\mathbf{R}}_{\zeta } } \right){\mathbf{e}}_{{\text{n}}}{\text{d}}x_{{\text{c}}} \\ \end{aligned}$$
(30)

Here, \({\mathbf{r}}_{{\text{i,cp}}}^{{{\text{tran}}}} , \, {\mathbf{r}}_{{\text{i,cp}}}^{{{\text{rot}}}} , \, {\mathbf{r}}_{{\text{i,cp}}}^{{{\text{coup}}}} {\text{ and }}{\mathbf{r}}_{{\text{i,cp}}}^{{{\text{am}}}}\) identify the pressure centers of the local strip (in the inertial frame), as determined by

$${\mathbf{r}}_{{\text{i,cp}}}^{*} = {\mathbf{R}}_{\varphi } {\mathbf{R}}_{\alpha } {\mathbf{R}}_{\eta } {\mathbf{R}}_{\xi } \left[ {\begin{array}{*{20}c} {x_{{\text{c}}} } & { - c_{{1}} \tilde{d}_{{{\text{cp}}}}^{*} } & {0} \\ \end{array} } \right]^{{\text{T}}}$$
(31)

in which the superscript “*” denotes various force components. On the basis of Sect. 2.2, \(F_{n}^{{{\text{tran}}}} ,F_{n}^{{{\text{rot}}}} {\text{and }}F_{n}^{{{\text{coup}}}}\) are inextricably linked to the generalized velocities, while \(F_{n}^{{{\text{am}}}}\) is affected by the generalized accelerations. Thus, through removing components of acceleration-related in Qaero

$${\mathbf{Q}}_{{{\text{aero}}}} ={\tilde{\mathbf{Q}}}_{{{\text{aero}}}} -{\mathbf{M}}_{{{\text{am}}}} {\ddot{\mathbf{q}}}$$
(32)

where \(\tilde{Q}_{{{\text{aero}}}}\)represents the aerodynamic loads with respect to the generalized velocity, and the effect of added-mass is responsible for the mass matrix Mam.Therefore, Eq. (14) can be rewritten as

$${\mathbf{M}\ddot{\mathbf{q}}} = -{\mathbf{Q}}_{{{\text{ela}}}} + \left[ {\begin{array}{*{20}c}{Q_{\varphi } } & {{\mathbf{0}}_{1 \times 8} } \\ \end{array} }\right]^{{\text{T}}} +{\tilde{\mathbf{Q}}}_{{{\text{aero}}}} -{\mathbf{Q}}_{{\text{V}}}$$
(33)

whereM is the sum of Mw and Mam.

Actuators can drive and direct the rigid body's flapping motion in this model. Hence, Eq. (33) may be kinematically bound through φ, and the constraint is enforced by applying an external driving torque.

$$\left[ {\begin{array}{*{20}c}{{\mathbf{M}}_{1 \times 1} } & {{\mathbf{M}}_{1 \times 8} } \\{{\mathbf{M}}_{8 \times 1} } & {{\mathbf{M}}_{8 \times 8} } \\\end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{\varphi }}\\ {{\ddot{\mathbf{q}}}_{i} } \\ \end{array} } \right] = - \left[{\begin{array}{*{20}c} { - k_{\varphi } \left( {\varphi -\varphi_{{\text{w}}} } \right)} \\{{\tilde{\mathbf{Q}}}_{{{\text{ela}}}} } \\ \end{array} } \right] +\left[ {\begin{array}{*{20}c} {Q_{\varphi } } \\ {{\mathbf{0}}_{1 \times 8} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c}{\tilde{Q}_{\varphi }^{{{\text{aero}}}} } \\{{\tilde{\mathbf{Q}}}_{i}^{{{\text{aero}}}} } \\ \end{array} }\right] - \left[ {\begin{array}{*{20}c} {Q_{\varphi }^{{\text{V}}} }\\ {{\mathbf{Q}}_{i}^{{\text{V}}} } \\ \end{array} } \right]$$
(34)

The unknown generalized accelerations \(\mathbf{{\ddot{q}}}_{{\text{i}}}\)and external driving torque Qφ are approximated by

$${\mathbf{M}}_{8 \times 8}{\ddot{\mathbf{q}}}_{i} = - {\tilde{\mathbf{Q}}}_{{{\text{ela}}}} +{\tilde{\mathbf{Q}}}_{i}^{{{\text{aero}}}} -{\mathbf{Q}}_{i}^{{\text{V}}} - {\mathbf{M}}_{8 \times 1}\ddot{\varphi }$$
(35)
$$\begin{aligned} Q_{\varphi } = &\underbrace {{\left( {{\mathbf{M}}_{1 \times 1} - {\mathbf{M}}_{1 \times 8} {\mathbf{M}}_{8 \times 8}^{ - 1} {\mathbf{M}}_{8 \times 1}} \right)\ddot{\varphi } - {\mathbf{M}}_{1 \times 8} {\mathbf{M}}_{8 \times 8}^{ - 1} {\mathbf{Q}}_{i}^{{\text{V}}} + Q_{\varphi }^{{\text{V}}} }}_{{{\text{inertial}}}} \\& \quad \underbrace {{ +{\mathbf{M}}_{1 \times 8} {\mathbf{M}}_{8 \times 8}^{ - 1}{\tilde{\mathbf{Q}}}_{i}^{{{\text{aero}}}} - \tilde{Q}_{\varphi }^{{{\text{aero}}}} }}_{{{\text{aerodynamic}}}}\underbrace {{ -{\mathbf{M}}_{1 \times 8} {\mathbf{M}}_{8 \times 8}^{ - 1}{\mathbf{Q}}_{{{\text{ela}}}} { + }k_{\varphi } \left( {\varphi -\varphi_{{\text{w}}} } \right)}}_{{{\text{elastic}}}} \\\end{aligned}$$
(36)

Taking β = 1/2 and γ = 1/4, the Newmark-Raphson method is utilized to solve Eqs. (35)–(36). A sensitivity analysis shows that the wing is discretized along the span using a total of 50 strips,and a single flapping cycle can be divided into 400-time steps. The power consumption P and transient lift L can be estimated using the generalized coordinate solution

$$L = \int_{{r_{0} }}^{{r_{0} + R}}{{\mathbf{e}}_{yi}^{{\text{T}}} \left( {{\mathbf{R}}_{\varphi }{\mathbf{R}}_{\alpha } {\mathbf{R}}_{\eta } {\mathbf{R}}_{\zeta } }\right){\text{d}}{\mathbf{F}}_{{{\text{aero}}}} }$$
(37)
$$P = Q_{\varphi } \dot{\varphi }$$
(38)

The efficiency of lift production \(\overline{{{\text{PL}}}}\) is

$$\overline{{{\text{PL}}}} = \frac{{\overline{L}}}{{\overline{P}}}$$
(39)

where \(\overline{L}\) and \(\overline{P}\) represent the mean values of a flapping cycle L and P, respectively.

3 Validation

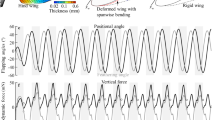
In order to verify the accuracy of the current model, we compared the digitized data obtained from the photographs of the hindwing of the rhinoceros beetle (Allomyrina dichotoma) with our predictions of flapping, pitching and twisting angles. The hindwing of rhinoceros beetles has been measured by Phan and Park [47] for flapping kinematics, wing geometry and mass distribution as shown in Table 1. However, their study did not report the elastic stiffness (E) and the root stiffness (kα and kφ) of the hindwing. According to the scaling rules [48], E is set at 30 MPa, kα is calculated to be 5 × 10–4 N·m·rad−1 [49], and kφ is assigned a value of 3 × 10–4 N·m·rad−1 by comparative verification (Fig. 2a). Moreover, the hindwing can be reinforced via veins, resulting in complex distributions of mass and stiffness, whereas the present model uses a uniform assumption.

Table 1 Parameters for the hindwing of rhinoceros beetles [47]
Full size table
Fig. 2
figure 2

Model validation by comparing with a beetle’s hindwing: a angle of flapping, angle of pitching at b 25% wingspan, c 50% wingspan and d 75% wingspan

Full size image

The real rigid-body flapping motion (φ) of these beetles is fitted as a smoothed triangular waveform \(\varphi \left( t \right) = \varphi_{{\text{m}}} \arcsin \left[ {K\sin \left( {2\pi ft} \right)} \right]/\arcsin \left( K \right)\) with K = 0.9 [50]. In our model, φ is equal to φw by setting kφ = 0, which means the influence of thorax muscles is eliminated. As shown in Fig. 2a, the fitted function is in good agreement with the real rigid-body flapping motion, which indicates that the adopted rigid-body flapping motion model is feasible. On this basis, we change the torsional stiffness kφ and calculated the optimal torsional stiffness of the model considering the effect of thorax muscle in subsequent research. The FSI model incorporates the conformed flapping angle to forecast the pitching motion at 25%, 50% and 75% of the wingspan, which includes the wing-root pitching in addition to the local twisting motion, as shown in Fig. 2b–d. The model shows good agreement with previous experiments in terms of local pitch angle (α + η); however, the pitching angle deviation at 75% of the wingspan is more pronounced compared to the wing root. This difference is most likely due to the rectangular platform assumption, which results in an inaccuracy in the local aerodynamic force induced by the beetle wing's local chord length drop about the wingtip. Though the QS model can estimate a wing strip’s aerodynamic loads with any chord length, in this study, a rectangular wing platform is utilized and disregards the change in chord lengths near the wingtip. It is a simplification for the FSI model while preserving most of the performance within the 75% wingspan. Nevertheless, it shows that our model is feasible and thus can be a strong tool for quickly evaluating the aeroelastic characteristics of both flexible flapping wing models and real insect wings.

4 Results and discussion

4.1 A benchmark case

As a benchmark case, an analysis of the flexible flapping wing has been conducted using the kinematics and shape of a real hawkmoth's wing (see Table 2 for details) [49, 51]. Although in actual situations, the rigid-body flapping motion (φ) of hawkmoth does not exactly follow the simple harmonic motion [52], the trend of the rigid-body flapping motion (φ) is consistent with the trend of simple harmonic motion [6]. Therefore, the trigonometric function is reasonable and convenient to model and analyze the flapping motion of insects [6, 53].

Table 2 Parameters for a flexible flapping wing [49, 51]
Full size table

In this study, the trigonometric function \(\dot{\varphi }\left( t \right) = 2\pi f\varphi_{{\text{m}}} \cos \left( {2\pi ft} \right)\) [49] is adopted to describe the rigid-body flapping motion (φ). The flapping frequency f = 25 Hz and amplitude φm = 60° are close to the measured values of hawkmoth wings [49, 52]. Figure 3 shows a comparison of the flapping motion for the flexible flapping wing between considering thoracic muscle effect (considering TM) and ignoring thoracic muscle effect (ignoring TM). It is seen that considering TM does not change the tendency of the flapping motion, but it changes the phase of the flapping motion. Under the effect of thoracic muscle, the flapping motion slightly lags.

Fig. 3
figure 3

Flapping angle in the benchmark case. Gray boxes delineate the downstrokes. Consider TM (considering the influence of thoracic muscles); ignore TM (ignoring the influence of thoracic muscle)

Full size image

Figure 4 displays a comparison between the wingtip and wing-root passive deformation. When ignoring TM, the pitching angle α peaks in advance. Considering TM can delay the pitching motion and reduce its magnitude (Fig. 4a). It can be seen from Fig. 4b that considering TM reduces the amplitude of the spanwise twist. For both cases, the peak of bending angle along the span occurs near the stroke reversal, as well as the maximum angle of the wingtip bending for considering TM is roughly 2°, which is lower than that ignoring TM (Fig. 4c). In other words, considering TM can inhibit the production of spanwise bending of the flexible flapping wing.

Fig. 4
figure 4

The benchmark case’s passive pitching angle and wing deformation: angle of a wing-root pitching, b wingtip twisting, c wingtip bending

Full size image

In Fig. 5, the transient lift for the two cases is compared, where \(\tilde{t}\) = 0.25–0.75 represents the downstroke (gray boxes). Considering TM, the lift peaks immediately after each mid-stroke. In contrast, the peak for ignoring TM appears before the mid-stroke with a larger amplitude. In other words, considering TM causes a lag in the lift peak and reduces its magnitude. This is because considering TM inhibits the deformation production of the flexible flapping wing, resulting in a reduction in lift (Fig. 4b and c). Hence, considering TM can decrease the cycle-averaged lift (0.027N when ignoring TM and 0.022N when considering TM).

Fig. 5
figure 5

Transient lift in the benchmark case

Full size image

Figure 6 further shows the decomposition of the transient lift for both cases. For both cases, the rotational lift and added-mass lift have similar trends and amplitudes, indicating that the average lift reduction is mainly caused via the translation-rotation coupling effect and translational lift. Particularly, there is a substantial increase in the negative lift resulting from the translation-rotation coupling effect after the stroke reversal when considering TM (Fig. 6c). This is comparable to the negative lift formation observed in a rigid flapping wing that is undergoing a delayed wing rotation [9, 54]. As shown in Fig. 4a, though the pitching angle nearly approaches the neutral position during each stroke reversal, the pitching angular velocity exhibits an asymmetric trend, and the decrease in transient lift is led by a rapid increase in pitching angle at the beginning of the following stroke. Therefore, as shown in Fig. 5, it results in a negative lift generation.

Fig. 6
figure 6

The benchmark case’s transient lift decompositions: a Ltran, translational lift, b Lrot, rotational lift, c Lcoup, translation-rotational coupling lift and d Lam, added-mass lift

Full size image

Figure 7 depicts a comparison the benchmark case’s transient power. Generally, for both cases, the transient power consumption is almost the same within a flapping cycle, but considering TM results in lower cycle-averaged power (0.078W for considering TM and 0.09W for ignoring TM). The flexible flapping wing slightly reduces the total power consumption because of the reduction in aerodynamic forces when considering TM (Fig. 7a). As shown in Fig. 7b, considering TM has a slight effect on the inertial power. Moreover, in both cases, the peak of the elastic power is observed following each stroke reversal indicates that the stored energy in the torsional springs and wing structure is employed to balance the aerodynamic power (Fig. 7c and d). Considering TM can enhance the elastic energy contribution to overcome the aerodynamic drag. Thus, assuming a perfect recovery system, the total power consumption can be decreased by a flexible flapping wing considering TM.

Fig. 7
figure 7

The benchmark case’s transient power: a P, total transient power, b Paero, aerodynamic power, c Piner, inertial power and d Pelas, elastic power

Full size image

4.2 Influences of root stiffness design

The root stiffness effect on the flexible wing considering TM is discussed in this section. As can be seen in Fig. 8a, a larger kα (kα = 7 × 10–4 N·m·rad−1 and kφ = 0 N·m·rad−1) creates a strong average lift (\(\overline{L}\)) with a value of about 0.026N. When the spanwise torsional spring stiffness is extremely low, the lift generation is significantly decreased and even produces negative lift. In addition, as shown by the lines (\(\overline{L}\) = 0.02 N) in Fig. 8a, the coupling effect of kα and kφ needs to be maintained for achieving a given lift. It can be seen from Fig. 8b, the maximum power consumption (\(\overline{P}\)) appears at kα = 1 × 10–4 N·m·rad−1 and kφ = 0 N·m·rad−1. Considering TM can significantly reduce the power consumption of flapping wings, while the stiffness change of chordwise torsional spring has little influence on the power consumption. In addition, as shown in Fig. 8c, the peak of efficiency (\(\overline{{{\text{PL}}}}\)) occurs at a lower value of lift production. It shows a balance between lift production and efficiency in the root stiffness design when considering TM. As Fig. 8a illustrates those various combinations of kα and kφ produce similar lift generation, the influences of kφ and kα on the amplitudes of pitching and flapping at the wing root and wingtip are explored in Fig. 8d–g. For cases with a comparable lift formation, the amplitudes are different. Moreover, it can be concluded that kα barely changes the flapping amplitude (Fig. 8f).

Fig. 8
figure 8

Aerodynamic performance and passive kinematics considering TM at different kα and kφ: average a lift, b power, amplitude of c power loading, d wing-root pitching, e wingtip pitching, f wing-root flapping and g wingtip bending

Full size image

In order to clarify the role of thoracic muscles in the effectiveness, Fig. 9 compares the transient power and lift in the high \(\overline{{{\text{PL}}}}\) status. As shown in Table 3, the high \(\overline{{{\text{PL}}}}\) considering TM is 23% higher than that ignoring TM. The high \(\overline{{{\text{PL}}}}\) status ignoring TM is achieved at kα = 5 × 10–4 N·m·rad−1 and kφ = 0 N·m·rad−1 [44], while considering TM, they are kα = 7 × 10–4 N·m·rad−1 and kφ = 1 × 10–4 N·m·rad−1. Generally, considering TM can reduce the lift generation and power consumption (Fig. 9a and b). The improvement in efficiency is due to the fact that the reduction in cycle-averaged power being greater than the reduction in cycle-averaged lift. Based on Fig. 9c, the reduction in lift when considering TM is mainly due to translational-rotational coupling lift (green lines) and translational lift (red lines), where the Ltran peak around mid-stroke is attenuated and the negative Lcoup after stroke reversal is increased. In addition, because of a larger root stiffness, the decrease of power is mainly caused by the reduce of the inertial component (blue lines in Fig. 9d).

Fig. 9
figure 9

Comparison of transient aerodynamic performance for high \(\overline{{{\mathbf{PL}}}}\) cases: a lift, b power, components of c lift and d power

Full size image
Table 3 Aerodynamic parameters of the high \(\overline{{{\text{PL}}}}\) state
Full size table

5 Conclusion

In this research, the thoracic muscle effect on dynamic performance of flexible flapping wings of insects is studied. The thoracic muscle effect is simulated by the chordwise torsional spring, whose stiffness is derived from a comparison test with the results of real insect experiments. The von Kármán nonlinear plate theory is employed to simulate the elastic deformation of the flexible flapping wing. An aerodynamic force is approximated using a quasi-steady aerodynamic model according to the blade element theory, and the bending and twisting along the span are described using quadratic polynomials. The Newmark-Raphson method is used to solve the equations of motion. Our results show that considering TM leads to lower cycle-averaged lift and power. However, compared to the case ignoring TM, considering TM can enhance the efficiency of lift production by about 23% of insect flight. This provides a more efficient design solution for FWMAVs. Furthermore, although the movement trends of the flapping motion are approximately the same for the cases with and without thoracic muscle effect, considering TM delays the pitching motion while reducing its magnitude. These findings contribute to the design of FWMAVs.