1 Introduction

Sandwich structures consist of two stiff thin face layers and one thick, soft layer placed between them. As a result of this configuration, several excellent properties are achieved, such as high stiffness and strength, low weight and high-energy absorption capability. Due to these desirable properties, sandwich structures are widely used in astronautic, aeronautic, automotive and marine applications.

In practical engineering applications, highly flexible laminated composite structures are prone to large deflections and post-buckling. Thus, instability phenomena in sandwich structures have attracted more and more attention. Several works on sandwich beam-like structures considering the geometrically nonlinear problem have been carried out during the last thirty years. According to several reviews (Carrera and Brischetto [1], Hu et al. [2], Sayyad and Ghugal [3]), classical laminate theory, first-order shear deformation theory, high-order theory [4] and zig-zag theory [5] have been proposed for modelling sandwich composites.

Due to the mismatch and heterogeneity in material properties between the skin layer and the core layer, compressed sandwich structures show more complex instability behaviours than structures made of homogeneous material. According to the buckling wavelength, instability can be divided into two prominent cases: (1) global buckling, whose wavelength value is of the order of a representative global dimension, (2) local buckling (wrinkling) [6], whose wavelength is comparable to the thickness of the core layer [7]. In addition to these uncoupled instabilities, the global–local-coupled instability, also called interactive buckling [8], is another widespread phenomenon. Many valuable theories and models have been proposed to describe these phenomena in the past decades in the literature (see Vonach and Rammerstorfer [9]). The global and local buckling behaviours of sandwich beams were studied by Frostig and Baruch [10] via using a high-order sandwich panel theory. Analytical, numerical and experimental studies were carried out by Jasion et al. [11] for the global and local buckling of sandwich beams and circular sandwich plates. The critical loads obtained by an analytical model, a FEM model, and experimental investigations were compared. Ji and Waas [12] proposed a numerical model based on the finite element method for both isotropic and orthotropic sandwich structures with different aspect ratios. This study provided a benchmark for sandwich structures’ buckling problems with different geometrical and material parameters. A sandwich model for detecting the global and local instability phenomena was proposed by Leotoing et al. [13]. By a parametric analysis, several geometrical and material parameters were assessed to control the global and local instability. Based on the displacement assumption of Leotoing, Hu et al. [14] developed a finite element sandwich beam model to describe global and local instability, and Yu et al. [15] further extended this model to the sandwich plate problem. On this basis, Liu et al. [16] and Huang et al. [17] used the Fourier series to develop an envelope model independent of the wavelength. The sandwich structure models mentioned above are valuable but not universal enough. It is often necessary to select models of different orders to solve different problems. Huang et al. [6] recently proposed a model, where the middle layer uses a model that can change the expansion order, whereas the skin layer is described by the Euler beam model. However, this kind of low-order beam theory is not practical for the description of the mechanical field of a thicker core layer of the sandwich structure. The description of the displacement field in a thick core layer can also use cubic functions (Choe et al. [18], Huang et al. [19], Yu et al. [15]) or MacLaurin expansions (Neves et al. [20]).

In this article, a CUF-based sandwich beam model is proposed to analyse sandwich beam-like structures considering the geometrically nonlinear problem. The kinematics in the cross section can be refined through a compact notation for a priori displacement field approximation. The governing equations are derived via the Principle of Virtual Displacements (PVD) in the form of fundamental nuclei. Based on the PVD, both a closed-form Navier-type analytical solution [21], as well as a weak form finite element solution, can be derived. Regarding the approximation of the physical field, a continuous function such as MacLaurin polynomial can be used globally, or a piecewise polynomial such as Lagrange polynomial can be applied locally. In this article, the Lagrangian polynomial is taken for the description of the mechanical field in sandwich structures. Carrera’s Unified Formulation (CUF) has been previously extended for modelling the beam structures on free vibration problem (Hui et al. [22]), failure problem (Carrera and Giunta [23]), thermal problem (Giunta et al. [24]) and hygro-thermal problem (Moleiro [25]). It is worth mentioning that D’Ottavio [26] proposed the Sublaminate Generalised Unified Formulation (S-GUF) as an extension of CUF-based laminated models [27], which allows to freely select the order of the through-thickness polynomial approximation at sublaminate level. S-GUF was exploited to study sandwich buckling and wrinkling problems by D’Ottavio et al. [28] and Vescovini et al. [29]. Recently, CUF-based beam models were applied to geometric nonlinear problems (Hui et al. [30, 31], De Pietro et al. [32, 33]) and multiscale geometric nonlinear problems (Hui et al. [34]). The latter work extends the framework of the CUF-based beam models by coupling it with the \(\text {FE}^{2}\) method (Feyel et al. [35], Xu et al. [36]). Some recent developments of the \(\text {FE}^{2}\) method can be found in Yang et al. [37], Huang et al. [38] and Raju et al. [39]. Carrera et al. [40, 41] and Wu et al. [42] studied the geometrically nonlinear problem of laminated composite beams by Taylor expansion and Lagrange expansion CUF models and the arc-length method was used as the nonlinear solver. As far as the nonlinear solver is concerned, ANM is a continuation method that associates a perturbation technique with a discretisation principle [43]. Under this framework, the computation of a solution path is achieved step by step, where at each step, the solution is represented by a truncated power series. Many studies presented in the literature show that the ANM is more robust and efficient than classical nonlinear solvers (e.g., Newton–Raphson’s method, modified

Newton–Raphson’s method and Riks’ method). Azrar et al. [44] gave a time-cost comparison between ANM and modified Newton–Raphson and concluded that ANM is more efficient and robust. Hui et al. [31] made a detailed comparison between the Newton–Raphson method and the ANM method in CPU calculation time. When the numerical model is the same (CUF-based beam model), the ANM solver’s time is one-fifth of the Newton–Raphson method. For comparison purposes, results of FEM solutions from the commercial code ABAQUS were employed.

The layout of the paper is as follows. Section 2 is devoted to introducing the studied problem, the notation and the preliminary governing equations. Section 3 provides an overview of the theoretical derivation of the hierarchical beam finite elements for sandwich structures. A mechanical analysis of sandwich structures is carried out via a weak form finite element solution based on CUF. Numerical results and discussions are presented in Sect. 4, where the accuracy, computational efficiency and robustness of the proposed models are discussed. Finally, conclusions are presented in Sect. 5.

2 Preliminaries

Fig. 1
figure 1

Sketch of a sandwich beam

Full size image

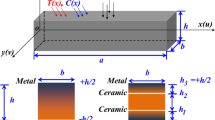
A sandwich beam structure of width b, thickness \(h_{t}\) and length L is displayed in Fig. 1. The displacement \({\mathbf {u}}\) of the top, bottom and core layers can be decomposed into a separated representation of the space coordinates (\(X=(x,z)\)):

$$\begin{aligned} {{\mathbf {u}}}^{(\zeta )}({\mathbf {X}})={{\mathbf {u}}}^{(\zeta )}\left( x,z\right) = \left\{ \begin{array}{cc} u^{(\zeta )}_x \left( x,z\right) &{} u^{(\zeta )}_z \left( x,z\right) \\ \end{array} \right\} ^T\!\!,\quad \zeta =t, b, c, \end{aligned}$$
(1)

where “T” stands for the transpose operator. The corresponding first-order derivatives components can be written as:

$$\begin{aligned} {{\varvec{\theta }}^{(\zeta )}({{\mathbf {u}}}^{(\zeta )})} = \left\{ \begin{array}{cccc} u^{(\zeta )}_{x,x} &{} u^{(\zeta )}_{x,z} &{} u^{(\zeta )}_{z,x} &{} u^{(\zeta )}_{z,z} \\ \end{array} \right\} ^{T}, \end{aligned}$$
(2)

where \(\varvec{\theta }\) is the displacement gradient vector. Considering geometric nonlinearity, the Green–Lagrange strain can be written as follows:

$$\begin{aligned} {{\mathbf {E}}}^{(\zeta )} =\left\{ \begin{array}{ccc} {E}^{(\zeta )}_{xx} \\ {E}^{(\zeta )}_{zz} \\ {E}^{(\zeta )}_{xz} \\ \end{array} \right\} =\left[ \begin{array}{ccc} {u}^{(\zeta )}_{x,x} \\ {u}^{(\zeta )}_{z,z} \\ {u}^{(\zeta )}_{x,z}+{u}^{(\zeta )}_{z,x} \\ \end{array} \right] + \frac{1}{2} \left[ \begin{array}{ccc} {{u}^{(\zeta )}_{x,x}}^{2}+{{u}^{(\zeta )}_{z,x}}^{2} \\ {{u}^{(\zeta )}_{x,z}}^{2}+{{u}^{(\zeta )}_{z,z}}^{2} \\ 2{u}^{(\zeta )}_{x,x}{u}^{(\zeta )}_{x,z}+2{u}^{(\zeta )}_{z,x}{u}^{(\zeta )}_{z,z} \\ \end{array} \right] =\left[ {\mathbf {H}} +\dfrac{1}{2} {{\mathbf {A}}}^{(\zeta )} \left( {\varvec{\theta }}^{(\zeta )} \right) \right] {{\varvec{\theta }}^{(\zeta )}}, \end{aligned}$$
(3)

where the matrices \({\mathbf {H}}\) and \({{\mathbf {A}}}^{(\zeta )}\left( {\varvec{\theta }}^{(\zeta )}({{\mathbf {u}}}^{(\zeta )})\right) \) are defined as:

$$\begin{aligned} {\mathbf {H}}= & {} \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 1 &{} 1 &{} 0 \\ \end{array} \right] , \end{aligned}$$
(4)
$$\begin{aligned} {{\mathbf {A}}}^{(\zeta )}\left( {\varvec{\theta }}^{(\zeta )}({{\mathbf {u}}}^{(\zeta })\right)= & {} \left[ \begin{array}{cccc} {u}^{(\zeta )}_{x,x} &{} 0 &{} {u}^{(\zeta )}_{z,x} &{} 0 \\ 0 &{} {u}^{(\zeta )}_{x,z} &{} 0 &{} {u}^{(\zeta )}_{z,z} \\ {u}^{(\zeta )}_{x,z} &{} {u}^{(\zeta )}_{x,x} &{} {u}^{(\zeta )}_{z,z} &{} {u}^{(\zeta )}_{z,x} \\ \end{array} \right] . \end{aligned}$$
(5)

A virtual variation in strain can be written in the following form:

$$\begin{aligned} \delta {{\mathbf {E}}}^{(\zeta )}= \delta \left\{ {\mathbf {H}} {{\varvec{\theta }}^{(\zeta )}} + \dfrac{1}{2} {{\mathbf {A}}}^{(\zeta )}{\varvec{\theta }}^{(\zeta )} \right\} ={\mathbf {H}} \delta {\varvec{\theta }}^{(\zeta )}+ {{\mathbf {A}}}^{(\zeta )} \delta {\varvec{\theta }}^{(\zeta )}, \end{aligned}$$
(6)

where \(\delta \) stands for a virtual variation. For a two-dimensional problem, the material stiffness matrix can be written in the following matrix form:

$$\begin{aligned} {{\mathbf {C}}}^{(\zeta )}= \left[ \begin{array}{ccc} {{C}}^{(\zeta )}_{11} &{} {{C}}^{(\zeta )}_{13} &{} {{C}}^{(\zeta )}_{15} \\ {{C}}^{(\zeta )}_{13} &{} {{C}}^{(\zeta )}_{33} &{} {{C}}^{(\zeta )}_{35} \\ {{C}}^{(\zeta )}_{15} &{} {{C}}^{(\zeta )}_{35} &{} {{C}}^{(\zeta )}_{55} \\ \end{array} \right] . \end{aligned}$$
(7)

The second Piola–Kirchhoff stress of each layer can be written into the following vector form:

$$\begin{aligned} {\mathbf {S}}^{(\zeta )} = \left\{ \begin{array}{ccc} S^{(\zeta )}_{xx} &{} S^{(\zeta )}_{zz} &{} S^{(\zeta )}_{xz} \\ \end{array} \right\} ^{T}\!\!. \end{aligned}$$
(8)

Thus, the constitutive law for each layer is defined by the following expression:

$$\begin{aligned} {{\mathbf {S}}}^{(\zeta )} = {{\mathbf {C}}}^{(\zeta )} {{\mathbf {E}}}^{(\zeta )}={{\mathbf {C}}}^{(\zeta )}\left( {{\mathbf {H}} {\varvec{\theta }}^{(\zeta )} } + {\dfrac{1}{2} {{\mathbf {A}}}^{(\zeta )} {\varvec{\theta }}^{(\zeta )}}\right) . \end{aligned}$$
(9)

The virtual internal \({\mathscr {L}}_{int}\) and external \({\mathscr {L}}_{ext} \) virtual work satisfies the following relationship:

$$\begin{aligned} \delta {\mathscr {L}}_{int} - \delta {\mathscr {L}}_{ext} = 0. \end{aligned}$$
(10)

The whole sandwich structure’s internal work is obtained by summing contributions from top, bottom and core layers as follows:

$$\begin{aligned} \displaystyle \delta {\mathscr {L}}_{int}= & {} \delta {\mathscr {L}}_{int}^{(t)} +\delta {\mathscr {L}}_{int}^{(c)}+\delta {\mathscr {L}}_{int}^{(b)} \nonumber \\ \displaystyle= & {} {\sum }_{\zeta =t,b,c} \int _{V_0} \delta {\mathbf {E}}^{(\zeta )T} {\mathbf {S}}^{(\zeta )} d V\nonumber \\ \displaystyle= & {} {\sum }_{\zeta =t,b,c} \int _{V_0^{\zeta }} {\delta {\varvec{\theta }}^{(\zeta )}}^{T} {\left[ {\mathbf {H}} + {{\mathbf {A}}}^{(\zeta )} ({\varvec{\theta }}^{(\zeta )}({{\mathbf {u}}}^{(\zeta )})) \right] }^{T} {\mathbf {S}}^{(\zeta )} d V, \end{aligned}$$
(11)

where \(V_0^{\zeta }\) is the undeformed volume of a layer. By neglecting the body forces and considering an external force proportional to a scalar parameter \(\lambda \), the external work can be written in the following form:

$$\begin{aligned} \delta {\mathscr {L}}_{ext}=\lambda \delta {\mathbf {u}}^{T} {\mathbf {F}}, \end{aligned}$$
(12)

where \({\mathbf {F}}\) is an external force vector. Based on the equations above, a weak formulation of the governing equations of the sandwich structure reads:

$$\begin{aligned} \begin{array}{lll} \displaystyle {\sum }_{\zeta =t,b,c} \int _{{V}^{\zeta }_{0}} \delta {\varvec{\theta }}^{(\zeta )T} {\left[ {\mathbf {H}} + {{\mathbf {A}}}^{(\zeta )} \right] }^{T} {{\mathbf {S}}}^{(\zeta )} d V={{\lambda }} \delta {\mathbf {u}}^T {\mathbf {F}},\\ \displaystyle {{\mathbf {S}}}^{(\zeta )}= {{\mathbf {C}}}^{(\zeta )} {{\mathbf {E}}}^{(\zeta )},\\ \displaystyle {{\mathbf {E}}}^{(\zeta )}= \left[ {\mathbf {H}} +\dfrac{1}{2} {{\mathbf {A}}}^{(\zeta )} \right] {\varvec{\theta }}^{(\zeta )}.\\ \end{array} \end{aligned}$$
(13)

These equations are the starting point for developing geometrically non-linear hierarchical finite elements using Carrera’s Unified Formulation.

3 Hierarchical beam finite elements of sandwich structures

In this section, the CUF is used to rewrite Eq. (13) for sandwich beam structures. For both transverse and axial displacement components, CUF is used to approximate the through-the-thickness behaviour (variation versus the z coordinate), whereas the finite element method is used to approximate the variation versus the axial coordinate x.

Fig. 2
figure 2

Shape function corresponding to the axial direction and the thickness direction in the cross-section

Full size image

As shown in Fig. 2, the idea of the proposed CUF-based model is to separate the displacement field of different layers with the corresponding Lagrangian functions \(F^{(t)}_{\tau }\), \(F^{(c)}_{\tau }\) and \(F^{(b)}_{\tau }\). To be noticed, top, core and bottom layer shares the same shape functions along the axial direction. The maximum number of terms in \(F^{(t)}_{\tau }\), \(F^{(c)}_{\tau }\) and \(F^{(b)}_{\tau }\) is \(N^{(t)}_{u}\), \(N^{(c)}_{u}\) and \(N^{(b)}_{u}\), respectively. The maximum number of shape function along the axial direction \(N_{i}\) is \(N^{e}_{n}\). The displacement approximation can be rewritten as follows for a generic layer:

$$\begin{aligned} \begin{array}{ll} {{\mathbf {u}}} \left( x,z\right) = F^{(\zeta )}_{\tau } \left( z \right) N_i \left( x \right) {\mathbf {q}}_{\tau i}, \\ \tau = 1, \ 2, \ \dots , \ N^{(\zeta )}_{u}; \quad \zeta =t, b, c; \quad i = 1, \ 2, \ \dots , \ N^{e}_{n}, \end{array} \end{aligned}$$
(14)

where \({\mathbf {q}}_{\tau i}\) is the generalised nodal displacement vector \({\mathbf {q}}_{\tau i}^{(\zeta )T} = \left\{ \begin{array}{cc} q_{\tau i}^{(\zeta ) u} &{} q_{\tau i}^{(\zeta ) w} \\ \end{array} \right\} \). Based on Einstein’s notation, a twice-repeated subscript implicitly represents a summation. Thus, the displacement gradient in Eq. (2) can be defined as follows:

$$\begin{aligned} \varvec{\theta }^{(\zeta )} = \left\{ \begin{array}{cccc} F_{\tau }^{(\zeta )} N_{i_{,x}} {q}^{u}_{\tau i} &{} F_{\tau _{,z}}^{(\zeta )} N_i {q}^{u}_{\tau i} &{} F_{\tau }^{(\zeta )} N_{i_{,x}} {q}^{w}_{\tau i} &{} F_{\tau _{,z}}^ {(\zeta )} N_i {q}^{w}_{\tau i} \\ \end{array} \right\} ^{T}= {{\mathbf {G}}}_{\tau i}^{(\zeta )} {\mathbf {q}}_{\tau i}, \end{aligned}$$
(15)

where \({\mathbf {G}}^{(\zeta )}_{\tau i}\) is as follows:

$$\begin{aligned} {\mathbf {G}}^{(\zeta )}_{\tau i} = \left[ \begin{array}{cc} F_{\tau }^{(\zeta )} N_{i_{,x}} &{} 0 \\ F_{\tau _{,z}}^{(\zeta )} N_i &{} 0 \\ 0 &{} F_{\tau }^{(\zeta )} N_{i_{,x}} \\ 0 &{} F_{\tau _{,z}}^{(\zeta )} N_{i}. \\ \end{array} \right] . \end{aligned}$$
(16)

The following expressions for virtual variations are derived within the CUF framework:

$$\begin{aligned} \begin{array}{ll} \delta {\mathbf {u}}^{(\zeta )} = F_{\tau }^{(\zeta )} N_{i} \delta {{\mathbf {q}}}_{\tau i}^{(\zeta )} ,\\ \delta \varvec{\theta }^{(\zeta )} = {\mathbf {G}}_{\tau i}^{(\zeta )} \delta {{\mathbf {q}}}_{\tau i}^{(\zeta )}. \end{array} \end{aligned}$$
(17)

The governing equation of the sandwich model in Eq. (13) then can be written as follows:

$$\begin{aligned} \begin{array}{lll} \displaystyle \sum _{\zeta = t,c,b}\delta {{\mathbf {q}}}_{\tau i}^{(\zeta )T} \int _{{V}^{(\zeta )}_0} {\mathbf {G}}_{\tau i}^{(\zeta )T} {\left[ {\mathbf {H}} + {{\mathbf {A}}}^{(\zeta )} \left( {\varvec{\theta }}^{(\zeta )}\right) \right] }^{T} {{\mathbf {S}}}^{(\zeta )} d V={\delta {{\mathbf {q}}}^{T}_{\tau i}} {\lambda }^{1} N_{i}^T F_{\tau }^{T} {\mathbf {F}}, \\ \displaystyle {{\mathbf {S}}}^{(\zeta )}= {{\mathbf {C}}}^{(\zeta )} {{\mathbf {E}}}^{(\zeta )}, \\ \displaystyle {{\mathbf {E}}}^{(\zeta )}= \left[ {\mathbf {H}} +\dfrac{1}{2} {{\mathbf {A}}\left( {\varvec{\theta }}^{(\zeta )}\right) } \right] {\mathbf {G}}_{s j}^{(\zeta )} \delta {{\mathbf {q}}}_{s j}^{(\zeta )}.\\ \end{array} \end{aligned}$$
(18)

The details of the perturbation form and the fundamental nucleus have been shown by Hui et al. [30, 31, 34]. They are not reported here for the sake of brevity. The resulting nonlinear problem in Eq. (18) is solved by the ANM. A brief introduction on ANM for the resolution of nonlinear problems is given in Appendix A.

4 Numerical results

Three cases are shown in this section. The first problem is a static analysis and it aims at validating the proposed numerical models. The second case addresses a global buckling analysis. The third case is devoted to a discussion on the coupling phenomenon of global and local buckling. For all the presented results, a quadratic beam element is used (3-node elements).

4.1 Static analysis

Fig. 3
figure 3

Static analysis: a sandwich beam under a transverse force

Full size image

As shown in Fig. 3, a bending problem of a sandwich beam is considered, in which the transverse and axial displacements of four corners are fixed and a transverse force is applied at the mid span. In this case, the proposed sandwich models and a FEM solution based on two-dimensional solid elements implemented in the commercial code ABAQUS are compared. Eight degrees of freedom from four corners of the beam are constrained. The transverse concentrated force \(\lambda F\) is applied with \(F=1\) N at the point \((L/2, h_{t}/2)\) as shown in Fig. 3. The material of each layer is isotropic. The geometrical and material parameters are: \(h_{t}=1\) m, \(h_{s}= h_{c}/10\), \(E_{s}=6.9 \times 10^{10}\) Pa, \(E_{c}=6.9 \times 10^{6}\) Pa, \(\nu _{s}=\nu _{c}=0.3\). The subscripts “s” and “c” stand for skin and core, respectively, whereas “t" stands for total. For the ABAQUS FEM model meshed with CPS8 elements, the Riks arc-length method is selected as the nonlinear solver. The initial, minimum, maximum arc-length increments are set as \( 10^{-5}\), \( 10^{-5}\) and 1000, respectively. A slenderness ratio \(L/h_{t}=50\) is considered. A coarse and a refined mesh grid is considered as reference results. When the slenderness ratio equals 50, for the refined mesh, the number of elements along the axial direction \(N_{ex}\) is 1200. \(N_u^{(c)}\) stands for the number of nodes for the core layer, \(N_u^{(s)}\) represents the number of nodes for the skin layers, since the number of nodes of top layer \(N_u^{(t)}\) and the number of nodes of the bottom layer \(N_u^{(b)}\) are equal. The number of elements along the thickness for the skin layers is 2, whereas for the core layer is 20, and the mesh along the thickness of the cross-section is addressed as (2, 20, 2). For the coarse mesh, the number of sub-domains along the thickness of the skin layers is 1, and the number of elements along the thickness of the core layer is 10, solution addressed as (1, 10, 1). The number of elements along the axial direction \(N_{ex}\) is 600. Each element’s length-to-thickness ratio is set to be 1, which can guarantee an accurate result.

Table 1 Static analysis: the displacement \(u_{z}\) at point (L/2, h/2) with a load parameter \(\lambda =1.0261 \times 10^{6}\)
Full size table

Table 1 shows the results obtained by selecting different number of axial elements \(N_{ex}\) and expansion order of skin and core layers \(N_u^{(s)}\), \(N_u^{(c)}\). It can be observed that when \(N_u^{(c)} = 6\), \(N_u^{(s)} = 3\) and \(N_{ex}=120\), the relative error \(\Delta \) is \(0.60\%\). By increasing the number of skin layers’ sub-domains \(N_u^{(s)}\) to 5, the relative error can be reduced to \(0.13\%\) if other parameters (including the core layer’s node number \(N_u^{(c)}\) and the number of axial elements \(N_{ex}\)) are unchanged. The models with \(N_u^{(s)}=5\) predict a more accurate displacement than the models with \(N_u^{(s)}=3\). Increasing the number of axial elements can improve the accuracy of the results, whereas only increasing the number of sub-domains in the core layer will not significantly affect the results. One may notice that the responses seem to be dependent more on \(N_u^s\) than on \(N_u^c\) in this case. This may be due to the concentrated load rather than the nonlinearity of the global solution. Meanwhile, all solutions in Table 1 present less than \(2\%\) discrepancy compared to the reference solutions. Table 2 shows the total degrees of freedom (DOFs) for 1D CUF models and 2D ABAQUS FEM models. 1D CUF model marked as “\(\text {1D CUF} ~ N_{ex}=80, N_u^{(c)}=6, N_u^{(s)}=6\)” has the highest degrees of freedom in the framework of CUF solution, the value is 5, 144. 2D ABAQUS FEM model marked as “\(\text {2D FEM} ~ N_{ex}=600, N_{ez}=(1,10,1)\)” has the lowest number of degrees of freedom, the value is 45, 650. 1D CUF models require \(88.71\%\) less dofs than the 2D ABAQUS FEM model.

Table 2 Static analysis: total degrees of freedom (DOFs) for 1D CUF models and 2D ABAQUS FE models
Full size table
Fig. 4
figure 4

Load–displacement curves of the 1D CUF-based sandwich model (\(N_u^{(s)}=6\)) and 2D FEM model (based on ABAQUS). The thickness of the core layer versus the skin layer \(h_{c}/h_{s}\) equals 10, and the slenderness ratio is 50

Full size image
Fig. 5
figure 5

Load–displacement curves of the 1D CUF-based sandwich model (\(N_u^{(s)}=3, 4, 5, 6\)) and 2D FEM model (based on ABAQUS). The thickness of the core layer versus the skin layer \(h_{c}/h_{s}\) equals 10, and the slenderness ratio is 50

Full size image

The results in Figs. 4 and 5 illustrate the comparison with the 2D FEM solutions. Figure 4 shows the results of the four sets of 1D CUF models (represented by the marked symbols) and the results of the two sets of 2D FEM models (represented by the dotted line). The number of nodes along the thickness in the skin layers used in the 1D CUF model is \(N_u^{(s)} = 6\). As the number of nodes along the thickness in the core layer \(N_u^{(c)}\) is increased, the accuracy of the 1D CUF model is further improved to be entirely consistent with the reference FEM model. In Fig. 5, the value of the reference point’s displacement is shown by changing the number of skin layers’ nodes \(N_u^{(s)}\) when the node number \(N_u^{(c)}\) along the core layer’s thickness is fixed to 6. It can be seen that when \(N_u^{(s)}\) equals 6, the result is consistent with the reference solution in the range \(\lambda \in [0, 2 \times 10^6]\). The results of the 1D CUF model with \(N_u^{(s)}=3, 4, 5\) and the reference solution are different in the range of \(\lambda \ge 1.5 \times 10^6\). For the sake of brevity, the cases of the slenderness ratio \(L/h_{t}=10\) and \(L/h_{t}=20\) are not shown here since they present a similar trend.

4.2 Buckling analysis

Fig. 6
figure 6

Global buckling analysis: a sandwich beam under compressive loads

Full size image
Table 3 Boundary and loading conditions in terms of nodal degrees of freedom (DOFs) for 1D CUF model and 2D FEM model
Full size table

This case investigates the global buckling and post-buckling analysis of sandwich structures as in Huang et al. [6]. A sandwich beam subjected to four concentrated forces is considered as shown in Fig. 6. To trigger the post-buckling analysis, a small perturbation force of magnitude \(F \times 10^{-5} [N]\) is applied at the point \((L/2,(h_c+h_s)/2)\). The length L and thickness \(h_{t}\) are 0.5 m and 0.025 m, respectively. The slenderness ratio is equal to 20. The width is assumed to be equal to the unit. The material properties are the same as the previous analysis. The details of boundary and loading conditions are presented in Table 3. The core-to-skin thickness ratio \(h_{c}/h_{s}\) is equal to 1, 10, 50, and 80.

Table 4 Buckling analysis: the total degrees of freedom (DOFs) for 1D CUF model and 2D FEM model
Full size table

Table 4 shows the comparison of DOFs. The DOFs of the 2D FEM model are 3, 241, 298 for a refined mesh scheme and 813, 770 for a coarse mesh scheme. When the degree of freedom of the 1D CUF-based model is the largest, it is only 2662, which is \(0.08\%\) of that of refined mesh 2D FEM model and \(0.33\%\) of that of the coarse mesh of the 2D FEM model. The obvious difference in DOFs is due to the limitation of the aspect ratio of the 2D FEM model. The elemental length-to-width ratio is set to be close to 1 to ensure convergence.

Fig. 7
figure 7

Nonlinear equilibrium paths of the proposed 1D CUF-based model and 2D FEM model (based on ABAQUS). The core-to-skin thickness ratio \(h_{c}/h_{s}\) equals 80, 50, 10 and 1, and the slenderness ratio is 20

Full size image

In Fig. 7, the four sub-figures show the load-deflection curves of sandwich structures with four different core-to-skin thickness ratios that are obtained by the 1D CUF sandwich model and the 2D FEM model. The adopted models can accurately predict the instability curve and are consistent with the bifurcation results in Huang et al. [6]. As the thickness ratio decreases, the buckling load increases. However, the degrees of freedom of the proposed model are much less than that of ABAQUS, which is shown in Table 4. Then, due to the use of ANM, under the same displacement conditions, the number of inversions of the stiffness matrix is greatly reduced, and the computation cost is further reduced in terms of the nonlinear solver. One can see that all nonlinear equilibrium paths from the proposed 1D CUF sandwich model match well the curve from the FEM model before the post-buckling. However, only the model named “1D \(\text {CUF } N_u^{(c)}=7, N_u^{(s)}=3\)” can predict the post-buckling behaviour accurately.

This model only needs to increase the order in the thickness direction to get the correct result. This is also a significant advantage of the CUF approach: the order of the model can be adjusted arbitrarily so that it can be easily used for various types (thick or thin) sandwich beam problems. One notes that a “softening" post-buckling behaviour can be observed for the case with the largest core-to-skin thickness ratio \((h_c/h_s=80)\), whereas stable post-buckling responses are found for the cases with smaller core-to-skin thickness ratios. This is because the local wrinkling occurs in the post-buckling stage in the former case, which results in a global–local-coupled buckling pattern that will be investigated in detail in the following subsection.

4.3 Global–local-coupled buckling analysis

The problem of global–local-coupled buckling is relatively common in engineering, and it is a strongly nonlinear problem involving two bifurcation points, which is usually difficult to solve, requiring accurate numerical models and efficient path tracking methodologies [45]. Two cases of global–local-coupled buckling are here presented. In the first case, the global buckling mode appears first; in the second one, the local buckling mode occurs first. Except for the geometric parameters, the two cases have the same material properties, boundary conditions and loads as reported in Sect. 4.2. For the first case, the beam length is 0.5 m, and the thickness of skins and core layer is 0.0005 m and 0.024 m, respectively. For the second case, the beam length is 0.25 m, and the thickness of skins and core layer is 0.0003 m and 0.0244 m, respectively. This difference in geometrical parameters leads to total different buckling behaviours in the two cases [7, 18, 46]. To trigger the post-buckling analysis, a perturbation force of 1/20000 of a concentrated force is applied to the center points of the skin layers.

Fig. 8
figure 8

Nonlinear equilibrium paths for the global–local-coupled instability of the proposed CUF-based beam model and 2D FEM model

Full size image
Table 5 Global buckling analysis: total degrees of freedom (DOFs) for 1D CUF FE model and 2D FE model
Full size table
Fig. 9
figure 9

Contour plots of displacement component \(u_z\) [m]: global buckling at \(\lambda F \times 10^{-4} = 2.86 ~N\) and global–local-coupled buckling at \(\lambda F \times 10^{-4} = 2.73 ~N\). The results are obtained with 1D CUF model

Full size image
Fig. 10
figure 10

Nonlinear equilibrium paths for the local–global-coupled instability of the proposed CUF-based beam model and 2D FEM model (point A in  Fig. 11)

Full size image
Fig. 11
figure 11

Contour plots of displacement component \(u_z\) [m]: local buckling at \(\lambda F \times 10^{-4} = 2.57~N\) and local–global-coupled buckling at \(\lambda F \times 10^{-4} = 2.51~N\). The results are obtained with 1D CUF model

Full size image

For the first case, the nonlinear equilibrium paths of global and local coupled instability are shown in Fig. 8, which corresponds to \(u_{z}\) at point \((L/2,(h_c+h_s)/2)\). Figure 8a represents the overall situation, where \(u_{z}\) is in the range of 0.012 to 0 [m]. Five curves are presented, four of which marked “1D CUF” are from the proposed CUF-based model, and one of them labelled “2D FEM" is obtained from the FEM model in the ABAQUS software. The DOFs comparison is found in Table 5. The overall trends of these five curves are consistent. The first bifurcation point is around \((-8.38 \times 10^{-4} [m], 2.84 \times 10^4 [N])\), which corresponds to the instability mode of global buckling (see Fig. 9a). The second bifurcation point is near \((-6.65 \times 10^{-3} [m],2.86 \times 10^4 [N])\), which corresponds to the instability mode of global–local-coupled buckling (see Fig. 9b). The enlarged picture Fig. 8b shows more details around these two bifurcation points. From the point (0, 0) to the second bifurcation point, four curves marked “1D CUF” model are all slightly higher than the curve labelled “2D FEM”. This relative error is around \(0.35\%\). From the second bifurcation point to the leftmost endpoint, the models with the number of nodes along the thickness of skin layers \(N_u^{(s)}=5\) yield better results than the ones with \(N_u^{(s)}=3\). The curve marked 1D CUF \(N_u^{(c)}=7\), \(N_u^{(s)}=5\) and the curve marked 2D FEM almost perfectly overlap. However, the relative error between the model with \(N_u^{(s)}=3\) and the reference model is relatively high. This is because the accurate simulation of the global buckling mode requires fewer nodes along the axis, while more longitudinal nodes are needed to ensure the accurate simulation of the global–local coupled buckling. The instability patterns and the displacement contour plots generated from the 1D CUF model are shown in Fig. 9. The sandwich beam first undergoes the stage of overall buckling, as shown in Fig. 9a. During the deformation process, corrugated local instability occurs in the transverse middle area of the sandwich beam, as shown in Fig. 9b.

For the second case, the nonlinear equilibrium paths for the local–global-coupled instability of the proposed CUF-based beam model and 2D FEM model are shown in Fig. 10. The first bifurcation point is around \((-9.86 \times 10^{-5} [m], 2.57 \times 10^{4} [N])\), which corresponds to the local anti-symmetric wrinkling (see Fig. 11a) that is the dominant buckling mode for sandwich beams with isotropic linear elastic core [7, 9, 28]. Then, the sandwich structure immediately evolves into the second bifurcation point near \((-1.84 \times 10^{-4} [m],2.57 \times 10^{4} [N])\), which demonstrates the local–global-coupled buckling pattern (see Fig. 11b). Four curves corresponding to the 1D CUF model are consistent with the curve trends of the 2D FEM model. It was not until the second bifurcation point that the results of the 1D CUF and 2D FEM models show a more obvious difference. The results of the 1D CUF model gradually approach the reference solution by increasing the number of nodes along the thickness of the core layer, and the relative error is about \(0.83\%\) only. In order to clearly determine the position of the first and second bifurcation points, the nonlinear equilibrium paths shown in Fig. 10 correspond to the results at point \((37L/320,(h_c+h_s)/2)\)). The buckling instability mode diagram and displacement contour plot of the two stages (local buckling and local–global-coupled buckling) are shown in Fig. 11, respectively. Compared with the global–local-coupled buckling mode in the first case, the local buckling in the local–global-coupled buckling mode in the second case occurs over the entire axial length and not just around the middle area.

5 Conclusions

This paper presents a numerical sandwich model to solve the geometrically nonlinear problem through the Carrera Unified Formulation and the Asymptotic Numerical Method. The CUF-based model is firstly validated with the comparison of a FEM model from ABAQUS for static analysis. In some cases, the DOFs are reduced by \(99.88\%\). Then, the proposed model is applied to the global buckling case. Besides, an application of this model to detect the global–local-coupled instability is demonstrated herein. Two cases of global–local-coupled buckling are presented. In the first case, the global buckling mode occurs first; in the second case, the local buckling mode occurs first. The nonlinear equilibrium paths have been evaluated. The accuracy is comparable to the two-dimensional FEM-based reference solutions with a considerably reduced computational cost.