1 Introduction

SAW devices have been widely used in wireless communication systems. The advantage of these devices is the high sensitivity to external disturbances because the acoustic energy is concentrated near the surface within a few wavelengths [1]. In order to improve the quality of the received signal in modern electronic devices, the unwanted signals and noise should be suppressed. So, SAW filters with high performance [2,3,4] are very important for advanced communication technologies.

Glass et al. [5, 6] found that a band gap (in which the propagation of elastic waves is suppressed) exists in the band structures when Rayleigh waves propagate in a semi-infinite isotropic elastic medium with a periodic corrugated surface. This provides an effective method to filter elastic waves by designing periodically corrugated surfaces. Maznev and Every [7] obtained the dispersion relations of Rayleigh waves in a supported film with periodic mass loading at the surface by using the plane wave expansion method. It was found that the ellipticity of the particle motion in the surface waves plays an important role in determining the width of the band gaps. Low-frequency band gaps of SAWs were opened by the interaction of the locally resonant modes and the surface modes when the cylindrical pillars were placed on the surface of a semi-infinite substrate periodically [8]. The band gap features such as location, number, and width could be tuned by the cylindrical pillars’ height, radius, and lattice symmetry [9,10,11,12]. Furthermore, the propagation of SAWs in a semi-infinite substrate with periodic composite pillars, which consists of a cap metallic pillar and a bottom epoxy pillar, was investigated [13]. The study showed that the bottom pillar has an important role in engineering the band structures when the Young’s modulus is one order of magnitude smaller than that of the cap pillar.

SH waves (including BG waves [14,15,16] and Love waves [17,18,19]) are widely used in signal-processing devices due to their high performance and simple particle motion [20]. The performance of SH wave filters is a key parameter of microwave devices and needs to be investigated comprehensively. Tsutsumi and Kumagai [21] studied the propagation characteristics of BG waves in a periodically corrugated piezoelectric substrate with the aid of a singular perturbation procedure. It was found that a wide band gap is obtained by choosing the piezoelectric constant suitably. Xu et al. [22] studied the dispersion relation of BG waves in a magneto-electro-elastic (MEE) substrate with a periodically inertial load surface based on the Bloch’s theorem and the coupling of modes approximation. Wilcox et al. [23] investigated the propagation of SH waves in an elastic substrate covered by an elastic layer of another material with a sinusoidal corrugated surface. The study found that SH waves exist in the structure when the shear wave velocity in the layer is greater than that in the substrate, which is different from the well-known existence condition of SH waves in layered structures [17,18,19]. This is because the corrugation traps the mechanical energy of SH waves and this contribution is larger than the resistance of the surface layer for the SH wave formation. The power reflection [24] and dispersion relations [25,26,27] of Love waves in an elastic layered structure with a corrugated interface or surface were discussed in detail. Pang et al. [28] analyzed the propagation characteristics of SH waves in an MEE substrate with thin metal strips deposited periodically on the surface and effects of the metal gratings on band gap features of SH waves were investigated. In above analysis [21,22,23,24,25,26,27,28], the small corrugations were considered and the effects of the corrugations’ dimensions on wave motion were not analyzed. The dispersion relation of SH waves in an elastic substrate with periodic gratings of the large-amplitude was studied and more high-frequency branches appeared in the band structures when the height of the gratings was large enough [29]. Laude et al. [30,31,32] further studied the dispersion relations of SH and vertical polarization (VP) modes in the piezoelectric substrates with periodic metal gratings on the surface. Although the effects of the gratings’ height on propagation features of SH waves were discussed [29,30,31,32], the influence of the material properties of the gratings on band structures was not investigated.

With the development of material technology, functionally graded materials (FGMs) can be manufactured and used as substrates to improve the propagation characteristics of SH waves [33,34,35,36,37,38,39,40,41,42,43]. Based on these properties, the band gap features of SH waves in homogeneous substrates with corrugated surfaces [21,22,23,24,25,26,27,28,29,30,31,32] could be improved efficiently by the gradient change of the material properties. This study investigates the propagation characteristics of SH waves in an FGPM substrate with periodic gratings on the surface. Effects of the material properties and height of the gratings as well as the gradient coefficient of the piezoelectric substrate on band structures of SH waves are investigated. The surface modes are convert into the bulk modes and the propagating modes are transformed into the resonant modes by tuning the gradient coefficient of the FGPM substrate. Consequently, a new low-frequency band gap is opened and SH modes with high frequencies are trapped in the gratings completely. This article aims to provide an efficient method to design SAW devices with high-performance based on FGPMs.

2 Statement of the problem

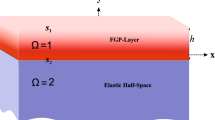
The transversely isotropic FGPM substrate with periodic dielectric gratings on the surface and the coordinate system are shown in Fig. 1. z-axis is the poling direction, which is perpendicular to x–y plane. The plane at x = 0 is the surface of the substrate (it is also the interface between the substrate and gratings). The material constants in the substrate change gradually along the x-axis direction and the SH waves propagate along the positive direction of the y-axis. The gratings’ period, width, and height are a, l, and h, respectively.

Fig. 1
figure 1

The FGPM substrate with periodic gratings (Color figure online)

Full size image

For SH waves propagation in the proposed structure shown in Fig. 1, the mechanical displacement components and electrical potential are described as follows

$$ u = v = 0,\quad w = w\left( {x,y,t} \right),\quad \varphi = \varphi \left( {x,y,t} \right), $$
(1)

where u, ν, and w are the displacement components of SH waves along the x-axis, y-axis, and z-axis, respectively. φ is the electrical potential.

The motion differential equation of SH waves in the transversely isotropic FGPM (x > 0) can be expressed as follows [34, 43]

$$ \begin{aligned} c_{44} \left( x \right)\nabla^{2} w_{1} + e_{15} \left( x \right)\nabla^{2} \varphi_{1} + \frac{{\partial c_{44} \left( x \right)}}{\partial x}\frac{{\partial w_{1} }}{\partial x} + \frac{{\partial e_{15} \left( x \right)}}{\partial x}\frac{{\partial \varphi_{1} }}{\partial x} = &\, \rho \left( x \right)\frac{{\partial^{2} w_{1} }}{{\partial t^{2} }}, \\ e_{15} \left( x \right)\nabla^{2} w_{1} - \varepsilon_{11} \left( x \right)\nabla^{2} \varphi_{1} + \frac{{\partial e_{15} \left( x \right)}}{\partial x}\frac{{\partial w_{1} }}{\partial x} - \frac{{\partial \varepsilon_{11} \left( x \right)}}{\partial x}\frac{{\partial \varphi_{1} }}{\partial x} = &\, 0, \\ \end{aligned} $$
(2)

where w1 and φ1 are the mechanical displacement and electrical potential of SH waves in the FGPM substrate. c44(x), e15(x), ε11(x) and ρ(x) are the elastic constant, piezoelectric constant, dielectric constant, and mass density in the substrate respectively. ∇2 is the two-dimensional Laplace operator. t is the time.

The nonzero stress τij and electric displacement Di components induced by SH waves in the FGPM substrate are given [34]

$$ \begin{aligned} \tau_{xz} = &\, c_{44} \left( x \right)\frac{{\partial w_{1} }}{\partial x} + e_{15} \left( x \right)\frac{{\partial \varphi_{1} }}{\partial x},\quad \tau_{yz} = c_{44} \left( x \right)\frac{{\partial w_{1} }}{\partial y} + e_{15} \left( x \right)\frac{{\partial \varphi_{1} }}{\partial y},\quad \\ D_{x} = &\, e_{15} \left( x \right)\frac{{\partial w_{1} }}{\partial x} - \varepsilon_{11} \left( x \right)\frac{{\partial \varphi_{1} }}{\partial x},\quad D_{y} = e_{15} \left( x \right)\frac{{\partial w_{1} }}{\partial y} - \varepsilon_{11} \left( x \right)\frac{{\partial \varphi_{1} }}{\partial y}.\quad \\ \end{aligned} $$
(3)

In the FGPM substrate, the variations of material constants along the thickness direction (x-axis) with the same exponential function are assumed without loss of generality [34, 38, 43]

$$ c_{44} \left( x \right) = c_{44}^{0} e^{\alpha x} ,\quad e_{15} \left( x \right) = e_{15}^{0} e^{\alpha x} ,\quad \varepsilon_{11} \left( x \right) = \varepsilon_{11}^{0} e^{\alpha x} ,\quad \rho \left( x \right) = \rho^{0} e^{\alpha x} , $$
(4)

where α is the exponential coefficient indicating the profile of the material gradient along the x-axis direction and the quantities with superscript 0 are the corresponding values of these parameters at the surface x = 0.

Equation (4) is substituted into Eq. (2), the following field equations can be obtained

$$\begin{aligned} c_{44}^{0} \left( {\nabla^{2} w_{1} + \alpha \frac{{\partial w_{1} }}{\partial x}} \right) + e_{15}^{0} \left( {\nabla^{2} \varphi_{1} + \alpha \frac{{\partial \varphi_{1} }}{\partial x}} \right) = & \, \rho^{0} \frac{{\partial^{2} w_{1} }}{{\partial t^{2} }}, \\ e_{15}^{0} \left( {\nabla^{2} w_{1} + \alpha \frac{{\partial w_{1} }}{\partial x}} \right) - \varepsilon_{11}^{0} \left( {\nabla^{2} \varphi_{1} + \alpha \frac{{\partial \varphi_{1} }}{\partial x}} \right) = & \,0. \\ \end{aligned} $$
(5)

In the region –h < x < 0, the dielectric gratings and air gaps are periodically stacked along the y-axis direction. The motion differential equation of SH waves in this region could be expressed as follows [29, 38, 43]

$$\begin{aligned} c^{\prime}_{44} \left( y \right)\nabla^{2} w_{2} + \frac{{\partial c^{\prime}_{44} \left( y \right)}}{\partial y}\frac{{\partial w_{2} }}{\partial y} = & \, \rho^{\prime}\left( y \right)\frac{{\partial^{2} w_{2} }}{{\partial t^{2} }}, \\ \varepsilon^{\prime}_{11} \left( y \right)\nabla^{2} \varphi_{2} + \frac{{\partial \varepsilon^{\prime}_{11} \left( y \right)}}{\partial y}\frac{{\partial \varphi_{2} }}{\partial y} = & \, 0, \\ \end{aligned} $$
(6)

with the nonzero stress \(\tau^{\prime}_{ij}\) and electric displacement \(D^{\prime}_{i}\) components

$$ \tau^{\prime}_{xz} = c^{\prime}_{44} \left( y \right)\frac{{\partial w_{2} }}{\partial x},\quad \tau^{\prime}_{yz} = c^{\prime}_{44} \left( y \right)\frac{{\partial w_{2} }}{\partial y},\quad D^{\prime}_{x} = - \varepsilon^{\prime}_{11} \left( y \right)\frac{{\partial \varphi_{2} }}{\partial x},\quad D^{\prime}_{y} = - \varepsilon^{\prime}_{11} \left( y \right)\frac{{\partial \varphi_{2} }}{\partial y}. $$
(7)

where w2 and φ2 are the mechanical displacement and electrical potential of SH waves in the region –h < x < 0. \(c^{\prime}_{44} \left( y \right)\), \(\varepsilon^{\prime}_{11} \left( y \right)\) and \(\rho^{\prime}\left( y \right)\) are the elastic constant, dielectric constant, and mass density in the region –h < x < 0, respectively.

Usually, the dielectric constant ε0 of air is much smaller than that of the dielectric gratings and is negligible. Thus the space in the region x < –h can be treated as vacuum. The electrical potential function φ0(x, y, t) satisfies the following Laplace equation [38, 43]

$$ \nabla^{2} \varphi_{0} = 0, $$
(8)

with the nonzero electric displacement \(D_{i0}\) components

$$ D_{x0} = - \varepsilon_{0} \frac{{\partial \varphi_{0} }}{\partial x},\quad D_{y0} = - \varepsilon_{0} \frac{{\partial \varphi_{0} }}{\partial y}. $$
(9)

The wave motion in the proposed structure in Fig. 1 should satisfy the continuity conditions at x = 0 and boundary conditions at x =  − h, which are described as follows.

(1) The continuity conditions at x = 0

$$ \begin{aligned} w_{1} \left( {0,y} \right) = &\, w_{2} \left( {0,y} \right),\quad \tau_{xz} \left( {0,y} \right) = \tau^{\prime}_{xz} \left( {0,y} \right), \\ \varphi_{1} \left( {0,y} \right) = & \, \varphi_{2} \left( {0,y} \right),\quad D_{x} \left( {0,y} \right) = D^{\prime}_{x} \left( {0,y} \right), \\ \end{aligned} $$
(10a)

(2) The boundary conditions at x =  − h

$$ \tau^{\prime}_{xz} \left( { - h,y} \right) = 0,\quad \varphi_{2} \left( { - h,y} \right) = \varphi_{0} \left( { - h,y} \right),\quad D^{\prime}_{x} \left( { - h,y} \right) = D_{x0} \left( { - h,y} \right), $$
(10b)

(2) The attenuation conditions at x →  ± ∞

$$ \begin{gathered} w_{1} ,\;\varphi_{1} \to 0,\quad \quad {\text{for }}x \to + \infty , \hfill \\ \quad \varphi_{0} \to 0,\quad \quad \;{\kern 1pt} {\text{for }}x \to - \infty , \hfill \\ \end{gathered} $$
(10c)

3 Solutions of the problem

3.1 Solutions in the FGPM substrate

For the FGPM substrate described above, the solutions of Eq. (5) can be expressed in the following forms

$$ \begin{aligned} w_{1} \left( {x,y,t} \right) = & \, W_{1} \left( x \right)\exp \left( {iky - i\omega t} \right), \\ \varphi_{1} \left( {x,y,t} \right) = & \, \Phi_{1} \left( x \right)\exp \left( {iky - i\omega t} \right), \\ \end{aligned} $$
(11)

where W1(x) and Φ1(x) are the functions to be determined. k is the wavenumber and ω is the circular frequency. \(i = \sqrt { - 1}\) is the imaginary unit.

Equation (11) is substituted into Eq. (5), the following field equations can be obtained

$$ \begin{aligned} c_{44}^{0} \left( {W^{\prime\prime}_{1} + \alpha W^{\prime}_{1} - k^{2} W_{1} } \right) + e_{15}^{0} \left( {\Phi^{\prime\prime}_{1} + \alpha \Phi^{\prime}_{1} - k^{2} \Phi_{1} } \right) = & - \rho^{0} \omega^{2} W_{1} , \\ e_{15}^{0} \left( {W^{\prime\prime}_{1} + \alpha W^{\prime}_{1} - k^{2} W_{1} } \right) - \varepsilon_{11}^{0} \left( {\Phi^{\prime\prime}_{1} + \alpha \Phi^{\prime}_{1} - k^{2} \Phi_{1} } \right) = & \, 0, \\ \end{aligned} $$
(12)

in which, the prime on W1 and Φ1 denotes differentiation with respect to x coordinate.

The second expression of Eq. (12) provides

$$ \left( {\Phi^{\prime\prime}_{1} + \alpha \Phi^{\prime}_{1} - k^{2} \Phi_{1} } \right) = \frac{{e_{15}^{0} }}{{\varepsilon_{11}^{0} }}\left( {W^{\prime\prime}_{1} + \alpha W^{\prime}_{1} - k^{2} W_{1} } \right). $$
(13)

Equation (13) is substituted into the first expression of Eq. (12) and yields

$$ \overline{c}_{44} \left( {W^{\prime\prime}_{1} + \alpha W^{\prime}_{1} - k^{2} W_{1} } \right) = - \rho^{0} \omega^{2} W_{1} , $$
(14)

with \(\overline{c}_{44} = c_{44}^{0} + {{\left( {e_{15}^{0} } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {e_{15}^{0} } \right)^{2} } {\varepsilon_{11}^{0} }}} \right. \kern-0pt} {\varepsilon_{11}^{0} }}.\)

For SH surface waves considered in the article, the solution of Eq. (14) is

$$ W_{1} \left( x \right) = A_{1} e^{rx} , $$
(15)

with \(r = - \frac{\alpha }{2} - \sqrt {\frac{{\alpha^{2} }}{4} + \left( {k^{2} - \frac{{\omega^{2} }}{{{{\overline{c}_{44} } \mathord{\left/ {\vphantom {{\overline{c}_{44} } {\rho^{0} }}} \right. \kern-0pt} {\rho^{0} }}}}} \right)} .\) A1 is the unknown coefficient.

According to Eq. (13), the undetermined function Φ1(x) can be obtained [15]

$$ \Phi_{1} \left( x \right) = A_{2} e^{px} + \frac{{e_{15}^{0} }}{{\varepsilon_{11}^{0} }}A_{1} e^{rx} , $$
(16)

with \(p = - \frac{\alpha }{2} - \sqrt {\frac{{\alpha^{2} }}{4} + k^{2} } .\) A2 is the unknown coefficient.

Then, the mechanical displacement and electrical potential in the FGPM substrate are shown

$$ \begin{aligned} w_{1} \left( {x,y,t} \right) = & \, A_{1} e^{rx} \exp \left( {iky - i\omega t} \right), \\ \varphi_{1} \left( {x,y,t} \right) = & \, \left( {A_{2} e^{px} + \frac{{e_{15}^{0} }}{{\varepsilon_{11}^{0} }}A_{1} e^{rx} } \right)\exp \left( {iky - i\omega t} \right). \\ \end{aligned} $$
(17)

According to the Floquet−Bloch theorem, the expressions in Eq. (17) are expanded in the Fourier series in the y-axis direction

$$ \begin{aligned} w_{1} \left( {x,y,t} \right) = & \sum\limits_{m = - \infty }^{ + \infty } {A_{1m} e^{{r_{m} x}} \exp \left( {ik_{m} y - i\omega t} \right)} , \\ \varphi_{1} \left( {x,y,t} \right) = & \sum\limits_{m = - \infty }^{ + \infty } {\left( {A_{2m} e^{{p_{m} x}} + \frac{{e_{15}^{0} }}{{\varepsilon_{11}^{0} }}A_{1m} e^{{r_{m} x}} } \right)\exp \left( {ik_{m} y - i\omega t} \right)} , \\ \end{aligned} $$
(18)

where km = k + 2mπ/a, k is restricted in the first Brillouin zone [− π/a, π/a]. \(r_{m} = - \frac{\alpha }{2} - \sqrt {\frac{{\alpha^{2} }}{4} + \left( {k_{m}^{2} - \frac{{\omega^{2} }}{{{{\overline{c}_{44} } \mathord{\left/ {\vphantom {{\overline{c}_{44} } {\rho^{0} }}} \right. \kern-0pt} {\rho^{0} }}}}} \right)}\) and \(p_{m} = - \frac{\alpha }{2} - \sqrt {\frac{{\alpha^{2} }}{4} + k_{m}^{2} } .\)

3.2 Solutions in the region − h < x < 0

In the region –h < x < 0, the material constants are periodic functions of y with the period a due to the periodic arrangement of the dielectric gratings and air gaps. Then, these constants are expended in the Fourier series

$$ c^{\prime}_{44} \left( y \right) = \sum\limits_{{m^{\prime} = - \infty }}^{ + \infty } {c^{\prime}_{{44\left( {m^{\prime}} \right)}} e^{{im^{\prime}\frac{2\pi }{a}y}} } ,\quad \varepsilon^{\prime}_{11} \left( y \right) = \sum\limits_{{m^{\prime} = - \infty }}^{ + \infty } {\varepsilon^{\prime}_{{11\left( {m^{\prime}} \right)}} e^{{im^{\prime}\frac{2\pi }{a}y}} } ,\quad \rho^{\prime}\left( y \right) = \sum\limits_{{m^{\prime} = - \infty }}^{ + \infty } {\rho^{\prime}_{{\left( {m^{\prime}} \right)}} e^{{im^{\prime}\frac{2\pi }{a}y}} } , $$
(19)

with the Fourier coefficients given as follows

$$ c^{\prime}_{{44\left( {m^{\prime}} \right)}} \left( {\varepsilon^{\prime}_{{11\left( {m^{\prime}} \right)}} ,\rho^{\prime}_{{\left( {m^{\prime}} \right)}} } \right) = c^{\prime}_{44} \left( {\varepsilon^{\prime}_{11} ,\rho^{\prime}} \right) \times \left\{ \begin{gathered} \frac{l}{a},\quad \quad \quad \quad \quad \quad m^{\prime} = 0, \hfill \\ \frac{{\sin \left( {m^{\prime}\pi \frac{l}{a}} \right)}}{{m^{\prime}\pi }},\quad \quad m^{\prime} \ne 0. \hfill \\ \end{gathered} \right. $$
(20)

The mechanical displacement and electrical potential in this region are expressed as follows

$$ \begin{aligned} w_{2} \left( {x,y,t} \right) = & \sum\limits_{m = - \infty }^{ + \infty } {W_{2m} \left( x \right)\exp \left( {ik_{m} y - i\omega t} \right)} , \\ \varphi_{2} \left( {x,y,t} \right) = & \sum\limits_{m = - \infty }^{ + \infty } {\Phi_{2m} \left( x \right)\exp \left( {ik_{m} y - i\omega t} \right)} , \\ \end{aligned} $$
(21)

where W2m(x) and Φ2m(x) are the functions to be determined.

Substituting Eqs. (19) and (21) into Eq. (6), the undetermined functions W2m(x) and Φ2m(x) can be obtained

$$ \begin{aligned} W_{2m} \left( x \right) = & \sum\limits_{s = 1}^{ + \infty } {\left( {a_{1s} e^{{\lambda_{1s} x}} + b_{1s} e^{{ - \lambda_{1s} x}} } \right)} \beta_{1m}^{s} , \\ \Phi_{2m} \left( x \right) = & \sum\limits_{s = 1}^{ + \infty } {\left( {a_{2s} e^{{\lambda_{2s} x}} + b_{2s} e^{{ - \lambda_{2s} x}} } \right)} \beta_{2m}^{s} , \\ \end{aligned} $$
(22)

where a1s, b1s, a2s, and b2s are the weighting coefficients. \(\lambda_{1s}\) and \(\beta_{1m}^{s}\) are the sth eigenvalue and mth component of the corresponding eigenvector in the following nonstandard eigenvalue problem

$$ \lambda_{1s}^{2} \sum\limits_{m = - \infty }^{ + \infty } {c^{\prime}_{{44\left( {q - m} \right)}} \beta_{1m}^{s} } = \sum\limits_{m = - \infty }^{ + \infty } {\left( {k_{q} c^{\prime}_{{44\left( {q - m} \right)}} k_{m} - \omega^{2} \rho^{\prime}_{{\left( {q - m} \right)}} } \right)\beta_{1m}^{s} } , $$
(23)

similarly, \(\lambda_{2s}\) and \(\beta_{2m}^{s}\) are the sth eigenvalue and mth component of the corresponding eigenvector in the nonstandard eigenvalue problem shown below

$$ \lambda_{2s}^{2} \sum\limits_{m = - \infty }^{ + \infty } {\varepsilon^{\prime}_{{11\left( {q - m} \right)}} \beta_{2m}^{s} } = \sum\limits_{m = - \infty }^{ + \infty } {k_{q} \varepsilon^{\prime}_{{11\left( {q - m} \right)}} k_{m} \beta_{2m}^{s} } , $$
(24)

where \(q = m + m^{\prime}\) and \(q,\;m = 0, \pm 1, \pm 2, \pm 3, \cdots\).

The mechanical displacement and electrical potential in the region –h < x < 0 are obtained by substituting Eq. (22) into Eq. (21)

$$ \begin{aligned} w_{2} \left( {x,y,t} \right) = & \sum\limits_{m = - \infty }^{ + \infty } {\sum\limits_{s = 1}^{ + \infty } {\left( {a_{1s} e^{{\lambda_{1s} x}} + b_{1s} e^{{ - \lambda_{1s} x}} } \right)} \beta_{1m}^{s} \exp \left( {ik_{m} y - i\omega t} \right)} , \\ \varphi_{2} \left( {x,y,t} \right) = & \sum\limits_{m = - \infty }^{ + \infty } {\sum\limits_{s = 1}^{ + \infty } {\left( {a_{2s} e^{{\lambda_{2s} x}} + b_{2s} e^{{ - \lambda_{2s} x}} } \right)} \beta_{2m}^{s} \exp \left( {ik_{m} y - i\omega t} \right)} . \\ \end{aligned} $$
(25)

3.3 Solutions in the region x <  − h

There is no mechanical disturbance in the region x < –h, which is treated as the vacuum. Then, the electrical potential function φ0(x, y, t) can be obtained by considering Eqs. (8) and (10c)

$$ \varphi_{0} \left( {x,y,t} \right) = \sum\limits_{m = - \infty }^{ + \infty } {A_{0m} e^{{\sqrt {k_{m}^{2} } x}} \exp \left( {ik_{m} y - i\omega t} \right)} , $$
(26)

where A0m is the unknown coefficient.

3.4 Dispersion equation

Equations (18), (25), and (26) with the corresponding stress and electric displacement components in Eqs. (3), (7), and (9) are substituted into Eqs. (10a) and (10b) yields an infinite set of linear equations

$$ \begin{aligned} & \,A_{1q} - \sum\limits_{s = 1}^{ + \infty } {\left( {a_{1s} + b_{1s} } \right)} \beta_{1q}^{s} = 0, \\ & \,\overline{c}_{44} r_{q} A_{1q} + e_{15}^{0} p_{q} A_{2q} - \sum\limits_{s = 1}^{ + \infty } {\lambda_{1s} \left( {a_{1s} - b_{1s} } \right)} \sum\limits_{m = - \infty }^{ + \infty } {c^{\prime}_{{44\left( {q - m} \right)}} } \beta_{1m}^{s} = 0, \\ & \,A_{2q} + \frac{{e_{15}^{0} }}{{\varepsilon_{11}^{0} }}A_{1q} - \sum\limits_{s = 1}^{ + \infty } {\left( {a_{2s} + b_{2s} } \right)} \beta_{2q}^{s} = 0, \\ & \,\varepsilon_{11}^{0} p_{q} A_{2q} - \sum\limits_{s = 1}^{ + \infty } {\lambda_{2s} \left( {a_{2s} - b_{2s} } \right)} \sum\limits_{m = - \infty }^{ + \infty } {\varepsilon^{\prime}_{{11\left( {q - m} \right)}} } \beta_{2m}^{s} = 0, \\ & \,\sum\limits_{s = 1}^{ + \infty } {\lambda_{1s} \left( {a_{1s} e^{{ - \lambda_{1s} h}} - b_{1s} e^{{\lambda_{1s} h}} } \right)} \sum\limits_{m = - \infty }^{ + \infty } {c^{\prime}_{{44\left( {q - m} \right)}} } \beta_{1m}^{s} = 0, \\ & \,\sum\limits_{s = 1}^{ + \infty } {\left( {a_{2s} e^{{ - \lambda_{2s} h}} + b_{2s} e^{{\lambda_{2s} h}} } \right)} \beta_{2q}^{s} - A_{0q} e^{{ - \sqrt {k_{q}^{2} } h}} = 0, \\ & \,\sum\limits_{s = 1}^{ + \infty } {\lambda_{2s} \left( {a_{2s} e^{{ - \lambda_{2s} h}} - b_{2s} e^{{\lambda_{2s} h}} } \right)} \sum\limits_{m = - \infty }^{ + \infty } {\varepsilon^{\prime}_{{11\left( {q - m} \right)}} } \beta_{2m}^{s} - \varepsilon_{0} \sqrt {k_{q}^{2} } A_{0q} e^{{ - \sqrt {k_{q}^{2} } h}} = 0, \\ \end{aligned} $$
(27)

in which, A1q, A2q, a1s, b1s, a2s, b2s, and A0q are undetermined coefficients. In practice, Eq. (27) is reduced to a finite set by limiting q and m to the range − M < q, m < M, where M is the positive integer and is large enough to ensure the accuracy of the calculated results. Then, s ranges from 1 to 2 M + 1 and Eq. (27) becomes a set of 14 M + 7 linear equations with 14 M + 7 unknown coefficients. To obtain the nontrivial solution, the determinant of the coefficient matrix of Eq. (27) has to vanish

$$ \det \left| {Q\left( {k,\omega } \right)} \right| = 0, $$
(28)

which yields the dispersion relation ω = ω(k) for the SH waves propagation in the structure depicted in Fig. 1.

4 Numerical results and discussion

In numerical calculations, the piezoelectric material ZnO [38] is selected as the substrate and different dielectric materials, such as SiO2 [38], Pb glass [43], and Si [44] are chosen as the gratings for comparison. The material constants are summarized in Table 1. The dielectric constant of air is ε0 = 8.854 × 10–12 (F/m). The period of the gratings a is 10 mm and l/a is fixed at 0.5. 5 Bloch harmonic waves (M = 2, − 2 ≤ q, m ≤ 2) are adopted appropriately for solving the dispersion equation (Eq. 28) by an effective numerical root finding method in the complex-value domain [45] and the theoretical results are verified by numerical simulation implemented by the finite element software COMSOL Multiphysics 5.0a. In Comsol simulation, the thickness of the substrate is 20a and the variation of the material constants in the FGPM substrate is realized by the analytical function, in which the expressions of the material constants along the substrate thickness are input, under the material properties option in the model builder.

Table 1 Material constants for numerical calculation [38, 43, 44]
Full size table

4.1 The effect of the material properties of the gratings on band structures

The effect of the material properties of the gratings on band structures of SH waves is shown in Fig. 2. The violet hexagons represent the sound line that is defined as ω1 = kcsh, where ω1 is the cutoff frequency and \(c_{sh} = \sqrt {{{\overline{c}_{44} } \mathord{\left/ {\vphantom {{\overline{c}_{44} } {\rho^{0} }}} \right. \kern-0pt} {\rho^{0} }}} = {2841}{\text{.4}}\;{\text{m/s}}\) is the shear wave velocity in the FGPM substrate. Note that the mechanical energy of SH waves is radiated into the surrounding medium when the circular frequency ω is greater than ω1 and the surface waves become leaky or pseudo surface waves [46], which are not considered in the article. It is seen from Fig. 2 that the band structures obtained by the theoretical calculation almost coincide with the FEM results. The correctness of the theoretical calculation in the article is verified to a certain extent. As can be seen, the frequencies of the first two modes in the band structures decrease and more surface modes appear in the band structures as the shear wave velocity \(c^{\prime}_{sh}\) in the dielectric gratings decreases (\(c^{\prime}_{sh} = \sqrt {{{c^{\prime}_{44} } \mathord{\left/ {\vphantom {{c^{\prime}_{44} } {\rho^{\prime}}}} \right. \kern-0pt} {\rho^{\prime}}}} = {5840}{\text{.1}}\;{\text{m/s}}\) in Si, \(c^{\prime}_{sh} = {3765}{\text{.9}}\;{\text{m/s}}\) in SiO2, and \(c^{\prime}_{sh} = {2370}{\text{.7}}\;{\text{m/s}}\) in Pb glass). This is because the mechanical energy of SH waves is more easily trapped in the soft gratings (the shear wave velocity is small). The flat frequency bands shown in Fig. 2 indicate that the group velocity \(c_{g} = {{d\omega } \mathord{\left/ {\vphantom {{d\omega } {dk = 0}}} \right. \kern-0pt} {dk = 0}}\) and the resonance is formed in the gratings.

Fig. 2
figure 2

Band structures of SH waves in the FGPM substrate with different dielectric gratings at h = 4a, α = 0 obtained by the theoretical calculation (black circles) and FEM (dark yellow balls), a the material of the dielectric gratings is Si; b the material of the dielectric gratings is SiO2; c the material of the dielectric gratings is Pb glass (Color figure online)

Full size image

In order to explore the resonant modes formed in the gratings, the mode shapes of displacements at ka/π = 1 marked by the red balls shown in Fig. 2 are displayed in Fig. 3. As can be seen, the low-frequency modes are more easily trapped in the gratings than the high-frequency modes because the modes become more and more heavily damped with the increasing frequency by radiating the mechanical energy into the substrate (seen in the mode shapes of B1, C2, D3, and E3). Consequently, SH waves could propagate through the proposed structure in Fig. 1 by the evanescent coupling of the resonant modes. The results obtained in this section show that the desired filter properties of SAW devices could be realized by choosing the material components of the gratings properly.

Fig. 3
figure 3

Mode shapes of displacements at ka/π = 1 marked by the red balls, A1 and B1 in Fig. 2a; A2, B2, and C2 in Fig. 2b; A3, B3, C3, D3, and E3 in Fig. 2c (Color figure online)

Full size image

4.2 The effect of the gratings’ height on band structures

The effect of the gratings’ height on band structures of SH waves is shown in Fig. 4. It is seen from Fig. 4 that the band structures obtained by the theoretical calculation and FEM simulation have a good agreement. There is only one frequency band in the band structures when the grating height h is no more than a shown in Fig. 4a. As h increases from 0.5a to a, the frequency band moves down and gets more flat. When h increases from a to 2a, one more frequency band (high-order mode) falls into the band structure shown in Fig. 4b and the first frequency band becomes flatter than that at h = a. This illustrates that more and more mechanical energy is trapped in the higher gratings and the quality of the energy trapping (the first frequency band) is improved by increasing the grating height because the group velocity \(c_{g} = {{d\omega } \mathord{\left/ {\vphantom {{d\omega } {dk}}} \right. \kern-0pt} {dk}}\) decreases and the localization of SH waves is strengthened.

Fig. 4
figure 4

The effect of the gratings’ height on band structures of SH waves in the structure shown in Fig. 1 with the material of the gratings is SiO2 at α = 0 obtained by the theoretical calculation (black circles, blue circles, olive circles) and FEM (dark yellow balls), (a) h = 0.5a, 0.7a, and a; (b) h = 2a (Color figure online)

Full size image

To illustrate the localization of SH waves in the gratings with different heights clearly, the mode shapes of displacements at ka/π = 1 marked by the red balls shown in Fig. 4 are displayed in Fig. 5. As seen in Fig. 5, the mechanical energy of SH waves is not confined in the gratings completely and more mechanical energy is trapped in the gratings with the increase of the grating height by radiating a small fraction of the mechanical energy into the substrate. As can be seen, the penetration depth of SH waves decreases as the grating height increase. When the grating height is large enough (h = 2a), the mechanical energy of the A4 mode is almost localized in the gratings but the mechanical energy of the high-order mode (B4 mode) is hard to be harvested completely. Although the quality of the energy trapping could be improved by increasing the grating height, the dimensions of SAW devices would increase inevitably. It is not desirable in the application of microwave devices. However, this problem could be solved effectively by choosing the material component and height of the gratings properly.

Fig. 5
figure 5

Mode shapes of displacements at ka/π = 1 marked by the red balls in Fig. 4 A1, A2, A3 in Fig. 4a; A4 and B4 in Fig. 4b (Color figure online)

Full size image

4.3 The effect of the gradient coefficient of the FGPM substrate on band structures

The effect of the gradient coefficient (α < 0) of the FGPM substrate on band structures of SH waves is shown in Fig. 6. The band structures obtained by the theoretical calculation almost coincide with that obtained by FEM simulation. As can be seen, the frequency bands move down as the gradient coefficient α decreases from 0 to − 3000. The reason is that rm (shown in Table 2) under Eq. (18), which represents the attenuation per unit length along the thickness direction, decreases as the gradient coefficient decreases. More and more mechanical energy is radiated into the substrate with the increase of the penetration depth of SH waves, which decreases the waves’ phase velocity at the substrate’s surface.

Fig. 6
figure 6

The effect of the gradient coefficient α (α < 0) on band structures of SH waves in the structure shown in Fig. 1 with the material of the gratings is SiO2 at h = 4a obtained by the theoretical calculation (black circles, blue circles, olive circles) and FEM (dark yellow balls) (Color figure online)

Full size image
Table 2 Values of rm at ka/π = 1 under different gradient coefficients (α ≤ 0, h = 4a)
Full size table

The mode shapes of displacements at ka/π = 1 marked by the red balls shown in Fig. 6 are displayed in Fig. 7. Compares the mode shapes of A2 mode, B2 mode, and C2 mode shown in Fig. 3 with Fig. 7, it is found that the penetration depth of the same modes (A0, A1, A2; B0, B1, B2; C0, C1, C2) increase as the gradient coefficient α decreases. This phenomenon is different from the above results shown in Figs. 2–5 that the mechanical energy of SH waves with the lower frequency is more easily trapped in the gratings. It is seen from Figs. 2 and 4 that the frequency bands of SH waves with low frequencies are flatter than that of the same modes with high frequencies, which indicates the high quality of the energy trapping. In Fig. 6, the frequency bands of SH waves with the lower frequency caused by the negative gradient coefficient become more inclined, indicating that the quality of the energy trapping decreases. As can be seen, the penetration depth of the high-order mode is more significant than that of the low-order mode because the attenuation coefficient rm of the high-order mode is smaller than that of the low-order mode shown in Table 2. This makes the proposed structure shown in Fig. 1, which consists of a FGPM substrate with negative gradient coefficients and periodic dielectric gratings, suitable to serve as a transducer by converting the surface modes into the bulk modes.

Fig. 7
figure 7

Mode shapes of displacements at ka/π = 1 marked by the red balls in Fig. 6, A0, B0, and C0 for α =  − 3000; A1, B1, and C1 for α =  − 1000 (Color Figure online)

Full size image

The effect of the gradient coefficient (α > 0) of the FGPM substrate on band structures of SH waves is shown in Fig. 8. The band structures obtained by the theoretical calculation agree well with that obtained by FEM simulation. It is seen from Fig. 8 that the cutoff frequency (start point of each mode) of SH waves increases as the gradient coefficient increases. An interesting physical phenomenon is found that the flat bands are obtained as the gradient coefficient increases to 3000. The possible reason is that the attenuation per unit length along the thickness direction rm (shown in Table 3) increases as the gradient coefficient increases. More and more mechanical energy is trapped in the gratings with the decrease of the penetration depth of SH waves, which increases the waves’ phase velocity at the substrate’s surface. As can be seen, the flat bands are generated due to the propagating modes are transformed into the resonant modes induced by the positive gradient coefficient and a new low-frequency band gap is opened under the first frequency band as the gradient coefficient increases to 100.

Fig. 8
figure 8

The effect of the gradient coefficient α (α > 0) on band structures of SH waves in the structure shown in Fig. 1 with the material of the gratings is SiO2 at h = 4a obtained by the theoretical calculation (black circles, blue circles, olive circles) and FEM (dark yellow balls) (Color figure online)

Full size image
Table 3 Values of rm at ka/π = 1 under different gradient coefficients (α ≥ 0, h = 4a)
Full size table

The mode shapes of displacements at ka/π = 1 marked by the red balls shown in Fig. 8 are displayed in Fig. 9. Compares the mode shapes of A2 mode, B2 mode, and C2 mode shown in Fig. 3 with Fig. 9, it is found that the penetration depth of the same modes (A2, A3, A4; B2, B3, B4; C2, C3, C4) decrease as the gradient coefficient α increases because the attenuation coefficient rm increases as the gradient coefficient α increases shown in Table 3. In the above analysis (Figs. 2–5), the high quality of the energy trapping of SH waves with the low frequency can be realized due to the flat bands, which represents the localization of SH waves. However, the quality of the energy trapping of SH waves with the high frequency is improved effectively by tuning the positive gradient coefficient shown in Fig. 9. The mechanical energy of SH waves with high frequencies could be stored into the gratings completely by tuning the positive gradient coefficient, which could not be realized in the same structure with the homogeneous substrate. This makes the proposed structure shown in Fig. 1, which consists of an FGPM substrate with positive gradient coefficients and periodic dielectric gratings, suitable to serve as resonators and filters by transforming the propagating modes into the resonant modes.

Fig. 9
figure 9

Mode shapes of displacements at ka/π = 1 marked by the red balls in Fig. 8, A3, B3, C3 for α = 100; A4, B4, and C4 for α = 3000 (Color figure online)

Full size image

5 Conclusions

The propagation characteristics of SH waves in an FGPM substrate with periodic dielectric gratings have been investigated in the article. An effective numerical root finding method is adopted to solve the dispersion equation of SH waves in the complex-value domain and the theoretical results are verified by FEM simulation. Effects of the material properties and height of the gratings as well as the gradient coefficient of the FGPM substrate on band structures of SH waves and mode shapes of displacements are investigated in detail. The numerical results show that more SH modes are trapped in the gratings when the shear wave velocity in the gratings decreases or the gratings’ height increases. The surface modes are converted into the bulk modes by tuning the negative gradient coefficient. The propagating modes are transformed into the resonant modes and a new low-frequency band gap is opened by tuning the positive gradient coefficient. The mechanical energy of SH waves with high frequencies could be trapped in the gratings completely by tuning the positive gradient coefficient, which could not be realized in the same structure with the homogeneous substrate. The results obtained in the article provide a theoretical basis for designing high performance SAW transducers, resonators, and filters.