1 Introduction

In 1962, Huston proposed the concept of a piezoelectric semiconductor based on his previous research [1]. This new type of functional material has both piezoelectric and semiconductor properties. With these two special properties, a new type of piezoelectric sensing test system integrating sensors and electronic circuits can be developed, and applied to micro/nanoelectromechanical systems [2]. There have been many studies on the propagation characteristics of sound waves in piezoelectric structures and piezoelectric composite structures with electromechanical coupling characteristics. On this basis, a piezoelectric semiconductor adds the carrier density field in addition to the displacement field and electric field, and then the semiconductor characteristics are taken into account. In piezoelectric semiconductors, the transmission of acoustic charge is dependent on the electric field generated by the piezoelectric effect when acoustic waves propagate. Therefore, the elastic dynamics of piezoelectric semiconductors needs to be improved. Recently, many studies have been done on different wave patterns with different structures, e.g., gap wave in a piezoelectric ceramic half-space with a thin semiconductor film and an air gap between the film and the half-space [3], extensional wave in a piezoelectric semiconductor rod [4], one-dimensional dynamic equations of a piezoelectric semiconductor beam with a rectangular cross section [5], SH wave in a piezoelectric semiconductor half-space [6], SH wave in multiplied piezoelectric semiconductor plates [7] and multiplied coupled wave in a transversely isotropic piezoelectric semiconductor slab sandwiched by two piezoelectric half-spaces [8]. All these researches are useful for the controlling of elastic waves propagation in the semiconductor structures.

Among all kinds of piezoelectric structures, piezoelectric functional gradients or graded materials are also a widely used intelligent materials. The material properties of the functionally gradient material change uniformly in a certain direction to eliminate the macro-interface in the material and then exhibit a kind of stress relaxation characteristic that makes it adapt to the more severe stress environment. Functional gradient materials have potential application prospects in biomedical, aerospace and other fields [9,10,11]. The application of functionally gradient materials brings some new changes to the propagation of elastic waves. Glushkov et al. [12] studied the surface wave excitation and propagation at the functionally gradient layer, the properties of which change with depth and coating in a half-space. Li and Wei [13] investigated the propagation of shear surface waves at the free traction surface of half-infinite functionally graded magneto-electro-elastic material, and it was found that the surface wave speed decreased gradually with increasing of the absolute value of the gradient index. Lan and Wei [14] studied the bandgaps of a piezoelectric/piezo-magnetic phononic crystal with a functionally graded interlayer. Wu et al. [15] studied the elastic wave propagation in one-dimensional phononic crystals with functionally graded materials. Cao et al. [16] studied the propagation of Rayleigh surface waves in a transversely isotropic graded piezoelectric half-space with material properties varying continuously along the depth direction. Ezzin et al. [17] studied the Rayleigh wave behavior at the surface of a FGM medium covering on a semi-infinite substrate. Niu et al. [18] investigated the nonlinear dynamics of a FGM conical panel with initial imperfections. Jin Zhang [19] studied the piezopotential properties of graded InGaN NWs through multiscale modeling. To sum it up, it is found that the functional materials composed of semiconductors and functionally gradient materials are rarely studied.

In this paper, we study the propagation of shear surface waves in a functionally gradient piezoelectric half-space with semiconductor characteristics and discuss the effects of semiconductor properties and the material gradient coefficient on the surface wave velocity. For the convenience of the analysis, we assume that the material parameters change exponentially with depth; that the wave velocity of the shear surface wave is obtained from the governing equation with displacement, electric and carrier density fields; and that we can use free-traction boundary conditions.

2 Basic physical equations of shear surface wave

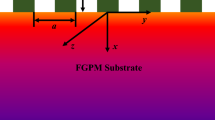
The surface wave propagation behavior at the surface of a transversely isotropic functionally gradient piezoelectric semiconductor (FGPS) half-space, as shown in Fig. 1, is taken into account. The surface traction of the half-space is free. The wave propagation direction is along the \({x}_{2}\)—direction, the poling direction is along the \({x}_{1}\)—axis, and the \(O{x}_{2}{x}_{3}\) plane is transversely isotropic. The material coefficients vary continuously along the depth direction.

Fig. 1
figure 1

Half-infinite functionally gradient piezoelectric semiconductor material

Full size image

The linear theory for small and dynamic signals consists of motion (Newton’s law), Gauss’s law of electrostatics and the conservation of charge [6, 20, 21]:

$$\begin{gathered} \sigma_{ji,j} = \rho \ddot{u_{i}} \hfill \\ D_{i,i} = qp \hfill \\ q\dot{p} + J_{i,i} = 0 \hfill \\ \end{gathered}$$
(1)

where \({\sigma }_{ij}\) is the stress tensor, \(\rho\) is the mass density, \({u}_{i}\) is the displacement vector, \({D}_{i}\) is the electric displacement vector, \(q\) is the carrier charge, \(p\) is the perturbation of the carrier density and \({J}_{i}\) is the electric current vector.

The constitutive equations of piezoelectric semiconductors can be written as:

$$\begin{gathered} \sigma_{ij} = c_{ijkl} \varepsilon_{kl} - e_{kij} E_{k} \hfill \\ D_{i} = e_{ikl} \varepsilon_{kl} + \kappa_{ij} E_{j} \hfill \\ J_{i} = q\overline{p}\mu_{ij} E_{j} + qp\mu_{ij} \overline{E}_{j} - qd_{ij} p_{,j} \hfill \\ \end{gathered}$$
(2)

where \({c}_{ijkl}\), \({e}_{kij}\) and \({\kappa }_{ij}\) are the elastic, piezoelectric and dielectric constants, respectively;\({\mu }_{ij}\) and \({d}_{ij}\) are the carrier mobility and diffusion constants, respectively; \(\overline{p }\) is the steady-state carrier density; \({\overline{E} }_{i}\) is the uniform biasing electric field; \({\varepsilon }_{ij}\) is the strain tensor and \({E}_{k}\) is the electric field. The expressions of \({\varepsilon }_{ij}\) and \({E}_{i}\) are given as:

$${\varepsilon }_{ij}=\frac{1}{2}\left({u}_{i,j}+{u}_{j,i}\right), {E}_{i}=-{\phi }_{,i}$$
(3)

where \(\phi\) is the electric potential.

We specialize the general equations to antiplane motions of crystals of class 6 mm. Consider the piezoelectric semiconductor half-space in Fig. 1. Antiplane motions are described by the following fields:

$${u}_{1}={u}_{2}=0,{u}_{3}={u}_{3}\left({x}_{1},{x}_{2},t\right)$$
$$\phi =\phi \left({x}_{1},{x}_{2},t\right),p=p\left({x}_{1},{x}_{2},t\right)$$
(4)

For the transversely isotropic piezoelectric semiconductor with the polarized direction along the \({x}_{3}\) axis, the constitutive equations of the crystals of class 6 mm become:

$${\sigma }_{13}=2{c}_{44}{\varepsilon }_{13}-{e}_{15}{E}_{1}$$
$${\sigma }_{23}=2{c}_{44}{\varepsilon }_{23}-{e}_{15}{E}_{2}$$
$${D}_{1}=2{e}_{15}{\varepsilon }_{31}+{\kappa }_{11}{E}_{1}$$
$${D}_{2}=2{e}_{15}{\varepsilon }_{23}+{\kappa }_{11}{E}_{2}$$
(5)
$${J}_{1}=q\overline{p}{\mu }_{11}{E}_{1}-q{d}_{11}{p}_{,1}$$
$${J}_{2}=q\overline{p}{\mu }_{11}{E}_{2}+qp{\mu }_{11}{\overline{E} }_{2}-q{d}_{11}{p}_{,2}$$

where \({\overline{E} }_{1}=0\) was assumed. \({\overline{E} }_{2}\) is along the wave propagation direction.

The material constants are assumed to vary exponentially along the thickness direction, i.e.:

$${c}_{ij}\left({x}_{1}\right)={c}_{ij}^{0}{e}^{k{x}_{1}}, {e}_{ij}\left({x}_{1}\right)={e}_{ij}^{0}{e}^{k{x}_{1}}, {\mu }_{11}\left({x}_{1}\right)={\mu }_{11}^{0}$$
$${\kappa }_{ij}\left({x}_{1}\right)={\kappa }_{ij}^{0}{e}^{k{x}_{1}},q\left({x}_{1}\right)={q}^{0}{e}^{k{x}_{1}}, {d}_{11}\left({x}_{1}\right)={d}_{11}^{0}, \rho \left({x}_{1}\right)={\rho }^{0}{e}^{k{x}_{1}}$$
(6)

where \(\left\{{c}_{ij}^{0}, {e}_{ij}^{0}, {\kappa }_{ij}^{0},{q}^{0},{\rho }^{0},{\mu }_{11}^{0},{d}_{11}^{0}\right\}=\left\{{c}_{ij},{e}_{ij},{\kappa }_{ij},q, \rho ,{\mu }_{11},{d}_{11}\right\}\left(0\right)\), and \(k\) is the functional gradient index characterizing the material gradient degree along \({x}_{1}\)- direction. When \(k=0\) in Eq. (6), the parameters with superscript 0 corresponds to a homogeneous material degenerated from the FGPS material.

Inserting Eqs. (3)–(6) into Eq. (1) leads to the governing equations as:

$${c}_{44}^{0}{\nabla }^{2}{u}_{3}+{e}_{15}^{0}{\nabla }^{2}\phi +k\left({c}_{44}^{0}{u}_{\mathrm{3,1}}+{e}_{15}^{0}{\phi }_{,1}\right)={\rho }^{0}{\ddot{u}}_{3}$$
$${e}_{15}^{0}{\nabla }^{2}{u}_{3}-{\kappa }_{11}^{0}{\nabla }^{2}\phi +k\left({e}_{15}^{0}{u}_{\mathrm{3,1}}-{\kappa }_{11}^{0}{\phi ,}_{1}\right)={q}^{0}p$$
(7)
$$\dot{p}-\overline{p}{\mu }_{11}^{0}{\nabla }^{2}\phi -{d}_{11}^{0}{\nabla }^{2}p+{\mu }_{11}^{0}{\overline{E} }_{2}{p}_{,2}-k\left(\overline{p}{\mu }_{11}^{0}{\phi ,}_{1}+{d}_{11}^{0}{p}_{,1}\right)=0$$

3 Wave velocity equation

Assume that the solution of Eq. (7) is in the form as:

$$\left\{{u}_{3},\phi ,p\right\}=\left\{A,B,D\right\}{e}^{-\xi \beta {x}_{1}}{e}^{i\xi \left({x}_{2}-ct\right)}$$
(8)

where \(\mathrm{c}\) is the wave velocity,\(\upxi\) is the wave number which is taken to be real and positive and \(\upbeta\) is the complex number which describes the decay rate from the free surface. Instituting Eq. (8) into Eq. (7), a system of homogeneous linear equations with respect to \(A, B,D\) is obtained as:

$$\left[{c}_{44}^{0}\left({\xi }^{2}{\beta }^{2}-{\xi }^{2}-k\xi \beta \right)+{\rho }^{0}{\xi }^{2}{c}^{2}\right]A+{e}_{15}^{0}\left({\xi }^{2}{\beta }^{2}-{\xi }^{2}-k\xi \beta \right)B=0$$
$${e}_{15}^{0}\left({\xi }^{2}{\beta }^{2}-{\xi }^{2}-k\xi \beta \right)A-{\kappa }_{11}^{0}\left({\xi }^{2}{\beta }^{2}-{\xi }^{2}-k\xi \beta \right)B-{q}^{0}D=0$$
(9)
$$\overline{p}{\mu }_{11}^{0}\left({\xi }^{2}{\beta }^{2}-{\xi }^{2}-k\xi \beta \right)B+\left[{d}_{11}^{0}\left({\xi }^{2}{\beta }^{2}-{\xi }^{2}-k\xi \beta \right)+i\xi c-i\xi {\mu }_{11}^{0}{\overline{E} }_{2}\right]D=0$$

For nontrivial solutions of \(A,B\), and \(D\), the value of the determinant of the coefficient matrix in Eq. (9) must vanish and turns to:

$$\alpha \{{d}_{11}^{0}\left({c}_{44}^{0}{\kappa }_{11}^{0}+{{e}_{15}^{0}}^{2}\right){\alpha }^{2}+[{d}_{11}^{0}{\kappa }_{11}^{0}{\rho }^{0}{c}^{2}{\xi }^{2}+i\xi \left(c-{\mu }_{11}^{0}{\overline{E} }_{2}\right)\left({\kappa }_{11}^{0}{c}_{44}^{0}+{{e}_{15}^{0}}^{2}\right)$$
$$-{c}_{44}^{0}{q}^{0}\overline{p}{\mu }_{11}^{0}]\alpha +[i\xi \left(c-{\mu }_{11}^{0}{\overline{E} }_{2}\right){\kappa }_{11}^{0}-{q}^{0}\overline{p}{\mu }_{11}^{0}]{\xi }^{2}{\rho }^{0}{c}^{2}\}=0$$
(10)

where \(\alpha ={\xi }^{2}{\beta }^{2}-k\xi \beta -{\xi }^{2}\). There are three roots derived from Eq. (10) as:

$${\alpha }_{1}=0, {\alpha }_{2}=\frac{-b{^{\prime}}+\sqrt{{b{^{\prime}}}^{2}-4a{^{\prime}}c{^{\prime}}}}{2a{^{\prime}}}, {\alpha }_{3}=\frac{-b{^{\prime}}-\sqrt{{b{^{\prime}}}^{2}-4a{^{\prime}}c{^{\prime}}}}{2a{^{\prime}}}$$
(11)

where

$$a{^{\prime}}={d}_{11}^{0}\left({c}_{44}^{0}{\kappa }_{11}^{0}+{{e}_{15}^{0}}^{2}\right)$$
$$b{^{\prime}}={d}_{11}^{0}{\kappa }_{11}^{0}{\rho }^{0}{c}^{2}{\xi }^{2}+i\xi \left(c-{\mu }_{11}^{0}{\overline{E} }_{2}\right)\left({c}_{44}^{0}{\kappa }_{11}^{0}+{{e}_{15}^{0}}^{2}\right)-{c}_{44}^{0}{q}^{0}\overline{p}{\mu }_{11}^{0}$$
$$c{^{\prime}}=\left[i\xi \left(c-{\mu }_{11}^{0}{\overline{E} }_{2}\right){\kappa }_{11}^{0}-{q}^{0}\overline{p}{\mu }_{11}^{0}\right]{\xi }^{2}{\rho }^{0}{c}^{2}$$
(12)

From Eq. (10), it can be found that \(\alpha\) depends on the wave velocity \(c\) and wave number \(\xi\). Then, \(\beta\) can be obtained with a determined \(\alpha\). Only the three roots of \(\beta\) with positive real parts are taken and denoted by \({\beta }_{m} \left(m=1, 2, 3\right)\). Corresponding to each \({\beta }_{m}\), the ratios among the amplitudes \(A, B\), and \(D\) can be determined from Eq. (9) as:

$${P}_{m}=\frac{{A}_{m}}{{B}_{m}}=-\frac{{e}_{15}^{0}\left({\xi }^{2}{\beta }_{m}^{2}-k\xi {\beta }_{m}-{\xi }^{2}\right)}{{c}_{44}^{0}\left({\xi }^{2}{\beta }_{m}^{2}-k\xi {\beta }_{m}-{\xi }^{2}\right)+{\rho }^{0}{\xi }^{2}{c}^{2}}$$
$${Q}_{m}=\frac{{D}_{m}}{{B}_{m}}=\frac{1}{{q}^{0}}\left({\xi }^{2}{\beta }_{m}^{2}-k\xi {\beta }_{m}-{\xi }^{2}\right)\left({e}_{15}^{0}{P}_{m}-{\kappa }_{11}^{0}\right)$$
(13)

The solutions of the surface waves can be rewritten as:

$$\left\{{u}_{3},\phi ,p\right\}=\sum_{m=1}^{3}\left\{{P}_{m}{B}_{m}{,B}_{m},{Q}_{m}{B}_{m}\right\}{e}^{-\xi {\beta }_{m}{x}_{1}}{e}^{i\xi \left({x}_{2}-ct\right)}$$
(14)

Combining Eqs. (5) and (14), the stress component \({\sigma }_{13}\), the electric displacement component \({D}_{1}\) and the electric current component can also be rewritten in the form of wavelet superposition.

In the free half-space, the electric potential \({\phi }_{0}\) and electric displacement \({D}_{0}\) with continuous boundary conditions [6, 21] are given as:

$${\phi }_{0}=\sum_{m=1}^{3}{B}_{m}{e}^{\xi {x}_{1}}{e}^{i\xi \left({x}_{2}-ct\right)}$$
$${D}_{0}=-{\varepsilon }_{0}{\phi }_{\mathrm{0,1}}=-{\varepsilon }_{0}\xi \sum_{m=1}^{3}{B}_{m}{e}^{\xi {x}_{1}}{e}^{i\xi \left({x}_{2}-ct\right)}$$
(15)

At the surface of the piezoelectric half-space, the continuous boundary conditions are given as:

$${\sigma }_{13}=0$$
$${\dot{D}}_{1}+{J}_{1}={\dot{D}}_{0}$$
(16)
$$p=0$$

Inserting Eqs. (14) and (15) into Eq. (16) leads to:

$$\sum_{m=1}^{3}\left({c}_{44}^{0}{P}_{m}+{e}_{15}^{0}\right){\beta }_{m}{B}_{m}=0$$
$$\sum_{m=1}^{3}\left[i{\xi }^{2}c{\beta }_{m}\left({e}_{15}^{0}{P}_{m}-{\kappa }_{11}^{0}\right)+\xi {q}^{0}{\beta }_{m}\left(\overline{p}{\mu }_{11}^{0}+{d}_{11}^{0}{Q}_{m}\right)-i{\xi }^{2}{\varepsilon }_{0}c\right]{B}_{m}=0$$
(17)
$$\sum_{m=1}^{3}{Q}_{m}{B}_{m}=0$$

Due to the existence of the nontrivial solution, Eq. (17) yields that the coefficient determinant must equal to zero, and then the velocity \(c\) of the surface wave is obtained.

4 Numerical results and discussion

The piezoelectric material used in this calculation is ZnO, and the material parameters are \({c}_{44}^{0}=43\,{\text{GPa}}, {e}_{15}^{0}=-0.48\,{\text{C/{m}}}^{2},{\varepsilon }_{11}^{0}=7.61\times {10}^{-11}\,{\text{F/m}}, {\rho }^{0}=\)

\(5700{\mkern 1mu} {\text{kg}}/{\text{m}}^{3} ,q^{0} = 1.602 \times 10^{{ - 19}} C,\,\mu _{{11}}^{0} = 1{\mkern 1mu} {\text{m}}^{2} /{\text{Vs}},d_{{11}}^{0} = \mu _{{11}}^{0} K^{0} T^{0} /q^{0}\) in which \({K}^{0}\) is the Boltzmann constant and \({T}^{0}\) is the absolute temperature [6, 21]. At room temperature, \({K}^{0}{T}^{0}/{q}_{e}=0.026\,{\text{V}}\), where \({q}_{e}=1.602\times {10}^{-19}\) coulomb is the electronic charge [22]. For the carriers, we consider holes with \(q={q}_{e}\). The present technology can make materials with \(\overline{p }\) of any value between zero and \({10}^{19}/{m}^{3}\). \(\overline{p }\) is varied in the following calculation. We use the speed of the shear wave in a nonconducting piezoelectric half-space as a normalizing speed: \({c}_{BG}^{2}=\frac{{\overline{c} }_{44}}{{\rho }^{0}}\left[1-\frac{{\overline{\kappa }}_{15}^{4}}{{(1+{\kappa }_{11}^{0}/{\varepsilon }_{0})}^{2}}\right]\) where \({\overline{c} }_{44}={c}_{44}^{0}+\frac{{{e}_{15}^{0}}^{2}}{{\kappa }_{11}^{0}},\) \({\overline{\kappa }}_{15}^{2}=\frac{{{e}_{15}^{0}}^{2}}{{\kappa }_{11}^{0}{\overline{c} }_{44}}\) and adopt a normalized electric field \(\gamma ={\mu }_{11}^{0}{\overline{E} }_{2}/{c}_{BG}.\)

4.1 Influence of the functional gradient index \({\varvec{k}}\) on the wave velocity

The magnitude of the gradient coefficient \(k\) is related to the wavelength, so it is greater than 103. Figure 2 shows, (1) the existence of the gradient index \(k\) causes abnormal dispersion of the surface wave; (2) the existence of the gradient index \(k\) causes the wave velocity to decrease, which means that the adoption of FGPS material hinders the wave propagation; (3)when the absolute value of the gradient index \(k\) increases, the wave velocity in the low frequency region decreases obviously while that in the high frequency region is smaller; and (4) when \(k\) is nonzero, the wave velocity is always less than that of the BG wave. When \(k\) is zero and the wave number \(\xi\) is much larger (> 10 × 103/\(m\)), the wave velocity tends to that of the BG wave.

Fig. 2
figure 2

Effect of the gradient index \(k\) on the wave velocity for \({\overline{E} }_{2}=0\)

Full size image

4.2 Influence of the steady-state carrier density \(\overline{{\varvec{p}} }\) on the wave velocity

The dimensionless electric field intensity γ and the functional gradient index \(k\) in Fig. 3a are taken as 0, and only the carrier density \(\overline{p }\) is taken into account. When the carrier density increases, the wave velocity decreases correspondingly, which means that the carrier density hinders the propagation of the surface wave. The influence on the high-frequency region (with larger ξ) is relatively smaller and that on the low frequency region is much greater. When \(k=0\), Fig. 3a reproduces the results of paper [6] in which the horizontal surface waves in a transversely isotropic piezoelectric conductor are studied. Then, the correctness of the results in this paper is further verified. In Fig. 3b, the influence of the carrier density is observed without biasing the electric field in the FGPM half-space. Since both \(k\) and \(\overline{p }\) can hinder the wave propagation, the reduction of the wave velocity becomes much larger.

Fig. 3
figure 3

a Effect of \(\overline{p }\) without FGPM and biasing field. b Effect of \(\overline{p }\) with FGPM and without biasing field

Full size image

4.3 Influence of the biasing electric field \({\overline{{\varvec{E}}} }_{2}\) on the wave velocity

In Fig. 4a, the carrier concentration \(\overline{p }\) is taken as \({10}^{15}\), and the functional gradient index \(k\) is taken as 0 which means that the half-space material is uniform. When the electric field intensity \(\gamma\) increases, the wave velocity also increases. That is, the electric field amplifies the wave propagation, and the influence can be observed clearly when ξ is smaller while hardly when ξ is larger. These results also reproduce the work in the reference [6]. The wave velocity under a biasing electric field has an upper limit, that is, \(c<{c}_{BG}\). When considering that the material of the half-space is FGPM (\(k\ne 0\)), Fig. 4b is obtained in view of the opposite influence of γ and \(k\) on the wave velocity. Obviously, the change becomes tiny in the whole frequency range.

Fig. 4
figure 4

a Effect of \(\gamma\) without FGPM on the wave velocity with carrier density \(\overline{p }={10}^{15}\)/\({\mathrm{m}}^{3}.\) b Effect of \(\gamma\) with FGPM on the wave velocity with carrier density \(\overline{p }={10}^{15}\)/\({\mathrm{m}}^{3}\)

Full size image

5 Conclusion

In this paper, the influences of the functional gradient index, the biasing electric field and the steady-state carrier density on the velocity of surface waves propagating on the surface of the FGPS half-space are observed. The effects of carrier density and electric field intensity are consistent with those in the non-functionally-graded transversely isotropic piezoelectric semiconductor materials. That is, the carrier density hinders the wave propagation and the biasing electric field along the \({x}_{2}\)—direction amplifies the wave propagation. These results are obvious in the low frequency region, but less obvious in the high frequency region. The gradient index also hinders the wave propagation. This result is consistent with the conclusion of classical nonsemiconductor functionally graded materials. This can be explained by the fact that the functionally graded materials increase the scattering of waves, which is not beneficial to the propagation of waves. These conclusions provide a theoretical basis for the application of acoustic surface devices made of functionally graded semiconductors.