1 Introduction

The rapid development of microelectromechanical systems (MEMS) and nanoelectromechanical systems (NEMS) in the past decades has been fueled by the fast growth of the nanotechnology. Piezoelectric elements such as beams, plates and shells have been widely utilized as the building blocks in the MEMS and NEMS as sensors, actuators, and others [1]. Flexoelectric elements are the other promising building blocks in the next-generation MEMS and NEMS devices [2,3,4,5], besides of the state-of-the-art piezoelectric devices. Unlike piezoelectricity, flexoelectricity is a universal electromechanical coupling which exists in all dielectrics due to the local inversion symmetry breaking by the strain gradient. Unexpectedly, the flexoelectric coefficients for certain perovskite ferroelectrics such as lead magnesium niobate (PMN) [6], barium strontium titanate (BST) [7], lead zirconate titanate (PZT) [8], and barium titanate (BT) [9] are three to five orders magnitude larger than those of the theoretical predictions [10, 11] and first-principle calculations [12, 13]. These experiment results triggered the investigation of flexoelectricity in the fundamental mechanical elements.

From the continuum mechanics point of view, the strain gradient elasticity is considered as a higher-order gradient theory. The study of higher-order strain gradient elasticity and couple stress theory can be traced back to the work of Mindlin [14], Mindlin and Eshel [15], and Toupin [16]. Later, the study of higher-order gradient and generalized continua mechanics goes back to the nonlocal elastic theory by Eringen [17, 18]. The theory of flexoelectricity for elastic dielectrics can be considered as a higher-order electromechanical coupling theory. The origin of the elastic dielectrics with flexoelectricity might be found in the earlier work of Mindlin [19], in which the polarization gradient has been involved in the framework of the continuum elastic dielectrics. Sharma and co-workers [20], and Cross and co-workers proposed a modified phenomenological model for the flexoelectric effects in solid dielectrics. Sharma and co-workers [21,22,23,24] have extended Mindlin’s work by including the strain gradient terms. In Cross’s work, the flexoelectric effects have been investigated from the viewpoint of equilibrium thermodynamics. The physical fundamental of the flexoelectricity for elastic dielectrics can be found in Shen and Hu [25,26,27], in which the electrostatic force, surface piezoelectric and flexoelectric effect were all take into consideration in the continuum theoretical frameworks.

Based on the above-mentioned continuum theoretical frameworks, Jiang and co-workers [28,29,30] investigated the static bending and vibration of piezoelectric nanobeams with flexoelectricity. Liang et al [31,32,33] studied the static bending, buckling, and vibration behaviors of piezoelectric nanostructures with consideration of the surface and flexoelectric effect. The electromechanical response of piezoelectric nanostructures and flexoelectric nanostructures can be also found in various previous works [34,35,36]. Further, flexoelectricity has been verified to play an important role in the magnetoelectric behaviors of a multiferroic composite, which provides a novel notion for designing multiferroic devices [37, 38]. The forced vibration of piezoelectric and flexoelectric beams due to steady loads is a very important issue in engineering applications. However, exact solutions for the forced vibration of piezoelectric and flexoelectric Euler–Bernoulli beams (EBs) are still limited As pointed out by the previous investigation, the static measurement offers only a rough estimation of the flexoelectric effect, and it is generally inaccurate in comparison to dynamic measurements [39]. The forced vibration of Euler–Bernoulli beams (EBs) and Timoshenko beams (TBs) has been rigorously studied by means of the Green’s functions [40, 41]. In the light of the dynamic experimental measurement of the flexoelectric coefficient for perovskite ceramics and polymer materials [42,43,44,45], it is essential to present the dynamic response of piezoelectric and flexoelectric beams. To the author’s knowledge, mechanical structural design and functionally graded composite can greatly enhance the electromechanical behaviors of dielectrics, leading to a higher performance and a wider range of application in energy conversion devices [46,47,48,49]. Here we propose a novel way based on the size-dependent electromechanical couplings to fabricate BT-based materials with ultrahigh piezoelectric coefficient, which can be a guideline for designing new flexoelectric devices.

2 Piezoelectric and flexoelectric Euler–Bernoulli beams

In order to simplify the discussion, the higher-order gradients terms (fifth and sixth strain gradient terms) are neglected. The electric enthalpy in considering both the piezoelectric and flexoelectric effects can be written as [50, 51]

$$\begin{aligned} H=-\frac{1}{2}a_{kl} E_{k} E_{l} +\frac{1}{2}c_{ijkl} \varepsilon _{ij} \varepsilon _{kl} -e_{ijk} \varepsilon _{ij} E_{k} -\mu _{ijkl} E_{k} \varepsilon _{ij,l} \end{aligned}$$
(1)

where \(a_{ij} \) and \(c_{ijkl} \) are the second-rank dielectric constant and elastic stiffness constant, respectively. In addition, \(e_{ijk} \) is the third-rank piezoelectric constant, while \(\mu _{ijkl} \) is the fourth-rank flexoelectric constant.

The displacement components for EBs can be written as

$$\begin{aligned} u( {x,y,z,t} )=-z\frac{\partial w_{0} }{\partial x}, \,\, v( {x,y,z,t} )=0, \,\, w( {x,y,z,t} )=w_{0} ( {x,t} ) \end{aligned}$$
(2)

where \(w_{0} ( {x,t} )\) is the deflection of the neutral plane.

The elastic strains can be then derived from Eq. (2) from the displacement–strain relation as

$$\begin{aligned} \varepsilon _{xx} =\frac{\partial u}{\partial x}=-z\frac{\partial ^{2}w_{0} }{\partial x^{2}}. \end{aligned}$$
(3)

The only nontrivial gradients of strain are

$$\begin{aligned} \eta _{xxx} =\frac{\partial \varepsilon _{xx} }{\partial x}=-z\frac{\partial ^{3}w_{0} }{\partial x^{3}}, \,\, \eta _{zxx} =\frac{\partial \varepsilon _{xx} }{\partial z}=-\frac{\partial ^{2}w_{0} }{\partial x^{2}}. \end{aligned}$$
(4)

For a flexoelectric beam with electrodes on its top and bottom surfaces, the electric field is assumed in the thickness direction, as pointed out in our previous works [32]. The electric potential is assumed in the form as \(\varphi =\varphi ( {z,t} )\); therefore, the electric field can be written as \(E_{z} ( {z,t} )=-\partial \varphi /\partial z\).

From Eq. (1), the constitutive equation for the piezoelectric EBs with flexoelectric effect can be written as

$$\begin{aligned} \sigma _{xx} =c_{11} \varepsilon _{xx} -e_{31} E_{z} , \,\, \tau _{zxx} =-\mu _{31} E_{z}. \end{aligned}$$
(5)

And the electric displacement and higher-order electric displacement are

$$\begin{aligned} D_{z} =a_{33} E_{z} +e_{31} \varepsilon _{xx} +\mu _{\text {31}} \eta _{zxx}. \end{aligned}$$
(6)

In case of open-circuit condition, the electric displacement on the surface is zero, \(\left. {D_{z} } \right| _{a} =0\). And considering the Gauss’s Law of the electric displacement, \(\partial D_{z} /\partial z=0\), one gets that the electric displacement should be equal to zero. Thus, from Eq. (6) one gets

$$\begin{aligned} E_{z} =-\frac{e_{31} }{a_{33} }\varepsilon _{xx} -\frac{\mu _{31} }{a_{33} }\eta _{zxx}. \end{aligned}$$
(7)

Then, substituting Eq. (7) into Eq. (5) yields

$$\begin{aligned} \begin{aligned} \sigma _{xx}&= \left( {c_{11} +\frac{e_{31}^{2} }{a_{33} }} \right) \varepsilon _{xx} +\frac{e_{31} \mu _{31} }{a_{33} }\eta _{zxx}, \\ \tau _{zxx}&=\frac{e_{31} \mu _{31} }{a_{33} }\varepsilon _{xx} +\frac{\mu _{31}^{2} }{a_{33} }\eta _{xxz}. \end{aligned} \end{aligned}$$
(8)

The equilibrium equations and boundary conditions of the beam can then be derived from Hamilton’s principle [52],

$$\begin{aligned} \delta \int _{t_{1} }^{t_{2} } {L\text {d}t} +\int _{t_{1} }^{t_{2} } {\delta W\text {d}t} =0, \end{aligned}$$
(9)

where L is the Lagrange density defined by

$$\begin{aligned} L=\int _V {\left( {\frac{1}{2}\rho {\dot{u}}_{i} {\dot{u}}_{i} -H}. \right) \text {d}V} \end{aligned}$$
(10)

As pointed out by Tiersten [52], the Lagrange density in Eq. (10) is the kinetic energy minus the electric enthalpy as in piezoelectric media, rather than the kinetic energy minus the internal energy as in pure elasticity.

The work done by the external force p( x, t ) can be expressed as

$$\begin{aligned} W=\int _0^L {P( {x,t} )w_{0} ( {x,t} )\text {d}x}. \end{aligned}$$
(11)

Substituting Eqs. (2), (8), and (11) into Eq. (9) gives

$$\begin{aligned} \begin{aligned}&\delta \int _{t_{1} }^{t_{2} } {L\text {d}t} +\int _{t_{1} }^{t_{2} } {\delta W\text {d}t} \\&\quad =\int _{t_{1} }^{t_{2} } {\text {d}t} \int _V {( {\rho {\dot{w}}_{0} \delta {\dot{w}}_{0} -\sigma _{xx} \delta \varepsilon _{xx} -\tau _{zxx} \delta \eta _{zxx} } )\text {d}V} +\int _{t_{1} }^{t_{2} } {\text {d}t} \int _0^L {p( {x,t} )\delta w_{0} ( {x,t} )\text {d}x} \\&\quad =\int _{t_{1} }^{t_{2} } {\left. {\left[ {( {M+P} )\delta \left( {\frac{\partial w_{0} }{\partial x}} \right) } \right] } \right| _{0}^{L} \text {d}t} -\int _{t_{1} }^{t_{2} } {\left. {\left[ {\left( {\frac{\partial ( {M+P} )}{\partial x}}\right) \delta w_{0} } \right] } \right| _{0}^{L} \text {d}t} \\&\qquad +\int _{t_{1} }^{t_{2} } {\text {d}t} \int _0^L {\left[ {\frac{\partial ^{2}( {M+P} )}{\partial x^{2}}-\rho A{\ddot{w}}_{0} +p( {x,t} )} \right] \delta w_{0} dx} \\ \end{aligned} \end{aligned}$$
(12)

where M and P are the bending moment and higher-order bending moment on the cross section, respectively. These internal generalized forces are defined by

$$\begin{aligned} M( x )=- \left( {c_{11} +\frac{e_{31}^{2} }{a_{33} }} \right) I\frac{\partial ^{2}w_{0} }{\partial x^{2}}, \,\, P=-\frac{\mu _{31}^{2} A}{a_{33} }\frac{\partial ^{2}w_{0} }{\partial x^{2}}. \end{aligned}$$
(13)

Due to the arbitrariness of \(\delta w_{0} \), the governing equations for the piezoelectric and flexoelectric EBs are

$$\begin{aligned} \frac{\partial ^{2}M}{\partial x^{2}}+\frac{\partial ^{2}P}{\partial x^{2}}-\rho A{\ddot{w}}_{0} +p( {x,t} )=0. \end{aligned}$$
(14)

And the corresponding boundary conditions for a cantilever beam are

$$\begin{aligned} \begin{array}{ll} w_{0} ( {x=0} )=0, &{} \left. {\left[ {\frac{\partial M}{\partial x}+\frac{\partial P}{\partial x}} \right] } \right| _{x=L} =0, \\ \left. {\frac{\partial w_{0} }{\partial x}} \right| _{x=0} =0, &{} \left. {( {M+P} )} \right| _{x=L} =0. \\ \end{array} \end{aligned}$$
(15)

By substituting Eq. (13) into Eq. (14), one gets the governing equations expressed by displacement \(w_{0} \) as

$$\begin{aligned} \frac{\partial ^{4}w_{0} }{\partial x^{4}}+\frac{\rho A}{( {EI} )^{\mathrm{eff}}}{\ddot{w}}_{0} =\frac{1}{( {EI} )^{\mathrm{eff}}}p( {x,t} ) \end{aligned}$$
(16)

where \(( {EI} )^{\mathrm{eff}}\) is the effective bending rigidity, defined by

$$\begin{aligned} ( {EI} )^{\mathrm{eff}}= \left( {c_{11} +\frac{e_{31}^{2} }{a_{33} }} \right) I+\frac{\mu _{31}^{2} A}{a_{33}}, \end{aligned}$$
(17)

In the case of the short-circuit condition, the electric field \(E_{z} ( {x,t} )\) is equal to zero. Hence, the higher-order couple stresses vanish. Equation  (5) reduces to \(\sigma _{xx} =c_{11} \varepsilon _{xx}\).

The explicit governing equations are then reduced to

$$\begin{aligned} c_{11} I\frac{\partial ^{4}w_{0} }{\partial x^{4}}+\rho A{\ddot{w}}_{0} =p( {x,t} ). \end{aligned}$$
(18)

Under this condition, the governing equations reduce to the same form as the classical EBs without electromechanical coupling. However, the electric charge on the upper and lower surface can be detected to measure the flexoelectric coefficient,

$$\begin{aligned} D_{z} =e_{31} \varepsilon _{xx} +\mu _{31} \eta _{xxz}. \end{aligned}$$
(19)

When the electric charge on the surface is detected, then one has

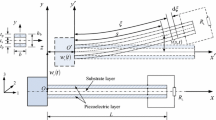
$$\begin{aligned} \Delta Q=\frac{Q^{\text {upper}}-Q^{\text {lower}}}{2}=\mu _{31} A_{e} \frac{\partial ^{2}w_{0} }{\partial x^{2}} \end{aligned}$$
(20)

where \(Q^{\text {upper}}\) and \(Q^{\text {lower}}\) have the same magnitude but with opposite sign because of the pure bending state, and \(A_{e}\) is the area of the electrode on the upper and lower surface. When the tip displacement of cantilever beams is detected, the expression of the displacement can be expressed by the tip displacement so that the flexoelectric coefficient can be determined by Eq. (20); the schematic graph for measuring the flexoelectric coefficient is shown in Fig. 1a. It should be noticed that the detected electric charge is contributed to only the flexoelectric effect. Figure 1b displays that the upper part of the beam is in opposite mechanical state with the lower part of the beam; therefore, the electric charge induced by the piezoelectric effect has the same sign on both the upper and lower surfaces. There is no current flow in the circuit under short- circuit condition. However, flexoelectric effect-induced bound charge has opposite sign on the upper and lower electrodes; therefore, weak electric current should be detected. Similarly, piezoelectricity doesn’t contribute to the electric potential, which will be discussed in detail in the following Sections. The elimination of the piezoelectric effect in pure bending leads to the measurement of the flexoelectric effect practically.

Fig. 1
figure 1

a Experiment arrangement for the measurement of flexoelectric coefficient; b illustration of the electric response under short-circuit condition and open-circuit condition. The polarization direction is given by the arrows (red for piezoelectric effect, yellow for flexoelectric effect)

Full size image

3 Green’s function solutions for the forced vibration

In order to obtain the analytical solution for the forced vibration of piezoelectric and flexoelectric EBs, we use the Green’s function. Considering the piezoelectric and flexoelectric EBs excited by a harmonic force, then, the method of separation of variables and the synchronous motion hypothesis give

$$\begin{aligned} \begin{aligned} p( {x,t} )&=P( x )e^{i\omega t}, \\ w_{0} ( {x,t} )&=W( x )e^{i\omega t}. \end{aligned} \end{aligned}$$
(21)

By substituting Eqs. (21) into the governing Eqs. (16), one gets the governing equations for the piezoelectric and flexoelectric EBs with open-circuit condition as

$$\begin{aligned} W^{( 4 )}( x )-a_{1} W( x )=b_{1} P( x ) \end{aligned}$$
(22)

where \(a_{1} =\rho A\omega ^{2}/( {EI} )^{\mathrm{eff}}\), \(b_{1} =1/( {EI} )^{\mathrm{eff}}\).

If the flexoelectric effect is neglected, letting \(\mu _{31} =0\), the governing equation (22) reduces to that of the classical piezoelectric Euler–Bernoulli beam model with effective bending rigidity \(( {EI} )^{\mathrm{eff}}=c_{11} +e_{31}^{2} /a_{33} \). Note that the external force has an opposite direction in our model compared with that in Ref. [41]. We focus on the electromechanical coupling behaviors so that we do not try to deal with the damping effect in our work. And the definition of the effective bending rigidity for EB under various physical conditions can also be found in our previous works [32, 33, 53, 54].

To obtain the solution for the governing equation (22) with the superposition principle, we present the transverse displacement W(x) as an integral equation of a Green’s function as

$$\begin{aligned} W( x )=\int _0^L {P( {x_{0} } )G( {x,x_{0} } )\text {d}x} \end{aligned}$$
(23)

where the Green’s function \(G( {x,x_{0} } )\) means its response of a unit concentrated force acting at an arbitrary position \(x_{0} \), and \(P( {x_{0} } )\) is the amplitude of the external force.

First we consider an unit concentrated force applied at an arbitrary position \(x_{0} \), i.e., \(P( x )=\delta ( {x-x_{0} } )\); then, Eq. (23) can be expressed as \(W( x )=G( {x,x_{0} } )\). And mathematically, \(G( {x,x_{0} } )\) is the solution of the following equation:

$$\begin{aligned} G^{( 4 )}-a_{1} G=b_{1} \delta ( {x-x_{0} } ). \end{aligned}$$
(24)

After using the Laplace transform method with respect to the variable x, the Green’s function can be expressed as

$$\begin{aligned} {\hat{G}}( {s,x_{0} } )=\frac{R( s )}{s^{4}-a_{1} }. \end{aligned}$$
(25)

The characteristic equation of Eq. (24) has the form

$$\begin{aligned} s^{4}-a_{1} =0. \end{aligned}$$
(26)

The roots of Eq. (26) are

$$\begin{aligned} s_{1} =a_{1}^{1 /4} , \,\, s_{2} =-a_{1}^{1 / 4} , \,\, s_{3} =ia_{1}^{1 /4} , \,\, s_{4} =-ia_{1}^{1 /4}. \end{aligned}$$
(27)

This gives the solution in the form of

$$\begin{aligned} {\hat{G}}( {s,x_{0} } )=\frac{R( s )}{( {s-s_{1} } )( {s-s_{2} } )( {s-s_{3} } )( {s-s_{4} } )}. \end{aligned}$$
(28)

The inverse transform of \({\hat{G}}( {s,x_{0} } )\) gives

$$\begin{aligned} \begin{aligned} G( {x,x_{0} } )&=H( {x-x_{0} } )\Phi _{1} ( {x-x_{0} } )+\Phi _{2} ( x )G( 0 ) \\&\quad +\Phi _{3} ( x )G^{( 1 )}( 0 )+\Phi _{4} ( x )G^{( 2 )}( 0 )+\Phi _{5} ( x )G^{( 3 )}( 0 ) \end{aligned} \end{aligned}$$
(29)

where \(\Phi _{i} \, ( {i=1,2,...,5} )\) are defined by

$$\begin{aligned} \begin{aligned}&\Phi _{1} ( {x-x_{0} } )=\sum \limits _{i=1}^4 {b_{1} A_{i} ( {x-x_{0} } )} , \,\, \Phi _{2} =\sum \limits _{i=1}^4 {A_{i} ( x )( {s_{i}^{3} +a_{1} s_{i} })} , \\&\Phi _{3} =\sum \limits _{i=1}^4 {A_{i} ( x )( {s_{i}^{2} +a_{1} } )} , \,\, \Phi _{4} =\sum \limits _{i=1}^4 {A_{i} ( x )s_{i} } , \,\, \Phi _{5} =\sum \limits _{i=1}^4 {A_{i} ( x)}. \end{aligned} \end{aligned}$$
(30)

Where \(A_{i} \, ( {i=1,2,...,4} )\) are functions given by

$$\begin{aligned} \begin{aligned} A_{1} ( x )&=\frac{e^{s_{1} x}}{( {s_{1} -s_{2} } )( {s_{1} -s_{3} } )( {s_{1} -s_{4} } )}, \,\, A_{2} ( x )=\frac{e^{s_{2} x}}{( {s_{1} -s_{2} } )( {s_{3} -s_{2} } )({s_{4} -s_{2} } )}, \\ A_{2} ( x )&=\frac{e^{s_{3} x}}{( {s_{3} -s_{1} } )( {s_{3} -s_{2} } )( {s_{3} -s_{4} } )}, \,\, A_{4} ( x )=\frac{e^{s_{4} x}}{( {s_{4} -s_{1} } )( {s_{4} -s_{2} } )({s_{4} -s_{3} } )}. \end{aligned} \end{aligned}$$
(31)

4 Determination of the constants by boundary conditions

Various derivatives of \(G( {x,x_{0} } )\) can be derived from Eq. (29) as

$$\begin{aligned} G^{( 1 )}( {x,x_{0} } )= & {} \Phi _{1}^{( 1 )} ( {x-x_{0} } )+\Phi _{2}^{(1 )} ( x)G( 0 ) \nonumber \\&+\,\Phi _{3}^{( 1 )} ( x )G^{( 1 )}( 0 )+\Phi _{4}^{( 1 )} ( x )G^{( 2 )}( 0 )+\Phi _{5}^{( 1 )} ( x )G^{( 3 )}( 0 ), \end{aligned}$$
(32)
$$\begin{aligned} G^{( 2 )}( {x,x_{0} } )= & {} \Phi _{1}^{( 2 )} ( {x-x_{0} } )+\Phi _{2}^{( 2 )} ( x)G( 0 ) \nonumber \\&+\,\Phi _{3}^{( 2 )} ( x )G^{( 1 )}( 0 )+\Phi _{4}^{( 2 )} ( x )G^{( 2 )}( 0 )+\Phi _{5}^{( 2 )} ( x )G^{( 3 )}( 0 ), \end{aligned}$$
(33)
$$\begin{aligned} G^{( 3 )}( {x,x_{0} } )= & {} \Phi _{1}^{( 3 )} ( {x-x_{0} })+\Phi _{2}^{( 3 )} ( x)G( 0 ) \nonumber \\&+\,\Phi _{3}^{( 3 )} ( x )G^{( 1 )}( 0 )+\Phi _{4}^{( 3 )} ( x )G^{( 2 )}( 0 )+\Phi _{5}^{( 3 )} ( x)G^{( 3 )}( 0 ). \end{aligned}$$
(34)

Equations (29), (32-34) establish the relations between the quantities at arbitrary cross section x. Particularly, at the boundary \(x=L\), one gets

$$\begin{aligned} \left[ \begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {\Phi _{2} ( L )} &{} {\Phi _{3} ( L )} &{} {\Phi _{4} ( L )} &{} {\Phi _{5} ( L )} \\ {\Phi _{2}^{( 1 )} ( L )} &{} {\Phi _{3}^{( 1 )} ( L )} &{} {\Phi _{4}^{( 1 )} ( L )} &{} {\Phi _{5}^{( 1 )} ( L )} \\ {\Phi _{2}^{( 2 )} ( L )} &{} {\Phi _{3}^{( 2 )} ( L )} &{} {\Phi _{4}^{( 2 )} ( L )} &{} {\Phi _{5}^{( 2 )} ( L )} \\ {\Phi _{2}^{( 3 )} ( L )} &{} {\Phi _{3}^{( 3 )} ( L )} &{} {\Phi _{4}^{( 3 )} ( L )} &{} {\Phi _{5}^{( 3 )} ( L )} \\ \end{array} \right] \left\{ \begin{array}{l} G( 0 ) \\ G^{( 1 )}( 0 ) \\ G^{( 2 )}( 0 ) \\ G^{( 3 )}( 0 ) \\ \end{array} \right\} = \left\{ \begin{array}{l} G( {L,x_{0} } )-\Phi _{1} ( {L-x_{0} } ) \\ G^{( 1 )}( {L,x_{0} } )-\Phi _{1}^{( 1 )} ( {L-x_{0} } ) \\ G^{( 2 )}( {L,x_{0} } )-\Phi _{1}^{( 2 )} ( {L-x_{0} } ) \\ G^{( 3 )}( {L,x_{0} } )-\Phi _{1}^{( 3 )} ( {L-x_{0} } ) \\ \end{array} \right\} . \end{aligned}$$
(35)

By setting \(\Phi _{1} =0\), one obtains the free vibration of the piezoelectric and flexoelectric Euler–Bernoulli beam. The constants G(0), \(G^{( 1 )}( 0 )\), \(G^{( 2 )}( 0 )\), and \(G^{( 3 )}( 0 )\) can be determined by the corresponding boundary conditions. For a cantilever beam which is clamped at \(x=0\) and free at \(x=L\), the corresponding boundary conditions are given in Eqs. (15). The boundary conditions then can be rewritten by the Green’s function \(G( {x,x_{0} } )\) as shown in Table 1.

Table 1 Boundary conditions of the piezoelectric and flexoelectric cantilever beam
Full size table

With the boundary conditions in Table 1 and relations in Eqs. (35), one can obtain

$$\begin{aligned} \left[ \begin{array}{ll} {\Phi _{4}^{( 2 )} ( L )} &{}\quad {\Phi _{5}^{( 2 )} ( L )} \\ {\Phi _{4}^{( 3 )} ( L )} &{}\quad {\Phi _{5}^{( 3 )} ( L )} \\ \end{array} \right] \left\{ \begin{array}{l} G^{( 2 )}( 0 ) \\ G^{( 3 )}( 0 ) \\ \end{array} \right\} = \left\{ \begin{array}{l} -\Phi _{1}^{( 2 )} ( {L-x_{0} } ) \\ -\Phi _{1}^{( 3 )} ( {L-x_{0} } ) \\ \end{array} \right\} . \end{aligned}$$
(36)

Thus, Green’s function for the cantilever EB is determined as

$$\begin{aligned} G( {x,x_{0} } )=H( {x-x_{0} } )\Phi _{1} ( {x-x_{0} } )+\Phi _{4} ( x )G^{( 2 )}( 0 )+\Phi _{5} ( x )G^{( 3 )}( 0 ). \end{aligned}$$
(37)

Then, the explicit expression of the transverse displacement excited by a unit harmonic force can be written as

$$\begin{aligned} w( {x,t} )=\left[ {H( {x-x_{0} } )\Phi _{1} ( {x-x_{0} } )+\Phi _{4} ( x )G^{( 2 )}( 0 )+\Phi _{5} ( x )G^{( 3 )}( 0 )} \right] \sin \omega t \end{aligned}$$
(38)

where \(\omega =2\pi f\) is the circular frequency of the external excited force.

After obtaining the dynamic mechanical response of EB, we can gain the output charge under short-circuit condition and output voltage under open circuit. Under open-circuit condition, the total electric displacement on the top and bottom surface is zero. Thus,

$$\begin{aligned} \int _{S_{e} } {( {a_{33} E_{3} +e_{31} \varepsilon _{11} +\mu _{31} \partial _{3} \varepsilon _{11} } )\text {d}S} =0. \end{aligned}$$
(39)

With the help of the Green’s function \(G( {x,x_{0} } )\), the average electric field can be written as

$$\begin{aligned} \bar{{E}}_{3} ( {x,t} )=\frac{1}{a_{33} S_{e} }\int _{S_{e} } {\left[ {e_{31} zG^{( 2 )}( {x,x_{0} } )+\mu _{31} G^{( 2 )}( {x,x_{0} } )} \right] \text {d}S}. \end{aligned}$$
(40)

The dynamic output of the electric potential can be written as

$$\begin{aligned} \varphi ( t )=-\int _{-\frac{h}{2}}^{\frac{h}{2}} {E_{z} dz} \sin \omega t=-\frac{\mu _{31} }{a_{33} S_{e} /Bh}\int _0^L {G^{( 2 )}( {x,x_{0} } )\text {d}x} \sin \omega t. \end{aligned}$$
(41)

It should be noticed that the electric potential induced by piezoelectricity is zero because of the symmetry through thickness. Thus, only flexoelectricity contributes to the dynamic output of the electric potential, as shown in Fig. 1b.

Under short circuit, the electric field along the thickness is zero; thus, the electric displacement can be written as

$$\begin{aligned} D_{3} =( {e_{31} \varepsilon _{11} +\mu _{31} \partial _{3} \varepsilon _{11} } )\sin \omega t. \end{aligned}$$
(42)

Then, the output charge along the thickness of the beam can be written as

$$\begin{aligned} Q( t )=\frac{1}{h}\int _V {D_{3} \text {d}V} =-\mu _{31} B\int _0^L {G^{( 2 )}( {x,x_{0} } )\text {d}x} \sin \omega t. \end{aligned}$$
(43)

5 Numerical results and discussion

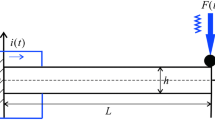
Considering a unit force loaded at the free end of the cantilever beam, the external force can be expressed as \(p( {x,t} )=\delta ( {x-L} )e^{i\omega t}\). The width–thickness ratio is taken \(b=2h\). We introduce the following dimensionless quantities:

$$\begin{aligned} \xi =\frac{x}{L}, \,\, \beta =\frac{h}{L}, \,\, g( \xi )=\frac{G( {x,L} )}{w_{\max } }. \end{aligned}$$
(44)

Material properties in the numerical calculations are chosen as \(c_{11} =1\) 08 GPa, \(a_{33} =\text {1.12}\times 10^{-8} \, \text {F/m}\), \(e_{31} =-4.4 \, \text {C/m}^{2}\), \(\mu _{31} = 10 \,\upmu \text {C/m}\) [9], and \(\rho =\text {5}780 \, \text {kg/m}^{3}\).

The static solution for the deflection of the beam is

$$\begin{aligned} w( x )=\frac{F( {x-3L} )x^{2}}{6( {EI} )^{\mathrm{eff}}}. \end{aligned}$$
(45)

To maintain the elastic deformation, we choose\(F=\frac{Ebh^{4}}{80L^{3}}\) .

In this Section, we consider the forced vibration of the Euler–Bernoulli piezoelectric and flexoelectric beam driven by a unit force loaded at the free end of the cantilever beam; therefore, the deflection of the beam can be expressed by the Green’s function G( x, L).

Fig. 2
figure 2

Dynamic deflection of the beam versus time at \(x=L\), a \({H}=1 \, \hbox {mm}\); b \({H} = 1\,\upmu \hbox {m}\)

Full size image

When considering \(\beta =20\), \(f=1\text {Hz}\), the dynamic deflection of the beam versus time at the position \(x=L\) is illustrated in Fig. 2. ‘E’, ‘P’, ‘F’, and ‘\(\hbox {P}{+}\hbox {F}\)’ in Fig. 2 represents elastic beam, piezoelectric beam, flexoelectric beam, and piezoelectric and flexoelectric beam, respectively. In Fig. 2a, the applied force is about 0.3 N, and the thickness of the beam is one millimeter. It is obvious that the dynamic deflection of the elastic beam, piezoelectric beam, flexoelectric beam, and piezoelectric and flexoelectric beam almost equal each other. This implies that the effect of piezoelectricity, flexoelectricity or both does not affect the dynamic deflection significantly at the macroscopic level. However, the dynamic deflection of the elastic beam, piezoelectric beam, flexoelectric beam, and piezoelectric and flexoelectric beam is separated when the thickness of the cantilever beam reduces to ten micrometer, as shown in Fig. 2b. The applied force is about 0.3 µN to maintain the beam in elastic deformation. Therefore, the elastic strain is almost in the same level in Fig. 2a, b. The elastic strain gradient is, however, inversely proportional to the beam thickness. The elastic strain gradient in Fig. 2b is much larger than that in Fig. 2a. The dynamic deflection of the elastic beam is equal to that of the piezoelectric beam in Fig. 2b, while the dynamic deflection of the flexoelectric beam is smaller than that of the elastic and piezoelectric beam. Moreover, the dynamic deflection of the flexoelectric beam is equal to that of the piezoelectric and flexoelectric beam. Therefore, Fig. 2b reveals that the difference in the dynamic deflection could be ascribed to the effect of flexoelectricity. The results in Fig. 2 imply that the effect of flexoelectricity becomes significant when the beam thickness reduces to microscale. For short-circuit condition, however, the effects of piezoelectricity and flexoelectricity do not affect the dynamic deflection because the elastic modulus remains constant. As a result, one may determine the flexoelectric coefficient for beams by a pure elastic technique at the microscale, such as testing the bending rigidity of the beam or determining the dynamic deflection of the flexoelectric beam under open-circuit condition.

The dynamic output voltage versus time of the Euler–Bernoulli beam is illustrated in Fig. 3. Obviously, elastic and piezoelectric Euler–Bernoulli beam will not cause any output voltage, owing to the tensile state of the upper part in the beam while the compressive state is in the lower part of the beam, as displayed in Fig. 1b. The flexoelectric Euler–Bernoulli beam, however, will cause output voltage due to the flexoelectric effect.

Fig. 3
figure 3

Dynamic output voltage versus time a \({H}=1 \, \hbox {mm} {\sim } 10\,\upmu \hbox {m}\); b different length–thickness ratios when \({H} = 1\,\hbox {mm}\)

Full size image

We find that the peak voltage for a flexoelectric Euler–Bernoulli beam is 0.164 V, and this value remains almost constant when the beam thickness reduces to fifty micrometers. This can be explained via the static solution of the output voltage, which can be expressed as

$$\begin{aligned} \varphi =\frac{3\mu _{31}}{40a_{33} \beta ^{2}}. \end{aligned}$$
(46)

The dynamic output voltage for a flexoelectric Euler–Bernoulli beam will be increasingly remarkable when the length–thickness ratio \(\beta \) decreases (Fig. 3b). The results above throw light on enhancing the dynamic output voltage by changing the size of the beam, besides increasing the intrinsic flexoelectric coefficient.

Moreover, these results lead us to rethink some of the existing works [55,56,57]. In these works, \({\text {BaTiO}}_{3}\) nanowires or nanowire arrays were used to harvester energy from the environmental vibration. The flexible nanogenerator based on single \({\text {BaTiO}}_{3}\) nanowire can generate an output voltage of up to 0.21 V and has been found in the previous works [57]. Our results imply that the flexoelectric effect might play an important role in the dynamic output voltage of the nanogenerators.

Fig. 4
figure 4

a Dynamic output charge versus time with \({H}=1\,\hbox {mm}\), \(\beta \,=\,\text {20}\); b piezoelectric coefficient \({\text {d}}_{33}\) of doped BT [58] and effective piezoelectric coefficient \({\text {d}}_{33}\) of an Euler–Bernoulli flexoelectric beam

Full size image

Figure 4a illustrates the dynamic output charge versus time under short-circuit condition. As stated above, the electric charge induced by piezoelectricity has the same sign on both surfaces, and only flexoelectricity contributes to the current flow. However, the peak output charge rapidly decreases to 0.075 pC when the beam thickness reduces to one micrometer, which is hard to measure practically. This phenomenon can also be directly explained by the static solution of the output charge,

$$\begin{aligned} Q=\frac{3\mu _{31} bh}{40L}=\frac{3\mu _{31} h}{20\beta }. \end{aligned}$$
(47)

The results above give us a new understanding of measuring the flexoelectric coefficients, that is, to get detectable electric charge output, the beam size should be avoided to made too small. Moreover, we introduce the effective piezoelectric coefficient, which can be expressed as

$$\begin{aligned} d_{33}^{\mathrm{eff}} =\frac{6\mu _{31} \beta ^{2}}{Eh}. \end{aligned}$$
(48)

We can see that the coefficient is inversely proportional to the beam thickness; hence, it can be significantly enhanced when the beam thickness decreases to microscale, as illustrated in Fig. 4b. The toxicity and environmental impacts of lead have shifted the attention from the most widely used lead zirconate titanate piezoceramics to alkaline bismuth titanate-based piezoelectric ceramics. Chemical modification or microstructurally engineering BT-based materials have been fabricated and selected to substitute for lead zirconate titanate piezoceramics. As compared in Fig. 4b, the effective piezoelectric coefficient \({\text {d}}_{33}\) (222 pC/N) is comparable with the piezoelectric- doped BT (largest value, 454 pC/N) when the beam thickness is at one millimeter; however, the effective piezoelectric coefficient \({\text {d}}_{33}\) (2222 pC/N) will be much stronger than that of the piezoelectric doped BT ceramics. Furthermore, the effective piezoelectric coefficient \({\text {d}}_{33}\) is size dependent of the beam thickness; this gives a novel way to design piezoelectric materials by flexoelectricity.

6 Conclusions

This work presents the forced vibration of a piezoelectric and flexoelectric Euler–Bernoulli beam by the Green’s function solution. The exact solutions for the harmonically excited beams are derived for cantilevers with different beam thicknesses. The tip deflection, dynamic output voltage, and dynamic output charge were selected to demonstrate the effect of the flexoelectric effect. Numerical results for \({\text {BaTiO}}_{3}\) cantilevers showed that the tip deflection would be smaller than that predicted by the classical piezoelectric beam theory. The dynamic output voltage and charge are negligible when the beam thickness reduces to microscale; however, several methods are proposed here to effectively enhance the electric response, such as changing the length–thickness ratio or introduce the effective piezoelectric coefficients. Our results imply that pure mechanical experiments can be used to determine the flexoelectric effect with different electrical boundary conditions. Moreover, our results showed that mechanical structural design can be another novel way to fabricate BT-based piezoelectric materials with ultrahigh piezoelectric coefficient.