1 Introduction

Functionally graded (FGMs) plate and shell structures are made of materials that are characterized by a continuous variation of the mechanical and thermo-physical properties through the thickness direction by combining two different materials, usually ceramic and metal. The ceramic materials have excellent characteristics in heat resistance with low thermal conductivity, while metal has excellent strength and toughness. In addition, FGM structures have a continuous and smooth variation of the material properties from one surface to the other, which eliminates abrupt changes in the stress and displacement distributions. Nowadays, the metal-ceramic FGM shell structures are widely used in many industrial applications such as aircraft, space vehicles, reactor vessels, and other high-temperature environments scientific and engineering applications. A common phenomenon in these advanced applications that can cause serious performance and safety problems is vibration. Vibrations are oscillations in mechanical dynamic systems which often refer to systems that can oscillate freely without applied forces. Due to the wide applications of functionally graded shells in high-temperature environments, the study of dynamic behaviour of these structures in thermal conditions is of the key importance. Numerous studies have been performed analytically on the free vibration of FGM plate/shell structures. Among them, Huang et al. [1] examined the nonlinear vibration of FGM plates in thermal environments using HSDT. The equation of motion was solved by an improved perturbation technique to determine the nonlinear frequencies of functionally graded plates. Kim [2] used a theoretical method to identify vibration characteristics of FGM plates, in which the Rayleigh–Ritz method was applied to obtain the frequency equation. Kadoli et al. [3] analysed free vibration of functionally graded cylindrical shells. The FSDT with Fourier series expansion of the displacement variables was used to model the FGM shell. Matsunaga [4] extracted the natural frequencies of higher-order theory FGM plates by using Hamilton's principle to derive the governing dynamic equations. Han et al. [5] worked on free vibration of FGM plate and shell structures. The FSDT shell element formulation was based on a quasi-conforming shell element. Zhao et al. [6] studied the free vibration of functionally graded plates using the element-free kp-Ritz method. The equation of motion was determined by the Ritz procedure to the energy functional of the system. The vibration analysis of solar functionally graded plates with using SSDT was performed by Shahrjerdi [7]. The equilibrium equations were derived using the energy method, and the solution was based on Fourier series. Nguyen-Xuan et al. [8] presented an improved finite element approach with node-based strain smoothing, applied for static, free vibration, and mechanical/thermal buckling problems of FGM plates. Kar et al. [9] investigated the free vibration responses of shear deformable functionally graded single/doubly curved panels with higher-order shear deformation theory. In Fazzolari [10], the author performed free vibration of functionally graded plates with temperature-dependent materials, using advanced hierarchical higher-order equivalent single layer plate theories developed using the method of power series expansion of displacement components. Parida et al. [11] presented higher-order shear deformation theory of finite element model for free vibration analysis of a rotating FGM plate with thermal effect. Parida et al. [12] studied the free vibration of a skew FGM plate in thermal environment with higher-order shear deformation theory. Burlayenko et al. [13] generated an ABAQUS routine to study the free vibrations of FGM sandwich plates under thermal load, using a solid brick finite element. Shakouri [14] studied the vibration of rotating functionally graded conical shells with temperature-dependent material properties. The governing equations were employed by using Donnel shell theory. Hong [15] analysed the nonlinear static bending and nonlinear free vibration of 2D third-order shear deformation theory of FGM plates. Moita et al. [16] worked on the free vibration performance of FGM axisymmetric plate/shell structures. The numerical solution was obtained by expanding the variables in Fourier series in the circumferential direction and using conical frustum finite elements in the meridional direction.

Porosities may appear in FGMs as a result of the manufacturing process or by design, and therefore, it is necessary to consider the effects of porosity on the vibration performance of these highly engineered materials. Wattanasakulpong et al. [17] presented linear and nonlinear vibration analyses of FGM elastically end restrained porous beams. Ebrahimi et al. [18] studied the thermo-mechanical vibration behaviour of FG porous beams by presenting Navier solution and employing a semi-analytical differential transform method. Ghadiri et al. [19] studied the free vibration analysis of a functionally graded porous cylindrical micro-shell under thermal effect, based on the FSDT and the modified couple stress theories. Trinh et al. [20] investigated the fundamental frequencies of functionally graded sandwich shells with double curvature under thermo-mechanical loadings with porosities. The Bubnov–Galerkin procedure was employed to derive the governing equations. Talebizadehsardari et al. [21] examined the vibration of macro–micro-nano-functionally graded porous plates and shells with introducing a closed-form solution. The governing equations were derived by third-order plate and shell theories. Tran et al. [22] studied bending, buckling, and free vibration of a FGP nano-shell resting on an elastic foundation. Katiyar et al. [23] presented free vibration analysis of an geometrically imperfect and discontinuous porous functionally graded bidirectional plate resting on an elastic foundation under thermal environment. Several other works on free vibration of FGM porous plates and shells have been presented in recent years, see, for instance, [24,25,26,27,28,29]. However, as far as the authors know free vibrations of FGM shell structures with temperature-dependent material properties are mainly limited to free-vibration response of shell structures in particular cylindrical shells with the presence of porosity distribution. Therefore, as such studies are important to the structural designers the present paper examines the free vibration response of functionally graded porous shell structures under thermal environment with temperature-dependent material properties using a doubly curved shell finite element. This shell element is an 8-node curved degenerated shell element formulated using the principle of virtual displacement with thermal stresses effect. Translational and rotary inertia effects are considered in the mass matrix formulation. The material is assumed to be porous with temperature-dependent properties functionally graded in the thickness direction according to the power-law distribution of volume fractions of the constituent materials. In this work, the influence of porosity distribution with temperature gradient through-thickness direction, besides the effect of material constituents, material gradient, boundary conditions, and radius to thickness ratio on the frequency characteristics is presented and discussed.

2 Material properties of an FGM

The effective properties of an FGM plate/shell are assumed to be continuously changing through the thickness direction. The power-law function (P-FGM) [30] is commonly used to describe the gradually varying volume fraction of the constituent materials as:

$$V_{c} \left( z \right) = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{n}$$
(1)

where (n) stands for the power-law index. It is a non-negative real number; (h) is the shell thickness, and (z) is the thickness direction coordinate (− 0.5 h ≤  z ≤  0.5 h).

In this study, the functional material is considered to be porous with an evenly distributed porosity. The porosity distribution through an FGM material is depicted in Fig. 1.

Fig. 1
figure 1

Porosity distribution in a FG material

Full size image

In the case of a porous FGM, based on the rule of mixture, the through-thickness material properties, such as the elasticity modulus E, Poisson's ratio \(\nu\), mass density \(\rho\), thermal expansion coefficient \(\alpha\), and thermal conductivity \(K\), are given in several references [31,32,33,34] by the following equation:

$$P\left( {z,\,\,T} \right) = \left( {P_{c} (T) - P_{m} (T)} \right)V_{c} (z) + P_{m} (T) - \left( {P_{c} (T) + P_{m} (T)} \right)\frac{a}{2}$$
(2)

where Pc, Pm denote the effective material properties of the ceramic and metal phases, respectively, and (a) is the volume fraction of porosity. However, during this investigation, we noticed that Eq. (2) provides negative thermal conductivity (K) when approaching the ceramic-rich surface, and, in thermal analysis, this equation provides an erroneous distribution of temperature. In order to elucidate this inaccuracy, let us consider a porous FGM with a porosity volume fraction (a), distributed equally in the ceramic and metal phases, and the modified rule of mixture reads:

$$P = P_{m} \left( {V_{m} - \frac{a}{2}} \right) + P_{c} \left( {V_{c} - \frac{a}{2}} \right),$$
(3)

In Refs. [31,32,33,34], it is assumed that the total volume fraction of the metal and ceramic complies with the following equation: Vm + Vc = 1, which leads to Eq. (2). This equation provides several inconsistencies in the obtained FGM properties, especially in the through-thickness temperature distribution. For instance, if we have a ceramic phase (Vm = 0 and Vc = 1) then, Eq. (2) yields:

$$P\left( {z,\,\,T} \right) = P_{c} \left( T \right)\left( {1 - \frac{a}{2}} \right) + P_{m} \left( { - \frac{a}{2}} \right),$$
(4)

As the thermal conductivity (K) of the metal phase is much higher than that of the ceramic phase, see Table 8, Eq. (7) provides a negative value of the thermal conductivity (K) of the porous FGM.

In order to solve this problem, let us consider a porous homogenous material with a porosity volume fraction (a) for which Pc = Pm = P. Then, Eq. (3) yields:

$$P = P\left( {V_{m} - \frac{a}{2}} \right) + P\left( {V_{c} - \frac{a}{2}} \right) = P\left( {V_{m} + V_{c} - a} \right)$$
(5)

which yields:

$$V_{m} + V_{c} = 1 + a.$$
(6)

Equation (6) represents the correct correlation between the metal and ceramic volume fractions in a porous FGM. By substituting Eq. (6) into Eq. (2), we get:

$$P\left( {z,\,T} \right) = \left( {P_{c} (T) - P_{m} (T)} \right)V_{c} (z) + P_{m} (T) - \left( {P_{c} (T) - P_{m} (T)} \right)\frac{a}{2}.$$
(7)

Equation (7) represents the correct formula of the rule of mixture of porous FGMs with evenly distributed porosity. The evenly distributed porosity is defined as P-I. For another type of porous FGM having uneven distribution of porosities, in which the porosity increases linearly from (0) “at the metal phase” to (a) “at the ceramic phase” is defined as P-II, the following rule of mixture is applied:

$$P\left( {z,T} \right) = \left( {P_{c} (T) - P_{m} (T)} \right)V_{c} (z) + P_{m} (T) - \left( {P_{c} (T) - P_{m} (T)} \right)\frac{a}{4}\left( {1 + 2\frac{z}{h}} \right),$$
(8)

Another type of porous FGM having uneven distribution of porosities, in which, the porosity decreases linearly from (a) “at the metal phase” to (0) “at the ceramic phase” is defined as P-III, with the following rule of mixture:

$$P\left( {z,T} \right) = \left( {P_{c} (T) - P_{m} (T)} \right)V_{c} (z) + P_{m} (T) - \left( {P_{c} (T) - P_{m} (T)} \right)\frac{a}{4}\left( {1 - 2\frac{z}{h}} \right),$$
(9)

The fourth type of porous FGM having uneven distribution of porosities, in which the porosity increases linearly from (0) “at the metal phase” to (a) “at the mid surface h/2”, then decreases linearly from (a) “at the mid surface” to (0) “at the ceramic phase” is defined as P-IV, with the following rule of mixture:

$$P\left( {z,\,T} \right) = \left( {P_{c} (T) - P_{m} (T)} \right)V_{c} (z) + P_{m} (T) - \left( {P_{c} (T) - P_{m} (T)} \right)\frac{a}{4}\left( {1 - 2\frac{\left| z \right|}{h}} \right),$$
(10)

If considering the temperature dependency of the mechanical and thermo-physical properties of the constituent materials, the properties of the metal or ceramic phases are given by:

$$P\left( T \right) = P_{0} \left( {P_{ - 1} T^{ - 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} } \right)$$
(11)

where T = T0 + ∆T is the material temperature (in Kelvin), T0 stands for the reference stress-free temperature (usually taken as 300 K), ∆T denotes the temperature change, and P0, P−1, P1, P2, and P3 are the coefficients of temperature, which are unique for each constituent.

The temperature variation is assumed to occur only in the thickness direction. Due to the smooth variation of the effective properties of an FGM through the thickness direction, the through-thickness temperature distribution is non-uniform as depicted in Figs. 2 and 3. When a heat shock passes through the FGM, the temperature changes from slow to fast due to the functional conductivity of the material mixture. This functionality is controlled by gradually varying the volume fractions of the two materials in between the two surfaces. Moreover, the temperature distribution can be non-uniform, even for a homogenous material mixture, due to the effect of a hierarchic porosity, as depicted in Fig. 4. The temperature can change from fast to slow or from slow to fast according to the porosity distribution as shown in Fig. 4.

Fig. 2
figure 2

Through-thickness temperature distributions in a P-I porous FGM with different porosity volume fractions

Full size image
Fig. 3
figure 3

Through-thickness temperature distributions in a porous FGM with different power-law indexes

Full size image
Fig. 4
figure 4

Through-thickness temperature distributions in a porous FGM with different porosity types; n = 0

Full size image

The non-uniform temperature distribution through the thickness can be determined by solving the one-dimensional steady-state heat transfer problem [35]:

$$\frac{{\text{d}}}{{{\text{d}}z}}\left[ {K\left( z \right)\frac{{{\text{d}}T}}{{{\text{d}}z}}} \right] = 0,\;T\left( {z = {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}} \right) = T_{c} ,\;T\left( {z = {{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}} \right) = T_{m}$$
(12)

where K(z) is the thermal conductivity, evaluated using Eq. (7). Tc and Tm denote the temperature of the ceramic-rich and metal-rich surfaces of the shell, respectively. The solution for Eq. (12) is given by:

$$T\left( z \right) = T_{m} + \Delta T \cdot \eta \left( z \right),\;\Delta T = T_{c} - T_{m} ,\;\eta \left( z \right) = \left( {{{\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{z} {\frac{{{\text{d}}z}}{K\left( z \right)}} } \mathord{\left/ {\vphantom {{\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{z} {\frac{{{\text{d}}z}}{K\left( z \right)}} } {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\frac{{{\text{d}}z}}{K\left( z \right)}} }}} \right. \kern-\nulldelimiterspace} {\int\limits_{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}} {\frac{{{\text{d}}z}}{K\left( z \right)}} }}} \right),$$
(13)

The integrals of Eq. (13) are evaluated using numerical integration.

To show the change in the temperature distribution between the perfect and porous FGMs in thermal environments, the temperature distribution with the thickness coordinate in an aluminium–zirconia material mixture is plotted in Fig. 2. Here, different power-law indexes are considered, and the porosity volume fraction is set as a = 0, a = 0.1, a = 0.2 and a = 0.3. In Fig. 3, different porosity volume fractions are considered, and the power-law index is set as n = 0.5, n = 1, n = 2, and n = 5.

To show the change in the temperature distributions between the four porosity distributions P-I, P-II, P-III and P-IV in thermal environments, the temperature distribution with the thickness coordinate in an aluminium–zirconia material mixture is plotted in Figs. 4, 5, and 6. Here, different porosity volume fractions are considered, and the power-law index is set as n = 0, n = 0.1, and n = 0.5.

Fig. 5
figure 5

Through-thickness temperature distributions in a porous FGM with different porosity types; n = 0.1

Full size image
Fig. 6
figure 6

Through-thickness temperature distributions in a porous FGM with different porosity types; n = 0.5

Full size image

Figures 5 and 6 show the variations of temperature with the thickness coordinate in a porous FGM with different porosity distributions. It can be seen that the uneven porosity P-III provides a pattern of temperature distribution similar to that due to the variation of the volume fractions of the two materials in between the two surfaces (the power-law index). As we can see from Fig. 6, the effect of porosity P-III vanishes rapidly with the increase of the power-law index. However, the uneven porosity P-II provides a pattern of temperature distribution symmetric to that due to the variation of the volume fractions of the two materials in between the two surfaces.

To show the change of material properties due to porosity in a porous FGM, the variations of Young’s modulus with the thickness coordinate aluminum-zirconia material mixture are plotted in Figs. 7, 8, and 9 for the four porosity distributions P-I, P-II, P-III, and P-IV. Here, the different porosity volume fractions are considered, and the power-law index is set as n = 0, n = 0.1, and n = 5.

Fig. 7
figure 7

Through-thickness elasticity moduli distribution in a porous FGM with different porosity types; n = 0

Full size image
Fig. 8
figure 8

Through-thickness elasticity moduli distributions in a porous FGM with different porosity types; n = 0.1

Full size image
Fig. 9
figure 9

Through-thickness elasticity moduli distributions in a porous FGM with different porosity types; n = 5

Full size image

3 Formulation of the shell finite element

To derive the formulation of the presented degenerated curved shell element in thermal environments, the sixteen-node solid element can be degenerated into an 8-node curved shell element in few steps as shown in Fig. 10. We are using the main shell assumption of straight normal remaining straight and inextensible after deformation [36], and neglecting the strain energy associated with the stresses perpendicular to the middle surface (plane stress condition).

Fig. 10
figure 10

An 8-node degenerated shell element

Full size image

3.1 Geometry and kinematics of the shell

The position vector of an arbitrary point “p” on the shell is determined by the iso-parametric interpolation of the global coordinates using the nodal coordinates and direction cosines of the director vectors of all nodes of an element “e” [37, 38]. Then, the Cartesian coordinates \({\varvec{r}} = \left\{ {\begin{array}{*{20}c} x & y & z \\ \end{array} } \right\}^{T}\) of a point “p” inside an element “e” are given by:

$${\varvec{r}}\left( {\xi ,\eta ,\zeta } \right) = \sum\limits_{i = 1}^{n} {N_{i} \left( {\xi ,\eta } \right)} \, {\varvec{r}}_{i} + \frac{\zeta }{2}h\sum\limits_{i = 1}^{n} {N_{i} } \left( {\xi ,\eta } \right){\varvec{v}}_{3i}$$
(14)

where \({\varvec{r}}_{i}\) denotes the Cartesian coordinates of nodal points, ζ defines the position of the point in the thickness direction, n is the number of element nodes, and \(N_{i} \left( {\xi ,\eta } \right)\) is the two-dimensional interpolation function.

The nodal normal vector at node (i) can be obtained by the cross product of two vectors that are tangent to the reference surface at (i):

$${\varvec{v}}_{3i} = \sum\limits_{j = 1}^{n} {\left( {\frac{{\partial N_{j} \left( {\xi_{i} ,\eta_{i} } \right)}}{\partial \xi }{\varvec{r}}_{0j} \wedge \frac{{\partial N_{j} \left( {\xi_{i} ,\eta_{i} } \right)}}{\partial \eta }{\varvec{r}}_{0j} } \right)}$$
(15)

where \({\varvec{r}}_{0j}\) defines the position vector of a point on the reference surface. Then, the director vector is given by: \({\varvec{v}}_{3i} = \frac{{{\varvec{v}}_{3i} }}{{\left\| {{\varvec{v}}_{3i} } \right\|}}\).

The displacement vector of an arbitrary point “ p” inside the element “ e” having five degrees of freedom can be obtained from the following relation:

$${\varvec{u}}\left( {\xi ,\eta ,\zeta } \right) = \sum\limits_{i = 1}^{n} {N_{i} \left( {\xi ,\eta } \right)} \, {\varvec{u}}_{i} + \frac{\zeta }{2}h\sum\limits_{i = 1}^{n} {N_{i} } \left( {\xi ,\eta } \right)\left[ {\begin{array}{*{20}c} { - {\varvec{v}}_{2i} } & {{\varvec{v}}_{1i} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\alpha_{i} } \\ {\beta_{i} } \\ \end{array} } \right\}$$
(16)

where the two orthogonal unit vectors \({\varvec{v}}_{1i}\) and \({\varvec{v}}_{2i}\) are introduced to express the director vector in terms of \(\alpha_{i}\) and \(\beta_{i}\), where \(\alpha_{i}\) and \(\beta_{i}\) are the rotation angles of the director vector \({\varvec{v}}_{3i}\) about the tangent vectors \({\varvec{v}}_{1i}\) and \({\varvec{v}}_{2i}\), respectively.

Hence, each node has three global displacements and two rotations about the local in-plane axis, respectively, \(\user2{\hat{u} = }\left\{ {\begin{array}{*{20}c} u & v & w & {\theta_{x} } & {\theta_{y} } \\ \end{array} } \right\}^{T}\).

3.2 Stress and strain fields

Considering that the material of the shell is linearly thermo-elastic, the stress tensor in global Cartesian coordinates is obtained in terms of elastic strains and temperature change as:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{11} } \\ {\sigma_{22} } \\ {\sigma_{33} } \\ {\sigma_{12} } \\ {\sigma_{13} } \\ {\sigma_{23} } \\ \end{array} } \right\} = \left[ {\varvec{C}} \right]\left( {\left\{ {\begin{array}{*{20}c} {\varepsilon_{11}^{m} } \\ {\varepsilon_{22}^{m} } \\ {\varepsilon_{33}^{m} } \\ {2\varepsilon_{12}^{m} } \\ {2\varepsilon_{13}^{m} } \\ {2\varepsilon_{23}^{m} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\varepsilon_{11}^{th} } \\ {\varepsilon_{22}^{th} } \\ {\varepsilon_{33}^{th} } \\ {2\varepsilon_{12}^{th} } \\ {2\varepsilon_{13}^{th} } \\ {2\varepsilon_{23}^{th} } \\ \end{array} } \right\}} \right)$$
(17)

where the thermal strain in the global system coordinates, using Voigt notation, can be calculated as follows:

$${\varvec{\varepsilon}}^{th} = - \alpha \left( {T,z} \right)\Delta T\left( z \right) \cdot \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 0 & 0 & 0 \\ \end{array} } \right]^{T}.$$
(18)

There, ΔT(z) is the temperature change, and \(\alpha \left( {T,z} \right)\) is the effective thermal expansion coefficient. Note that \(\alpha \left( {T,z} \right)\) is variable with the thickness coordinate and temperature according to Eqs. (11) and (7), respectively. The temperature change ΔT is defined as:

$$\Delta T\left( z \right) = T\left( z \right) - T_{0}$$
(19)

where \(T_{0}\) is the reference temperature.

The Green strain in the global Cartesian system can be written in terms of displacements as:

$${\varvec{\varepsilon}}_{ij} = \frac{1}{2}\left( {\frac{{\partial {\varvec{u}}_{i} }}{{\partial {\varvec{r}}_{j} }} + \frac{{\partial {\varvec{u}}_{j} }}{{\partial {\varvec{r}}_{i} }}} \right).$$
(20)

After introducing finite element discretization, the linear strain vector can be expressed as: \({\varvec{\varepsilon}}_{ij} = {\varvec{B}}_{0} \,\hat{\user2{u}}\), where the B0 is the linear strain–displacement matrix and \(\user2{\hat{u} = }\left\{ {\begin{array}{*{20}c} u & v & w & {\theta_{x} } & {\theta_{x} } \\ \end{array} } \right\}^{T}\) stands for the vector of nodal degrees of freedom associated with the displacement field.

According to shell assumptions, the strain energy associated with the stresses along the thickness direction is neglected. Then, since the normal stress and strain along the thickness direction are ignored in the local convected coordinates, the following stress tensor is obtained in local coordinates, using Voigt notation:

$$\tilde{\user2{\sigma }} = \left\{ {\begin{array}{*{20}c} {\sigma_{11} } &\quad {\sigma_{22} } &\quad 0 &\quad {\sigma_{12} } &\quad {\sigma_{13} } &\quad {\sigma_{23} } \\ \end{array} } \right\}^{T},$$
(21)

Accordingly, the linear constitutive matrix is expressed in the local coordinates by:

$$\tilde{\user2{C}} = \left[ {\begin{array}{*{20}c} {C_{11} } &\quad {C_{12} } &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ {C_{12} } &\quad {C_{11} } &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad {C_{44} } &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad {C_{55} } & \quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad {C_{66} } \\ \end{array} } \right]$$
(22)

where

$$C_{11} = \frac{{E\left( {T,z} \right)}}{{1 - \nu^{2} \left( {T,z} \right)}},\;C_{12} = \nu \left( {T,z} \right)C_{11} ,\;C_{44} = C_{55} = C_{66} = k_{s} \left( {\frac{{1 - \nu \left( {T,z} \right)}}{2}} \right),$$
(23)

The elastic modulus \(E\left( {T,z} \right)\) and the Poisson's ratio \(\nu \left( {T,z} \right)\) vary with the thickness and temperature according to Eqs. (11) and (7). The shear correction factor \(k_{s}\) is introduced to improve the shear distribution across the shell thickness. A computational algorithm for the transverse shear correction factors can be found in [39, 40]. Then, the constitutive matrix \({\varvec{C}}\) in the global coordinates can be obtained by using the following transformation:

$${\varvec{C}} = {\varvec{Q}}^{T} \tilde{\user2{C}}\user2{ Q}$$
(24)

where Q stands for the transformation matrix given in [35].

4 Governing equations

The dynamic equilibrium equation for vibration analysis based on the virtual work principle can be written as:

$$\int_{V} {\delta {\varvec{\varepsilon}}_{ij}^{T} \cdot {\varvec{C}} \cdot {\varvec{\varepsilon}}_{ij \, } } {\text{d}}V = \int_{V} {\delta \dot{u}^{T} } M\dot{u}\;{\text{d}}V$$
(25)

where \({\varvec{\varepsilon}}_{ij}\) denotes the Green–Lagrange strain tensor, the right side of Eq. (25) is resulting from the element kinetic energy.

Once again, introducing finite element discretization, Eq. (25) can be written in the following matrix form:

$$\delta {\varvec{u}}_{e}^{T} \left( {\int_{V} {{\varvec{B}}_{0}^{T} {\varvec{C}}} {\varvec{B}}_{0} \, dV} \right) = \delta \dot{u}_{e}^{T} \left( {\int_{V} {{\varvec{S}}^{T} \user2{\rho S}} {\text{d}}V} \right),$$
(26)

Due to thermal stresses, the element geometric stiffness matrix can be expressed as:

$${\varvec{K}}_{\sigma th} = \int_{V} {{\varvec{G}}^{T} {\varvec{H}}^{\text{th}}} {\varvec{G}}\,{\text{d}}V.$$
(27)

in which the nonlinear strain–displacement transformation G and the thermal stress Hth matrices are defined, respectively, as:

$$\begin{aligned} & \user2{G\hat{u}} = \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}}} &\quad {\frac{\partial v}{{\partial x}}} &\quad {\frac{\partial w}{{\partial x}}} &\quad {\frac{\partial u}{{\partial y}}} &\quad {\frac{\partial v}{{\partial y}}} &\quad {\frac{\partial w}{{\partial y}}} &\quad {\frac{\partial u}{{\partial z}}} &\quad {\frac{\partial v}{{\partial z}}} &\quad {\frac{\partial w}{{\partial z}}} \\ \end{array} } \right\}^{T} , \\ & {\varvec{H}}^{\text{th}} = \left[ {\begin{array}{*{20}c} {\sigma_{x}^{th} \cdot {\varvec{I}}} &\quad {\tau_{xy}^{th} \cdot {\varvec{I}}} &\quad {\tau_{xz}^{th} \cdot {\varvec{I}}} \\ {\tau_{xy}^{th} \cdot {\varvec{I}}} &\quad {\sigma_{y}^{th} \cdot {\varvec{I}}} &\quad {\tau_{yz}^{th} \cdot {\varvec{I}}} \\ {\tau_{xz}^{th} \cdot {\varvec{I}}} &\quad {\tau_{yz}^{th} \cdot {\varvec{I}}} &\quad {\sigma_{z}^{th} \cdot {\varvec{I}}} \\ \end{array} } \right],\;{\varvec{I}} = \left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 0 \\ 0 &\quad 1 &\quad 0 \\ 0 &\quad 0 &\quad 1 \\ \end{array} } \right]. \\ \end{aligned}$$
(28)

Finally, the free vibration equation, under thermal environment, is given by:

$$\left( {\left[ {{\varvec{K}} + {\varvec{K}}_{\sigma th} } \right] - \omega^{2} \left[ {\varvec{M}} \right]} \right)\left\{ u \right\} = 0$$
(29)

where \(\omega\) known as natural frequency, \(u\) is the corresponding eigenvector, and the element stiffness matrix can be obtained by:

$${\varvec{K}} = \int_{V} {{\varvec{B}}_{0}^{T} {\varvec{C}}} {\varvec{B}}_{0} \,{\text{d}}V.$$
(30)

The consistent mass matrix obtained from the kinetic energy including translational and rotary inertia effects is given by:

$${\varvec{M}} = \int_{V} {{\varvec{S}}^{T} \user2{\rho S}} \,{\text{d}}V$$
(31)

with S standing for the displacement matrix, and ρ is the density matrix defined as:

$${\varvec{S}} = \left[ {\begin{array}{*{20}c} {{\varvec{S}}^{1} } & {{\varvec{S}}^{2} } & {...} & {{\varvec{S}}^{8} } \\ \end{array} } \right],$$
(32)
$${\varvec{S}}^{i} = \left[ {\begin{array}{*{20}c} {N_{i} } &\quad 0 &\quad 0 &\quad { - h_{z} N_{i} l_{2i} } &\quad {h_{z} N_{i} l_{1i} } \\ 0 &\quad {N_{i} } &\quad 0 &\quad { - h_{z} N_{i} m_{2i} } &\quad {h_{z} N_{i} m_{1i} } \\ 0 &\quad 0 &\quad {N_{i} } &\quad { - h_{z} N_{i} n_{2i} } &\quad {h_{z} N_{i} n_{1i} } \\ 0 &\quad 0 &\quad 0 & \quad{N_{i} } &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad 0 &\quad {N_{i} } \\ \end{array} } \right],$$
(33)
$${\varvec{\rho}} = \left[ {\begin{array}{*{20}c} \rho &\quad 0 &\quad 0 &\quad {{{\rho h} \mathord{\left/ {\vphantom {{\rho h} 2}} \right. \kern-\nulldelimiterspace} 2}} &\quad 0 \\ 0 &\quad \rho &\quad 0 &\quad 0 &\quad {{{\rho h} \mathord{\left/ {\vphantom {{\rho h} 2}} \right. \kern-\nulldelimiterspace} 2}} \\ 0 &\quad 0 &\quad \rho &\quad 0 &\quad 0 \\ {{{\rho h} \mathord{\left/ {\vphantom {{\rho h} 2}} \right. \kern-\nulldelimiterspace} 2}} &\quad 0 &\quad 0 &\quad {{{\rho h^{2} } \mathord{\left/ {\vphantom {{\rho h^{2} } 4}} \right. \kern-\nulldelimiterspace} 4}} &\quad 0 \\ 0 &\quad {{{\rho h} \mathord{\left/ {\vphantom {{\rho h} 2}} \right. \kern-\nulldelimiterspace} 2}} &\quad 0 &\quad 0 &\quad {{{\rho h^{2} } \mathord{\left/ {\vphantom {{\rho h^{2} } 4}} \right. \kern-\nulldelimiterspace} 4}} \\ \end{array} } \right]$$
(34)

where \(\rho\) is the effective material density and \(h_{z} = \frac{\zeta }{2}h\).

5 Numerical results and discussion

In this Section, the free vibration response of functionally graded porous shell structures with temperature-dependent material properties under thermal environment is studied. The efficacy and validation of the presented finite element formulation are tested for the problems for which the analytical solutions are available in the literature. The temperature is assumed to be uniform on any surface that lies between the top and bottom surfaces and can be varied through the thickness direction only as a nonlinear function. The stiffness matrix is integrated using a modified 5-points reduced numerical integration scheme [41, 42] that provides a full rank stiffness matrix with no need for hourglass control, resulting in a highly efficient shell element.

5.1 Square plate

In order to validate the present formulation, the numerical results of a ZrO2/Ti-6Al-4V and Si3N4/SUS304 FGM square plate are compared with the analytical solution available in the literature [43]. The materials' “mechanical and thermo-physical” properties are taken as temperature-dependent, see Table 8 (Appendix A).

The square plate has a side length L = 0.2 m and thickness h = 0.025 m. The plate is simply supported on all its edges with no in-plane displacements, as shown in Fig. 11. The mesh consists of 3 × 3 square elements.

Fig. 11
figure 11

Simply supported square FGM plate with no in-plane displacements

Full size image

Tables 1 and 2 show the variation of the first non-dimensional frequency of the square plate with the volume fraction index (n) under different sets of thermal condition while porosity is not considered. For convenience, the non-dimensional natural frequency used in the analysis is defined as \(\omega^{ * } = \omega \left( {{{L^{2} } \mathord{\left/ {\vphantom {{L^{2} } h}} \right. \kern-\nulldelimiterspace} h}} \right)\sqrt {\left( {1 - \nu_{m}^{2} } \right){{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} }}} \right. \kern-\nulldelimiterspace} {E_{m} }}}\) where \(E_{m}\), \(\rho_{m}\), and \(\nu_{m}\) are the reference values at T0 = 300 K.

Table 1 Non-dimensional first natural frequency of a ZrO2/Ti-6Al-4V square plate in thermal environment
Full size table
Table 2 Non-dimensional natural frequency of an Si3N4/SUS304 square plate in thermal environment
Full size table

Three thermal loading cases are investigated, in which the bottom surface temperature is held constant Tm = 300 K, while the top surface temperature is taken as Tc = 300 K, 400 K, and 600 K for the first, second, and the third loading case, respectively.

In this test, the effect of volume fraction index (n) and temperature field on the first natural frequency is represented. The results are in good agreement with the analytical solution. It can be seen that the non-dimensional frequencies of the FGM plate are showing a descending trend from ceramic rich to metal rich, it is because the ceramic materials are well known for their higher stiffness than the metal ones. Besides, a decrease in the natural frequencies can be noticed when the material properties are considered as temperature dependent.

Tables 1 and 2 show the variation of the first four non-dimensional frequencies of the square plate with the volume fraction index (n) under different sets of thermal condition and with different porosity indexes. Indices in brackets (m, n) stand for the vibration mode in x and y axes.

The first mode frequencies depicted in Tables 3 and 4 are plotted in Fig. 12. It is observed that the non-dimensional frequency with the volume fraction index for the two investigated values of porosity (a = 0.1 and a = 0.2) tends to decrease with the increase of the power-law index in all the studied thermal conditions. Moreover, as the elasticity moduli decrease by the increase in temperature or the porosity, the non-dimensional frequency decreases with the increase in temperature and porosity.

Table 3 Non-dimensional natural frequencies of ZrO2/Ti-6Al-4V square plate in thermal environment with porosity parameter
Full size table
Table 4 Non-dimensional natural frequencies of Si3N4/SUS304 square plate in thermal environment with porosity parameter
Full size table
Fig. 12
figure 12

Non-dimensional first natural frequency of the porous FGM square plate in thermal environments: (a), (b)

Full size image

5.2 Cylindrical shell panel

In this example, the geometry of an FGM cylindrical panel is presented in Fig. 13. A 4 × 4 elements mesh is employed for the spatial discretization. The two curved edges of the panel are free, while the straight edges are simply supported. Free vibration analysis of a simply supported (Al/Al2O3) FGM shell was investigated analytically in [26]. It is extended here to investigate the free vibration of a porous cylindrical FGM shell in thermal environments.

Fig. 13
figure 13

Geometry of the cylindrical panel

Full size image

A ceramic–metal FGM that consists of alumina and aluminum (Al/Al2O3) is considered. The material properties of each constituent at temperature T = 300 K are listed in Table 5. Table 6 shows the obtained results against those reported in the literature [26].

Table 5 Material properties of (Al/Al2O3) [26]
Full size table
Table 6 Non-dimensional natural frequency \(\omega^{ * } = \omega \left( {{{L^{2} } \mathord{\left/ {\vphantom {{L^{2} } h}} \right. \kern-\nulldelimiterspace} h}} \right)\sqrt {{{\rho_{c} } \mathord{\left/ {\vphantom {{\rho_{c} } {E_{c} }}} \right. \kern-\nulldelimiterspace} {E_{c} }}}\) for FGM panel
Full size table

Herein, we investigated the free vibration behaviour of porous FG cylindricals panel under different thermal conditions. The material properties of the constituents are chosen from Table 8. The dimensionless frequency used in this analysis is \(\omega^{ * } = 100 \, \omega \, h \, \sqrt {{{\rho_{c} } \mathord{\left/ {\vphantom {{\rho_{c} } {E_{c} }}} \right. \kern-\nulldelimiterspace} {E_{c} }}}\) where \(E_{c}\) and \(\rho_{c}\) are the reference values at T0 = 300 K.

Table 7 Dimensionless frequency of isotropic clamped spherical shell
Full size table

The effect of temperature, power-law index (n), and porosity coefficients on the first fundamental natural frequency with simply supported (ssss) and clamped (cccc) edges is illustrated in Figs. 14, 15, and 16, respectively.

Fig. 14
figure 14

First non-dimensional frequency variation versus temperature (Tc) of the FG cylindrical panel: a simply supported, b clamped

Full size image
Fig. 15
figure 15

First non-dimensional frequency variation versus power-law index (n) of FG panel: a simply supported, b clamped

Full size image
Fig. 16
figure 16

First non-dimensional frequency variation versus porosity coefficients a of FG panel for: a simply supported, b clamped

Full size image

The temperature field is applied by holding the bottom surface temperature at Tm = 300 K, while the top surface is heated up to temperature Tc = 700 K. It can be observed from Fig. 14 that there is a significant difference between the responses depending on which the material properties are considered as temperature-dependent or not. It is clear that the effect of considering the material properties as temperature-dependent on the natural frequency is highly affected and goes in descending trend as temperature increases.

It can be also seen that the non-dimensional frequencies decrease as the temperature of the ceramic surface (Tc) increases. This is due to the decrease of the constituent materials′ stiffness with the temperature increases.

The effect of the power-law index (n) on the natural frequency is depicted in Fig. 15 for two boundary conditions. The temperature field is applied by holding the bottom surface temperature at constant temperature Tm = 300 K, while the top surface temperature is held at Tc = 600 K. The non-dimensional frequency decreases nonlinearly with the power-law index (n) increase. Due to the fact that Young’s modulus of the ceramic material is higher than that of the metallic material, the non-dimensional frequency becomes highly sensitive to the power-law index (n) minor variation.

Figure 16 shows the effect of porosity factor (a) on the free vibration of the FG cylindrical panel. Generally, the increasing of the porosity factor decreases the non-dimensional frequency. It can be noticed that the non-dimensional frequency decreases proportionally to the porosity factor increase. Furthermore, one can notice that taking the material properties as temperature dependent can have a significant outcome on the overall vibration response, especially in high-temperature environments.

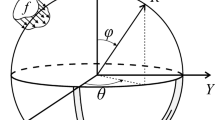
5.3 Spherical cap shell

In this example, the clamped spherical cap shown in Fig. 17 is studied. At first we assessed the free vibration response of an isotropic clamped spherical cap reported in the literature [29]. Material and geometric properties of the spherical shell are taken as R = 1 m, h = 0.05 m, E = 211 GPa, ρ = 7800 kg/m3, and v = 0.3. The spherical cap is modelled using the mesh shown in Fig. 17.

Fig. 17
figure 17

Geometry and mesh of the spherical cap

Full size image

The free vibration response of the isotropic clamped spherical cap shell is represented by the non-dimensional frequency \(\omega^{ * } = \omega \, R \, \sqrt {{\rho \mathord{\left/ {\vphantom {\rho E}} \right. \kern-\nulldelimiterspace} E}}\) for the first four modes of vibration listed in Table 7 fort two angles disposition (θ = 45°, 60°). Note that the number in brackets (m, n) indicates the vibration mode, with m being the number of half-waves along the generatrix, and n is the circumferential wave number.

The present results are found to be in good agreement with those reported by [29], and the difference between the results at the second and the third mode is due to the different solution strategies used in the studies. The corresponding modes shapes of the first four natural frequencies of the clamped spherical shells (θ = 45°) are illustrated in Fig. 18.

Fig. 18
figure 18

The first four mode shapes of an isotropic clamped spherical cap shell (θ = 45°)

Full size image

However, no results are available in the literature concerning free vibration analysis of an FGM porous spherical cap shell in thermal environments. We investigated the free vibration response of an FGM porous spherical cap (θ = 45°) under different thermal fields. Two different material mixtures are considered, the first one is the (ZrO2/Ti-6Al-4V), and the second one is the (Si3N4/SUS304). The materials′ mechanical and thermo-physical properties are taken as temperature-dependent. Two cases of boundary conditions are also considered: Hinged BC (hhhh): u = v = w = 0 at H = 0 and clamped BC (cccc) at H = 0 all d.o.fs = 0. For convenience, the dimensionless frequency is defined by \(\omega^{ * } = \omega \, R \, \sqrt {{{\rho_{c} } \mathord{\left/ {\vphantom {{\rho_{c} } {E_{c} }}} \right. \kern-\nulldelimiterspace} {E_{c} }}}\) where \(E_{c}\) and \(\rho_{c}\) are the reference values at T0 = 300 K. Figures 19, 20, and 21 show the variation of the first dimensionless frequency ω* of a hinged and clamped FGM spherical cap as function of temperature fields, power-law index (n), and porosity coefficient (a), respectively.

Fig. 19
figure 19

Non-dimensional frequency variation versus temperature (Tc) of FGM spherical cap: a hinged, b clamped

Full size image
Fig. 20
figure 20

Non-dimensional frequency variation versus power-law index (n) of FGM spherical cap: a hinged, b clamped

Full size image
Fig. 21
figure 21

Non-dimensional frequency variation versus porosity coefficients a of FGM spherical cap: a hinged, b clamped

Full size image

Based on the obtained results, it can be seen that the increase in temperature gradient, power-law index (n) or the porosity (a) leads to a decrease in natural frequencies; however, the temperature dependency of materials' properties can have considerable consequences on the free vibration response of the spherical cap. Moreover, the natural frequencies decrease proportionally with the increase in porosity. This behaviour matches the porosity contribution in the rule of mixture of Eq. (7). Meanwhile, the decrease of the natural frequencies with the increase of the power-law index is highly nonlinear. This correlation follows the power-law index contribution in the rule of mixture of Eq. (7). It can also be seen that this behaviour is exhibited in the investigated plate, cylindrical and spherical shell.

The effect of radius to thickness ratio (R/h) on the dimensionless frequency ω* of hinged and clamped FGM porous spherical caps is investigated and depicted in Fig. 22. Note that: n = 2, Tm = 300 K, Tc = 600 K, and a = 0.4. It is observed that the dimensionless frequency decreases dramatically when the ratio (R/h) increases. We can also observe that when the ratio (R/h) increases from 5 to 25, at the beginning, the dimensionless frequency decreases quickly, and the rate becomes gentler with further increase of the radius to thickness ratio (R/h). This means that the rising of the curvature of the shell causes a decrease in the stiffness, which causes a rapid decrease of the dimensionless frequency of the spherical cap. Moreover, the FGM spherical shell behaves as a thin structure with low rigidity, and the natural frequencies become hence as steady-state motion.

Fig. 22
figure 22

Variation of non-dimensional frequency of FGM porous spherical cap with (R/h) ratio for hinged and clamped BCs

Full size image

6 Conclusions

In this paper, the free vibration response of functionally graded plate, cylindrical and spherical porous shells subjected to high-temperature field with temperature-dependent material properties has been investigated. The equation of motion is developed based on a curved 8-node degenerated shell element formulation using the principle of virtual work. Some convergence studies are provided to assess the effectiveness and accuracy of the present formulation. The numerical results show a significant impact of different sets of thermal environmental conditions, different values of volume fraction index (n), porosity coefficients (a), radius to thickness ratio (R/h), and boundary conditions on the dimensionless frequency ω* of FGM cylindrical and spherical shells. It is shown that considering the material properties as temperature dependent has a significant consequence on the vibration response of FGM shells. It is shown that the influence of temperature on the effective material properties such as Young’s modulus and thermal expansion coefficient is non-negligible, especially at higher temperatures. Moreover, the effect of the porosity is more observable at high temperatures.