Free vibration analysis of a fluid-filled functionally graded spherical shell subjected to internal pressure

Abstract

An analytical solution is developed to study the free vibration of a thin functionally graded (FG) spherical shell under initial internal static pressure based on Love’s first approximation theory. A coupled vibro-acoustic analytical model is presented for spherical shells filled with compressible nonviscous fluid. The non-homogenous material properties are assumed to be graded according to a power-law distribution of the constituents through the shell thickness. By introducing a stress function, the reformulated coupled equations of motion of FG spherical shells under the influence of initial stresses are obtained. The wave equation is used to model the internal acoustic domain. The boundary conditions of continuity of fluid and shell velocities, as well as the normal pressure acting on the internal surface of the shell from the fluid are imposed. The frequency equation of the coupled system is obtained utilizing modal expansion along with the orthogonality properties of the mode shapes. Exact solutions for the free vibration of pressurized empty and fluid-filled shells are obtained in terms of products of trigonometric and Legendre functions in a spherical coordinate system. Numerical results are validated with the results of simple cases available in the literature as well as finite element modeling. Effects of different parameters including material constants, geometry, initial pressure and vibro-acoustic coupling on natural frequencies are studied. The presented analytical solution is an attempt to describe the vibrational behavior of FG pressurized fluid-filled spherical shells.

1 Introduction

Studying the vibrational characteristics of thin shells of different shapes and boundary conditions is one of the problems with numerous applications in engineering structures [1, 2]. Such structures can be subjected to a variety of static or dynamical loadings, such as internal or external fluids. Among these, free vibration of a pressurized elastic spherical shell is a problem that is applicable to many structures, such as spherical pressure vessels, sport balls, biological organs, airbags, and balloons. One possible application of such a study is a method for noninvasively monitoring pressure changes inside sealed containers [3, 4], intracranial pressure in human heads [5, 6], and intraocular pressure in the eye [7, 8]. The cross section of the head or eye resembles an engineering layered sphere in which material properties change through the thickness direction. In the following, a brief review on the most important papers regarding the vibration of fluid-filled spherical shells is presented.

Strutt and Rayleigh [9] were the first who studied the axisymmetric vibrations of a fluid enclosed in a rigid spherical shell. Extensional axisymmetric free vibrations of an isotropic elastic spherical shell were first solved by Lamb [10]. Then, Love [11] investigated the problem of free and forced vibrations of a spherical shell filled with an incompressible fluid based on the exact elasticity theory. Morse and Feshbach [12] presented the free vibration analysis of a fluid-filled spherical membrane. Rand and DiMaggio [13] treated the axisymmetric extensional vibrations of fluid‐filled isotropic spherical shells and obtained the analytic forms of frequency equations and mode shapes. In order to present a theoretical model of the human head, Engin and Liu [14] studied the axisymmetric torsionless vibration of a thin homogeneous fluid-filled spherical shell, including both membrane and bending effects. Kenner and Goldsmith [15] obtained the response of a spherical shell filled with a nonviscous compressible fluid under normal dynamic loading. Su [16] examined the effect of fluid viscosity on the axisymmetric vibrations of a fluid-filled spherical shell and observed a reduction in frequencies with the increase of viscosity. Zhang and Geers [17] used the Laplace transform and separation of variables method to solve the transient response of a fluid‐filled submerged thin spherical shell excited by a plane step wave. Chen and Ding [18] investigated the nonaxisymmetric natural vibration of a spherically isotropic spherical shell filled with a compressible inviscid fluid based on the three-dimensional elasticity. In a similar work, they studied the free vibration of a fluid-filled FG spherical shell [19] in which they did not take into account the effect of initial internal static pressure on natural frequencies. Hu et al. [20] investigated the axisymmetric vibrations of submerged piezoelectric sphere filled with viscous fluid and noted that the fluid inside the shell had a dominant effect on the vibrational behavior of the submerged shell. Piacsek et al. [3] conducted experiments on an aluminum spherical shell filled with either air or water subjected to static internal pressure and observed that resonance frequencies increase as the pressure increases. Fazelzadeh and Ghavanloo [21] studied the coupled axisymmetric oscillation of homogeneous spherical membrane shell filled with an inviscid fluid based on nonlocal elasticity theory. They observed that the natural frequencies change when the size effect is considered. El Baroudi et al. [22] presented analytical and numerical analyses of vibrational modes for the system of brain, cerebro-spinal fluid and skull in spherical coordinate. The influences of the cerebro-spinal fluid compressibility and thickness on natural frequencies were investigated. Tamadapu et al. [23] studied the axisymmetric vibrations of a submerged fluid-filled spherically isotropic thick microspherical shell with partial-slip interface condition. The influences of partial-slip, surface tension, spherical isotropy and density variation along the thickness on the resonance spectrum were examined. Kuo et al. [24] developed a model appropriate to free vibrations of an inflated balloon as an elastic spherical shell and considered the influence of skin tension due to initial pressure and the inertial effect of fluid. They presented analytical solution for the natural frequencies and compared the results with experimental ones. More recently, Eslaminejad et al. [4] used experimental modal analysis to study the effect of internal fluid pressure on the frequencies, damping ratio and mode shapes of an aluminum hemispherical shell filled with water.

In order to facilitate the solution procedure, there were always attempts to reformulate the governing equations (in terms of displacement field variables) into a reduced number of differential equations in terms of some potential functions. Gol’denveizer reduced the three governing equations of circular cylindrical shells within classical theory into one eighth-order equation in terms of some potential functions [25, 26]. Vlasov [27] introduced the governing equations of classical Donnell-Mushtari-Vlasov theory of thin shells of revolutions in terms of transverse deflection and stress function with total order of eight and extended the procedure into nonshallow spherical shells within Love’s first approximation theory [1, 28]. Here, the procedure will be extended to motion equations of FG spherical shells with initial stress and filled with fluid which facilitates the solution procedure greatly. Recently, Fallah et al. [28, 29] reformulated the governing equations of FG and multilayered cylindrical shells [28] as well as sandwich circular plates [29] within first-order shear deformation theory with total order of ten into three equations in terms of transverse displacement, stress function and a boundary-layer function. It is worth mentioning that another procedure for decoupling the governing equations of FG and composite structures may be to introduce the concept of physical neutral surface through the thickness of structure so that the stretching-bending coupling will disappear [30, 31].

The above review indicates that while there are number of researchers who have studied the vibrational characteristics of fluid-filled spherical shells, there exists no analytic solution on the free vibration of a thin FG spherical shell filled with compressible inviscid fluid and subjected to initial internal pressure. In the present paper, based on the Love’s first approximation theory and introduction of a stress function, the coupled equations of motion for a pressurized FG spherical shell are reformulated. The motion of compressible inviscid fluid contained within the spherical shell and the fluid–solid interaction are taken into account. The exact solution for frequency equation and mode shapes are derived in terms of trigonometric and Legendre functions. Finally, the effects of material distribution, shell geometry, initial internal pressure and internal acoustic wave on membrane and bending natural frequencies are studied. The analytical formulation and frequency results presented here can serve as a benchmark for various approximate theories or numerical approaches.

2 Formulation

2.1 Governing equations

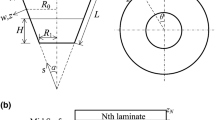
Consider a thin FG spherical shell of uniform thickness $h$ and radius $R$, described in a spherical coordinate system $\left( {r,\varphi ,\theta } \right)$ as shown in Fig. 1. The FG material is modelled as a non-homogenous isotropic linear elastic material whose properties vary continuously through the thickness of the shell as a function of the volume fraction and properties of the constituents as follows:

(1)

where $g$ is the power-law index and the subscripts $m$ and $c$ indicate metal and ceramic, respectively. Also, $z$ is the distance measured along the outward normal to the middle surface (see Fig. 1). Equation (1) is used as a model for the effective Young's modulus (E) and mass density ($\rho$). Here, it is assumed that Poisson’s ratio ($\nu$) is constant through the shell thickness. It is worth mentioning that the following formulation is applicable to any distribution of Young's modulus and mass density through the shell thickness and their distribution may be assumed to be different from each other according to different laws. Based on Love’s first approximation theory, the shell displacement field is given as [1]:

$$\begin{aligned} & U_{\varphi } \left( {\varphi ,\theta ,z,t} \right) = u_{\varphi } \left( {\varphi ,\theta ,t} \right) + z \beta_{\varphi } \left( {\varphi ,\theta ,t} \right), \\ & U_{\theta } \left( {\varphi ,\theta ,z,t} \right) = u_{\theta } \left( {\varphi ,\theta ,t} \right) + z \beta_{\theta } \left( {\varphi ,\theta ,t} \right), \\ & U_{z} \left( {\varphi ,\theta ,z,t} \right) = w\left( {\varphi ,\theta ,t} \right), \\ \end{aligned}$$

(2)

where $u_{\varphi }$, $u_{\theta }$, and $w$ are the in-plane and transverse displacements of a point on the middle surface of the shell. In addition, $\beta_{\varphi }$ and $\beta_{\theta }$ represent rotation functions. Assumption of neglecting transverse shear deformation leads to:

$$\begin{aligned} & \beta_{\varphi } = \frac{1}{R}\left( {u_{\varphi } - \frac{\partial w}{{\partial \varphi }}} \right), \\ & \beta_{\theta } = \frac{1}{R}\left( {u_{\theta } - \frac{1}{\sin \varphi }\frac{\partial w}{{\partial \theta }}} \right). \\ \end{aligned}$$

(3)

Fig. 1

Geometry of FG spherical shell, its loading and the coordinate system

Using Love’s strain–displacement relations of elasticity [1], the nonzero components of strain are found to be as follows:

$$\begin{aligned} & \varepsilon_{\varphi } = \varepsilon_{\varphi }^{0} + zk_{\varphi } , \\ & \varepsilon_{\theta } = \varepsilon_{\theta }^{0} + zk_{\theta } , \\ & \varepsilon_{\varphi \theta } = \varepsilon_{\varphi \theta }^{0} + zk_{\varphi \theta } , \\ \end{aligned}$$

(4)

where the membrane normal and shear strains ($\varepsilon_{\varphi }^{0} ,\varepsilon_{\theta }^{0} ,\varepsilon_{\varphi \theta }^{0}$) as well as the changes in bending and twisting curvatures ($k_{\varphi } ,k_{\theta } ,k_{\varphi \theta }$) are:

$$\begin{aligned} & \varepsilon_{\varphi }^{0} = \frac{1}{R}\left( {\frac{{\partial u_{\varphi } }}{\partial \varphi } + w} \right), \\ & \varepsilon_{\theta }^{0} = \frac{1}{R}\left( {\frac{1}{\sin \varphi }\frac{{\partial u_{\theta } }}{\partial \theta } + \cot \varphi u_{\varphi } + w} \right), \\ & \varepsilon_{\varphi \theta }^{0} = \frac{1}{R}\left( {\frac{{\partial u_{\theta } }}{\partial \varphi } - \cot \varphi u_{\theta } + \frac{1}{\sin \varphi }\frac{{\partial u_{\varphi } }}{\partial \theta }} \right), \\ \end{aligned}$$

(5)

$$\begin{aligned} & k_{\varphi } = k_{\varphi }^{0} + \varepsilon_{\varphi }^{0} /R, \\ & k_{\theta } = k_{\theta }^{0} + \varepsilon_{\theta }^{0} /R, \\ & k_{\varphi \theta } = k_{\varphi \theta }^{0} + \varepsilon_{\varphi \theta }^{0} /R, \\ \end{aligned}$$

(6)

$$\begin{aligned} & k_{\varphi }^{0} = - \frac{1}{{R^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial \varphi^{2} }} + w} \right), \\ & k_{\theta }^{0} = - \frac{1}{{R^{2} }}\left( {\frac{1}{{\sin^{2} \varphi }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} + \cot \varphi \frac{\partial w}{{\partial \varphi }} + w} \right), \\ & k_{\varphi \theta }^{0} = \frac{2}{{R^{2} \sin \varphi }}\left( {\cot \varphi \frac{\partial w}{{\partial \theta }} - \frac{{\partial^{2} w}}{\partial \varphi \partial \theta }} \right). \\ \end{aligned}$$

(7)

By using Hamilton’s principle and neglecting the transverse shear deformation and rotatory inertia, Love’s differential equations of motion under the influence of initial stresses are obtained [32]:

$$\frac{\partial }{\partial \varphi }\left( {\sin \varphi N_{\varphi } } \right) + \frac{{\partial N_{\varphi \theta } }}{\partial \theta } - \cos \varphi N_{\theta } + \sin \varphi Q_{\varphi } = \overline{\rho }hR\sin \varphi \frac{{\partial^{2} u_{\varphi } }}{{\partial t^{2} }},$$

(8a)

$$\frac{\partial }{\partial \varphi }\left( {\sin \varphi N_{\varphi \theta } } \right) + \frac{{\partial N_{\theta } }}{\partial \theta } + \cos \varphi N_{\varphi \theta } + \sin \varphi Q_{\theta } = \overline{\rho }hR\sin \varphi \frac{{\partial^{2} u_{\theta } }}{{\partial t^{2} }},$$

(8b)

$$\frac{\partial }{\partial \varphi }\left( {\sin \varphi Q_{\varphi } } \right) + \frac{{\partial Q_{\theta } }}{\partial \theta } - \sin \varphi \left( {N_{\varphi } + N_{\theta } } \right) + \frac{{\sin \varphi N^{r} }}{R}\nabla^{2} w = \overline{\rho }hR\sin \varphi \frac{{\partial^{2} w}}{{\partial t^{2} }} - qR\sin \varphi ,$$

(8c)

$$\begin{aligned} & R\sin \varphi Q_{\varphi } = \frac{\partial }{\partial \varphi }\left( {\sin \varphi M_{\varphi } } \right) + \frac{{\partial M_{\varphi \theta } }}{\partial \theta } - \cos \varphi M_{\theta } , \\ & R\sin \varphi Q_{\theta } = \frac{\partial }{\partial \varphi }\left( {\sin \varphi M_{\varphi \theta } } \right) + \frac{{\partial M_{\theta } }}{\partial \theta } + \cos \varphi M_{\varphi \theta } , \\ \end{aligned}$$

(9)

in which $Q_{\varphi }$ and $Q_{\theta }$ are transverse shear stress resultants, $q\left( {\varphi ,\theta ,t} \right)$ is the net external distributed load in normal direction, $N^{r} = PR/2$ for an spherical shell under uniform internal radial static pressure ($P$), $\overline{\rho } = \frac{1}{h}\mathop \smallint \limits_{ - h/2}^{h/2} \rho \left( z \right){\text{d}}z$, and $\nabla^{2} = \frac{1}{\sin \varphi }\frac{\partial }{\partial \varphi }\left( {\sin \varphi \frac{\partial }{\partial \varphi }} \right) + \frac{1}{{\sin^{2} \varphi }}\frac{{\partial^{2} }}{{\partial \theta^{2} }}.$ The membrane forces and bending moments in (8) and (9) are defined as follows:

$$\begin{aligned} & \left( {N_{\varphi } ,N_{\theta } ,N_{\varphi \theta } } \right) = \mathop \int \nolimits_{ - h/2}^{h/2} \left( {\sigma_{\varphi } ,\sigma_{\theta } ,\sigma_{\varphi \theta } } \right){\text{d}}z, \\ & \left( {M_{\varphi } ,M_{\theta } ,M_{\varphi \theta } } \right) = \mathop \int \nolimits_{ - h/2}^{h/2} \left( {\sigma_{\varphi } ,\sigma_{\theta } ,\sigma_{\varphi \theta } } \right)z{\text{d}}z. \\ \end{aligned}$$

(10)

Using the linear constitutive relations of an isotropic material, the membrane forces and bending moments of FG spherical shells are obtained:

$$\begin{aligned} & N_{\varphi } = A\left( {\varepsilon_{\varphi }^{0} + \nu \varepsilon_{\theta }^{0} } \right) + B\left( {k_{\varphi } + \nu k_{\theta } } \right), \\ & N_{\theta } = A\left( {\varepsilon_{\theta }^{0} + \nu \varepsilon_{\varphi }^{0} } \right) + B\left( {k_{\theta } + \nu k_{\varphi } } \right), \\ & N_{\varphi \theta } = \frac{{A\left( {1 - \nu } \right)}}{2}\varepsilon_{\varphi \theta }^{0} + \frac{{B\left( {1 - \nu } \right)}}{2}k_{\varphi \theta } , \\ \end{aligned}$$

(11)

$$\begin{aligned} & M_{\varphi } = B\left( {\varepsilon_{\varphi }^{0} + \nu \varepsilon_{\theta }^{0} } \right) + D\left( {k_{\varphi } + \nu k_{\theta } } \right), \\ & M_{\theta } = B\left( {\varepsilon_{\theta }^{0} + \nu \varepsilon_{\varphi }^{0} } \right) + D\left( {k_{\theta } + \nu k_{\varphi } } \right), \\ & M_{\varphi \theta } = \frac{{B\left( {1 - \nu } \right)}}{2}\varepsilon_{\varphi \theta }^{0} + \frac{{D\left( {1 - \nu } \right)}}{2}k_{\varphi \theta } , \\ \end{aligned}$$

(12)

where $\left( {A,B,D} \right) = \mathop \smallint \nolimits_{ - h/2}^{h/2} E\left( z \right)\left( {1,z,z^{2} } \right){\text{d}}z/\left( {1 - \nu^{2} } \right)$ are stiffness coefficients of the FG spherical shell. Substitution of relations (6) into (11) leads to:

$$\begin{aligned} & N_{\varphi } = \left( {A + B/R} \right)\left( {\varepsilon_{\varphi }^{0} + \nu \varepsilon_{\theta }^{0} } \right) + B\left( {k_{\varphi }^{0} + \nu k_{\theta }^{0} } \right), \\ & N_{\theta } = \left( {A + B/R} \right)\left( {\varepsilon_{\theta }^{0} + \nu \varepsilon_{\varphi }^{0} } \right) + B\left( {k_{\theta }^{0} + \nu k_{\varphi }^{0} } \right), \\ & N_{\varphi \theta } = \frac{{\left( {A + B/R} \right)\left( {1 - \nu } \right)}}{2}\varepsilon_{\varphi \theta }^{0} + \frac{{B\left( {1 - \nu } \right)}}{2}k_{\varphi \theta }^{0} . \\ \end{aligned}$$

(13)

By introducing relations (6) and (13) into (12) we have:

$$\begin{aligned} & M_{\varphi } = \overline{D}\left( {k_{\varphi }^{0} + \nu k_{\theta }^{0} } \right) + \frac{R}{\xi }N_{\varphi } , \\ & M_{\theta } = \overline{D}\left( {k_{\theta }^{0} + \nu k_{\varphi }^{0} } \right) + \frac{R}{\xi }N_{\theta } , \\ & M_{\varphi \theta } = \frac{{\overline{D}\left( {1 - \nu } \right)}}{2}k_{\varphi \theta }^{0} + \frac{R}{\xi }N_{\varphi \theta } , \\ \end{aligned}$$

(14)

in which $\overline{D} = D - BR/\xi$ and $\xi = R\left( {B + AR} \right)/\left( {D + BR} \right)$. Upon substitution of the relations (14) into the moment equation (9), and using the first two equations of motion (8a) and (8b), the transverse shear stress resultants are found as follows:

$$\begin{aligned} & Q_{\varphi } \left( {1 + \frac{1}{\xi }} \right) = - \frac{{\overline{D}}}{{R^{3} }}\frac{\partial }{\partial \varphi }\left( {\nabla^{2} w + 2w} \right) + \frac{{\overline{\rho }hR}}{\xi }\frac{{\partial^{2} u_{\varphi } }}{{\partial t^{2} }}, \\ & Q_{\theta } \left( {1 + \frac{1}{\xi }} \right) = - \frac{{\overline{D}}}{{R^{3} }}\frac{1}{\sin \varphi }\frac{\partial }{\partial \theta }\left( {\nabla^{2} w + 2w} \right) + \frac{{\overline{\rho }hR}}{\xi }\frac{{\partial^{2} u_{\theta } }}{{\partial t^{2} }}. \\ \end{aligned}$$

(15)

In the following, we consider the fact that $\xi$ is a very large number for a thin spherical shell and assume $\left( {1 + \xi } \right) \approx \xi$ (see Fig. 5). For a homogenous isotropic spherical shell ($B=0,$$A=Eh/(1-\nu^2) \ {\text{and}} \ D=Eh^3/12(1-\nu^2 )$), we have $\xi = 12R^{2} /h^{2}$. Now, we introduce a stress function $F\left( {\varphi ,\theta ,t} \right)$ through the following relations [1]:

$$\begin{aligned} & N_{\varphi } = \frac{1}{{R^{2} }}\left( {\frac{1}{{\sin^{2} \varphi }}\frac{{\partial^{2} F}}{{\partial \theta^{2} }} + \cot \varphi \frac{\partial F}{{\partial \varphi }} + F - \frac{{\overline{\rho }R^{2} \left( {1 + \nu } \right)}}{{\overline{E}}}\frac{{\partial^{2} F}}{{\partial t^{2} }} + \frac{{\overline{D}}}{R}\left( {\nabla^{2} w + 2w} \right)} \right), \\ & N_{\theta } = \frac{1}{{R^{2} }}\left( {\frac{{\partial^{2} F}}{{\partial \varphi^{2} }} + F - \frac{{\overline{\rho }R^{2} \left( {1 + \nu } \right)}}{{\overline{E}}}\frac{{\partial^{2} F}}{{\partial t^{2} }} + \frac{{\overline{D}}}{R}\left( {\nabla^{2} w + 2w} \right)} \right), \\ & N_{\varphi \theta } = \frac{1}{{R^{2} }}\left( {\frac{\cos \varphi }{{\sin^{2} \varphi }}\frac{\partial F}{{\partial \theta }} - \frac{1}{\sin \varphi }\frac{{\partial^{2} F}}{\partial \varphi \partial \theta }} \right), \\ \end{aligned}$$

(16)

where $\overline{E} = \mathop \smallint \nolimits_{ - h/2}^{h/2} E\left( z \right){\text{d}}z/h$. By substituting relations (16) into Eqs. (8a) and (8b), also using the transverse shear stress resultants in relations (15), the terms containing the effect of tangential inertia are obtained as:

$$\begin{aligned} & \overline{\rho }hR\frac{{\partial^{2} u_{\varphi } }}{{\partial t^{2} }} = - \frac{{\overline{\rho }\left( {1 + \nu } \right)}}{{\overline{E}}}\frac{\partial }{\partial \varphi }\left( {\frac{{\partial^{2} F}}{{\partial t^{2} }}} \right), \\ & \overline{\rho }hR\frac{{\partial^{2} u_{\theta } }}{{\partial t^{2} }} = - \frac{{\overline{\rho }\left( {1 + \nu } \right)}}{{\overline{E}}}\frac{1}{\sin \varphi }\frac{\partial }{\partial \theta }\left( {\frac{{\partial^{2} F}}{{\partial t^{2} }}} \right). \\ \end{aligned}$$

(17)

By substitution of relations (15), (16) and (17) into the third equation of equilibrium (8c) and carrying out some manipulations, the first reformulated differential equation of motion in terms of $w$ and $F$ is obtained as follows:

$$\frac{1}{{R^{2} }}\left( {\nabla^{2} F + 2F} \right) + \frac{{\overline{\rho }\left( {1 + \nu } \right)}}{{\overline{E}}}\left( {\frac{{\nabla^{2} }}{\xi } - 2} \right)\frac{{\partial^{2} F}}{{\partial t^{2} }} + \frac{{\overline{D}}}{{R^{3} }}\left( {\nabla^{2} + 2} \right)\left( {\nabla^{2} w + 2w} \right) + \overline{\rho }hR\frac{{\partial^{2} w}}{{\partial t^{2} }} - \frac{1}{R}N^{r} \nabla^{2} w = qR.$$

(18)

Next, we use the compatibility equation in spherical coordinates [1]:

$$\frac{\partial }{\partial \varphi }\left( {\sin^{2} \varphi \frac{{\partial \varepsilon_{\theta }^{0} }}{\partial \varphi }} \right) + \frac{{\partial^{2} \varepsilon_{\varphi }^{0} }}{{\partial \theta^{2} }} - \sin \varphi \cos \varphi \frac{{\partial \varepsilon_{\varphi }^{0} }}{\partial \varphi } + 2\sin^{2} \varphi \varepsilon_{\varphi }^{0} - \frac{{\sin^{2} \varphi }}{R}\left( {\nabla^{2} w + 2w} \right) = \frac{\partial }{\partial \varphi }\left( {\sin \varphi \frac{{\partial \varepsilon_{\varphi \theta }^{0} }}{\partial \theta }} \right).$$

(19)

The membrane strains are obtained from relations (13) in terms of membrane forces and transverse displacement as

$$\begin{aligned} & \varepsilon_{\varphi }^{0} = \frac{R}{{\left( {1 - \nu^{2} } \right)\left( {B + AR} \right)}}\left( {N_{\varphi } - \nu N_{\theta } } \right) - \frac{BR}{{B + AR}}k_{\varphi }^{0} , \\ & \varepsilon_{\theta }^{0} = \frac{R}{{\left( {1 - \nu^{2} } \right)\left( {B + AR} \right)}}\left( {N_{\theta } - \nu N_{\varphi } } \right) - \frac{BR}{{B + AR}}k_{\theta }^{0} , \\ & \varepsilon_{\varphi \theta }^{0} = \frac{2R}{{\left( {1 - \nu } \right)\left( {B + AR} \right)}}N_{\varphi \theta } - \frac{BR}{{B + AR}}k_{\varphi \theta }^{0} . \\ \end{aligned}$$

(20)

Upon substitution of the relations (20) into (19) as well as using Eqs. (7) and (16), the compatibility equation is rewritten as follows:

$$\frac{1}{{R^{2} }}\left[ {\nabla^{2} F + \left( {1 - \nu } \right)F} \right] - \frac{{\overline{\rho }\left( {1 - \nu^{2} } \right)}}{{\overline{E}}}\frac{{\partial^{2} F}}{{\partial t^{2} }} + \frac{{\overline{D}}}{{R^{3} }}\left( {1 - \nu } \right)\left( {\nabla^{2} w + 2w} \right) - \frac{{\overline{E}h}}{R}w = 0.$$

(21)

Therefore, the dynamic behavior of thin FG spherical shells under the influence of initial stresses (e.g. a pressurized shell) can be predicted by solving the coupled equations in (18) and (21).

2.2 Natural frequencies of pressurized FG spherical shells

Here, the frequency equations for pressurized FG spherical shells without considering the internal acoustic domain (the solution of equations in (18) and (21)) are obtained. By assumption of zero normal loading ($q = 0$) as well as $F = F^{*} \left( {\varphi ,\theta } \right)e^{i\omega t}$ and $w = w^{*} \left( {\varphi ,\theta } \right)e^{i\omega t}$ for time-harmonic vibrations, the differential equations of motion in (21) and (18) are reduced to

$$\begin{aligned} & \frac{{\nabla^{2} + 1 - \nu + \left( {1 - \nu^{2} } \right)\Omega^{2} }}{{R^{2} }}F^{*} + \left[ {\frac{{\overline{D}}}{{R^{3} }}\left( {1 - \nu } \right)\left( {\nabla^{2} + 2} \right) - \frac{{\overline{E}h}}{R}} \right]w^{*} = 0, \\ & \frac{{\nabla^{2} + 2 - \left( {1 - \nu^{2} } \right)\Omega^{2} \left( {\frac{{\nabla^{2} }}{\xi } - 2} \right)}}{{R^{2} }}F^{*} + \left[ {\frac{{\overline{D}}}{{R^{3} }}\left( {\nabla^{2} + 2} \right)\left( {\nabla^{2} + 2} \right) - \frac{{\overline{E}h}}{R}\Omega^{2} - \frac{{N^{r} }}{R}\nabla^{2} } \right]w^{*} = 0, \\ \end{aligned}$$

(22)

in which $\Omega^{2} = \overline{\rho }R^{2} \omega^{2} /\overline{E}$ is the square of normalized natural frequency and $\omega$ is the angular frequency. After some mathematical manipulations, Eqs. (22) are reduced to two sixth-order differential equations with the same form and coefficients governing the behavior of $F^{*}$ and $w^{*}$ as follows:

$$\begin{aligned} & \nabla^{6} \left\{ {\begin{array}{*{20}c} {w^{*} } \\ {F^{*} } \\ \end{array} } \right\} + c_{1} \nabla^{4} \left\{ {\begin{array}{*{20}c} {w^{*} } \\ {F^{*} } \\ \end{array} } \right\} + c_{2} \nabla^{2} \left\{ {\begin{array}{*{20}c} {w^{*} } \\ {F^{*} } \\ \end{array} } \right\} + c_{3} \left\{ {\begin{array}{*{20}c} {w^{*} } \\ {F^{*} } \\ \end{array} } \right\} = 0, \\ & c_{1} = 4 + \left( {1 - \nu^{2} } \right)\Omega^{2} - \frac{{R^{2} }}{{\overline{D}}}N^{r} , \\ & c_{2} = \frac{{R^{2} }}{{\overline{D}}}\left\{ {\overline{E}h\left( {1 - \Omega^{2} } \right) - N^{r} \left[ {1 - \nu + \left( {1 - \nu^{2} } \right)\Omega^{2} } \right]} \right\}, \\ & c_{3} = \frac{{\overline{E}hR^{2} }}{{\overline{D}}}\left\{ {2 + \Omega^{2} \left[ {1 + 3\nu - \left( {1 - \nu^{2} } \right)\Omega^{2} } \right]} \right\}. \\ \end{aligned}$$

(23)

In the following, the general solution for $w^{*}$ is presented and it is obvious that $F^{*}$ will have the same general solution. To this end, Eq. (23) is rewritten in the following form:

$$\left( {\nabla^{2} + \lambda_{1} } \right)\left( {\nabla^{2} + \lambda_{2} } \right)\left( {\nabla^{2} + \lambda_{3} } \right)w^{*} = 0,$$

(24)

where the parameters $\lambda_{\alpha } \left( {\alpha = 1,2,3} \right)$ satisfy the cubic equation

$$- \lambda^{3} + c_{1} \lambda^{2} - c_{2} \lambda + c_{3} = 0.$$

(25)

The general solution of (24) can be expressed as:

$$\begin{aligned} & w^{*} = \mathop \sum \limits_{\alpha = 1}^{3} w_{\alpha } , \\ & \left( {\nabla^{2} + \lambda_{\alpha } } \right)w_{\alpha } = 0,\,\,\alpha = 1,2,3 \\ \end{aligned}$$

(26)

The general solution of the differential equation in (26) in the spherical coordinate system can be written as [1]:

$$\begin{aligned} & w_{\alpha } = \mathop \sum \limits_{m = 0}^{\infty } \left[ {A_{\alpha m} P_{{\mu_{\alpha } }}^{m} \left( {\cos \varphi } \right) + B_{\alpha m} Q_{{\mu_{\alpha } }}^{m} \left( {\cos \varphi } \right)} \right]\left[ {{\text{C}}_{{\alpha {\text{m}}}} \cos \left( {m\theta } \right) + D_{\alpha m} \sin \left( {m\theta } \right)} \right], \\ & \lambda_{\alpha } = \mu_{\alpha } \left( {\mu_{\alpha } + 1} \right), \\ \end{aligned}$$

(27)

in which $A_{\alpha m} ,B_{\alpha m} ,C_{\alpha m} ,D_{\alpha m}$ are unknown coefficients, and $P_{{\mu_{\alpha } }}^{m} \left( {\cos \varphi } \right)$ and $Q_{{\mu_{\alpha } }}^{m} \left( {\cos \varphi } \right)$ denote the Legendre functions of first and second kinds of degree $\mu_{\alpha }$ and order $m$. Because the Legendre functions of the second kind are singular at $\varphi = 0$, the coefficients $B_{\alpha m}$ should be set to zero in relation (27), i.e., $B_{\alpha m} = 0$. Also, in order to have a valid solution, the Legendre functions $P_{{\mu_{\alpha } }}^{m}$ which are singular at $\varphi = \pi$, must be substituted by Legendre polynomials. Therefore, $\mu_{\alpha }$ must be an integer ($n = 0,1,2, \ldots$). Finally, the general solution becomes:

$$w^{*} = \mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{m = 0}^{n} w_{nm} ,$$

(28a)

$$w_{nm} = P_{n}^{m} \left( {\cos \varphi } \right)\left[ {{\text{C}}_{{{\text{nm}}}} \cos \left( {m\theta } \right) + D_{nm} \sin \left( {m\theta } \right)} \right],$$

(28b)

where $w_{nm}$ satisfies the relation

$$\nabla^{2} w_{nm} = - \lambda_{n} w_{nm} , \lambda_{n} = n\left( {n + 1} \right)$$

(28c)

and $P_{n}^{m} \left( {\cos \varphi } \right)$ denote the Legendre polynomials of degree $n$ and order $m$ [33]. Upon substitution of relation (28a) in (23) and utilizing the orthogonality properties of mode shapes presented in (28b), the frequency equations for vibration of FG spherical shells under initial stress are obtained:

$$\begin{aligned} & 2a\Omega_{1}^{2} = b - \sqrt {b^{2} - 4ac} ,\,\,2a\Omega_{2}^{2} = b + \sqrt {b^{2} - 4ac},\, \\ & a = 1 - \nu^{2} , \\ & b = 1 + 3\nu + \left( {1 + \frac{{1 - \nu^{2} }}{{\overline{E}h}}N^{r} } \right)\lambda_{n} + \frac{{\overline{D}\left( {1 - \nu^{2} } \right)}}{{\overline{E}hR^{2} }}\lambda_{n}^{2} , \\ & c = - 2 + \left( {1 - \frac{1 - \nu }{{\overline{E}h}}N^{r} } \right)\lambda_{n} - \frac{{\overline{D}}}{{\overline{E}hR^{2} }}\left( {4 - \frac{{R^{2} }}{{\overline{D}}}N^{r} } \right)\lambda_{n}^{2} + \frac{{\overline{D}}}{{\overline{E}hR^{2} }}\lambda_{n}^{3} . \\ \end{aligned}$$

(29)

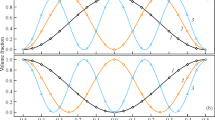
So, the natural frequencies arrange themselves into two branches, where the $\Omega_{1}$ branch is dominated by transverse motion and the $\Omega_{2}$ branch is dominated by in-plane motion (see Fig. 2).

Fig. 2

a The first six dominant bending mode shapes and b two dominant in-plane mode shapes for a homogenous spherical shell

2.3 Natural frequencies of Pressurized fluid-filled FG spherical shells: The coupled vibro-acoustic analytical model

The motion of the compressible inviscid fluid medium contained within the spherical shell of radius $R$ is governed by the following wave equation [34]:

$$\nabla^{2} \phi = \frac{1}{{c_{f}^{2} }}\frac{{\partial^{2} \phi }}{{\partial t^{2} }},\,\,{\mathbf{v}} = \nabla \phi ,\,\,p = - \rho_{f} \frac{\partial \phi }{{\partial t}},$$

(30)

where $c_{f}$ and $\rho_{f}$ are the speed of sound and the density of the fluid, $p$ is the acoustic pressure and $\phi \left( {\varphi ,\theta ,r,t} \right)$ is the acoustic velocity potential. The general solution of wave equation in spherical coordinate system may be written as [34]:

$$\phi = \mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{m = 0}^{n} \phi_{nm} e^{i\omega t} ,$$

(31a)

$$\phi_{nm} = j_{n} \left( {\frac{\omega }{{c_{f} }}r} \right)P_{n}^{m} \left( {\cos \varphi } \right)\left[ {A_{{{\text{nm}}}} \cos \left( {m\theta } \right) + B_{nm} \sin \left( {m\theta } \right)} \right],$$

(31b)

where $j_{n}$ is the spherical Bessel functions. The continuity of elastic shell’s velocity and fluid particles’ velocity, and the net normal force acting on the shell are as follows:

$$\frac{\partial w}{{\partial t}} = \frac{\partial \phi }{{\partial r}},$$

(32a)

$$q = - \rho_{f} \frac{\partial \phi }{{\partial t}} - f,$$

(32b)

where $f\left( {\varphi ,\theta ,t} \right)$ is the external distributed load (see Fig. 1). Now, the governing equations of motion in (18) and (21) while coupled with the internal acoustic domain through Eq. (32) are solved. To this end, the expansions of $w$ and $F$ in terms of the associated normal modes are considered as follows:

$$w = \mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{m = 0}^{n} w_{nm} e^{i\omega t} , F = \mathop \sum \limits_{n = 0}^{\infty } \mathop \sum \limits_{m = 0}^{n} F_{nm} e^{i\omega t} ,$$

(33a)

$$w_{nm} = P_{n}^{m} \left( {\cos \varphi } \right)\left[ {{\text{C}}_{{{\text{nm}}}} \cos \left( {m\theta } \right) + D_{nm} \sin \left( {m\theta } \right)} \right],$$

(33b)

$$F_{nm} = P_{n}^{m} \left( {\cos \varphi } \right)\left[ {G_{{{\text{nm}}}} \cos \left( {m\theta } \right) + H_{nm} \sin \left( {m\theta } \right)} \right].$$

(33c)

By direct substitution of expansions (31) and (33) into the continuity equation (32a), one gets

$$i\omega C_{nm} = A_{nm} \frac{\omega }{{c_{f} }}j_{n}^{^{\prime}} \left( {\frac{\omega }{{c_{f} }}R} \right), \,\,i\omega D_{nm} = B_{nm} \frac{\omega }{{c_{f} }}j_{n}^{^{\prime}} \left( {\frac{\omega }{{c_{f} }}R} \right).$$

(34)

By assumption of zero external load and introducing the relations (31), (32b) and (33) into the equations of motion (18) and (21), we obtain the same equations for the pairs ($G_{nm} , C_{nm} )\,{\text{and }}\left( {H_{nm} , D_{nm} } \right)$:

$$\begin{aligned} & \left[ {\frac{{ - \lambda_{n} + 1 - \nu }}{{R^{2} }} + \frac{{\overline{\rho }\left( {1 - \nu^{2} } \right)}}{{\overline{E}}}\omega^{2} } \right]G_{nm} + \left[ {\frac{{\overline{D}}}{{R^{3} }}\left( {1 - \nu } \right)\left( {2 - \lambda_{n} } \right) - \frac{{\overline{E}h}}{R}} \right]C_{nm} = 0, \\ & \left[ {\frac{{2 - \lambda_{n} }}{{R^{2} }} + \frac{{\overline{\rho }\left( {1 + \nu } \right)}}{E}\omega^{2} \left( {\frac{{\lambda_{n} }}{\xi } + 2} \right)} \right]G_{nm} \\ & \; + \left[ {\frac{{\overline{D}}}{{R^{3} }}\left( {2 - \lambda_{n} } \right)^{2} - \overline{\rho }hR\omega^{2} + \frac{{\lambda_{n} N^{r} }}{R} - \rho_{f} R\omega c_{f} \frac{{j_{n} \left( {\frac{\omega }{{c_{f} }}R} \right)}}{{j_{n}^{^{\prime}} \left( {\frac{\omega }{{c_{f} }}R} \right)}}} \right]C_{nm} = 0, \\ \end{aligned}$$

(35)

Finally the natural frequencies of the coupled system are calculated by setting the corresponding coefficient matrix of relations (35) equal to zero.

3 Numerical examples

Here, verification examples and case studies are presented. In Sect. 3.1, two verification examples for natural frequencies of homogenous and FG spherical shells are presented and compared with the existing ones in the literature. In Sect. 3.2, the effects of internal static pressure, geometrical parameters, fluid to solid wave velocity and density ratio on the dynamical behavior of fluid-filled homogenous shells are studied. In Sect. 3.3, FG spherical shells are considered and the effects of material gradient, initial internal pressure, vibro-acoustic coupling, and thickness to radius ratio on their natural frequencies are studied. For the purpose of numerical illustrations, the geometric and mechanical properties of homogenous and FG spherical shells as well as properties of internal fluid are considered as presented in Table 1. Due to lack of relevant studies on the subject, most parametric studies in Sects.3.2 and 3.2 are validated with the results of finite element modeling (ABAQUS [35]). It is to be noted that up to 2,400 eight-node doubly curved thin shell, reduced integration "S8R5" elements were used in the FE modeling of homogenous and FG spherical shells. Moreover, 15,200 20-node quadratic acoustic brick "AC3D20" elements were used in meshing of the fluid part.

Table 1 Geometric parameters and mechanical properties of homogenous and FG spherical shells as well as internal fluid

3.1 Verification examples

Here, two verification examples for natural frequencies of homogenous and FG spherical shells are presented and compared with the available results in the literature. In addition, it is to be emphasized that most parametric studies in Sects. 3.2 and 3.3 are validated with the results obtained through finite element modeling.

Example 1

The normalized natural frequencies ($\Omega_{1,2}^{2} = \overline{\rho }R^{2} \omega^{2} /\overline{E}$.) for a homogenous isotropic spherical shell (see Table 1) are obtained and compared with the results of Ref. [1] in Table 2. Excellent agreement is observed.

Table 2 Comparison of normalized natural frequencies of an isotropic homogenous spherical shell with the results of Ref. [1]

Example 2

An empty FG spherical shell of inner radius $a$ and outer radius $b$ is considered. The material properties are assumed to vary in radial direction according to a power law $E = E_{0} \left( {r/b} \right)^{\eta }$, $\rho = \rho_{0} \left( {r/b} \right)^{\eta }$ as defined in Ref. [36] and Poisson’s ratio is considered to be constant through the shl thickness. In Ref. [36] the axisymmetric radial free vibration of hollow FG sphere is investigated using 3D elasticity theory. Table 3 compares the dimensionless breathing mode natural frequency, $\beta = a\omega \sqrt {\rho_{0} \left( {1 + \nu } \right)\left( {1 - 2\nu } \right)/E_{0} \left( {1 - \nu } \right)}$, of functionally graded ($\eta = 5$) empty spheres ($b/a = 1.02, 1.05, 1.1$ and $1.25$) with the results of Ref. [36]. It is to be noted that the vibration analysis in [36] is based on 3D elasticity theory while the present formulation is based on the classical shell theory. The results of present study for thin shells ($b/a = 1.02, 1.05)$ are in good agreement with the ones reported in [36]. As the shell becomes thicker, the difference between the results increases.

Table 3 Comparison of normalized breathing mode frequencies of functionally graded empty sphere with the results of Ref. [36]

3.2 Dynamical behavior of homogenous shells

In order to study the effect of initial membrane stresses on natural frequencies of spherical shells, a thin spherical steel shell with geometric parameters and mechanical properties as given in Table 1, under different values of initial stress ($N^{r} = 0, 2, 10 \,{\text{MN}}/{\text{m}}$) is considered. Table 4 presents the lowest normalized eigenfrequencies ($\Omega_{1,2}^{2} = \overline{\rho }R^{2} \omega^{2} /\overline{E}$) obtained via the present analytical study and the FEM modeling. Good agreement is seen to exist between the results. Also, the corresponding mode shapes of dominant bending and in-plane modes are illustrated in Figs. 2a and b, respectively. It can be seen that an increase in internal pressure is associated with an increase specially in bending vibrational natural frequencies ($\Omega_{1}$). Also, when the thickness to radius ratio becomes larger, the difference between the analytical and FEM results increases, due to the thin classical shell theory used in the formulation.

Table 4 Normalized natural frequencies of an isotropic homogenous spherical shell for different values of initial stress and thickness, along with FEM results

Figures 3a and b display the variations of bending normalized natural frequency ($\Omega_{1}$) versus the membrane stress ($N^{r}$) for homogenous spherical shells of thickness $h = 0.005{\text{ m}}$ and $h = 0.001{\text{ m}}$, respectively. As can be seen, a compressive membrane stress reduces the natural frequencies to zero at critical buckling loads, while a tensile membrane stress increases the natural frequencies. Additionally, the rate of change in magnitude of natural frequencies with respect to membrane stress is larger for a higher mode number ($n$).

Fig. 3

Variations of normalized bending natural frequency ($\Omega_{1}$) versus the membrane stress ($N^{r}$) for a homogenous spherical shell of thickness a $h = 0.005\,{\text{ m}}$ and b $h = 0.001\,{\text{ m}}$

Next, a homogenous spherical shell (see Table 1) is considered and supposed to be filled with water under internal pressure. Table 5 presents the analytical and FEM results of lowest normalized natural frequencies ($\Omega^{2} = \overline{\rho }R^{2} \omega^{2} /\overline{E}$) of homogenous fluid-filled spherical shells with different values of initial stress $\left( {N^{r} = 0, 2, 10 {\text{MN}}/{\text{m}}} \right)$. It can be seen that the natural frequencies obtained through the solution of coupled system of equations have a great accuracy when compared with the FEM results. Compared with the results presented in Table 4, it is observed that the natural frequencies of fluid-filled shells are smaller than those of empty ones. It is also observed that as the shell becomes thinner, the effect of vibro-acoustic coupling on natural frequencies increases. This effect reduces for higher mode numbers ($n$) as the bending becomes dominant.

Table 5 Comparison of normalized natural frequencies of a homogenous spherical shell filled with water with the results of FEM for different values of initial stress and thickness

Furthermore, Fig. 4 illustrates the variations of normalized natural frequency ($\Omega$) of homogenous spherical shells with the ratio of fluid to solid wave velocities ($c_{f} /c_{s}$), where $c_{s} = \sqrt {E/2\left( {1 + \nu } \right) }$. Two different values of density ratio ($\rho_{f} /\rho = 0.1, 0.5$) and shell thickness $h = 0.005{\text{ m}}$ and $h = 0.001{\text{ m}}$ are considered. It is observed that an increase in fluid to solid wave velocity ratio is associated with an increase in all natural frequencies and except for the breathing mode ($n = 0$) whose corresponding frequency grows unboundedly, all other frequencies converge to specific values. In addition, for higher fluid to solid density ratio, the effect of fluid on the dynamic behavior of coupled system is dominant and the frequency convergence happens in lower velocity ratios. Also, normalized natural frequencies decrease for higher density ratios (due to the added inertia effect) and lower shell thickness.

Fig. 4

Variations of normalized natural frequency ($\Omega$) versus the ratio of fluid to solid wave velocities ($c_{f} /c_{s}$) for a homogenous spherical shell of thickness $h = 0.005{\text{ m}}$ and $h = 0.001{\text{ m}}$, and density ratios of $\rho_{f} /\rho = 0.1, 0.5$

3.3 Dynamical behavior of FG shells

In the remaining, FG spherical shells are considered and the effects of material gradient, initial internal pressure, vibro-acoustic coupling, and thickness to radius ratio on their natural frequencies are studied. To this end, thin spherical aluminum–alumina shells with geometric parameters and mechanical properties as given in Table 1, under different values of initial stress ($N^{r} = 0, 2, 10 {\text{MN}}/{\text{m}}$) are considered.

The results obtained through analytical solution for normalized natural frequencies ($\Omega_{1,2}^{2} = \overline{\rho }R^{2} \omega^{2} /\overline{E}$) of FG spherical shells with power-law index, $g = 3,$ and different values of initial stress and thickness are presented in Table 6 and are compared with the results of FEM modeling. The results are in good agreement. As explained before, the difference of analytical and FEM results increases for larger thickness to radius ratios and an increase in internal pressure is associated with an increase in bending vibrational natural frequencies ($\Omega_{1}$). In order to model through-the-thickness variations of mechanical properties of FGM in ABAQUS, the FG shell is considered to be laminated with10 sub-layers.

Table 6 Normalized natural frequencies of functionally graded spherical shell $\left( {g = 3} \right)$ for different values of initial stress and thickness, along with FEM results

Figure 5 shows the variations of non-dimensional parameter $\xi$ with power-law index $g$ for FG spherical shells of radius $R = 0.1 {\text{m}}$ and thickness $h = 0.005{\text{ m}}$ as well as $h = 0.001{\text{ m}}$. This parameter is considered to be large and assumed that $\left( {1 + \xi } \right) \approx \xi$ in relations (15). Figure 4 shows the correctness of this assumption. Moreover, it can be seen that parameter $\xi$ has a maximum value when material is homogenous and has a minimum value when the power-law index is near to $g = 1$.

Fig. 5

Variations of non-dimensional parameter $\xi$ of FG spherical shell of thickness $h = 0.005{\text{ m}}$ and $h = 0.001{\text{ m}}$ with power-law index $g$

Figure 6a presents the variations of normalized bending natural frequencies ($\Omega_{1}$) of FG spherical shells (see Table 1) with zero initial stress versus power-law index for the first nine bending mode shapes ($n = 2 \ldots 10)$. It can be observed that the variations in normalized natural frequencies with power-law index are more pronounced for higher mode numbers for which the effect of bending is dominant (see Fig. 2). The results for mode numbers $n = 2$ and $n = 10$ are depicted in separate figures in Fig. 6b for the sake of clarification. It is observed that the natural frequencies of all modes of vibration have the same trend of variations with material power-law index and minimum normalized frequency occurs when power-law index is close to $g = 2$. Similarly, Fig. 7a shows the variations of first four dominant membrane natural frequencies ($\Omega_{2}$) versus power-law index. For more clarification, the results are also depicted in separate figures in Figs. 7b. The trend of variations of all membrane normalized natural frequencies with power-law index is the same but the changes are small specially when compared with changes in bending natural frequencies in Fig. 6. So, it is concluded that material index has a considerable effect on dominant bending frequencies and this effect becomes more pronounced for higher mode numbers ($n$). The normalized membrane and bending natural frequencies of FG spherical shells of thickness $h = 0.005{\text{ m}}$ and $h = 0.001{\text{ m}}$, for different material constants ($g = 0.1, 1, 10$) are given in Table 7. It is observed that as the shell becomes thinner, the material constant has a smaller effect on normalized frequencies with the same trend of variations as discussed in Figs. 6 and 7.

Fig. 6

a Variations of normalized bending natural frequencies ($\Omega_{1}$) of FG spherical shells ($R = 0.1 {\text{m}}, h = 0.005{\text{ m}}$) with zero initial stress versus power-law index for nine bending mode shapes ($n = 2 \ldots 10)$ and b repeated results for $n = 2, 10$

Fig. 7

a Variations of four dominant normalized membrane natural frequencies ($\Omega_{2}$) of FG spherical shells ($R = 0.1 \,{\text{m}}, h = 0.005\,{\text{ m}}$) with zero initial stress versus power-law index and b repeated results for $n = 0, 3$

Table 7 Normalized natural frequencies of functionally graded spherical shell for different values of material constant and thickness

Finally, Table 8 provides analytical results for natural frequencies of FG fluid-filled spherical shells (see Table 1) with power-law index ($g = 3$) under different values of internal pressure ($N^{r} = 0, 2, 10 \,{\text{MN}}/{\text{m}}$). The results of analytical vibro-acoustic model are also compared with the ones obtained through FEM modeling. As before, results are in good agreement. As expected, the natural frequencies increase for a thicker shell and for higher values of internal pressure. Also, compared with the results presented in Table 6, the natural frequencies of pressurized fluid-filled shells are smaller than those of pressurized empty shells.

Table 8 Comparison of normalized natural frequencies of a functionally graded spherical shell $\left( {g = 3} \right)$ filled with water, for different values of initial stress and thickness with the results of FEM

4 Conclusions

In the present work, the vibration of a thin spherical FG shell under internal pressure is revisited using the Love’s first approximation theory. Also, a coupled vibro-acoustic analytical solution is given for a fluid-filled pressurized FG spherical shell. Coupled governing equations of motion are reformulated by introduction of stress function. This reformulation conveniently makes it possible to present exact solution in terms of product of trigonometric and Legendre functions. The results of the present analytical solution are validated with the ones available in the literature and the results of FEM modeling. The current study confirms that the flexural dynamic characteristics of spherical FG shells are notably influenced by initial membrane stress and material distribution. In particular, it is observed that.

• Higher mode number frequencies have greater rate of change with respect to initial membrane stress.

• Natural frequencies decrease when the pressurized spherical shell is filled with fluid and the internal acoustic domain is considered.

• Normalized natural frequencies increase when the fluid to solid wave velocity ratio increases.

• FG material index has a considerable effect on dominant bending frequencies and this effect becomes more pronounced for higher mode numbers. The minimum normalized frequency of different mode shapes occurs around $g = 2$.