1 Introduction

Dispersed droplets can be generated, transported, sorted, merged, and manipulated, in the microfluidic channel [1,2,3,4]. A fundamental physical understanding of droplet deformation, [5,6,7,8], droplet breakup [9, 10], and droplet coalescence [11,12,13] are essential subjects for development of rheological and drug delivery models.

Droplet coalescence in a microfluidic channel has been experimentally and numerically studied in recent years. Wasan et al. were the first researchers who studied the droplet coalescence in enhanced oil recovery [14]. When two or more droplets approach to each other, the liquid film between droplets forms thinner by squeezing at the plateau border. The thinning rate of liquid film strongly depends on the capillary pressure and disjoining pressure [15, 16]. The thickness of liquid film is estimated by the ratio of interfacial tension and viscous force [17]. Droplet coalescence by geometrically mediated flow in microchannel has been experimentally studied by Tan et al. [18]. They have found three different types of droplet fusion regimes. Reichert and Walker have experimentally studied the coalescence dynamics of oil coated in irreversibly adsorbed surfactant layers [19]. They have suggested two types of coalescence behavior including fast coalescence at low surface coverage and slow coalescence at high surface coverage. The effect of droplet size and surfactant concentration on the coalescence stability have been experimentally studied by Politova et al. [20]. They have investigated the relation between the surfactant concentration and droplet lifetime. By using the micofluidic method, Dudek et al. have measured the coalescence time and coalescence angle. They have found that the increase of salinity decreases the coalescence time [21].

Motivated by recent experimental work [22], Williams et al. have studied the population balance modeling to predict the droplet coalescence kinetics of oil-in-water emulsions [23]. They have investigated the effect of droplet size, droplet volume fraction, and viscosity ratio on the coalescence kinetics of oil-in-water emulsions. Coalescence and conjunction of two bubbles at low Reynolds number have been numerically and experimentally by Feng et al. [24]. They have found two different coalescence regimes listing no conjunct coalescence which is divided into a contact stage and a drainage stage, and conjunct coalescence which has an extra conjunct stage.

The deformation and coalescence of droplets under electric and magnetic fields have been widely studied in the past two decades. Magnetocoalescence of ferrofluid droplets in a straight microchannel has been numerically studied by Kadivar [13]. His results indicate that the droplets elongate in the magnetic field direction. Huang et al. have experimentally and numerically studied coalescence dynamics of water droplets under a direct current electric field [25]. They have investigated the effect of viscosity ratio and electric capillary number on the coalescence of water droplets. The occurrence of different coalescence regimes is summarized in the phase diagrams.

The droplet dynamics including deformation [8, 26, 27], migration [28, 29], coalescence [13, 25], and breakup [30, 31] strongly depends on the channel geometry. T-junction, Y-junction, and sudden expansion channels are important types of microfluidic channels. The effect of droplet size and flow rate ratio on the droplet coalescence in T-junction microchannel has been experimentally studied by Christopher et al. [32]. They have investigated the effect of droplet velocity on droplet coalescence. Their results indicate that the droplet velocity is an important parameter in the coalescence behavior. Three regimes of coalescence dynamics in T-junction channels have been reported by Yang et al. [33]. They have studied the effect of viscosity ratio and liquid velocity on the coalescence dynamics. The effect of Y-junction angle on the coalescence dynamics in microchannel have been experimentally studied by Liu et al [34]. They have reported a critical capillary number for each value of bifurcation angle which droplet–droplet coalescence occurs. Droplet deformation and droplet coalescence in the sudden expansion microchannel have been experimentally and numerically investigated. Brosseau et al. have used expansion channel to measure the surfactant adsorption dynamics by measuring droplet deformation [35]. Kadivar and Farrokhbin have numerically studied deformation and relaxation of a droplet flowing through a sudden expansion channel [36].

The incompressible Newtonian flow in a symmetric plane sudden expansion is an interesting subject. The sudden expansion channel geometry is relatively simple. However, the resulting flow is very complex and it depends on control parameters such as the inlet boundary conditions, the Reynolds number and Deborah number, and the expansion ratio. This channel geometry is widely used in the microfluidic devices. For example, Brosseau et. al. have investigated the surfactant adsorption kinetics via interfacial tensiometry in a series of sudden expansion channels [35]. Droplet coalescence and self-assembly of droplets in sudden expansion microchannel have been experimentally studied by Schirrmann et. al [37]. Their experimental results indicate that the droplet coalescence at sudden expansion channel depends on the droplet length, droplet–droplet distance, and droplet velocity. Ferrás et. al. have studied the effect of slip boundary conditions for Newtonian and viscoelastic fluids in a sudden expansion channel. They have investigated the effect of slip coefficient on the streamline and flow type in the 1:4 expansion channel [38].

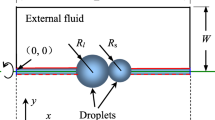
In this work, a numerically study of coalescence dynamics of monodisperse emulsion droplets flow through a sudden expansion microchannel is presented. Figure 1 presents the geometry considered in this work. The microchannel consists a straight channel of width \(W_1\), which suddenly expands symmetrically with right angles to a wide long channel of width \(W_2\) (\(W_1<W_2)\). In this study, we consider a two-phase flow which consists of two fluids separated by an interface. We assume that a flow past two-dimensional droplet containing a droplet phase labeled, 2, and suspended in continuous phase labeled, 1. Viscosity of continuous phase is \(\mu _1\) and viscosity of droplet phase is \( \mu _2\). In this work, we apply Brinkman equation to describe the droplets motion in the two-dimensional flow. By Using Green’s theorem, we convert the Brinkman partial differential equation to boundary integral equation and solved them by applying the boundary element method. Finally the dynamics of droplet coalescence is discussed as function of droplet–droplet distance, droplet size, viscosity ratio, capillary number, and channel width ratio.

Fig. 1
figure 1

Sketch of the microfluidic channel considered. The width of inlet and outlet channels are labeled by \(W_{1}\) and \(W_{2}\), respectively

Full size image

This paper is structured as follows: In the following Sect. 2, we will formulate the Brinkman equation and boundary conditions for the velocity field and normal component of the stress tensor at the droplet-continuous phase interface as well as at the channel walls. The numerical implementation to solve the boundary integral representation equation for the velocity field as well as for local droplet velocity are also contained in Sect. 2.3. The results of our numerical solutions, including the dynamics of droplet coalescence, are reported in Sect. 3. Finally, in Sect. 4 we summarize our findings, conclude, and give an outlook on possible future work in this field.

2 Governing equations

In this study, the coalescence of deformable droplets in the sudden expansion microfluidic channel is investigated by using boundary integral equation of interface dynamics for the depth-averaged Brinkman equation. We consider a two-dimensional flow past deformable droplets containing a droplet phase called, 2, and suspended in carrier phase called, 1. Viscosity of carrier phase and droplet phase are labeled by \(\mu _1\) and \( \mu _2\), respectively. We also define viscosity of droplet phase to carrier phase by \(\mu =\mu _2/\mu _1\) The considered channel geometry consists a narrow straight channel of width \(W_1\), which suddenly expands symmetrically with right angles to a wide long channel of width \(W_2\) (\(W_1<W_2)\). Figure 1 illustrates the top view of our studied microfluidic channel.

In order to report our numerical results in dimensionless numbers, we divide all lengths by the length scale \(L_0=W_1\), traveling time by time scale \(T_0=\mu _1 W_1/\gamma \) (\(\gamma \) is interfacial tension), droplet velocity by velocity scale \(\gamma /\mu _1\). In this way, we use capillary number to describe the relative effect of viscous drag forces versus surface tension forces acting across the droplet surface.

In the Hele-Shaw limit where the ratio of channel width to channel height is much larger than one, the droplets are confined between the top and bottom channel walls. In the microfluidic channel, the flow rate is in the range of \(\mu l/\mathrm{min}\), the Reynolds number is usually smaller than one, and, hence, the fluidic resistance in the microfluidic channel is high. In the low Reynolds number limit, the nonlinear inertial terms are negligible. According to experimental observations and numerical studies [39,40,41,42], in the Hele-Shaw limit, the velocity field is almost constant in the channel width direction. In this direction, a deviation from the constant value in the vicinity of channel walls is observed. In the height direction, however, the flow velocity follows locally a Poiseuille profile. In the low Reynolds number limit, the dynamics of droplet motion can be described by either the Stokes equation or the Brinkman equation. The analytical solutions of three-dimensional Stokes equation and Brinkman equation in a narrow straight microchannel illustrate that the velocity profiles are not far from each other [41, 42]. Therefore, we apply the depth-averaged Brinkman equation instead of three-dimensional stokes equation. In this way, the flows of droplet phase and carrier phase are described by the Brinkman equation and the conversion of mass as the following equations [43]:

$$\begin{aligned} \varvec{\nabla }P^{(i)}= & {} \alpha _i (\varvec{\nabla }^2{\mathbf {V}}^{(i)}-k^2 {\mathbf {V}}^{(i)}) \quad \mathrm{on} \quad \Omega _i \quad \mathrm{with} \quad i \in \{ { 1},{ 2} \}, \end{aligned}$$
(1)
$$\begin{aligned} \varvec{\nabla }.{\mathbf {V}}^{(i)}= & {} 0 \quad \mathrm{on} \quad \Omega _i \quad \mathrm{with} \quad i \in \{ { 1},{ 2} \}, \end{aligned}$$
(2)

where P(x, y) is the dimensionless pressure, \({\mathbf {V}}\) is the depth averaged dimensionless velocity, \(k=\sqrt{12}/H\), and \(\alpha _i=\mu _i/\mu _1\).

2.1 Boundary conditions

2.1.1 On the droplet surface

The first boundary condition on the droplet surface is discontinuity of normal component of stress tensor across the droplet-continuous phase interface. The discontinuity condition on the normal stress at the two phase interface is given by [40]

$$\begin{aligned} {\varvec{\sigma }}{^{\mathbf {(2)}}{\mathbf {\cdot n}}-{\varvec{\sigma }}^{\mathbf {(1)}}}{\mathbf {\cdot n}}=\gamma \left( \frac{\pi }{4}\, \kappa _{\parallel }+\kappa _{\perp }\right) {\mathbf {n}}, \end{aligned}$$
(3)

where \(\varvec{\sigma }\) is stress tensor and \(\varvec{\sigma }\cdot {\mathbf {n}}\) is normal component of stress tensor, \(\gamma \) is surface tension, \({\mathbf {n}}\) is unit normal vector pointing from the interior of the droplet phase into the continuous phase, \(\kappa _{\parallel }\) is local curvature in-plane, and \(\kappa _{\perp }\) is curvature in the thin direction. The prefactor \(\pi /4\) corresponds to non-wetting condition at the top and bottom walls of the Hele-Shaw cell [44].

The second boundary condition on the droplet surface apples on the normal and tangential components of velocity. According to continuity equation, Eq. (2), there is no mass transfer through the two phase interface. Therefore, the normal and tangential components of fluid velocity is continuous across the droplet-continuous phase interface. This boundary condition reads

$$\begin{aligned} {\mathbf {V}}^{(1)}={\mathbf {V}}^{(2)}\ne 0 \quad \mathrm{on} \quad \Gamma _{{ 12}}~, \end{aligned}$$
(4)

where \(\Gamma _{{ 12}}\) is the two-dimensional droplet contour.

2.1.2 On the channel walls and inlet

On the channel walls, no-slip boundary condition is applied. According to the no-slip boundary condition, the normal and tangential components of the carrier velocity are zero on the channel walls.

Finally, we assume that the initial position of droplet is far the inlet. Hence, Darcy–Brinkman velocity of single phase is applied at the channel inlet [43]:

$$\begin{aligned} V_{in} ^{(1)} (y)=Ca\frac{\cosh (kW_1/2)-\cosh (ky)}{\cosh (kW_1/2)-1}, \end{aligned}$$
(5)

where Ca is the capillary number.

2.2 Integral representation

In order to investigate motion dynamics of microfluidic droplets, we compute the velocity components of the droplet interface including the \(V_x\) and \(V_y\) on the droplet surface. One way to obtain the relevant boundary data of the velocity field is to numerically compute a self-consistent integral equation for velocity field V on the liquid–liquid boundary as well as on the channel walls. Following the formulation of boundary integral equations [40, 45], the velocity field at point (\({\mathbf {r}}_0)\) that lies in the continuous fluid satisfies a self-consistent integral equation of the form

$$\begin{aligned} V_j ^{(1)}({\mathbf {r}}_0)= & {} \frac{1}{C_l} \oint _{\Gamma _{{ w}},\Gamma _{{ o}}} [V_i ^{(1)}({\mathbf {r}})T^B_{ijk} ({\mathbf {r}},{\mathbf {r}}_0)n_k- \sigma ^{(1)} n_i G^B _{ij}({\mathbf {r}},{\mathbf {r}}_0)] \mathrm{d}\ell \nonumber \\&+\frac{1}{C_l}\oint _{\Gamma _{{ 12}}} \left[ (\alpha _2-1) V_i ^{(1)} ({\mathbf {r}}) T^B _{ijk} ({\mathbf {r}},{\mathbf {r}}_0)n_k - \gamma \left( \frac{\pi }{4}\, \kappa _{\parallel }+\kappa _{\perp }\right) n_i G^B _{ij}({\mathbf {r}},{\mathbf {r}}_0)\right] \mathrm{d}\ell , \end{aligned}$$
(6)

where \({\mathbf {r}}=(x,y)\), \({\mathbf {r}}_0=(x_0,y_0)\) are the field and the singular points, respectively. When integration point \({\mathbf {r}}\) approaches the evaluation point \(\mathbf {r_0}\), the integrands exhibit a singularity. When the singular point \(\mathbf {r_0}\) is placed on the channel domain the coefficient \(C_l=\frac{1}{2}\) and if it is placed on the liquid–liquid interface \(C_l=\frac{1+\alpha _2}{2}\). \(\Gamma _{{ w}}\) is the channel wall contour and \(\Gamma _o\) is a straight line cutting through the open ends of the microfluidic channel. \(G^B _{ij}\) and \(T^B _{ijk}\) are velocity and stress tensor Green’s functions of Brinkman’s equation, respectively. Free-space Green’s functions of Brinkman’s equation are given by [40, 45]

$$\begin{aligned} G^B _{ij} ({\mathbf {r}},\mathbf {r_0})= & {} -\delta _{ij}A(k\rho )+\frac{{\hat{\rho }}_i{\hat{\rho }}_j}{\rho ^2}B(k\rho ), \end{aligned}$$
(7)
$$\begin{aligned} T^B _{ijk}= & {} \delta _{ij}\frac{{\hat{\rho }}_j}{\rho ^2}2[B(k\rho )-1]+\frac{\delta _{ij}{\hat{\rho }}_k+\delta _{kj}{\hat{\rho }}_i}{\rho ^2}C(k\rho ) -4\frac{{\hat{\rho }}_i{\hat{\rho }}_j{\hat{\rho }}_k}{\rho ^4}D(k\rho ), \end{aligned}$$
(8)

where

$$\begin{aligned} A(\rho )= & {} 2\left[ \frac{1}{k^2\rho ^2}-\frac{K_1(k\rho )}{k\rho }-K_0(k\rho )\right] ,\nonumber \\ B(\rho )= & {} 2\left[ \frac{2}{k^2\rho ^2}-2\frac{K_1(k\rho )}{k\rho }-K_0(k\rho )\right] ,\nonumber \\ C(\rho )= & {} \frac{8}{k^2\rho ^2}-4K_0(k\rho )-2\left( k\rho +\frac{4}{k\rho }\right) K_1(k\rho ),\nonumber \\ D(\rho )= & {} C(k\rho )+k\rho K_1(k\rho ). \end{aligned}$$
(9)

\({\hat{{\varvec{\rho }}}}={\mathbf {r}}-\mathbf {r_0}\), \(\rho =|{\hat{{\varvec{\rho }}}}|\), and \(K_0(k\rho )\), \(K_1(k\rho )\) are modified Bessel functions.

The domain integral on the right-hand side of Eq. (6) is directly computed by domain discretization followed by numerical integration.

2.3 Boundary element discretization

In this study, the boundary element method is applied to generate the numerical solutions to the integral equation (6). The process of numerical implementation can be briefly described as follow:

  • Discretize the boundary into the collocation elements.

  • Approximate the self-consistent integral equation (6) with sums of integrals over the boundary elements.

  • Replace the unknown boundary distribution of velocity with constant function over the each element.

  • Compute the integrations over the each element by using the Gauss–Legendre quadrature.

  • Solve the linear system of equations that results from its discretization.

The first step in the implementation of the boundary element method is to discretize the boundary into finite numbers of elements which are defined boundary elements. We discretize the channel walls, inlet and outlets into a collection of N straight segments defined by the element end-points. The deformable droplet is discretized by applying the periodic cubic-spline method which periodicity conditions for the first and second derivative at the first and last nodes. The coordinates of each cubic spline element are presented in parametric form by the cubic polynomial.

The grid independence study was performed by calculation of the droplet area as function of time. According to continuity equation, the droplet area is constant over the travel time. We have found that 120 points for droplet contour and 388 straight elements for fixed boundaries are satisfactory and any increase beyond this mesh size would lead to insignificant changes in results.

In the next step, the boundary integrals of Brinkman equation are discretized over contours with sums of integrals over the boundary elements. The integrals over each boundary element should be computed accurately by the Gauss-Legendre quadrature with 12 nodes. In this way, the integral of a nonsingular function over the interval \([-1,1]\) is approximated with a weighted sum of the values of the integrand at selected points:

$$\begin{aligned} \int _{-1}^{1} {f(x)\mathrm{d}x}\approx \sum _{i=1}^{12}{w}_i{f}({x}_i), \end{aligned}$$
(10)

where \({w}_i\) are quadrature weights, and \({x}_i\) are the roots of the nth Legendre polynomial. It is clear that, as the field point \({\mathbf {r}}\) approaches the singular point \(\mathbf {r_0}\), the integrands of Eq. (6) exhibit the weak (logarithmic) and strong (high-order) singularities of the Green’s functions. The logarithmic singularity should be integrated analytically. The high-order singularity disappears as the field point \({\mathbf {r}}\) approaches the singular point \(\mathbf {r_0}\). In this case, the normal unit vector is perpendicular to \(({\mathbf {r}}-\mathbf {r_0})\).

The local velocity at each collection point has been numerically computed by numerical solving of the linear system of equations that results from the boundary integral discretization. The system of linear algebraic equations was solved by Gaussian elimination method. By using the local velocity at each location point, the new position of the collection point has been calculated by using an explicit Euler method:

$$\begin{aligned} x^{(n+1)}= & {} \int _{t=n} ^{t=n+1} V_x \mathrm{d}t+x^{(n)},\nonumber \\ y^{(n+1)}= & {} \int _{t=n} ^{t=n+1} V_y \mathrm{d}t+y^{(n)}, \end{aligned}$$
(11)

where \({\mathbf {V}}\) is the velocity field obtained by solving the boundary integral equation (6) at the each collection point. Since relative positions of the points on the droplet contour are changed over time, we have to remesh the splines at each time step. When the relative position of two adjacent nodes on the interface is twice as big or twice as small as the initial size, the points are remeshed equidistantly using a cubic interpolation. In this way, we have calculated the time evolution of droplet shape and droplet motion at each time step. Since the boundary element method is only implemented for boundaries which are discretized, it is unnecessary to remesh the whole domain as the interface evolves. After determining the new position of nodes, it is necessary to find the shortest distance between the droplet–droplet interface at each time step. In the numerical simulation, the coalescence behavior can be described in two stages: At first stage, two or more droplets approach to each other. At second stage, when the shortest distance value extremely close to zero, droplet–droplet coalescence occurs.

The advantage of this model is that only values of the unknown function on boundaries need to be found. It means that the velocity field is explicitly written in terms of the stress and velocity functions on the boundaries. No discretization of elements inside the droplet is required to solve for the flow fields. Furthermore, the boundary element method results are obtained with considerably less computational effort which is one of the other advantages of this method

3 Results

In this study, the effect of viscosity ratio, capillary number, width ratio, and droplet area on coalescence dynamics in a sudden expansion microchannel are numerically studied. The microchannel consists of two straight channels which calls narrow and wide channel. The narrow channel is connected to wide channel by two rectangle walls. The width of narrow and expansion channels are called by \(W_{1}\) (inlet) and \(W_{2}\) (outlet), respectively. We also define width ratio of narrow channel to wide channel as \(W=W_{2} /W_{1}\). Figure 1 illustrates the schematic geometry of the present study. The channel height, H, is assumed to be much smaller than the inlet channel width, \(W_{1}/H=8\). The channel length of inlet and outlet is kept fixed to \(8W_{1}\). The continuous phase is injected from the narrow channel. We consider two droplets passing through the narrow channel. The droplet radius, droplet area, inter-droplet distance are indicated by R, \(A_d\), and D, respectively.

Figure 2 illustrates the subsequent snapshots of droplet flowing in the sudden expansion microchannel. When a droplet enters into the sudden expansion channel, its velocity decreases and it starts to deform under the normal stress in the sudden expansion area. Figure 3 indicates the velocity of droplets as a function of time for droplet–droplet coalescence regime. Due to velocity field of continuous phase in the entrance of the wide channel, the droplet velocity decreases as the droplet enters into the sudden expansion channel. Therefore, as the first droplet enters into sudden expansion channel, its velocity reduces. Meantime, the second droplet is moving forward at a larger velocity in the narrow channel thereby decreasing its distance to the first droplet. Finally, when the second droplet completely enters the sudden expansion, it has a similar velocity. Depending on control parameters (such as droplet area and capillary number), we found two scenarios as the second droplet enters into the sudden expansion channel. In the first scenario, the second droplet touch the back surface of the first droplet and droplet–droplet coalescence occurs in the wide channel. This regime is named “coalescence regime”. Figure 2a indicates the subsequent snapshots of coalescence regime. We observe that for sufficiently droplet–droplet distance, the two droplet coalesced into a large droplet (see video in Online Supplementary Materials). If the initial droplet distance larger than the critical distance, \(D>D_c\), the droplet coalescence does not occur. The second regime is named “non-coalescence regime” when two droplets do not touch each other. Figure 2b shows the non-coalescence regime. In this work, we will investigate the effect of control parameters on the droplet coalescence. In this way, we want to find the critical separation of two droplets where the coalescence of the droplets is inhibited. The results of transition between coalescence regime and non-coalescence regime are included in the phase diagrams.

Fig. 2
figure 2

Subsequent snapshots of droplets motion in a sudden expansion channel. a Coalescence regime. b Non-coalescence regime

Full size image
Fig. 3
figure 3

Droplet velocity as a function of time. The numerical parameters are: \(A_d=0.32\), \(\mathrm{Ca}=0.05\) and \(W=3\)

Full size image

3.1 Influence of droplet area

In order to investigate the effect of droplet area on the droplet coalescence, we fix the capillary number and droplet area and vary the initial droplet distance to find the critical value which droplet coalescence occurs. Several simulations were performed with varying droplet–droplet distance. Figure 4 illustrates the phase diagram of droplet coalescence for droplet area as a function of critical droplet–droplet distance for different given values of capillary number. The numerical prediction for droplet area illustrates that by increasing the droplet area, the critical droplet distance decreases. The solid line indicates transition from the coalescence regime to non-coalescence regime. In addition, at given value of droplet area, by increasing the capillary number, the critical droplet distance increases. This result is in a good qualitative agreement with experimental reports [37].

Fig. 4
figure 4

Droplet area as a function of critical droplet distance for the different values of capillary number. The solid curves are drawn only to guide the eye. This line indicates transition from the coalescence regime to non-coalescence regime

Full size image

3.2 Effect of channel width ratio

In order to investigate the effect of channel width ratio on the droplet coalescence, capillary number and droplet area were kept fixed and the initial droplet–droplet distance was varied. Several simulations were carried out for different values of droplet–droplet distance. Figure 5 indicates the diagram mapping the coalescence dynamics as a function of droplet area and critical droplet–droplet distance. Symbols illustrate the critical droplet–droplet distance for each given value of droplet size at two given values of width ratio. Numerical results indicate that by increasing the width ratio, the critical droplet–droplet distance increases. Indeed, the velocity of the front droplet decreases by increasing the width ratio. The rate of velocity decrease at the sudden expansion is higher at higher width ratios. This behavior of the front droplet velocity leads to critical coalescence at larger distances. In other words, a smaller width ratio, W, is associated with a smaller drop in velocity of droplet in the sudden expansion. Therefore, requiring more closely spaced droplets in the narrow channel for a droplet coalesces with an adjacent droplet. As one can see in Fig. 5, by increasing the width ratio, the transition between coalescence regime and non-coalescence regime occurs at large initial droplet–droplet distance. We have found a good quantitative agreement of our numerical results with the experimental results [37].

Fig. 5
figure 5

Droplet area as a function of critical droplet distance for the different values of channel width ratio. The solid curves are drawn only to guide the eye. This line indicates transition from the coalescence regime to non-coalescence regime

Full size image

3.2.1 Influence of capillary number

It is clear that the droplet deformation strongly depends on the capillary number [7]. On the other hand, the droplet coalescence depends on the droplet shape. In this way, we investigate the effect of capillary number on the critical droplet–droplet coalescence dynamics. Figure 6 illustrates the effect of capillary number on the droplet–droplet distance. Numerical results indicate that by increasing the capillary number, the critical droplet–droplet distance increases. We also find that, at given value of capillary number, the critical droplet–droplet distance increases by increasing the width ratio. The physical reason for this behavior is that by increasing the capillary number, the droplet deformation at the entrance of the sudden expansion channel increases. When the droplet approaches the sudden expansion, the droplet velocity decreases and the droplet interface experiences a stronger hydrodynamics force due to hyperbolic flow field at sudden expansion channel and higher width ratio. Therefore, the critical coalescence occurs at larger droplet–droplet distance

Fig. 6
figure 6

Diagram mapping the coalescence dynamics as a function of critical droplet–droplet distance and capillary number for the three different values of channel width ratio

Full size image

Figure 7 indicates the diagram mapping the coalescence dynamics as a function of critical droplet–droplet distance and capillary number for the three different values of viscosity ratio of two fluids. One can see find that the by increasing the capillary number, the critical droplet–droplet distance increases. Numerical results indicate that at given value of capillary number, the critical droplet–droplet distance increases by reducing the viscosity ratio of droplet phase to continuous phase.

Fig. 7
figure 7

Diagram mapping the coalescence dynamics as a function of critical droplet–droplet distance and capillary number for the three different values of viscosity ratio

Full size image

3.3 Effect of viscosity ratio

According to previous studies [8, 26], deformation of droplet depends on the viscosity ratio of droplet phase to carrier phase. Now, we investigate the effect of viscosity ratio on the droplet–droplet coalescence dynamics. In this way, we kept all parameters fixed and changing the viscosity ratio. To change the value of the viscosity ratio without affecting the capillary number, we kept the viscosity of carrier phase fixed and changed the droplet viscosity. Figure 8 illustrates the effect of viscosity ratio on the droplet–droplet distance. Numerical results indicate that by reducing the viscosity ratio, the critical droplet–droplet distance increases. The physical reason for this behavior was found to be that the droplet coalescence depends on the system properties, and in particular the viscosity and surface tension. The kinetic energy increases by increasing the droplet viscosity. Hence, requiring more closely spaced droplets in the inlet channel for a droplet coalesces with an adjacent droplet.

Fig. 8
figure 8

Diagram mapping the coalescence dynamics as a function of critical droplet–droplet distance and viscosity ratio of droplet phase to carrier phase for the three different values of width ratio

Full size image

4 Conclusion

In this work, we have presented a numerical study of droplet coalescence of two droplets flowing through a sudden expansion microfluidic. We have numerically solved the integral equation of the Brinkman’s differential equation using the boundary element method. We have focused our attention on the coalescence mechanism where the two droplets touch each other. Two different regimes which are governed by the relative separation of droplets have been identified: coalescence regime and non-coalescence regime. The transition between the coalescence and non-coalescence regimes was discussed in the phase diagrams. We have found that the critical separation distance of two droplets depends on the capillary number, viscosity ratio, droplet size, and ratio outlet to inlet channel width. Numerical results indicate that critical droplet–droplet distance increases by decreasing the droplet size and viscosity ratio of droplet phase to carrier phase. However, we have found that the critical separation distance of droplets increases by increasing the capillary number. Our numerical results are in good quantitative agreement with the previous experimental study [37].

This model has many applications and can be used in the drug deliver or petroleum industry where the separation or coalescence of droplets is one of the most important processes. Our goal is to model microstructure development during manipulation processes. After solving for the velocity field in the industrial microfluidic devices, one could apply our theory to track the dynamics of the droplet throughout the flow. Indeed, the numerical methods typical of such complex flow modeling should also allow the implementation of our rheological model, so the channel geometry and flow problems could be directly coupled. This method is able to accurately predict the droplet motion in the microfluidic devices.