Introduction

Dispersed droplets are an important subject in the rheological science. The droplet deformation (Delaby et al. 1995; Malkin et al. 2004), droplet breakup (Marshall and Walker 2019; Niedzwiedz et al. 2010), and droplet coalescence (Grizzuti and Bifulco 1997; Verdier and Brizard 2002) are interesting subject of rheological studies, due to practical application as well as due to rheological effects. Dispersed droplet generation and its manipulation are two important processes in the droplet dynamics in the microfluidic systems. The channel geometry has good ability to produce and control the external and internal forces that create, flow, breakup, and coalesce droplets (Bremond et al. 2008a; Baret et al. 2009; Baret 2012; Salkin et al. 2013). In recent years, numerous studies have been carried out on the dynamics of droplet motion in microchannels such as droplet deformation (Chang et al. 2019; Trégouët et al. 2018), droplet sorting (Kadivar et al. 2013; Kadivar 2016), droplet breakup (Link et al. 2004; Salkin et al. 2013), and droplet coalescence (Bremond et al. 2008b; Huang et al. 2019; Baret et al. 2009; Kadivar 2014).

Taylor was the first researcher who formulated the droplet deformation in terms of viscosity ratio and capillary number Taylor (1932, 1934). There are several theoretical models to describe the effect of droplet deformation on the rheology properties. These theories are able to the prediction of droplet breakup. The surface tension, droplet size, shear rate, and viscosity ratio are important parameters on the rheological properties of droplets. The effect of droplet size on the rheological properties of a dispersion of water droplet in continuous oil phase has been studied by Malkin et al. (2004).

Deng et al. have applied Lagrangian-Eulerian algorithm for studying the droplet deformation and droplet breakup in Convective flows (Deng and Jeng 1992). By using the hydrodynamic interactions between deformable droplets, Manga and Stone have applied the three-dimensional boundary integral for systems containing two, three, or four droplets to study the droplets motion in low Reynolds number suspensions. They have also investigated the effect of deformation on the droplet coalescence in this regime (Manga and Stone 1995).

Droplet deformation and droplet breakup depend on the concentration of insoluble surfactant. The effect of surfactant concentration on the droplet deformation and droplet breakup has been numerically studied by Bazhlekov et al. (2006). They have solved the Stokes equation together with equation of state by applying the boundary element method to evolve the droplet shape as a function of surfactant concentration, viscosity ratio, and elasticity number.

The behavior of droplet dynamics under extensional flow is of considerable scientific interest (Mulligan and Rothstein 2011; Kadivar and Farrokhbin 2017; Ulloa et al. 2014; Cabral and Hudson 2006; Kadivar 2018). The effect of droplet deformation on the rheological properties of suspensions in elongational flow has been investigated by Delaby et al. (Delaby et al. 1995). The effect of Marangoni stress on the droplet deformation in an extensional flow has been studied by Pawar and Stebe (Pawar and Stebe 1996). They have solved the Stokes equation by using the boundary element method in the presence of Marangoni boundary condition (Pawar and Stebe 1996). Their results indicate that the droplet deformation in the presence of Marangoni stress is higher than with respect to case where surface tension is fixed (Pawar and Stebe 1996). The deformation of water droplets in confined shear and extensional flow has been experimentally studied by Mietus et al. (2002). In their experimental work, they passed the water droplets dispersed in castor oil through a horizontal annular Couette flow cell. Their experimental results indicate that the droplet size and droplet deformation depend on flow history (Mietus et al. 2002).

The influence of confinement on the deformation and orientation of a single droplet during steady-shear flow has been experimentally studied by Vananroye et al. (2011). Their results illustrate that at high viscosity ratio, confinement strongly increases the droplet deformation. They have also found that by increasing the degree of confinement, the droplet deformation increases (Vananroye et al. 2011). By applying the boundary integral method, Cunha and Oliveira have numerically investigated the effect of viscosity ratio and capillary number on the droplet deformation of a droplet flowing through a cylindrical tube (Cunha and Oliveira 2019). The effect of viscosity on droplet formation and droplet deformation has been experimentally investigated by Tice et al. (2004). Their experimental results illustrate that the droplet shape depends on the capillary number and contrast between the viscosity of droplet phase and continuous phase. Mulligan et al. have investigated the influence confinement-induced flow shear on droplet deformation and breakup under extensional flow. Their experimental results indicate that the droplet deformation decreases by reducing the channel confinement. Cabral and Hudson have been measured the surface tension of droplet under extensional flow by analyzing the droplet deformation (Cabral and Hudson 2006). Kadivar and Farrokhbin have been investigated the droplet deformation and droplet relaxation of a droplet flowing through a narrow channel opening to a planar sudden expansion. They have found two different regimes of droplet deformation. At the first regime, droplet deformation is proportional to droplet volume while in the second one, droplet deformation is independent of droplet size (Kadivar and Farrokhbin 2017).

T-junction, Y-junction, and cross-junction are most common structures used in microfluidic systems (Kadivar 2016; Jullien et al. 2009; Hoang et al. 2013; Brosseau et al. 2014; Gai et al. 2016; Khor et al. 2017; Kadivar and Alizadeh 2017). Jullien et al. have experimentally studied the droplet deformation and droplet breakup in microfluidic T-junction at the small capillary numbers (Jullien et al. 2009). The dynamics of droplet deformation in the three dimensional T-junction has been numerically investigated by Hoang et al. (2013). The interaction, deformation, and breakup of droplet pairs in the Y-junction have been investigated by Khor et al. (2017). Ulloa et al. experimentally studied the droplet deformation in a microfluidic cross-junction at the low Reynolds numbers and large aspect ratio of droplet radius to channel height (Ulloa et al. 2014).

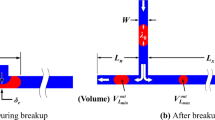
In this work, a numerically study of monodisperse emulsion droplet flow through a microchannal non-orthogonal intersection is presented. Figure 1 presents the geometry considered in this work. The microchannal consists a non-orthogonal intersection having two inlets and two outlets. The inlet channels are along the x-axis and the angle between the outlet channels and right inlet is called θ. The width of inlet channel and outlet channel call win and wout, respectively. In this study, we consider a two-phase flow which consists of two fluids separated by an interface. We assume that a flow past two-dimensional droplet containing a droplet phase labeled, d, and suspended in continuous phase labeled, c. Viscosity of continuous phase is μc and viscosity of droplet phase is μd. In this study, we apply Brinkman equation to describe the droplets dynamics in the Hele-Shaw limit. In this way, the Brinkman partial differential equation is converted to boundary integral equation and solved by using the boundary element method as well. Finally the dynamics of droplet deformation and droplet breakup are discussed as function of droplet size, capillary number, and channel geometry.

Fig. 1
figure 1

Sketch of the microfluidic channel considered. The inlet channels are along x-axis. The width of inlet and outlet channels is labeled by win and wout, respectively

Full size image

This paper is structured as follows: In the following “Governing equations”, we will formulate Brinkman equation and boundary conditions for the velocity field and normal component of stress tensor at the droplet-continuous phase interface as well as at channel walls. The numerical implementation to solve the boundary integral representation equation for the velocity field as well as for local droplet velocity is also contained in “Boundary element discretization’. The results of our numerical solutions, including the dynamics of droplet deformation and droplet breakup, are reported in “Results”. Finally, in “Conclusion”, we summarize our findings, conclude, and give an outlook on possible future work in this field.

Governing equations

In the Hele-Shaw limit where straight width channel is much larger than channel height, h, experimental observations indicate that droplets are confined between the top and bottom walls of the microfluidic channel. The fluidic resistance decreases as the ratio of channel width to channel height (cross-sectional area) increases. Therefore, the flow rate is usually in the range from nl/min to mu l/min with flow velocity in the order of mm/s. Numerical studies and experimental observations illustrate that in the very narrow straight channel, the velocity field is almost constant in the channel width direction (Gondret et al. 1997; Nagel and Gallaire 2015; Gallaire et al. 2014; Langlois and Deville 2014). In the channel width direction, one can find a deviation from the constant value in the vicinity of channel walls. Although in the height axis, z-axis, the velocity profile is parabolic shape. In the microfluidic channel, the Reynolds number is much smaller than one. Therefore, Stokes equation or Brinkman equation (modified Darcy equation) is used in analyzing the dynamics of droplet motion. The analytical solutions of Stokes equation and Brinkman equation in a narrow straight microchannel illustrate that the velocity profiles are not far from each other (Gallaire et al. 2014; Langlois and Deville 2014). In the present study, we will solve depth-averaged Brinkman equation instead of solving 3D stokes equation. In this way, we consider a two-phase flow which consists of two fluids separated by an interface. We assume that a flow past two-dimensional droplet containing a droplet phase labeled, d, and suspended in continuous phase labeled, c. Viscosity of continuous phase is μc and viscosity of droplet phase is μd. In order to report data with dimensionless numbers, we select length scale L0, time scale μcL0/γ, pressure scale γ/L0, velocity scale γ/μc, and capillary number Ca = μcU0/γ. The dimensionless droplet area, ad, is defined as the droplet area divided by the squared length scale. Here, and in the remainder of this article, we will denote all non-dimensional rescaled lengths and physical quantities by lower case symbols. In the microfluidic systems, because the channel size is in the micrometer range, we can neglect the gravitational effect. The homogeneous dimensionless Brinkman equation in the droplet phase (d) and carrier phase (c) is given by:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\nabla}p^{(i)}=\lambda (\boldsymbol{\nabla}^{2}\mathbf{u}^{(i)}-\alpha^{2} \mathbf{u}^{(i)}) ~~\text{ on }~~ {\Omega}_{i} ~~\text{ with }~~ i \in \{ \mathrm{c},\mathrm{d} \}~, \end{array} $$
(1)

In addition, the continuity equation must be satisfied in both droplet and continuous regions:

$$ \begin{array}{@{}rcl@{}} \boldsymbol{\nabla}.\mathbf{u}^{(i)}=0 \qquad \text{on} \quad {\Omega}_{i} \quad \text{with} \quad i \in \{ \mathrm{c},\mathrm{d} \} \end{array} $$
(2)

where p(x, y) is the dimensionless pressure, u is the depth averaged dimensionless velocity, \(\alpha =\sqrt {12}/h\), λ = 1 and λ = μd/μc for the carrier phase and droplet phase, respectively.

Boundary conditions on droplet interface and channel walls

In the absence of Marangoni and thermocapillary effects, because of surface tension, the normal component of stress tensor is discontinuous across the the droplet-continuous phase interface. The discontinuity condition on the normal stress at the two phase interface is given by:

$$ \boldsymbol{\Delta}\mathbf{f}= \mathbf{\sigma^{(d)}\cdot n^{(cd)}}-\mathbf{\sigma^{(c)}\cdot n^{(cd)}}=\gamma(\frac{\pi}{4} \kappa_{\parallel}+\kappa_{\perp}) \mathbf{n^{(cd)}}, $$
(3)

where σ is stress tensor and σ ⋅n(cd) is normal component of stress tensor, γ is surface tension, n(cd) is unit normal vector pointing from the interior of the droplet phase into the continuous phase, κ∥ is local curvature in-plane, and κ⊥ is curvature in the thin direction. Prefactor π/4 corresponds to non-wetting condition at the top and bottom walls of the Hele-Shaw cell (Park and Homsy 1984). The effect of prefactor on the droplet dynamics was discussed in more detail by Park and Homsy (1984).

The other boundary condition on the droplet-continuous phase interface apples on the normal and tangential components of velocity. According to continuity equation, Eq. 2, there is no mass transfer through the two phase interface. Therefore, the normal component of fluid velocity is continuous across the droplet-continuous phase interface. On the other hand, we assume no-slip boundary conditions, so the flow velocity is continuous across the droplet-carrier liquid interface. This boundary condition reads:

$$ \mathbf{u}^{(c)}=\mathbf{u}^{(d)}\neq0 \qquad \text{on} \qquad {\Gamma}_{\text{cd}}~, $$
(4)

where Γcd is the two-dimensional droplet contour.

Finally, the no-slip boundary condition requires that the velocity must vanish over all channel walls.

Integral representation

In order to investigate the droplet shape under extensional flow, we will calculate the velocity components of the droplet interface ux and uy as the droplet moves through the microchannal. One way to obtain the relevant boundary data of the velocity field is to numerically compute a self-consistent integral equation for velocity field u on the liquid-liquid boundary and channel walls. Following the formulation of Pozrikids (2002), the velocity field at point (r0) that lies in the continuous fluid satisfies a self-consistent integral equation of the following form:

$$ \begin{array}{@{}rcl@{}} \lefteqn{u_{j}^{(c)}(\mathbf{r}_{0}) = \frac{1}{C_{l}} \oint_{{\Gamma}_{\mathrm{w}},{\Gamma}_{\mathrm{o}}} [u_{i}^{(c)}(\mathbf{r})T^{B}_{ijk} (\mathbf{r},\mathbf{r}_{0})n_{k}- f^{(c)}_{i} G^{B}_{ij}(\mathbf{r},\mathbf{r}_{0})] \mathrm{d}\ell}\\ &\qquad\quad\!+\frac{1}{c_{l}}\oint_{{\Gamma}_{\text{cd}}} [ (1-\mu_{d}/\mu_{c}) u_{i}^{(c)}(\mathbf{r}) T^{B}_{ijk} (\mathbf{r},\mathbf{r}_{0})n_{k} -{\Delta}\mathbf{f}_{i} G^{B}_{ij}(\mathbf{r},\mathbf{r}_{0})] \mathrm{d}\ell, \end{array} $$
(5)

where r = (x, y), r0 = (x0, y0) are the field and the singular points, respectively. When integration point r approaches the evaluation point r0, the integrands exhibit a singularity. If the singularity at r0 is placed on the channel domain the coefficient \(c_{l}=\frac {1}{2}\) and if it is located on the liquid-liquid interface \(c_{l}=\frac {\mu _{c}+\mu _{d}}{2\mu _{c}}\). Γw is the channel wall contour and Γo is a straight line cutting through the open ends of the microfluidic channel. \(G^{B}_{ij}\) and \(T^{B}_{ijk}\) are velocity and stress tensor Green’s functions of Brinkman’s equation, respectively. Free-space Green’s functions of Brinkman’s equation are given by Pozrikids (2002)

$$ G^{B}_{ij} (\mathbf{r},\mathbf{r_{0}})=-\delta_{ij}A(\alpha\rho)+\frac{\hat{\rho}_{i}\hat{\rho}_{j}}{\rho^{2}}B(\alpha\rho), $$
(6)
$$ \begin{array}{@{}rcl@{}} T^{B}_{ijk} & = & \delta_{ij}\frac{\hat{\rho}_{j}}{\rho^{2}}2[B(\alpha\rho)-1]+\frac{\delta_{ij}\hat{\rho}_{k}+\delta_{kj}\hat{\rho}_{i}}{\rho^{2}}C(\alpha\rho) \\ & & -4\frac{\hat{\rho}_{i}\hat{\rho}_{j}\hat{\rho}_{k}}{\rho^{4}}D(\alpha\rho), \end{array} $$
(7)

where

$$ \begin{array}{@{}rcl@{}} A(\rho)=2[\frac{1}{\alpha^{2}\rho^{2}}-\frac{K_{1}(\alpha\rho)}{\alpha\rho}-K_{0}(\alpha\rho)],\\ B(\rho)=2[\frac{2}{\alpha^{2}\rho^{2}}-2\frac{K_{1}(\alpha\rho)}{\alpha\rho}-K_{0}(\alpha\rho)],\\ C(\rho)=\frac{8}{\alpha^{2}\rho^{2}}-4K_{0}(\alpha\rho)-2(\alpha\rho+\frac{4}{\alpha\rho})K_{1}(\alpha\rho)\\ D(\rho)=C(\alpha\rho)+\alpha\rho K_{1}(\alpha\rho). \end{array} $$
(8)

\(\hat {\mathbf {\rho }}=\mathbf {r}-\mathbf {r_{0}}\), \(\rho =|\hat {\mathbf {\rho }}|\), and K0(αρ), K1(αρ) are modified Bessel functions.

One may calculate the domain integral on the right-hand side of Eq. 5 either directly by domain discretization followed by numerical integration, or indirectly by the method of approximate particular solutions or the dual reciprocity method. In the next subsection, we will discuss the numerical procedure to solve the integral representation equation.

Boundary element discretization

The first step in the implementation of the boundary element method is to discretize the boundary into a finite number of elements which are called boundary elements. We discretize fixed boundaries like walls and open ends into a collection of N straight segments defined by the element end-points or nodes, whereas the droplet is discretized by using the cubic-spline method. The advantage of cubic spline method is that slope and curvature of each cubic spline at the end point of elements are continuous. On the other hand, the cubic spline elements improve the accuracy of boundary element method solutions. The coordinates of each cubic spline element are presented in parametric form by the cubic polynomial. Because the droplet is closed surface, we used the periodic cubic-spline which periodicity conditions for the first and second derivative at the first and last nodes are imposed.

The grid independence study was performed by calculation of the droplet area as function of time. According to continuity equation, the droplet area is constant over the travel time. We have found that 98 points for droplet contour and 352 straight elements for fixed boundaries are satisfactory and any increase beyond this mesh size would lead to insignificant changes in results.

The boundary integrals of Brinkman equation are discretized over contours with sums of integrals over the boundary elements. The integrals over each boundary element should be computed accurately by the Gauss-Legendre quadrature with 12 nodes. In this way, the integral of a non-singular function over the interval [− 1, 1] is approximated with a weighted sum of the values of the integrand at selected points. However, when the field point r approaches the singular point r0, the integrands of the Eq. 5 exhibit the weak (logarithmic) and strong (high-order) singularities of the Green’s functions. The logarithmic singularity should be integrated analytically. The high-order singularity disappears as the field point r approaches the singular point r0. In this case, the normal unit vector is perpendicular to (r −r0).

After computing the local velocity at the collection points, we update the position of the points by using an explicit Euler method. Using the explicit Euler, the interface droplet is advanced in discrete time steps:

$$ \begin{array}{@{}rcl@{}} x^{(n+1)}={\int}_{t=n}^{t=n+1} u_{x} dt+x^{(n)} \enspace,\\ y^{(n+1)}={\int}_{t=n}^{t=n+1} u_{y} dt+y^{(n)}\enspace, \end{array} $$
(9)

where u is the velocity field obtained by solving the boundary element problem at node r(n). Since relative positions of the points on the droplet contour are changed over time, it is necessary to remesh the splines at each time step. When the relative position of two adjacent nodes on the interface is twice as big or twice as small as the initial size, the points are remeshed equidistantly using a cubic interpolation (Kadivar et al. 2013). Since the boundary element method is only implemented for boundaries which are discretized, it is unnecessary to remesh the whole domain as the interface evolves.

Results

In this study, the droplet deformation and droplet breakup in the flat microfluidic non-orthogonal cross-section have been numerically studied. The microfluidic channel consists two inlets and two outlets. The angle between each side outlet microchannel and the right inlet microchannel calls θ. In this way, we define the x-axis along the the inlet channels. Figure 1 presents the channel geometry of the present study. The width of inlets and outlets is equal to win and wout, respectively. The channel height, h, is assumed to be much smaller than the channel widths, win/h = 8. The channel length of inlets and outlets is fixed by 10 times win. The carrier fluid is injected from two opposite sides into the microfluidic channel. It is clear that the velocity of carrier fluid at the outlets depends on the θ and wout. Therefore, we call the flow rate of the inlet channel by qin. In this way, the outlet flux is well controlled by total flow rate. We assume that at the left inlet, a droplet of radius r and viscosity ηd is suspended in a carrier liquid of viscosity ηc. Here, and in the remainder of this article, the droplet phase and carrier phase will be labeled with d and c, respectively.

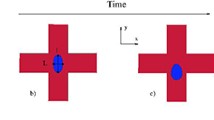
When a droplet arrives at oblique symmetric cross-junction, the droplet velocity decreases and droplet deforms. Figure 2 shows subsequent snapshots in time of the droplet deformation in the microfluidic channel. The time evolution of the droplet deformation is also illustrated at the bottom of snapshot series in Fig. 2. The droplet deformation is calculated by δ = (b − a)/(b + a), where a and b are diameters of the droplet along the x- and y-axes, respectively. Figure 3 presents the droplet velocity and droplet deformation as a function of its dimensionless distance from the intersection center, \(|l|=\sqrt {x^{2}+y^{2}}\). The negative sign of droplet velocity indicates that the droplet flows through downward outlet. Figure 3.b illustrates the droplet deformation as a function of droplet distance from the center of intersection zone when the droplet flows into (red line) and out of (green line) the cross-intersection. The negative value of δ denotes that the droplet is lengthened in the x-axis while the positive value indicates that the droplet is stretched along the y-axis. The zero value of δ indicates that the droplet approaches to the its circular shape.

Fig. 2
figure 2

Subsequent snapshots and droplet deformation as a function of droplet size. The numerical parameters are as follows: r = 0.43, Ca = 0.35, and θ = π/4

Full size image
Fig. 3
figure 3

Droplet velocity and droplet deformation as a function of droplet distance from the center of oblique intersection, |l| when the droplet flows into (red line) and out of (green line) the cross-intersection. The numerical parameters are as follows: r = 0.43, Ca = 0.35, and θ = π/4

Full size image

It is clear that the droplet deformation increases monotonically as the droplet approaches the cross-intersection zone. Finally, the droplet deformation reaches its maximum value where the droplet velocity is zero. However, the droplet deformation backs into a circular shape when it flows into the upward or downward outlet (see the movie given as Supplementary Material). As one can see, the two curves of droplet deformation do not match exactly due to variation in the velocity profile. When the droplet approaches the cross-intersection, it experiences a diverging flow field and slows down there. However, a droplet flowing out of the cross-intersection experiences a convergent flow. It means that droplet deformation in the cross-junction microfluidic channel is an irreversible phenomenon.

The experimental observations and numerical studies indicate that the droplet formation and breakup dynamics strongly depend the channel geometry, capillary number, and droplet size. In this work, we will investigate the droplet deformation and droplet breakup in an oblique intersection. In the following subsection, we will investigate the effect of control parameters on the maximum droplet deformation. The results of droplet breakup including the breakup phase diagram are contained in the “Droplet breakup”.

Droplet deformation

Influence of capillary number

In order to investigate the effect of capillary number on the droplet deformation, we have calculated the maximum deformation of droplet at given values of droplet size. In this way, the channel geometry was kept fix, and we have varied the capillary number at different given values of droplet size. In a dynamic regime where the droplet deforms but does not breakup when passing through the cross-intersection, we have changed the capillary number in the range of 0.08–0.3 by varying the flow rate or surface tension. Figure 4 illustrates the maximum droplet deformation as a function of capillary number for different given values of droplet size. The symbols depict the numerical data, and the dashed-dotted curves show the best numerical fit. The inset shows a logarithmic plot. In the Hele-Shaw limit, the droplets are confined across the channel height axis. However, when the droplet diameter is larger than the channel width, they are also confined the channel width. Figure 5 indicates the subsequent snapshots in the time of the droplet motion for two different values of droplet size. We have found two regimes of droplet deformation with a dependency on the droplet size. A first regime, when the undeformed droplet diameter is smaller than the channel width, we have found that the droplet deformation increases linearly by increasing the capillary number. The results of our numerical fitting show that the maximum droplet deformation scales with power law with capillary number with an exponent 1.07. This behavior is in qualitative agreement with previous theoretical predictions and experimental observation. Taylor predicted that the droplet deformation in the steady shape is proportional to the capillary number with a power law exponent 1 (Taylor 1934). As one can see in Fig. 4, by increasing the droplet size, a deviation from Taylor theory is visible. For example, droplets having a radius 0.44 are not confined along the channel width direction. However, they are confined along the channel height direction. Therefore, droplets of different sizes touch edge flow to different degrees. The effects of confinement become much stronger when the droplets are also confined along the channel width direction (as demonstrated in Figs. 4 and 5 ). The experimental results of Ulloa et al. indicate the the maximum droplet deformation is proportional to the capillary number with power 0.92 (Ulloa et al. 2014). However, dependency of maximum droplet deformation on the capillary number is completely different for the second regime, in which the droplet diameter is larger than channel width. The solid circle points of Fig. 4 presents the maximum droplet deformation as a function of capillary number for droplet diameter 1.04. The main focus of the present study on the small droplet in which the undeformed droplet diameter is smaller than the channel width.

Fig. 4
figure 4

Maximum droplet deformation as a function of capillary numbers for the different values of droplet size. The differently shaped dots are the numerical data and the dashed-dotted lines show the numerical fit of each curve. The solid circle points correspond to the second regime, in which the droplet diameter is larger than the channel width. The inset is a log-log plot

Full size image
Fig. 5
figure 5

Subsequent snapshots in the time of the droplet motion for two different values of droplet size: (a) First regime: r = 0.43, (b) Second regime: r = 0.52

Full size image

Effect of droplet size

As one can see in Fig. 4, the prefactor of the best power law fit to our numerical results depends on the droplet size. In order to investigate the effect of droplet size on the droplet deformation, we ran the program for three different values of capillary number. Figure 6 presents the rescaled deformation as a function of undeformed radius of droplet, r, for three different values of capillary number. The symbols denote the numerical data, and the dashed-dotted curves present the best power law fit. The inset is a log-log plot. The best power law fit \(\delta _{\max \limits }/Ca^{1.07}= A r^{\alpha }\) leads to α = 3.08. This result is in good agreement with previous studies (Brosseau et al. 2014; Shapira and Haber 1990).

Fig. 6
figure 6

Dependency of the maximum droplet deformation on dimensionless droplet radius. The colored dashed-dotted curves illustrate the best fit to the data. The inset is a log–log plot

Full size image

Influence of intersection angle

To explain the influence of the intersection angle of the microchannel on the maximum droplet deformation, we keep the droplet size and capillary number fixed and vary the intersection angle. The simulations were implemented for intersection angle varying from π/6 to π/2 at an increment of π/18. The θ = π/2 corresponds to orthogonal intersection geometry. Figure 7 shows subsequent snapshots in time of the droplet deformation in the different values of intersection angle. As one can see, the maximum droplet deformation increases by increasing the intersection angle. Figure 8 presents the rescaled droplet deformation as a function of intersection angle. The inset of Fig. 8 indicates the logarithmic plot of the rescaled droplet deformation. The different symbols illustrate the numerical data. On the log-log scale, the data can be fitted by a straight line, indicating that the maximum droplet deformation illustrates a power-law behavior of the form

$$ \delta_{\max}\propto\theta^{\upbeta} $$
(10)

where β = 0.50. The dashed-dotted curves on Fig. 8 show the best power law fit. This result is in a good agreement with previous numerical study (Kadivar 2018).

Fig. 7
figure 7

Snapshots of a droplet deformation in the orthogonal and oblique symmetric cross-junction microchannel at different values of intersection angles. (a) θ = π/2, (b) θ = π/3, (c) θ = π/4, and (d) θ = π/6. The numerical parameters are as follows: r = 0.43, Ca = 0.35, and w = 1

Full size image
Fig. 8
figure 8

Droplet deformation as a function of intersection angle for two different values of capillary number. The dashed-dotted line presents the best fit to the data. The inset is a log–log plot

Full size image

Effect of width ratio

Now, we investigate the effect of the ratio of the outlet channel width to inlet channel width on the droplet deformation. In this way, the inlet and outlet channels are both equal initially and then the outlet width is varied to study the effects of different width of outlets to the maximum deformation of droplet. The ratio of the outlet channel width to inlet channel width is defined as w = wout/win. The simulations were performed for ratio of outlet/inlet varying from 0.7 to 1.0. Figure 9 illustrates the rescaled droplet deformation as a function of ratio of the outlet channel width to inlet channel width. It is important to mention that the flow through the channel intersection is irreversible. This irreversibility is one reason that the droplet deformation depends on the width ratio. The dashed-dotted line indicates the best power-law fit to our numerical data. According to the fitting curve shown on the graph in Fig. 9, the maximum droplet deformation should be rescaled as:

$$ \delta_{\max}= 7.30 Ca^{1.07} r^{3.08} \theta^{0.50} w^{-1.08} $$
(11)
Fig. 9
figure 9

Droplet deformation as a function of ratio of the outlet/inlet width for two different values of capillary number. The dashed-dotted lines present the best fit to the data. The numerical parameters are as follows: r = 0.43 and θ = π/2

Full size image

Droplet breakup

When a droplet arriving at orthogonal intersection(θ = π/2), the droplet velocity decreases and droplet deforms. The deformation of a droplet flowing through the intersection area increases by increasing the capillary number, until the droplet shape is no longer and droplet breakup takes place at a critical value of capillary number. Therefore, depending on the droplet size and capillary number, single droplet can break into two smaller daughter ones at the cross-junction or do not break, choosing one branch of the intersection. For the geometry studied in this paper, we will provide information on how the numerical parameters affect the droplet breakup phenomenon. Figure 10 illustrates an example of the temporary evolution of symmetric droplet breakup.

Fig. 10
figure 10

Evolution of symmetric droplet breakup in an orthogonal intersection microfluidic channel

Full size image

As the tip of the droplet enters the intersection area, the droplet front interface experiences a stronger hydrodynamic force due to hyperbolic flow field. Therefore, its tip becomes elongated perpendicular to the direction of travel. As the droplet moves further in the intersection area, its tip and rear become more elongated parallel to y-axis. In the low capillary number, when the droplet center reaches close to the center of intersection zone, front and rear of the droplet contour start taking a concave shape. Therefore, the radius of curvature of the front and rear becomes negative. By passing time, a parabolic-like neck is formed at the center of intersection zone and narrows with time. The neck thickness monotonically decreases as the droplet approaches the intersection center. The droplet breakup takes place as the neck thickness reaches a critical value. Depending on the droplet size and capillary number, a single droplet may splits into into two identical daughter ones (see the Supplementary Material).

Figure 11 presents the various regimes of breakup and non-breakup on the capillary-droplet radius diagram. The symbols represent the critical capillary number for a given value of droplet size which above that the mother droplet splits into two daughter droplets. To investigate the effect of droplet size on the droplet breakup dynamics, several simulation were carried out for droplet size varying from 0.34 to 0.42. Our numerical results indicate that the critical capillary number decreases by increasing the undeformed droplet radius.

Fig. 11
figure 11

A phase diagram indicating the mechanism of droplet breakup as a function of the droplet size

Full size image

Conclusion

In this work, we have presented a 2D simulation of a droplet flowing through a microfluidic non-orthogonal intersection junction. In order to investigate the dynamics of droplet deformation and droplet breakup, we have numerically solved the depth-averaged Brinkman equation, describing the carrier fluid motion, as well as to track the fluid-fluid interface. The effect of the capillary number, droplet size, intersection angle, and ratio of outlet channel width to inlet channel width on droplet deformation have been studied. In this way, the maximum droplet deformation has been scaled as a function of capillary number, droplet size, intersection angle, and ratio of outlet channel width to inlet channel width. We have found the maximum scales with capillary number with power law with an exponent 1.07. Our numerical results indicate the the maximum droplet deformation scales with undeformed droplet radius and intersection angle with exponents 3.08 and 0.5, respectively. Our numerical results are in a good agreement with previous experimental and theoretical studies (Taylor 1934; Ulloa et al. 2014; Brosseau et al. 2014; Kadivar 2018). In the second part of the current study, we have studied the droplet breakup phenomenon in an orthogonal intersection junction. It is clear that by increasing the capillary number, the deformation of a droplet traveling in cross-junction region becomes larger, until the droplet shape is no longer observed and droplet breakup takes place at a critical value of capillary number. We have presented a phase diagram for droplet breakup as a function of undeformed droplet radius. Our numerical results indicate that the critical capillary number decreases with increasing the undeformed droplet radius.