1 Introduction

Nowadays, there is a strong request for elimination of the low-frequency vibration in the real systems. This request is satisfied with vibration isolators of passive type, with low rigidity and high static loading, whose natural frequency is almost the quarter of the frequency of the system [1]. The issue of obtaining low stiffness and high load isolator is a problem known for a long time [2]. It is found that the problem is possible to be solved with the so-called quasi-zero-stiffness (QZS) system. It is an elastic system with an almost flat area on its static force characteristic, i.e., an area with stiffness near zero [3]. The QZS system allows to obtain simultaneously high static load and low dynamic stiffness. The most widely model of the system contains three linear springs connected in one point and with a configuration which gives the nonlinear geometric property. Statics and dynamics of the model are investigated in [4,5,6,7,8]. It is obtained that if one spring is vertical and the other two inclined, at the static equilibrium the dynamic stiffness is zero, while near this position it increases with displacement and remains much less than the static stiffness [9]. The mathematical model of the QZS is [5]

$$\begin{aligned} \ddot{x} + c {\dot{x}} + x \left( 1- {\frac{1}{\sqrt{1+x^{2}}}}\right) = F_{0} \cos \, (\omega t) \end{aligned}$$
(1)

where c is the damping coefficient, \(F_{0}\) is the amplitude, and \(\omega \) is the frequency of the excitation force. Due to nonlinearity in system (1), bifurcation phenomena [10] occur. For certain parameters, the motion of the system is chaotic [11] and strange attractors exist [12].

Nowadays, other methods for obtaining QZS are developed: “scissor-like” system with spring [13], buckled beam instead of inclined springs [14], systems with pneumatic [15, 16] or magnetic elements [17], etc. For all of the models with QZS it is common that they have better absorption properties than linear isolators [18]. However, it is concluded that the system has several disadvantages, including design complexity, configuration requirements, and manufacturing [19].

In the literature, the other paradigm of the low-frequency isolator is the so-called smooth and discontinual (SD) oscillator which is developed from a simple arch model [20]. The SD oscillator with negative stiffness is connected in parallel with the vertical support to obtain the geometric configuration of QZS [10]. The mathematical model is

$$\begin{aligned} \ddot{x} + c {\dot{x}} + x \left( 1- {\frac{1}{\sqrt{a^{2}+x^{2}}}}\right) = F_{0} \cos \, (\omega t) \end{aligned}$$
(2)

where the parameter \(\alpha \) is the control parameter for smoothness or discontinuity. Comparing (1) and (2), it is seen that Eq. (2) is the generalized form of (1) where the parameter \(\alpha \) need not be 1. Namely, (1) and (2) are equal for \(\alpha =1\). In addition, the order of nonlinearity in both models is the same.

Assuming that \(x \ll a\) and using the first two terms of the series expansion of the function \(\sqrt{\alpha ^{2}+x^{2}}=a ({1+\frac{1}{2}\frac{x^{2}}{\alpha ^{2}}+ O({\frac{x^{2}}{\alpha ^{2}}})})\), i.e., \(\frac{1}{\sqrt{\alpha ^{2}+x^{2}}}\approx \frac{1}{a} ({1-\frac{1}{2}\frac{x^{2}}{\alpha ^{2}}})\), Eq. (2) transforms into

$$\begin{aligned} \ddot{x} + c {\dot{x}} + x \left( 1- {\frac{1}{\alpha }}\right) + {\frac{x^{3}}{2\alpha ^{3}}} = F_{0} \cos \, (\omega t). \end{aligned}$$
(3)

It is obvious that Eq. (3) is with cubic nonlinearity. A significant number of papers is published considering the dynamics of the nonlinear systems (for example [21,22,23]). Various asymptotic approaches for solving these nonlinear differential equations are developed.

There are two main directions of designing a QZS isolator: (a) to produce a system where that effect can be obtained with a cam–roller–spring mechanism [24] or (b) to manufacture a compact low-frequency vibration isolator [25]. The isolator in the form of a single item is designed, and prototypes of different shapes and materials are made [26, 27]. In the QZS isolator with the cam–roller system, where the cam is designed to convert the vertical displacement of the cam into horizontal displacement of the roller, for a given vertical displacement of the cam the horizontal displacement of the roller is expressed with a polynomial [28]. The compact low-frequency isolator, made of two-component polyurethane, has a high advantage in comparison with the conventional spring and rubber vibration isolators due to smaller dimensions. The isolators are applied for driver seats [29], for reducing dynamic loads on the foundation [30], for sensors for measurement of absolute vibration displacement of a moving platform [31], for machine rotors [32], etc. Experimental measurements on the QZS isolators are also done [33]. It is concluded that the results obtained experimentally qualitatively correspond to those obtained analytically, but there is quantitative difference.

The aim of the paper is to improve the physical and mathematical models of the QZS system by generalizing the form of nonlinearity of the system. The new model has to be able to create a compact, light vibration isolator with quasi-zero stiffness, which would have minimum parts and components, according to an engineering requirement nowadays, especially in application where size or weight is limited. Namely, instead of linear, the nonlinear springs are connected in parallel with the vertical support which gives not only geometric but also physical nonlinearity. The influence of the order of nonlinearity on the vibration of the system is investigated.

The paper is divided into six sections. In Sect. 2, the model of the string–mass structure is suggested. The motion of the system is described with a second-order differential equation with strong nonlinear elastic term. In Sect. 3, a mathematical procedure for solving of the differential equation of the truly nonlinear string–mass system is developed. Free and forced vibrations excited with multi-frequency force are considered. The exact vibration is given in the form of the Ateb (inverse Beta) function. In Sect. 4, the influence of the preloading string force on the vibration property of the string–mass structure is investigated. Two cases are considered: one, when the preloading force in the string is constant, and second, when the force is a time variable function. In Sect. 5, a numerical example is presented. The paper ends with Conclusions.

2 Model of the system

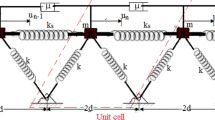
Using the archetypal model [34], the system is designed as a mass–string system shown in Fig. 1. The slider with mass m is connected with two nonlinear strings in parallel with the vertical support.

Fig. 1
figure 1

Force distribution in the strings

Full size image

Motion of the mass is in perpendicular direction to the string orientation. The displacement of slider causes deformation of the string (see Fig. 1)

$$\begin{aligned} \varDelta L=\sqrt{L^{2}+X^{2}}-L \end{aligned}$$
(4)

where L is the initial length of the string and x is the displacement. Using the relation for the stress

$$\begin{aligned} \sigma =\frac{T}{A} \end{aligned}$$
(5)

and also the stress–strain expression [35]

$$\begin{aligned} \sigma =\varepsilon ^{\beta } E, \end{aligned}$$
(6)

the force T follows as

$$\begin{aligned} T=AE \left( \frac{\Delta L}{L}\right) ^{\beta } \end{aligned}$$
(7)

where E is Young’s modulus, A is the cross section of the string, \(\varepsilon \) is the strain, and \(\beta \in {R}\) (integer or non-integer) is the order of nonlinearity. Varying the position of the free end of the string, the preloading force in the string can be varied. For the preloading force \(T_{0}\), the total string force is obtained as

$$\begin{aligned} T=T_0 +EA \left( \sqrt{1+\left( \frac{X}{L}\right) ^{2}}-1\right) ^{\beta }. \end{aligned}$$
(8)

Using the first two terms of the series expansion of (8) for the case when \(x/L \ll 1\), it is

$$\begin{aligned} T=T_0 +\frac{EA}{2^{\alpha }}\left( \frac{X}{L}\right) ^{2\beta }. \end{aligned}$$
(9)

For the angle \(\theta \), formed between the initial and deformed position of the string, when \(\sin \theta \approx {\tan }\theta =X/L\), the approximate restitution force in x direction is

$$\begin{aligned} F=T_0 \frac{X}{L}+\frac{EA}{2^{\beta }}\frac{X}{L} \left( \frac{X}{L}\right) ^{2\beta }. \end{aligned}$$
(10)

Using (4) and the assumption that the linear damping force and an excitation force act, the differential equation of motion follows

$$\begin{aligned} m {\ddot{X}} + T_{0} {\frac{X}{L}} + {\frac{EA}{2^{\beta }}} {\frac{X}{L}} \left( {\frac{X}{L}}\right) ^{2\beta } + c {\dot{X}} = F_{e} (t). \end{aligned}$$
(11)

Let us introduce the dimensionless variables and parameters

$$\begin{aligned} x=\frac{X}{L}, \quad t^{*}=t \Omega _{e}, \quad \omega ^{2}= \frac{T_0}{mL}, \quad c=\frac{c}{m\Omega _e}, \quad k_\mathrm{la} =\frac{\omega ^{2}}{\Omega _e^2}, \quad k_\mathrm{na} =\frac{EA}{mL\Omega _e^2}, \end{aligned}$$
(12)

where \(\Omega _{e}\) is the frequency of the excitation force, while \(k_\mathrm{la}\) and \(k_\mathrm{na}\) are coefficients of linearity and nonlinearity. Substituting (12) in (11) and introducing the notation \(\alpha =2\beta +1\), the dimensionless equation of motion is obtained,

$$\begin{aligned} \ddot{x} + k_\mathrm{la} x + k_\mathrm{na} x |x|^{\alpha - 1} + c {\dot{x}} = {\frac{1}{mL \Omega _{e}^{2}}} F (t^{*}). \end{aligned}$$
(13)

Equation (13) is: (a) truly nonlinear for \(k_\mathrm{la} = 0\), (b) linear with small nonlinearity if \(k_\mathrm{la} \gg k_\mathrm{na}\) and (c) strongly nonlinear if \(k_\mathrm{na} \gg k_\mathrm{la}\). Which type of equation will follow depends mainly on the value of the preloading force \(T_{0}\). Thus, if \(T_{0}\) is zero, the coefficient of the linear term is zero, and we have the nonlinear energy sink. Otherwise, as in the real string \(T_{0} \ll {\textit{EA}}\) the nonlinear equation cannot degenerate into a linear one in spite of the fact that \(x \ll L\). The nonlinear term is dominant in comparison with the linear one, and Eq. (13) is strongly nonlinear.

3 Strongly nonlinear string structure

If the damping and excitation force are small in comparison with the nonlinear term, Eq. (13) transforms into

$$\begin{aligned} \ddot{x} + k_\mathrm{na} x |x|^{\alpha - 1} = {\frac{\varepsilon }{mL \Omega ^{2}}} F (t^{*}) - \varepsilon k_\mathrm{la} x - \varepsilon c \dot{x} \end{aligned}$$
(14)

where \(\varepsilon \ll 1\) is a small parameter.

Two special cases of motion of the system are investigated: the free and the forced vibrations.

3.1 Free vibration of the string–mass system

For the case when \(\varepsilon =0\) and the damping and the excitation force are omitted, Eq. (14) transforms into

$$\begin{aligned} \ddot{x} + k_\mathrm{na} x |x|^{\alpha - 1} = 0. \end{aligned}$$
(15)

Equation (15) is the mathematical model of the free vibration of the string–mass system. It is a truly nonlinear second-order differential equation with the exact solution [36]

$$\begin{aligned} x=Cca (\alpha , 1, \Omega t^{*}+\theta ) \end{aligned}$$
(16)

where ca is the cosine Ateb (inverse beta) function with amplitude C, phase angle \(\theta \) and frequency \(\Omega \). Namely, using (16) and time derivatives [37],

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t^{*}}ca ({\alpha , 1, \Omega {{t}}^{*} + \theta })= & {} -\frac{2 \Omega ^{*}}{\alpha +1} sa ({1, \alpha , \Omega {t}^{*} + \theta }), \end{aligned}$$
(17)
$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t^{*}}sa ({1, \alpha , \Omega {{t}}^{*} + \theta })= & {} \Omega ca^{\alpha } ({\alpha , 1, \Omega {t}^{*} + \theta }) \end{aligned}$$
(18)

where sa is the sine Ateb function which satisfies the relation

$$\begin{aligned} ca^{\alpha +1} ({\alpha , 1, \Omega {t}^{*} + \theta }) + sa^{2} ({1, \alpha , \Omega {t}^{*} + \theta })=1, \end{aligned}$$
(19)

and substituting in (15), the frequency of the function follows as

$$\begin{aligned} \Omega = \sqrt{\frac{k_\mathrm{na} C^{\alpha -1}}{2({\alpha +1})}}. \end{aligned}$$
(20)

The period of functions \(sa ({1, \alpha , \Omega {t}^{*} + \theta })\) and \(ca ({\alpha , 1, \Omega {t}^{*} + \theta })\) is according to [38]

$$\begin{aligned} P=\frac{2B\left( {\frac{1}{\alpha +1},\frac{1}{2}} \right) }{\Omega } \end{aligned}$$
(21)

where B is the beta function. Using (20) and (21), the frequency of vibration is computed as

$$\begin{aligned} \omega ^{*} = \frac{\pi }{B\left( {\frac{1}{\alpha +1},\frac{1}{2}} \right) }\sqrt{\frac{2C^{\alpha -1}}{\alpha +1}k_\mathrm{na}}, \end{aligned}$$
(22)

i.e., for (12)

$$\begin{aligned} \omega ^{*} = \frac{\pi }{B \left( {\frac{1}{\alpha +1},\frac{1}{2}} \right) }\sqrt{\frac{2C^{\alpha -1}}{\alpha +1}\frac{EA}{mL \Omega ^{2}}}. \end{aligned}$$
(23)

Analyzing (23), it can be concluded that the frequency of vibration is higher for higher rigidity of the string. If the mass of the absorber is smaller, the frequency of the vibration is higher. The frequency of vibration depends on the length of the string: The longer the string, the smaller is the frequency. The frequency of vibration depends on the initial deflection and on the order of nonlinearity, too.

3.2 Forced vibration of the string–mass system

Let us assume the multi-harmonic excitation given in the general form. In [39], it is suggested that the most suitable form of the excitation force is a cosine Ateb periodic function

$$\begin{aligned} f=F_0 ca ({\alpha , 1, \Omega _e t}) |{ca ({\alpha , 1, \Omega _e t})}|^{\alpha -1} \end{aligned}$$
(24)

where \(F_{0}\) is the amplitude and \(\Omega _{\mathrm{e}}\) is the frequency of the function. Namely, it is known that the ca function has a cosine Fourier series expansion. Introducing the dimensionless coefficients

$$\begin{aligned} \Omega ^{*}= \frac{\Omega _e}{\omega }, \quad f_0 =\frac{F_0}{mL \Omega _e^2}, \end{aligned}$$
(25)

and considering the forced vibration, the mathematical model of the forced vibration of the system is

$$\begin{aligned} \ddot{x} + k_\mathrm{na} x |x|^{\alpha - 1} = f_{0} ca (\alpha , 1, \Omega ^{*} t^{*}) |ca (\alpha , 1, \Omega ^{*} t^{*})|^{\alpha - 1}. \end{aligned}$$
(26)

For the known excitation parameters \(F_{0}\) and \(\Omega ^{*}\), Eq. (26) has an exact analytical solution

$$\begin{aligned} x=Cca ({\alpha , 1, \Omega ^{*} t^{*}}) \end{aligned}$$
(27)

where C is the amplitude of vibration which satisfies the relation

$$\begin{aligned} -\frac{2C}{\alpha +1} \Omega ^{*2} + k_\mathrm{na} C |C|^{\alpha -1}=f_0, \end{aligned}$$
(28)

i.e., the expression with real coefficients

$$\begin{aligned} -\frac{C}{\beta +1}\frac{m^{2}L^{2} \Omega _e^4}{T_0} + EAC |C|^{2\beta } =F_0. \end{aligned}$$
(29)

For the case when the excitation force \(F_0\) is of the order of EA and much higher than \(\frac{m^{2}L^{2} \Omega _e^4}{T_0}\), the approximate value of the amplitude of vibration is

$$\begin{aligned} C= \left( \frac{F_0}{EA}\right) ^{\frac{1}{2\beta +1}}. \end{aligned}$$
(30)

The amplitude depends on the order of nonlinearity of the string material \(\beta \): The higher the coefficient \(\beta \), is the smaller is the amplitude of vibration.

4 Influence of the preloading force on the vibration

If the preloading force of the string, i.e., the linear term, and also the damping term exist, the equation of motion is

$$\begin{aligned} \ddot{x} + k_\mathrm{na} x |x|^{\alpha -1} = - \varepsilon k_\mathrm{na} x - \varepsilon c {\dot{x}}. \end{aligned}$$
(31)

Equation (31) is a strongly nonlinear equation with small perturbation terms with small parameter \(\varepsilon \). Comparing (15) and (31), it is concluded that Eq. (31) is the perturbed version of Eq. (15). For this assumption, it is obvious that the solution of (31) has to be the perturbed version of the solution of (15). Based on this assumption, the following procedure for solving (31) is introduced:

  • First, the exact solution of (15) is determined.

  • The solution of (31) and its derivative are assumed in the form of the solution of (15) and its derivative.

  • The first derivative of the assumed solution of (31) is computed and compared with the assumed first derivative of (15). Equating the relations a first-order equation is obtained.

  • Substituting the assumed solution in (31), the additional first-order equation is obtained.

  • The second-order differential Eq. (31) is transformed into two first-order differential equations where the new variables are the amplitude and phase of vibration.

  • For solving of the first-order differential equations, the averaging procedure is introduced.

If the length of the string and the preloading string force \(T_{0}\) are not varying, parameters \(k_\mathrm{la}\) and \(k_\mathrm{na}\) are constant, and Eq. (31) is with constant coefficients. Otherwise, if the length of the string and the preloading force are varying in time, parameters \(k_\mathrm{la}\) and \(k_\mathrm{na}\) are also time variable and Eq. (31) is with time variable coefficients.

4.1 System with constant string force

According to the suggested procedure, the solution of (31) and its first derivative are assumed in the form (16) but with the time variable parameters, i.e.,

$$\begin{aligned} x=C ({t^{*}}) ca ({\alpha , 1, \psi ({t^{*}})}), \quad {\dot{x}} = - {\frac{2 \Omega ^{*} (t^{*})}{\alpha + 1}} C (t^{*}) sa (1, \alpha , \psi (t^{*})) \end{aligned}$$
(32.1,2)

where \(C = C (t^{*})\) is the time variable amplitude and \(\psi = \psi (t^{*})\) is the time variable phase that satisfies the relation

$$\begin{aligned} {\dot{\psi }} (t^{*}) = \Omega (t^{*}) + {\dot{\theta }} (t^{*}). \end{aligned}$$
(33)

Comparing (32.2) with the complete time derivative of (32.1), the following constraint is obtained:

$$\begin{aligned} {\dot{C}} ca - C {\dot{\theta }} {\frac{2}{\alpha + 1}} sa = 0 \end{aligned}$$
(34)

where \(C = C(t^{*})\), \(\psi = \psi (t^{*})\), \(\theta = \theta (t^{*})\), \({\textit{ca}} = ca (\alpha , 1, \psi )\), and \({\textit{sa}} = {\textit{sa}}(1,\alpha , \psi )\). Using the time derivative of (32.2) and substituting in (31), we obtain

$$\begin{aligned} ({\dot{C}} \Omega + C {\dot{\Omega }}) {\frac{2}{\alpha + 1}} sa + C\Omega {\dot{\theta }} {\frac{2}{\alpha + 1}} ca^{\alpha } = \varepsilon k_\mathrm{la} Cca-\varepsilon cC \Omega \frac{2}{\alpha +1}sa. \end{aligned}$$
(35)

Equations (34) and (35) correspond to the second-order differential equation (31). After some modification, it is

$$\begin{aligned} {\dot{C}} \Omega= & {} \varepsilon k_\mathrm{la} Csaca - \varepsilon c C \Omega {\frac{2}{\alpha + 1}} sa^{2}, \end{aligned}$$
(36)
$$\begin{aligned} C \Omega {\dot{\theta }} {\frac{2}{\alpha + 1}}= & {} \varepsilon k_\mathrm{la} Cca^{2} - \varepsilon c C \Omega {\frac{2}{\alpha + 1}} saca. \end{aligned}$$
(37)

For simplification, we average equations (36) and (37) over the period P of the Ateb function. The averaged equations are

$$\begin{aligned} {\dot{C}} \Omega= & {} -\varepsilon cC\Omega {\frac{2}{\alpha + 1}} \langle sa^{2} \rangle , \end{aligned}$$
(38)
$$\begin{aligned} C \Omega {\dot{\theta }} {\frac{2}{\alpha + 1}}= & {} \varepsilon k_\mathrm{la} C \langle ca^{2} \rangle \end{aligned}$$
(39)

where

$$\begin{aligned} \langle sa^{2}\rangle = \frac{1}{P}{\int }_0^P \, sa^{2}\hbox {d}\psi =\frac{\alpha +1}{\alpha +3}, \quad \langle ca^{2}\rangle = \frac{1}{P}{\int }_0^P \, ca^{2}\hbox {d}\psi , \quad \langle sa \, ca \rangle = \frac{1}{P}{\int }_0^P \, sa \, ca \, \hbox {d}\psi =0 \end{aligned}$$

Solving Eq. (38), it is

$$\begin{aligned} C=C_0 \exp \left( {-\frac{2\varepsilon c}{\alpha +3}t^{*}} \right) \end{aligned}$$
(40)

where \(C_{0}\) is the arbitrary initial value. Substituting (40) in (39), the time variation of the phase is

$$\begin{aligned} \psi ({t^{*}}) = {\int }_0^{t^{*}} \left( \Omega + \frac{\varepsilon k_\mathrm{la}}{\Omega } \frac{\alpha +1}{2}ca^{2}\right) \hbox {d}t^{*}. \end{aligned}$$
(41)

Using the amplitude and phase relation, the relative motion of the string–mass system is approximately expressed as

$$\begin{aligned} X=(C_0 L)\exp \left( {-\frac{2\varepsilon c}{\alpha +3}\sqrt{\frac{T_0}{mL}}t} \right) ca ({\alpha , 1, \psi (t)}). \end{aligned}$$
(42)

Based on (42), we conclude that the amplitude of vibration decrease depends not only on the damping coefficient and mass of the slider, but also on the length of the string, preloading force, and order of nonlinearity.

Numerical example

For the real mechanism with mass \(m = 1\) kg, string length \(L = 1\) m, cross section of the string \(A = 125 \, {\hbox {mm}}^{2}\), modulus of elasticity \(E = 200\) GPa, and the order of nonlinearity 2.73 (see [21]), the dimensionless coefficient of nonlinearity is \(k_\mathrm{na} = 10.3\). It is known that for standard construction materials it is always true that \({\textit{EA}}\gg T_{0}\), since \(T_{0}/A\) is smaller than the break tension, and break tension is much smaller than E. Then, for tensioning a string with a safety factor 2 with respect to break, it follows that \(T_{0} < {\textit{EA}}/400\). Assuming the preloading force \(T_{0} = 15 \, \hbox {N}\) and the damping coefficient \(c = 1 \, \hbox {kg/s}\), we calculate the dimensionless parameters \(\varepsilon k_\mathrm{la} =0.12\), \(\varepsilon c=0.833\) and \(\Omega =1.175 C^{0.865}\).

For this set of parameters, the equations of motion (36) and (37) are

$$\begin{aligned} {\dot{C}} = 0.10213 C^{0.135} saca - 0.4465 Csa^{2}, \qquad {\dot{\theta }} = 0.19047 ca^{2} C^{-0.865} - 0.833 saca. \end{aligned}$$
(43)

The averaged equations (38) and (39) transform into

$$\begin{aligned} {\dot{C}} = -0.29075 C, \quad {\dot{\theta }} = 0.16231 C^{-0.865}. \end{aligned}$$

Integrating the equations for the initial conditions \(C(0) = 0.5\) and \(\theta (0) = 0\), the averaged amplitude and phase variations are \(C=0.5 \exp \, ({-0.29075t^{*}})\) and \(\theta =0.33031 (\exp (0.25150t^{*})-1)\). In Fig. 2, the solution of the exact equation (43) obtained numerically and the averaged amplitude of vibration \(C-t^{*}\) obtained analytically is plotted. It is obvious that the averaged amplitude is on the top of the exact curve and the difference is negligible.

Fig. 2
figure 2

Numerical solution of the exact equations (43) (full line) and the analytically obtained averaged amplitude curve (dotted line)

Full size image

4.2 System with time variable string force

In the system shown in Fig. 1, the length of the string and the preloading force can be varied. The effect of their variation is mathematically recognized as the time variation of the coefficients \(k_{\mathrm{na}}\) and \(k_{\mathrm{la}}\). If the change of parameters is slow and the function of the so-called slow time \(\tau = \varepsilon t\), the equation of motion (31) is transformed into

$$\begin{aligned} \ddot{x} + k_\mathrm{na} (\tau ) x |x|^{\alpha -1} = - \varepsilon k_\mathrm{la} (\tau ) x - \varepsilon c {\dot{x}}. \end{aligned}$$
(44)

To solve Eq. (44), we introduce the solution and its time derivative in form (32) with frequency function \(\Omega \) which depends on the amplitude of vibration C and on the slow time \(\tau \). Introducing the assumed solution, Eq. (44) transforms into

$$\begin{aligned} {\dot{C}} \left( \Omega + C {\frac{\partial \Omega }{\partial C}}\right) {\frac{2}{\alpha + 1}} sa + C \Omega {\dot{\theta }} {\frac{2}{\alpha + 1}} ca^{\alpha } = \varepsilon k_\mathrm{la} Cca - \varepsilon c C\Omega {\frac{2}{\alpha + 1}} sa - \varepsilon C {\frac{\partial \Omega }{\partial \tau }} {\frac{2}{\alpha + 1}} sa. \end{aligned}$$
(45)

Equations (34) and (45) are two first-order differential equations which represent the rewritten version of (44) in new variables C and \(\psi \), i.e., \(\theta \). After some transformation and using the relation (20), it is

$$\begin{aligned} {\dot{C}} \Omega= & {} \varepsilon k_\mathrm{la} Csaca - \varepsilon c C\Omega {\frac{2}{\alpha + 1}} sa^{2} - \varepsilon C {\frac{\partial \Omega }{\partial C}} {\frac{2}{\alpha + 1}} sa^{2}, \end{aligned}$$
(46)
$$\begin{aligned} C \Omega {\dot{\theta }} {\frac{2}{\alpha + 1}}= & {} \varepsilon k_\mathrm{la} Cca^{2} - \varepsilon c C\Omega {\frac{2}{\alpha + 1}} saca - \varepsilon C {\frac{\partial \Omega }{\partial C}} {\frac{2}{\alpha + 1}} saca. \end{aligned}$$
(47)

To solve the system of Eqs. (46) and (47) is not an easy task. It is at this moment the averaging over the period of Ateb functions is introduced. The averaged equations are

$$\begin{aligned} {\dot{C}}= & {} - \varepsilon C \left( {\frac{1}{\Omega }} {\frac{\partial \Omega }{\partial \tau }} + c\right) {\frac{2}{\alpha + 1}} \langle sa^{2} \rangle , \end{aligned}$$
(48)
$$\begin{aligned} \Omega {\dot{\theta }} {\frac{2}{\alpha + 1}}= & {} \varepsilon k_\mathrm{la} \langle ca^{2} \rangle . \end{aligned}$$
(49)

Using (20) and the initial amplitude \(C_{0}\), after integration the expression for amplitude variation is obtained,

$$\begin{aligned} \frac{C}{C_0} = \left( {\frac{\Omega _0}{\Omega (\tau )}} \right) ^{\frac{2}{\alpha +3}}\exp \left( {-\frac{2c}{m\left( {\alpha +3} \right) }{\int }_0^\tau \sqrt{\frac{T_0 (\tau )}{L(\tau )}}\hbox {d}\tau } \right) , \end{aligned}$$
(50)

where

$$\begin{aligned} \frac{\Omega _0}{\Omega (\tau )} = \left( {\frac{C_0}{C}} \right) ^{\frac{\alpha -1}{2}}\sqrt{\frac{k_\mathrm{na0}}{k_\mathrm{na}}}. \end{aligned}$$

\(k_{\mathrm{na0}}\) is the initial value of the coefficient. According to (12), the relation is rewritten into

$$\begin{aligned} C=C_0 \left( {\frac{L(\tau )}{L}} \right) ^{\frac{1}{2({\alpha +1})}}\exp \left( {-\frac{c}{m({\alpha +1})}{\int }_0^\tau \sqrt{\frac{T_0 (\tau )}{L(\tau )}}\hbox {d}\tau } \right) . \end{aligned}$$
(51)

For the case when the length of the string is constant, the amplitude variation is

$$\begin{aligned} C=C_0 \exp \left( {-\frac{c}{mL({\alpha +1})}{\int }_0^\tau \sqrt{T_0 (\tau )}\hbox {d}\tau } \right) . \end{aligned}$$
(52)

The amplitude decreases in time. The velocity of amplitude decrease depends on the preloading force variation. The higher the preloading force in the string, is the faster the amplitude decrease is.

However, if the damping is neglected and the length of the string is varying, the amplitude of vibration is

$$\begin{aligned} C = C_0 \left( {\frac{L(\tau )}{L}} \right) ^{\frac{1}{2({\alpha +1})}}. \end{aligned}$$
(53)

For \(\alpha =3\), relation (53) gives the result which is already published in [40].

The variation of phase angle (49) is

$$\begin{aligned} {\dot{\theta }} = \varepsilon k_\mathrm{la} {\frac{\alpha + 1}{2}} {\sqrt{{\frac{2 (\alpha + 1)}{k_\mathrm{na} c^{\alpha - 1}}}}} \langle ca^{2} \rangle . \end{aligned}$$
(54)

It is evident that the phase angle \(\theta \) tends to increase in time. The phase angle variation depends on the amplitude of vibration, i.e., not only on the damping coefficient and order of nonlinearity, but also on the string force time variation.

Using the previously obtained results, we can calculate the amplitude variation due to the variation of the preloading force. On the contrary, for the known preloading force–time function, we can predict the amplitude of vibration of the string–mass system.

5 Discussion

To give an appropriate explanation for the obtained analytical results, a numerical example is considered. For the real system, where the cross section of the string is \(125 \, {\hbox {mm}}^{2}\), modulus of elasticity \(E = 200\) GPa, and the order of nonlinearity 2.73 (see [21]), the dimensionless differential equation of motion (31) for the preloading force \(T = 15 \, \hbox {N}\) is

$$\begin{aligned} {\ddot{x}} + 10.3 x |x|^{1.73} = - 0.12x - 0.833 {\dot{x}}. \end{aligned}$$
(55)

In Fig. 3a, the analytical solution (43) and the numerical solution of (55) are compared. They are in good agreement.

In Fig. 3b, the influence of the constant preloading string force on the vibration of the system is considered. The equation of motion is solved numerically. Two different values for the force are applied. It is obtained that for higher value of the preloading the vibration decrease is faster and the period of vibration is shorter.

Fig. 3
figure 3

Displacement–time curves: a numerically (black line) and analytically (red line) obtained solutions; b numerically obtained solutions for various preloading forces: \(T=23 \, \hbox {N}\) (red line) and \(T =34 \, \hbox {N}\) (black line) (color figure online)

Full size image

In this Section, the dynamics of the string–mass system where the preloading string force is varying is considered. Two types of force variation are assumed: (a) preloading force decreases, and (b) the preloading force increases in slow time.

If there is the slow time relaxation of the string force described as

$$\begin{aligned} T=\frac{T_0 }{(1+p\tau )^{2}}, \end{aligned}$$

the amplitude variation is

$$\begin{aligned} C=\frac{C_0 }{(1+p\tau )^{\frac{p_1 }{p}}} \end{aligned}$$

where p is the parameter of the force decrease in time, and

$$\begin{aligned} p_1 =\frac{cT_0 }{mL({\alpha +1})}. \end{aligned}$$

For \(p=\frac{p_1 }{2}\), the decrease in the amplitude corresponds to the force decrease. Otherwise, for \(p = 1\) and \(p_{1} > 2\) the amplitude decrease is faster than the decrease in the preloading force.

For \(m = 1 \, \hbox {kg}\), \(c = 1 \, \hbox {kg/s}\), \(L = 1 \, \hbox {m}\), \(\alpha = 2.73\), \(T_{0} = 10 \, \hbox {N}\), various values of parameter p, the \(T-\tau \) and \(C-\tau \) diagrams are plotted (Fig. 4). It is obtained that for higher values of the parameter p the decrease in the preloading force is faster than for small p. However, the amplitude decrease is slower in time for higher values of p than for smaller ones. To obtain the faster amplitude decrease, we need smaller values of parameter p and the slow preloading force decrease.

In Fig. 5, the \(T-\tau \) and \(C-\tau \) diagrams for various values of the initial preloading force \(T_{0}\) are plotted. It is obvious that the variation of the initial preloading force has influence on the velocity of amplitude decrease. The amplitude decrease is faster for higher values of the initial preloading force.

Fig. 4
figure 4

\(T{-}\tau \) (red full line) and \(C{-}\tau \) (blue dotted line) diagrams for various p (color figure online)

Full size image
Fig. 5
figure 5

\(T{-}\tau \) (red full line) and \(C{-}\tau \) (blue dotted line) diagrams for various \(T_{0}\) (color figure online)

Full size image

If there is the preloading force increasing in time,

$$\begin{aligned} T=\frac{T_0 }{(1-p\tau )^{2}}, \end{aligned}$$

the amplitude of vibration is

$$\begin{aligned} C=C_0 (1-p\tau )^{\frac{p_1 }{p}}. \end{aligned}$$

In Fig. 6, the influence of parameter p on the variation of the string force and on the vibration amplitude is plotted. It is obtained that for higher values of parameter p the increase in the preloading force is faster than for the smaller values of p. The same holds for the amplitude of vibration: For higher value of p, the velocity of the amplitude decrease is higher.

Fig. 6
figure 6

\(T{-}\tau \) (red full line) and \(C{-}\tau \) (blue dotted line) diagrams for various p (color figure online)

Full size image
Fig. 7
figure 7

\(T{-}\tau \) (red full line) and \(C{-}\tau \) (blue dotted line) diagrams for various \(T_{0}\) (color figure online)

Full size image

In Fig. 7, the \(T{-}\tau \) and \(C{-}\tau \) diagrams for various values of the initial preloading force are considered. It is obtained that the initial value of the preloading force has influence on the variation of the amplitude of vibration. For smaller values of the initial preloading force, the amplitude decrease is faster.

6 Conclusions

In the paper, the dynamics of the SD oscillator, modeled as a string–mass structure which is the sub-system of a vibration absorber, is investigated. The influence of the preloading force of the string on the dynamics of the mass–string system is studied. The motion of the system is described with a strong nonlinear differential equation where the order of nonlinearity is a positive real number (an integer or non-integer). It defines the geometric and physical nonlinearity of the string. The solution of the nonlinear differential equation is suggested in the form of the Ateb function. The solution procedure is based on the solution of the truly nonlinear equation and represents the modified version of the linear solving treatment. Amplitude and phase of vibration are time dependent, while the frequency depends on the amplitude of vibration, too. It is concluded that the analytically obtained results agree with numerical ones.

In addition, it is seen that the preloading force in the string has significant influence on the mass motion in the system: The higher the preloading is, the faster the vibration damping is, and the period of vibration is shorter. In addition, it is concluded that velocity of the variation of the preloading force has an effect on the system motion. If the preloading force is decreasing and we start with a high value of the initial preloading force, the amplitude of vibration would decrease faster than if the initial preloading force is small. However, if the preloading force is increasing, the small initial preloading force is more convenient for faster amplitude decrease. Thus, the preloading force can be used as the control parameter of the system. The mass–string structure suggested in the paper is suitable to be applied for vibration mitigation caused by any multi-harmonic excitation (earthquake or wind force) as the string tension tunes the frequency of the device with excitation one.