Stability of modulated signals in the damped mechanical network of discontinuous coupled system oscillators with irrational nonlinearities

Abstract

The behavior of mechanical network consisting of discontinuous damped system oscillators elastically coupled with strong irrational nonlinearities, excited at one of its end by the modulated signal, is investigated. By using the Newton second law, the set of discrete damped equations governing the dynamics of this network are established. These set of equations have strong irrational nonlinearities, with smooth or discontinuous characteristics depending just to the inclination angles of strings. By using next the perturbation method, these set of discrete equations are reduced to the nonlinear cubic Landau–Ginzburg (CGL) equation governing the small dissipative amplitude modulated signal. As this CGL equation is not integrable, the dissipative modulated pulse and dark solitons as solutions are approximated via perturbation method, which is confirmed by using the conserved quantities as well as numerical investigations. Finally the conditions for modulational instability are found and proved to be sensitive both to inclination angle and dissipative coefficient.

1 Introduction

The mathematical modeling of discrete systems behaviors by continuous partial differential (PD) equations has always attracted enormous attentions in linear and nonlinear sciences [1,2,3,4]. When the size of discrete systems is sufficiently large, they are viewed as continuous media, from where different perturbation methods are usually applied to reduce their discrete equations to PD equations easy to solve, and each method is chosen according to the desired solution. To name just a few, the Korteweg de Vries (KdV) [3, 4], the Boussinesq [4] and the sine-Gordon [5,6,7] equations are usually found for envelope solitons, while the nonlinear Schrödinger (NLS) [1, 2] and the Ginzburg Landau (GL) [8] equations are found for modulated solitons. Soliton being a well-known and intriguing aspect of nonlinear behavior in a continuous systems [9]. Among the above-mentioned equations, some are integrable and easy to solve, while the others, as the GL equation, are non-integrable and their solutions need to be approximated. The non-integrability of the last equations is due to the fact that their parameters are complex, and obtained for dissipative networks. One of the key properties of a dissipative dynamical system is that the total energy stored in the system decreases with time [10]. Discrete systems are designed and used for their potential applications in several branches of physics including electronic [2, 4, 11], optic [12] and mechanics [13]. In electronic for example, the discrete nonlinear transmission lines (NLTL) are used as waveguide for the propagation of signal voltages for one place to another but with strong losses due to the presence of resistors. NLTLs are also used as signal amplifiers or as generators of solitary wave trains (see [14] and references therein). In optics, the optical fibers have been proved to be adequate for signal light transmission and solitons generations without considerably losses [12]. In mechanics the chain of string or pendulum leads to mechanical networks adequate for solitons generation [1].

With regard to non-integrable nonlinear differential equations usually found in nonlinear science, perturbation methods are usually used to approximate their solutions, by starting from the exact solution of a related solvable equations [15]. A critical feature of the technique is a middle step that breaks the model differential equations into both solvable and perturbative parts [4]. In perturbation theory, the solution is expressed as a power series in an arbitrary small parameter $\epsilon$ [15]. The first term being the known solution to the solvable part of the equation. While successive terms in the series at higher powers of $\epsilon$ usually become smaller. An approximate perturbation solution is obtained by truncating the series, usually by keeping only the first two terms, that is the solution to the solvable part and that of the first order perturbation correction. The small parameter $\epsilon$ usually vanishes in the resulting solution, taking into account to initial or/and boundary conditions. This is why this parameter must not be taken as tuning parameter of the system equation.

Very recently, Adoum Danao Adile et al. [1] proposed an undamped mechanical network (UMN) where each unit cell has irrational nonlinearity, which leads to the transition from smooth to discontinuous dynamics. It is important to mention that for the smooth dynamics, the restoring force created by inclined springs is a continuous function, while for that discontinuous, the restoring force is discontinuous for particular values of parameters [16]. This nonlinear oscillator being comprised a lumped mass, linked by a pair of inclined elastic linear springs. As a consequence the nonlinearity obtained was strong and due just to the inclination. Adoum Danao Adile et al. found that although the network obtained had riches dynamics, the absence of dissipation leads to solutions with infinite amplitude near resonant frequency which is not suitable for real applications. In order to prove that this network can find its application in industry and technology, Fabien Kenmogne et al. [13] proposed then a model of sand sieve, which has at the entrance the driven Van der Pol oscillator, which is coupled at the output to sand sieve through the damped mechanical network described here, while its dynamics have being studied in details. However in both previous works, any attention has been focussed on the propagation of signals and modulational instability (MI) in this UMN which could lead to other potential applications. These two items will then constitute the main purpose of the present work. Thus, the rest of the paper is organized as follows:

In Sect. 2 we will describe the model and derive the governing equations. Section 3 will be devoted to effects of damping on the envelope solitons like signals; then we have derived the cubic Guinzburg equation describing small amplitude signal propagation, following by the seeking of dissipative envelope solitons like signals. Finally Sect. 4 is devoted to find the condition under which the modulated plane wave propagating in the system will become instable to a small perturbation (the MI).

2 Description of the system model and equations of motion

We consider the mechanical network consisting of a discontinuous coupled system oscillator with strong irrational nonlinearities in which each unit cell is consisting of a lumped identical mass m, linked by a pair of inclined elastic springs of stiffness k, capable of resisting both tensions and compressions and which are pinned to their rigid supports (T). Although each of the inclined springs provides linear restoring resistance, it has been proved that the resulting force has a strong irrational nonlinearity due to the geometric configuration [1, 13]. Each unit cell is coupled to the first neighbors through the elastic springs of stiffness $k_s$, while the lumped mass make frictions on horizontal bar with the friction coefficient $\mu$. By applying the Newton second law, one can have the following ordinary differential equation:

$$\begin{aligned} m\ddot{u}_n+f(u_n)+k_s(2u_n-u_{n+1}-u_{n-1})+\mu (2\dot{u}_n-\dot{u}_{n+1}-\dot{u}_{n-1})=0\nonumber \\ ,\quad for \quad n=1,...,N, \end{aligned}$$

(1)

governing the displacement $u_n(t)$ of the n th mass. In the above equation the dots are derivatives with respect to time t. $f(u_n)$ defined as

$$\begin{aligned} f(u_n)=2ku_n-k\sqrt{d^2+h^2}\left( \frac{u_n+d}{\sqrt{(u_n+d)^2+h^2}}+ \frac{u_n-d}{\sqrt{(u_n-d)^2+h^2}}\right) \end{aligned}$$

(2)

is the nonlinear restoring force created by inclined springs. This force is a continuous function of $u_n$, leading to smooth dynamics, except when $h\equiv 0$, which takes the form $f(u_n)=2ku_n-k\sqrt{d^2+h^2}\left( sign(u_n+d)+ sign(u_n-d)\right)$. sign(x) being the signum function. For this last case, $f(u_n)$ isn’t a continuous function for $u_n\approx \pm d$, leading to the fact that the dynamics is discontinuous.

Fig. 1

Schematic diagram of the mechanical network

In order to write the governing equation of the system in dimensionless form, let us first take into account the angle $\theta$ (with $\tan (\theta )=h/d$) between the direction of inclined strings and the horizontal direction, and secondly make the following change of variables and parameters:

$$\begin{aligned} U_n=u_n/\sqrt{d^2+h^2},\quad \tau =t\omega _0,\quad \omega _0^2=k/m,\quad \varepsilon _r=k_s/k,\quad \mu _s=\frac{\mu \omega _0}{k}, \end{aligned}$$

(3)

leading to the following set of equations;

$$\begin{aligned}&\ddot{U}_n+2U_n-\left( \frac{U_n+\cos (\theta )}{\sqrt{(U_n+\cos (\theta ))^2+\sin ^2(\theta )}}+ \frac{U_n-\cos (\theta )}{\sqrt{(U_n-\cos (\theta ))^2+\sin ^2(\theta )}}\right) \nonumber \\&\quad +\left( \varepsilon _r+\mu _s\frac{d}{d\tau }\right) (2U_n-U_{n+1}-U_{n-1})=0,\quad for \quad n=1,...,N. \end{aligned}$$

(4)

The restoring force (2) of the system can easily be written as

Fig. 2

The nonlinear irrational restoring force

$$\begin{aligned} f(U_n)=2U_n-\left( \frac{U_n+\cos (\theta )}{\sqrt{(U_n+\cos (\theta ))^2+\sin ^2(\theta )}}+ \frac{U_n-\cos (\theta )}{\sqrt{(U_n-\cos (\theta ))^2+\sin ^2(\theta )}}\right) . \end{aligned}$$

(5)

Figure 2 plotted for different values of $\theta$ shows the discontinuity for $\theta \equiv 0$ and a continuity elsewhere, which means the irrational character of the restoring force.

3 Effects of damping on the envelope solitons like signals

3.1 Cubic Guinzburg equation

The set of the above differential equations are very difficult to solve, and their solutions need to be approximated via the integrable equations easy to solve [4, 17, 18]. In order to simplify the above set of equations in a form easily solvable, let us consider that the total number of cell N is large and the distance between two adjacent cells d weak, i.e the well-known continuum limit would be applied. For this parameter regime, the system allows as solution the signal with long wavelength [4, 19]. Then ${U}_n(t)$ is supposed to vary slowly from one cell to another so that the discrete expression of Eq. (4) can be approximated by the a third-order Taylor expansion about $U_{n\pm 1}(t)$. Let us adopt here the reductive perturbation approach in the semi-discrete approximation [14, 20], according to which the time dependence of the displacement at lattice site n is expressed approximately as

$$\begin{aligned} U_n(t)=\epsilon U_1(x,\tau )e^{-\chi n}e^{i\phi (n,t)}+cc \end{aligned}$$

(6)

where c.c. denotes the complex conjugation, $\chi$ the dissipation coefficient, and the functions $U_1(x,\tau )$ is to be determined. The phase variable $\phi$ and the envelope variables x and $\tau$ are defined as

$$\begin{aligned} \phi (n,t)=kn-\omega t,\quad x=\epsilon \left( n-v_gt\right) ,\quad \tau =\epsilon ^2t. \end{aligned}$$

(7)

Substituting the solution (6) into the set of Eqs. (4) and taking into account only the coefficients of the first harmonic (coefficients proportional to $e^{i\phi (n,t)}$) one obtains:

$\blacktriangle$ At order $\epsilon ^1e^{i\phi (n,t)}$, the following dispersion relation:

$$\begin{aligned} \Omega _m^2-\omega ^2+(\varepsilon _r-i\omega \mu _s)\left( 2-e^{-\chi }e^{ik}-e^{\chi }e^{-ik}\right) =0, \end{aligned}$$

(8)

where $\Omega _m$ is defined as $\Omega _{m}^{2} = 2\cos ^{2} (\theta )$. Separating this equation into real and imaginary parts yield:

$$\begin{aligned} \omega ^2-\Omega _m^2-2\mu _s\omega \sin (k)\sinh (\chi )-2\varepsilon _r\left[ 1-\cos (k)\cosh (\chi )\right] =0, \end{aligned}$$

(9)

for the real part, and

$$\begin{aligned} \chi =\ln \left( \frac{\omega \mu _s+\sin (k)\sqrt{\varepsilon _r^2+\omega ^2\mu _s^2}}{\varepsilon _r\sin (k)+\omega \mu _s\cos (k)}\right) , \end{aligned}$$

(10)

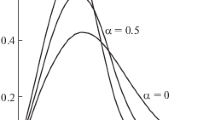
for the imaginary part. In Fig. 3, $\omega$ and $\chi$ are plotted for $\mu _s=0.01$, and $\varepsilon _r=1$. As one can see the system has the band pass filter character, and the dissipation coefficient increases with increasing value of k. Otherwise, the lower gap frequency decreases as $\theta$ increases, leading at $\theta =\pi /2$ to the lower pass filter.

Fig. 3

a Dispersion relation, and b dissipation coefficient, obtained for $\varepsilon _r=1$ and for varying values of $\theta$. with $\mu _s=0.01$, blue. As one can see, the dissipation coefficient tends to increase the maximum of the band pass frequency

$\blacktriangle$ At order $\epsilon ^2e^{i\phi (n,t)}$, one obtains the group velocity $v_g=v_{gr}+iv_{gi}$, with

Fig. 4

Group velocity with same parameters as in Fig. 6. a The real part, b The imaginary part

$$\begin{aligned}&v_{gr}=\frac{2\left[ \mu _s\left( \Gamma _1\Gamma _2-4\varepsilon _r^2\omega ^2\right) \cos (k)\sinh (\chi )+ 2\omega \varepsilon _r\left( \varepsilon _r^2+\mu _s^2\Omega _m^2\right) \sin (k)\cosh (\chi )\right] }{4\varepsilon _r^2\omega ^2+\mu _s^2\omega _r^4},\nonumber \\&v_{gi}=\frac{2\left[ \mu _s\left( \Gamma _1\Gamma _2-4\varepsilon _r^2\omega ^2\right) \sin (k)\cosh (\chi )- 2\omega \varepsilon _r\left( \varepsilon _r^2+\mu _s^2\Omega _m^2\right) \cos (k)\sinh (\chi )\right] }{4\varepsilon _r^2\omega ^2+\mu _s^2\omega _r^4}, \end{aligned}$$

(11)

in which

$$\begin{aligned} \Gamma _1=\omega ^2-\omega _m^2,\quad \Gamma _2=\varepsilon _r^2-\mu _s^2\omega ^2,\quad D=4\varepsilon _r^2\omega ^2+\mu _s^2\omega _r^4,\quad \omega _r=\sqrt{\omega ^2+\Omega _m^2}. \end{aligned}$$

(12)

$\blacktriangle$ At order $\epsilon ^3e^{i\phi (n,t)}$, one obtains the following partial differential equation:

Fig. 5

Real and imaginary parts of P, with same parameters as in Fig. 6

Fig. 6

Real and imaginary parts of Q, with same parameters as in Fig. 6

$$\begin{aligned} i\frac{\partial U_1}{\partial \tau }+\left( P_r+iP_i\right) \frac{\partial ^2 U_1}{\partial x^2}+\left( Q_r+iQ_i\right) H(n,U_1)U_1=0, \end{aligned}$$

(13)

with $H(n,U_1)=e^{-2\chi n}\left\| U_1\right\| ^2$, and

$$\begin{aligned}&P_r=\left[ \omega \left( 2\varepsilon _r^2+\mu _s^2\omega _r^2\right) \left( v_{gr}^2-v_{gi}^2+ \mu _s\sin (k)\xi _1+\cos (k)\xi _2\right) -2\mu _s\varepsilon _r\Gamma _1\left( 2v_{gr}v_{gi}+\right. \right. \nonumber \\&\left. \left. \mu _s\cos (k)\xi _3+\sin (k)\xi _4\right) \right] /\left( {4\varepsilon _r^2\omega ^2+\mu _s^2\omega _r^4}\right) ,\nonumber \\&P_i=-\left[ \omega \left( 2\varepsilon _r^2+\mu _s^2\omega _r^2\right) \left( 2v_{gr}v_{gi}+ \mu \cos (k)\xi _3+\sin (k)\xi _4\right) +2\mu _s\varepsilon _r\Gamma _1\left( v_{gr}^2-v_{gi}^2\right. \right. \nonumber \\&\qquad \left. \left. +\mu _s\sin (k)\xi _1+\cos (k)\xi _2\right) \right] /\left( {4\varepsilon _r^2\omega ^2+\mu _s^2\omega _r^4}\right) ,\nonumber \\&Q_r=3\sigma ^2\omega \frac{\left( 2\varepsilon _r^2+\mu _s^2\omega _r^2\right) }{4\varepsilon _r^2\omega ^2+\mu _s^2\omega _r^4},\quad Q_i=-3\sigma ^2\mu _s\varepsilon _r \frac{\Gamma _1}{4\varepsilon _r^2\omega ^2+\mu _s^2\omega _r^4} \end{aligned}$$

(14)

in which

$$\begin{aligned}&\xi _1=-\omega \sinh (\chi )+v_{gi}\cosh (\chi ),\quad \xi _2=\varepsilon _r\cosh (\chi )+\mu _sv_{gr}\sinh (\chi ),\nonumber \\&\xi _3=\omega \cosh (\chi )-v_{gi}\sinh (\chi ),\quad \xi _4=\varepsilon _r\sinh (\chi )+\mu _sv_{gr}\cosh (\chi ). \end{aligned}$$

(15)

By considering that the modulated signal evolves slowly from one site to another, the term $e^{-2\chi n}$ in Equation can be supposed independent to variable x. Setting then $\psi =U_1e^{-\chi n}$, Eq. (13) can be reduced to the following cubic Ginzburg differential equation:

$$\begin{aligned} i\frac{\partial \psi }{\partial \tau }+\left( P_r+iP_i\right) \frac{\partial ^2 \psi }{\partial x^2}+\left( Q_r+iQ_i\right) \left\| \psi \right\| ^2\psi =0, \end{aligned}$$

(16)

governing weak amplitude modulated signals in the system.

3.2 Dissipative envelope solitons like signals

3.2.1 Analytical findings

In order to find the solution of Eq. (16) and then analyze the dissipative effect of the network, it is important to mention that many wave equations consist in generalizations of the integrable equations like the NLS equation and, sometimes, additional terms may be considered as small perturbations. The basic idea of the perturbation approach is to look for a solution of a perturbed nonlinear equation in terms of certain natural fast and slow variables. We assume that $P_i=\epsilon P_{ai}$, $Q_i=\epsilon Q_{ai}$, and we look for a solution $\psi$ is of the form:

$$\begin{aligned} \psi =\psi _0+\epsilon \psi _1+..., \end{aligned}$$

(17)

where $\psi _1,...$ are corrections, while the independent variables are transformed into several variables $\tau _j=\epsilon ^j\tau$. Substituting the above expression of $\psi$ into Eq. (16) and collecting the powers of $\epsilon$ we obtain the series of equations which leads:

$\blacktriangle$ At the lowest order $\epsilon ^0$ to the well-known NLS equation:

$$\begin{aligned} i\frac{\partial \psi _0}{\partial \tau _0}+P_r\frac{\partial ^2 \psi _0}{\partial x^2}+Q_r\left\| \psi _0\right\| ^2\psi _0=0, \end{aligned}$$

(18)

where the solution can be written as

$$\begin{aligned} \psi _0=A_0(\tau _1,...)sech\left( \tilde{\eta }_1\right) e^{i\tilde{\eta }_2}, \end{aligned}$$

(19)

with the constraints:

$$\begin{aligned} \frac{\partial \eta _1}{\partial x}=A_0(\tau _1,...)\sqrt{\frac{Q_r}{2P_r}}, \quad \frac{\partial \eta _1}{\partial \tau _0}=-Q_r A_0^2(\tau _1,...),\quad \frac{\partial \eta _2}{\partial x}=A_0(\tau _1,...)\sqrt{\frac{Q_r}{2P_r}},\quad \frac{\partial \eta _2}{\partial \tau _0}=0. \end{aligned}$$

(20)

provided that $P_rQ_r>0$, which corresponds to pulse soliton with stationary phase or

$$\begin{aligned} \psi _0=A_0(\tau _1,...)tanh\left( \tilde{\eta }_1\right) e^{i\tilde{\eta }_2}, \end{aligned}$$

(21)

with

$$\begin{aligned}&\frac{\partial \eta _1}{\partial x}=A_0(\tau _1,...)\sqrt{-\frac{Q_r}{2P_r}}, \quad \frac{\partial \eta _1}{\partial \tau _0}=-v_e \frac{\partial \eta _1}{\partial x},\quad \frac{\partial \eta _2}{\partial x}=\frac{v_e}{2P_r},\quad \frac{\partial \eta _2}{\partial \tau _0}=-v_p\frac{\partial \eta _2}{\partial x},\nonumber \\&2v_ev_p-v_e^2+4PQA_0^2(\tau _1,...)=0, \end{aligned}$$

(22)

corresponding to dark soliton with the constraint $P_rQ_r<0$ [21].

$\blacktriangle$ At order $\epsilon ^1$, one has the following linear inhomogeneous equation in $\psi _1$

$$\begin{aligned} \tilde{L}_r\psi _1=-i\left( \frac{\partial \psi _0}{\partial \tau _1}+P_{ai}\frac{\partial ^2 \psi _0}{\partial x^2}+Q_{ai}\left\| \psi _0\right\| ^2\psi _0\right) , \end{aligned}$$

(23)

where $\tilde{L}_{r}$ is the linear operator defined by

$$\begin{aligned} \tilde{L}_r=i\frac{\partial }{\partial \tau _0}+P_r\frac{\partial ^2 }{\partial x^2}+Q_r\left( 2\left\| \psi _0\right\| ^2+\psi _0^2conj\right) , \end{aligned}$$

(24)

with $conj\psi =\bar{\psi }$ and $\psi \bar{\psi }=\bar{\psi }\psi =\Vert \psi \Vert ^2$. Denoting by $\rho _i(i = 1, . . . ,M)$ the $i^{th}$ solution of the homogeneous adjoint problem $\tilde{L}_r^A(\rho _i) = 0$, where $\tilde{L}_r^A$ defined by

$$\begin{aligned} \tilde{L}_r^A=i\frac{\partial }{\partial \tau _0}+P_r\frac{\partial ^2 }{\partial x^2}+Q_r\left\| \psi _0\right\| ^2, \end{aligned}$$

(25)

is the adjoint operator to $\tilde{L}_r$, we obtain by multiplying Eq. (23) by $\bar{\rho _i}$ the following differential equation:

$$\begin{aligned} \left( \tilde{L}_r\psi _1\right) \bar{\rho _i}-\left( \tilde{L}_r^A \rho _i\right) \bar{\psi _1}=-i\left( \frac{\partial \psi _0}{\partial \tau _1}+P_{ai}\frac{\partial ^2 \psi _0}{\partial x^2}+Q_{ai}\left\| \psi _0\right\| ^2\psi _0\right) \bar{\rho _i}, \end{aligned}$$

(26)

which may be integrated to give the following secularity condition:

$$\begin{aligned} -i\int _{-\infty }^{+\infty }\bar{\rho _i}\left( \frac{\partial \psi _0}{\partial \tau _1}+P_{ai}\frac{\partial ^2 \psi _0}{\partial x^2}+Q_{ai}\left\| \psi _0\right\| ^2\psi _0\right) d\eta _1=0. \end{aligned}$$

(27)

Setting $\rho _i=\phi _0$ and by considering first solution given by (19), the above equation can be integrated to give the following secularity condition:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial \eta _2}{\partial \tau _1}+P_{ai}\frac{\partial ^2 \eta _2}{\partial x^2}=0, \\ \frac{\partial A_0}{\partial \tau _1}-P_{ai}\left[ \left( \frac{\partial \eta _2}{\partial x}\right) ^2+\frac{1}{3}\left( \frac{\partial \eta _1}{\partial x}\right) ^2\right] A_0+\frac{2}{3}Q_{ai}A_0^3=0. \end{array}\right. \end{aligned}$$

(28)

Accounting to constraints Eq. (20), it is obvious that:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial \eta _2}{\partial \tau _1}+P_{ai}\frac{\partial ^2 \eta _2}{\partial x^2}=0,\\ \frac{\partial A_0}{\partial \tau _1}+\frac{2}{3}\left( \frac{Q_{ai}P_r-P_{ai}Q_r}{P_r}\right) A_0^3=0. \end{array}\right. \end{aligned}$$

(29)

From Eq. (20), the first line of the above equation leads to ${\partial \eta _2}/{\partial \tau _1}=0$, while its second line leads to the solution:

$$\begin{aligned} A_0\left( \tau _1\right) =\tilde{A}_0\sqrt{\frac{3P_r}{3P_r+4\left( Q_{ai}P_r-P_{ai}Q_r\right) \tilde{A}_0^2\tau _1}}. \end{aligned}$$

(30)

By remembering that $\tau _1=\epsilon \tau$, one has $A(\tau )=\tilde{A}_0\sqrt{\vartheta _b(\tau )}$, with:

$$\begin{aligned} \vartheta _b(\tau )=\frac{3P_r}{3P_r+4\left( Q_{i}P_r-P_{i}Q_r\right) \tilde{A}_0^2\tau }. \end{aligned}$$

(31)

while from the set of Eqs.(32), one has:

$$\begin{aligned} \psi (x,\tau )&=\tilde{A}_0\sqrt{\vartheta _b(\tau )}sech\left[ \tilde{A}_0\sqrt{\frac{Q_r}{2P_r}\vartheta _b(\tau )}\left( x- \tau \tilde{A}_0\sqrt{2P_rQ_r \vartheta _b(\tau )}\right) \right] \nonumber \\&\quad \times exp\left( i x \tilde{A}_0\sqrt{\frac{Q_r}{2P_r} \vartheta _b(\tau )}\right) . \end{aligned}$$

(32)

By remembering to original variables, the dissipative modulated bright solution (32) of the network equation can be rewritten as:

$$\begin{aligned}&U(n,t)=\rho (t)sech\left[ \mu (t)(n-tv_r(t))\right] \cos [t\Omega _i(t)]\cos [K(t)n-t\Omega _r(t)]\exp [t\Omega _i(t)]\times \nonumber \\&\left( \frac{1-\tan [t\Omega _i(t)]\tan [K(t)n-t\Omega _r(t)]\tanh \left[ \mu (t)(n-tv_r(t))\right] }{1-\sin ^2[t\Omega _i(t)]sech^2\left[ \mu (t)(n-tv_r(t))\right] }\right) \end{aligned}$$

(33)

with

$$\begin{aligned}&\rho (t)=U_0/\sqrt{{1+\frac{\left( Q_{i}P_r-P_{i}Q_r\right) }{3P_r}U_0^2t}},\quad \mu (t)=\frac{\rho (t) }{2}\sqrt{\frac{Q_r}{2P_r}},\quad K(t)=k+\mu (t),\nonumber \\&v_r(t)=v_{gr}+\frac{\rho (t) }{2}\sqrt{2{P_r}{Q_r}},\quad \Omega _i(t)=\mu (t)v_{gi},\quad \Omega _r(t)=\omega +v_{gr}\mu (t). \end{aligned}$$

(34)

For the dark solution (21), the integration given by Eq. (27) is infinite and needs to be renormalized as:

$$\begin{aligned} -i\int _{-\infty }^{+\infty }\bar{\rho _i}\left( 1-\frac{\left\| \psi _0\right\| ^2}{A_0^2}\right) \left[ \frac{\partial \psi _0}{\partial \tau _1}+P_{ai}\frac{\partial ^2 \psi _0}{\partial x^2}+Q_{ai}\left\| \psi _0\right\| ^2\psi _0\right] d\eta _1=0. \end{aligned}$$

(35)

Substituting then the solution (21) into the above equation leads by equating the resulting real and imaginary parts to:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial \eta _2}{\partial \tau _1}+P_{ai}\frac{\partial ^2 \eta _2}{\partial x^2}=0, \\ \frac{\partial A_0}{\partial \tau _1}-P_{ai}\left[ \left( \frac{\partial \eta _2}{\partial x}\right) ^2+\frac{4}{5}\left( \frac{\partial \eta _1}{\partial x}\right) ^2\right] A_0+\frac{3}{5}Q_{ai}A_0^3=0. \end{array}\right. \end{aligned}$$

(36)

In order to simplify our investigations, let us set $v_e=v_p$, leading from Eq. (22) to $v_e=v_p=2A_0(\tau _1,..)\sqrt{-P_rQ_r}$, and from Eq. (36), one has:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial \eta _2}{\partial \tau _1}+P_{ai}\frac{\partial ^2 \eta _2}{\partial x^2}=0,\\ \frac{\partial A_0}{\partial \tau _1}+\left( \frac{3Q_{ai}P_r+7P_{ai}Q_r}{5P_r}\right) A_0^3=0, \end{array}\right. \end{aligned}$$

(37)

leading to the solution $\frac{\partial \eta _2}{\partial \tau _1}=0$ and accounting to original variables to $A_0\left( \tau \right) =\tilde{A}_0 \sqrt{\vartheta _d\left( \tau \right) }$, with

$$\begin{aligned} \vartheta _d\left( \tau \right) =\frac{5P_r}{5P_r+2\left( 3Q_{i}P_r+7P_{i}Q_r\right) \tilde{A}_0^2 \tau }. \end{aligned}$$

(38)

One can then find the following dissipative modulated dark soliton:

$$\begin{aligned}&\psi (x,t)=\tilde{A}_0\sqrt{\vartheta _d\left( \tau \right) }tanh\left[ \tilde{A}_0\sqrt{\frac{-Q_r}{2P_r}\vartheta _d\left( \tau \right) }\left( x- 2\tau \tilde{A}_0\sqrt{-P_rQ_r\vartheta _d\left( \tau \right) }\right) \right] \times \nonumber \\&exp\left( i \tilde{A}_0\sqrt{\frac{-Q_r}{P_r}\vartheta _d\left( \tau \right) }\left( x- 2\tau \tilde{A}_0\sqrt{-P_rQ_r\vartheta _d\left( \tau \right) }\right) \right) . \end{aligned}$$

(39)

3.2.2 Validity of results via conserved quantities

When the parameters of Eq. (16) introduced by the dissipation coefficient $P_i=Q_i=0$, the resulting equation admits a certain number of conserved quantities among which the norm and the momentum

$$\begin{aligned} N=\int _{-\infty }^{\infty }\Vert \psi \Vert ^2dx,\quad M=i\int _{-\infty }^{\infty }\left( \psi \frac{\partial \bar{\psi }}{\partial x}- \bar{\psi }\frac{\partial \psi }{\partial x}\right) dx \end{aligned}$$

(40)

as well as the Hamiltonian

$$\begin{aligned} H=\int _{-\infty }^{\infty }\left( -P\left\| \frac{\partial \psi }{\partial x}\right\| ^2+\frac{Q}{2}\Vert \psi \Vert ^4\right) dx. \end{aligned}$$

(41)

The system has constant shape if the norm is invariant as the time evolves. Thus in order to prove that the norm is the conserved quantity, let us multiply Eq. (16) by $\bar{\psi }$ and make the difference with the complex conjugation of the resulting Equation, one has:

$$\begin{aligned} \frac{\partial \Vert \psi \Vert ^2}{\partial \tau }-iP_r\frac{\partial }{\partial x}\left( \bar{\psi }\frac{\partial \psi }{\partial x}- \psi \frac{\partial \bar{\psi }}{\partial x}\right) +P_i\left( \bar{\psi }\frac{\partial ^2 \psi }{\partial x^2}+\psi \frac{\partial ^2 \bar{\psi }}{\partial x^2}\right) +2Q_i\left\| \psi \right\| ^4 =0, \end{aligned}$$

(42)

which for the bright solution can be integrated as

$$\begin{aligned} \frac{\partial }{\partial \tau }\int _{-\infty }^{\infty }\Vert \psi \Vert ^2dx+2\int _{-\infty }^{\infty }\left[ \frac{P_i}{2}\left( \bar{\psi }\frac{\partial ^2 \psi }{\partial x^2}+\psi \frac{\partial ^2 \bar{\psi }}{\partial x^2}\right) +Q_i\left\| \psi \right\| ^4\right] dx =0. \end{aligned}$$

(43)

It then obvious that when $P_i=Q_i=0$, one has $\frac{\partial }{\partial \tau }\int _{-\infty }^{\infty }\Vert \psi \Vert ^2dx=\frac{\partial }{\partial \tau }N=0$, and as a consequence, the norm is time independent and is a conserved quantity.

In order to study the effect of the dissipation of the system equation, let us consider that $P_i\ne Q_i\ne 0$, By setting the ansatz

$$\begin{aligned} \psi (x,t)=A(t)sech(\eta (x,t))\exp (i\xi (x,t)), \end{aligned}$$

(44)

with the constraint $\frac{\partial (\eta (x,t))}{\partial x}=\mu (t)=A(t)\sqrt{\frac{Q_r}{2P_r}}$, $\frac{\partial (\xi (x,t))}{\partial x}=\gamma (t)=A(t)\frac{\sqrt{2P_rQ_r}}{2P_r}$, and replacing the variable of integration x of Eq. (43) by $\eta$, one has the following ordinary differential equation:

$$\begin{aligned} \frac{\partial A}{\partial \tau }-P_i\left( \frac{1}{3}\left( \frac{\partial \eta }{\partial x}\right) ^2+\left( \frac{\partial \xi }{\partial x}\right) ^2\right) A+\frac{2}{3}Q_iA^3=0, \end{aligned}$$

(45)

which is identical to Eq. (28) and where its solution can be given by Eq. (30).

For the dark solitary solution, it is important to mention that when one renormalizes Eq. (43) by multiplying it by $1-(\Vert \psi (x,t)\Vert /A_0(t))^2$, one obtains after integration the differential equation similar to Eq. (36), by taking the ansatz $\psi (x,t)=A(t)\tanh (\eta (x,t))\exp (i\xi (x,t))$.

3.2.3 Numerical validation

In this section we present the details and the result of the numerical investigations performed both on cubic Ginzburg differential equation (16) and on the exact discrete equations given by the set of differential Eq. (1) . Firstly, in order to verify the validity of the analytical solution (32), we perform here numerical integrations of the cubic Ginzburg differential equation (16), which is an approximation of the exact equation governing modulated wave propagation in the network. The fourth- order Runge–Kutta scheme is used with normalized integration time step $\Delta \tau =0.001$. The parameters has been chosen as $P_r=Q_r=1$, $Q_i=0.001$ and $P_i=-0.001$. As initial condition, the dissipative solution (32) is used with the initial time $\tau _0=0$. Then Fig. 7 shows the propagation and head on collision of two bright solitary signals, with the amplitudes $A_0 = 0.8$ and $A_0=1$, initially located at $x_0=-20$ and $x_0=20$, respectively. As time goes on both these initial bright solitary waves propagate without changes of their initial profiles but with amplitudes which slightly decrease in propagation. However, these signals survey collusion, confirming that (32) is the dissipative bright soliton.

Next in order to prove that the damped pulse solution (33) is the approximated solution of the set of ordinary differential equation (4), the numerical investigations are performed here using as above the fourth- order Runge- Kutta scheme with the normalized integration time step $\Delta \tau =0.02$ and with parameters: $\theta =\pi /6$, $k=\pi /4$ leading to $\omega = 1.4442$, $\mu _s=0.002$ and $\varepsilon _r=1$. In Fig. 8, we have shown the propagation of the bright modulated signal, that amplitude decreases in propagation due to dissipation.

Fig. 7

Numerical investigation obtained by solving the cubic Ginzburg differential equation (16), showing the propagation and head collision of two bright solitary waves, obtained for $P_r=Q_r=1$, $Q_i=0.001$ and $P_i=-0.001$. As one can see, both these two signals survey collision, but their amplitudes decrease in propagation due to dissipation

Fig. 8

Propagation of signal in the network governed by Eq. (4), with parameters: $\theta =\pi /6$, $k=\pi /4$ leading to $\omega = 1.4442$, $\mu _s=0.002$ and $\varepsilon _r=1$. As one can see, the signal attenuates in propagation due to dissipation

4 Modulational instability

In this section we study the conditions under which a modulated plane wave propagating in the waveguide described by the complex Ginzburg Eq. (13) can become unstable against a small perturbation. This equation has the exact plane wave solution

$$\begin{aligned} \psi (x,\tau )=A_0\exp {i\left( K_0-\Omega _0\tau \right) },\quad K_0=A_0\sqrt{\frac{Q_i}{P_i}}, \quad \Omega _0=-\left( Q_r-\frac{Q_i}{P_i}P_r\right) A_0^2, \end{aligned}$$

(46)

with the constraint $P_iQ_i\ge 0$. Using the procedure outlined in [17, 22], the linear stability of this solution can be investigated by first considering a longitudinal perturbation of the amplitude and by looking for a solution in the form:

$$\begin{aligned} \psi (x,\tau )=[A_0+a(x,\tau )]\exp {i\left( K_0-\Omega _0\tau \right) }, \end{aligned}$$

(47)

where $a(x,\tau )$ is a complex function and describes a perturbation which is assumed to be small as compared to the carrier wave parameter $A_0$. Substituting the solution (47) into Eq. (13) and neglecting nonlinear terms in $a(\tau ,x)$ leads to the following evolution equation for a:

$$\begin{aligned} i\frac{\partial a}{\partial \tau }+(P_r+iP_i)\left( 2iA_0\sqrt{\frac{Q_i}{P_i}}\frac{\partial a}{\partial x}+ \frac{\partial ^2 a}{\partial x^2}\right) +2(Q_r+iQ_i)A_0^2R_e(a)=0 \end{aligned}$$

(48)

where by Re(a), we mean the real part of a. Next, by introducing the Fourier transforms :

$$\begin{aligned} \hat{a}_1(t,K)=\int _{-\infty }^{\infty }a(\tau ,x)\exp (iKx)dx, \end{aligned}$$

(49)

one has

$$\begin{aligned} i\frac{\partial \hat{a}_1}{\partial \tau }+(P_r+iP_i)\left( 2A_0K\sqrt{\frac{Q_i}{P_i}} -K^2\right) \hat{a}_1+2(Q_r+iQ_i)A_0^2R_e(\hat{a}_1)=0. \end{aligned}$$

(50)

Decomposing the perturbation into real and imaginary parts, $\hat{a}_1=u_1+iu_2$, leads to the following set of ordinary differential equation in K space $\partial _t \hat{U}=B\hat{U}$, where the vector $\hat{U}$ and matrix B are defined as

$$\begin{aligned} \hat{U}=\left[ \begin{array}{c} \hat{u_1} \\ \hat{u_2} \end{array} \right] , \quad B=\left[ \begin{array}{cc} \left( K^2-2A_0K\sqrt{\frac{Q_i}{P_i}}\right) P_i-2Q_iA_0^2 &{} P_r\left( K^2-2A_0K\sqrt{\frac{Q_i}{P_i}}\right) \\ -P_r\left( K^2-2A_0K\sqrt{\frac{Q_i}{P_i}}\right) +2Q_rA_0^2 &{} P_i\left( K^2-2A_0K\sqrt{\frac{Q_i}{P_i}}\right) \end{array} \right] . \end{aligned}$$

(51)

The eigenvalues of the matrix B, obtained by setting the solution proportional to $\exp (i\Omega t)$ are then given by $\Omega =i\Gamma (K)\pm P_r\sqrt{ g(K)}$ with

$$\begin{aligned} \Gamma (K)= & {} 2Q_iA_0^2-P_i\left( K-A_0\sqrt{\frac{Q_i}{P_i}}\right) ^2, \nonumber \\ g(k)= & {} \left( \left( K-A_0\sqrt{\frac{Q_i}{P_i}}\right) ^2-\frac{\left( P_rQ_i+Q_rP_i\right) }{P_rP_i}A_0^2\right) ^2 -\frac{\left( Q_r^2+Q_i^2\right) }{P_r^2}A_0^4. \end{aligned}$$

(52)

The plane-wave is stable against small modulation if $g(K)>0$ and $\Gamma (K)\ge 0$. Otherwise, two complex numbers $\Omega =i(\Gamma (K)\pm G(K))$, with

$$\begin{aligned} G(K)=P_r\left[ \frac{\left( Q_r^2+Q_i^2\right) }{P_r^2}A_0^4- \left( \left( K-A_0\sqrt{\frac{Q_i}{P_i}}\right) ^2-\frac{\left( P_rQ_i+Q_rP_i\right) }{P_rP_i}A_0^2\right) ^2 \right] ^{1/2} \end{aligned}$$

(53)

are solutions of Eq. (53) and the perturbation a(X, t) diverges with time leading to an exponential growth of the amplitude with the growth rate or MI gain described by G(K). The MI occurs then whether the following constraint is satisfied

$$\begin{aligned} \frac{Q_r}{P_r}\left( 1+\frac{P_rQ_i}{P_iQ_r}-\sqrt{1+\frac{Q_i^2}{Q_r^2}}\right) A_0^2< \left( K-A_0\sqrt{\frac{Q_i}{P_i}}\right) ^2< \frac{Q_r}{P_r}\left( 1+\frac{P_rQ_i}{P_iQ_r}+\sqrt{1+\frac{Q_i^2}{Q_r^2}}\right) A_0^2 \end{aligned}$$

(54)

Fig. 9

a Sign of $\gamma$, (red for $\gamma >0$ and black elsewhere), b Sign of $P_iQ_i$ (red for $P_iQ_i>0$ and black elsewhere). The parameters of the system are: $\mu _s=0.01$, $\varepsilon _r=1$

provided that $\gamma ={Q_r}{P_r}\left( 1+\frac{P_rQ_i}{P_iQ_r}+\sqrt{1+\frac{Q_i^2}{Q_r^2}}\right) >0$ and $P_iQ_i\ge 0$.

Fig. 10

Modulational instability (MI) of the plane wave observed for $\varepsilon _r=1$ $\theta =\pi /6$, $k=\pi /6$ and $\mu _s=0.001$ leading from the dispersion relation to the frequency of $\omega =1.3296$ and dissipation coefficient $\chi = 3.5628\times 10^{-4}$. a input signal, b cell 50, c cell 100 and (d) cell 200. The initial amplitude is $U_0 =0.5$, whereas the modulation rate is $M = 1\%$, and the modulation frequency is $\omega _m=0.13$

Fig. 11

Same as in Fig. 10 but with $\mu _s=0.01$, leading from the dispersion relation to: $\omega =1.3296$ and $\chi =3.5626\times 10^{-3}$

is the linear operator defined by In order to confirm our analytical findings, the numerical simulations of the exact discrete Eq. (4) has been performed by using as above the fourth-order Runge-Kutta scheme, with the time step always kept $\delta \tau =2.10^{-2}$. The parameters $\varepsilon _r=1$, $\theta =\pi /6$ and $k=\pi /6$ are kept constant while $\mu _s$ is the tuning parameter. As initial condition, we applied at the entrance (cell 1) the following input signal voltage:

$$\begin{aligned} U_1(t)=U_0\left( 1+Mcos(\omega _m t)\right) cos(\omega t) \end{aligned}$$

(55)

in which $V_m$ designates the amplitude of the unperturbed plane wave with angular frequency $\omega = 2\pi f$. M and $\omega _m= 2\pi f_m$, respectively, stand for the rate and the angular frequency of the modulation.

The obtained results are shown in Fig. 10 for $\mu _s=0.001$ and in Fig. 10 for $\mu _s=0.01$. As one can see for both curves, the modulated signal leads to a train of impulses signals in propagation. However for the case whose perturbation is more weak ( that is $\mu _s=0.001$), the magnitude of the propagating signal increases, while for the other case $\mu _s=0.01$ which is not weak enough, the modulated signal vanishes in propagation.

5 Concluding remarks

We have investigated the damping effects on the propagation of modulated signals of the mechanical network consisting of discontinuous elastically coupled system oscillators with strong irrational nonlinearities. By means of the Newton second law, the set of damped discrete equations governing signals generation by the system have been found. This set of equations have smooth characteristics for weak values of the displacement $U_n$, or discontinuous characteristics when the inclination angle is weak enough. Then, in order to find modulated signals as solution of the system equation, the nonlinear cubic complex Guinzburg (NCCG) Equation governing the small amplitude modulated signals in the network was found from the perturbation method. Moreover, the time scale perturbation method [4, 19] applied on this NCCG equation is used to find the modulated dissipative pulse and dark solitons as approximated solutions of the network equation. and next we confirmed our results by using the conserved quantities. Then the numerical investigations performed both on the NCCG Equation and the exact equation of the network show the decreasing of signals in propagation due to damping. Finally the conditions to have modulational instability in the system was found and verify through numerical investigations, from where it appeared that when the dissipation coefficient is weak enough, the small amplitude perturbed signal decomposed into a train of pulse soliton in propagation, with amplitude larger than the initial signal, while for large value of the dissipation coefficient, the perturbed modulation signal decomposed into a train of pulse soliton, but with amplitude which vanishes.