1 Introduction

Variations in oceanic/sea waves are usually characterized as stochastic. It is therefore not surprising that the development and application of emerging data mining techniques have received noteworthy attention in the ocean-/sea wave–analyzing community. From a coastal operation/engineering perspective, data mining techniques were typically applied to develop wave parameters forecasting models using long-term measurements of oceanic/climatic variables (e.g., Tsai et al. 2002; Kazeminezhad et al. 2005; Özger 2011; Vouterakos et al. 2012; Akpınar et al. 2014; Aydoğan et al. 2013; Hadadpour et al. 2014; Duan et al. 2016; Tsai et al. 2018; Law et al. 2020; Zubier 2020).

Artificial neural networks (ANN) are of the earliest data mining techniques that were applied for wave parameter prediction. In a seminal paper by Deo and Naidu (1998), ANNs were used for real-time wave forecasting in Yanam, along the east coast of India. The authors demonstrated that ANNs exhibited higher covariation between the predicted and observed significant wave height than the classic autoregressive (AR) models. In a similar study, the promising role of ANNs for tide prediction was also reported by Deo and Chaudhari (1998). Agrawal and Deo (2002) compared the efficiency of different ANN models with classic linear time series modeling approaches of autoregressive moving average (ARMA) and autoregressive integrated moving average (ARIMA) and showed that ANNs produce more accurate predictions of wave heights than the linear time series schemes when shorter intervals of predictions (3 h and 6 h) were involved. For long-range predictions (12 h and 24 h), both the classic and ANN models showed similar performance. Makarynskyy et al. (2005) utilized ANNs in wave predictions on the west coast of Portugal and showed that ANNs can be successfully applied to predict significant wave heights and zero-up-crossing wave periods with short-term warning times. Mandal and Prabaharan (2006) reported the potential use of recurrent neural networks (RNNs) through a comprehensive case study in Marmugao, west coast of India. The results indicated that RNNs with exogenous inputs recurrent algorithms can be used for significant wave heights forecasting directly from measured waves. Zamani et al. (2008) showed that ANNs provide higher accuracy than instance-based learning when they applied for significant wave heights forecasting in the Caspian Sea. Londhe and Panchang (2007) and Londhe (2008) proved that ANNs can recognize the nonlinear correlation between buoy networks that could be beneficial in the estimation of missing wave parameters via correlating oceanographic data from multiple stations. Kamranzad et al. (2011) used wind speed, direction, and wave height as input parameters for an ANN model for significant wave height prediction for the Persian Gulf. More recently, Zubier (2020) demonstrated that ANN can be satisfactorily employed for the significant wave heights prediction in Eastern Central Red Sea for up to 12 h in advance.

For several years, genetic programming (GP) has been successfully used to solve forecasting and classification problems in hydro-climatological applications (Danandeh Mehr et al. 2018). Regarding ocean engineering, some examples include prediction of significant wave height and average zero-cross wave period (Kambekar and Deo 2012), wave runup (Power et al. 2019), and sea level (Ghorbani et al. 2010) as well as filling up gaps in wave data (Ustoorikar and Deo 2008), and optimizing pumping strategies for coastal aquifer management (Sreekanth and Datta 2010). Owing to the explicit structure of GP-based models, recent studies have also used GP to develop new formulae to optimize the design of coastal structures. For example, Formentin and Zanuttigh (2019) presented a new GP-based formula for parametrization of the reductive effects induced by crown walls and bullnoses on the average wave overtopping discharge at coastal structures. Most recently, the multigene GP technique was used by Lee and Suh (2020) to develop stability formula for rock armor and Tetrapods. The authors demonstrated that the multigene GP model is more accurate than previous empirical formulae as well as ANN-based models.

To cope with uncertainties available in wave-borne data, hybrid data mining models were suggested in the recent studies (Balas et al. 2010; Koç and Balas 2012). The hybrid models either integrate the capabilities of various data mining models or created through linking a data-preprocessing approach with a data mining technique (Danandeh Mehr 2018). For instance, an adaptive neuro-fuzzy inference system (ANFIS) is a hybrid technique that was suggested and applied by Mahjoobi et al. (2008) for wave parameters hindcasting in Lake Ontario. The authors compared ANFIS with ANN and FIS models and demonstrated that ANFIS is marginally more accurate than its counterparts. ANFIS was also used by Tür and Balas (2010) for accurate forecasting of daily significant wave height in the Black Sea. The authors used daily average wave height and wave period data recorded at different time intervals and compared the ANFIS results with those of ANN (Deo and Naidu 1998) and FIS (Kazeminezhad et al. 2005). The results showed that ANFIS is generally superior to the standalone models. A similar study conducted by Akpınar et al. (2014) indicated the promising role of ANFIS for significant wave heights and period forecasting in the Black Sea. Zanaganeh et al. (2009) introduced a hybrid genetic algorithm–ANFIS model in which both clustering and rule base parameters in the prediction of significant wave height and peak spectral period are simultaneously optimized using genetic algorithm and ANNs. The results showed that the hybrid model is superior to ANFIS and Shore Protection Manual methods in terms of their prediction accuracy. Combining wavelet decomposition with ANN, a hybrid neuro-wavelet model was suggested by Dixit et al. (2015) and Dixit and Londhe (2016) which was able to satisfactorily predict extreme wave heights and remove timing error in standalone ANN, respectively. Duan et al. (2016) demonstrated that AR models are adaptive for wave forecasting. However, they have limitations in forecasting nonlinear and non-stationary waves. Inspired by the capability of empirical mode decomposition (EMD), the authors suggested a hybrid EMD-AR model for significant wave height forecasting using the data from the National Data Buoy Center, USA. More recently, Buyukyildiz and Tezel (2017) showed that hybridization of particle swarm optimization algorithm with ANN and ANFIS may increase sea level forecasting accuracy in Lake Beysehir Turkey.

The review showed that the prediction of wave parameters is of great importance for planning of many operation-related activities in the oceans/seas and the design of coastal structures. The issue has been investigated by numerous researchers utilizing various data mining techniques. While the previous studies have mostly been focused on the prediction of significant wave height for different lead times, the maximum wave height (Hmax) hindcasting for concurrent data using GP techniques has not been investigated yet. Therefore, the main objective of this study is to explore a novel hybrid GP-based model that may increase the accuracy of standalone GP to forecast Hmax 1 h in advance. The method presented in this paper follows the ideas of the ensemble GP models proposed by Rahmani-Rezaeieh et al. (2019) and Khozani et al. (2020) for streamflow and incipient sediment motion modeling, respectively. However, instead of different types of GP, the proposed model integrates simple linear models with a classic GP variant which may yield in hybrid models simpler than those of previous studies that guarantee its novelty.

2 Study area, wave parameter monitoring, and data preparation

The direct wave height measurement has been started in Turkey in recent years. In the earlier studies, long-term wind data was typically used to estimate wave parameters (height and period) that yielded in Turkish deep-sea wave-wind atlas (Aydoğan et al. 2013). The data used in the study is from a buoy station located in Antalya Bay (36°43′00″ N - 31°01′00″ E), approximately 20 km offshore and 350 m deep, Mediterranean Sea, Turkey (Fig. 1). Atmospheric data (instantaneous wind velocity and direction, maximum wind velocity and direction, temperature, humidity, and pressure) and marine data (significant wave height and period, maximum wave height, wave direction, current velocity, current direction, salinity, and conductivity) are measured continuously at the station. The station is of tower type anchored to the seabed (Fig. 1). The station provides transmission of measurement data via GPS (Global Positioning System) and GPRS (General Packet Radio Service). Considering the sea depth, the station is in the deep sea and the waves are not transformed.

Fig. 1
figure 1

Location of the buoy station (star) at Antalya coast

Full size image

The hourly data from April 1, 2015 till March 31, 2016 were collected and used in this study. Because of a pronounced variation in the variance of measured wave heights, we divided the entire measurements into four subsamples of AMJ (April-May-June), JAS (July-August-September), OND (October-November-December), and JFM (January, February, March). Statistical characteristics of observed Hmax values were tabulated in Table 1. There are 2185 observations in each season. The samples at each season are also divided into two subsamples of training (70 days, 1640 observations) and holdout testing (20–21 days, 545 observations) periods. After detecting the best models, the testing data is used to control forecasting accuracy. Timeseries plot of the observations given in Fig. 2 provides a general view of the variation of the Hmax in different seasons. Presence of extreme waves with heights greater than 3 m is pronounced in the OND period. Due to short period (3-month) of each series, the plots reveal no seasonal component.

Table 1 Statistical characteristics of maximum wave height measured at different seasons
Full size table
Fig. 2
figure 2

Hourly values of maximum wave height measured at different seasons

Full size image

Figure 3 presents the directional wave rose showing the frequency of Hmax. It is observed from the figure that during the AMJ season, the waves smaller than 1 m are approached to the coast from S-SSW directions, and the higher waves come from SSW direction. In the JAS season, the waves mostly come from S-SSW directions. In the OND season, the waves below 1 m are seen from the SSW-S-SSE and SE directions, and the higher waves come predominantly from the SE direction. Finally, in the JFM season, the waves smaller than 1 m mostly appear from the S direction, and waves with maximum height in the range 1–2 m come from the SSW, SE, and WNW, and the higher ones come from the SSW and SE directions.

Fig. 3
figure 3

Seasonal wave rose at the buoy station; a AMJ, b JAS ) OND, and d JFM seasons

Full size image

Considering the annual wave directions, it is implied that waves smaller than 1 m are predominant and come from S and SSW directions. Larger waves appear to come mainly from the SSW and SE directions during the JFM and OND seasons. It is worth to mention that the wave directions obtained in the study agree with the wind-blowing directions in the region. Historical observations showed that most of the coastal damages were occurred by the waves coming from these directions during JFM and OND seasons.

3 Methodology

Successive observations of stochastic wave events are typically correlated, so future values may be predicted from past values. The discrete stochastic Hmax time series is analyzed in this study using simple descriptive techniques integrated with symbolic regression tools. The aim is to construct mathematical model which explains the observed variability in the data so that we can predict, with some confidence, future observations. As previously mentioned, two linear schemes including a simple linear regression (LR) and ARIMA model together with two nonlinear schemes including ANN and GP are used to model Hmax in each season. Besides, a new ensemble approach is suggested in this study that is described in this section.

3.1 The benchmark linear regression (LR) model

The ordinary LR model is the most basic type of statistical technique that is widely used to establish a linear relationship between two variables and forecast new observations. In the latter, the existing relationship about the observations is used to forecast unobserved values. It is known that wave height impacts on each other over the time and therefore, the previous values (Hmaxt − 1) can be used to forecast the current value (Hmaxt). On average, they might follow a linear pattern and, therefore, the linear equation to represent them could be expressed as:

$$ {Hmax}_t={\beta}_0+{\beta}_1{Hmax}_{t-1}+\varepsilon $$
(1)

where β1is the slope coefficient of the linear line plot between the current and previous Hmax values, β0 is the constant term or intercept, and ε is the error term which is going to be minimized to get the best linear fit.

3.2 Overview of ARIMA model

ARIMA process is of the most general time series modeling approach that allows the modeler to model nonstationary time series. In the ARIMA process, instead of predicting the time series itself, differences of the time series from one time step to the previous time step are predicted. It basically means that instead of predicting Hmaxt, a transformation is carried out so that Zt = Hmaxt + 1 − Hmaxt as difference between consecutive values of Hmax is modeled and predicted. The basic form of ARIMA (p, d, q) is presented as follows:

$$ {Z}_t={\sum}_{i=1}^P\left({\varphi}_i.{Z}_{t-i}\right)-{\sum}_{j=1}^q\left({\theta}_j.{\varepsilon}_{t-j}\right)+{\varepsilon}_t $$
(2)

where φiis the coefficient of AR model, θjis the coefficient of moving average (MA) model, and εt denotes the error in the current time step. The parameters p, q, and d represent the orders of AR, MA, and integrated part, respectively.

To identify the best ARIMA (p, d, q) models, first, the model parameters are determined. To determine order of integration, the parameter d, Augmented Dicky-Fuller (ADF) unit root test, is used in this study which indicates whether the time series does need to be differenced to make it stationary. For example, d = 1 means it needs to be differenced one time to make it stationary. The null hypothesis for an ADF unit root test is that the series contains a unit root against the alternative that the series does not contain a unit root because the series appears to be stationary around a constant. If the null hypothesis is rejected, then d equals to zero which means the data series does not need to be differenced to be made stationary, and therefore, the ARIMA (p, d, q) becomes the ARMA (p, q). Once Zt is predicted, the Hmaxt + 1 that the modeling process originally started with can be recovered using the following equation:

$$ {Hmax}_{t+1}={Z}_t+{Hmax}_t. $$
(3)

Comparing to the classic Dickey-Fuller test, the ADF allows for testing the higher-order autoregressive processes. The other alternatives include (but are not limited to) ADF-GLS (Elliott et al. 1996) and KPSS (Kwiatkowski et al. 1992) tests.

3.3 Overview of ANN

An ANN model imitates human brain activity and it consists of neurons and some layers which are processing units. A feedforward neural network is a type of ANN algorithm that consists of two or more layers with neurons in each layer. The network response is:

$$ {y}_i=f\left({\sum}_{i=1}^n{w}_i{x}_i-{b}_j\right) $$
(4)

where n denotes the total number of input values (i.e., observed Hmax) and their weights, xi parameter are the input values of a perceptron, parameter wiwi are weights for each input, bj value is the bias of the perceptron, and yj refers to output of a perceptron that states activation function values of summation.

There are hidden layers between the input and the output layers. Each neuron layer receives input from the previous layer and gets in contact with the next layer by sending an output. The output y of a perceptron for hyperbolic tangent, or tanh, function in the hidden layers is denoted as:

$$ y=f(z)=\mathit{\tanh}(z)=\frac{e^z-{e}^{-z}}{e^z+{e}^{-z}} $$
(5)

where parameter z denotes the output of a perceptron summation.

3.4 Overview of genetic programming

GP is a domain-independent, problem-solving approach in which computer programs are evolved to find solutions to problems. It is based on the Darwinian principle of “survival of the fittest.” The programs are typically characterized by a tree structure known as genome. Figure 4 illustrates a genome and corresponding mathematical equation using a root node (multiplication), inner nodes of addition, multiplication, and subtraction as well as terminal nodes of x1, x2, and random numbers of 2.25 and 1.75. Each node in a GP tree can adopt a function or terminal variables. Some of the main issues in the GP-based modeling is the selection of a set of appropriate functions, input variables, and maximum depth (also referred to as height) of GP trees.

Fig. 4
figure 4

A tree-shaped genomes and corresponding mathematical representations

Full size image

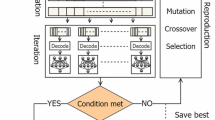
No matter what the problem is, GP algorithm begins with creation of initial population of programs called potential solutions. Then, the solutions that show higher performance during training phase survive to the next generation of population where they are considered as parents to create offspring. To this end, typically three evolutionary operators are used. The operators that act on the genomes include reproduction, crossover, and mutation. Reproduction is transferring the best single solution into the new population set of offspring without any morph. The process commences with the goodness of fit assessment of initial programs and ends after the identification of the best fitted one. Crossover is an operation that needs two of the best solutions as parents. The operation yields two offspring by replacing of genetic material of the parents. The offspring are solutions that possess genetic materials of their parents. Many studies have shown that offspring fits to the training set better than their parents. Mutation is the third genetic operation in which genetic materials of a single parent is replaced with new genetic materials (a new subtree) at the mutation point (Karimi et al. 2019). These operations are repeated using the population of offspring as the new set of parents till an individual shows a desired level of fit to the training data set. If the individual shows favorite accuracy for the testing data, then it is called the best solution and the model is not overfitted. Different variants of GP and their applications in water engineering were reviewed by Danandeh Mehr et al. (2018). The reader is referred to this paper for the relevant details.

3.5 Ensemble GP (EGP) model

To overcome the problem of the use of single input in both linear and nonlinear forecasting models, a new ensemble learning method that combines the multiple models results to improve the accuracy of the forecasts is suggested and verified in this study. In the ensemble model, which is called EGP, a new GP tree is created so that the evolutionary algorithm tries to minimize error between new model outputs and observed data at training period, however, the best model is selected among those of potential solutions that provide the highest accuracy in validation dataset. The idea came from the unique feature of GP that can provide a population of models for a single problem having more or less the same accuracy at training data, but different at validation set. In this way, the modeler would be avoided from overfitting problem. The other advantage of the proposed model is the automatic sensitivity analysis of standalone models using GP engine. When ensemble inputs are used, GP would be able to give more weights to the more effective inputs and reject the less effective inputs which may yield not only more accurate forecast but also a parsimonious structure. According to several researches in ensemble modeling, it is confirmed that combining the results of different models could enhance the prediction accuracy (Rahmani-Rezaeieh et al. 2019; Nourani et al. 2020).

3.6 Performance evaluation of the models

The models’ performances are compared using two statistical indicators, Nash-Sutcliff Efficiency (NSE) and Root Mean Square Error (RMSE) as expressed below.

$$ NSE=1-\frac{\sum_{i=1}^n{\left({X}_i^{obs}-{X}_i^{pre}\right)}^2}{\sum_{i=1}^n{\left({X}_i^{obs}-{X}_{mean}^{obs}\right)}^2} $$
(6)
$$ RMSE=\sqrt{\frac{\sum_{i=1}^n{\left({X}_i^{obs}-{X}_i^{pre}\right)}^2}{n}} $$
(7)

where \( {X}_i^{obs} \)is the wave height measured in the buoy, \( {X}_i^{pre} \)is the height calculated by the models, and n is the number of measurements.

4 Results and discussion

In this section, at first, the outcomes of standalone modeling via LR, ARIMA, ANN, and GP techniques are presented. Then the results of the new ensemble model and discussion on different models are presented.

4.1 Evolution of standalone linear and nonlinear models

The best LR models attained for AMJ, JAS, OND, and JFM seasons were presented in Eqs. 8 to 10, respectively.

$$ {Hmax}_t=0.032+0.9454{Hmax}_{t-1}+\varepsilon $$
(8)
$$ {Hmax}_t=0.0674+0.834{Hmax}_{t-1}+\varepsilon $$
(9)
$$ {Hmax}_t=0.018+0.9722{Hmax}_{t-1}+\varepsilon $$
(10)
$$ { Hm ax}_t=0.041+0.9659{Hm\mathrm{a}x}_{t-1}+\varepsilon $$
(11)

The constant term in all models are close to 0.0 and coefficient for the Hmaxt − 1 is close to 1.0. These equations show that for every meter increase in Hmax, the next hour it will rise by 0.9 on average.

As previously described, to develop an ARIMA model, the relevant parameters must be identified first. Here, the ADF test was applied for each time series to figure out the order of integration d. To make sure to include enough lags, the max lag of ADF test was selected equal to 24 which is two times more than the cube root of the sample size (~ 11.8). Therefore, the test is started with 24 lags and test down using a 10% significant level to determine number of lags to include in the ADF unit root test. As the mean value of each series is not zero (see Table 1), the test was done with a constant. The p values of AMJ, JAS, OND, and JFM seasons were calculated equal to 7.445e−10, 0.001166, 0.0006641, and 1.749e−5 which imply that the null hypothesis of a unit root can be rejected. This means that the Hmax observations at each season does not have to be differenced to be made stationary and thus, d = 0.

To determine the parameters p and q, the correlogram of the series were plotted and the patterns of autocorrelation function (ACF) and partial ACF (PACF) visually inspected as depicted in Fig. 5. Both are decaying but an oscillation pattern is seen for JAS season. As expected, there is no significant partial correlation after the first lag. These patterns point to p and q being equal to one in all the series. Thus, the model would be ARIMA (1,0,1) which is also called ARMA (1,1). Therefore, the evolved models have the form given in Eq. (12). The associated parameters attained for each season at training period were presented in Table 2.

$$ {Hmax}_{t+1}=\varphi .{Hmax}_t+{\varepsilon}_t-\theta .{\varepsilon}_{t-1} $$
(12)
Fig. 5
figure 5

Correlogram of the maximum wave height time series in a AMJ, b JAS, c OND, and d JFM seasons

Full size image
Table 2 Parameter values obtained for ARMA (1,1) models at each season
Full size table

In the evolution of nonlinear data mining models (here ANN and GP), dimensions of the inputs together with the types of transfer functions within the computation units of the models (if any) must be taken into consideration before training the models. To attain dimensionally correct ANN and GP models in this study, the observed Hmax series were scaled to the range between 0.1 and 0.9 as follows.

$$ {Hmax}_{nt}=0.8\times \frac{Hmax_t-{Hmax}_{min}}{Hmax_{max}-{Hmax}_{min}}+0.1 $$
(13)

To develop ANN models, the well-known Levenberg-Marquardt algorithm existing in neural network toolbox of MATLAB was used. Several three-layer feed-forward networks with hyperbolic tangent and pure linear transfer functions, as the activation functions in the hidden and output layers, respectively, were trained and tested. To achieve an appropriate topology at each season, different numbers of hidden neurons were used in the training process. The results from training process at all the seasons showed that the best performance at testing period is produced when only two hidden neurons are used. Although increasing the number of hidden neurons may slightly intensify the models’ performance at training sets, it may not increase the performance at testing set, which means the models are overfitted to the training data set.

To develop GP models, GPdotNET software packages (Hrnjica and Danandeh Mehr 2019) were used in this study. The package evolves hundreds of potential models via the combination of input parameters, user defined functions, and some random constants. Like the ANN models, RMSE was used as the fitness fiction to be minimized during the training process. Rank selection method was utilized to select the successful individuals among the potential models during the evolutionary process (model generation), and the best model was considered as the one which provides the least RMSE at the training data sets after 500 generation. The probability of crossover, mutation, and reproduction operations were equal to 0.8, 0.2, and 0.1, respectively. The mathematical expressions of the best attained GP models for AMJ, JAS, OND, and JFM seasons were presented in Eqs. 14 to 17, respectively.

$$ {Hmax}_{nt}={Hmax}_{nt-1}+\left(\left(\left(\mathit{\cos}\left({Hmax}_{nt-1}\ \right)\right)-0.97607\ \right)\times 0.00326\right) $$
(14)
$$ {Hmax}_{nt}={Hmax}_{nt-1}-\left(\left(\mathit{\sin}\left(\left(0.1996\times \left(\mathit{\sin}\left(\left({Hmax}_{nt-1}-0.1996\ \right)\right)\right)\right)\right)\right)\right) $$
(15)
$$ {Hmax}_{nt}={Hmax}_{nt-1}\times \left(\mathit{\cos}\left(\left(0.67758\ {\left({Hmax}_{nt-1}\right)}^2\times \left({Hmax}_{nt-1}\times \left(\mathit{\cos}\left({\left({Hmax}_{nt-1}\right)}^2\right)\right)\right)\right)\right)\right) $$
(16)
$$ {Hmax}_{nt}={Hmax}_{nt-1}\times \Big(\mathit{\cos}\left(\left(\left(\left(\mathit{\sin}\left({Hmax}_{nt-1}\ \right)\right)\times \left({Hmax}_{nt-1}\right)\times \left(\left(\cos {Hmax}_{nt-1}\right)\right)\times \left(\mathit{\cos}\left({Hmax}_{nt-1}\right)\right)\right)\right)\right) $$
(17)

4.2 Comparison of classic linear and data mining nonlinear models

For further assessment of the standalone models, the performance measures of each model during training and testing periods were summarized in Table 3 and the scatter plots of the forecasts vs observations were presented in Fig. 6. Since the actual data for the testing period is available, the static method, aka one step ahead or rolling forecast, was used instead of dynamic forecasts. In other words, the forecasts in testing periods are based on actual hold out series rather than the forecasted value.

Table 3 The summary of standalone models for one-step ahead maximum wave height forecasting
Full size table
Fig. 6
figure 6

Scatter plots of the standalone model estimation vs. observed experimental training (top panel) and testing (bottom panel) data sets

Full size image

According to Table 3, both linear and nonlinear models show more or less same accuracy at each season. While they are not well enough in AMJ, their forecasting accuracy is acceptable (NSE > 0.9) in the OND season. However, the maximum forecasting error during training period is 0.15 m which belongs to the ARMA model in OND season. The reason behind is perhaps the extreme wave height (Hmax = 4.33m) observed in this season.

According to Fig. 6, the GP and LR forecasts have distributed closer to the 1:1 line in AMJ season. The ARMA exhibited the worst performance in this case. Considering the distribution of the results in JAS season, it is seen that ARMA still scattered far away from diagonal line and tends to underestimate Hmax. As already mentioned, the best forecasts were obtained in OND season with slight superiority of GP to its counterparts.

4.3 Evolution of ensemble models

As previously mentioned in the ensemble modeling, the results of the best LR, ARMA, ANN, and GP models are recombined through a nonlinear scheme. Thus, the ensemble results are not sensitive to the limit of a single input used in standalone models. To attain an optimum ensemble model in this stage, the GP engine was executed again to minimize mean absolute error as the secondary fitness function, and the maximum depth of genes (up to seven to secure parsimony condition) as well as the optimum rate of evolutionary operations were obtained via a trial–error process. Given an extra attempt, a simple averaging (called ensemble mean; EM) model was also considered as another benchmark in which arithmetic mean of the standalone models’ (i.e., LR, ARIMA, ANN, GP) forecasts were calculated as the new forecasts. Table 4 compares the efficiency results of the best evolved ensemble models at different seasons.

Table 4 Performance indices obtained for the ensemble models at each season
Full size table

The results indicated that the EM scheme did not necessarily increase forecasting accuracy of the standalone models. However, the EGP significantly improved the forecasting results. The scheme decreases the forecasting errors to 0.03 m on average. The reason behind such promising results is further postprocessing of the forecasts of linear/nonlinear models so that the results of the effective models were recombined to achieve higher accuracy in testing period. Figure 7 compares ensemble models’ forecasts with corresponding observations during the testing period. Although both ensemble models can capture the stochastic feature of the highly fluctuating, they slightly underestimate Hmax values higher than 1 m in AMJ and JAS seasons. The EGP is superior to EM and can capture the global and local maxima better than EM and all the standalone models.

Fig. 7
figure 7

Observed and ensemble model forecasts of maximum wave height hydrograph and their scatter plot during testing period

Full size image

As previously mentioned, the EGP model is explicit and can be expressed in the tree genome. The corresponding genome of the best evolved EGP models were illustrated as depicted in Fig. 8. The GP and LR models appeared in all the seasons more frequently which implies higher efficiency of the associated models in the accuracy of final solutions. The ARMA model appeared only in the EGP model of OND season.

Fig. 8
figure 8

The best EGP tree evolved for maximum wave height forecasting in a AMJ, b JAS, c OND, and d JFM seasons

Full size image

5 Conclusions

The tremendous growth in offshore operational activities demands enhanced wave forecasting models. In this study, a comparative study between classic linear and data mining nonlinear methods was accomplished and a new ensemble model was proposed for Hmax forecasting. The models were trained and verified using hourly wave measurements from a buoy station located in the route of intensive maritime trade in Mediterranean Sea, Antalya region, Turkey.

The results showed that both linear and nonlinear models are generally qualified to 1-h ahead forecast of Hmax in the study region. As the forecasts obtained in seasonal scale, it can be concluded that the use of ordinary linear regression models, with a given confidence, would be applicable in practice. While a higher degree of accuracy is needed, the proposed ensemble modeling methodology can be implemented.

From a modeling perspective, despite being hybrid, the new EGP model is explicit and allows the modeler to improve the accuracy of standalone models through a secondary fitness function. The other important feature of the proposed ensemble model which highlights its superiority over the existing ensemble models (e.g., Nourani et al. 2020; Tehrany et al. 2019, among others) is that it meets simplicity conditions via an internal sensitivity analysis. These features encourage the EGP model to be applied by practitioners. This study was limited to 1-h ahead forecast of Hmax for a single station in the Mediterranean Sea. Future studies may explore the performance of EGP approach for Hmax prediction with higher lead times. Increasing the number of stations along the sea gives more accurate results on the modeling of the entire coast. Moreover, efficiency of the proposed approach for wind-wave models could be investigated, however, their complexity and inclusion of errors due to sudden changes in wind measurements must be carefully addressed.