1 Introduction

Researches related to geophysical fluid dynamics have attracted more and more attention from scholars in recent years, such as the recent results on the general governing equations of geophysical fluid flows in the ocean [1,2,3,4,5,6,7], and in the atmosphere [8,9,10,11]. The dynamics of the atmospheric boundary-layer is very important in applications, such as weather prediction, climate studies, air pollution, dewfall, frost formation and so on.

The Ekman layer theory is of great significance for understanding the dynamics of atmospheric boundary layer, and it applies to many areas, including the bottom of the atmosphere(near the Earth’s surface and the Ocean), the bottom of the Ocean (near the Ocean flat) and surface waters (near the air-sea interface). The classic Ekman theory [12] requires a balance among the Coriolis force, the pressure gradient force and the frictional force (the dominant momentum balance for steady wind-driven currents is between the wind stress, frictional forces and the Coriolis force) [13,14,15,16]. But in equatorial areas, the Coriolis effect vanishes, the nonlinear effects have to be accounted for [17,18,19,20]. By assuming a constant vertical eddy viscosity and ignoring the nonlinear effects, the Ekman spiral solution is established. It is the first explicit solution of the Ekman model, three predictions are obtained from this solution, two of which have been confirmed by some data in non-equatorial regions. However, the other prediction of the three, in the aspect of the deflection angle of the surface flow from the wind direction, there is a big difference between the forecast and the actual data [21,22,23,24]. This difference is naturally attributed to the assumption of constant vorticity. For the past few years, there exist some results about explicit solutions for non-constant eddy viscosity, whether in the context of atmospheric flows [8,9,10, 25,26,27,28] or regarding wind-generated ocean currents [29,30,31,32,33,34].

In [10], the authors considered the atmospheric Ekman layer with height-dependent eddy viscosities which are some quadratic or rational power functions, they obtained the new solutions respectively. The authors in [33] constructed an explicit solution in the case of a piecewise-constant eddy viscosity with two distinct values, and investigated how variations in the ratio of the two values affect the deflection angle at the surface, while the author in [34] considered non-equatorial steady Ocean currents with a three-value constant eddy viscosity, an explicit solution and a formula for the surface deflection angle are constructed. In [35], the authors investigated transients in the oceanic Ekman layer, in the presence of time-varying winds, they solved the problem by means of Laplace transforms, and gave an explicit formula for the surface current. The authors in [36] discussed the atmospheric Ekman layer with two types of eddy viscosities, in the case of quadratic function, an explicit solution was constructed by using different method from [31], and in the case of piece-constant in two layers, the solution and a formula for the surface deflection angle were obtained.

In this paper, we focus on the atmospheric Ekman flows with three cases of the eddy coefficient which are the fractional and integer powers functions with respect to height, we constructed the explicit solutions and gave the formulas for the surface deflection angle, respectively. These results will be an extension of the corresponding results in [34, 36].

2 The governing equations

The Ekman layer is governed by the following equations in the non-equatorial region of the Northern Hemisphere:

$$\begin{aligned} {\left\{ \begin{array}{ll} f(v-v_{g})=-\frac{\partial }{\partial z}(k\frac{\partial u}{\partial z}),\\ f(u-u_{g})=\frac{\partial }{\partial z}(k\frac{\partial v}{\partial z}), \end{array}\right. } \end{aligned}$$
(1)

which is the standard \(f-\)plane Ekman-flow for variable eddy viscosity, under adequate heat forcing [37, 38]. Here u, v are the components of the wind in the x and y directions, \(u_{g}\) and \(v_{g}\) are the corresponding constant geostrophic wind components, \(f=2\Omega \sin \theta \) is the Coriolis parameter at the fixed latitude \(\theta \) (\(\theta \in (0, \frac{\pi }{2}]\) denotes the angle of latitude in right-handed rotating spherical coordinates) and k is the eddy viscosity coefficient.

We use the following boundary conditions for (1) as

$$\begin{aligned} u&=0,~~~v=0~~~\text{ at } ~~z=z_{0}, \end{aligned}$$
(2)
$$\begin{aligned} u&\rightarrow u_{g},~~~v\rightarrow v_{g}~~~\text{ for } ~~z\rightarrow \infty , \end{aligned}$$
(3)

where \(z_{0}\) is called the roughness height. Let \(\Psi =(u-u_{g})+i(v-v_{g})\), and from (1), we will get

$$\begin{aligned} k(z)\frac{\partial ^{2}\Psi }{\partial z^{2}}+\frac{\partial k}{\partial z}\frac{\partial \Psi }{\partial z}-i\cdot f\Psi =0, \end{aligned}$$
(4)

the boundary conditions (2) and (3) become

$$\begin{aligned} \Psi =-(u_{g}+iv_{g})~~~\text{ at } ~~z=z_{0}, \end{aligned}$$
(5)

and

$$\begin{aligned} \Psi \rightarrow 0~~~\text{ for } ~~z\rightarrow \infty , \end{aligned}$$
(6)

we can write (4) as

$$\begin{aligned} (k(z)\Psi '(z))'=if\Psi (z), \end{aligned}$$

we integrate this equation and obtain

$$\begin{aligned} (k(z)\Psi '(z))=if\int \Psi (z)dz, \end{aligned}$$
(7)

we denote

$$\begin{aligned} \omega (z)=\int \Psi (z)dz, \end{aligned}$$
(8)

the Eq. (7) will become

$$\begin{aligned} k(z)\omega ''(z)=if\omega (z), \end{aligned}$$
(9)

If \(k=\)constant, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} u(z)=u_{g}+e^{\gamma (z_{0}-z)}[-u_{g}\cos (\gamma (z_{0}-z))+v_{g}\sin (\gamma (z_{0}-z))],\\ v(z)=v_{g}-e^{\gamma (z_{0}-z)}[u_{g}\sin (\gamma (z_{0}-z))+v_{g}\cos (\gamma (z_{0}-z))], \end{array}\right. } \end{aligned}$$
(10)

where \(\gamma =\sqrt{\frac{f}{2k}}.\) However, if \(k\ne \)constant, then solving (1) will be more interesting and complex, here, we consider the following cases.

3 Main results

3.1 Case (I)

We assume

$$\begin{aligned} k(z)=fz^{-\frac{8}{3}}, \end{aligned}$$
(11)

then (9) can be written in the form

$$\begin{aligned} \omega ''(z)=iz^{-\frac{8}{3}}\omega (z). \end{aligned}$$
(12)

Thus we have the following result.

Theorem 3.1

The solution of (4) with (5) and (6) can be expressed by the following formula

$$\begin{aligned} \Psi (z)=\left( 1-3\sqrt{i}z^{-\frac{1}{3}}+3iz^{-\frac{2}{3}}\right) Be^{3\sqrt{i}z^{-\frac{1}{3}}}, \end{aligned}$$
(13)

here

$$\begin{aligned} B&=\frac{F\cos \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) +G\sin \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) }{E}e^{-\frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}}\\&+\frac{G\cos \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) -F\sin \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) }{E}e^{-\frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}}i, \end{aligned}$$

where

$$\begin{aligned} E&=\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-1 \right) ^{2}+\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-3z_{0}^{-\frac{2}{3}}\right) ^{2}, \\ F&=u_{g}\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-1 \right) +v_{g}\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-3z_{0}^{-\frac{2}{3}}\right) , \end{aligned}$$

and

$$\begin{aligned} G=v_{g}\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-1 \right) -u_{g}\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-3z_{0}^{-\frac{2}{3}}\right) . \end{aligned}$$

Proof

We assume

$$\begin{aligned} \omega (z)=A \left( z+3\sqrt{i}z^{\frac{2}{3}}\right) +B \left( z-3\sqrt{i}z^{\frac{2}{3}}\right) e^{3\sqrt{i}z^{-\frac{1}{3}}}, \end{aligned}$$
(14)

where A and B are constants which are determined later.

From (14), we have

$$\begin{aligned} \omega '(z)=A \left( 1+3\sqrt{i}z^{-\frac{1}{3}}+3iz^{-\frac{2}{3}}\right) e^{-3\sqrt{i}z^{-\frac{1}{3}}}+ B \left( 1-3\sqrt{i}z^{-\frac{1}{3}}+3iz^{-\frac{2}{3}}\right) e^{3\sqrt{i}z^{-\frac{1}{3}}}, \end{aligned}$$

and

$$\begin{aligned} \omega ''(z)=A \left( iz^{-\frac{5}{3}}+3i\sqrt{i}z^{-2}\right) e^{-3\sqrt{i}z^{-\frac{1}{3}}}+ B \left( iz^{-\frac{5}{3}}-3i\sqrt{i}z^{-2} \right) e^{3\sqrt{i}z^{-\frac{1}{3}}}, \end{aligned}$$

thus \(\omega (z)\) satisfied the (9), and \(\Psi (z)\) satisfied the (4) by using the definition of \(\omega (z)\).

From the conditions (5) and (6), we know that

$$\begin{aligned} A=0 \end{aligned}$$

and

$$\begin{aligned} B=\frac{u_{g}+iv_{g}}{-1+3\sqrt{i}z_{0}^{-\frac{1}{3}}-3iz_{0}^{-\frac{2}{3}}}e^{-3\sqrt{i}z_{0}^{-\frac{1}{3}}}, \end{aligned}$$

by direct calculation, we complete the proof. \(\square \)

If we set

$$\begin{aligned} B_{1}=\frac{F\cos \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) +G\sin \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) }{E}e^{-\frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}}, \end{aligned}$$

and

$$\begin{aligned} B_{2}=\frac{G\cos \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) -F\sin \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) }{E}e^{-\frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}}, \end{aligned}$$

from Theorem 3.1, we have

$$\begin{aligned} \Psi (z)=\left( 1-3\sqrt{i}z^{-\frac{1}{3}}+3iz^{-\frac{2}{3}}\right) (B_{1}+B_{2}i)e^{3\sqrt{i}z^{-\frac{1}{3}}}, \end{aligned}$$

using the definition of \(\Psi (z)\), we obtain

$$\begin{aligned} u=\;&u_{g}+\left[ \left( 1-\frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) B_{1}+\left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}-3z^{-\frac{2}{3}}\right) B_{2}\right] \cos \left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) \\&-\left[ \left( 1-\frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) B_{2}-\left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}-3z^{-\frac{2}{3}}\right) B_{1}\right] \sin \left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) \end{aligned}$$

and

$$\begin{aligned} v=\;&v_{g}+\left[ \left( 1-\frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) B_{2}-\left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}-3z^{-\frac{2}{3}}\right) B_{1}\right] \cos \left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) \\&+\left[ \left( 1-\frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) B_{1}+\left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}-3z^{-\frac{2}{3}}\right) B_{2}\right] \sin \left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) . \end{aligned}$$

If we assume the geostrophic wind is purely zonal, that is \(v_{g}=0\), then we have

$$\begin{aligned} B_{1}=\frac{u_{g}\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-1 \right) \cos \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) -u_{g}\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-3z_{0}^{-\frac{2}{3}}\right) \sin \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) }{E} e^{-\frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}}, \end{aligned}$$

and

$$\begin{aligned} B_{2}=\frac{-u_{g}\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-1 \right) \sin \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) -u_{g}\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-3z_{0}^{-\frac{2}{3}}\right) \cos \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) }{E} e^{-\frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}}. \end{aligned}$$

Now we set

$$\begin{aligned} B'_{1}=\left[ \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-1 \right) \cos \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) -\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-3z_{0}^{-\frac{2}{3}}\right) \sin \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) \right] e^{-\frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}}, \end{aligned}$$

and

$$\begin{aligned} B'_{2}=\left[ -\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-1 \right) \sin \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) -\left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}-3z_{0}^{-\frac{2}{3}}\right) \cos \left( \frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}\right) \right] e^{-\frac{3}{\sqrt{2}}z_{0}^{-\frac{1}{3}}}. \end{aligned}$$

We denote the angle between the wind vector at any height and the geostrophic vector by \(\beta (z)\), then we have

$$\begin{aligned} \begin{aligned} \beta (z)=&\arg \frac{u+iv}{u_{g}+iv_{g}}=\arctan \frac{v}{u}\\ =&\arctan \frac{P\cos \left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) +Q\sin \left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) }{E+Q\cos \left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) -P\sin \left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) }, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} P=\left[ \left( 1-\frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) B_{2}'- \left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}-3z^{-\frac{2}{3}}\right) B_{1}' \right] \end{aligned}$$

and

$$\begin{aligned} Q=\left[ \left( 1-\frac{3}{\sqrt{2}}z^{-\frac{1}{3}}\right) B_{1}'+ \left( \frac{3}{\sqrt{2}}z^{-\frac{1}{3}}-3z^{-\frac{2}{3}}\right) B_{2}' \right] . \end{aligned}$$

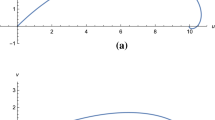
One can draw the graphs of \(\beta (z)\) for \(z_{0}=0.1\) m and \(z_{0}=0.2\) m, respectively, we find that \(\beta (z)\) decrease for all \(z>z_{0}\), which demonstrated on Figs. 1 and 2.

Fig. 1
figure 1

The graph of \(arctan(v/u), z_{0}=0.1\) m

Full size image
Fig. 2
figure 2

The graph of \(arctan(v/u), z_{0}=0.2\) m

Full size image

3.2 Case (II)

We consider an eddy viscosity k(z) given by

$$\begin{aligned} k(z)=fz^{\frac{12}{7}}. \end{aligned}$$
(15)

then the Eq. (9) will become

$$\begin{aligned} \omega ''(z)=iz^{-\frac{12}{7}}\omega (z), \end{aligned}$$
(16)

By following, the example 2.14, for the exponent \(\alpha =-\frac{12}{7}\), and the constant \(c=i\), we denote by \(q=\frac{1}{2}\alpha +1\), then we have \(q=\frac{1}{7}\), so \(\frac{1}{q}=7\) is an odd number, the general solution of (16) is the Cayley solution given by

$$\begin{aligned} \omega (z)=\;&A \left( 1-7\sqrt{i}z^{\frac{1}{7}}+\frac{98}{5}iz^{\frac{2}{7}}-\frac{686}{15}i\sqrt{i}z^{\frac{3}{7}}\right) e^{7\sqrt{i}z^{\frac{1}{7}}}\\ \nonumber&+B \left( 1+7\sqrt{i}z^{\frac{1}{7}}+\frac{98}{5}iz^{\frac{2}{7}}+\frac{686}{15}i\sqrt{i}z^{\frac{3}{7}}\right) e^{-7\sqrt{i}z^{\frac{1}{7}}}, \end{aligned}$$
(17)

so we have

$$\begin{aligned} \Psi (z)=A \left( -\frac{7}{5}iz^{-\frac{7}{5}}+\frac{686}{15}z^{-\frac{3}{7}}\right) e^{7\sqrt{i}z^{\frac{1}{7}}} +B \left( -\frac{7}{5}iz^{-\frac{7}{5}}+\frac{686}{15}z^{-\frac{3}{7}}\right) e^{-7\sqrt{i}z^{\frac{1}{7}}}. \end{aligned}$$
(18)

The conditions (6) and (5) lead to

$$\begin{aligned} A=0 \end{aligned}$$

and

$$\begin{aligned} B&=\frac{u_{g}+iv_{g}}{\frac{7}{5}iz_{0}^{-\frac{7}{5}}-\frac{686}{15}z_{0}^{-\frac{3}{7}}}e^{7\sqrt{i}z_{0}^{\frac{1}{7}}} \\&=\frac{-F\cos \left( \frac{7z_{0}^{\frac{1}{7}}}{\sqrt{2}}\right) -G\sin \left( \frac{7z_{0}^{\frac{1}{7}}}{\sqrt{2}}\right) }{E}+\frac{G\cos \left( \frac{7z_{0}^{\frac{1}{7}}}{\sqrt{2}}\right) -F\sin \left( \frac{7z_{0}^{\frac{1}{7}}}{\sqrt{2}}\right) }{E}i \\&=B_{1}+B_{2}i, \end{aligned}$$

where

$$\begin{aligned} E&=\left( \frac{686}{15}z_{0}^{-\frac{3}{7}}\right) ^{2}+\left( \frac{7}{5}z_{0}^{-\frac{7}{5}}\right) ^{2}, \\ F&=\left( u_{g}\frac{686}{15}z_{0}^{-\frac{3}{7}}+v_{g}\frac{5}{7}z_{0}^{-\frac{5}{7}}\right) e^{\frac{7z_{0}^{\frac{1}{7}}}{\sqrt{2}}}, \end{aligned}$$

and

$$\begin{aligned} G=\left( u_{g}\frac{7}{5}z_{0}^{-\frac{7}{5}}-v_{g}\frac{686}{15}z_{0}^{-\frac{3}{7}}\right) e^{\frac{7z_{0}^{\frac{1}{7}}}{\sqrt{2}}}. \end{aligned}$$

Thus from (18), we have

$$\begin{aligned} \Psi (z)&=(B_{1}+B_{2}i) \left( {-\frac{7}{5}iz^{-\frac{7}{5}}+\frac{686}{15}z^{-\frac{3}{7}}}\right) e^{-7\sqrt{i}z^{\frac{1}{7}}} \\&=\left[ \left( B_{1}\frac{686}{15}z^{-\frac{3}{7}}+B_{2}\frac{7}{5}z^{-\frac{7}{5}}\right) e^{-\frac{7}{\sqrt{2}}z^{\frac{1}{7}}}- i \left( \frac{7}{5}B_{1}z^{-\frac{7}{5}}+\frac{686}{15}z^{-\frac{3}{7}}B_{2}\right) e^{-\frac{7}{\sqrt{2}}z^{\frac{1}{7}}}\right] e^{-\frac{7}{\sqrt{2}}z^{\frac{1}{7}}i}. \end{aligned}$$

From the definition of the \(\Psi (z)\), we obtain

$$\begin{aligned} u=u_{g}+P\cos \left( \frac{7}{\sqrt{2}}z^{\frac{1}{7}}\right) -Q\sin \left( \frac{7}{\sqrt{2}}z^{\frac{1}{7}}\right) \end{aligned}$$

and

$$\begin{aligned} v=v_{g}-P\sin \left( \frac{7}{\sqrt{2}}z^{\frac{1}{7}}\right) -Q\cos \left( \frac{7}{\sqrt{2}}z^{\frac{1}{7}}\right) , \end{aligned}$$

where

$$\begin{aligned} P=\left( B_{1}\frac{686}{15}z^{-\frac{3}{7}}+B_{2}\frac{7}{5}z^{-\frac{7}{5}}\right) e^{-\frac{7}{\sqrt{2}}z^{\frac{1}{7}}}, \end{aligned}$$

and

$$\begin{aligned} Q=\left( \frac{7}{5}B_{1}z^{-\frac{7}{5}}+\frac{686}{15}z^{-\frac{3}{7}}B_{2}\right) e^{-\frac{7}{\sqrt{2}}z^{\frac{1}{7}}}. \end{aligned}$$

We denote the angle between the wind vector at any height and the geostrophic vector by \(\beta (z)\), that is

$$\begin{aligned} \begin{aligned} \beta (z)=\arg \frac{u+iv}{u_{g}+iv_{g}}=\arg \frac{u_{g}u+vv_{g}+i(vu_{g}-uv_{g})}{u^{2}_{g}+v^{2}_{g}} =\arctan \frac{vu_{g}-uv_{g}}{uu_{g}+vv_{g}}. \end{aligned} \end{aligned}$$

If we assume the geostrophic wind is purely zonal, that is \(v_{g}=0\), then we have

$$\begin{aligned} \begin{aligned} \beta (z)=\arg \frac{u+iv}{u_{g}+iv_{g}}=\arctan \frac{v}{u}. \end{aligned} \end{aligned}$$

Now we set

$$\begin{aligned} \begin{aligned} P_{0}=\frac{\cos \left( \frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}\right) \frac{686}{15}z_{0}^{-\frac{3}{7}} -\frac{7}{5}z_{0}^{-\frac{7}{5}}\sin \left( \frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}\right) }{E}e^{\frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}} \frac{686}{15}z^{-\frac{3}{7}} \\ +\frac{\cos \left( \frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}\right) \frac{7}{5}z_{0}^{-\frac{7}{5}} -\frac{686}{15}z_{0}^{-\frac{3}{7}}\sin \left( \frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}\right) }{E}e^{\frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}} \frac{7}{5}z^{-\frac{7}{5}} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} Q_{0}=&\frac{\cos \left( \frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}\right) \frac{686}{15}z_{0}^{-\frac{3}{7}} -\frac{7}{5}z_{0}^{-\frac{7}{5}}\sin \left( \frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}\right) }{E}e^{\frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}} \frac{7}{5}z^{-\frac{7}{5}} \\&+\frac{\cos \left( \frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}\right) \frac{7}{5}z_{0}^{-\frac{7}{5}} -\frac{686}{15}z_{0}^{-\frac{3}{7}}\sin \left( \frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}\right) }{E}e^{\frac{7}{\sqrt{2}}z_{0}^{\frac{1}{7}}} \frac{686}{15}z^{-\frac{3}{7}}, \end{aligned} \end{aligned}$$

we will get

$$\begin{aligned} \begin{aligned} \beta (z)=\arctan \frac{v}{u}=\arctan \frac{P_{0}\sin \left( \frac{7}{\sqrt{2}}z^{\frac{1}{7}}\right) +Q_{0}\cos \left( \frac{7}{\sqrt{2}}z^{\frac{1}{7}}\right) }{e^{\frac{7}{\sqrt{2}}z^{\frac{1}{7}}}+P_{0}\cos \left( \frac{7}{\sqrt{2}}z^{\frac{1}{7}}\right) -Q_{0}\sin \left( \frac{7}{\sqrt{2}}z^{\frac{1}{7}}\right) }. \end{aligned} \end{aligned}$$

The graphs of \(\beta (z)\) for \(z_{0}=0.2\) m and \(z_{0}=0.3\) m will be shown on Figs. 3 and 4, respectively, we find that \(\beta (z)\) decrease for all \(z>z_{0}\).

Fig. 3
figure 3

The graph of \(arctan(v/u), z_{0}=0.2\) m

Full size image
Fig. 4
figure 4

The graph of \(arctan(v/u), z_{0}=0.3\) m

Full size image

3.3 Case (III)

We consider an eddy viscosity k(z) given by

$$\begin{aligned} k(z)=fz^{4}, \end{aligned}$$

then the Eq. (9) will become

$$\begin{aligned} \omega ''(z)=iz^{-4}\omega (z), \end{aligned}$$
(19)

Let

$$\begin{aligned} \omega =z\mu (z), \end{aligned}$$
(20)

and

$$\begin{aligned} z=\frac{1}{s}, \end{aligned}$$

using the chain rule, we have

$$\begin{aligned} \omega '(z)=u-\frac{1}{z}\frac{d\mu }{ds} \end{aligned}$$

and

$$\begin{aligned} \omega ''(z)=-\frac{1}{z^{3}}\frac{d^{2}\mu }{ds^{2}}. \end{aligned}$$

By the direct calculation, (19) is reduced to

$$\begin{aligned} \frac{d^{2}\mu }{ds^{2}}+i\mu =0, \end{aligned}$$

the general solution

$$\begin{aligned} \mu =c_{1}e^{\frac{1+i}{\sqrt{2}}s}+c_{2}e^{-\frac{1+i}{\sqrt{2}}s} \end{aligned}$$

is obtained for two arbitrary constants \(c_{1}\) and \(c_{2}\). Using the definition of \(\omega (z)\) and (20), we obtain

$$\begin{aligned} \Psi (z)=c_{1}e^{\frac{1-i}{\sqrt{2}z}}-c_{1}\frac{1-i}{\sqrt{2}z}e^{\frac{1-i}{\sqrt{2}z}}+c_{2}e^{-\frac{1-i}{\sqrt{2}z}}+c_{2}\frac{1-i}{\sqrt{2}z}e^{-\frac{1-i}{\sqrt{2}z}}. \end{aligned}$$

The conditions (6) and (5) lead to

$$\begin{aligned} c_{1}+c_{2}=0 \end{aligned}$$

and

$$\begin{aligned} c_{1}e^{\frac{1-i}{\sqrt{2}z_{0}}}-c_{1}\frac{1-i}{\sqrt{2}z_{0}}e^{\frac{1-i}{\sqrt{2}z_{0}}}+c_{2}e^{-\frac{1-i}{\sqrt{2}z_{0}}} +c_{2}\frac{1-i}{\sqrt{2}z_{0}}e^{-\frac{1-i}{\sqrt{2}z_{0}}}=-(u_{g}+iv_{g}). \end{aligned}$$

So we have

$$\begin{aligned} c_{1}=-c_{2} \end{aligned}$$

and

$$\begin{aligned} c_{2}=\frac{u_{g}+iv_{g}}{e^{\frac{1-i}{\sqrt{2}z_{0}}}-\frac{1-i}{\sqrt{2}z_{0}}e^{\frac{1-i}{\sqrt{2}z_{0}}} -e^{-\frac{1-i}{\sqrt{2}z_{0}}}-\frac{1-i}{\sqrt{2}z_{0}}e^{-\frac{1-i}{\sqrt{2}z_{0}}} } \end{aligned}$$

If we assume the geostrophic wind is purely zonal, that is \(v_{g}=0\), similar to the procedure discussed in Sect. 3.2, then we can obtain the formula for the angle between the wind vector at any height and the geostrophic vector by \(\beta (z)\).