1 Introduction

Hydraulic fracturing has significantly contributed to the development of unconventional reservoirs. This operation usually results in the formation of complex fracture networks with nonplanar and multistranded shapes, where pre-existing natural fractures play an important role (Gale et al. 2007; Cao and Sharma 2022a). The formation of complex fracture networks in naturally fractured rocks has been supported by cores and mine-back experiments (Fu et al. 2022; Gale et al. 2021; Raterman et al. 2017; Warpinski and Teufel 1987). Multiple numerous fracture diagnostic techniques, which can be simply divided into near-wellbore and far-field, also provide evidence for the generation of complex fracture networks (Warpinski et al. 2014). These techniques include tracer methods, microseismic mapping, pressure interference analysis, and fiber optic-based sensing (Craig et al 2021). The contact area of the complex fracture network with the reservoir is increased, which affects the reservoir drainage area and the production of hydrocarbons. The conductive path connecting the stimulated reservoir region and the wellbore can also change due to alterations in the subsurface formation and fracture conductivity. Therefore, it is essential and vitally important to (1) create a realistic discrete fracture network for pre-existing natural fractures; (2) capture the formation of complex fracture networks formed by the interaction of hydraulic fractures with natural fractures; (3) assess production from wells producing from such complex fracture networks while considering pore pressure depletion and changes in the stress field.

Natural fractures are usually represented as planes of weakness that tend to be reactivated during fracturing operations. This reactivation of these planes of weakness can be modeled by a DFN approach. The interaction between hydraulic fractures (HFs) and natural fractures (NFs) plays a key role in the formation of complex fracture networks. This interaction and fracture propagation in naturally fractured formations have been investigated by researchers using different models, such as boundary element methods (Cao and Sharma 2022b; Wu and Olson 2015), pipe-interface element methods (Sun and Yu 2022; Yan and Yu 2022; Yan et al. 2021), peridynamics (Agarwal et al. 2020; Ouchi et al. 2015), cracking particle methods (Rabczuk and Belytschko 2004), cracking elements methods (Zhang and Zhuang 2019), discrete element methods (Shang et al. 2019), discontinuous deformation analysis (Choo et al. 2016), phase-field theory (Miehe and Mauthe 2016), finite element/extended finite element methods (Li et al 2017), and finite volume methods (Zheng et al. 2019). As compared to other methods, the displacement discontinuity method (DDM), a class of boundary element methods, reduces the dimension of problems by one and only discretizes the boundary (fractures) of the domain, which significantly reduces the computational cost and easily captures the interaction between hydraulic and natural fractures. Gu and Weng (2010) extended an analytical crossing criterion, developed by Renshaw and Pollard (1995), for the non-orthogonal intersection of NF and HF. Then, Wu and Olson (2015) modified the criterion to consider both mode I and mode II in the propagation of hydraulic fractures using a simplified three-dimensional DDM to solve fracture mechanics. Cao et al. (2021) conducted a detailed sensitivity analysis for hydraulic fracture propagation in natural fractures using a three-dimensional DDM-based fracturing simulator.

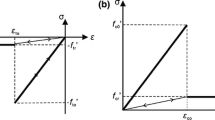
During flowback, a loss of fracture conductivity occurs during the flow from reservoirs to fractures to the wellbore. Thus, incorporating this dynamic process of fracture conductivity loss is important. An empirical exponential relationship (Fig. 1) was proposed to capture the evolution of fracture conductivity, and an exponential index \(\gamma\) (named permeability modulus) is introduced to characterize the change in fracture conductivity with effective stress (Wu et al. 2017). In this paper, this empirical relationship is incorporated into our simulator to take into consideration the effect of conductivity change. Kumar et al. (2018) adopted this relation to investigate the effect of drawdown on fracture conductivity. Zheng et al. (2019) simulated production from complex fracture networks considering the effect of geomechanics and the closure of fractures.

Fig. 1
figure 1

(adapted from Wu et al. 2017)

Loss of fracture conductivity as a function of the effective stress

Full size image

HFTS-2 is a large collaborative field-based project in the Permian Delaware Basin, funded by the US Department of Energy, which aims to improve the understating of the hydraulic fracturing process and the created hydraulic fractures (Ciezobka 2021). Multiple advanced diagnostics have been applied to describe fracture geometry, help maximize the efficiency of hydraulic fracturing, and increase the production of hydrocarbons. These diagnostic techniques include a microseismic survey, geochemical analysis, and core analysis of the core taken from a slant well. The core data can be used to build a DFN for the formation. The algorithm for generating a realistic DFN is provided in the section on natural fracture characterization.

In this paper, we have used the data obtained from the HFTS-2 slant core as a reference to establish the DFN to describe the spatial distribution of natural fractures. An algorithm is developed to generate the DFN automatically until the best realization is found. Then, a fully coupled hydraulic fracturing simulator is used to propagate hydraulic fractures in natural fractures. After that, flowback from the generated DDM-based complex fractures is simulated. Finally, history matching is conducted to compare the simulation results with the field production data. It is our expectation that this process will generate reservoir pore pressure depletion patterns that are much more realistic than those obtained by assuming planar fractures. These depletion patterns can then be used to make important operational decisions such as well spacing and fracturing size.

2 Model Description

The workflow starts with building a discrete fracture network based on core data. This is followed by fracture propagation modeling in this discrete natural fracture network, and finally production history matching. These steps involve the following key elements that we have coupled together into a single model: a DFN simulator, a hydraulic fracturing simulator, and a black oil simulator. The organization of this paper follows this workflow (Fig. 2).

Fig. 2
figure 2

Flowchart for the DFN-fracturing-reservoir simulation workflow

Full size image

The recorded data obtained by multiple fracture diagnostic techniques indicates field-scale vertical (sub-vertical) fractures (Craig et al. 2021). The DFN approach is applied to create realistic natural fracture networks. The key parameters for natural fractures include fracture density, orientation, and length distribution. The details of how to build a realistic and statistically representative natural fracture network are provided in the section on natural fracture characterization. The length distribution of natural fractures follows a power law relationship, which is expressed as (Segall and David 1983),

$$f\left(l\right)=a{l}^{-b}$$
(1)

where b is a constant exponent index, a is a constant depending on the constraints on length, and l is the natural fracture length. Two dominant orientations (NE-SW and WNE-ESE) are observed for natural fractures (Gale et al. 2021). A Gaussian distribution is used to describe the orientation distribution of the natural fractures. The density is a to-be-determined parameter, which is obtained by calibrating with core data.

After the establishment of a realization of a natural fracture network, a DDM-based hydraulic fracturing simulator is used to propagate hydraulic fractures. This simulator fully couples fracture mechanics solved by DDM and fluid flow inside fractures solved by a finite volume method. A fully implicit numerical scheme is used to solve for width and pressure simultaneously at each time step. The growth of fractures through the formation is described in terms of a stress intensity factor (SIF). When the SIF at the tip of the fracture is larger than the critical SIF the fracture is allowed to propagate. A Mohr–Coulomb-based crossing criterion is used to model the interaction between a natural fracture and a hydraulic fracture. Natural fractures can be reactivated when the normal stress is at least equal to the tensile strength, or the shear stress meets the Mohr–Coulomb criteria. Then, the reactivated natural fracture element is converted into a hydraulic fracture element. The mechanical opening of these fractures is now coupled with the fluid flow in the fracture (as is the case with all fractures categorized as hydraulic fractures). As a boundary condition, a uniform pressure is exerted on each fracture surface. The details of the DDM model, discretization of equations, algorithms, and the interaction between hydraulic fractures and natural fractures can be found in Cao and Sharma 2022c. The governing equations are provided here for a better understanding of the basics behind the fracturing simulator. The equilibrium equation is expressed as,

$${\sigma }_{ij,j}+{f}_{i}=0$$
(2)

where \(\sigma\) is the stress tensor and \({f}_{i}\) is the body force in the \(i\) direction.

The strain–displacement relation is given by

$${\varepsilon }_{ij}=\frac{{u}_{i,j}+{u}_{j,i}}{2}$$
(3)

where \(u\) is the displacement, subscripts \(i,j\) represent the derivative in the \(i\) direction with respect to \(j\), and \(\varepsilon\) is the strain.

The governing equation for fluid flow inside fractures is given by,

$$\frac{\partial (\rho w)}{\partial t}-\nabla \cdot \left(\frac{{\mathrm{\rho w}}^{3}}{12\upmu }\right)+{\dot{m}}_{leak-off}={\dot{m}}_{injection}$$
(4)

where w is the fracture width, \(\rho\) is the density of injection fluids, \(\mu\) is the fluid viscosity, \({\dot{m}}_{leak-off}\) is the leak-off term that is determined by Carter’s leak-off equation, and \({\dot{m}}_{injection}\) is the injection term from the wellbore to the fracture. For simplicity, it is assumed that a hydraulic fracture is connected to a perforation cluster, and the injection fluid is distributed equally into each perforation cluster. This assumption can be relaxed by using a more complex wellbore model that computes the fluid and proppant distribution into each perforation cluster (Yi et al. 2021; Zheng et al. 2021).

The generated complex fracture geometry from this DDM-based fracturing simulator is taken as an input for the black-oil reservoir simulator, which allows three fluid phases: water, oil, and gas. While a finite volume method is used for the reservoir domain, a finite area method is used for the fracture domain. It is assumed that (1) water and oil phases are immiscible; (2) gas can be solution gas in the oil. The mass conservation equations for water, oil and gas phases are expressed in Eqs. (5)-(7).

$$\frac{\partial }{\partial t}\left(\frac{\phi {S}_{w}}{{B}_{w}}\right)=\nabla \cdot \left[\frac{k{k}_{rw}}{{\mu }_{w}{B}_{w}}\nabla {\psi }_{w}\right]-{q}_{w}$$
(5)
$$\frac{\partial }{\partial t}\left(\frac{\phi {S}_{o}}{{B}_{o}}\right)=\nabla \cdot \left[\frac{k{k}_{ro}}{{\mu }_{o}{B}_{o}}\nabla {\psi }_{o}\right]-{q}_{o}$$
(6)
$$\frac{\partial }{\partial t}\left[\phi \left(\frac{{S}_{g}}{{B}_{g}}+\frac{{R}_{sw}{S}_{w}}{{B}_{w}}+\frac{{R}_{so}{S}_{o}}{{B}_{o}}\right)\right]=\nabla \cdot \left[\frac{k{k}_{rg}}{{\mu }_{g}{B}_{g}}\nabla {\psi }_{g}+\frac{{R}_{sw}k{k}_{rw}}{{\mu }_{w}{B}_{w}}\nabla {\psi }_{w}+\frac{{R}_{so}k{k}_{ro}}{{\mu }_{o}{B}_{o}}\nabla {\psi }_{o}\right]-{q}_{g}$$
(7)

where \(\phi\) represents porous media porosity, \(k\) is permeability tensor. \({S}_{w}\), \({S}_{g}\), and \({S}_{o}\) represent saturation of water, gas, and oil, respectively. \({B}_{w}\), \({B}_{g}\), and \({B}_{o}\) represent formation volume factor (FVF) of water, gas, and oil, respectively. \({k}_{rw}\), \({k}_{rg}\), and \({k}_{ro}\) represent relative permeability of water, gas, and oil, respectively. \({\psi }_{w}\), \({\psi }_{g}\), and \({\psi }_{o}\) represent potential of water, gas, and oil, respectively, wherein \({\psi }_{i}={p}_{i}-{\rho }_{i}gz\). \({p}_{i}\) and \({\rho }_{i}\) are pressure and density of three phases. \({q}_{w}\), \({q}_{g}\), and \({q}_{o}\) represent volumetric rate of water, gas, and oil, respectively. \({R}_{sw}\) and \({R}_{so}\) are the solution gas ratio in the water and oil phases. Stone’s II Model is used to characterize the relative permeability of three phases. The normalized Stone’s Model II can be expressed as (Lotfollahi 2015; Baker 1988; Stone 1970)

$${k}_{ro}={k}_{rocw}[\left(\frac{{k}_{row}}{{k}_{rocw}}+{k}_{rw}\right)\left(\frac{{k}_{rog}}{{k}_{rocw}}+{k}_{rg}\right)-({k}_{rw}+{k}_{rg})]$$
(8)

where \({k}_{rocw}\) is the oil relative permeability at connate water and zero gas, \({k}_{ro}\), \({k}_{rg}\), \({k}_{rw}\) are the oil, gas, and water relative permeability, respectively. \({k}_{row}\) is the oil relative permeability in oil–water system, and \({k}_{rog}\) is the oil relative permeability in gas–liquid system.

The formation volume factor (FVF) is used to convert volumes at reservoir conditions to its equivalent volumes at standard conditions. The formation volume factor (\({B}_{i}\)) is defined as

$${B}_{i}={V}_{i,rc}/{V}_{i,sc}$$
(9)

where subscripts \(rc\) and \(sc\) represent volumes at reservoir conditions and standard conditions, and \(i\) represents water, oil, and gas. Formation volume factors are usually measured through PVT experiments. Equations relating formation volume factors with pressure can be found in Lotfollahi (2015). These equations are listed in this paper. For slightly compressible fluids (water and dead-oil), FVF at constant temperature can be calculated as

$${B}_{i}=1-{c}_{i}(p-{p}_{sc})$$
(10)

where \({p}_{sc}\) is the standard condition pressure, and \({c}_{i}\) is the fluid compressibility. For gas at reservoir condition, the FVF can be expressed as

$${B}_{g}=\frac{{p}_{sc}}{{T}_{sc}}\frac{T}{p}Z$$
(11)

where \(Z\) is gas compressibility factor.

The integration of the mass conservation equations for each phase gives the pressure equations for the reservoir domain, which is expressed as (Zheng and Sharma 2021; Nguyena et al. 2017)

$$\frac{1}{M}\frac{\partial p}{\partial t}=\left({B}_{w}-{R}_{sw}{B}_{g}\right)\left[\nabla \cdot \left(\frac{k{k}_{rw}}{{\mu }_{w}{B}_{w}}\nabla {\psi }_{w}\right)-{q}_{w}\right]+\left({B}_{o}-{R}_{so}{B}_{g}\right)\left[\nabla \cdot \left(\frac{k{k}_{ro}}{{\mu }_{o}{B}_{o}}\nabla {\psi }_{o}\right)-{q}_{o}\right]+{B}_{g}[\nabla \cdot \left(\frac{k{k}_{rg}}{{\mu }_{g}{B}_{g}}\nabla {\psi }_{g}+\frac{{R}_{sw}k{k}_{rw}}{{\mu }_{w}{B}_{w}}\nabla {\psi }_{w}+\frac{{R}_{so}k{k}_{ro}}{{\mu }_{o}{B}_{o}}\nabla {\psi }_{o}\right)-{q}_{g}]$$
(12)

Where \(\frac{1}{M}=\frac{\alpha -\phi }{{K}_{s}}+\frac{\phi }{{K}_{f}}.\) \(M\) is named Biot modulus, \({K}_{f}\) is the fluid bulk modulus, and \({K}_{s}\) is the solid bulk moduli.

In a similar way, the mass conservation equations and pressure equation for fluids inside fractures are given by (Zheng et al. 2021)

$$\frac{\partial }{\partial t}\left(\frac{V{S}_{w}}{{B}_{w}}\right)=\mathrm{V}\nabla \cdot \left[\frac{k{k}_{rw}}{{\mu }_{w}{B}_{w}}\nabla {\psi }_{w}\right]+{q}_{w}$$
(13)
$$\frac{\partial }{\partial t}\left(\frac{V{S}_{o}}{{B}_{o}}\right)=\mathrm{V}\nabla \cdot \left[\frac{k{k}_{ro}}{{\mu }_{o}{B}_{o}}\nabla {\psi }_{o}\right]+{q}_{o}$$
(14)
$$\frac{\partial }{\partial t}\left[V\left(\frac{{S}_{g}}{{B}_{g}}+\frac{{R}_{sw}{S}_{w}}{{B}_{w}}+\frac{{R}_{so}{S}_{o}}{{B}_{o}}\right)\right]=\mathrm{V}\nabla \cdot \left[\frac{{w}^{2}}{12}\left(\frac{{k}_{rg}}{{\mu }_{g}{B}_{g}}\nabla {\psi }_{g}+\frac{{R}_{sw}{k}_{rw}}{{\mu }_{w}{B}_{w}}\nabla {\psi }_{w}+\frac{{R}_{so}{k}_{ro}}{{\mu }_{o}{B}_{o}}\nabla {\psi }_{o}\right)\right]+{q}_{g}$$
(15)
$$c_{f} w\frac{\partial p}{{\partial t}} = \left( {B_{w} - R_{sw} B_{g} } \right)\left[ {\nabla \cdot \left( {\frac{{w^{3} }}{12}\frac{{k_{rw} }}{{\mu_{w} B_{w} }}\nabla \psi_{w} } \right) + q_{w} } \right] + \left( {B_{o} - R_{so} B_{g} } \right)\left[ {\nabla \cdot \left( {\frac{{w^{3} }}{12}\frac{{k_{ro} }}{{\mu_{o} B_{o} }}\nabla \psi_{o} } \right) + q_{o} } \right] + B_{g} \left[ {\nabla \cdot \frac{{w^{3} }}{12}\left( {\frac{{k_{rg} }}{{\mu_{g} B_{g} }}\nabla \psi_{g} + \frac{{R_{sw} k_{rw} }}{{\mu_{w} B_{w} }}\nabla \psi_{w} + \frac{{R_{so} k_{ro} }}{{\mu_{o} B_{o} }}\nabla \psi_{o} } \right) + q_{g} } \right]$$
(16)

where \(V=wS\) is the fracture control volume, \(S\) is the fracture surface area, and \(w\) is the fracture width. \({c}_{f}={S}_{w}{c}_{fw}+{S}_{o}{c}_{fo}+{S}_{g}{c}_{fg}\), wherein \({c}_{fi}\) is the compressibility of phase \(i\).

The constraints between phase pressure and saturation in fractures and reservoirs are listed below,

$${p}_{cow}={p}_{o}-{p}_{w}$$
(17)
$${p}_{cgo}={p}_{g}-{p}_{o}$$
(18)
$${S}_{w}+{S}_{o}+{S}_{g}=1$$
(19)

where \({p}_{cow}\) and \({p}_{cgo}\) are capillary pressure at the oil/water and gas/oil interface, respectively.

The well index of a fractured well is calculated by the modified Peaceman well model (Moinfar 2013), which is given by,

$$WI=\frac{{k}_{f}w}{\mathrm{ln}\frac{{\left({L}_{f}^{2}+{h}_{f}^{2}\right)}^{1/2}}{{r}_{w}}-1.966}$$
(20)

where \({k}_{f}\) is the effective fracture permeability, \(WI\) is the well index of a fractured well, \({h}_{f}\) is the fracture height relative to the block, \({L}_{f}\) is the fracture length in the block.

3 Natural Fracture Characterization

One-dimensional slant cores through the stimulated volume were acquired in HFTS-2 for fracture description. The one-dimensional core only provides a description of the orientation distribution and number of fractures intersected by the core (Gale et al. 2021). These data are used to characterize and calibrate the properties and distribution of a discrete fracture network. We build the natural fracture network with a to-be-determined areal density and length distribution and match the number of fractures per unit length of synthetic cores with the actual core measurements. The natural fractures, similar to those observed in the HFTS-1, are oriented NE-SW and WNE-ESE. A random Gaussian distribution (with a mean and standard deviation) is used to vary the fracture orientation. The length distribution of natural fractures is simulated using a power law distribution. The areal density of natural fractures in formations and the length distribution of natural fractures are determined by matching the simulated number of intersections with the average number from HFTS-2 data.

The discrete natural fracture network (represented by grey lines) generated by our simulator is automatically calibrated by the number of intersections of natural fractures (represented by red lines) with a synthetic core (represented by a black cylinder), as seen in Fig. 3. The computed number of intersected natural fractures is then taken as a key index for the establishment of the areal density of natural fractures. Nine synthetic cores (Fig. 4), 100 m in length and at 10-m intervals, are analyzed from the created DFN. Take core #1 as an example, for better visualization of the intersected natural fractures in this DFN realization, the natural fracture network is removed except for the fractures that intersect the wellbore (Fig. 5). A comparison of the number of intersected natural fractures by synthetic cores and the results for HFTS-2 slant cores, represented by a green line, shows good agreement and consistency across the entire DFN (see Fig. 6). The average number of intersected natural fractures obtained by Gale et al. (2021) is used. This method results in an areal density of 0.28 fractures/m2 and a power law distribution for fracture length with a lower bound of 2.0 m and an upper bound of 10.0 m.

Fig. 3
figure 3

Schematic for the intersections of natural fractures with a synthetic core

Full size image
Fig. 4
figure 4

Top view of nine cores and a natural fracture network. Five colors are used to represent nine cores with specified locations due to the symmetry

Full size image
Fig. 5
figure 5

Side view of natural fractures intersected by Core #1. A red rectangle enclosed by grey lines represents a natural fracture element, and the synthetic core is represented by a black cylinder

Full size image
Fig. 6
figure 6

The number of intersected natural fractures for nine cores

Full size image

4 Hydraulic Fracturing Simulation

A hydraulic fracturing simulation is conducted to capture the final geometry of fractures after propagation in the calibrated natural fracture network by using a DDM-based hydraulic fracturing simulator. The simulation case is initialized with a domain of 300 m by 400 m, where 33,593 natural fractures are distributed (see Fig. 7). A single-stage fracturing treatment with three perforation clusters (see Fig. 7) is simulated. The parameters used for hydraulic fracture propagation are listed in Table 1.

Fig. 7
figure 7

Schematic for a single-stage fracturing treatment (three perforation clusters) in a naturally fractured formation. A single fracture propagates from one cluster represented by a red line. Natural fractures are represented by grey lines

Full size image
Table 1 Parameters used for fracture propagation in natural fracture networks
Full size table

Figure 8a shows the final complex fracture network after hydraulic fracturing. It is shown that the overall propagation direction for all three fractures initially tends to be in the direction of the maximum horizontal stress (along the Y-axis). Two dominant orientations of natural fractures can cause the continuous re-orientation of hydraulic fractures. Multiple local complex fracture networks are also observed. The following reasons account for this result: (1) a high density of natural fractures increases the probability of the interaction between propagating hydraulic fractures and natural fractures; (2) natural fractures are registered in the form of weak planes which tend to be reactivated; (3) the weak planes make hydraulic fractures tend to turn along the direction of natural fractures as the interaction occurs; (4) fracture bifurcations, usually originating from the location of the interaction between hydraulic fractures and planes of weakness, provide an additional branch and increase the probability of subsequent bifurcations. This phenomenon induces complexity in the fracture networks.

Fig. 8
figure 8

The final geometry of fracture networks after fracture growth in a natural fracture network. In a, the generated hydraulic fractures are represented by black lines, and the simulated natural fractures are represented by grey lines. In b, the width of the propagated fractures is represented by colored lines

Full size image

Well productivity from complex fracture networks is proportional to the contact area between the fractures and the reservoir matrix. In addition, it is related to the width or conductivity of the fractures. Figure 8b shows the width profile for the generated fracture networks, and the color represents the magnitude. It is observed that the minimum width only exists at the tip of fractures, which indicates a good fracture conductivity for fluid flow. Figure 9 shows the dynamic evolution of fracture area versus time as the hydraulic fractures grow in a DFN. The large area of the connected fractures controls the well productivity.

Fig. 9
figure 9

The area of hydraulic fractures as a function of simulation time (single stage)

Full size image

Maxwell et al. (2015) indicated that microseismicity induced by hydraulic fracturing can be divided into “wet” events, induced by the deformations directly related to hydraulic fracturing, and “dry” events, resulting from the failure of remote natural fractures. In this paper, only wet events are registered during the propagation of hydraulic fractures in natural fractures. The magnitude of microseismicity is represented by its moment magnitude, which is expressed as (Aki and Richards 2002)

$${M}_{w}=\frac{2}{3}({\mathrm{log}}_{10}{M}_{0}-16.1)$$
(21)

where \({M}_{0}\) is the seismic moment, which is given by (Aki and Richards 2002)

$${M}_{0}=\mu Ad$$
(22)

where \(\mu\) is the shear modulus, \(d\) is the average slip, and \(A\) is the area.

The results for microseismicity indicate a large number of registered microseismic events during the hydraulic fracturing treatment (Fig. 10). The high density of weak pre-existing natural fractures increases the probability of reactivation when HFs and NFs interact. The moment magnitude of wet events is in the range of − 4 and − 1, which is consistent with the results from field experiments (Warpinski et al. 2013; Grechka et al. 2021). The temporal distribution of microseismicity is shown in Fig. 11. This spatiotemporal distribution of microseismic events allows us to quantify event size and incorporate microseismicity into the hydraulic fracturing model.

Fig. 10
figure 10

Top view of the microseismic cloud (represented by colored solid circles) generated from fracture propagation in natural fractures. The color represents the moment magnitude obtained from the simulation

Full size image
Fig. 11
figure 11

The time evolution of microseismic events. (1) Red for N < 2, (2) Green for 2 ≤ N < 4, (3) Blue for 4 ≤ N < 6, (4) Cyan for 6 ≤ N < 8, (5) Magenta for 8 ≤ N < 10, and (6) Yellow for 10 ≤ N

Full size image

5 Flowback and History-Matching

A black oil reservoir simulator is used to simulate flowback from the complex fracture network generated by the hydraulic fracturing treatment. Two grids need to be established, including the fracture mesh and the reservoir mesh. The grids for fractures obtained from fracture propagation are named DDM grids. The DDM grids are in an unstructured format as indicated by white lines in Fig. 12. The unstructured reservoir mesh, represented by grey blocks enclosed by blue lines, is established when the best embedment of the unstructured DDM grids for fracture geometry is found (see Fig. 12). This approach allows complicated fracture networks to comply with the configuration of the reservoir. The parameters used for the flowback simulation are listed in Table 2.

Fig. 12
figure 12

Computation mesh for production from complex fracture networks in the reservoir. DDM grids are used to represent fracture mesh, and the reservoir mesh is formed in an unstructured format

Full size image
Table 2 Parameters used for reservoir simulation
Full size table

Cases are set up to simulate the production of the fractured well from complex fracture networks and subsequently to conduct history matching with the HFTS-2 field data. The evolution of fracture conductivity during the flowback process is captured by the use of an empirical exponential relationship. The monthly gas rate is chosen as an index to evaluate the history-matching results.

The evolution of reservoir drainage area is reflected in the pore pressure profile (Fig. 13). Two snapshots (180 days and 720 days) during flowback are used to show this process, and the pressure is rescaled for each stage for better visualization. The results indicate that at the start of production, the drainage area is immediately around the complex fracture network. As flowback continues, reservoir drainage area expands in all directions, which is affected by the shape of the generated fracture network.

Fig. 13
figure 13

Pore pressure profile at different times: a 180 days and b 720 days

Full size image

A comparison between the simulation results and field well production data shows good agreement (Fig. 14). It is noted that the dimensionless monthly rate is defined as the simulated/field monthly rate divided by a selected value for comparison convenience. The developed workflow in this paper can be applied for completion optimization and drawdown strategy improvement to enlarge reservoir drainage area and increase well productivity from complex fracture networks.

Fig. 14
figure 14

A comparison between simulation results and field data (production rate during flowback). The red line representing field data is bold for better visualization

Full size image

6 Impact of Natural Fractures

For simplicity, natural fractures are often not taken into consideration when simulating fracture propagation and production. To clearly demonstrate the impact of natural fractures on the fracture geometry and reservoir depletion, the base case in the previous sections was rebuilt without natural fractures. All the other parameters were kept the same (except for the removal of pre-existing natural fractures).

Figure 15 shows the geometry of the propagated hydraulic fractures in the reservoir without considering natural fractures. The black line represents the wellbore and the three white lines represent the propagated hydraulic fractures. The geometry of the hydraulic fractures without natural fractures shows: (1) symmetry with respect to the middle perforation cluster; (2) two non-planar hydraulic fractures due to the effect of stress shadow; (3) much longer hydraulic fractures along the direction of maximum horizontal stress because there are no interactions with natural fractures.

Fig. 15
figure 15

Computation meshes for production from propagated fractures in the reservoir without natural fractures

Full size image

The well is flowed back and the simulated pore pressure at the end of 720 days is presented in Fig. 16a. It is clearly seen that the reservoir drainage without natural fractures is significantly different from those when natural fractures are accounted for. The reservoir drainage without natural fractures extends much further from the well. A wider drainage area is observed with natural fractures. The comparison of monthly rate (see Fig. 17) and cumulative production (see Fig. 18) shows small differences in production rate with and without natural fractures. It is noted that the dimensionless cumulative rate is defined as the simulated/field cumulative rate divided by a selected value for comparison convenience. Pre-existing natural fractures enhance well productivity, but the production comes from a more compact reservoir region closer to the production well. The differences in the fracture geometry, reservoir drainage area, and well productivity without considering natural fractures have very important implications for fracture design and well spacing in naturally fractured reservoirs. A smaller well spacing and a larger cluster spacing may be recommended for this particular naturally fractured reservoir based on the shape of the reservoir drainage volume.

Fig. 16
figure 16

A comparison between simulation results for pressure profile without (a) and with (b) natural fractures at 720 days

Full size image
Fig. 17
figure 17

A comparison between simulation results for monthly rate with (blue lines) and without (red lines) natural fractures

Full size image
Fig. 18
figure 18

A comparison between simulation results for cumulative rate with (blue lines) and without (red lines) natural fractures

Full size image

7 Discussion

Building a realistic representation of a naturally fractured reservoir includes the following three steps: natural fracture characterization, creation of complex fracture networks by propagating hydraulic fractures in this naturally fractured domain, and finally reservoir simulation calibrated by history matching.

The first and most important step is the establishment of a realistic DFN describing the spatial distribution of natural fractures based on the direct observation of fractures in a core. The core provides information about fracture density, fracture orientation, and fracture type (hydraulic fractures, subvertical natural fractures, drilling-induced fractures, and core-handling fractures) (Gale et al 2021). The inherent one-dimensional nature of the core limits our ability to create a two-dimensional DFN. Under this constraint, the representation of natural fractures in naturally fractured formations is made consistent with core observations. In addition, the interaction between NFs and HFs plays an important role in the formation of complex fracture networks, which in turn suggests the importance of propagating hydraulic fractures in a realistic DFN.

A three-dimensional hydraulic fracturing simulator, fully coupling fracture mechanics and fluid flow, is used to propagate hydraulic fractures in natural fractures and subsequently provides the geometry of complex fractures for reservoir simulation. It is observed that (1) the final geometry of hydraulic fractures can be quite complex and asymmetric, (2) multiple local bifurcations and reorientations can occur and enhance the network complexity. Microseismic events are important diagnostic indicators of the areal extent of the fracture network.

Unstructured grids for both fractures and reservoirs are chosen so the complex DDM fracture grids can be explicitly embedded into a reservoir grid for flowback simulations. At this step, it is necessary to capture the reservoir drainage area evolution, reflected in the dynamic reservoir pore pressure profile, since the well productivity is significantly affected by the drainage area once the geometry of fracture networks is given. A permeability modulus is introduced to take into consideration the change of fracture conductivity during flowback. It should be pointed out that the permeability modulus represents the loss of fracture conductivity with effective stress and is related to the mineral composition of the rock. A comparison of the simulated monthly gas rate with field data shows a good match. This suggests that the reservoir and fracture flow has captured all first-order effects and can be used for completion optimization and for estimating reservoir depletion and drainage.

For a realization of a naturally fractured reservoir, different results will be observed if the properties of the natural fractures, the in-situ stress conditions, the reservoir conditions, and other model parameters are changed. For the specified field (HFTS-2), the uncertainties are induced by the one-dimensional nature of the core and to-be-determined natural fracture length and density when the distribution of natural fracture orientation and the number of natural fractures intersected by the wellbore are known. The methodology we proposed can eliminate these induced uncertainties to some degree by calibrating the proposed model with core data and field data. The accuracy can be further improved if outcrop data and image log data with interpreted natural fractures are available.

8 Conclusions

A complete and practical workflow is proposed and demonstrated to investigate the impact of complex fracture networks on well productivity. This work can serve as a template for how to build a realistic natural fracture network from one-dimensional core data, generate realistic instances of complex fracture networks, and simulate well productivity while considering the dynamic evolution of fracture conductivity. Based on the results obtained, the following conclusions are made.

  1. (1)

    A methodology for accurately accounting for pre-existing natural fractures in naturally fractured rocks including their distribution of orientation, density, and length is presented.

  2. (2)

    The accuracy and reliability of the generated DFN and the created hydraulic fracture network (HFN) are demonstrated by comparing them with core data and history-matching production data.

  3. (3)

    The high density of fractures in the core showing various orientations of hydraulic and natural fractures suggests the high frequency of bifurcation, branching and reorientation in the process of hydraulic fracture propagation. This behavior is also observed in the simulation results.

  4. (4)

    The geometry, production and drainage area are very different when natural fractures are not taken into account (only planar fractures are considered). This can have very important implications for decisions regarding well spacing and fracture design.

  5. (5)

    A large number of reactivated natural fractures are observed in hydraulic fracturing simulations and in the field core.

  6. (6)

    Based on the good history-matching results, the fracturing-reservoir simulator can be used to provide guidance on completion optimization, well spacing and drawdown strategies to enlarge reservoir drainage area and increase well productivity.