FracProp: Stochastic Fracture Propagation Model

Abstract

This paper presents a geometric, mechanics-based, stochastic model—FracProp—that was developed to predict fracture initiation and propagation in rock. FracProp is capable of quantifying uncertainties associated with the point of fracture initiation and direction of fracture propagation. The current version of FracProp uses compounded probability distributions that are continuously fitted based on mechanical principles (stress distribution and material properties). The model assumes that fracture initiation and propagation depend on the stress profiles around the fracture (flaw) tip in a rock block subjected to vertical, horizontal, and internal loading. To develop the model, we studied the mechanics of a rock block containing one single flaw (pre-existing opening) with the Finite Element (FE) software ABAQUS. Stress profiles obtained in the modeling were used with the model’s probabilistic processes to dynamically simulate (model) crack/fracture propagation. FracProp was validated with the results of experiments under various loading conditions done at the Massachusetts Institute of Technology (MIT) geomechanics laboratory.

1 Background

The study of fracture initiation and propagation is very important in rock mechanics and engineering. It is essential for the understanding how rock masses behave when subjected to loading that affects natural and engineered structures, such as tunnels and foundations as well as hydraulic fracturing in the context of hydrocarbon extraction and Enhanced Geothermal System (EGS) e.g. Tester (2006).

The mechanics of initiation and propagation of newly created and existing fractures have been studied extensively but more work is required for complete understanding. Field data are difficult to obtain and interpret, thus laboratory testing and numerical modeling play a major role in understanding fracturing in rocks.

Since the early 1900s, many researchers developed criteria to describe the initiation and propagation of cracks in brittle materials. Griffith (1921, 1924) was the first to understand that the presence of cracks in brittle materials led to the decrease of their tensile strength and used Inglis’ (1913) mathematical linear elastic solution for the stress field surrounding an ellipse.

Since then, many other researchers have developed criteria based on stress, strain, and energy fields around a flaw tip to describe the initiation and propagation of cracks in brittle materials (e.g. Erdogan and Sih 1963; Rice 1968; Sih 1974). Many of these have been implemented in Boundary Element (BE) codes (e.g. Chan 1986; Bobet 1997 and 2000; Shen and Stephansson 1993; Vásárhelyi and Bobet 2000; Isaksson and Ståhle 2002) and in Finite Element (FE) codes (e.g. Ingraffea and Heuze 1980; Reyes 1991; Gonçalves da Silva 2009; Gonçalves da Silva and Einstein 2013). Other implementations and methods to simulate crack propagation include hybrid experimental–numerical methods (e.g. Kobayashi 1999; Yu and Kobayashi 1994; Guo and Kobayashi 1995), Extended Finite Element models (XFEM) (e.g. Fagerström and Larsson 2008; Xu and Yuan 2011; Liu et al. 2011) and peridynamics (e.g. Agwai et al. 2011 and Silling and Askari 2005).

In this paper, we propose a hybrid mechanics-based probabilistic model to simulate fracture initiation and propagation. The advantages of the method include the incorporation of uncertainties, both of the initiation point and of the propagation direction of the fracture. The model has also a fast-computational speed, making it ideal to be incorporated in existing Discrete Fracture Networks (DFNs) to model artificially and naturally induced fractures (e.g. Geofrac, Ivanova et al. 2014; EllipFrac, Abdulla 2018; Fracman, Dershowitz 1998).

2 FracProp Assumptions

Initial assumptions concerning the fracturing phenomenon were made so that the model is tractable and computationally efficient. For modeling fracture initiation and propagation, two types of assumptions are made, namely, material-related and fracture-related. The major assumptions are detailed below.

Material-related assumptions:

• (a)Homogeneous material: this implies that the rock material possesses spatially uniform mechanical properties, specifically Young’s modulus and Poisson’s ratio (methods for measuring the homogeneity of rock masses are found in Kulatilake et al. 1990, 1997 and Fiechter 2004).

• (b)Linear elastic material: This assumption allows one to use the principles of superposition to calculate the stresses for any desired loading conditions.

Fracture-related assumptions:

• (c)Stepwise propagation: the fracture propagates in quasi-continuous steps of deterministic length.

• (d)Fracture tip shape is assumed to be semicircular with a deterministic radius. This applies to the existing fracture and to each fracture propagation step.

• Fracture initiation point is assumed to be at the tip of the fracture and to follow a von Mises distribution.

• (e)Fracture initiation criterion: fracture is assumed to initiate if the maximum major principal stress exceeds a threshold, specifically the tensile strength of the material (${\Gamma }_{rock}$) [convention: tensile stresses are positive].

• (f)Fracture propagation direction: the propagation direction is assumed to be perpendicular to the major principal direction and to follow a von Mises distribution.

• (g)Markovian propagation memory: the next propagation step depends solely on the current propagation step.

Note that the convention used in this paper is tensile stresses are positive and compression stresses negative.

Figure 1 shows a schematic of the stepwise propagation in FracProp.

Fig. 1

Schematic of the FracProp stepwise fracture propagation. Note that the propagation (at each step) occurs only if ${\sigma }_{Imax}>{\Gamma }_{rock}$ (maximum principal stress is greater than the tensile strength of the rock)

3 FracProp Methodology

Fracture initiation and propagation in FracProp depend on the stress profiles around the fracture tip in a rock block subjected to vertical, horizontal and/or internal loading with a single pre-existing fracture (i.e. pre-existing flaw). To obtain the required stress profiles, a mechanics database was built using ABAQUS simulations of rock blocks containing one single flaw with different inclination angles (${\theta }_{f}$) and subjected to a unit load for vertical (V_L) horizontal (H_L) and internal fluid pressure (W_P) loading (see Fig. 2), which are applied individually to build a database of stress profiles that can be used to obtain any desired loading condition using superposition. This follows the process developed by Gonçalves da Silva (2009) and Gonçalves da Silva and Einstein (2013). The database of stress profiles will be detailed Sect. 4.

Fig. 2

Schematic of ABAQUS model used to simulate the MIT experimental tests. We simulated tests of rock blocks subject to unit load for different flaw inclinations ${\theta }_{f}$. These correspond to the three models on the right. The figure also shows how the unit loads can be combined to simulate any desired loading

The database is used to obtain the stress profiles around the tip, which are used in a fitting process of the two von Mises distributions that model the initiation and propagation direction sequentially. Sampling from these distributions results in potentially different realizations of the fracture initiation and propagation path along the rock allowing one to capture uncertainties associated with the fracturing process (i.e. the fact that if several samples are tested under the same conditions different fractures patterns are observed). More specifically, for a given load, using the database and assuming linear elasticity and using the principle of superposition, the normal and shear stress profiles around the tip of a flaw are calculated for any desired loading condition. The database contains normal and shear stresses for unit loading under vertical, horizontal and internal water pressure conditions. The extension from single individual unit loading into combined generic-valued loading is straightforward due to the linear elastic assumption (see Fig. 2). Once the stress profiles for a desired load are obtained, the major principal stresses around the tip are calculated. The point at which the major principal stress is maximized is used as the mean of the von Mises distribution for initiation, from where samples will be drawn and considered as the initiation point. At the initiation point, the state of stress is obtained from the mechanics database, and the principal directions are calculated. The second von Mises distribution—propagation direction distribution, is then fitted such that its mean is perpendicular to the major principal stress (sign-convention used: positive for tension and negative for compression). Consequently, a sample direction is drawn from this distribution and a propagation step is imposed, and the fracture geometry is updated. This process continues until the stoppage criteria are met. The stoppage criteria are: (a) the maximum principal stress is less than the tensile strength of the material (${\Gamma }_{rock}$) or (b) the fracture path ends outside the rock block, i.e. complete separation.

The FracProp’s methodology outlined above is now detailed below. It involves a preparation step (step 0), which consists of the development of the database of stress profiles, followed by a set of iterative steps.

3.1 Step 0 (Preparation Step): Building a Database of Stress Profiles of Unit Loads (W _p = 1, V _L = 1, H _L = 1) (MPa)

To develop the model, we started by studying the fracturing process of a flaw (in a rock specimen) when subjected to internal hydraulic pressure, and vertical and horizontal external stresses (leading to the initiation and propagation of new cracks). We did this with a finite element model, using ABAQUS. We model the MIT experimental tests (used to validate FracProp), which were done on 5 cm by 10 cm specimens with a 1 cm long flaw in the center, with varying orientations ${\theta }_{f}$, subjected to unit internal pressure (${W}_{P}$), vertical load (${V}_{L}$) and horizontal load (${H}_{L}$), separately, to build a database of stress profiles around the flaw (see Sect. 4). Based on the ABAQUS simulations’ results, we can simulate any desired loading conditions using the principle of superposition. This step follows the work of Gonçalves da Silva 2009 and Gonçalves da Silva and Einstein 2014. Figure 2 shows a schematic of the MIT test specimen. In the figure, one can see how the simulation results of the individual unit loads (${V}_{L}=1MPa$,${H}_{L}=1MPa$,${W}_{P}=1MPa$) are used to obtain the results for any desired combined load, through superposition due to the assumption of elasticity.

Once the database was developed, the following set of iterative steps (step 1 to step 8) is used to model and generate several realizations for the fracture initiation and propagation patterns.

3.2 Step 1: Determining the Normal and Shear Stress Profiles around the Flaw Tip for a Given Load (W _p , V _L , H _L )

Given a particular load (${W}_{P}$, ${V}_{L}$, ${H}_{L}$), and a particular flaw orientation ${\theta }_{f}$, normal and shear stress profiles around the flaw tip are obtained from the database of the stress profiles (developed in the preparation step 0) using the principle of superposition. Figure 3 illustrates how FracProp uses the database of unit load stress profiles to determine the stress profiles for any desired load.

Fig. 3

Schematic of how FracProp uses the mechanics database to determine the state of stress around the tip of the flaw for any desired loading condition. The inputs are the loading conditions (${W}_{P}$, ${V}_{L}$, ${H}_{L}$) and the flaw inclination ${\theta }_{f}$. FracProp searches for the state of stress profiles generated by the unit loads for the input flaw inclination, and then, through superposition (given the elasticity assumption), generates the stress profiles around the tip for the input loading conditions. In addition, FracProp allows one to obtain the state of stress at any point along the stress path, which is helpful when considering the von Mises distribution sampling

3.3 Step 2: Determining the Principal Stresses and Directions Around the Flaw Tip

Based on the normal and shear stress profiles calculated in step 1, the principal stresses (magnitude and direction) around the flaw tip are calculated.

3.4 Step 3: Checking if the Fracture Initiation Occurs

If the maximum major principal stress is greater than a pre-defined tensile strength threshold (${\Gamma }_{rock}$), then, fracture initiation occurs. Otherwise, no initiation occurs, and the simulation stops.

3.5 Step 4: Modeling the Fracture Initiation Point (Primary Stochastic Process)

If the criterion in step 3 is satisfied, then initiation starts. The point of initiation is assumed to be the point at the tip where the major principal stress is maximized. This point is then used to define/fit the von Mises distribution for fracture initiation, i.e. the point (its value) will become the mean parameter of the von Mises distribution that models the fracture initiation in FracProp.

3.6 Step 5: Sampling a Fracture Initiation Point

A fracture initiation point is sampled from the von Mises distribution defined/fitted in step 4. This is done to represent the uncertainties associated with the initiation point such as spatial variability of material properties.

3.7 Step 6: Modeling the Fracture Propagation Direction (Secondary Stochastic Process)

The principal directions are calculated at the sampled initiation point (in step 5) and the secondary stochastic process is then started using the minor principal direction as the mean of the von Mises distribution that models the direction of fracture propagation.

3.8 Step 7: Sampling the Fracture Propagation Orientation

A propagation direction is sampled from the von Mises distribution for propagation direction defined in step 6.

3.9 Step 8: Fracture Propagation

A fracture propagation step is imposed using the propagation direction sampled in step 7 in combination with the user defined step length l, and the fracture geometry is updated.

Steps 1–8 are repeated while the stoppage criteria are not met. These criteria are:

• a. The maximum principal stress is less than the tensile strength of the material (${\Gamma }_{rock}$).

• b. The fracture path ends outside the rock block, i.e. complete separation.

Figure 4 shows the methodology used by FracProp and how the database of stress profiles interacts with the algorithms of the model, numbered as per the order of the corresponding step. Figure 5 shows the stepwise process of FracProp.

Fig. 4

Methodology used by FracProp. This figure shows how the database interacts with the algorithms in FracProp to model fracture initiation and propagation. This process will be further detailed in the next sections. VM: von Mises; PDF: probability distribution function

Fig. 5

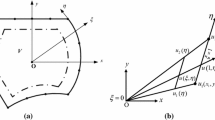
Stepwise process for fracture propagation: (1) input parameters are the loading conditions (${W}_{P}$, ${V}_{L}$, ${H}_{L}$) and the flaw inclination ${\theta }_{f}$, (2) state of stress around the fracture tip is determined using the mechanics database, (3) determine the angle $\psi$ for which the principal stress ${\sigma }_{I}$ is maximum. The value of this angle is used to calibrate the first stochastic process: fracture initiation, from which a value is sampled to obtain the initiation point $\widehat{{\varvec{p}}}$, (4) find the state of stress at point $\widehat{{\varvec{p}}}$ and determine the maximum principal direction ${\mathbf{v}}_{1}$. This value is used to start the second stochastic process: fracture propagation, from which a propagation direction $\widehat{\omega }$ is sampled, (5) a step propagation with length l and direction $\widehat{\omega }$ is imposed

4 Database of Stress Profiles

To develop the model, we started by studying the fracturing process of a flaw (in a rock specimen) when subjected to internal hydraulic pressure, vertical and horizontal stress (leading to the initiation and propagation of new cracks). For this, we built a finite element model, using ABAQUS, of the MIT tests using 5 by 10 cm specimen with a 1 cm long flaw with an aperture of 0.1 cm with varying orientations, subjected to a unit internal pressure, a unit vertical load and a unit horizontal load, separately. This is done so that we can simulate any desired loading condition using the principle of superposition. Stress profiles were created for the test specimen shown in Fig. 6.

Fig. 6

ABAQUS model of MIT test specimen

The boundary conditions of the model are as follows:

• 1. The left-hand-side edge is fixed in the x direction. i.e. ${U}_{1}=0$ in ABAQUS terminology.

• 2. The bottom edge is fixed in the $y$ direction. i.e. ${U}_{2}=0$ in ABAQUS terminology.

A total number of 273 cases were simulated as described in Table 1. This covers the integer inclination angles, ${\theta }_{f}$ $\in [0^\circ ;90^\circ ]$. The profiles for the remaining inclinations, i.e. for range ${\theta }_{f}\in \left[91^\circ ;360^\circ \right)$ can be obtained from the results of the simulations with inclination angles of ${\theta }_{f}$ $\in [0^\circ ;90^\circ ]$. Table 2 shows how the results of the simulations for ${\theta }_{f}$ $\in \left[0^\circ ;90^\circ \right]$ can be used to determine the stress profiles for the remaining flaw inclination angles ${\theta }_{f}$.

Table 1 ABAQUS experiments inclination angles ${\theta }_{f}$ and loading conditions

Table 2 Process to obtain the normal stress and shear stress profiles for ${\theta }_{f}\in$ [$91^\circ ;360^\circ$]: $Y = flip(X)$ returns array $Y$ of the same size as $X$, but with the order of the elements reversed

Figure 7 shows three examples which demonstrate how the stress profiles of = ${\theta }_{f}${120°, 240°, 300°} can be obtained from the stress profiles of ${\theta }_{f}$=60 ^o following the rules presented in Table 2.

Fig. 7

Normal and shear stressed at different inclination angles: 60° vs. 120°, 60° vs. 240°, and 60° vs. 300°

The performance of FracProp was compared with the results of lab experiments conducted on gypsum rocks (detailed later in Sect. 6); thus, the database was developed using the mechanical properties of gypsum listed in Table 3.

Table 3 Mechanical properties of gypsum used in the ABAQUS modeling

The normal and shear stress profiles are extracted along the semicircular path centered around the center of the flaw tip that is $1.03$ times the radius r of the tip as shown in Fig. 8. The value of 1.03 $r$ was chosen based on preceding work by Gonçalves da Silva (2009) and Gonçalves da Silva and Einstein (2014).

Fig. 8

Semicircular path used to extract stress profiles around the flaw tip in the ABAQUS model and angle $\psi$ sign convention. $\psi$ is used to indicate the points along the circular path of $1.03r$ radius, ${\theta }_{f}$ is the inclination angle of the fracture (step)

An example of a stress profile for a flaw with an inclination angle ${\theta }_{f}=$ 45° subjected to a unit internal pressure (${W}_{P}=1MPa$) is presented in Figs. 9 and 10. Figure 9 presents the distribution of stresses ($x$ component, ${\sigma }_{x}$) from ABAQUS (${S}_{11}$ in ABAQUS is ${\sigma }_{x}$, the horizontal stress). Figure 10 shows the stress profiles for ${\sigma }_{x}$, for different flaw inclinations ${\theta }_{f}$, along the pre-defined path in red in Fig. 9 and defined in Fig. 8. One can observe in Fig. 10 that for a flaw angle ${\theta }_{f}$ of 0, i.e. for a vertical flaw the ${\sigma }_{x}$ stress profile is symmetric with two maxima at $\psi$ = 60° and $\psi$ = $-$ 60°. As the angle ${\theta }_{f}$ changes from 0° to 90°, the stress profile has only one maximum value for ${\sigma }_{x}$, which shifts from $\psi$ =$-$ 60°, at ${\theta }_{f}$ = 0° (vertical flaw) to $\psi$ = 0° at ${\theta }_{f}$ = 90° (horizontal flaw). All stress profiles ($xx, yy$ and $xy$ components, i.e. ${\sigma }_{x}, {\sigma }_{y}$ and ${\tau }_{xy}$, respectively) resulting from simulations with different flaw orientations ${\theta }_{f}$ were stored in a database and indexed by the corresponding inclination angle ${\theta }_{f}$ and loading condition so that they are programmatically easily accessible by the stochastic processes of FracProp.

Fig. 9

Simulated stress (${\sigma }_{x}$) distribution around a flaw tip for inclination ${\theta }_{f}$= 45° and pre-defined path (in red). Note that ${S}_{11}$ in ABAQUS is ${\sigma }_{x}$

Fig. 10

Stress profile (${\sigma }_{x}$) for different flaw tip inclinations along the pre-defined path in Fig. 9. The sign convention for angle $\psi$ is presented in Fig. 8

The ABAQUS model is elastic and, therefore, for any combination of vertical, horizontal, and/or internal pressure, the combined stress profiles can be calculated using superposition. Figure 11 shows the normal (${\sigma }_{x}$, ${\sigma }_{y}$) and shear (${\tau }_{xy})$ stress profiles for a load of $HL=1 MPa$, $VL =4.5 MPa$ and $WP=6.72 MPa$. These are the loading values used in one of the experiments conducted at MIT, which was used for validating the model (See Sect. 6). The calculated major and minor principal stresses, ${\sigma }_{I}$ and ${\sigma }_{II}$, and the maximum shear stress, ${\tau }_{max}$ are shown in Fig. 12.

Fig. 11

Normal (${\sigma }_{x}$, ${\sigma }_{y}$) and shear stress (${\tau }_{xy}$) profiles for one single flaw with ${\theta }_{f}\in$ {0°, 30°, 45°, 60°, 90°} subject to the combined loading of ${H}_{L}= 1MPa, {V}_{L}=4.5MPa, {W}_{P}=6.72MPa$

Fig. 12

Major and minor principal stresses and maximum shear stress profiles for one single flaw with ${\theta }_{f}$ $\in$ {0°, 30°, 45°, 60°, 90°} subject to the combined loading of ${H}_{L}= 1MPa, {V}_{L}=4.5MPa, {W}_{P}=6.72MPa$

For the case of combined loading ${H}_{L}= 1MPa, {V}_{L}=4.5MPa, {W}_{P}=6.72MPa$, Fig. 13 relates the angle ${\psi }^{*}$, which corresponds to the point at which the major principal stress ${\sigma }_{I}$ is maximized, to the flaw inclination angle ${\theta }_{f}$. Note that ${\psi }^{*}$ denotes the angle that maximizes the major principal stress at the tip path given a specific inclination angle as mathematically described in Eq. (4) in Sect. 5. This value is used as the mean of the von Mises distribution for initiation in the first stochastic process of FracProp. One can observe that for ${\theta }_{f}=0^\circ$, i.e. a horizontal flaw, the expected point at which fracture might initiate is 60° clockwise with respect to the horizontal (see Fig. 14). Inspecting Fig. 13, one can notice that the pattern for ${\theta }_{f}=[0^\circ ,180^\circ ]$ is almost an exact replica of the pattern observed for ${\theta }_{f}=(180^\circ ,360^\circ )$. This is understandable as a 0°-inclined flaw is like a 180°-inclined flaw; simply the flaw is flipped and so is the described pattern. The relations in Fig. 13 have a stair-like appearance. We believe that this is due to the FE discretization resolution of the model used and that a smoother increase is expected with a higher resolution of the FE discretization.

Fig. 13

${\psi }^{*}$ vs.${\theta }_{f}$ for a combined load ${H}_{L}= 1MPa, {V}_{L}=4.5MPa, {W}_{P}=6.72MPa$

Fig. 14

Expected initiation point and principal directions for a single flaw with different inclination angles ${\theta }_{f}$ subjected to combined load $VL = 4.5 MPa; HL = 1 MPa; WP = 6.72 MPa$ (sign-convention used: positive for tension and negative for compression)

Figure 14 shows the expected initiation point and principal directions at that point, for a single flaw with different inclination angles ${\theta }_{f}$ for the combined load $VL = 4.5 MPa; HL = 1 MPa; WP = 6.72 MPa$. The initiation points deviate from the midpoint of the flaw tip due to the existence of the horizontal and vertical loads.

5 FracProp Model: Stochastic Process and Algorithms

The preceding sections described the basic concepts underlying FracProp, which are now used to explain the computational details.

5.1 Stochastic Processes: von Mises Probability Distribution

FracProp is a stochastic geometric mechanics-based model. It uses two compounded stochastic processes to model fracture initiation and propagation. Both processes use von Mises probability distributions to model the fracture initiation point and the fracture propagation orientation.

The directional probability distribution function (PDF) of the von Mises distribution is used to stochastically model directions in 2-D space. It has been used in several fields of applications such as bioinformatics (Mardia et al. 2008) and seasonality of disease onset (Gao et al. 2006) to name a few.

A direction in 2-D space is defined by one angle, as for example $\psi$, and this angle is the random variable in the von Mises distribution. The circular random variable, $\psi$ is assumed to follow a von Mises distribution if its PDF is given by Eq. (1).

$$f(\psi |\mu_{0} ,\kappa ) = \frac{1}{{2\pi I_{0} (\kappa )}}e^{{\kappa \cos (\psi - \mu_{0} )}} ,\psi \in [ - \pi ,\pi ],\kappa > 0,\mu_{0} \in [ - \pi ,\pi ]$$

(1)

where:

${\mu }_{0}$—the mean direction $\psi$, i.e. $E\left[\psi \right]={\mu }_{0}$

$\kappa$—concentration parameter.

${I}_{0}(\kappa )$—modified Bessel function of order zero as defined in Eq. (2).

$$I_{0} (\kappa ) = \sum\limits_{r = 0}^{\infty } {\frac{1}{{r!^{2} }}\left( {\frac{1}{2}\kappa } \right)}^{2r}$$

(2)

As one can observe from Eq. (1), the von Mises distribution is defined by two parameters: the mean direction, ${\mu }_{0}$ and the concentration parameter, $\kappa$. ${\mu }_{0}$ represents the most likely, or expected, direction, while $\kappa$ describes how wide the distribution is. A simpler interpretation for $\kappa$ is that it represents the reciprocal of the variance. That is, the higher the value of $\kappa$, the narrower (more certain) the distribution is.

Figure 15 plots the von Mises PDF defined in Eq. (1) for different values of the concentration parameter $\kappa$ and a mean direction ${\mu }_{o}$=0. Note that for $\kappa =0$, the von Mises distribution becomes similar to the uniform distribution in the range $[-\pi ;\pi ]$.

Fig. 15

von Mises PDF in Eq. (1) for different values of the concentration parameter $\kappa$ and a mean direction ${\mu }_{o}=0$

5.2 Primary Stochastic Process: Modeling Fracture Initiation Point

FracProp assumes that the initiation point is limited to the tip (represented by a half-circle in Fig. 16) of the fracture and that it follows a von Mises distribution. In addition, it is assumed that the expected initiation point is the point at which, the major principal stress is maximized, which can be obtained using the database described in Sect. 4. To represent any initiation candidate point, i.e. $p$, on the fracture tip, the polar notation is used. That is, any point on the semicircular path is represented by the angle $\psi$ and the length, $r$, which is the radius of the semicircular tip as shown in Fig. 16. The coordinates of $p$ are calculated by the following equation:

$$p = [r \cdot \cos (\psi )\quad r \cdot \sin (\psi )]^{T}$$

(3)

Fig. 16

Initiation point notation in polar format (c center of the flaw tip, r radius of the flaw tip, p initiation point)

The expected initiation point is represented by the corresponding angle ${\psi }^{*}$ which is obtained from the database described in Sect. 4 based on the flaw inclination angle and the loading conditions. ${\psi }^{*}$ is mathematically defined as in the following equation:

$$\psi * = \arg \mathop {\max }\limits_{\psi \in \Psi } \{ \sigma_{I} (\psi )\} |_{{\theta_{f} }}$$

(4)

where

${\psi }^{*}$ is the angle that corresponds to the expected initiation point.

${\sigma }_{I}(\psi )$ is the major principal stress profile along the path of interest.

The value of ${\psi }^{*},$ obtained through Eq. (4), is then used as an input in the primary stochastic process, more specifically, the initiation von Mises distribution is fitted with the mean μ₀ = ${\psi }^{*}$ and with a user defined concentration parameter ${\upkappa }_{1}$ which is based on material properties (the greater the homogeneity of the material, the greater ${\upkappa }_{1}$). In this paper, we assume a homogeneous material (gypsum), and therefore a high value of ${\upkappa }_{1}$ is used. Then, a directional angle, $\widehat{\psi }$ is sampled from the von Mises distribution and is used to represent the initiation point in the current propagation step. Algorithm 1 shows the pseudo code for generating the initiation point at any fracture propagation step. This corresponds to steps 4 and 5 in Sect. 3.

Algorithm 1 Obtaining initiation point at any propagation step, r is the radius of the flaw tip or the radius of the tip of the propagation step
Determine $V_{L}, H_{L}, W_{p}, \kappa _{1}$
For the $i^{th}$ propagation step, find $\theta _{f}^{(i)}$
Use the database to get:
$\sigma _{I}^{(i)} = \mathcal {F} \Big (V_{L}, H_{L}, W_{p}, \theta _{f}^{(i)} \Big )$
$\psi ^{*} = \text {arg max}_{\psi } \big \{ \sigma ^{(i)}_{I}(\psi ) \big \}$
Fit von Mises PDF: $f_{\Psi }\big (\psi | \mu _{o}=\psi ^{*}, \kappa _{1} \big )$
Sample $\hat{\psi } \sim f_{\Psi }\big (\psi | \mu _{o}=\psi ^{*}, \kappa _{1} \big )$
Calculate initiation point: $p_{(i)} = \begin{bmatrix} r \ \cos (\hat{\psi })&r \ \sin (\hat{\psi }) \end{bmatrix}$

It should be mentioned that to impose a fracture propagation step i (i.e. define the ${\theta }_{f}^{(i)})$, two pieces of information should be provided: 1. the initiation point, generated by the primary stochastic process (pseudo-algorithm 1) detailed in this Sect. 2. the propagation direction or orientation which is addressed in the following section.

5.3 Secondary Stochastic Process: Modeling Propagation Direction

The expected propagation direction is assumed to be perpendicular to the major principal direction (sign convention: positive for tension and negative for compression). Given an inclination angle (${\theta }_{f}$), loading conditions and the sampled initiation point, ${\varvec{p}}$, the state of stress at that point (${\varvec{p}}$) can be obtained from the database described in Sect. 4.

Specifically, given the inclination angle (${\theta }_{f}$) of a flaw, loading conditions and the sampled initiation point, ${\varvec{p}}$, the state of stress at that point (${\varvec{p}}$) is calculated and stored in the form of a 2 × 2 matrix as in the following equation:

$$S_{{p_{i} }} = \left[ {\begin{array}{*{20}c} {\sigma_{x}^{{(p^{(i)} )}} } & {\sigma_{xy}^{{(p^{(i)} )}} } \\ {\sigma_{xy}^{{(p^{(i)} )}} } & {\sigma_{y}^{{(p^{(i)} )}} } \\ \end{array} } \right]$$

(5)

where:

${S}_{{p}_{i}}$—state of stress at point ${\varvec{p}}$ on the tip of the flaw in the $i$^th step.

${\sigma }_{x}^{({p}^{\left(i\right)})}$, ${\sigma }_{y}^{({p}^{\left(i\right)})}$—normal stresses in the $x$ and $y$ directions, respectively, at point ${\varvec{p}}$ at the tip of the flaw $i$^th step.

${\sigma }_{xy}^{({p}^{\left(i\right)})}$—shear stress at point $p$ at the tip of the flaw in the $i$^th step.

From the matrix in Eq. (5), the principal directions, major and minor, are obtained using singular value decomposition (SVD) (Wunch 2006) to calculate the eigenvalues ${\lambda }_{1}$ and ${\lambda }_{2}$ and the corresponding eigenvectors v1 and v2. Assuming ${\lambda }_{1}\ge {\lambda }_{2}$, then, v1 is the major principal directional vector, and v2 is the minor principal directional vector. Consequently, the expected propagation direction is perpendicular to the directional vector v1, equivalently, along the v2 directional vector. These directional vectors can be represented by the following equation:

$${\mathbf{v}} = \left[ {\begin{array}{*{20}c} {{\mathbf{v}}_{x} } & {{\mathbf{v}}_{y} } \\ \end{array} } \right]^{T} \to \omega_{{\text{v}}} = \tan^{ - 1} \left( {\frac{{{\mathbf{v}}_{{\text{y}}} }}{{{\mathbf{v}}_{{\text{x}}} }}} \right)$$

(6)

where

$\mathbf{v}$—directional vector of interest.

${\omega }_{\mathrm{v}}$—the angle corresponding to the direction vector $\mathbf{v}$ measured from the $x$ axis.

In FracProp, the propagation direction is represented in terms of the propagation angle, i.e. ${\Omega }_{\mathrm{v}}$ is the random angle describing the propagation direction. To model this, the von Mises distribution, with the PDF in Eq. 1, is used. Algorithm 2 shows the pseudo code that is used to obtain the fracture propagation direction for the $i$th propagation step.

Algorithm 2 Obtaining propagation direction
Determine $V_{L}, H_{L}, W_{p}, \kappa _{2}, \theta _{f}^{(i-1)}$ and step length l
Use Algorithm 1 to get current propagation point, $p_{i-1}$
Use the database to obtain state of stress matrix at the selected initiation point, i.e. $S_{p_{i-1}}$
Calculate the eigenvectors and eigenvalues of $S_{p_{i-1}}$: $\mathbf{v }_{1}, \mathbf{v }_{2}, \lambda _{1}, \lambda _{2}, \lambda _{1} \ge \lambda _{2}$
Calculate the mean propagation directional angle, $\omega ^{*} = \tan ^{-1} \bigg ( \frac{\mathbf{v }_{2_{y}}}{\mathbf{v }_{2_{x}}} \bigg )$
Calibrate a von Mises PDF: $f_{\Omega } \Big (\omega | \mu _{o}= \omega ^{*}, \kappa _{2} \Big )$
Sample a propagation directional angle, $\hat{\omega } \sim f_{\Omega } \Big (\omega | \mu _{o}= \omega ^{*}, \kappa _{2} \Big )$
Propagate according to the sampled angle such that the fracture propagates from $p_{i-1}$ to $p_{i}$ such that:
$p_{i} = p_{i-1} + l \begin{bmatrix} \cos (\hat{\omega })&\sin (\hat{\omega }) \end{bmatrix}^{T}$
Calculate the new inclination angle: $\theta _{f}^{(i)} = \hat{\omega }$

Algorithm 2 is used to model the fracture propagation direction stochastically. The parameter $\kappa$₂ controls the uncertainty in the propagation direction. Low values of $\kappa$₂ lead to high uncertainty and vice versa.

The overall model and how the components described in the previous sections come together are explained in more detail below.

5.4 Overall Model

In this section, we explain how FracProp uses its two components—mechanics database and the stochastic processes (based on the von Mises distribution)—to stochastically model fracture initiation and propagation.

Figure 17 shows the flowchart of the FracProp model. The inputs for the model are listed below.

Fig. 17

FracProp model flowchart

1. Loading conditions: ${V}_{L}; {H}_{L}; {W}_{P}$.

2. Initiation and propagation concentration parameters ${\kappa }_{1}$ and ${\kappa }_{2},$ respectively.

3. Material tensile strength Γrock in $MPa$.

4. Initial flaw dimensions: ${l}_{o}$ and ${w}_{o}$ for length and width (aperture), respectively.

5. Initial flaw inclination angle ${\theta }_{f}^{(1)}$

6. Initial flaw tip center ${c}_{1}$.

7. Fracture propagation steps dimensions: $l$ and $w$ for length and width (aperture), respectively.

The initial flaw has semicircular tip that has a width (aperture) $w$ which is equal to twice the radius of the tip ($2r$)—see Fig. (6)—and so does each of the propagation step. In FracProp, each propagation step has semicircular tip with the same width as the initial flaw. Though, FracProp is equipped with the mathematical capabilities to adapt to any width (aperture) as calculated in the following equation:

$$r_{i} = \left\{ \begin{gathered} \frac{{w_{0} }}{2}\quad i = 1 \hfill \\ \frac{w}{2}\quad i > 1 \hfill \\ \end{gathered} \right.$$

(7)

where

${w}_{0}$—width (aperture), of the initial flaw.

$w$—assumed width of the propagating crack (propagation step).

${r}_{1}$—radius of the tip of the initial flaw.

${r}_{i} \mathrm{for }i>1$—radius of the tip of each propagating crack (propagation step), which is assumed to be constant in this work for all propagation steps (In this work, we assume that ${r}_{i}=\frac{{w}_{o}}{2}, \exists i=\mathrm{1,2}\dots$).

FracProp starts by calculating the major principal stress around the tip of the fracture using the inclination angle ${\theta }_{f}$, mechanics database, and principles of superposition. Initiation and propagation of a new fracture are determined depending on the maximum major principal stress compared to the tensile strength of the rock. If the maximum principal stress is greater than the tensile strength of the material, then the initiation/propagation takes place. The von Mises distribution for fracture initiation is obtained with the calculated mean (${\psi }_{i}^{*}$) and using the input concentration parameter (${\kappa }_{1}$). Then, a sample initiation point is drawn from this von Mises distribution, i.e. ${\widehat{\psi }}_{i}$ (the $i$—index denotes the ith step), which determines the point where the propagation step starts. Since ${\widehat{\psi }}_{i}$ is an angle, the coordinates of the initiation point are calculated using linear algebra by extending the vector initiating from the center of the flaw tip of the ${i}^{th}$ step (${c}_{i}$) along the ${\widehat{\psi }}_{i}$ angle with step length ${r}_{i}$ as in the following equation:¹

$$p_{i} = c_{i} + r_{i} [\cos \hat{\psi }_{i} \quad \sin \hat{\psi }_{i} ]^{T}$$

(8)

The state of stress ${S}_{{p}_{i}}$ at the calculated point ${p}_{i}$ is determined based on its location with respect to the fracture tip from the mechanics database.

The eigenvalues (${\lambda }_{1, 2}$) and eigenvectors (${\mathbf{v}}_{\mathrm{1,2}}$) are then found for the corresponding stress state ${S}_{{p}_{i}}$. The ${\lambda }_{1, 2}$ correspond to the principal stresses, ${\mathbf{v}}_{\mathrm{1,2}}$ correspond to the principal directions. Assuming ${\lambda }_{1}\ge {\lambda }_{2}$, then, ${\mathbf{v}}_{1},{\mathbf{v}}_{2}$ are the major and minor principal directions, respectively, since the analysis is in 2D, and the expected propagation direction is perpendicular to ${\mathbf{v}}_{1}$ (i.e. along ${\mathbf{v}}_{2}$). To find the expected propagation angle (${\omega }^{*}$) from the vector ${\mathbf{v}}_{2}={\left[\begin{array}{cc}{v}_{2x}& {v}_{2y}\end{array}\right]}^{T}$, Eq. (9) is used where the $i$ index denotes the propagation step.

$$\omega_{i}^{*} = \tan^{ - 1} \left( {\frac{{v_{2y}^{(i)} }}{{v_{2x}^{(i)} }}} \right)$$

(9)

The fracture propagation direction angle, ${\omega }_{i}^{*}$, is used as the mean of the von Mises distribution (as discussed previously in Sect. 5.2), in addition to the concentration parameter ${\kappa }_{2}$ specified by the user. A sample direction angle, ${\widehat{\omega }}_{i}$, is drawn from the fitted distribution. This angle is the propagation angle for the ith step. In addition, a propagation step of length $l$ is imposed from the ${c}_{i}$ along ${\widehat{\omega }}_{i}$ as in Eq. (10) yielding into the new center (${c}_{i+1}$).

$$c_{i + 1} = c_{i} + l\left[ {\sin \hat{\omega }_{i} \quad \cos \hat{\omega }_{i} } \right]^{T}$$

(10)

where ${c}_{i}$ is the center of the flaw tip at the $i$^th step (Fig. 16).

Once the propagation step is imposed, the inclination angle ${\theta }_{f}^{(i)}$ is updated as the propagation direction ${\widehat{\omega }}_{i}$ as shown in Eq. (11).

$$\theta_{f}^{(i + 1)} = \hat{\omega }_{i}$$

(11)

This process continues until the maximum major principal stress is either no longer larger than the tensile strength of the material (${\Gamma }_{rock}$) or until the fracture completely separates the rock block.

To quantify the uncertainties associated with fracture initiation and propagation, FracProp uses the Monte Carlo technique, i.e. the procedure in Fig. 17 is repeated several times yielding several realizations of the initiation and propagation.

It is important to discuss the effect of the length of each propagation step on the final fracture pattern: currently, FracProp assumes deterministic propagation step length , which is provided by the user. To select this value, one should understand that the smaller the value of$l$, the larger the number of steps of propagation and the more “continuous” the propagation pattern looks like. Nonetheless, this is associated with higher computational expenses and hence, a balance should be sought between the desire to have continuous fracture pattern and the available computational resources.

Finally, it is important to point out that the von Mises distributions for initiation and propagation are not independent. That is, the fracture propagation direction—controlled by the fracture propagation von Mises distribution (secondary stochastic process)—depends on the sampled initiation point from the first von Mises distribution (primary stochastic process, which models the fracture initiation), as the state of stress at this point determines the mean of the fracture propagation von Mises distribution.

6 Model Validation

To validate FracProp, we performed laboratory experiments at MIT. The experimental setup, developed by the MIT rock mechanics group, allows one to observe and record the fracturing processes with high-speed and high-resolution photography. With it, one can, for instance, distinguish tensile and shear cracking in detail. In addition, the flow of the hydraulic fracturing fluid can be observed including aspects such as fluid lag or lead. Acoustic emissions are also recorded as the tests are performed. Tests are done on prismatic specimens with pre-existing flaw(s) under uniaxial and biaxial external loads and pressurization of the flaw(s). Figure 18 shows a schematic of the principle of the experimentation at MIT, while the overall experimental setup is shown in Fig. 19. It should be mentioned that the concentration parameter, $\kappa$, for both von Mises distributions is set to 25 (see Eq. 2 to check how $\kappa$ affects von Mises distribution).

Fig. 18

Principle of the experimentation at MIT

Fig. 19

Photo of testing equipment, high-resolution and high-speed cameras and acoustic emissions equipment (Morgan 2015)

Two experiments were compared:

7 Comparison 1

The model results were compared with a hydraulic fracture test on gypsum specimens with biaxial loading (${V}_{L} = 4.5 MPa; {H}_{L} = 1 MPa$) and flaw pressure ${(W}_{P} = 6.72 MPa)$. The flaw inclination angle was ${\theta }_{f}^{(1)}=90^\circ$. The results of the simulation and the lab results are shown in Fig. 20 in which the stochastic nature of FracProp is well illustrated in the 10-simulation case (on the right).

Fig. 20

FracProp simulations and MIT lab experiment for the combined loading case ${V}_{L} = 4.5 MPa; {H}_{L} = 1 MPa; {W}_{P} = 6.72 MPa$

8 Comparison 2

This experiment was a dry fracture test on gypsum specimens with uniaxial loading conditions (${V}_{L} = 4.5 MPa$). Figure 21 shows the results of one run of the model for a vertical stress of $30 MPa$ (on the left). The same figure, on the right, shows 10 runs of the model for the same conditions. The model results compare well with the experiments by Wong (2008) (center of Fig. 21).

Fig. 21

FracProp simulations and MIT lab experiment for loading case ${V}_{L}= 30MPa; {H}_{L} = 0 MPa; {W}_{P} = 0 MPa$

We also compared the performance of FracProp with one of the most widely used commercial DEM software—UDEC from Itasca. The results are shown in Fig. 22. The results show similar fracture patterns; however, FracProp takes a fraction of the time to run when compared with UDEC, i.e. few seconds vs. 3.5 h.

Fig. 22

FracProp simulations, MIT lab experiment and UDEC simulation for (wet) combined loading case ${V}_{L} = 4.5 MPa; {H}_{L} = 1 MPa; {W}_{P} = 6.72 MPa$

9 Conclusions

In this paper, we introduced FracProp, a model and software for stochastic modeling of fracture propagation. FracProp assumes that fractures initiate on the tip of the fracture, with the expected initiation point being the point where the major principal stress is maximized. The expected propagation direction is assumed to be perpendicular to the major principal direction (tension). This is repeated in a stepwise process with the next fracture (crack) propagating at the tip of the preceding one. Two sources of uncertainties are addressed in this model: (1) uncertainties associated with initiation point and (2) uncertainties associated with propagation direction. To model fracture initiation and propagation, FracProp uses two compounded stochastic processes based on the Von Mises distribution. To obtain the mean of these two distributions, extensive mechanics simulations were conducted in ABAQUS, with the aim of obtaining the normal and shear stress profiles for flaws subjected to different individual loading conditions with different inclination angles. The results of these simulations were arranged in the form of a database. FracProp uses this database to dynamically retrieve normal and shear stress profiles. Using superposition, FracProp calculates the total normal and shear stresses for any combined loading case and the corresponding major principal stresses. Also, it fits the two von Mises distributions (for initiation and propagation) accordingly at each step of the propagation. Monte Carlo simulation is used to provide several realizations of the potential fracture patterns. FracProp was validated with laboratory experiments from MIT, one for hydraulic fracturing with biaxial external stress (with injected fluid, vertical and horizontal loading) and one for a uniaxial test both conducted on gypsum specimens. The results of the model were in good agreement with the test results. Since FracProp adopts the assumption that fractures are expected to initiate on the tip where the major principal stress is maximized, it cannot—in its current version—model anti-wing cracks, nonetheless, FracProp can be improved to do so by considering shear stresses contribution to fracture initiation and propagation.