Applications of Rock Failure Process Analysis (RFPA) to Rock Engineering

Abstract

The rock failure process analysis (RFPA) method has been developed to simulate fractures that develop progressively in rock engineering. The code of RFPA incorporates the mesoscopic heterogeneity in rock mechanical parameters including Young’s modulus, rock strength characteristic, etc. In numerical models of rock masses, values of Young’s modulus and rock strength are realized according to a given distribution function, such as the Weibull distribution, in which the distribution parameters represent the level of heterogeneity of the medium. Another notable feature of this method is that no priori assumptions need to be made about where and how fracture and failure will occur, i.e., cracking can occur spontaneously and exhibit a variety of mechanisms when certain local stress conditions are met. These unique features have made RFPA capable for simulating the whole fracturing process of initiation, propagation and coalescence of fractures in rock engineering under a variety of loading conditions.

1 Introduction

Landslides are a global geophysical hazard (Kirschbaum et al. 2010). Indeed, nonseismically triggered landslides are estimated to have resulted more than 30,000 fatalities worldwide between 2004 and 2010 (Petley 2012). In particular, landslides pose a significant hazard in Mainland China. Millions of landslides are located in Mainland China, and most of them are concentrated in the southern region of China (i.e., east of the Qinghai-Tibet Plateau and south of Mt. Qinling). Landslides kill hundreds of people and cost tens of billions of Renminbi (RMB) in economic losses every year. Landslide hazards have increased in China since the 1980s, likely due to increasing construction activities and changes in climatic conditions (Huang 2015). For example, the Xikou landslide that occurred in the town of Xikou in Sichuan Province on July 10, 1989 was one of the most significant Chinese geological disasters of the 1980s. In this event, nearly 1,000,000 m³ of soil slid on a steep slope from a relative height of more than 500 m, destroying four villages, killing 221 people, and resulting in a direct economic loss of more than six million RMB. The landslide caused by the Wenchuan earthquake on May 12, 2008 resulted in large numbers of people dead and injured and houses destroyed. Landslides with debris volumes of more than 1,000,000 m³ occurred in the town of Guanling in Guizhou Province on June 28, 2010, killing 99 people. The landslide in the city of Dujiangyan on July 10, 2013 resulted in 30 fatalities and 123 missing. In recent years, construction activities in southwest China have profoundly reduced slope stability . Following the construction of the Three Gorges Dam on the Yangtze River, more than 3800 landslides were observed along the banks of this huge reservoir (Fourniadis et al. 2007).

Great efforts have been put forth to analyse the stability of rock slopes using various approaches. In general, the stability of a rock slope can be evaluated using limit equilibrium methods, whereas complex slope deformation and failure can be analysed in depth using numerical modelling techniques. Numerical methods have been developed and applied because of their ability to better simulate actual slope failure mechanisms (Jiang et al. 2015). The rock failure process analysis (RFPA) is one of the most popular methods and has been widely applied in slope stability analysis. The advantages of the RFPA to study slope stability are threefold. (1) The stress-strain relation of soil or rock is considered, and thus more accurate mechanical behaviours can be computed, such as non-linear deformation and the influence of water and earthquakes. (2) No assumptions are applied in advance related to the interslide forces and their directions, or the shape or location of the slip surface. The critical slip surface is determined automatically, and the slope fails naturally. (3) Complex slope geometries can be addressed, and parametric studies can be conducted. (4) It can effectively simulate the crack initiation , propagation and coalescence processes of rock during the small deformation stage (Tang 1997; Tang and Tang 2012; Tang and Tang 2015).

Simultaneously, many problems in geotechnical engineering involve large deformations, intact rock movement, the post-failure behaviour of a sliding slope or landslide, and the post-failure of soil due to liquefaction or debris flow. In rock engineering, a rock mass contains many joints, faults, inclined strata, and weak zones, etc., and such discontinuities can significantly affect the mechanical behaviour of rock mass (Hoek et al. 2002). Moreover, rock slope instability mechanisms occur not only along existing discontinuities but also as complex internal processes associated with shear or tensile fracture in the intact rock, particularly in massive natural rock slopes and deep engineered slopes (Eberhardt et al. 2004; Wong and Wu 2014). However, with RFPA, it is difficult to study block movement, toppling and landsliding, which can be easily modelled by discontinuous deformation analysis (DDA ) method pro-posed by Shi (1988). Therefore, the RFPA method is further improved by combining the advantages of DDA and the novel discontinuous deformation and displacement (DDD) analysis method has been proposed for the whole-process failure process simulation of rock masses.

2 Governing Equations of RFPA

• 1. Heterogeneity in intact rock

Rock heterogeneity plays a significant role in determining the deformation behaviours and progressive failure process of rock materials (Manthei 2005). Weibull distribution , which is a statistical method, has been widely used to study the effect of heterogeneity on the mechanical behaviour of quasi-brittle materials (Basu et al. 2009; Weibull 1939), and is given as follows:

$$ \varphi \left(\sigma \right)=\frac{m}{\sigma_0}\cdot {\left(\frac{\sigma }{\sigma_0}\right)}^{m-1}\cdot {e}^{-{\left(\frac{\sigma }{\sigma_0}\right)}^m} $$

(17.1)

where σ is the strength or elastic modulus of the element, σ ₀ is the mean value of σ and m is defined as the homogeneity index of the material in the RFPA method.

The distribution of parameter σ is shown in Fig. 17.1. A greater value of m indicates a more homogeneous of material, and vice-versa.

Fig. 17.1

Weibull distribution with different homogeneity index m

• 2. Failure criteria within the RFPA method

The stress state at any point in the damage surface is in an elastic state which can be expressed as follows:

$$ F\left({\sigma}_1,{\sigma}_2,{\sigma}_3\right)<0 $$

(17.2)

However, when the stress state at a point is on the damage surface, it satisfies the following equation

$$ F\left({\sigma}_1,{\sigma}_2,{\sigma}_3\right)=0 $$

(17.3)

There is another stress state at a point, i.e.

$$ F\left({\sigma}_1,{\sigma}_2,{\sigma}_3\right)>0 $$

(17.4)

which indicates that the current stress is higher than the yield strength of the element. Although this stress state does not exist in practice, it occurs during numerical simulation . This is because each load step in a numerical simulation cannot be infinitely small; therefore, if a small load increment △F is applied to an element that has a stress state very close to its critical damage threshold, the stress of this element may exceed that of its damage surface, i.e. in the stress state described by Eq. (17.4).

The damage process of rock is shown in Fig. 17.2. There are two damaged surfaces, i.e. the initial damage surface and the residual strength of the element. For elements within the elastic zone, their mechanical behaviour can be described by the elastic solution (Fig. 17.2 ①); however, when the initial damaged surface (i.e. F ₁) is reached, a brittle stress drop occurs (Fig. 17.2 ②). It is commonly recognized that rock is not a perfectly brittle material; instead, it has a certain residual strength after failure. Therefore, in this study, a residual strength surface (F ₂) is considered. After a brittle stress drop, the damaged surface suddenly lands on the residual strength surface; thus the element is in a damaged state while containing a certain residual strength. Under incremental loading, the stress state of the damaged element will keep on the residual strength surface until a threshold is reached (stress states at point ③). At this moment, the element is fully damaged or is in contact with other elements. As can be seen from Fig. 17.2, if the element is an ideal elastic-plastic material, there is no brittle drop in stress when the stress state meets the initial damage surface F ₁; instead, the damage would further evolve along F ₁. In this study, a residual strength coefficient, λ, which is defined as the ratio between the residual strength and the initial strength, is introduced into the numerical model. Therefore, λ = 1 corresponds to an ideal elastic-plastic model, in which the damage surfaces F ₁ and F ₂ overlap completely. However, when 0 ≤ λ < 1, an elastic-brittle damage model is represented.

Fig. 17.2

Damage surface evolution , where ①, ② and ③ are the three stress states of an element (i.e. elastic, damage and failure) and (a), (b) and (c) are the corresponding stress responses

In this study, the Mohr-Coulomb criterion with a tensile cut-off is used as the damage surface. The tensile damage function is expressed as follows:

$$ {F}_t\left(\sigma \right)=-{\sigma}_3-{f}_t=0 $$

(17.5)

where F _t is the tensile damage surface and f _t is the tensile strength .

The Mohr-Coulomb criterion is used to determine whether the meso-element is damaged in a shear mode, i.e.

$$ {F}_s\left(\sigma \right)={\sigma}_1-{\sigma}_3\frac{1+\sin \phi }{1-\sin \phi }-{f}_c=0 $$

(17.6)

where σ ₁ and σ ₃ are the major and minor principal stresses of the meso-element, respectively, φ is the internal friction angle and f _c is the uniaxial compressive strength.

• 3. Damage evolution of meso-element

When considering the ‘modified effective stress’ concept , the damage variable d (0 ≤ d ≤ 1) is defined as follows:

$$ \boldsymbol{\sigma} ={\boldsymbol{E}}_0\left(1-d\right)\boldsymbol{\varepsilon} $$

(17.7)

The damage in this study refers to the damage at the mesoscopic level, i.e. damage to the meso-elements. Macro fractures are the extension of these meso-damages. The damage constitutive law is shown in Fig. 17.3.

Fig. 17.3

Brittle damage constitutive law of meso-element

When the meso-elements are damaged in the tensile model, the parameter d can be expressed as follows:

$$ d=\left\{\begin{array}{ll}0& \varepsilon <{\varepsilon}_{t0}\\ {}1-\frac{{\lambda \varepsilon}_{t0}}{\varepsilon }& {\varepsilon}_{t0}\le \varepsilon <{\varepsilon}_{tu}\\ {}1& \varepsilon \ge {\varepsilon}_{tu}\end{array}\right. $$

(17.8)

where λ is the residual strength coefficient, ε _t0 is the maximum elastic strain, and ε _tu is the ultimate tensile strain of the meso-element, which indicates whether the element has had a complete loss of its bearing capacity.

If the meso-element is subjected to multiaxial stresses, the strain, ε, in Eq. (17.8) needs to be replaced by the equivalent strain, $\overline{\varepsilon},$ which can be determined by

$$ \overline{\varepsilon}=-\sqrt{{\left\langle {\varepsilon}_1\right\rangle}^2+{\left\langle {\varepsilon}_2\right\rangle}^2+{\left\langle {\varepsilon}_3\right\rangle}^2} $$

(17.9)

where ε ₁, ε ₂ and ε ₃ are the principal strains and the operator〈〉is defined as follows:

$$ \left\langle x\right\rangle =\left\{\begin{array}{ll}x& x\le 0\\ {}0& x>0\end{array}\right. $$

(17.10)

When a meso-element is damaged in shear model, the parameter d is defined as follows:

$$ d=\left\{\begin{array}{ll}0& \varepsilon <{\varepsilon}_{c0}\\ {}1-\frac{\sigma_{cr}}{\varepsilon {E}_0}& \varepsilon \ge {\varepsilon}_{c0}\end{array}\right. $$

(17.11)

where σ _cr is the residual uniaxial strength and ε _c0 is the compressive threshold strain , which can be expressed as follows:

$$ {\varepsilon}_{c0}={f}_c/{E}_0 $$

(17.12)

For the meso-element in the multiaxial stress state , the effect of other principal stresses on its compressive threshold strain , ε _c0, at peak strength must be considered. This effect is expressed as follows:

$$ {\varepsilon}_{c0}=\frac{1}{E_0}\left[{\sigma}_{c0}+\frac{1+\sin \phi }{1-\sin \phi }{\sigma}_3-\nu \left({\sigma}_1+{\sigma}_2\right)\right] $$

(17.13)

where ν is Poisson’s ratio.

• 4. Improve RFPA with the DDA theory.

To simulate the whole failure processes of landsliding, there are two stages that should be studied: the crack growth stage and the block movement stage. The RFPA method is used to model the first stage and the DDA method is used to study the second stage.

In RFPA, FEM is used to analyse the stress and strain distributions. Then, the damage module is used to check whether there is damage to any of the meso-elements. A meso-element is assumed to be damaged if its stress state lies below the failure envelope. If there are any newly formed damage elements, the stress and deformation distributions for all of the elements are recomputed with new parameters under the same loading condition to attain a new equilibrium state. This process is repeated until no additional element damage occurs and then incremental loading is applied. The stress redistribution caused by damage to one meso-element may induce additional damage to the neighbouring meso-elements. Coalescence of these damaged meso-elements gradually leads to the formation of macrocracks, resulting in structural failure.

In the DDA method, under the given displacement mode, the total equivalence equation is built up for the total potential energy of the block system, according to the minimum potential energy principle, as follows:

$$ \left[\begin{array}{llll}{K}_{11}& {K}_{12}& \cdots & {K}_{1n}\\ {}{K}_{21}& {K}_{22}& \cdots & {K}_{2n}\\ {}\vdots & \vdots & \ddots & \vdots \\ {}{K}_{n1}& {K}_{n2}& \cdots & {K}_{nn}\end{array}\right]\left\{\begin{array}{c}{D}_1\\ {}{D}_2\\ {}\vdots \\ {}{D}_n\end{array}\right\}=\left\{\begin{array}{c}{F}_1\\ {}{F}_2\\ {}\vdots \\ {}{F}_n\end{array}\right\} $$

(17.14)

where K _ij is a 6 × 6 sub-matrix, F _i is the external load sub-matrix and D _i is the deformation variable sub-matrix of Block i, which contains six variables:

$$ {D}_i=\left\{{u}_0\kern0.48em {\nu}_0\kern0.48em {r}_0\kern0.48em {\varepsilon}_x\kern0.48em {\varepsilon}_y\kern0.48em {\gamma}_{xy}\right\} $$

(17.15)

where u ₀ and v ₀ are the rigid body displacement of the point (x ₀, y ₀) in Block i; r ₀ is the block rotational angle around the centre (x ₀, y ₀); ε _x and ε _y represent the mormal strain; and γ _xy represents the shear strain. By solving the equilibrium equation, D _i can be obtained. Then, the new geometric boundaries and the displacement of any point in Block i can be calculated as follows:

$$ \left\{\begin{array}{c}u\\ {}v\end{array}\right\}={T}_i{D}_i $$

(17.16)

$$ {T}_i=\left[\begin{array}{llllll}1& 0& -\left(y-{y}_0\right)& \left(x-{x}_0\right)& 0& \left(y-{y}_0\right)/2\\ {}0& 1& \left(x-{x}_0\right)& 0& -\left(y-{y}_0\right)& \left(x-{x}_0\right)/2\end{array}\right] $$

(17.17)

where T _i is the transformation displacement matrix.

It can be seen from Eq. (17.14) that the stiffness matrix between the FEM and DDA methods are the same and can be solved by a uniform algebraic equation solver.

Figure 17.4 shows the solution process in the proposed DDD method. First, the geometric model is meshed as finite elements. Note that the joints and faults are modelled as small, weak solid elements. Then, the RFPA module is used for crack growth study, including the crack initiation , propagation and coalescence processes. In each loading step, the FE model is checked for the presence of large deformed elements. If none are present, the next loading step is applied on the boundary of the FE model. Otherwise, the program will automatically generate new DDA blocks for all of the large deformed elements; this is called the DDA module. In this process, the FE mesh is divided into two domains, i.e. the RFPA domain and the DDA domain, which can be seen in Fig. 17.5. In the DDA domain, each element is considered as a single DDA block, whereas the joint properties, including tensile strength and cohesive strength, are assumed to follow Weibull distribution to model the heterogeneity features of joints. In the RFPA domain, the FEM method is used to simulate the stress and displacement distributions. Note that the boundary of the RFPA domain is considered to be the boundary of the DDA domain, as indicated by the red dashed line in Fig. 17.5.

Fig. 17.4

Flowchart of the DDD method

Fig. 17.5

Schematic of the DDA method, in which the RFPA is a discontinuous deformation analysis module and the DDA is a discontinuous displacement analysis module. The red dashed line is the boundary between the RFPA domain and the DDA domain

Next, the DDA module is used to simulate the block movements. Note that the block in DDA and the element in RFPA are connected by nodes . Therefore, the displacement and force within the blocks are transferred by the connecting nodes. When there is no block movement, the vertex forces and displacements on the boundary between the RFPA and the DDA domains, calculated by the DDA module, are transferred to the nodes on the same boundary within the RFPA domain. Then, the RFPA module is invoked to analyse the stress, displacement and damage in the next loading step. The above-mentioned process continues until it reaches the maximum step, as set by the user.

From the solving process in the DDD method, it can be seen that only large displacement elements in the FE mesh are included within the DDA calculation. Therefore, the number of blocks that need to be calculated by DDA is greatly reduced, significantly improving the computational efficiency of large displacement analyses. Furthermore, the DDD method can automatically search slopes for potential slip surfaces using damage evolution process modelling.

3 Numerical Verification

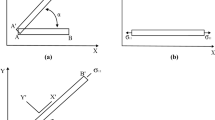
• 1. The geometry conditions

The geometry of the excavated slope model studied here is shown in Fig. 17.6. Importantly, this geometry is the same as that used in the experiments of Zhang et al. (2008). If we consider the same material, the elastic modulus, tensile strength and Poisson’s ratio in the numerical specimen should be 50 MPa, 5 kPa and 0.32, respectively. The cohesion and friction angle are taken as 40 kPa and 32°, respectively. The left and right boundaries of slope are fixed in the x-direction but the y-direction is free, whereas the bottom boundary is fixed in the y-direction but free in the x-direction.

Fig. 17.6

The geometry of the modelled slope. The slope angle is given by α

• 2. Formation of a slip surface

Figure 17.7 shows the failure pattern of the rock slope modelled by FEM when the slope angle α is 75°. Noted that the displacement of the slope is relatively small before the sliding surface forms. Indeed, only minor damage (cracks) can be observed during the initial stages of slope failure in our numerical model (Fig. 17.7a), in agreement with observations from both experimental investigations and geological surveys. Figure 17.7a shows that a long crack formed at the top of the slope, and that a few smaller cracks formed within the slope and at the toe of the slope. Importantly, the long crack at the top of the slope has a surface expression (i.e. visible at the surface), while the smaller cracks, even those at the toe of the slope, do not break the surface (Fig. 17.7a). The numerical result agrees with the in-site observations that, prior to a landslide, many slopes display surface cracks at the top of the sloe (as shown in Fig. 17.8) but few visible cracks at the toe of the slope. Generally, shear cracks occur near the toe of the slope, and tensile cracks initiate at the slope crest. Shear fractures are unlikely to produce visible cracks because the slip surfaces remain in contact. Tensile failures (i.e. opening-mode fracture), however, result in fracture surfaces that separate and are therefore easily observed (Fig. 17.8). One of the advantages of numerical modelling is can provide images of the slope at progressively higher displacements, which makes it easy to follow the progression of slope failure. Figure 17.7b, c show the same slope as in Fig. 17.7a but the displacement has been enlarged 10 and 50 times, respectively. The image of Fig. 17.7c shows that the sliding surface has formed and has divided the slope into a sliding region and a rigid region. As explained above, the large displacement and movement of the sliding region must be subsequently studied using the DDA module.

Fig. 17.7

The failure pattern of the rock slope modelled by FEM for a slope angle of α = 75°, where (a), (b) and (c) show images of the sliding region with displacement enlarged to 1, 10 and 50 times, respectively

Fig. 17.8

In-site observation of surface cracks at the top of a slope

Figure 17.9 shows the displacement distribution during failure of the 75°-angle slope. The displacement is normalized in each step to highlight the largest displacement area (warm colours indicate high-displacement and cold colours indicate low-displacement). The results indicate that, when the gravitational acceleration is relatively small (i.e. 19g ₀), the largest displacement area is located at the top-right corner, and the smallest displacement is located at the bottom of the slope. With each additional increment of gravity, the zone of largest displacement is gradually transferred to the sloping sides, such as when g = 30 g ₀ (Fig. 17.9). When g increases to 37g ₀ or 40g ₀, the largest displacement area is mainly concentrated in the vicinity of the sloping sides, but it is difficult to judge from these images whether the slope is unstable. Further increments of gravity accelerate the localization of the large displacement, which can be clearly observed when g = 45 g ₀. Finally, the largest displacement is concentrated only near the sloping sides when g = 49 g ₀. To better understand whether the slope has transferred into an unstable state, we use the model to plot the displacement vector fields for the slope. The displacement vector fields for gf = 48 g ₀ and gf = 49 g ₀ show that there is a sudden increment of displacement in the sliding region at gf = 49 g ₀ (Fig. 17.10), indicating that the critical gravitational acceleration of this slope model is gf = 49 g ₀.

Fig. 17.9

The evolution of displacement in a slope with a slope angle of α = 75° at different gravity step increments, from 19g ₀ to 49g ₀. The colour bar shows the normalized displacement in each gravity increment step. Warm colours indicate high-displacement and cold colours indicate low-displacement. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article)

Fig. 17.10

Displacement vector evolution of the slope (α = 75°) at g = 48 g ₀ and g = 49 g ₀. The arrow direction and size represents the direction and size of the displacement, respectively

Figure 17.11 presents the simulated initiation , propagation, and coalescence of the fractures in the slope model for increasing gravitational acceleration steps, and Fig. 17.12 presents the corresponding stress distribution throughout the numerical slope. The results indicate that cracks initiate first at the toe of the slope and propagate upward along the slope (i.e., 30g ₀ and 35g ₀) (Figs. 17.11 and 17.12). Figure 17.13 shows the types and locations of failures that occurred during increasing increments of gravitational acceleration. Figure 17.13 shows that both tensile (red circles) and shear failures (blue circles) occur in the heterogeneous material, which agrees with the finding of Pells (1993) that non-homogeneity in the material itself can lead to non-uniform stress across the section. Due to the effect of heterogeneity on mechanical behaviour, microfailures (i.e. fractures at a length scale much shorter than the eventual slip surface) can occur at locations of high-stress, and also initiate at weak locations due to the presence of local discontinuities . The stress distribution in Fig. 17.12 further indicates that the heterogeneity of the rock causes non-homogeneous stress to be distributed throughout the slope, causing particularly large stress fluctuations that result in distributed failures at the beginning of loading, as shown in Fig. 17.13, where many isolated shear fractures form at the toe of the slope (i.e., at 15g ₀). With further increments in loading, the number of shear failures (blue circles) increases, and tensile failures (red circles) occur in the regions where shear failures have been generated (i.e., 20g ₀ and 25g ₀, as shown in Fig. 17.13). Many tensile failures are generated when g = 30 g ₀, which results in an observable crack at the toe of the slope, as shown in Figs. 17.11 and 17.12. Tensile failures begin to localize and finally lead to the formation of macrocracks. It is interesting to note that when gravitational acceleration increases to a certain value (such as 40g ₀), a crack appears in the top of the slope (see Figs. 17.11 and 17.12), similar to that shown in Fig. 17.8. The failure types shown in Fig. 17.13 indicate that such surface cracks are caused by the initiation and propagation of tensile failures (red circles).

Fig. 17.11

Images of the failure process of a slope with a slope angle α = 75° at different gravity step increments, from 19g ₀ to 49g ₀

Fig. 17.12

Images showing the evolution of shear stress with in a slope with a slope angle of α = 75° at different gravity step increment, from 19g ₀ to 49g ₀. The colour bar shows the normalized shear stress in each gravity increment step. Bright colours indicate high-stress and dark colours indicate low-stress. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article)

Fig. 17.13

Images showing the location of tensile (red circles) and shear (blue circles) failure events within a slope with a slope angle of α = 75° at different gravity step increments, from 15g ₀ to 40g ₀. The green dashed line shows region of shear-failure coalescence . (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article)

The failure types and locations shown in Fig. 17.13 facilitate a deeper understanding of the mechanism of the slope. The failure process indicates that shear failures (blue circles) occur at the slope toe, which in turn cause load transfer to the adjacent areas (such as at 15g ₀). Because of the heterogeneity of rock, shear failures are scattered near the toe of the slope. According to fracture mechanics , stress concentrates at the tip of an existing shear crack and likely leads to crack extension due to tensile stresses . For this reason, tensile failures (red circles) appear in the region where earlier shear failures occurred, as shown in Fig. 17.13 when g = 20 g ₀. As loading progresses (i.e., g = 25 g ₀ and 30 g ₀), shear failures occur closer and closer to the top of the slope. At the same time, tensile failures are also produced in the shear failure region near the slope toe. The number of shear failures is larger than of the number of tensile failures at the beginning of loading, but the opposite situation occurs when the loading increment reaches a certain value, such as 35g ₀. With subsequent loads, shear failure may continue to occur, but tensile fracture is the main type of failure in the slope, especially in the region of the top surface. The coalescence of mixed tensile-shear crack development from the toe of the slope and tensile crack development from the upper surface results in a sliding resistance force that is lower than the sliding force and subsequently leads to slope-scale instability . It can be observed that the cracks that form between the tensile-failure clusters at the top and the toe of the slope are mainly attributed to shear failure, as shown in Fig. 17.13 when g = 40 g ₀ (the shear failure coalescence region is indicated by a dashed green line). This coalescence region is also observed in the stress distribution shown in Fig. 17.12, which shows that large shear stresses (indicated by brighter colours) are concentrated in the coalescence region. The failure process of the slope indicates that both tensile failures and shear failures must be implemented in the numerical model to more deeply understand the failure mechanism of different slopes.

Figure 17.14 presents the different failure patterns of slopes with different slopes angles (45°, 75° and 85°). It can be observed that the cracks tend to initiate from the slope toe when the slope angle is relatively large. When the angle is smaller, the cracks are more likely to start above the slope toe. Figure 17.15 shows the experimentally obtained failure patterns of a slope when the slope angle is 85°, taken from the work of Zhang et al. (2008). The final gravitational acceleration required for slope failure in the experiment was 45g ₀. The critical slip surface obtained from our numerical modelling agrees well with that observed in the experiment of Zhang et al. (2008) (similar findings were also reported in Hu et al. (2010). In both the numerical and experimental results, tensile fractures were observed at the top of the slope, which agrees with the common failure mode for full-scale in-situ slopes (as shown in Fig. 17.8).

• 3. Large displacement and block movement modelling of the slope

Fig. 17.14

Slope failure patterns in slopes with different slope angles (displacement enlarged 50 times)

Fig. 17.15

Photograph of an experimentally obtained slope failure patterns for a slope with a slope angle of 85° (Hu et al. 2010)

As soon as the slip surface forms in the slope, the sliding region will experience large displacements and block movement. Figures 17.4 and 17.5 show that the DDA module is invoked to address the mechanical behaviour in the post-failure slope. Jing (1998) noted that the chief disadvantage of DDA is the requirement of knowing the exact geometry of the fracture systems in the problem domain. However, when the DDA geometry is inherited from that of the FEM grid, especially when the FEM module automatically delineates the slip surface, the DDA method is more convenient for modelling the post-failure process of the slope. In this study, when the FEM module prepares data for DDA module, the friction angle, cohesion and tensile strength of new cracks are assumed to be zero, and other joints (element edges shown in Fig. 17.5) are consistent with the elements. Only gravitational loading is applied to the slope, which is equal to the gravitational acceleration at failure. Figure 17.16 shows the input geometry in DDA modelling of the post-failure slope with an initial slope angle α = 75° in which the sliding region includes 16,451 small blocks (elements). The post-failure process of this slope modelled by the DDA module is shown in Fig. 17.17 in which the large-scale movement and rotations of blocks are clearly demonstrated. This type of deformation mode is highly difficult to simulate by conventional FEM or other continuum-based numerical methods. The result shows that the sliding region moves along the slip surface (see Fig. 17.17a) at the beginning of sliding. With further landslide progression, the sliding region is divided into many blocks, including large and small blocks (Fig. 17.17b). We note that most of the small blocks are mainly distributed near the slip surface. These small blocks are elements that failed during the FE modelling, and their accumulation is the main reason for the position of the slip surface. Many small blocks slide or roll together as post-failure slope deformation continues, accompanied by fragmentation of large blocks. Because the slip surface (red solid line in Fig. 17.17) is not smooth (same as on-site or experimental observation) and the blocks move against each other, the velocities of movement of those blocks are different from one another, which leads to the rolling of blocks. Furthermore, such mechanical behaviour also results in joint failure during the landslide processes, subsequently forming smaller blocks, as shown in Fig. 17.17d–f, in the forefront of landslide zone (indicated by the red dashed line in (f)). This phenomenon agrees with the failure characteristics of slopes with large slope angles. Finally, because of large gravitational loading, the sliding mass moves far from its original position, as shown in Fig. 17.17h.

Fig. 17.16

Input geometry for the DDA modelling. Example shown is the post-failure slope configuration for a slope with an initial slope angle α = 75°, as provided by the FEM modelling

Fig. 17.17

Images showing block movement, rotation, and fracturing processes during the post-failure displacement of a slope with and initial slope angle α = 75° at different time increments (from 0.37 to 29.11 s). Solid red lines delineate the sliding surface . The dashed red line in (f) shows zone of broken, smaller blocks (see text for details). The dashed red line in (h) shows the fragmental nature of the forefront of the sliding region (for comparison with Fig. 17.18d; see text for details). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.) (Tang et al. 2017)

Figure 17.18 shows the post-failure process of a slope with α = 85°. The most notable difference between α = 75° and α = 85° is that the fragments at the forefront of the sliding region in the slope with α = 85° are smaller than those in slope with α = 75° (see the zone within the red dashed line in Figs. 17.17h and 17.18d). The reason for this result lies in the fact that most of the gravity of the overlying sliding mass loads the mass at the toe of the slope (red dashed region shown in Fig. 17.18a) if the slope angle is large, but such a load is mostly supported by the rigid region in the slope with a small slope angle . During the landslide process, the movement of blocks adjacent to the contact between the sliding region and the rigid region results in block fragmentation at the contact zone, as shown by the red dashed zone shown in Fig. 17.18c. The results also indicate that the sliding distance is longer when the slope angle is higher (at the same time following slip surface initiation ).

Fig. 17.18

Images showing block movement, rotation, and fracturing processes during the post-failure displacement of a slope with an initial slope angle α = 85° at different time increments (from 0.32 to 29.27 s). Solid red lines delineate the sliding surface . The dashed red line in (d) shows the fragmental nature of the forefront of the sliding region (for comparison with Fig. 17.17h; see text for details). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.) (Tang et al. 2017)

The failures during the FE modelling stage are considered in the modelling of the sliding process by the DDA module, as shown in Fig. 17.17 and 17.18. In the classic DDA modelling, most studies did not consider failures during the initiation of the slip surface. To study the effect of such failures on the characteristics of the landslide, the following simulation of a landslide by the DDA module assumes that the input parameters (friction angle, cohesion and tensile strength ) of the joints on the sliding surface are zero, and other joints in the sliding region (shown in Fig. 17.16) are consistent with the initial values of the elements, i.e., the joints at the edges of failed elements are not set to zero but are equal to the initial parameters of such elements. The modelling result is shown in Fig. 17.19, where the slope angle is 75°. It can be observed that the integrated sliding region slides along the sliding surface during the initial stages of post-failure slope deformation. Because of the roughness of the slip surface, the sliding region is broken into many large blocks, which differs from results with a homogeneous slip surface (Bui et al. 2011). During the movement of the blocks, the larger ones can be split again and generate smaller blocks, as shown in Fig. 17.19f–g for the splitting process of block ①. Furthermore, similar to that shown in Fig. 17.17, block fragmentation is most efficient near the boundary between the sliding region and rigid region.

Fig. 17.19

Images showing block movement, rotation, and fracturing processes during the post-failure displacement of a slope with an initial slope angle α = 75° without consideration of the element failure in the DDA modelling (see text for details). Solid red lines delineate the sliding surface . Block splitting and rotation are indicated in panels (g) and (h) (see text for details). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.) (Tang et al. 2017)

The advantages of the combined FEM and DDA method in handling static failure and post-failure behaviour of the slope are clearly noted in the discussion presented above. For both small and large displacements, the automatic identification of the slip surface, fragmentation, block movement, and rotation are easily addressed by the combined method. This is because the continuum-based finite element method has the advantage of static crack initiation , propagation, and coalescence modelling, including localization of failures, and the discontinuous failure along the slip surface of the sliding block is simulated without any difficulties by the DDA method.

4 Engineering Applications

4.1 The Slope Instability at the Alpetto Open Pit Mine

• 1. Engineering geological conditions

On June 28–29, 1997, a serious slope instability happened at the Alpetto open pit mine, located in the north part of Cesana Brianza (Lecco), in Northern Italy. The topographic map of the Alpetto Mine is shown in Fig. 17.20, where two cross sections are highlighted, i.e. Section A and B. In this paper, Section A is elected as the typical profile for analysis. It is located in the eastern part of the mine. The instability occurred along Section A during a continuous and intensive rainfall process and extended from the toe to the crest of the main exploitation front, for a total height of 130 m, involving an estimated volume of 50,000 m³ (in Fig. 17.21). Investigation was carried out after the rock slide including geological mapping, borehole drilling , laboratory testing and so forth (Barla et al. 2012).

Fig. 17.20

Survey of Cesana Brianza in Northern Italy and plan view of the Alpetto Mine (Barla et al. 2012)

Fig. 17.21

Alpetto high rock cut slope (Cesana Brianza, Lecco, Italy) after the 1997 rock slide (Barla et al. 2012)

On the basis of rock properties, Section A can be characterized by a carbonatic stratigraphic sequence (Early Jurassice-Middle-Early Cretaceous) where the following geologic formations may be distinguished: Maiolica (MAI; Middle Cretaceous), Rosso ad Aptici (RAP; Late Jurassic), Radiolariti (RLS; Middle-Late Jurassic), Rosso Ammonitico Lombardo (RAL; Early-Middle Jurassic), Calcare di Domaro (DOM; Early-Middle Jurassic), and Calcare di Moltrasio (MOT; Early Jurassic). The RAL geological formation also includes some black shale levels.

According to the geological survey, the stratigraphic sequence is characterized by the bedding planes with dip angles from 55 to 80°. The main fault of Section A in the eastern part is inside the MOT formation, and it is characterized by a dip angle of 80°, while the faults in the western area are characterized by an approximately N-S strike, displacing the stratigraphic series, occasionally with a consistent rotation of the rock formations. On the whole, the slope was created by cutting the rock mass, nearly parallel to the bedding with a dip angle of 60–65°.

• 2. Numerical model and parameters

This study focuses on the use of the DDD method to simulate the 1997 rock slide that happened in the eastern zone of the Alpetto mine, i.e. the geological profile of Section A is shown in Fig. 17.22.

Fig. 17.22

The geological profile of the high rock slope (Barla et al. 2012)

Then, a finite-element mesh was built to reflect the geometry of Section A by account for 13,457 quadrilateral elements and 13,777 nodes , as shown in Fig. 17.23. Five different rock formations were reproduced according to the geological survey and joints between different formations were simulated by setting up the thin, weak solid element layers. In terms of the boundary conditions , the surface was free and the horizontal displacements on the lateral sides were fixed. Meanwhile, the horizontal and vertical displacements at the bottom were fixed as well. And care is taken to avoid any influence of the boundary conditions in the numerical results to be obtained.

Fig. 17.23

Numerical model for DDD method

Several investigations have been carried out to determine the rock mass parameters after the rock sliding. These included site investigations and laboratory testing. The rock mass was classified in terms of the Geological Strength Index-GSI according to Hoek and Brown (1997), while strength and deformability parameters for the rock mass were determined by empirical correlations (Barla et al. 2003). The heterogeneity of the rock strength and deformation , as well as the joint strength, is concerned, and the homogeneity index m is set to be 3. The correlative parameters of weak layers between different formations are set as a third of the surrounding rock mass’.

• 3. Analysis and Results

Numerical analysis in plane strain condition was performed. The slope centrifugal method (Wang et al. 2009) was adopted for the simulation of progressive slope failure before sliding during the DDD analysis. The initial stress distribution in slope was calculated by applying gravity loading in first two steps, and then the slope centrifugal method was carried out until gaining the slipping surface and the large displacement zone. Figures 17.24 and 17.25 show different consecutive screenshots of the numerical simulation obtained using the DDD method, where Fig. 17.24a–d present the crack initiation , propagation and coalescence process modelled by the FEM, while Fig. 17.25a–f present the joint sliding and rock block movement processes modelled by the DDA method.

Fig. 17.24

The crack growth with the DDD method (Gong and Tang 2016)

Fig. 17.25

The slope sliding with the DDD method. (Gong and Tang 2016)

At first, the initial stress field is reproduced by applying gravity till equilibrium. Then, the slope centrifugal method, proposed by Wang et al. (2009), is adopted. What needs to emphasize is that, in the method, the horizontal acceleration is applied on slopes and the value of the acceleration increases step by step. It can be seen that the greater stresses accumulate at the Maiolica formation toe where failure occurs first. With further increasing of the horizontal acceleration, cracks gradually propagate to the upper surface along the interface between Maiolica and Radiolariti. Finally, as shown in Fig. 17.24d, the sliding mass is detached from the slope and starts to slide along the sliping surface. At this time, the FEM-based RFPA method is no longer suitable for the next simulation of the large displacement of the sliding mass. Therefore, the DDA module in the DDD method is applied to the analysis of the block movement process. To realize the transition from the continuum-based method to the discontinuum-based method, the mesh information for large displacement elements in the RFPA module is automatically imported into the DDA module. Note that only large displacement elements are included in the DDA computing, which significantly improve the computing efficiency.

When the slope surface occurs, it exists in a critical state. Figure 17.25 illustrates the modelling results of the block movement simulated by the DDA module. It can be seen that the sliding mass gets started to move in Fig. 17.25a and shear displacement occurs within the Maiolica formation toe because of stress concentration during the initial landsliding stage; moreover, many small blocks are formed as more elements fail and many small blocks slide or roll together. Finally, the sliding mass is stabilized and the failure pattern is shown in Fig. 17.25d. It indicates the sliding mass travels quite far away from its original location shown in Fig. 17.24d. It can be observed how the rock mass desegregates during the sliding and the broken rock mass covers the bottom area of the slope finally. Figure 17.26 shows a comparison of the final topographic profiles obtained by the three different numerical methods and the field observations. The modeling results of the DDD method were in a good agreement with the FDEM and PFC2D simulations (Barla et al. 2012). Most importantly, they were qualitatively similar to the field observations shown in Fig. 17.21 (Barla et al. 2012).

Fig. 17.26

Comparison of the observations and numerical simulations . (Gong and Tang 2016)

4.2 Coastal Cliff Recession

• 1. Engineering background

As a main coastal geologic risk, the cliff erosion threatens property and life in the touristic areas centered on beaches. Accidents resulting from cliff collapse should be aware of in order to achieve effective management, especially for coastal zones depending on the tourism, and where necessary, engineering intervention is inevitable. It is worth noting that the gravitational process plays an important role in the evolution of the cliffs that can be defined as a geographical feature in the form of denuded coastal escarpment in coastal geomorphology (Castedo et al. 2012). On rocky coasts, gravitational movements, such as falling, toppling and sliding, can not only cause the abrupt changes in coastline trend, but also result in geologic hazards. On the other hand, a limestone or chalk cliff often has a notch at its base due to the marine action and high solubility of these materials. These cliffs are widely distributed, for instance in the Ryukyu Islands (Kogure et al. 2006) and along the Eastern English Channel (Cossec et al. 2011). They are prone to slope mass movements caused by gravity. Large slope mass movements can even generate tsunamis and local earthquakes inducing damages whose influence is significantly beyond the collapse area of the cliff (Bolt 2004). Figure 17.27 shows the schematic profile of a typical cliff shore. From the perspective of predicting, preventing and minimizing the potential economic losses and casualties, improving the knowledge of cliff collapse and evolution mechanisms is of great importance in coastal engineering.

Fig. 17.27

The schematic profile of cliff shore

• 2. Numerical Model and Parameters

The coastal cliffs with a notch at their base are widely distributed in the world and prone to slope mass movements due to gravity. The whole processes of the gravity-induced collapses are much more complicated than simple prime modes, as explored analytically by, for example, Kogure and Matsukura (2012). Meanwhile, initial examination showed that it is necessary to consider both the strength and the structure features for modelling coastal cliff recession. Especially for rocky cliffs, the characteristic of structure is important for determining the cliff deformation and failure. In order to simulate the whole process of cliff collapse and investigate the effect of the geological structure and rock composition on cliff morphology, a numerical model of rocky cliff with well-developed jointing and bedding planes dissecting the rock mass presented by Carter et al. 2009 is chosen as shown in Fig. 17.28.

Fig. 17.28

Cliff models for numerical simulation : (a) Model I; (b) Model II

The height of the cliff is 20 m and a classic wave-cut notch caused by marine erosion is created by excavating the base of the cliff face. The notch depth is 3 m from the cliff face to the retreat point. Two different rock mass fabrics are considered: (1) one joint set with inclination of 80° measured counterclockwise from the horizontal axis and spacing of 5 m (Model I); (2) two orthogonal joint sets with inclination of −10° and 80° measured counterclockwise from the horizontal axis and spacing of 8 m and 5 m, respectively (Model II). Note that the joints are simulated by setting up the thin and weak solid-element layers.

To reasonably replicate the failure mechanisms, the physical-mechanical parameters are applied to the elements and contracts, as shown in Table 17.1, including density of the material ρ, elastic modulus E, Poisson’s ratio ν, cohesion c, friction angle φ, tensile strength σ _t, etc. The homogeneity index m is set to be 5. In terms of the boundary conditions , the surface of the model is free, the horizontal displacements of the lateral sides are fixed, and the horizontal and vertical displacements at the bottom are all fixed.

Table 17.1 Physical-Mechanical Parameters of rock masses

• 3. Analysis and Results

Figure 17.29a–d show the initiation and propagation of fractures during the small deformation stage of the cliff model with one joint set. It can be seen from Fig. 17.29a that the tensile ruptures occur at the back of the cliff initially. The upper part of the joints at the back gets fully damaged. Meanwhile, note that failure appears at the lower-middle part of the joint near the notch as well. Figure 17.29b indicates that with the gravity acceleration increasing gradually, the middle part of the second-nearest joint from the cliff face is damaged. Simultaneously, it is the stress concentrations occurring at the ends of the fractures that induce cracks developing along the joints. It is clear from Fig. 17.29c that there are large tensile stress concentration areas forming on the right side of each joint and compressive stress concentration areas forming on the left side of each joint, and the fractures at the back and near the notch develop upwards and downwards along the joints continuously, which triggers the structural failure shown in Fig. 17.29d. Moreover, a crack generating from the joint towards the notch and large compressive stresses concentrating at the notch can also be seen in Fig. 17.29d. When the toppling surface occurs, the cliff is in a critical state. From now on, the FEM-based RFPA method is no longer appropriate for the next calculation of the large displacement of the toppling masses, and the DDA method is therefore used for the block-movement analysis.

Fig. 17.29

Crack growth and cliff instability of Model I: (a) initial tensile cracks ; (b) stress induction; (c) crack propagation; (d) falling mass formation; (e) mass detachment; (f) toppling; (g) fragmentation; (h) failure pattern (Gong et al. 2018)

Figure 17.29e–h show the movement of blocks during the large displacement stage of the cliff model with one joint set. Figure 17.29e indicates that the rock masses are detached from the cliff and begin to move towards the free surface. Figure 17.29f shows that when the lower-right part of the toppling block hits the ground, many small blocks form above the notch and cracks occur at the lower-middle part of the whole block owing to the impact and rotation. Figure 17.29g shows the interaction between the formed blocks. They fall and roll together but with different velocities and modes. Finally, the falling masses are stabilized, and Fig. 17.29h shows the final failure pattern. We can see that the top masses travel very far from their initial locations in Fig. 17.29. From the calculation results, it is clear how the rock masses form and interact during toppling, and the broken rock masses cover the bottom area of the cliff eventually.

Figure 17.30a–d show the initiation and propagation of fractures during the small deformation stage of the cliff model with two orthogonal joint sets. It is clear from Fig. 17.30a that there are tensile ruptures occurring at the back of the cliff at the beginning of gravity increasing, which is the same as the precious model I. Besides the upper part of the joints at the back, the lower-middle part of the joint near the notch is completely damaged. Figure 17.30b shows the second-nearest joint from the cliff face is damaged gradually with the value of the gravity acceleration increasing step by step. At the same time, it is worth noting that there are significant stress concentrations existing at the ends of the fractures. It is the high stress values that induce cracks developing along the joints continuously. In addition, Fig. 17.30c indicates that the large tensile stress concentrates at the the right side of each joint, while the large compressive stress concentrates at the left side of each joint. Furthermore, unlike the model I, the cracks not only generate along the joints with inclination of 80° consistently but also start to develop along the perpendicular joint set. It can be seen from Fig. 17.30d that the raw of joints with inclination of −10° just above the notch are damaged more heavily than the raw of joints near the top surface of the cliff. Meanwhile, varying degrees of damages appear at different places of the raw of joints under the notch. When the critical state is reached, the FE mesh data for large displacement calculation in RFPA are imported into DDA automatically to achieve the continuum-to-discontinuum analysis .

Fig. 17.30

Crack growth and cliff instability of Model II: (a) initial tensile cracks ; (b) stress induction; (c) crack propagation; (d) falling mass formation; (e) mass detachment; (f) toppling; (g) fragmentation; (h) failure pattern. (Gong et al. 2018)

Figure 17.30e–h show the movement of blocks during the large displacement stage of the cliff model with two orthogonal joint sets. The detaching process presented in Fig. 17.30e demonstrates that the rock masses will fall in the form of toppling. When the toppling block hits the edge of the notch, it splits into two main blocks because of the formation of the crack along the joint in the middle, which is significantly different from the previous simulation, as shown in Fig. 17.30f. Figure 17.30g shows that several smaller blocks form above the nothch during the falling process. After translation, rotation and interaction, all the blocks are stabilized eventually and the brocken rock masses cover the bottom area of the cliff as shown in Fig. 17.30h. The complex failure pattern is in agreement with the observations and analysis reported by Halcrow Ltd. (1998) and Carter et al. (2009).

4.3 The Right Bank Slope of Dagangshan Hydropower Station during Reservoir Impounding

Based on the theory that energy release and dissipation during the damage process in rock are related to the rock strength (Xie et al. 2005), Xu et al. (2014) developed a microseismic damage model to evaluate the slope stability . The damage variable D of the rock mass can be defined as the ratio of the actual assigned energy ΔU of the rock mass element to the total releasable elastic strain energy U ^e. The actual assigned energy ΔU can be calculated according to the radiation energy U _M and the seismic efficiency g. Thus, the damage variable D can be calculated as follows:

$$ \mathrm{D}=\frac{\Delta U}{U^e}=\frac{U_M/\eta }{U^e}=\frac{U_M}{\eta {U}^e} $$

(17.18)

where U _M can be obtained from seismic source information; g is 0.001%, as obtained by blasting tests (Xu et al. 2014) on the right bank slope of Dagangshan hydropower station ; and U ^e can be calculated using Eq. (17.19) if the initial elastic modulus E ₀, Poisson’s ratio ν, and the three principal stresses of the rock mass are known (Fig. 17.31).

Fig. 17.31

Numerical results obtained for the right bank slope during impoundment (only part of the model is depicted to clearly illustrate the distributions of the damaged elements and the minimum principal stress among all the anti-shear galleries). (a) Distribution of the damaged elements, (b) distribution of the minimum principal stress (a negative value represents tensile stress ), and (c) distribution of the displacement in the x-direction in a typical section that includes all the anti-shear galleries. (Liu et al. 2017)

$$ {U}^e=\frac{1}{2{E}_0}\left[{\sigma}_1^2+{\sigma}_2^2+{\sigma}_3^2-2\upsilon \left({\sigma}_1{\sigma}_2+{\sigma}_2{\sigma}_3+{\sigma}_1{\sigma}_3\right)\right] $$

(17.19)

Slopes are unstable if the stress state satisfies the failure criterion. In the case of partial failure, the stress state varies within the slope, and the safety factor of the slope also varies. Reservoir impoundment is a long-term process, and failures within the slope during the process do not occur simultaneously. Progressive microseismic damage should be considered when evaluating the stability of a slope during impoundment. When the safety factor of the right bank slope of the Dagangshan hydropower station is calculated using RFPA^3D-Centrifuge during the impoundment period, the seepage effect and pore pressures are neglected. The microseismic events monitored during the impoundment process are again divided into four stages, and the seismic source information in each stage is processed individually and stored in four independent files; the files are then used in the safety factor calculation, which includes the effect of microseismic damage. To fully reflect the progressive damage and the changes in slope stability during the impoundment process, the material parameters used in the earlier stages of the safety factor calculation are adjusted to include the effects of microseismic damage for use in the later stages. For example, the material parameters used in stage two are determined based on the effects of microseismic damage recorded in stage one. If an element is not damaged in stage one, its initial material parameters are used in the second calculation stage. However, if the element is damaged in stage one, then the material parameters used in stage two are adjusted according to the following equations:

$$ {E}_1=\left(1-D\right){E}_0 $$

(17.20)

$$ {\sigma}_1=\left(1-D\right){\sigma}_0 $$

(17.21)

$$ {\upsilon}_1=\left(1-D\right){\upsilon}_0 $$

(17.22)

where D is the damage factor of the element damaged in the previous stage; E ₀, r ₀ and ν ₀ represent the initial elastic modulus, compressive strength and Poisson’s ratio, respectively; and E ₁, r ₁ and ν ₁ represent the elastic modulus, compressive strength and Poisson’s ratio in the current stage after considering the effects of microseismic damage. To consider progressive microseismic damage , the damage factor changes in different stages according to the microseismic events, and the material parameters in each stage change accordingly.

The finite element model was used to calculate the safety factor of the slope during the impoundment process. In the numerical model, the centrifugal loading coefficient was set to 1%. Figures 17.32 and 17.33 illustrate the distributions of the maximum principal stress and the damage elements, respectively. The model used the centrifugal loading method for the fourth stage of the monitored microseismic events to explain the failure process of the right bank slope. Figure 17.32 shows that the tensile stresses in the regions of the dikes, faults, unloading fissure zones and anti-shear galleries are greater than those in other regions; in addition, failure initially occurs in areas with high tensile stress. Two main slip surfaces exist in the right bank slope: One is the slip surface along unloading fissure zone XL-915, and the other comprises unloading fissure zone XL-316 and fault f231. Both slip surfaces form at the top of the slope and gradually extend to the toe of the slope with the accumulation of damaged elements. Because no reinforcement measures are installed in the unloading fissure zone XL-915, the integrated slip surface forms in calculation step 11, as shown in Fig. 17.33. However, because of the anti-shear galleries surrounding unloading fissure zone XL-316 and fault f231, the slip surface formed there does not cut through the anti-shear galleries in calculation step 11, as illustrated in Fig. 17.33. According to the finite element modelling, which incorporates the effects of progressive microseismic damage , the safety factor of the slope is calculated to be 1.10. According to calculation, the safety factor of the slope is 1.10 during the impoundment process; because this value is greater than 1.0, the right bank slope of the Dagangshan hydropower station is generally stable during reservoir impounding. Moreover, the numerical results for step 6, as depicted in Fig. 17.33, show that the damaged elements are mainly distributed along the main dikes (b43, b68, b83 and b85), sliding surface XL-915 and the upper part of sliding surface XL-316/f231 in accordance with the distribution of microseismic events captured by the microseismic monitoring system. According to the centrifugal loading method, the slope becomes unstable in calculation step 11; however, the distribution of microseismic events during impoundment agrees with the distribution of damage elements in calculation step 6, which again indicates that the slope remains stable during impoundment.

Fig. 17.32

Modelled failure process in the right bank slope in terms of the distribution of the maximum principal stress (a negative value represents tensile stress ). (Liu et al. 2017)

Fig. 17.33

Modelled failure process in the right bank slope in terms of the distribution of the damaged elements. (Liu et al. 2017)

The factors obtained from the numerical modelling that considers the effects of progressive microseismic damage are plotted in Fig. 17.34 together with the change in the microseismic event energy during impoundment. Figure 17.34 shows that the safety factor decreases as the water level increases, indicating that water storage has an adverse effect on slope stability . Moreover, the safety factor initially decreases quickly but then decreases slowly, which is related to the energy released by the microseismic events during each stage. Figure 17.34 clearly shows that the event with the largest energy appears in the second stage; correspondingly, the safety factor also decreases in this stage. As the event energy in the other impoundment stages is relatively small, no sudden decrease in the safety factor occurs in the other stages, which demonstrates the suitability of the proposed microseismic damage model for evaluating the slope stability. Slopes are considered unstable if the stress state satisfies the failure criterion. In the case of partial failure, the stress state varies within the slope, and the safety factor of the slope also varies. Additionally, the progressive microseismic damage considers the changes in the slope due to damage. The proposed progressive microseismic damage model provides a valuable tool for evaluating slope stability during reservoir impounding.

Fig. 17.34

Variation of the slope safety factor and the monitored microseismic event energy during impoundment. (Liu et al. 2017)

5 Conclusions

The RFPA method has been used extensively to simulate the failure process of rocks in a number of engineering fields. The unique feature of this code is that no priori assumptions need to be made about where and how fracture and failure will occur. Namely, cracking can occur spontaneously and can exhibit a variety of mechanisms when certain local stress conditions are exceeded. However, the progressive failure of a rock structure requires both continuous and discontinuous modelling. The continuous modelling must address the initiation , propagation and coalescences of cracks. The discontinuous modelling should be able to simulate the block movement and rotation, block contact, fragmentation and large displacements.

Considering the RFPA method only performs well in dealing with the crack initiation and growth, it is further improved by the DDA method to offer a comprehensive analysis approach which is able to account for cracks or discontinuities within rock masses and replicate the whole-processes of crack propagation, coalescence and contacts between blocks. The failure mechanism of slopes and tunnels, including crack initiation & propagation and post-failure characteristics, can be therefore modelled. The DDD method proposed by improving RFPA using the DDA theory is simple in concept, and the combined scheme is easy to implement. This method inherits the advantages of both RFPA and DDA methods and is able to provide a complete and unified description of the entire rock deformation process (including crack initiation and propagation ) and rock body movement (including translation, rotation and interaction), representing a distinct improvement over the conventional numerical methods.