Ultimate Bearing Capacity of Rock Mass Foundations Subjected to Seepage Forces Using Modified Hoek–Brown Criterion

Abstract

The experimental data shows that most rocks behave nonlinearly in nature. The modified nonlinear Hoek–Brown failure criterion was considered to investigate the bearing capacity problem of shallow rigid foundations on rock masses subjected to horizontal seepage forces. Two multi-wedge translational failure mechanisms, including symmetrical and non-symmetrical mechanisms were used in the closed-form of the upper bound method of the limit analysis theory. The symmetrical failure mechanism was used in the case of no seepage, while the seepage effect was considered in the non-symmetrical mechanism. The variation of seepage forces was obtained as a function of gradient ratio i(γ_w/γ_sub) in the developed formulation. The bearing capacity coefficients N_γ, N_q and N_σ are introduced for the case of seepage flow condition. The results show that the magnitude of the bearing capacity coefficients reduces continuously with an increase in the value of gradient ratio i(γ_w/γ_sub). The obtained results were compared and offered for functional use in foundation engineering.

1 Introduction

Most conventional bearing capacity calculations for soil beddings are based on the assumption that soil strength is governed by the linear Mohr–Coulomb failure criterion. In this context, a limit equilibrium expression for the ultimate bearing capacity of a strip footing is classically introduced by Terzaghi (1943) which can be written as:

$$q_{\text{u}} = c N_{c} + q_{0} N_{q} + 0.5 \gamma B_{0} N_{\gamma } .$$

(1)

Later, Michalowski (1997) and Soubra (1999) presented limit analysis upper bound solutions for the bearing capacity of soils based on the multi-wedge translation failure mechanism considering the linear Mohr–Coulomb failure criterion. The experiments have shown that the strength envelopes of most geomaterials, especially rocks, have the nature of nonlinearity, Hoek and Brown (1980), among others. Based on this fact, the ultimate bearing capacity of rock foundations has been studied by several investigators (Yang and Yin 2005; Merifield et al. 2006; Saada et al. 2008; Mao et al. 2012; Mansouri et al. 2019) among others, and the ultimate bearing capacity of rock mass foundations has also been introduced in the form:

$$q_{\text{u}} = s^{0.5} \sigma_{\text{ci}} N_{\sigma } + q_{0} N_{q} + 0.5 \gamma B_{0} N_{\gamma } .$$

(2)

Despite the fact that few special cases like the seismic bearing capacity of rock masses by Saada et al. (2011) and Yang (2009) and the bearing capacity of nearby footings resting on rock mass by Javid et al. (2015) have been investigated in the available literature, the authors were not aware of any qualitative study to determine the ultimate bearing capacity of rock mass foundations considering the presence of seepage forces. However, few studies like Imani et al. (2012) obtained the impact of stable groundwater on the ultimate bearing capacity of jointed rock foundations, considering two joint sets. In a recent paper, the effect of seepage on the bearing capacity of soil was investigated by Veiskarami and Kumar (2012) and Veiskarami and Habibagahi (2013). They used the kinematic approach of limit analysis using the Mohr–Coulomb failure criterion for soil mass. The effect of seepage was considered by non-dimensional ratio, i(γ_w/γ_sub), where, i is the hydraulic gradient, and γ_w and γ_sub refer to the unit weights of water and submerged soil mass, respectively.

In a recent work, Mao et al. (2012) obtained the ultimate bearing capacity of rock mass foundations based on upper bound solution using a multi-tangential technique for considering the nonlinear Hoek–Brown criterion. They considered that the angle between each velocity vector and the corresponding line is different in the entire failure mechanism. Using this approach, a higher number of degrees of freedom was added to the failure mechanism. This assumption was used in the present paper with the generalized multi-tangential lines technique to consider the nonlinearity of rock mass behavior. The motivation behind this paper is to investigate the effect of seepage on the bearing capacity of Hoek–Brown rock masses under the load of a strip footing, using the upper bound method. To the best of the authors’ knowledge, there is a dearth of analytical research carried out on this realm.

Two different failure mechanisms were considered including a symmetrical mechanism (named M1) for the case of a dry rock mass and a non-symmetrical failure mechanism (named M2) for the case of a rock mass subjected to horizontal seepage flow. The aim of this work is to incorporate the seepage force in the rock mass bearing capacity equation considering different failure mechanisms. The optimization of the obtained upper bound solution was performed using the genetic algorithm.

2 Modified Hoek–Brown Failure Criterion

A reliable estimate of strength and deformation characteristics of rock masses is needed for any rock engineering design. As an empirical criterion, the Hoek–Brown (HB) criterion has been updated several times in response to experiences gained with its use in practice and to handle sure sensible limitations (Hoek et al. 2002). The last updated version, that is used here, can be written as:

$$\sigma^{\prime}_{\;1} = \sigma^{\prime}_{\;3} + \sigma_{\text{ci}} \left( {m_{\text{b}} \frac{{\sigma^{\prime}_{\;3} }}{{\sigma_{\text{ci}} }} + s} \right)^{a} ,$$

(3)

where σ′₁ and σ′₃ are the major and minor effective principal stresses at failure, σ_ci is the uniaxial compressive strength of the intact rock material and m_b is given by

$$m_{\text{b}} = m_{\text{i}} \exp \left( {\frac{{{\text{GSI}} - 100}}{28 - 14D}} \right).$$

(4)

In which, m_i is the value of m for intact rock and can be obtained from the experiments, GSI is the geological strength index of the rock mass and D is a factor which depends upon the degree of disturbance. It varies from 0 for undisturbed in situ rock masses to 1 for very disturbed rock masses. s and a are constants for the rock mass given by the following relationships:

$$s = \exp \left( {\frac{{{\text{GSI}} - 100}}{9 - 3D}} \right)$$

(5)

$$a = \frac{1}{2} + \frac{1}{6}\left( {e^{{ - \frac{\text{GSI}}{15}}} - e^{{ - \frac{20}{3}}} } \right).$$

(6)

The HB failure criterion, which assumes a homogenous and isotropic rock mass, should only be applied to those rock masses in which there are sufficient numbers of closely spaced discontinuities, with similar surface characteristics, and that isotropic behavior involving failure on multiple discontinuities can be assumed. In these cases, the water or ‘pore’ pressures governing the effective stresses will be those generated in the interconnected discontinuities defining the particles in an equivalent isotropic medium.

3 Upper Bound of Limit Analysis Method for Shallow Foundations on Rock Masses

The upper bound technique of limit analysis was used to develop approximate solutions for the ultimate bearing capacity of rock masses obeying the Hoek–Brown failure criterion. In the upper bound formulation, the loads, determined by equating the external rate of work to the internal rate of energy dissipation in an assumed velocity field are not less than the true failure load. The dissipation of energy in plastic flow associated with such a field can be computed from the idealized stress/strain rate relation (or the so-called flow rule). Using this flow rule considerably simplifies the application of the limit analysis. In this paper, the rock mass was considered to be homogeneous and isotropic material obeying the associated flow rule, i.e., the dilatancy angle was considered to be equal to the friction angle.

For each discontinuity line of the failure mechanisms, the equivalent Mohr–Coulomb parameters were obtained using the generalized multi-tangential technique.

3.1 Generalized Multi-tangential Technique

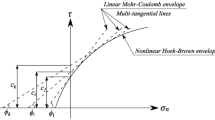
For a rock mass obeying the modified Hoek–Brown failure criterion, the failure envelope is nonlinear. In the σ_n–τ stress plane, where σ_n and τ are the normal and shear stresses, Yang and Yin (2005) replaced the nonlinear modified Hoek–Brown failure criterion by a linear Mohr–Coulomb failure criterion represented by a tangential line. This tangential line is given by

$$\tau = c_{\text{t}} + \sigma_{\text{n }} \tan \phi_{\text{t}} ,$$

(7)

where ϕ_t and c_t are the tangential friction angle and the intercept of the straight line to τ-axes, respectively. They introduced c_t in the following form:

$$\frac{{c_{\text{t}} }}{{\sigma_{\text{ci}} }} = \frac{{\cos \phi_{\text{t}} }}{2} \left[ {\frac{{ma(1 - \sin \phi_{\text{t}} )}}{{2\sin \phi_{\text{t}} }}} \right] ^{(a/1 - a) } - \frac{{\tan \phi_{\text{t}} }}{m}\left( {1 + \frac{{\sin \phi_{\text{t}} }}{a}} \right) \left[\frac{{ma(1 - \sin \phi_{\text{t}} )}}{{2\sin \phi_{\text{t}} }} \right] ^{(1/1 - a) } + \frac{s}{m}\tan \phi_{\text{t}} .$$

(8)

In which, σ_ci is the uniaxial compressive strength of the intact rock. Considering a single ϕ_t and the corresponding c_t in the whole failure mechanism would not have enough accuracy since the stress level in different discontinuity lines of the failure mechanism are not equal to each other. Hence, in the present paper, the nonlinear modified Hoek–Brown failure criterion [i.e., Eq. (3)]; was replaced by a series of linear Mohr–Coulomb failure criteria in Eq. (7), as shown in Fig. 1 to achieve different values of ϕ_t and the corresponding c_t. For this purpose, the tangential angles ϕ_t along all the discontinuity surfaces of the failure mechanisms were considered to be changeable. The optimum value of ϕ_t in each discontinuity line was obtained using an optimization procedure which is an important step in an upper bound analysis. Hence, in each discontinuity line, the nonlinear Hoek–Brown was replaced by an optimum approximate line. In this regard, the magnitude of c_t was also determined along each velocity discontinuity based on Eq. (8).

Fig. 1

Multi-tangential lines to modified HB failure criterion

3.2 Bearing Capacity of Foundations on Dry Rock Mass

Different solutions are available for calculating the bearing capacity of dry rock masses. Among them, the method presented by Mao et al. (2012) is more elaborated, since the multi-tangential technique with different values of ϕ was considered for each velocity discontinuity line. This method was applied in the present paper for developing the rock mass bearing capacity formulation in dry case and then adding the seepage effect in the formulation. To calculate the bearing capacity in the case of dry rock mass (without seepage effect), a symmetrical mechanism, named M1, was considered as shown in Fig. 2. The footing was considered to be rigid and its pressure (q_uD) and also the surcharge pressure (q₀) are shown in Fig. 2a. The internal energy dissipates along the interfaces of the two adjoining wedges (lines l_i) and at the base of the wedges (lines d_i). Since the mechanism is symmetric, only the velocity field and the hodograph for half of the problem domain is observed in Fig. 2b, c, respectively. Figure 2b is composed of k triangular wedges, the wedge i, moves with velocity V_i, which inclines at ϕ_i with respect to the base. Also the relative velocity V_i,i+1 inclines at ϕ_i,i+1 with respect to the interface of the two adjacent wedges. The incremental external work for different external forces can easily be obtained and the calculations are presented in Appendix 1. Energy is dissipated at the discontinuity surfaces d_i (i = 1, …, k) between the material at rest and the material in motion and at the discontinuity surfaces l_i (i = 1, …, k) within the radial shear zone.

Fig. 2

a A symmetrical failure mechanism M1 for determining the bearing capacity of dry rock masses. b Velocity field for half of the mechanism and c velocity hodograph for the first and ith triangular wedges

By equating the total energy dissipation with the total external work in the mechanism and after rearrangements, the upper bound of the ultimate bearing capacity of the rock foundation in the case of dry rock mass (without seepage effect) was obtained as follows:

$$q_{\text{uD}} = s^{0.5} \sigma_{\text{ci}} N_{\sigma } + q_{0} N_{q} + \frac{{\gamma B_{0} }}{2}N_{\gamma } ,$$

(9)

where γ is the unit weight of the rock mass and N_σ, N_q and N_γ are the bearing capacity coefficients that are as follows:

$$N_{\sigma } = 2(f_{1} + f_{2} + f_{3} )$$

(10)

$$N_{q} = - \;f_{4}$$

(11)

$$N_{\gamma } = - \;(f_{5} + f_{6} ),$$

(12)

where the non-dimensional functions f₁ to f₆ are reported in Appendix 1 of this paper. The best (lowest) upper bound solution of q_uD was obtained here by minimization of Eq. (9) with respect to the unknown parameters ϕ_i, ϕ_i,i+1, β_i, α_i and θ. The genetic algorithm of MATLAB program was used for minimization under the following constraints:

$$\begin{aligned} \beta_{i + 1} + \phi_{i} - \phi_{i + 1} - \alpha_{i} - \beta_{i} < 0,\quad \theta + \mathop \sum \limits_{i = 1}^{n} \alpha_{i} = \pi ,\quad \alpha_{i} + \beta_{i} \ge \beta_{i + 1} \hfill \\ \alpha_{i - 1} + \beta_{i - 1} + \phi_{i} - \phi_{i - 1} - \beta_{i} \le \pi ,\quad \phi_{i} \le \frac{\pi }{2},\quad \phi_{i,i + 1} \le \frac{\pi }{2},\quad \alpha_{i} + \beta_{i} < \pi . \hfill \\ \end{aligned}$$

(13)

3.3 Bearing Capacity of Foundations on Rock Mass Subjected to Seepage Forces

The forces exerted by the seepage flow play an important role in the bearing capacity of soil and rock masses. Considering the horizontal seepage force, it will result in transforming the shape of the failure mechanism from symmetrical to non-symmetrical. A recent study by Veiskarami and Kumar (2012), shows that the failure mechanism in the event of horizontal groundwater flow will become non-symmetrical with respect to the center line of the footing. In the present study, to calculate the bearing capacity of the rock mass subjected to horizontal seepage forces, a non-symmetrical mechanism, named M2, was considered as shown in Fig. 3.

Fig. 3

a A non-symmetrical failure mechanism M2 for determining bearing capacity of a rock mass subjected to seepage forces, b velocity field, c velocity hodograph

According to Fig. 3a, the distribution of seepage force is described by the gradient ratio i(γ_w/γ_sub), where, i is the hydraulic gradient, γ_w and γ_sub refer to the unit weights of water and the submerged rock mass, respectively. The term, i(γ_w/γ_sub) = 0, implies no seepage flow. Hansen and Roshanfekr (2012) studied the different values of gradient ratio verse factor of safety, and introduced the worst case for factors of safety against collapse failure, as a function of four different values of gradient ratio namely, 0, 0.1, 0.2, and 0.3 for dams in a parametric study. The results showed that the factor of safety of collapse failure decreased when the gradient ratio increased. These four different values of the gradient ratio were considered in the present study.

The horizontal seepage force was regarded as an external force contributing to the incremental external work W_i. Hence the total external force consists of the force acting on the foundation by the load of the superstructure, the weight of the rock mass in motion, the surcharge loading and the seepage forces. The seepage forces comprise the base shear load and the seepage forces of the rock mass in motion and the horizontal component of the surcharge load. The internal energy dissipation was calculated in a similar manner as described previously for dry rock masses. Calculations of the incremental external work and the internal energy dissipation in the whole mechanism are given in Appendix 2.

Equating the total external work to the total energy dissipation, and after rearrangements, the upper bound of the ultimate bearing capacity of a rock foundation subjected to seepage force (q_uS) is:

$$q_{\text{uS}} = s^{0.5} \sigma_{\text{ci}} N_{\sigma }^{S} + q_{0} N_{q}^{S} + \frac{{\gamma B_{0} }}{2}N_{\gamma }^{S} ,$$

(14)

where $N_{\sigma }^{S} ,$$N_{q}^{S}$ and $N_{\gamma }^{S}$ are the bearing capacity factors in the presence of water seepage which are given as follows:

$$N_{\sigma }^{S} = \frac{{[g_{1} + g_{2} ]}}{{\sin (\beta_{1} - \phi_{1} ) + i\left( {\frac{{\gamma_{\text{w}} }}{{\gamma_{\text{sub}} }}} \right)\cos (\beta_{1} - \phi_{1} )}},$$

(15)

$$N_{q}^{S} = - \frac{{\left[ { g_{3} + i\left( {\frac{{\gamma_{\text{w}} }}{{\gamma_{\text{sub}} }}} \right)g_{4} } \right]}}{{\sin (\beta_{1} - \phi_{1} ) + i\left( {\frac{{\gamma_{\text{w}} }}{{\gamma_{\text{sub}} }}} \right)\cos (\beta_{1} - \phi_{1} )}} ,$$

(16)

$$N_{\gamma }^{S} = - \frac{{\left[ { g_{5} + i\left( {\frac{{\gamma_{\text{w}} }}{{\gamma_{\text{sub}} }}} \right)g_{6} } \right]}}{{\sin (\beta_{1} - \phi_{1} ) + i\left( {\frac{{\gamma_{\text{w}} }}{{\gamma_{\text{sub}} }}} \right)\cos (\beta_{1} - \phi_{1} )}},$$

(17)

where the non-dimensional functions g₁ to g₆ were reported in Appendix 2. The best (lowest) upper bound solution of q_uS was obtained by minimization of Eq. (14) with respect to the unknown parameters ϕ_i, ϕ_i,i+1, β_i, α_i. The genetic algorithm of the MATLAB program was used for minimization under the following constraints:

$$\begin{aligned} \mathop \sum \limits_{i = 1}^{n} \alpha_{i} = \pi ,\quad 0 < \beta_{i + 1} - \phi_{i,i + 1} - \phi_{i + 1} < \pi ,\quad \alpha_{i} + \beta_{i} \ge \beta_{i + 1} \hfill \\ \alpha_{i - 1} + \beta_{i - 1} + \phi_{i} - \phi_{i - 1} - \beta_{i} \le \pi ,\quad \phi_{i} \le \frac{\pi }{2},\quad \phi_{i,i + 1} \le \frac{\pi }{2},\quad \alpha_{i} + \beta_{i} < \pi . \hfill \\ \end{aligned}$$

(18)

4 Results and Discussion

The upper bound of ultimate bearing capacity of a strip footing resting on homogenous rock masses was obtained by minimizing Eqs. (9) and (14), for two cases of without seepage (dry rock mass) and seepage forces (submerged rock mass), respectively. The number of triangular wedges in the mechanisms M1 was increased to 9 for half of the mechanism since according to Table 1, it was observed that the upper bound solution is improved by increasing the number of rigid blocks. However, the reduction in the values of the bearing capacity factor decreases with increasing the number of rigid blocks (k) and attains less than 0.1% for k = 9. In the case of the rock mass subjected to seepage forces, the number of triangular wedges in the mechanisms M2 was considered to be equal to 7 for the whole mechanism. It should be noted that for the M1 and M2 mechanisms, Soubra (1999) obtained the number of the wedges equal to 14 (for half of the M1 mechanism) and 12, respectively.

Table 1 N_σ value versus number of rigid blocks k, D = 0, γ = 0, q₀= 0, GSI = 30, σ_ci= 10 MPa and m_i= 10 for M1 symmetrical mechanism

It should be mentioned here that the values of the bearing capacity factors N_γ and N_q for the dry case and $N_{\gamma }^{S}$ and $N_{q}^{S}$ for the submerged case are not affected by the Hoek–Brown coefficients and are constant (see Appendices). Figure 4 shows the effect of bearing capacity factors versus gradient ratio i(γ_w/γ_sub).

Fig. 4

Effect of bearing capacity factor versus i(γ_w/γ_sub)

4.1 Dry Rock Masses

The results obtained by the M1 symmetrical mechanism were compared to those obtained by other existing solutions. For a foundation resting on the surface of a weightless rock mass, Eq. (9) changes to the following form:

$$q_{\text{uD}} = s^{0.5} \sigma_{\text{ci}} N_{\sigma 0} .$$

(19)

The factor N_σ0 is a function of D, GSI and m_i defining the strength parameters of the rock mass in the case of γ = 0 and q₀ = 0. Table 2 presents a comparison among the N_σ0 obtained from the present study (Eq. 19) after being divided by (s^0.5) with those obtained from Merifield et al. (2006) and Serrano et al. (2000) for the case of D = 0 and m_i= 30. The percentages of the difference between the results of the considered methods were also presented in this table. The results emphasize the efficiency of the method applied in the present work. The only exception to these observations occur for a small class of very poor quality rocks with GSI ≤ 10, where the method of Serrano et al. (2000) is more conservative and underestimates the bearing capacity factor up to − 15%, while the results from Merifield et al. (2006) represented the average finite element upper and lower bounds of the bearing capacity factor up to − 25%. Table 3 summarizes the computed bearing capacity coefficient N_σ for the ponderable rock mass, and a comparison was made to the methods of Yang and Yin (2005) and Saada et al. (2008) for the case of D = 0, m_i= 10 along with the relative difference among the results of the considered methods. The current method showed lower values for N_σ than other methods, which means that there is an improvement in N_σ values. The improvement occurred because of the generalized multi-tangential technique and the corresponding different friction angles in each discontinuity line assumed in the current study. Using this approach, a higher degree of freedom was added to the failure mechanism resulting in optimum bearing capacity.

Table 2 Bearing capacity factor N_σ0 for weightless rock: D = 0 and m_i= 30

Table 3 Dry bearing capacity factor N_σ for ponderable rock: D = 0 and m_i= 10

Figure 5 shows the critical slip surface obtained through optimization by considering k = 9, D = 0, γ = 0, q₀= 0, GSI = 60, σ_ci= 10 MPa and m_i= 17.

Fig. 5

Geometry of the critical failure surface (M1) for k = 9, D = 0, GSI = 60, σ_ci= 10 MPa, m_i= 17, γ = 0 and q₀= 0

Serrano et al. (2000) showed that the undisturbed parameter (D = 0) can be used for foundation analysis. Yang and Yin (2005) found that D has a small influence on the bearing capacity factors for D ≥ 0.3. In the present work, for investigating the effect of the disturbance factor, D, on the bearing capacity coefficient, N_σ, D = 0 and 0.1 were considered and the corresponding N_σ coefficients are presented in Table 4 for the ponderable rock masses. According to the results obtained, the bearing capacity factor decreased when D increased. The same result was also obtained by Yang and Yin (2005) for 0 ≤ D ≤ 0.3.

Table 4 Dry bearing capacity factor N_σ for five types of ponderable rocks: D = 0 and 0.1

As other results of the current study, the effects of the surcharge load, q₀, and the self-weight of the rock mass, γ, were also investigated and the results are presented in Figs. 6 and 7, respectively. For the case of m_i= 10, D = 0, σ_ci= 10 MPa, GSI = 30 and γ = 0, Fig. 6 represents the effects of q₀ on the ultimate bearing capacity. It is clear that by increasing the q₀, the ultimate bearing capacity will increase. The q_uD values obtained from the present study are better (lower) than those obtained by Saada et al. (2008) for all magnitudes of q₀, indicating the advantage of the present upper bound formulation with respect to Saada et al. (2008). Figure 7 shows the effects of γ on the ultimate bearing capacity for the case of m_i= 17, D = 0, σ_ci= 10 MPa and GSI = 30. It is observed from the figure that the weight of the rock mass has a very small effect on the bearing capacity.

Fig. 6

Effect of surcharge load q₀ on the ultimate bearing capacity

Fig. 7

Effect of rock mass unit weight γ on the ultimate bearing capacity

4.2 Rock Masses Subjected to Seepage Forces

4.2.1 Verification

It seems that there is not a quantitative study in the available literature considering the effect of seepage forces on the ultimate bearing capacity of rock mass foundations. Hence, a comparison was made with the available solutions for soil foundations subjected to seepage forces. The upper bound method applied by Veiskarami and Habibagahi (2013) and the lower bound method applied by Kumar and Chakraborty (2014) were used for comparison. To compare a Hoek–Brown rock mass with a Mohr–Coulomb soil, Hoek–Brown parameters of the rock mass were converted to the equivalent Mohr–Coulomb soil parameters (c and ϕ) using the following equations Hoek et al. (2002):

$$c^{\prime} = \frac{{\sigma_{\text{ci}} \left[ {(1 + 2a)s + (1 + a)m_{\text{b}} \sigma^{\prime}_{\;3n} } \right](s + m_{\text{b}} \sigma^{\prime}_{\;3n} )^{a - 1} }}{{(1 + a)(2 + a)\sqrt {1 + \left( {\frac{{6am_{\text{b}} (s + m_{\text{b}} \sigma^{\prime}_{\;3n} )^{a - 1} }}{(1 + a)(2 + a)}} \right)} }},$$

(20)

$$\phi^{\prime} = \sin^{ - 1} \left[ {\frac{{6am_{\text{b}} (s + m_{\text{b}} \sigma^{\prime}_{\;3n} )^{a - 1} }}{{2(1 + a)(2 + a) + 6am_{\text{b}} (s + m_{\text{b}} \sigma^{\prime}_{\;3n} )^{a - 1} }}} \right],$$

(21)

where σ′_3n= σ′_3max/σ_ci.

Note that the value of σ′_3max the upper limit of confining stress over which the relationship between the Hoek–Brown and the Mohr–Coulomb criteria is considered has to be determined for each individual case. These equations are provided in Roclab program that can be used easily in practical purposes. It should be noted that for the best conformity of the results, a constant value of the equivalent Mohr–Coulomb parameters was obtained in all discontinuity lines of the rock mass failure mechanism since in the above-mentioned methods for the soil beddings, constant values of Mohr–Coulomb parameters were used in the whole mechanism.

Using this technique, the rock mass was converted to an equivalent soil medium and the seepage bearing capacity formulation proposed in this paper for rock masses can be compared with the above-mentioned methods for soil medium. For a rock mass with GSI = 24, σ_ci= 30 MPa, m_i= 7, γ = 20 kN/m³ and ignoring the surcharge load (q₀), the equivalent Mohr–Coulomb parameters are obtained c = 0.8 MPa and ϕ = 20°. These values were used in the formulations developed in the present study to obtain q_uD and q_uS from M1 symmetrical and M2 non-symmetrical mechanisms, respectively. At the same time, the aforementioned equivalent c and ϕ were applied in the Veiskarami and Habibagahi (2013) and Kumar and Chakraborty (2014) methods. The results observed in Fig. 8, show the applicability of the proposed solution.

Fig. 8

Comparison of q_uS/q_uD versus i(γ_w/γ_sub) using the upper bound and lower bound solutions of Veiskarami and Habibagahi (2013) and Kumar and Chakraborty (2014), respectively, with present work

4.2.2 The Bearing Capacity Factor $N_{\sigma }^{S}$

For the foundation resting on the surface of weightless rock mass, Eq. (14) changes to the following form:

$$q_{\text{uS}} = s^{0.5} \sigma_{\text{ci}} N_{\sigma }^{S} .$$

(22)

Figures 9, 10, 11, 12, 13 show the $N_{\sigma }^{S}$ for weightless rock masses with different values of GSI and m_i, subjected to various seepage forces. The surcharge (q₀) was considered equal to zero. The effect of seepage was considered using non-dimensional factor i(γ_w/γ_sub) which varies from 0 to 0.3. This range covers most problems in practical interest (Hansen and Roshanfekr 2012). According to the figures, for a given GSI, increasing m_i leads to an almost linear increase in the bearing capacity factor, $N_{\sigma }^{S}$. In all cases, increasing the seepage forces (i.e., increasing the i(γ_w/γ_sub) factor) leads to a decrease in the bearing capacity factor $N_{\sigma }^{S}$ and thus reduction of ultimate bearing capacity. Figure 14 shows the effect of GSI on the $N_{\sigma }^{S}$ coefficient for m_i = 17 considering various i(γ_w/γ_sub) ratios. According to the figure, by increasing GSI values from 5 to 30 the $N_{\sigma }^{S}$ increased, while by increasing GSI values from 40 to 90, the $N_{\sigma }^{S}$ decreased. The same trend was also observed for other m_i values. Figure 15 shows the critical slip surface obtained by optimization of the M2 non-symmetrical mechanism in case of i(γ_w/γ_sub) = 0.3, corresponding to k = 7, D = 0, γ = 0, q₀= 0, GSI = 60, σ_ci= 10 MPa and m_i = 17.

Fig. 9

Upper bound values of seepage bearing capacity factor $N_{\sigma }^{S}$ for a GSI = 10, b GSI = 20

Fig. 10

Upper bound values of seepage bearing capacity factor $N_{\sigma }^{S}$ for a GSI = 30, b GSI = 40

Fig. 11

Upper bound values of seepage bearing capacity factor $N_{\sigma }^{S}$ for a GSI = 50, b GSI = 60

Fig. 12

Upper bound values of seepage bearing capacity factor $N_{\sigma }^{S}$ for a GSI = 70, b GSI = 80

Fig. 13

Upper bound values of seepage bearing capacity factor $N_{\sigma }^{S}$ for GSI = 90

Fig. 14

Upper bound values of seepage bearing capacity factor $N_{\sigma }^{S}$ for m_i= 17

Fig. 15

Geometry of the critical failure surface in the case of i(γ_w/γ_sub) = 0.3 for k  = 7, D  = 0, GSI = 60, σ_ci = 10 MPa, m_i = 17, γ  = 0 and q₀ = 0

4.2.3 Effect of Footing Width

Figure 16 shows the effect of the footing width, B₀, on the ultimate bearing capacity subjected to the seepage force in the case of σ_ci= 10 MPa, GSI = 60, m_i = 17, D = 0 and γ = 25 kN/m³, considering different values of gradient ratio, i.e., i = 0, 0.1, 0.2 and 0.3. It is observed from the figure that the footing width has very small effect on the bearing capacity.

Fig. 16

Ultimate bearing capacity (q_uS) subjected to the seepage for σ_ci= 10 MPa, GSI = 60, m_i= 17, D = 0 and γ = 25 kN/m³

4.3 Design Table for Practical Use

Table 5 provides the $N_{\sigma }^{S}$ factor considering m_i equal to 7, 10, 15, 17, and 25, GSI varying from 5 to 90 and D = 0. The effect of seepage forces was considered using the non-dimensional factor i(γ_w/γ_sub) which varies from 0 to 0.3. This table can easily be used by engineers in practical applications.

Table 5 Seepage bearing capacity factors $N_{\sigma }^{S}$ in term of i(γ_w/γ_sub), m_i and GSI, assuming D = 0

5 Summary and Conclusions

The bearing capacity of rock mass foundations subjected to seepage forces was investigated using the upper bound method of limit analysis. The generalized multi-tangential technique was used and two multi-wedge translational failure mechanisms, including symmetrical and non-symmetrical mechanisms were considered. The bearing capacity factor for the dry rock mass, N_σ, and the bearing capacity factor for the rock mass subjected to seepage forces, $N_{\sigma }^{S}$, were obtained that could easily be used in practical applications. The results obtained in this paper provide useful guidelines for designing foundations when seepage forces are present. The main conclusions of this paper are as follows:

• By increasing the disturbance factor, D, the bearing capacity factors N_σ and $N_{\sigma }^{S}$ decrease which results in a reduction in the bearing capacity.

• The weight of the rock mass has a small effect on the bearing capacity factors, N_σ and $N_{\sigma }^{S}$, since the main portion of the bearing capacity is due to the uniaxial compressive strength of the rock. So, in most previous researches, the weight effect was ignored. As a result, the width of the footing has an ignorable effect on the bearing capacity in both dry rock foundation and in the case of the existence of seepage.

• In all cases, increasing the seepage forces (i.e., increasing the i(γ_w/γ_sub) ratio) leads to a decrease in the bearing capacity factor $N_{\sigma }^{S}$ and thus reduces the ultimate bearing capacity.

• In all considered gradient ratios, for GSI < 30, the magnitude of $N_{\sigma }^{S}$ increases continuously with increasing the geological strength index, GSI. For GSI > 30, increasing the GSI results in decreasing the $N_{\sigma }^{S}$.

• The failure envelop of rock masses is not linear but slightly curved. Therefore, a linear approximation results in unacceptable bearing capacity magnitudes. For increasing the correctness of the results, one should replace the nonlinear failure envelop by several linear approximations. This method which was used in the present paper resulted in a considerable improvement in the bearing capacity of the rock masses for both the dry and seepage cases.

Appendices

Appendix 1: M1 Mechanism (Dry Rock Masses)

1.1 Geometry

For the triangular block i, the lengths l_i and d_i and the area S_i are given as follows:

$$l_{i} = \frac{{B_{0} }}{2\cos \theta }\mathop \prod \limits_{j = 1}^{i - 1} \frac{{\sin \beta_{j} }}{{\sin (\alpha_{j} + \beta_{j} )}}$$

(23)

$$d_{i} = \frac{{B_{0} }}{2\cos \theta } \frac{{\sin \alpha_{i} }}{{\sin (\alpha_{i} + \beta_{i} )}}\mathop \prod \limits_{j = 1}^{i - 1} \frac{{\sin \beta_{j} }}{{\sin (\alpha_{j} + \beta_{j} )}}$$

(24)

$$S_{i} = \frac{{B_{0}^{2} }}{2}\frac{{\sin \alpha_{i} \sin \beta_{i} }}{{4\cos^{2} \theta \sin (\alpha_{i} + \beta_{i} )}}\mathop \prod \limits_{j = 1}^{i - 1} \frac{{\sin^{2} \beta_{j} }}{{\sin^{2} (\alpha_{j} + \beta_{j} )}}$$

(25)

1.2 Internal Energy Dissipation

1. Along BC:

$$D_{\text{BC}} = c_{0,1} B_{0} f_{1} \left( {\alpha_{i} , \;\beta_{i} , \;\phi_{i} , \;\phi_{i,i + 1} , \;\theta } \right)V_{0} ,$$

(26)

where

$$f_{1} = \frac{{\cos \phi_{0,1} \cos (\beta_{1} - \theta - \phi_{1} )}}{{2\cos \theta \sin (\beta_{1} - \varphi_{1} - \phi_{0,1} )}} \times c_{0,1}$$

(27)

2. Along lines d_i (i = 1, …, k):

$$D_{{d_{i (i = 1, \ldots , k)} }} = c_{i} B_{0} f_{2} \left( {\alpha_{i} , \;\beta_{i} , \;\phi_{i} ,\; \phi_{i,i + 1} , \;\theta } \right)V_{0} ,$$

(28)

where

$$f_{2} = \frac{{ \cos (\theta - \phi_{0,1} ) }}{{2\cos \theta \sin (\beta_{1} - \phi_{1} - \phi_{0,1} )}} \mathop \sum \limits_{i = 1}^{k} \left[ {c_{i} \cos \phi_{i} \frac{{\sin \alpha_{i} }}{{\sin (\alpha_{i} + \beta_{i} )}}\mathop \prod \limits_{j = 1}^{i - 1} \frac{{\sin \beta_{j} \sin (\alpha_{j} + \beta_{j} - \phi_{j} - \phi_{j,j + 1} )}}{{\sin (\alpha_{j} + \beta_{j} )\sin (\beta_{j + 1} - \phi_{j + 1} - \phi_{j,j + 1} )}}} \right].$$

(29)

3. Along lines l_i (i = 2, …, k):

$$D_{{l_{i (i = 1, \ldots , k)} }} = c_{i,i + 1} B_{0} f_{3} \left( {\alpha_{i} , \;\beta_{i} ,\; \phi_{i} ,\; \phi_{i,i + 1} , \;\theta } \right)V_{0} ,$$

(30)

where

$$f_{3} = \frac{{ \cos (\theta - \phi_{0,1} ) }}{{2\cos \theta \sin (\beta_{1} - \phi_{1} - \phi_{0,1} )}}\sum\limits_{i = 2}^{k} {\left[ {c_{i,i + 1} \cos \phi_{i,i + 1} \frac{{\sin (\alpha_{i - 1} + \beta_{i - 1} + \phi_{i} - \phi_{i - 1} - \beta_{i} )}}{{\sin (\alpha_{i - 1} + \beta_{i - 1} - \phi_{i - 1} - \phi_{i,i - 1} )}} \times \mathop \prod \limits_{j = 1}^{i - 1} \frac{{\sin \beta_{j} }}{{\sin (\alpha_{j} + \beta_{j} )}} \times \mathop \prod \limits_{j = 1}^{i - 2} \frac{{\sin (\alpha_{j} + \beta_{j} - \phi_{j} - \phi_{j,j + 1} )}}{{\sin (\beta_{j + 1} - \phi_{j + 1} - \phi_{j,j + 1} )}}} \right]} .$$

(31)

Because of the symmetry of the M1 mechanism, the total energy dissipation in the whole mechanism is twice the summation of these three parts, i.e., Eqs. (24), (28), and (30):

$$\sum D = 2\left( {D_{\text{BC}} + D_{{d_{i (i = 1, \ldots , k)} }} + D_{{l_{i (i = 2, \ldots , k)} }} } \right)$$

(32)

1.3 External Work

1. External work due to the surcharge loading:

$$W_{{q_{0} }} = q_{0} B_{0} f_{4} \left( {\alpha_{i} , \;\beta_{i} , \;\phi_{i} , \;\phi_{i,i + 1} , \;\theta } \right)V_{0}$$

(33)

$$\begin{aligned} f_{4} = \frac{{ \cos \left( {\theta - \phi_{0,1} } \right) }}{{\cos \theta \sin \left( {\beta_{1} - \phi_{1} - \phi_{0,1} } \right)}}\frac{{\sin \beta_{k} }}{{\sin \left( {\alpha_{k} + \beta_{k} } \right)}}\sin \left( {\beta_{k} - \theta - \mathop \sum \limits_{j = 1}^{k - 1} \alpha_{j} - \phi_{k} } \right) \hfill \\ \times \mathop \prod \limits_{j = 1}^{k - 1} \frac{{\sin \beta_{j} \sin \left( {\alpha_{j} + \beta_{j} - \phi_{j} - \phi_{j,j + 1} } \right)}}{{\sin \left( {\alpha_{j} + \beta_{j} } \right)\sin \left( {\beta_{j + 1} - \phi_{j + 1} - \phi_{j,j + 1} } \right)}} \hfill \\ \end{aligned}$$

(34)

2. External work due to self-weight of the central triangular wedge, ABC:

$$W_{\text{ABC}} = \frac{{\gamma B_{0}^{2} }}{2}\left[ {f_{5} \left( {\alpha_{i} ,\; \beta_{i} , \;\phi_{i} , \;\phi_{i,i + 1} , \;\theta } \right)} \right]V_{0}$$

(35)

where

$$f_{5} = \frac{\tan \theta }{2}$$

(36)

3. External work due to self-weights of the remaining 2k triangular wedges:

$$\mathop \sum \limits_{i = 1}^{2k} W_{i} = \frac{{\gamma B_{0}^{2} }}{2}\left[ {f_{6} \left( {\alpha_{i} , \;\beta_{i} ,\; \phi_{i} ,\; \phi_{i,i + 1} , \;\theta } \right)} \right]V_{0}$$

(37)

where

$$f_{6} = \frac{{\cos (\theta - \phi_{0,1} )}}{{2\cos^{2} \theta \sin (\beta_{1} - \phi_{1} - \phi_{0,1} ) }}\sum\limits_{i = 1}^{k} {\left[ { \frac{{\sin \alpha_{i} \sin \beta_{i} }}{{\sin (\alpha_{i} + \beta_{i} )}}\sin \left( {\beta_{i} - \theta - \mathop \sum \limits_{j = 1}^{i - 1} \alpha_{j} - \phi_{i} } \right) \times \mathop \prod \limits_{j = 1}^{i - 1} \frac{{\sin^{2} \beta_{j} \sin (\alpha_{j} + \beta_{j} - \phi_{j} - \phi_{j,j + 1} )}}{{\sin^{2} (\alpha_{j} + \beta_{j} )\sin (\beta_{j + 1} - \phi_{j + 1} - \phi_{j,j + 1} )}}} \right].}$$

(38)

4. External work due to the footing load:

$$W_{{q_{\text{uD}} }} = q_{\text{uD}} V_{0} .$$

(39)

The total external work is the summation of the four contributions, i.e., Eqs. (33), (35), (37), and (39):

$$\sum W_{\text{ext}} = W_{{q_{0} }} + W_{\text{ABC}} + \mathop \sum \limits_{i = 1}^{2k} W_{i} + W_{{q_{\text{uD}} }} .$$

(40)

Appendix 2: M2 Mechanism (Rock Masses Subjected to Seepage)

2.1 Geometry

For the triangular block i, the lengths l_i and d_i, and the area S_i are given as follows:

$$l_{i} = B_{0} \frac{{\sin \beta_{1} }}{{\sin (\alpha_{1} + \beta_{1} )}}\mathop \prod \limits_{j = 2}^{i} \frac{{\sin \beta_{j} }}{{\sin (\alpha_{j} + \beta_{j} )}}$$

(41)

$$d_{i} = B_{0} \frac{{\sin \beta_{1} }}{{\sin (\alpha_{1} + \beta_{1} )}}\frac{{\sin \alpha_{i} }}{{\sin \beta_{i} }}\mathop \prod \limits_{j = 2}^{i} \frac{{\sin \beta_{j} }}{{\sin (\alpha_{j} + \beta_{j} )}}$$

(42)

$$S_{i} = \frac{{B_{0}^{2} }}{2}\frac{{\sin^{2} \beta_{1} }}{{\sin^{2} (\alpha_{1} + \beta_{1} )}}\frac{{\sin \alpha_{i} \sin (\alpha_{i} + \beta_{i} )}}{{\sin \beta_{i} }}\mathop \prod \limits_{j = 2}^{i} \frac{{\sin^{2} \beta_{j} }}{{\sin^{2} (\alpha_{j} + \beta_{j} )}}$$

(43)

2.2 Internal Energy Dissipation

1. Along lines d_i (i = 1, …, k):

$$D_{{d_{i (i = 1, \ldots , k)} }} = c_{i} B_{0} g_{1} \left( {\alpha_{i} , \;\beta_{i} , \;\phi_{i} , \;\phi_{i,i + 1} , \;\theta } \right)V_{0}$$

(44)

where

$$g_{1} = \frac{{\sin \beta_{1} }}{{\sin \left( {\alpha_{1} + \beta_{1} } \right)}}\sum\limits_{i = 1}^{k} {\left[ {c_{i} \cos \phi_{i} \frac{{\sin \alpha_{i} }}{{\sin \beta_{i} }} \times \mathop \prod \limits_{j = 2}^{i} \frac{{\sin \beta_{j} }}{{\sin \left( {\alpha_{j} + \beta_{j} } \right)}}\mathop \prod \limits_{j = 1}^{i - 1} \frac{{\sin \left( {\alpha_{j} + \beta_{j} - \phi_{j} - \phi_{j,j + 1} } \right)}}{{\sin \left( {\beta_{j + 1} - \phi_{j + 1} - \phi_{j,j + 1} } \right)}}} \right]}$$

(45)

2. Along lines l_i (i = 1, …, k − 1):

$$D_{{l_{i (i = 1, \ldots , k - 1)} }} = c_{i,i + 1} B_{0} g_{2} \left( {\alpha_{i} , \;\beta_{i} , \;\phi_{i} ,\; \phi_{i,i + 1} ,\; \theta } \right)V_{0}$$

(46)

where

$$g_{2} = \frac{{\sin \beta_{1} }}{{\sin (\alpha_{1} + \beta_{1} ) }}\sum\limits_{i = 1}^{k = 1} {\left[ {c_{i,i + 1} \cos \phi_{i,i + 1} \frac{{\sin (\alpha_{i} + \beta_{i} + \phi_{i + 1} - \phi_{i} - \beta_{i + 1} )}}{{\sin (\beta_{i + 1} - \phi_{i + 1} - \phi_{i,i + 1} )}}\mathop \prod \limits_{j = 2}^{i} \frac{{\sin \beta_{j} }}{{\sin (\alpha_{j} + \beta_{j} )}}\mathop \prod \limits_{j = 1}^{i - 1} \frac{{\sin (\alpha_{j} + \beta_{j} - \phi_{j} - \phi_{j,j + 1} )}}{{\sin (\beta_{j + 1} - \phi_{j + 1} - \phi_{j,j + 1} )}}} \right]} .$$

(47)

The total energy dissipation in the whole mechanism is equal to the summation of these two parts, i.e., Eqs. (44) and (46):

$$\sum {D = \left( {D_{{d_{i (i = 1, \ldots , k)} }} + D_{{l_{i (i = 2, \ldots , k)} }} } \right)} .$$

(48)

2.3 External Work

1. External work due to self-weights and seepage forces of the rock mass in motion of the k triangular rigid blocks:

$$W_{\text{rockmass}} = \frac{{\gamma B_{0}^{2} }}{2}\left[ {g_{3} + i\left( {\frac{{\gamma_{\text{w}} }}{{\gamma_{\text{sub}} }}} \right) g_{4} } \right]V_{1} ,$$

(49)

where

$$g_{3} = \frac{{\sin \beta_{1} }}{{\sin (\alpha_{1} + \beta_{1} )}}\sin \left( {\beta_{k} - \mathop \sum \limits_{j = 1}^{k - 1} \alpha_{j} - \phi_{k} } \right) \times \mathop \prod \limits_{j = 2}^{k} \frac{{\sin \beta_{j} }}{{\sin (\alpha_{j} + \beta_{j} )}}\mathop \prod \limits_{j = 1}^{k - 1} \frac{{\sin (\alpha_{j} + \beta_{j} - \phi_{j} - \phi_{j,j + 1} )}}{{\sin (\beta_{j + 1} - \phi_{j + 1} - \phi_{j,j + 1} )}}$$

(50)

$$g_{4} = \frac{{\sin \beta_{1} }}{{\sin (\alpha_{1} + \beta_{1} )}}\cos \left( {\beta_{k} - \mathop \sum \limits_{j = 1}^{k - 1} \alpha_{j} - \phi_{k} } \right) \times \mathop \prod \limits_{j = 2}^{k} \frac{{\sin \beta_{j} }}{{\sin (\alpha_{j} + \beta_{j} )}}\mathop \prod \limits_{j = 1}^{k - 1} \frac{{\sin (\alpha_{j} + \beta_{j} - \phi_{j} - \phi_{j,j + 1} )}}{{\sin (\beta_{j + 1} - \phi_{j + 1} - \phi_{j,j + 1} )}}$$

(51)

2. External work due to the surcharge loading and the corresponding seepage forces:

$$W_{{q_{0} }} = qB_{0} \left[ {g_{5} + i\left( {\frac{{\gamma_{\text{w}} }}{{\gamma_{\text{sub}} }}} \right) g_{6} } \right]V_{1} ,$$

(52)

where

$$g_{5} = \frac{{\sin^{2} \beta_{1} }}{{\sin^{2} (\alpha_{1} + \beta_{1} )}}\sum\limits_{i = 1}^{k} {\left[ {\frac{{\sin \alpha_{i} \sin (\alpha_{i} + \beta_{i} )}}{{\sin \beta_{i} }}\sin \left( {\beta_{i} - \mathop \sum \limits_{j = 1}^{i - 1} \alpha_{j} - \phi_{i} } \right) \times \mathop \prod \limits_{j = 2}^{i} \frac{{\sin^{2} \beta_{j} }}{{\sin^{2} (\alpha_{j} + \beta_{j} )}} \times \mathop \prod \limits_{j = 1}^{i - 1} \frac{{\sin (\alpha_{j} + \beta_{j} - \phi_{j} - \phi_{j,j + 1} )}}{{\sin (\beta_{j + 1} - \phi_{j + 1} - \phi_{j,j + 1} )}} } \right]}$$

(53)

$$g_{6} = \frac{{\sin^{2} \beta_{1} }}{{\sin^{2} (\alpha_{1} + \beta_{1} )}}\sum\limits_{i = 1}^{k} {\left[ {\frac{{\sin \alpha_{i} \sin (\alpha_{i} + \beta_{i} )}}{{\sin \beta_{i} }}\cos \left( {\beta_{i} - \mathop \sum \limits_{j = 1}^{i - 1} \alpha_{j} - \phi_{i} } \right) \times \mathop \prod \limits_{j = 2}^{i} \frac{{\sin^{2} \beta_{j} }}{{\sin^{2} (\alpha_{j} + \beta_{j} )}} \times \mathop \prod \limits_{j = 1}^{i - 1} \frac{{\sin (\alpha_{j} + \beta_{j} - \phi_{j} - \phi_{j,j + 1} )}}{{\sin (\beta_{j + 1} - \phi_{j + 1} - \phi_{j,j + 1} )}} } \right]}$$

(54)

3. External work due to the footing load and the corresponding seepage forces:

$$W_{{q_{\text{uS}} }} = q_{\text{uS}} \left[ {\sin (\beta_{1} - \phi_{1} ) + i\left( {\frac{{\gamma_{\text{w}} }}{{\gamma_{\text{sub}} }}} \right) \cos (\beta_{1} - \phi_{1} )} \right]V_{1} .$$

(55)

The total external work is the summation of the three contributions, Eqs. (49), (52), (55):

$$\sum W_{\text{ext}} = W_{\text{rockmass}} + W_{{q_{0} }} + W_{{q_{\text{uS}} }} .$$

(56)