Keywords

1 Introduction

Bearing capacity estimation is an important design consideration in the construction of foundations to support high-rise buildings, bridges, and other heavy structures. The type of geo-material supporting the foundation uniquely characterizes its bearing capacity. Various methods have been developed in past for the accurate estimation of bearing capacity of soil, the most widely used foundation material in case of shallow foundations. However, it has been observed that in specific cases foundations are also placed on rocks and majority of rocks have been proven to be an excellent foundation material. The engineering characteristics of rock have been found to be different from the soil. Thus, it is necessary to exclusively establish techniques for the bearing capacity estimation of rocks. However, unlike soil, simple closed form solutions or rigorous charts for bearing capacity estimation for rock-mass are limited owing to its more complex natural state as compared to soil.

In the past, efforts have been made to estimate the bearing capacity of rock-mass. The non-homogenous, discontinuous rock-matrix with the presence of naturally existing faults, bedding planes, and fractures makes it difficult to derive a simple expression for the bearing capacity estimation using the limit equilibrium method [1]. Largely, the bearing capacity estimation has been carried out using the nonlinear Hoek–Brown failure criterion [2] and its subsequent modifications, as the linear Mohr–Coulomb was found inconsistent in capturing the pressure dependent failure envelope exhibited by the rock-mass. Serrano et al. [3] have obtained the bearing capacity using the modified Hoek–Brown criterion [4] for a strip footing placed on a weightless rock medium using the method of stress characteristics. Further, MSC was employed by Keshavarz, Kumar [5] to obtain bearing capacity for strip and circular footings and by Keshavarz et al. [6] for seismic bearing capacity. Yang and Yin [7] employed the limit analysis theorems [8] to find the upper-bound solutions for ultimate bearing capacity using the modified HB criterion. Further, limit analysis theorem was employed by Merifield et al. [9] to obtain both the upper- and lower-bound estimates of the bearing capacity using the generalized HB criterion [10] and by Saada et al. [11] for its upper bound estimates. Numerical analysis also offers a good tool for the estimation of bearing capacity of rock-mass. However, it is difficult to explicitly model fractures and discontinuities that occur in rock mass using the displacement finite element method. So mostly bearing capacity estimation is carried out using the HB criterion in the elastoplastic domain of the conventional displacement-based finite element method. It is also observed that “Equivalent Mohr–Coulomb Parameters” as suggested by Hoek et al. [10] are used in the FE framework for the bearing capacity estimation. Clausen [12] implemented the modified HB criterion in the FE framework without any corner or apex approximations to obtain the bearing capacity of circular footings on rock-mass using the axis-symmetric FE model. However, such a comprehensive implementation of the HB criteria in the FE framework is limited and the use of “Equivalent Mohr–Coulomb Parameters” is quite prevalent.

The primary aim of this work is to carry out a comparative study of the two methods of implementing the HB criteria in the FE framework to understand and illustrate the fine intricacies involved in the implementation of the HB criterion.

2 Generalized Hoek–Brown Failure Criterion

It is evident from a substantial amount of experimental evidence that unlike soil, the failure envelope of almost all rock masses is nonlinear in the σ1−σ3 stress space. This nonlinearity has a significant effect on the bearing capacity estimation. Various researchers have given semi-empirical nonlinear failure criteria to capture the observed nonlinearity in the experiments. However, the Hoek–Brown failure criterion [2] given in 1980 and its subsequent updates in the year 1983, 1988, 1992, 1995, 1997, 2001, 2002, 2007, and 2018 has been the most widely accepted failure criterion. A detailed history of the development of the criteria over the years can be understood from [13].

In the present study, the generalized Hoek–Brown failure criterion [10] is used which is written in terms of principal stress as given in Eq. (1).

$$\sigma_{1}^{^{\prime}} = \sigma_{3}^{^{\prime}} + \sigma_{ci} \left( {m_{b} \tfrac{{\sigma_{3}^{^{\prime}} }}{{\sigma_{ci}^{^{\prime}} }} + s} \right)^{\alpha }$$
(1)

where σci represents the uniaxial compressive strength of intact rock mass obtained through experiment, σ1 and σ3 represent the major and minor principal stresses, respectively, and α, mb and s represent the dimensionless material parameters which are defined in Eqs. (2–4).

$$ \alpha = \tfrac{1}{2} + \tfrac{1}{6}(e^{\frac{-\text{GSI}}{15}} - e^{\frac{-20}{3}} ) $$
(2)
$$m_{b} = m_{i} \exp (\tfrac{{\text{GSI}} - 100}{{28 - 14D}})$$
(3)
$$s = \exp (\tfrac{{{\text{GSI}} - 100}}{9 - 3D})$$
(4)

where geological strength index (GSI) signifies the state of fracture in the natural state of the rock, varying between 10 to 100 with 10 and 100 representing highly fractured and unfractured state, respectively. D, Disturbance factor signifies the degree of disturbance in the rock matrix due to blasting, varying between 0 and 1 with 0 and 1 representing the undisturbed and highly disturbed state, respectively. Both of the parameters are non-dimensional in situ parameters obtained from the observation from the site. mi is a dimensionless parameter that represents the type of rock, varying from 4 for very fine weak rock like claystone to 33 for coarse igneous rock like granite. It is obtained experimentally however if the test data is not available then Hoek [14] has provided approximate values for five types of rocks.

Further, the unconfined strength of the rock-mass can be obtained from Eq. (1) by substituting σ3 = 0 and given as in Eq. (5).

$$\sigma_{c} = \sigma_{ci} s^{\alpha }$$
(5)

Here, it can be observed that the parameters s and α, which factor the fracture state of the rock, limit the value of the unconfined compressive strength of the fractured rock-mass to be less than the intact rock mass.

Also, the tensile strength of the rock-mass is given by Eq. (6).

$$\sigma_{t} = - \frac{{s\sigma_{ci} }}{{m_{b} }}$$
(6)

Here, it can be observed that parameter s limits the tensile strength to be less than the unconfined compressive strength of the intact rock. Also, it can be seen that mb reduces the tensile strength of the rock-mass as the rock type improves from soft carbonate rocks to hard igneous rocks owing to their brittle nature.

2.1 Equivalent Mohr–Coulomb Parameters

Mohr–Coulomb failure criteria are a well-established failure criterion for soil and it is widely used in the predefined constitutive models of the prevalent finite element tools. Owing to this fact, the developers of the HB failure criteria have given an “Equivalent Mohr–Coulomb Parameters” using the regression analysis in Hoek et al. [10]. An equivalent c′ and ϕ′ values were obtained by fitting an average linear Mohr–Coulomb relationship to the curve generated by solving Eq. 1 for a range of minor principal stress values defined by σt  <  σ3 <  \(\sigma_{3\text{max}}^{\prime}\). As a result of this regression analyses the values of c′ and ϕ′ were given by Eqs. (7–8).

$$c^{\prime} = \frac{{\sigma_{ci} \left[ {\left( {1 + 2\alpha } \right)s + \left( {1 - \alpha } \right)m_{b} \sigma_{3n}^{^{\prime}} } \right]\left( {s + m_{b} \sigma_{3n}^{^{\prime}} } \right)^{\alpha - 1} }}{{2\left( {1 + \alpha } \right)(2 + \alpha )\sqrt {1 + (6\alpha m_{b} (s + m_{b} \sigma_{3n}^{^{\prime}} )^{\alpha - 1} )} }}$$
(7)
$$\phi^{^{\prime}} = \sin^{ - 1} \left[ {\frac{{6\alpha m_{b} \left( {s + m_{b} \sigma_{3n}^{^{\prime}} } \right)^{\alpha - 1} }}{{2(1 + \alpha )\left( {2 + \alpha } \right) + 6\alpha m_{b} (s + m_{b} \sigma_{3n}^{^{\prime}} )^{\alpha - 1} }}} \right]$$
(8)

where σ3n =  \(\sigma_{3\text{max}}^{\prime}\)/σci. Rest other parameters are same as defined in Eq. (1–4). A major concern above is the selection of the maximum minor principal stress, \(\sigma_{3\text{max}}^{\prime}\) up to which the regression analysis gives satisfactory results. Hoek et al. [10] have provided a comprehensive guidelines for selecting the value of \(\sigma_{3\text{max}}^{\prime}\) for slopes as well as shallow and deep tunnels. However, in case of bearing capacity of foundation placed on rock, no such recommendation is provided. Only an approximate value of \(\sigma_{3\text{max}}^{\prime}\)  = 0.25 σci is suggested by Hoek, Brown [15] with a guideline to always verify the validity of the recommendation with respect to the stress range encountered in a specific problem.

Calibration with Hoek–Brown criterion. In the present study, the equivalent Mohr–Coulomb parameters have been obtained with the maximum minor principal stress, \(\sigma_{3\text{max}}^{\prime}\) considered to be equal to 0.25 times the unconfined compressive strength of the rock-mass, σci. The c′ and ϕ′ values obtained from Eqs. 7–8 have been used to define the Mohr–Coulomb criteria given by Eq. (9) for different input parameters of the Hoek–Brown failure criterion.

$$\tau = c + \sigma \tan \phi$$
(9)

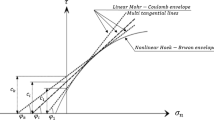
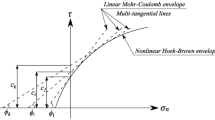
Further, the Mohr–Coulomb failure criterion has been expressed in terms of principal stresses, σ1 and σ3 using the Eq. (10) and plotted on the principal stress plane with the Hoek–Brown failure criterion so that the efficacy of this technique for different rock properties can be studied. Illustrative graphs were shown in Figs. 1 and 2.

$$\sigma_{1}^{^{\prime}} = \frac{{2c^{^{\prime}} \cos \phi^{^{\prime}} }}{{1 - \sin \phi^{^{\prime}} }} + \frac{{1 + \sin \phi^{^{\prime}} }}{{1 - \sin \phi^{^{\prime}} }}\sigma_{3}^{^{\prime}}$$
(10)
Fig. 1
figure 1

Failure criteria in principal stress plane for GSI = 10, a mi = 35 and b mi = 5

Full size image
Fig. 2
figure 2

Failure criteria in principle stress plane for mi = 10, a GSI = 90 and b GSI = 10

Full size image

It has been observed from Fig. 1 that as the mi value of the rock-mass increases, the curvature of Hoek–Brown failure criterion increases. The increase in curvature can be attributed to the improvement in the quality of rock, from being soft at lower mi and hard at higher values. With the increase in curvature, the two criteria lose agreement with each other.

Further, it has been observed from Fig. 2 that as the GSI value of rock increases the curvature of the Hoek–Brown failure criterion increases. The increase in curvature can be attributed to the improvement in the fracture state of rock, from being highly fractured at lower values to intact at higher values. With the increase in curvature, the agreement between the two graphs reduces.

It was also observed that as the fracture sate of rock improves with the increasing GSI the tensile strength of the rock also increases. The rock-mass gains its tensile strength from the intact.

From Figs. 1 and 2, it has been noted that for lower ranges of principal stresses, the equivalent Mohr–Coulomb failure criteria will overestimate the strength by a significant amount. This is a concerning issue particularly in the case of problems involving low over-burden pressure such as bearing capacity problem.

Further, it has been suggested that, since the Hoek–Brown failure criterion limits the tensile strength of the rock-mass by Eq. 6, it would be advantageous to estimate the bearing capacity factor using the modified Mohr–Coulomb criteria with a tension-cutoff corresponding to tensile strength of the rock-mass so that a more comprehensive comparative analysis could be done.

3 Comparative Study

In the present study, in order to understand and illustrate the cogency of the calibration technique involving “Equivalent Mohr–Coulomb Parameters,” a comparative study has been carried out by displacement-based finite element (DBFE) method using ABAQUS [16] and finite element limit analysis (FELA) method using OptumG2 [17].

3.1 DBFE with “Equivalent Mohr–Coulomb Parameters”

A DBFE analysis has been carried out to estimate the bearing capacity of the rock-mass whose strength was characterized using the “Equivalent Mohr–Coulomb parameters” in the Mohr–Coulomb and the modified Mohr–Coulomb material model with a tension cutoff. A 2D plane-strain FE model of a footing resting on the rock-mass has been developed. A DBFE analysis has been carried out to obtain the collapse load Q using the load–displacement curve and bearing capacity factor Nσ given by Eq. (11) as suggested by [9].

Finite element (FE) model. A 2D plane-strain FE model of a rigid strip footing resting on the rock mass has been developed as shown in Fig. 3. The dimensional domain and the mesh density, as shown in Fig. 3, has been ascertained after carrying out the sensitivity and convergence study. The base and the lateral boundaries of the model have been set as fixed in x & y directions and x-direction (as per the coordinate system shown in Fig. 3), respectively. The rigid foundation has been modeled as deformable elastic beam using two-node cubic beam (B23) and rock-mass having “Equivalent Mohr–Coulomb parameters” using the plane-strain quadratic (CPE8R) element with reduced integration. Both the Mohr–Coulomb and Modified Mohr–Coulomb failure criteria with a tension cutoff have been used to characterize the strength of rock-mass. An associated flow rule (ψ = ϕ, where ψ is the dilation angle) has been assumed to obtain the plastic strain.

Fig. 3
figure 3

FE model

Full size image

Load displacement curve. In order to obtain the load–displacement curve, a conventional displacement-based finite element method was employed in the elastoplastic framework. The strength criteria of the rock-mass defined the yield criteria in this framework. Forced displacement has been applied to the footing nodes corresponding to the footing displacement and the sum of the reactions at the footing node has been considered as the load carried by the rock-mass. The displacement and the load at each time step have been plotted to obtain the load displacement curve. The load carrying capacity of the rock-mass, Q, is considered corresponding to the yield as shown in Fig. 4

Fig. 4
figure 4

Load–displacement curve

Full size image

Estimation of Nσ: A non-dimensional bearing capacity factor, as proposed by Merifield et al. [9], is given by Eq. (11).

$$N_{\sigma } = \frac{{q_{u} }}{{\sigma_{ci} }}$$
(11)

where σci is the unconfined compressive strength of the rock-mass and qu is the bearing capacity of the rock-mass obtained by dividing the load carrying capacity, and Q is obtained from the load–displacement by the area of the footing.

3.2 FELA with Hoek–Brown Failure Criterion

A FELA has been carried out to estimate the bearing capacity of the rock-mass with the same properties as used in the DBFE analysis. However, the strength of the rock-mass was characterized using the Hoek–Brown failure criterion instead of the equivalent MC parameters. A 2D plane-strain FELA model of a footing resting on the rock-mass has been developed. A FE limit analysis has been carried out to obtain the collapse load Q using the limit analyses theorem as given by Chen [8] in the finite element FE framework provided in the OptumG2 software. Nσ has been similarly calculated using Eq. (11).

Finite element (FE) model. A 2D plane-strain FE model of a rigid footing resting on the rock-mass has been developed as shown in Fig. 5. The dimensional domain as shown in Fig. 5 has been ascertained after carrying out the sensitivity study. Adaptive meshing based on shear dissipation has been employed.

Fig. 5
figure 5

FELA model

Full size image

As shown in Fig. 5, at the base of the FE model, the displacement in both the directions (i.e., both x and y displacements) is restrained, while for the lateral boundaries, only vertical displacement is allowed (i.e., x displacement is zero). The strip foundation has been modeled using “plate” element. The interface material between the foundation and the surrounding rock-mass has been considered to be same as the rock-mass. An elastoplastic constitutive model based on Hoek–Brown failure criterion and following associated flow rule (ψ = ϕ, where ψ is the dilation angle) has been used for modeling of rock-mass using triangular elements with LB and UB formulations.

Estimation of Nσ: In the FELA framework, the load carrying capacity of the rock-mass, the upper-bound (UB) and lower-bound (LB) estimates of Q have been obtained using the limit analysis theorem. The average of UB and LB estimates has been further used to estimate the non-dimensional factor, Nσ in a similar manner as described in the above section.

3.3 Comparison and Discussion

The comparative study in this work has been done to primarily examine the efficacy of the “Equivalent Mohr–Coulomb parameters.” For this purpose, Nσ factors have been ascertained using the equivalent MC parameters with and without tension cutoff for the specified stress range (σt< σ3 < \(\sigma_{3\text{max}}^{\prime}\)   =  0.25σci) in the DBFE and using the HB criterion parameters in the FELA framework, respectively. The results are illustrated, compared, and validated with [9] in Table 1 and Fig. 6.

Table 1 Nσ values obtained using different analyses
Full size table
Fig. 6
figure 6

Nσ values corresponding to different analyses

Full size image

It has been observed that the bearing capacity factor, Nσ has a good aggrement with [9] when the nonlinear Hoek–Brown failure criteria is used in the bearing capacity estimation.

However, Nσ varies by a significant amount when estimated using the equivalent Mohr–Coulomb parameters. The variation varies from 40% at mi = 1 (i.e., for very soft rock) upto 54% at mi = 35 (i.e., for very hard rock). The difference in the values increases as the rock type improves from soft to hard rocks. This disagreement in values can be attributed to the disagreement in the failure criteria of the two techniques. Nσ values with the equivalent MC parameters are over-estimated because in the stress range usually encountered in the bearing capacity problem, the equivalent linear criterion over-estimates the strength in comparison to the nonlinear HB criterion.

Although the use of modified MC criteria with a tension cutoff reduces the Nσ value but the reduction is not significant. The tension cutoff although limits the MC criteria upto the tensile strength of the rock-mass as given in Eq. (6), but the limit to the strength is not leading upto significant reduction in the Nσ values as can be seen from Fig. 6.

This leads to the assertion that the over-estimation in the Nσis primarily due to the strength over-estimation by the linear MC failure criterion in the low stress range and marginally due to the incompetence of the linear MC criterion to incorporate the limiting tensile strength of the rock-mass.

4 Conclusions

In the present study, it is concluded that in case of bearing capacity estimation of footings placed on the highly fractured homogenous rock-mass, characterized by the nonlinear Hoek–Brown failure criterion, the usage of equivalent Mohr–Coulomb parameters as suggested by Hoek et al. [10] over-estimates the Nσ values by a significant amount.

This linearization technique has been found to be very sensitive to the stress range encountered in the problem, and thus should be implemented cautiously in the FE framework, with due consideration of the stress range ecountered in a specific problem.

As most of the available commercial software are provided with a graphical user interface (GUI)-based material model based on linear MC criteria, the use of equivalent MC criterion is quite prevalent. It is strongly recommended that in case of bearing capacity problems, the equivalent MC criteria should be implemented, cautiously.