Nonlinear torsional buckling and postbuckling analysis of cylindrical silicon nanoshells incorporating surface free energy effects

Abstract

In the present study, a size-dependent shell model is developed which can afford to describe the nonlinear torsional buckling and postbuckling characteristics of cylindrical nanoshells in the presence of surface stress effects. To accomplish this purpose, the Gurtin–Murdoch theory of elasticity together with the von Karman geometric nonlinearity is implemented into the first-order shear deformation shell theory. A linear variation through the thickness is considered for the normal stress component of the bulk to satisfy the balance conditions on the free surfaces of the nanoshell. By means of the virtual work principle, the non-classical governing differential equations are constructed in which the transverse displacement and Airy stress function are considered as independent variables. Thereafter, a boundary layer theory is employed including the effect of surface stress in conjunction with the nonlinear prebuckling deformations and the large postbuckling deflections. Subsequently, an efficient solution methodology based on an improved perturbation technique is put to use to obtain the size-dependent critical torsional buckling loads and the associated postbuckling equilibrium paths. It is observed that the torsional load exhibits a significant increase after reaching the minimum postbuckling load. Also, it is revealed that the effect of surface stress becomes negligible at high values of the deflection.

1 Introduction

Due to the distinguished mechanical and physical properties of nano-structured elements, they have attracted attention of scientific community and have considered being excellent candidates in wide range of application. Nanostructures produced by some molecular manipulations are viewed as the substantial building blocks for various nanosystems and nanodevices. In these applications, a nanostructure may be subjected to various loading conditions such as torsional load. As a consequence, an accurate model to predict the nonlinear buckling and postbuckling behavior of a nanoshell is necessary. Because the classical continuum theory is a scale independent theory, some modified continuum theories have been developed to characterize the size effect observed in nanoscale structures. Several investigations have been carried out in which the proposed modified continuum theories have been utilized as a bridge between the physics features at macroscale and nanoscale. Strain gradient elasticity theory, couple stress elasticity theory and nonlocal elasticity theory are examples of these non-classical theories which have been employed in several investigations.

For example, Shen and Zhang (2010) presented a size-dependent investigation on the torsional buckling and postbuckling of double-walled carbon nanotubes in thermal environments based on the nonlocal elasticity theory. Khademolhosseini et al. (2010) developed calibrated nonlocal shell models via molecular dynamics simulations for prediction of critical torsional buckling loads of single-walled carbon nanotube. Shen and Zhang (2011) proposed a nonlocal elastic beam model for nonlinear bending, buckling and vibration behaviors of carbon nanotubes on elastometric substrates. Ghavanloo and Fazelzadeh (2013) constructed a nonlocal shell model for radial vibration response of spherical nanoshells. Simsek (2014) used the nonlocal elasticity theory within the framework of the Euler–Bernoulli beam theory to analyze the nonlinear large amplitude free vibrations of nanobeams. Zhang et al. (2015) carried out a transient analysis of single-layered graphene sheets on the basis of the nonlocal theory of elasticity and using kp-Ritz method. Dehrouyeh-Semnani and Bahrami (2016) investigated the size-dependent mechanical behavior of Timoshenko microbeams on the basis of the modified couple stress beam element. Reddy et al. (2016) reported a finite element analysis within the framework of the modified couple stress theory for functionally graded circular microplates. Sahmani and Aghdam (2017a, b, c) employed the nonlocal elasticity theory for size-dependent nonlinear stability analysis of hybrid functionally graded nanoshells under different loading conditions. Nguyen et al. (2017) proposed a new and efficient isogeometric analysis including high-continuity elements on the basis of the modified couple stress theory for nonlinear analysis of functionally graded microplates. Yang et al. (2017) introduced a new size-dependent composite laminated beam model based on a re-modified couple stress theory and a refined zigzag theory. Sahmani and Aghdam (2017d, e, f, g) used the nonlocal strain gradient elasticity theory for size-dependent analysis of mechanical behaviors of micro/nano-structures made of multilayer functionally graded nanocomposites. Kim et al. (2018) studied the bending, buckling and free vibration responses of functionally graded porous microplates based on the modified couple stress elasticity theory. Tan and Chen (2018) investigated the size-dependent electro-thermo-mechanical behavior of multilayer microactuators by Joule heating based upon the modified couple stress elasticity theory. Sahmani and Aghdam (2017h, i, 2018a, b) developed nonlocal strain gradient continuum elastic models for capturing size effects on the nonlinear mechanical characteristics of lipid microtubules in a living cell. Wang and Zheng (2018) proposed a nonlinear size-dependent plate model based on the new modified couple stress theory for a pure polarized PLZT microplates. Fang et al. (2018) constructed a three-dimensional modified couple stress beam model to study the size-dependent free vibrations of functionally graded microbeams. Sahmani and Fattahi (2018) calibrated a nonlocal plate model via molecular dynamics simulation for axial buckling behavior of single-layered graphene sheets. Sahmani et al. (2018) presented an analytical mathematical solution for nonlocal strain gradient vibrations of postbuckled laminated functionally graded micro/nano-beams. Salehipour and Shahsavar (2018) reported the size-dependent frequency of functionally graded micro/nano-plates using a new plate model on the basis of the modified strain gradient and three dimensional elasticity theories. De Domenico and Askes (2018) employed stress gradient, strain gradient and inertia gradient beam models to simulate the flexural wave dispersion occurring in carbon nanotubes. Sahmani and Aghdam (2017j, 2018c) introduced a truncated cubic unit cell within the framework of the nonlocal strain gradient elasticity theory to analyze the nonlinear bending and primary resonance of porous micro/nano-beams. They also developed size-dependent continuum models for smart piezoelectric and piezomagnetic micro/nano-structures (Sahmani and Fattahi 2017; Sahmani and Aghdam 2018d; Sahmani and Khandan 2018).

Through decreasing the scale of a structure, the ratio of surface area to volume increases. In this manner, the material properties corresponding to boundary layers of the elastic media turn to be different from those of the bulk. This is attributed to this reason that the equilibrium requirements for the atoms located at or near free surface are different from those of the atoms in the bulk of structure. These extra properties known as surface free energies cause to change the mechanical characteristics of nanostructure which yields interesting behavior. Therefore, Gurtin and Murdoch (1975, 1978) proposed a generic theoretical framework based on the concepts of continuum mechanics that accounts surface free energy. According to this size-dependent elasticity theory, the surface layer of a solid is assumed as a mathematical layer of zero thickness having different material properties from the underlying bulk which is perfectly attached to the membrane. In recent years, much research has been performed in which Gurtin–Murdoch elasticity theory has been used in connection with the mechanical behavior of nanostructures.

Lim and He (2004) developed a size-dependent model to analyze the geometrically nonlinear response of thin elastic films with nanoscale thickness on the basis of continuum approach using surface elasticity theory. Li et al. (2006) studied the influence of surface free energy on the stress concentration around a spherical cavity in a linearly isotropic elastic medium based upon surface elasticity theory. Wang and Feng (2007) extended the surface elastic model to investigate the surface stress effects on contact problems based on a closed-form solution. He and Lilley (2008) reported the effects of surface stress on the static bending and bending resonance of nanowires with various boundary conditions. By using Gurtin–Murdoch elasticity theory, Mogilevskaya et al. (2008) solved a two-dimensional problem of multiple interacting circular nano-inhomogeneities and nano-pores. Zhao and Rajapakse (2009) examined the plane and axisymmetric problems corresponding to a surface-loaded elastic layer including effects of surface free energy. Fu et al. (2010) investigated the influences of surface free energy on the free vibration and buckling behavior of nanobeams in the both linear and nonlinear regimes using Galerkin’s technique. Through incorporation Gurtin–Murdoch elasticity theory into the different types of beam theory, Ansari and Sahmani (2011) predicted the bending and buckling behavior of nanoscale beams in the presence of surface stress effects. Also, Ansari and Sahmani (2011) studied the free vibration response of rectangular nanoplates based on surface elasticity theory and within the framework of different plate theories. Wang (2012) investigated the postbuckling characteristics of nanobeams containing internal flowing fluid incorporating the effects of surface stress. Gao et al. (2014) considered the surface stress effects in the analysis of nanowire buckling on elastomeric substrate. Sahmani et al. (2014, 2015) developed a non-classical beam model to study the nonlinear forced vibrations and free vibrations of postbuckled nanobeams on the basis of surface elasticity theory. Zhang et al. (2015) implemented the high-order surface stress model into the Bernoulli–Euler beam theory to analyze the transverse vibration of an axially compressed nanowire embedded in elastic medium. Liang et al. (2015) proposed a theoretical model to study the effects of surface stress on the postbuckling behavior of piezoelectric nanowires. Sahmani et al. (2015b, c, d, 2016a, b, c, d; Sahmani and Aghdam 2017k) explored the surface stress effects on the nonlinear stability behavior of cylindrical nanoshells subjected to various loading conditions. Sun et al. (2018) predicted the surface stress effect on the buckling characteristics of piezoelectric nanoshells under electro-mechanical load. Kamali et al. (2018) introduced an orthotropic elastic shell model for buckling analysis of microtubules under axial compression based on the surface elasticity theory. Dong et al. (2019) examined the buckling behavior of metal nanowires encapsulating carbon nanotubes in the presence of surface effects. Sarafraz et al. (2019) analyzed the nonlinear secondary resonance of silicon nanobeams under subharmonic and superharmonic external excitations including the effects of surface free energy.

In the current investigation, for the first time, the surface elasticity theory is incorporated within the framework of the first-order shear deformation shell theory to analyze the nonlinear torsional buckling and postbuckling of a nanoshell. Also, the surface stress effects in conjunction with the shear deformation in the large twist angle associated with the torsional postbuckling behavior of a silicon nanoshell is studied for the first time. To this end, the Gurtin–Murdoch elasticity theory is employed to develop a size-dependent shell model incorporating the effects of surface stress. After that, a boundary layer theory is employed including surface stress effects in conjunction with nonlinear prebuckling deformation and the large postbuckling deflections. Then by using an improved perturbation methodology, the size-dependent postbuckling equilibrium paths of nanosized shells under torsion are obtained corresponding to different values of the shell thickness, surface elastic constants, and surface residual stress.

2 Preliminaries

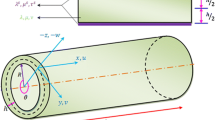
In Fig. 1, a cylindrical nanoshell with the length $L$, thickness $h$, and mid-surface radius $R$ is shown. The nanoshell includes a bulk part and two additional thin surface layers (inner and outer layers). For the bulk part, the material properties are Young’s modulus $E$ and Poisson’s ratio $\nu$. The two surface layers are assumed to have surface elasticity modulus of $E_{s}$, Poisson’s ratio $\nu_{s}$ and the surface residual tension $\tau_{s}$. According to a curvilinear coordinate system with its origin located on the middle surface of nanoshell, coordinates of a typical point in the axial, circumferential and radial directions are denoted by $x$, $y$ and $z$, respectively. Now, in accordance with the classical shell theory, the displacement field can be expressed as

Fig. 1

Schematic view of a cylindrical nanoshell with surface layers

$$u_{x} \left( {x,y,z} \right) = u\left( {x,y} \right) + z\psi_{x} \left( {x,y} \right),$$

(1a)

$$u_{y} \left( {x,y,z} \right) = v\left( {x,y} \right) + z\psi_{y} \left( {x,y} \right),$$

(1b)

$$u_{z} \left( {x,y,z} \right) = w\left( {x,y} \right),$$

(1c)

in which $u$, $v$ and $w$ denote the middle surface displacements along $x, y$ and $z$ axis, respectively.

Based on the von Karman kinematics of nonlinearity within the framework of the first-order shear deformation shell theory, the kinematical strain–displacement relationships can be expressed as follow

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} } \\ {\varepsilon_{yy}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\kappa_{xx} } \\ {\kappa_{yy} } \\ {\kappa_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \\ {\frac{\partial v}{\partial y} - \frac{w}{R} + \frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right)^{2} } \\ {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} + \frac{\partial w}{\partial x}\frac{\partial w}{\partial y}} \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\frac{{\partial \psi_{x} }}{\partial x}} \\ {\frac{{\partial \psi_{y} }}{\partial y}} \\ {\frac{{\partial \psi_{x} }}{\partial y} + \frac{{\partial \psi_{y} }}{\partial x}} \\ \end{array} } \right\},$$

(2a)

$$\left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\psi_{x} + \frac{\partial w}{\partial x}} \\ {\psi_{y} + \frac{\partial w}{\partial y}} \\ \end{array} } \right\},$$

(2b)

where $\varepsilon_{xx}^{0} ,\varepsilon_{xx}^{0} ,\gamma_{xy}^{0}$ stand for the strain components of the middle surface, and $\kappa_{xx} ,\kappa_{yy} ,\kappa_{xy}$ denote the curvature components of nanoshell.

Then, the constitutive relations can be given as

$$\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ {\sigma_{xz} } \\ {\sigma_{yz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\lambda + 2\mu } & \lambda & 0 & 0 & 0 \\ \lambda & {\lambda + 2\mu } & 0 & 0 & 0 \\ 0 & 0 & \mu & 0 & 0 \\ 0 & 0 & 0 & \mu & 0 \\ 0 & 0 & 0 & 0 & \mu \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\},$$

(3)

in which $\lambda = E\nu /\left( {\left( {1 - \nu } \right)(1 + 2\nu )} \right)$, $\mu = E/\left( {2\left( {1 + \nu } \right)} \right)$ are Lame’s constants.

Gurtin–Murdoch elasticity theory facilitates considering surface energy effects in the conventional continuum approach. In relation with the atomic features of nanostructures, there are always interactions between the elastic surface and bulk material. As a result, nanostructures mostly undergo in-plane loads in various directions. These in-plane loads on the surfaces of the bulk of nanoshell leads to surface stresses which can be obtained by using surface constitutive equations of Gurtin–Murdoch elasticity theory as follow (Gurtin and Murdoch 1975, 1978)

$$\begin{array}{*{20}l} {\sigma_{ij}^{s} = \tau_{s} \delta_{ij} + \left( {\tau_{s} + \lambda_{s} } \right)\varepsilon_{kk} \delta_{ij} + 2\left( {\mu_{s} - \tau_{s} } \right)\varepsilon_{ij} + \tau_{s} u_{i,j}^{s} } \hfill \\ {\sigma_{iz}^{s} = \tau_{s} u_{z,i}^{s} } \hfill \\ \end{array} ; \;\;\left( {i,j = x,y} \right),$$

(4)

where $\lambda_{s}$ and $\mu_{s}$ represent the surface Lame’s constants and $\tau_{s}$ is the surface residual stress under unstrained conditions. As a result, the components of surface stress can be determined with respect to the displacement components as below

$$\begin{aligned} \sigma_{xx}^{s} &= \left( {\lambda_{s} + 2\mu_{s} } \right)\varepsilon_{xx} + \left( {\tau_{s} + \lambda_{s} } \right)\varepsilon_{yy} + \tau_{s} - \frac{{\tau_{s} }}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} , \\ \sigma_{yy}^{s} &= \left( {\lambda_{s} + 2\mu_{s} } \right)\varepsilon_{yy} + \left( {\tau_{s} + \lambda_{s} } \right)\varepsilon_{xx} + \frac{{\tau_{s} }}{R}w + \tau_{s} - \frac{{\tau_{s} }}{2}\left( {\frac{\partial w}{\partial y}} \right)^{2} , \\ \sigma_{xy}^{s} &= \mu_{s} \gamma_{xy} - \tau_{s} \left( {\frac{\partial v}{\partial x} + \frac{\partial w}{\partial x}\frac{\partial w}{\partial y} + z\frac{{\partial \psi_{y} }}{\partial x}} \right) , \\ \sigma_{yx}^{s} &= \mu_{s} \gamma_{xy} - \tau_{s} \left( {\frac{\partial u}{\partial y} + \frac{\partial w}{\partial x}\frac{\partial w}{\partial y} + z\frac{{\partial \psi_{x} }}{\partial y}} \right), \\ \sigma_{xz}^{s} &= \tau_{s} \frac{\partial w}{\partial x},\;\; \sigma_{yz}^{s} = \tau_{s} \frac{\partial w}{\partial y}. \\ \end{aligned}$$

(5)

In the classical theories, as the stress component $\sigma_{zz}$ is small compared to the other normal stresses, so it is assumed that $\sigma_{zz} = 0$. Nevertheless, this assumption does not satisfy the surface conditions related to the Gurtin–Murdoch model. To tackle this problem, it is supposed that the stress component $\sigma_{zz}$ varies linearly through the thickness and satisfies the balance conditions on the surfaces of nanoshell. According to this assumption, $\sigma_{zz}$ can be obtained as

$$\sigma_{zz} = \frac{{\left( {\frac{{\partial \sigma_{xz}^{S + } }}{\partial x} + \frac{{\partial \sigma_{yz}^{S + } }}{\partial y}} \right) - \left( {\frac{{\partial \sigma_{xz}^{S - } }}{\partial x} + \frac{{\partial \sigma_{yz}^{S - } }}{\partial y}} \right)}}{2} + \frac{{\left( {\frac{{\partial \sigma_{xz}^{S + } }}{\partial x} + \frac{{\partial \sigma_{yz}^{S + } }}{\partial y}} \right) + \left( {\frac{{\partial \sigma_{xz}^{S - } }}{\partial x} + \frac{{\partial \sigma_{yz}^{S - } }}{\partial y}} \right)}}{h}z,$$

(6)

in which the superscripts $S^{ + }$ and $S^{ - }$ refer to the outer and inner surfaces of nanoshell, respectively. Through inserting Eq. (5) into Eq. (6), $\sigma_{zz}$ can be achieved as follows

$$\sigma_{zz} = \frac{{2\tau_{s} z}}{h}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right).$$

(7)

Now, by substituting the $\sigma_{zz}$ in the constitutive Eq. (3) corresponding to the normal stresses $\left( {\sigma_{xx} ,\sigma_{yy} } \right)$ for the bulk of the nanoshell, one will have

$$\sigma_{xx} = \left( {\lambda + 2\mu } \right)\varepsilon_{xx} + \lambda \varepsilon_{yy} + \frac{{\nu \sigma_{zz} }}{{\left( {1 - \nu } \right)}},$$

(8a)

$$\sigma_{yy} = \left( {\lambda + 2\mu } \right)\varepsilon_{yy} + \lambda \varepsilon_{xx} + \frac{{\nu \sigma_{zz} }}{{\left( {1 - \nu } \right)}}.$$

(8b)

Based on the continuum surface elasticity theory, the total strain energy of a cylindrical nanoshell incorporating the surface stress effects can be expressed as

$$\begin{aligned} \varPi_{s} & = \frac{1}{2}\mathop \int \limits_{S}^{ } \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2} }} \sigma_{ij} \varepsilon_{ij} dzdS + \frac{1}{2}\left( {\mathop \int \limits_{{S^{ + } }}^{ } \sigma_{ij}^{s} \varepsilon_{ij} dS^{ + } + \mathop \int \limits_{{S^{ - } }}^{ } \sigma_{ij}^{s} \varepsilon_{ij} dS^{ - } } \right) \\ & = \frac{1}{2}\mathop \int \limits_{S}^{ } \left\{ {v_{xx} \varepsilon_{xx}^{0} + \overline{N}_{yy} \varepsilon_{yy}^{0} + \overline{N}_{xy} \gamma_{xy}^{0} + \overline{M}_{xx} \kappa_{xx} + \overline{M}_{yy} \kappa_{yy} + \overline{M}_{xy} \kappa_{xy} + Q_{x} \gamma_{xz} + Q_{y} \gamma_{yz} } \right. \\ & \;\;\left. + \, { Q_{x}^{s} \frac{\partial w}{\partial x} + Q_{y}^{s} \frac{\partial w}{\partial y}} \right\}dS, \\ \end{aligned}$$

(9)

where $S$ is the area occupied by the middle surface of the nanoshell. In Eq. (9), the in-plane forces, bending moments and shear forces are obtained as

$$\begin{aligned} \overline{N}_{xx} & = N_{xx} + \sigma_{xx}^{s + } + \sigma_{xx}^{s - } = A_{11}^{*} \varepsilon_{xx}^{0} + A_{12}^{*} \varepsilon_{yy}^{0} + 2\tau_{s} - \tau_{s} \left( {\frac{\partial w}{\partial x}} \right)^{2} \\ \overline{N}_{yy} & = N_{yy} + \sigma_{yy}^{s + } + \sigma_{yy}^{s - } = A_{11}^{*} \varepsilon_{yy}^{0} + A_{12}^{*} \varepsilon_{xx}^{0} + \frac{{2\tau_{s} }}{R}w + 2\tau_{s} - \tau_{s} \left( {\frac{\partial w}{\partial y}} \right)^{2} \\ \overline{N}_{xy} & = N_{xy} + \frac{1}{2}\left( {\sigma_{xy}^{s + } + \sigma_{yx}^{s + } + \sigma_{xy}^{s - } + \sigma_{yx}^{s - } } \right) = A_{55}^{*} \gamma_{xy}^{0} - \tau_{s} \frac{\partial w}{\partial x}\frac{\partial w}{\partial y} \\ \overline{M}_{xx} & = M_{xx} + \frac{h}{2}\left( {\sigma_{xx}^{s + } - \sigma_{xx}^{s - } } \right) = D_{11}^{*} \kappa_{xx} + D_{12}^{*} \kappa_{yy} + E_{11}^{*} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) \\ \overline{M}_{yy} & = M_{yy} + \frac{h}{2}\left( {\sigma_{yy}^{s + } - \sigma_{yy}^{s - } } \right) = D_{11}^{*} \kappa_{yy} + D_{12}^{*} \kappa_{xx} + E_{11}^{*} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) \\ \overline{M}_{xy} & = M_{xy} + \frac{h}{4}\left( {\sigma_{xy}^{s + } + \sigma_{yx}^{s + } - \sigma_{xy}^{s - } - \sigma_{yx}^{s - } } \right) = D_{55}^{*} \kappa_{xy} \\ Q_{x} & = k_{s} A_{55} \gamma_{xz} ,\;\; Q_{y} = k_{s} A_{55} \gamma_{yz} \\ Q_{x}^{s} & = \sigma_{xz}^{s - } + \sigma_{xz}^{s + } = 2\tau_{s} \frac{\partial w}{\partial x},\;\; Q_{y}^{s} = \sigma_{yz}^{s - } + \sigma_{yz}^{s + } = 2\tau_{s} \frac{\partial w}{\partial y}, \\ \end{aligned}$$

(10)

where $k_{s}$ denotes the shear correction factor, and

$$\left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right\}dz, \;\; \left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right\}zdz,\;\; \left\{ {\begin{array}{*{20}c} {Q_{x} } \\ {Q_{y} } \\ \end{array} } \right\} = k_{s} \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xz} } \\ {\sigma_{yz} } \\ \end{array} } \right\}dz,$$

(11)

and

$$\begin{aligned} A_{11}^{*} & = \left( {\lambda + 2\mu } \right)h + 2\left( {\lambda_{s} + 2\mu_{s} } \right),\;\;A_{12}^{*} = \lambda h + 2\tau_{s} + 2\lambda_{s} , \;\;A_{55} = \mu h ,\;\; A_{55}^{*} = \mu h + 2\mu_{s} - \tau_{s} \\ D_{11}^{*} & = \frac{{\left( {\lambda + 2\mu } \right)h^{3} }}{12} + \frac{{\left( {\lambda_{s} + 2\mu_{s} } \right)h^{2} }}{2},\;\; D_{12}^{*} = \frac{{\lambda h^{3} }}{12} + \frac{{\left( {\tau_{s} + \lambda_{s} } \right)h^{2} }}{2}, \;\; E_{11}^{*} = \frac{{\nu h^{2} \tau_{s} }}{{6\left( {1 - \nu } \right)}}, \\ D_{55}^{*} & = \frac{{\mu h^{3} }}{12} + \frac{{\left( {2\mu_{s} - \tau_{s} } \right)h^{2} }}{4}. \\ \end{aligned}$$

(12)

By using virtual work’s principle as below

$$\delta \mathop \int \limits_{{t_{1} }}^{{t_{2} }} \varPi_{s} {\text{dt}} = 0,$$

(13)

and taking the variation of $u$, $v,$ and $w$ and integrating by parts, the non-classical governing differential equations can be derived as

$$\frac{{\partial \overline{N}_{xx} }}{\partial x} + \frac{{\partial \overline{N}_{xy} }}{\partial y} = 0 ,$$

(14a)

$$\frac{{\partial \overline{N}_{xy} }}{\partial x} + \frac{{\partial \overline{N}_{yy} }}{\partial y} = 0 ,$$

(14b)

$$\frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} + \frac{{\partial Q_{x}^{s} }}{\partial x} + \frac{{\partial Q_{y}^{s} }}{\partial y} + \frac{{\overline{N}_{yy} }}{R} + \overline{N}_{xx} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2\overline{N}_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + \overline{N}_{yy} \frac{{\partial^{2} w}}{{\partial y^{2} }} = 0,$$

(14c)

$$\frac{{\partial \overline{M}_{xx} }}{\partial x} + \frac{{\partial \overline{M}_{xy} }}{\partial y} - Q_{x} = 0,$$

(14d)

$$\frac{{\partial \overline{M}_{xy} }}{\partial x} + \frac{{\partial \overline{M}_{yy} }}{\partial y} - Q_{y} = 0.$$

The Airy stress function $f(x,y)$ can be defined as

$$\overline{N}_{xx} = \frac{{\partial^{2} f}}{{\partial y^{2} }} ,\;\; \overline{N}_{yy} = \frac{{\partial^{2} f}}{{\partial x^{2} }},\;\;\overline{N}_{xy} = - \frac{{\partial^{2} f}}{\partial x\partial y}.$$

(15)

As a result, the strain components can be expressed as below

$$\varepsilon_{xx}^{0} = - \varphi_{2} \frac{{\partial^{2} f}}{{\partial x^{2} }} + \varphi_{1} \frac{{\partial^{2} f}}{{\partial y^{2} }} - 2\tau_{s} \varphi_{2} \frac{w}{R} - \frac{{2\tau_{s} }}{{A_{11}^{*} + A_{12}^{*} }} + \tau_{s} \varphi_{1} \left( {\frac{\partial w}{\partial x}} \right)^{2} - \tau_{s} \varphi_{2} \left( {\frac{\partial w}{\partial y}} \right)^{2} ,$$

(16a)

$$\varepsilon_{yy}^{0} = - \varphi_{2} \frac{{\partial^{2} f}}{{\partial y^{2} }} + \varphi_{1} \frac{{\partial^{2} f}}{{\partial x^{2} }} + 2\tau_{s} \varphi_{1} \frac{w}{R} - \frac{{2\tau_{s} }}{{A_{11}^{*} + A_{12}^{*} }} + \tau_{s} \varphi_{1} \left( {\frac{\partial w}{\partial y}} \right)^{2} - \tau_{s} \varphi_{2} \left( {\frac{\partial w}{\partial x}} \right)^{2} ,$$

(16b)

$$\gamma_{xy}^{0} = - \varphi_{3} \frac{{\partial^{2} f}}{\partial x\partial y} + \tau_{s} \varphi_{3} \frac{\partial w}{\partial x}\frac{\partial w}{\partial y},$$

(16c)

in which

$$\varphi_{1} = \frac{{A_{11}^{*} }}{{\left( {A_{11}^{*} } \right)^{2} - \left( {A_{12}^{*} } \right)^{2} }},\;\; \varphi_{2} = \frac{{A_{12}^{*} }}{{\left( {A_{11}^{*} } \right)^{2} - \left( {A_{12}^{*} } \right)^{2} }} , \;\; \varphi_{3} = \frac{1}{{A_{55}^{*} }}.$$

(17)

Also, the geometrical compatibility equation for a perfect cylindrical shell is written as

$$\frac{{\partial^{2} \varepsilon_{xx}^{0} }}{{\partial y^{2} }} + \frac{{\partial^{2} \varepsilon_{yy}^{0} }}{{\partial x^{2} }} - \frac{{\partial^{2} \gamma_{xy}^{0} }}{\partial x\partial y} = \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} - \frac{1}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }}.$$

(18)

From differential equations of (14c) and (18) and with the aid of Eqs. (10) and (16a–16c), the nonlinear size-dependent governing differential equations can be derived as

$$\begin{aligned} - D_{11}^{*} \frac{{\partial^{3} \psi_{x} }}{{\partial x^{3} }} + \varphi_{4} \frac{{\partial^{3} \psi_{x} }}{{\partial x\partial y^{2} }} - D_{11}^{*} \frac{{\partial^{3} \psi_{y} }}{{\partial y^{3} }} + \varphi_{4} \frac{{\partial^{3} \psi_{y} }}{{\partial x^{2} \partial y}} - E_{11}^{*} \left( {\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} w}}{{\partial y^{4} }}} \right) \hfill \\ - 2\tau_{s} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) - \frac{1}{R}\frac{{\partial^{2} f}}{{\partial x^{2} }} = \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} f}}{{\partial y^{2} }} - 2\frac{{\partial^{2} w}}{\partial x\partial y}\frac{{\partial^{2} f}}{\partial x\partial y} + \frac{{\partial^{2} w}}{{\partial y^{2} }}\frac{{\partial^{2} f}}{{\partial x^{2} }}, \hfill \\ \end{aligned}$$

(19a)

$$\begin{aligned} \varphi_{1} \frac{{\partial^{4} f}}{{\partial x^{4} }} +& \left( {\varphi_{3} - 2\varphi_{2} } \right)\frac{{\partial^{4} f}}{{\partial x^{2} \partial y^{2} }} + \varphi_{1} \frac{{\partial^{4} f}}{{\partial y^{4} }} + \frac{{2\tau_{s} }}{R}\left( {\varphi_{1} \frac{{\partial^{2} w}}{{\partial x^{2} }} - \varphi_{2} \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right) + \frac{1}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & = \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} - 2\tau_{s} \varphi_{1} \left( {\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }}\frac{\partial w}{\partial x} + 2\left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} + \frac{{\partial^{3} w}}{{\partial x^{2} \partial y}}\frac{\partial w}{\partial y}} \right) \\ & \;\; + 2\tau_{s} \varphi_{2} \left( {\frac{{\partial^{3} w}}{{\partial x^{3} }}\frac{\partial w}{\partial x} + \frac{{\partial^{3} w}}{{\partial y^{3} }}\frac{\partial w}{\partial y} + \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} + \left( {\frac{{\partial^{2} w}}{{\partial y^{2} }}} \right)^{2} } \right) \\ & \;\; + \tau_{s} \varphi_{3} \left( {\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}}\frac{\partial w}{\partial y} + \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} + \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} + \frac{\partial w}{\partial x}\frac{{\partial^{3} w}}{{\partial x\partial y^{2} }}} \right), \\ \end{aligned}$$

(19b)

$$D_{11}^{*} \frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + D_{55}^{*} \frac{{\partial^{2} \psi_{x} }}{{\partial y^{2} }} - k_{s} A_{55} \left( {\psi_{x} + \frac{\partial w}{\partial x}} \right) + \varphi_{5} \frac{{\partial^{2} \psi_{y} }}{\partial x\partial y} + E_{11}^{*} \left( {\frac{{\partial^{3} w}}{{\partial x^{3} }} + \frac{{\partial^{3} w}}{{\partial x\partial y^{2} }}} \right) = 0,$$

(19c)

$$D_{11}^{*} \frac{{\partial^{2} \psi_{y} }}{{\partial y^{2} }} + D_{55}^{*} \frac{{\partial^{2} \psi_{y} }}{{\partial x^{2} }} - k_{s} A_{55} \left( {\psi_{y} + \frac{\partial w}{\partial y}} \right) + \varphi_{5} \frac{{\partial^{2} \psi_{x} }}{\partial x\partial y} + E_{11}^{*} \left( {\frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} + \frac{{\partial^{3} w}}{{\partial y^{3} }}} \right) = 0 ,$$

(19d)

where

$$\varphi_{4} = E_{11}^{*} - D_{11}^{*} ,\;\; \varphi_{5} = E_{11}^{*} - D_{12}^{*} - D_{55}^{*} .$$

(20)

It is assumed that the end supports of nanoshell are simply supported or clamped. Therefore, the boundary conditions at $x = 0,L$ can be expressed as

For simply supported edge supports: $w = 0, \;\overline{M}_{xx} = 0$.

For clamped edge supports: $w = 0, \frac{\partial w}{\partial x} = 0$.

Also, it is clear that

$$\mathop \int \limits_{0}^{2\pi R} \overline{N}_{xy} dy + 2\pi Rh\sigma_{xy} = 0 .$$

(21)

Moreover, the closed condition (periodicity) can be written as

$$\mathop \int \limits_{0}^{2\pi R} \frac{\partial v}{\partial y}dy = 0,$$

(22a)

which yields

$$\mathop \int \limits_{0}^{2\pi R} \left( { - \varphi_{2} \frac{{\partial^{2} f}}{{\partial y^{2} }} + \varphi_{1} \frac{{\partial^{2} f}}{{\partial x^{2} }} - 2\tau_{s} \varphi_{1} \frac{w}{R} - \frac{{2\tau_{s} }}{{A_{11}^{*} + A_{12}^{*} }} + \tau_{s} \varphi_{1} \left( {\frac{\partial w}{\partial y}} \right)^{2} - \tau_{s} \varphi_{2} \left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{w}{R} - \frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right)^{2} } \right)dy = 0.$$

(22b)

In other hand, the twist angle of nanoshell can be obtained as

$$\varTheta = \frac{1}{2\pi RL}\mathop \int \limits_{0}^{2\pi R} \mathop \int \limits_{0}^{L} \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)dxdy = \frac{1}{2\pi RL}\mathop \int \limits_{0}^{2\pi R} \mathop \int \limits_{0}^{L} \left( { - \varphi_{3} \frac{{\partial^{2} F}}{\partial x\partial y} + \left( {\tau_{s} \varphi_{3} - 1} \right)\frac{\partial w}{\partial x}\frac{\partial w}{\partial y}} \right)dxdy .$$

(23)

3 Solution procedure

3.1 Boundary layer-type governing equations

In order to perform the solution methodology, the following dimensionless parameters are defined

$$\begin{aligned} X& = \frac{\pi x}{L},\;\; Y = \frac{y}{R},\;\; \beta = \frac{L}{\pi R}, \;\; \eta = \frac{{L^{2} }}{{\pi^{2} h^{2} }},\;\; \epsilon = \frac{{\pi^{2} Rh}}{{L^{2} }} \hfill \\ \left\{ {a_{11}^{*} ,a_{12}^{*} ,a_{55}^{*} ,d_{11}^{*} ,d_{12}^{*} ,d_{55}^{*} ,e_{11}^{*} } \right\} &= \left\{ {\frac{{A_{11}^{*} }}{{A_{110} }},\frac{{A_{12}^{*} }}{{A_{110} }},\frac{{A_{55}^{*} }}{{A_{110} }},\frac{{D_{11}^{*} }}{{A_{110} h^{2} }},\frac{{D_{12}^{*} }}{{A_{110} h^{2} }},\frac{{D_{55}^{*} }}{{A_{110} h^{2} }},\frac{{E_{11}^{*} }}{{A_{110} h^{2} }}} \right\} \hfill \\ W &= \frac{ \epsilon w}{h} ,\;\; F = \frac{{ \epsilon ^{2} f}}{{A_{110} h^{2} }} ,\;\; \left\{ {\varPsi_{x} , \varPsi_{y} } \right\} = \frac{{ \epsilon ^{2} L}}{\pi h}\left\{ {\psi_{x} , \psi_{y} } \right\},\;\;\overline{\tau } = \frac{{\tau_{s} }}{{A_{110} }} \hfill \\ \left\{ {{\mathcal{M}}_{xx} ,{\mathcal{M}}_{yy} } \right\} &= \frac{{ \epsilon ^{2} L^{2} \left\{ {\overline{M}_{xx} ,\overline{M}_{yy} } \right\}}}{{\pi^{2} A_{110} h^{3} }}, \;\;{\mathcal{P}}_{s} = \frac{{\sigma_{xy} \sqrt L R^{3/4} }}{{\sqrt \pi A_{110} h^{5/4} }} ,\;\;\phi = \frac{{\varTheta \sqrt L R^{3/4} }}{{\sqrt \pi h^{5/4} }}, \hfill \\ \end{aligned}$$

(24)

in which $A_{110} = \left( {\lambda + 2\mu } \right)h$.

Consequently, the dimensionless form of the governing nonlinear differential equations based on the surface elasticity theory can be presented as follows

$$\begin{aligned} - d_{11}^{*} \epsilon \frac{{\partial^{3} \varPsi_{x} }}{{\partial X^{3} }} + \vartheta_{4} \epsilon \beta^{2} \frac{{\partial^{3} \varPsi_{x} }}{{\partial X\partial Y^{2} }} - d_{11}^{*} \epsilon \beta^{3} \frac{{\partial^{3} \varPsi_{y} }}{{\partial Y^{3} }} + \vartheta_{4} \epsilon \beta \frac{{\partial^{3} \varPsi_{y} }}{{\partial X^{2} \partial Y}} - 2\overline{\tau }\eta \epsilon ^{2} \frac{{\partial^{2} }}{{\partial X^{2} }} - 2\overline{\tau }\eta \epsilon ^{2} \beta^{2} \frac{{\partial^{2} }}{{\partial Y^{2} }} \hfill \\ - e_{11}^{*} \epsilon ^{2} \frac{{\partial^{4} W}}{{\partial X^{4} }} - 2e_{11}^{*} \epsilon ^{2} \beta^{2} \frac{{\partial^{4} W}}{{\partial X^{2} \partial Y^{2} }} - e_{11}^{*} \epsilon ^{2} \beta^{4} \frac{{\partial^{4} W}}{{\partial Y^{4} }} - \frac{{\partial^{2} F}}{{\partial X^{2} }} \hfill \\ = \beta^{2} \frac{{\partial^{2} F}}{{\partial X^{2} }}\frac{{\partial^{2} W}}{{\partial Y^{2} }} - 2\beta^{2} \frac{{\partial^{2} F}}{\partial X\partial Y}\frac{{\partial^{2} W}}{\partial X\partial Y} + \beta^{2} \frac{{\partial^{2} F}}{{\partial Y^{2} }}\frac{{\partial^{2} W}}{{\partial X^{2} }}, \hfill \\ \end{aligned}$$

(25a)

$$\begin{aligned} \vartheta_{1} \frac{{\partial^{4} F}}{{\partial X^{4} }} &+ \left( {\vartheta_{3} - 2\vartheta_{2} } \right)\beta^{2} \frac{{\partial^{4} F}}{{\partial X^{2} \partial Y^{2} }} + \vartheta_{1} \beta^{4} \frac{{\partial^{4} F}}{{\partial Y^{4} }} - 2\overline{\tau }\vartheta_{1} \frac{{\partial^{2} W}}{{\partial X^{2} }} + 2\overline{\tau }\vartheta_{2} \beta^{2} \frac{{\partial^{2} W}}{{\partial Y^{2} }} + \frac{{\partial^{2} W}}{{\partial X^{2} }} \\ & = - \beta^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{{\partial^{2} W}}{{\partial Y^{2} }} + \beta^{2} \frac{{\partial^{2} W}}{\partial X\partial Y}\frac{{\partial^{2} W}}{\partial X\partial Y} - 2\overline{\tau }\vartheta_{1} \beta^{2} \frac{{\partial^{3} W}}{{\partial X\partial Y^{2} }}\frac{\partial W}{\partial X} - 4\overline{\tau }\vartheta_{1} \beta^{2} \frac{{\partial^{2} W}}{\partial X\partial Y}\frac{{\partial^{2} W}}{\partial X\partial Y} \\ & \; - 2\overline{\tau }\vartheta_{1} \beta^{2} \frac{\partial W}{\partial Y}\frac{{\partial^{3} W}}{{\partial X^{2} \partial Y}} + 2\overline{\tau }\vartheta_{2} \frac{{\partial^{3} W}}{{\partial X^{3} }}\frac{\partial W}{\partial X} + 2\overline{\tau }\vartheta_{2} \beta^{4} \frac{{\partial^{3} W}}{{\partial Y^{3} }}\frac{\partial W}{\partial Y} + 2\overline{\tau }\vartheta_{2} \frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{{\partial^{2} W}}{{\partial X^{2} }} \\ & \; + 2\overline{\tau }\vartheta_{2} \beta^{4} \frac{{\partial^{2} W}}{{\partial Y^{2} }}\frac{{\partial^{2} W}}{{\partial Y^{2} }} + \overline{\tau }\vartheta_{3} \beta^{2} \frac{{\partial^{2} W}}{{\partial X^{2} }}\frac{{\partial^{2} W}}{{\partial Y^{2} }} + \overline{\tau }\vartheta_{3} \beta^{2} \frac{{\partial^{2} W}}{\partial X\partial Y}\frac{{\partial^{2} W}}{\partial X\partial Y} + \overline{\tau }\vartheta_{3} \beta^{2} \frac{{\partial^{3} W}}{{\partial X^{2} \partial Y}}\frac{\partial W}{\partial Y} \\ & \; + \overline{\tau }\vartheta_{3} \beta^{2} \frac{\partial W}{\partial X}\frac{{\partial^{3} W}}{{\partial X\partial Y^{2} }}, \\ \end{aligned}$$

(25b)

$$- k_{s} a_{55} \epsilon \frac{\partial W}{\partial X} + e_{11}^{*} \epsilon \frac{{\partial^{3} W}}{{\partial X^{3} }} + e_{11}^{*} \epsilon \beta^{2} \frac{{\partial^{3} W}}{{\partial X\partial Y^{2} }} - k_{s} a_{55} \varPsi_{x} + d_{11}^{*} \frac{{\partial^{2} \varPsi_{x} }}{{\partial X^{2} }} + d_{55}^{*} \beta^{2} \frac{{\partial^{2} \varPsi_{x} }}{{\partial Y^{2} }} + \vartheta_{5} \beta \frac{{\partial^{2} \varPsi_{y} }}{\partial X\partial Y} = 0,$$

(25c)

$$- k_{s} a_{55} \epsilon \beta \frac{\partial W}{\partial Y} + e_{11}^{*} \epsilon \beta \frac{{\partial^{3} W}}{{\partial X^{2} \partial Y}} + e_{11}^{*} \epsilon \beta^{3} \frac{{\partial^{3} W}}{{\partial Y^{3} }} - k_{s} a_{55} \varPsi_{y} + d_{55}^{*} \frac{{\partial^{2} \varPsi_{y} }}{{\partial X^{2} }} + d_{11}^{*} \beta^{2} \frac{{\partial^{2} \varPsi_{y} }}{{\partial Y^{2} }} + \vartheta_{5} \beta \frac{{\partial^{2} \varPsi_{x} }}{\partial X\partial Y} = 0,$$

(25d)

where

$$\begin{aligned} \vartheta_{1} & = \frac{{a_{11}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }} ,\;\; \vartheta_{2} = \frac{{a_{12}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }} , \;\; \vartheta_{3} = \frac{1}{{a_{55}^{*} }} , \\ \vartheta_{4} & = e_{11}^{*} - d_{11}^{*} , \;\; \vartheta_{5} = e_{11}^{*} - d_{12}^{*} - d_{55}^{*} . \\ \end{aligned}$$

(26)

Furthermore, the boundary conditions in dimensionless form will be at $X = 0, \pi$.

For simply supported edge supports: $W = 0, {\mathcal{M}}_{xx} = 0$.

For clamped edge supports: $W = 0, \frac{\partial W}{\partial X} = 0$.

Additionally, one will have

$$\frac{1}{2\pi }\mathop \int \limits_{0}^{2\pi } \beta \frac{{\partial^{2} F}}{\partial X\partial Y}dY + \varepsilon^{5/4} {\mathcal{P}}_{s} = 0 ,$$

(27)

and the closed condition becomes

$$\mathop \int \limits_{0}^{2\pi } \left( {\vartheta_{1} \frac{{\partial^{2} F}}{{\partial X^{2} }} - \vartheta_{2} \beta^{2} \frac{{\partial^{2} F}}{{\partial Y^{2} }} + \left( {1 - 2\overline{\tau }\vartheta_{1} } \right)W - \frac{{2\overline{\tau }\left( {\vartheta_{1} - \vartheta_{2} } \right)}}{{\beta^{2} }} - \overline{\tau }\vartheta_{2} \left( {\frac{\partial W}{\partial X}} \right)^{2} - \frac{{\beta^{2} }}{2}\left( {1 - 2\overline{\tau }\vartheta_{1} } \right)\left( {\frac{\partial W}{\partial Y}} \right)^{2} } \right)dY = 0.$$

(28)

In addition, the dimensionless the twist angle of nanoshell can be expressed as

$$\phi = \frac{1}{{4\pi^{2} \epsilon ^{5/4} }}\mathop \int \limits_{0}^{2\pi } \mathop \int \limits_{0}^{\pi } \left( { - \vartheta_{3} \beta \frac{{\partial^{2} F}}{\partial X\partial Y} + \left( {\overline{\tau }\vartheta_{3} - 1} \right)\beta \frac{\partial W}{\partial X}\frac{\partial W}{\partial Y}} \right)dXdY.$$

(29)

3.2 Singular perturbation technique

The classical perturbation method has been used in a wide range of application (Xu and Liu 2017; Henderson et al. 2018; Zhao et al. 2017; Scheidl and Mittibock 2018). In the preceding subsection, the important parameter $\epsilon$ was introduced. It has been revealed that practically, for a shell-type structure, one will always have $\epsilon \; \ll \;1$. As a consequence, Eqs. (25a–25d) represent the boundary layer type equations which consider the both nonlinear prebuckling deformations and large deflections in the postbuckling domain in conjunction with the effect of surface stress. Now, by assuming $\epsilon$ as a small perturbation parameter, the singular perturbation technique can be put to use which has been successfully applied to the nonlinear analyses of cylindrical shells at macroscale (Shen and Chen 1988; Shen 2008, 2014; Sahmani and Fattahi 2018b; Sahmani and Aghdam 2018e; Shen and Xiang 2018a, b; Sahmani et al. 2018a, b; Shen et al. 2018; Sahmani et al. 2019). On the basis of this technique, it is assumed that

$$W = \overline{W}\left( {X,Y, \epsilon } \right) + \tilde{W}\left( {X,Y, \epsilon ,\xi } \right) + \hat{W}\left( {X,Y, \epsilon ,\varsigma } \right) ,$$

(30a)

$$F = \overline{F}\left( {X,Y, \epsilon } \right) + \tilde{F}\left( {X,Y, \epsilon ,\xi } \right) + \hat{F}\left( {X,Y, \epsilon ,\varsigma } \right),$$

(30b)

$$\varPsi_{x} = \overline{\varPsi }_{x} \left( {X,Y, \epsilon } \right) + \tilde{\varPsi }_{x} \left( {X,Y, \epsilon ,\xi } \right) + \hat{\varPsi }_{x} \left( {X,Y, \epsilon ,\varsigma } \right),$$

(30c)

$$\varPsi_{y} = \overline{\varPsi }_{y} \left( {X,Y, \epsilon } \right) + \tilde{\varPsi }_{y} \left( {X,Y, \epsilon ,\xi } \right) + \hat{\varPsi }_{y} \left( {X,Y, \epsilon ,\varsigma } \right),$$

(30d)

where $\overline{W}\left( {X,Y, \epsilon } \right), \overline{F}\left( {X,Y, \epsilon } \right), \overline{\varPsi }_{x} \left( {X,Y, \epsilon } \right), \overline{\varPsi }_{y} \left( {X,Y, \epsilon } \right)$ denote regular solutions of the nanoshell, $\tilde{W}\left( {X,Y, \epsilon ,\xi } \right),\varvec{ }\tilde{F}\left( {X,Y, \epsilon ,\xi } \right),\varvec{ }\tilde{\varPsi }_{x} \left( {X,Y, \epsilon ,\xi } \right), \tilde{\varPsi }_{y} \left( {X,Y, \epsilon ,\xi } \right)$ and $\hat{W}\left( {X,Y, \epsilon ,\varsigma } \right), \hat{F}\left( {X,Y, \epsilon ,\varsigma } \right),\hat{\varPsi }_{x} \left( {X,Y, \epsilon ,\varsigma } \right)$, $\hat{\varPsi }_{y} \left( {X,Y, \epsilon ,\varsigma } \right)$ are the boundary layer solutions corresponding to $X = 0$ and $X = \pi$, respectively. These solutions can be expressed in the forms of perturbation expansions as below

$$\begin{aligned} \overline{W}\left( {X,Y, \in } \right) = & \mathop \sum \limits_{{i = 1}} \in ^{{i/4 + 1}} \overline{W}_{{i/4 + 1}} (X,Y)~, \\ ~\overline{F}\left( {X,Y, \in } \right) = & \mathop \sum \limits_{{i = 0}} \in ^{{i/4}} \overline{F}_{{i/4}} \left( {X,Y} \right) \\ \overline{\Psi }_{x} \left( {X,Y, \in } \right) = & \mathop \sum \limits_{{i = 1}} \in ^{{i/4}} \overline{\Psi }_{{x_{{i/4}} }} \left( {X,Y} \right)~, \\ ~\overline{\Psi }_{y} \left( {X,Y, \in } \right) = & \mathop \sum \limits_{{i = 1}} \in ^{{i/4}} \overline{\Psi }_{{y_{{i/4}} }} \left( {X,Y} \right) \\ \tilde{W}\left( {X,Y, \in ,\xi } \right) = & \mathop \sum \limits_{{i = 1}} \in ^{{i/4 + 1}} \tilde{W}_{{i/4 + 1}} \left( {X,Y,\xi } \right)\user2{~}, \\ \tilde{F}\left( {X,Y, \in ,\xi } \right) = & \mathop \sum \limits_{{i = 1}} \in ^{{i/4 + 2}} \tilde{F}_{{i/4 + 2}} \left( {X,Y,\xi } \right) \\ \tilde{\Psi }_{x} \left( {X,Y, \in ,\xi } \right) = & \mathop \sum \limits_{{i = 0}} \in ^{{i/4 + 3/2}} \tilde{\Psi }_{{x_{{i/4 + 3/2}} }} \left( {X,Y,\xi } \right)\user2{~}, \\ \user2{~}\tilde{\Psi }_{y} \left( {X,Y, \in ,\xi } \right) = & \mathop \sum \limits_{{i = 0}} \in ^{{i/4 + 2}} \tilde{\Psi }_{{y_{{i/4 + 2}} }} \left( {X,Y,\xi } \right) \\ \hat{W}\left( {X,Y, \in ,\varsigma } \right) = & \mathop \sum \limits_{{i = 1}} \in ^{{i/4 + 1}} \hat{W}_{{i/4 + 1}} (X,Y,\varsigma ), \\ \hat{F}\left( {X,Y, \in ,\varsigma } \right) = & \mathop \sum \limits_{{i = 1}} \in ^{{i/4 + 2}} \hat{F}_{{i/4 + 2}} (X,Y,\varsigma ) \\ \hat{\Psi }_{x} \left( {X,Y, \in ,\varsigma } \right) = & \mathop \sum \limits_{{i = 0}} \in ^{{i/4 + 3/2}} \hat{\Psi }_{{x_{{i/4 + 3/2}} }} (X,Y,\varsigma )~, \\ \hat{\Psi }_{y} \left( {X,Y, \in ,\varsigma } \right) = & \mathop \sum \limits_{{i = 0}} \in ^{{i/4 + 2}} \hat{\Psi }_{{y_{{i/4 + 2}} }} (X,Y,\varsigma ), \\ \end{aligned}$$

(31)

in which $\xi$ and $\varsigma$ stand for boundary layer variables which are defined as

$$\xi = \frac{X}{\sqrt \epsilon } ,\;\; \varsigma = \frac{\pi - X}{\sqrt \epsilon }.$$

(32)

By inserting Eqs. (30a–30d) and (31) in the surface elastic nonlinear governing differential Eqs. (25a–25d) and collecting the expressions with the same order of $\epsilon$, the sets of perturbation equations will be derived relevant to the both regular and boundary layer solutions. A tolerance limit $< 0.001$ is taken into consideration to determine the maximum order of $\epsilon$ associated with convergence of the solution methodology. Afterwards, it is assumed that $\overline{W}_{0} \left( {X,Y} \right) = {\mathcal{A}}_{00}^{(0)} , \overline{W}_{1/4} \left( {X,Y} \right) = \overline{W}_{1/2} \left( {X,Y} \right) = \overline{W}_{3/4} \left( {X,Y} \right) = \overline{W}_{1} \left( {X,Y} \right) = 0$ and $\overline{W}_{5/4} \left( {X,Y} \right) = {\mathcal{A}}_{00}^{(5/4)}$ in addition to $\overline{F}_{0} \left( {X,Y} \right) = - {\mathcal{B}}_{00}^{\left( 0 \right)} XY, \overline{F}_{1/4} \left( {X,Y} \right) = \overline{F}_{1/2} \left( {X,Y} \right) = \overline{F}_{3/4} \left( {X,Y} \right) = \overline{F}_{5/4} \left( {X,Y} \right) = 0$ and $\overline{F}_{1} (X,Y) = - {\mathcal{B}}_{00}^{(1)} XY$. Moreover, the initial buckling mode of the nanoshell is considered as follows

$$\overline{W}_{2} \left( {X,Y} \right) = {\mathcal{A}}_{00}^{\left( 2 \right)} + {\mathcal{A}}_{11}^{\left( 2 \right)} \sin \left( {mX - nY} \right)\sin \left( {nY} \right) + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right).$$

(33)

Through substitution of Eq. (33) into the sets of perturbation equations, the coefficients of $\overline{W}_{i} (X,Y)$, $\overline{F}_{i} \left( {X,Y} \right)$, $\overline{\Psi }_{{x_{{i/4}} }} (X,Y)$, $\overline{\Psi }_{{y_{{i/4}} }} (X,Y)$, can be extracted step by step, all of which are in terms of ${\mathcal{A}}_{11}^{\left( 2 \right)}$. The obtained asymptotic solutions corresponding to clamped edge supports are presented in "Appendix A".

Now, by using the given boundary, Eq. (27), closed conditions (28) and based on the unit twist angle (29), the postbuckling equilibrium paths can be derived as below

$${\mathcal{P}}_{s} = {\mathcal{P}}_{s}^{\left( 0 \right)} + {\mathcal{P}}_{s}^{\left( 2 \right)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon } \right)^{2} + {\mathcal{P}}_{s}^{\left( 4 \right)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon } \right)^{4} +\,\, \ldots ,$$

(34)

and

$$\phi = \phi^{(0)} + \phi^{(2)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon } \right)^{2} + \phi^{(4)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon } \right)^{4} +\,\, \ldots ,$$

(35)

where ${\mathcal{P}}_{s}^{\left( 0 \right)} , {\mathcal{P}}_{s}^{\left( 2 \right)} , {\mathcal{P}}_{s}^{\left( 4 \right)} , \phi^{(0)} , \phi^{(2)} , \phi^{(4)}$ are introduced in "Appendix B".

In accordance with the maximum dimensionless deflection of the nanoshell, ${\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon$ is considered as the second perturbation parameter which in contrast to the first small perturbation parameter $\epsilon$, it may be large. If it is assumed that the maximum deflection occurs at the dimensionless point of $\left( {X,Y} \right) = \left( {\pi /2m,\pi /2n} \right)$, one will have

$${\mathcal{A}}_{11}^{(2)} \epsilon = {\mathcal{W}}_{m} + {\mathcal{S}}_{1} {\mathcal{W}}_{m}^{2} + \ldots ,$$

(36)

in which ${\mathcal{W}}_{m}$ denotes the maximum dimensionless deflection of the nanoshell as

$${\mathcal{W}}_{m} = \frac{{w_{m} }}{h} + {\mathcal{S}}_{2} ,$$

(37)

where the symbols ${\mathcal{S}}_{1}$ and ${\mathcal{S}}_{2}$ are given in "Appendix B".

In order to determine the correct values of $m$ and $n$ corresponding to the maximum deflection, the minimum value of torsional buckling load obtained by Eq. (34) should be calculated by taking $W = 0$ (note that ${\mathcal{W}}_{m} \ne 0$).

4 Numerical results and discussion

In this section, the postbuckling equilibrium paths of cylindrical nanoshells subjected to torsion are presented including surface stress effects. The material properties of nanoshell made of Silicon are tabulated in Table 1. Also, in all of the preceding numerical results, the values of length and radius of nanoshells are selected as the ratios of $L^{2} /Rh = 200, \;\;R/h = 50$ are held constant, and it is assumed that the edge supports of nanoshells are clamped.

Table 1 Material properties of a cylindrical nanoshell made of Silicon (Miller and Shenoy 2000; Zhu et al. 2006)

At first, the validity of the present solving process is checked. In accordance with the best authors’ knowledge, there is no investigation in the open literature in which the torsional buckling and postbuckling of a nanoshell is studied based on the surface elasticity theory. Therefore, by ignoring the surface elastic terms, the critical buckling shear load of a cylindrical shell at usual scale is obtained via the current solving process and compared with those reported by Shaw and Simitses (1984) and Simitses (1968). In Table 2, the critical buckling shear load corresponding to each work is given. A very good agreement is found which confirms the validity and accuracy of the current study.

Table 2 Comparison of the critical buckling shear loads $N_{xy} ({\text{lbs/in)}}$ for an isotropic cylindrical shell under torsion

Depicted in Fig. 2 are the dimensionless postbuckling load–deflection curves of Silicon nanoshells with various thicknesses obtained by the classical and non-classical shell models. It can be seen that the both classical and non-classical paths are obviously nonlinear with a pattern as the torsional load exhibits a significant increase after reaching the minimum postbuckling load. It is indicated that for cylindrical nanoshells made of Silicon, surface stress effects cause to increase the critical buckling load. Moreover, it is found that through increase of shell thickness, the surface stress effect diminishes and the non-classical postbuckling curve tends to the classical one. Also, it is observed that the effect of surface stress becomes negligible at high values of deflection.

Fig. 2

Dimensionless postbuckling load–deflection curves of cylindrical nanoshells with different thicknesses

Figure 3 shows the classical and non-classical dimensionless postbuckling load-rotation curves of cylindrical nanoshells made of Silicon corresponding to different shell thicknesses. It is revealed again that the surface stress effects play more important role in the torsional buckling and postbuckling behavior of nanoshells with lower value of thickness. In addition, it is observed that by considering the effects of surface stress, the slope of prebuckling part of the load-rotation curve increases which means, it leads to decrease the critical buckling rotation of nanoshell under torsional load.

Fig. 3

Dimensionless postbuckling load-rotation curves of cylindrical nanoshells with different thicknesses

Figures 4 and 5 demonstrate, respectively, the influence of surface elastic constants on the postbuckling load–deflection and load-rotation curves of cylindrical nanoshell. It is observed that surface stress effect may cause to increase or decrease the stiffness of nanoshell against torsional load which depends on the sign of surface elastic constants. Furthermore, it can be seen that a positive value of surface elastic constants leads to increase the critical buckling load, but it decreases the critical buckling rotation. This pattern is reversed for a negative value of surface elastic constants. However, for the both positive and negative values of surface elastic constants, the effect of surface stress becomes negligible at high values of deflection.

Fig. 4

Effect of surface elastic constants on the dimensionless postbuckling load–deflection curves of cylindrical nanoshells $(h = 5 {\text{nm}})$

Fig. 5

Effect of surface elastic constants on the dimensionless postbuckling load-rotation curves of cylindrical nanoshells $(h = 5 {\text{nm}})$

Illustrated in Figs. 6 and 7 are, respectively, the dimensionless postbuckling load–deflection and load-rotation curves of nanoshell under torsion corresponding to various values of surface residual stress. It is shown that in contrast to a negative value of residual surface stress, a positive one causes to increase the critical buckling load, but it decreases the critical buckling rotation. So, a positive value of $\tau_{s}$ leads to decrease the slope of prebuckling part of the load-rotation curve, but a negative one causes to increase it.

Fig. 6

Effect of residual surface stress on the dimensionless postbuckling load–deflection curves of cylindrical nanoshells $(h = 5 {\text{nm}})$

Fig. 7

Effect of residual surface stress on the dimensionless postbuckling load-rotation curves of cylindrical nanoshells $(h = 5 {\text{nm}})$

5 Conclusion

In the present investigation, the nonlinear size-dependent buckling and postbuckling behavior of cylindrical nanoshells subjected to torsional load was studied incorporating the effects of surface stress. To this end, Gurtin–Murdoch elasticity theory was implemented into the classical shell theory to develop non-classical shell model which takes the effects of surface stress into account efficiently. Afterwards, a boundary layer theory was put to use including the surface stress effects in conjunction with the nonlinear prebuckling deformations and the large postbuckling deflections. Finally, a two-stepped singular perturbation technique was utilized to obtain the size-dependent postbuckling equilibrium paths of nanoshells under torsion.

It was seen that the torsional load exhibits a considerable increase after reaching the minimum postbuckling load. Additionally, it was found that through increase of shell thickness, the surface stress effect diminishes and the non-classical postbuckling curve tends to the classical one. Also, it was observed that the effect of surface stress becomes negligible at high values of deflection. Furthermore, it was revealed that a positive value of surface elastic constants leads to increase the critical buckling load, but it decreases the critical buckling rotation. For a negative value of surface elastic constants, this pattern is reversed. Moreover, it was indicated that, in contrast to a negative value of residual surface stress, a positive one leads to decrease the slope of prebuckling part of the load-rotation curve.

Appendices

Appendix A

The obtained asymptotic solutions are as below

$$\begin{aligned} W = {\mathcal{A}}_{00}^{(0)} + \epsilon^{5/4} \left[ {{\mathcal{A}}_{00}^{(5/4)} - {\mathcal{A}}_{00}^{(5/4)} \left( {\sin \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right) + \cos \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{\varGamma X}{\sqrt \epsilon }}} } \right. \hfill \\ \left. { - {\mathcal{A}}_{00}^{(5/4)} \left( {\sin \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + \cos \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \hfill \\ + \epsilon^{2} \left[ {{\mathcal{A}}_{00}^{\left( 2 \right)} + {\mathcal{A}}_{11}^{\left( 2 \right)} \sin \left( {mX - nY} \right)\sin \left( {nY} \right) + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right. \hfill \\ - \left( {{\mathcal{A}}_{00}^{(2)} + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right)\left( {\sin \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right) + \cos \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{\varGamma X}{\sqrt \epsilon }}} \hfill \\ \left. { - \left( {{\mathcal{A}}_{00}^{(2)} + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right)\left( {\sin \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + \cos \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \hfill \\ + \epsilon^{3} \left[ {{\mathcal{A}}_{00}^{\left( 4 \right)} + {\mathcal{A}}_{11}^{\left( 3 \right)} \sin \left( {mX - nY} \right)\sin \left( {nY} \right) + {\mathcal{A}}_{02}^{\left( 3 \right)} \cos \left( {2nY} \right)} \right] \hfill \\ + \epsilon^{4} \left[ {{\mathcal{A}}_{00}^{\left( 4 \right)} + {\mathcal{A}}_{11}^{\left( 4 \right)} \sin \left( {mX - nY} \right)\sin \left( {nY} \right) + {\mathcal{A}}_{20}^{\left( 4 \right)} \cos \left( {2mX - 2nY} \right)} \right. \hfill \\ \left. { + {\mathcal{A}}_{13}^{(4)} \sin \left( {mX - nY} \right)\sin \left( {3nY} \right) + {\mathcal{A}}_{02}^{(4)} \cos \left( {2nY} \right)\cos \left( {2nY} \right) + {\mathcal{A}}_{04}^{(4)} \cos (4nY)} \right] \hfill \\ + O\left( { \epsilon^{5} } \right), \hfill \\ \end{aligned}$$

(38)

$$\begin{aligned} F = - {\mathcal{B}}_{00}^{\left( 0 \right)} XY + \epsilon^{2} \left[ { - {\mathcal{B}}_{00}^{\left( 2 \right)} XY + {\mathcal{B}}_{11}^{\left( 2 \right)} \sin \left( {mX - nY} \right)\sin \left( {nY} \right) + {\mathcal{B}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right] \hfill \\ + \epsilon^{9/4} \left[ {{\mathcal{A}}_{00}^{{\left( {5/4} \right)}} \left( {b_{10}^{{\left( {9/4} \right)}} \sin \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right) + b_{01}^{{\left( {9/4} \right)}} \cos \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{\varGamma X}{\sqrt \epsilon }}} } \right. \hfill \\ \left. { + {\mathcal{A}}_{00}^{{\left( {5/4} \right)}} \left( {b_{10}^{{\left( {9/4} \right)}} \sin \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + b_{01}^{{\left( {9/4} \right)}} \cos \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \hfill \\ + \epsilon^{3} \left[ { - {\mathcal{B}}_{00}^{\left( 3 \right)} XY + {\mathcal{B}}_{02}^{\left( 3 \right)} \cos \left( {2nY} \right)} \right. \hfill \\ + \left( {{\mathcal{A}}_{00}^{\left( 2 \right)} + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right)\left( {b_{10}^{\left( 3 \right)} \sin \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right) + b_{01}^{\left( 3 \right)} \cos \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{\varGamma X}{\sqrt \epsilon }}} \hfill \\ \left. { + \left( {{\mathcal{A}}_{00}^{\left( 2 \right)} + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right)\left( {b_{10}^{\left( 3 \right)} \sin \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + b_{01}^{\left( 3 \right)} \cos \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \hfill \\ + \epsilon^{4} \left[ { - {\mathcal{B}}_{00}^{\left( 4 \right)} XY + {\mathcal{B}}_{20}^{\left( 4 \right)} \cos \left( {2mX - 2nY} \right) + {\mathcal{B}}_{13}^{\left( 4 \right)} \sin \left( {mX - nY} \right)\sin \left( {3nY} \right)} \right. \hfill \\ \left. { + {\mathcal{B}}_{02}^{\left( 4 \right)} \cos \left( {2nY} \right)} \right] + O\left( { \epsilon^{5} } \right), \hfill \\ \end{aligned}$$

(39)

$$\begin{aligned} \varPsi_{x} = \epsilon^{7/4} \left[ {{\mathcal{A}}_{00}^{{\left( {5/4} \right)}} \left( {c_{10}^{{\left( {9/4} \right)}} \sin \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right) + c_{01}^{{\left( {9/4} \right)}} \cos \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{\varGamma X}{\sqrt \epsilon }}} } \right. \hfill \\ \left. { + {\mathcal{A}}_{00}^{{\left( {5/4} \right)}} \left( {c_{10}^{{\left( {9/4} \right)}} \sin \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right) + c_{01}^{{\left( {9/4} \right)}} \cos \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] \hfill \\ + \epsilon^{2} \left[ {{\mathcal{C}}_{11}^{\left( 2 \right)} \cos \left( {mX - nY} \right)\sin \left( {nY} \right)} \right] \hfill \\ + \epsilon^{5/2} \left[ {\left( {{\mathcal{A}}_{00}^{(2)} + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right)\left( {c_{10}^{{\left( {5/2} \right)}} \sin \left( {\frac{\varGamma X}{\sqrt \epsilon }} \right) + c_{01}^{{\left( {5/2} \right)}} { \cos }\left( {\frac{\varGamma X}{\sqrt \epsilon }} \right)} \right)e^{{ - \frac{\varGamma X}{\sqrt \epsilon }}} } \right. \hfill \\ + \left( {{\mathcal{A}}_{00}^{(2)} + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right)} \right)\left( {c_{10}^{{\left( {5/2} \right)}} \sin \left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right. \hfill \\ \left. { + c_{10}^{{\left( {5/2} \right)}} { \cos }\left( {\frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }} \right)} \right)\left. {e^{{ - \frac{{\varGamma \left( {\pi - X} \right)}}{\sqrt \epsilon }}} } \right] + \epsilon^{3} \left[ {{\mathcal{C}}_{11}^{\left( 3 \right)} \cos \left( {mX - nY} \right)\sin \left( {nY} \right)} \right] \hfill \\ + \epsilon^{4} \left[ {{\mathcal{C}}_{11}^{\left( 4 \right)} \cos \left( {mX - nY} \right)\sin \left( {nY} \right) + {\mathcal{C}}_{20}^{\left( 4 \right)} \cos \left( {2mX - 2nY} \right)} \right. \hfill \\ \left. { +\,\, {\mathcal{C}}_{13}^{\left( 4 \right)} \cos \left( {mX - nY} \right)\sin \left( {3nY} \right)} \right], \hfill \\ \end{aligned}$$

(40)

$$\begin{aligned} \varPsi_{x} & = \epsilon ^{2} \left[ {{\mathcal{D}}_{11}^{\left( 2 \right)} \sin \left( {mX - nY} \right)\cos \left( {nY} \right)} \right] + \epsilon ^{3} \left[ {{\mathcal{D}}_{11}^{\left( 3 \right)} \sin \left( {mX - nY} \right)\cos \left( {nY} \right) + {\mathcal{D}}_{02}^{\left( 3 \right)} \sin \left( {2nY} \right)} \right] \\ & \;\; + \epsilon ^{4} \left[ {{\mathcal{D}}_{11}^{\left( 4 \right)} \sin \left( {mX - nY} \right)\cos \left( {nY} \right) + {\mathcal{D}}_{02}^{\left( 4 \right)} \sin \left( {2nY} \right) + {\mathcal{D}}_{13}^{\left( 4 \right)} \sin \left( {mX - nY} \right)\cos \left( {3nY} \right)} \right], \\ \end{aligned}$$

(41)

in which

$$\varGamma = \sqrt {\frac{a}{2}} \text{ },\;\;\text{ }a = \sqrt {\frac{{1 + 2\overline{\tau }\vartheta_{1} }}{{\vartheta_{1} \vartheta_{4} }}} .$$

Appendix B

The periodicity condition yields

$${\mathcal{A}}_{00}^{(0)} = \frac{{2\overline{\tau }\left( {\vartheta_{1} - \vartheta_{2} } \right)}}{{\beta^{2} \left( {1 - 2\overline{\tau }\vartheta_{1} } \right)}},$$

(42)

$${\mathcal{A}}_{00}^{(5/4)} = 0 ,$$

(43)

$${\mathcal{A}}_{00}^{(2)} = 0 ,$$

(44)

$${\mathcal{A}}_{00}^{(4)} = \frac{{\overline{\tau }\vartheta_{2} m^{2} + \beta^{2} n^{2} \left( {1 - 2\overline{\tau }\vartheta_{1} } \right)}}{{4\left( {1 - 2\overline{\tau }\vartheta_{1} } \right)}}\left( {{\mathcal{A}}_{11}^{\left( 2 \right)} } \right)^{2} + 2\beta^{2} n^{2} \left( {1 - 2\overline{\tau }\vartheta_{1} } \right)\left( {{\mathcal{A}}_{02}^{\left( 2 \right)} } \right)^{2} .$$

(45)

The parameters in Eqs. (34–37) are as follow

$${\mathcal{P}}_{s}^{\left( 0 \right)} = \left( {K_{0} + \epsilon ^{2} K_{3} \beta } \right) \epsilon ^{ - 1} ,$$

(46)

$$\begin{aligned} {\mathcal{A}}_{00}^{(4)} &= \frac{{\overline{\tau }\vartheta_{2} m^{2} + \beta^{2} n^{2} \left( {1 - 2\overline{\tau }\vartheta_{1} } \right)}}{{4\left( {1 - 2\overline{\tau }\vartheta_{1} } \right)}}\left( {{\mathcal{A}}_{11}^{\left( 2 \right)} } \right)^{2} \\ &\;\;+ 2\beta^{2} n^{2} \left( {1 - 2\overline{\tau }\vartheta_{1} } \right)\left( {{\mathcal{A}}_{02}^{\left( 2 \right)} } \right)^{2} . \end{aligned}$$

(47)

$$\begin{aligned} {\mathcal{P}}_{s}^{\left( 4 \right)} & = \left( {\frac{{K_{0}^{2} K_{1} K_{10} K_{14}^{2} \left( {K_{0} + K_{1} } \right) + 2K_{0}^{2} K_{1} K_{11} K_{14} - K_{0}^{2} K_{14}^{2} \left( {K_{0} + K_{1} } \right)\left( {9K_{7} - K_{8} } \right) + 2K_{0}^{3} K_{11} K_{14} }}{{K_{2}^{2} \left( {K_{0} K_{10} + 9K_{7} - K_{8} } \right)}}} \right. \\ & \;\; - \frac{{4K_{0}^{3} K_{9} K_{14} K_{16} \left( {K_{7} - K_{8} } \right) - 8\beta K_{0}^{3} K_{9}^{2} + \beta K_{0}^{3} K_{9} }}{{2K_{2}^{2} \left( {K_{7} - K_{8} } \right)^{2} }} \\ & \;\;\left. { - \frac{{\beta K_{0}^{3} K_{10} K_{14} K_{16} \left( {K_{0} + K_{1} } \right) + 2\beta K_{0}^{3} K_{11} }}{{K_{2}^{2} \left( {K_{0} K_{10} + 9K_{7} - K_{8} } \right)\left( {K_{7} - K_{8} } \right)}}} \right) \epsilon ^{ - 5/4} , \\ \end{aligned}$$

(48)

$$\phi^{(0)} = \frac{{{\mathcal{P}}_{s} \vartheta_{3} }}{2},$$

(49)

$$\phi^{(2)} = - \left[ {\frac{{\left( {\overline{\tau } \vartheta_{3} - 1} \right)\beta mn}}{4}} \right] \epsilon ^{{\frac{3}{4}}} ,$$

(50)

$$\phi^{(4)} = \left[ {\left( {\frac{{\left( {\overline{\tau }\vartheta_{3} - 1} \right)\beta mn}}{2}} \right)\left( {\left( {\frac{{K_{0} K_{14} + 4K_{5} }}{{4\left( {K_{0} - K_{4} } \right)}}} \right)^{2} + \left( {\frac{{K_{13} }}{{K_{0} K_{12} + 4\left( {K_{7} - K_{8} } \right)}}} \right)^{2} } \right)} \right] \epsilon ^{11/4} ,$$

(51)

where $K_{i} (i = 0, \ldots ,16)$ are the parameters in terms of $\vartheta_{1} ,\vartheta_{2} ,\vartheta_{3} , \vartheta_{4} , \vartheta_{5} ,m, n, \beta$ obtained via the sets of perturbation equations.

$${\mathcal{S}}_{1} = \frac{{K_{0} }}{{K_{2} }} \epsilon ^{ - 1} - \left( {\frac{{\overline{\tau }\vartheta_{2} m^{2} + \beta^{2} n^{2} \left( {1 - 2\overline{\tau }\vartheta_{1} } \right)}}{{4\left( {1 - 2\overline{\tau }\vartheta_{1} } \right)}}} \right) \epsilon ,$$

(52)

$${\mathcal{S}}_{2} = - \left( {\frac{{2\overline{\tau }\left( {\vartheta_{1} - \vartheta_{2} } \right)}}{{\beta^{2} \left( {1 - 2\overline{\tau }\vartheta_{1} } \right)}}} \right) \epsilon ^{ - 1} .$$

(53)