1 Introduction

Because of intrinsic elecromechanical coupling characteristics, piezoelectric materials have been widely used in various nanostructures such as gallium nitride nanoscaled wires (Tanner et al. 2007) and aluminum nitride nanofilms (Karabalin et al. 2009; Sinha et al. 2009) as good choices to design nanootransducers, nanoelectromechanical switches and energy harvesters. In such applications, size effects play a substantial role in the mechanical behavior, so in order to have a proper design for smart nanosystems, it is vital to consider these small scale effects.

On the other hand, due to the lack of generality of the classical continuum theory to characterize the size dependency in mechanical response of nanostructures, several higher-order continuum elasticity theories have been proposed and utilized during the past decade, for instances, modified couple stress elasticity theory (Mindlin and Tiersten 1962; Mindlin 1963), strain gradient elasticity theory (Aifantis 1999; Lam et al. 2003), surface elasticity theory (Gurtin and Murdoch 1975, 1978) and nonlocal elasticity theory (Eringen 1972). Among this variety of non-classical theories, the nonlocal elasticity theory is the most commonly successful applied one. In accordance with this nonconventional elasticity theory, it is supposed that the stress tensor at a reference point of body is related not only to strain components of that position, but also to all other points in the continuum. Based on the nonlocal continuum elasticity, the size-dependent behavior of various nanostructures has been extensively studied.

On the basis of nonlocal Euler–Bernoulli and Timoshenko beam models, Wang and Liew (2007) presented explicit solutions for scale effect on the static deformation of nanorods and nanotubes. Hu et al. (2008) focused on the influence of carbon nanotube (CNT) microstructure on the elastic transverse wave dispersion of single- and double-walled CNTs using a nonlocal shell model. Liu et al. (2008) introduced a novel model based on nonlocal Timoshenko beam model to analyze delaminating buckling occurred in microwedge indentation experiment. Ansari et al. (2010) proposed a nonlocal late model to calculate the natural frequencies of single-layered graphene sheets, the results of which are compared with those of molecular dynamics simulations. Aydogdu (2009) developed a generalized nonlocal beam model to predict different mechanical characteristics of beams at nanoscale corresponding to various types of the classical beam theories. Yan et al. (2010) examined the nonlocal size effect on the static bending behavior of triple-walled CNTs including initial stress and subjected to temperature field. Hao et al. (2010) used a nonlocal multiple-shell model to obtain the critical shear force of multi-walled CNTs under torsional load in the presence of thermal environments and elastic foundation. Ansari et al. (2011) applied nonlocal continuum elasticity within the framework of the Donnell shell theory to predict the axial buckling response of single-walled CNTs including temperature changes. Şimşek (2011) studied analytically the forced vibration of two CNTs connected elliptically with each other on the basis of nonlocal continuum theory. Ansari and Sahmani (2012) investigated the free vibrational response of single-walled CNTs on the basis of various types of nonlocal beam models and then extracted the proper value of nonlocal parameter via molecular dynamics simulation. Wang and Wang (2013) developed a nonlocal Timoshenko beam model to study the vibration of embedded nanotubes including stress and strain gradients. Potapov (2013) described size-dependent oscillations of a nanobeam under stochastic load using nonlocal Euler–Bernoulli beam model. Wang and Li (2014) obtained the amplitude-frequency response of a nanobeam under nonlinear primary resonance including nonlocality effect. Peng et al. (2015) studied the nonlocality scale effect on the buckling characteristics of bilayer composite plates under non-uniform axial compression. Yan et al. (2015) derived exact asymptotic solutions for bending deflection of nanobeams and nanoplates through applying nonlocal continuum theory. Li and Hu (2016) proposed nonlocal strain gradient beam models corresponding to the frameworks of Euler–Bernoulli and Timoshenko beam theories to determine the nonlinear bending deflection and nonlinear natural frequencies of nanoscaled beams.

Lately, some investigations have been carried out to apply nonlocal elasticity theory in prediction of size-dependent mechanical behavior of piezoelectric nanostructures. For instance, Asemi et al. (2014) implement nonlocal continuum theory to examine nonlinear vibration of piezoelectric nanoresonators subjected to electric voltage. Li et al. (2015) provided the nonlinear frequencies of grapheme/piezoelectric laminated sheets subjected to electric field in the presence of nonlocal effect.

Li and Wang (2016) reported the nonlocality influence in sensing moving force related to the nonlinear dynamic characteristics of grapheme/piezoelectric sandwich films. Arefi (2016) presented a nonlocal solution for wave propagation in functionally graded piezoelectric nanorods.

The main objective of the present study is to focus on size dependency in the large deflection and postbuckling response of piezoelectric nanoshells under axial compression combined with external lateral electric field and thermal environments. The basic equations of nonlocal piezoelectricity are firstly proposed within the framework of the first-order shear deformation shell theory and von Karman nonlinear strain–displacement kinematics. Then the nonlinear size-dependent governing equations are deduced to boundary layer-type ones and solved with the aid of a perturbation-based solution methodology to derive explicit asymptotic solutions for thermo-electro-mechanical postbuckling response of piezoelectric nanoshells.

2 Theoretical formulations of nonlocal piezoelectric shell model

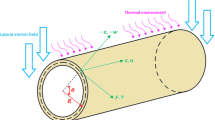
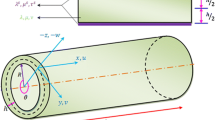
The schematic representation of a piezoelectric nanoshell with associated Cartesian coordinate system and in thermal environment is shown in Fig. 1 with length \( L \), radius \( R \) and thickness \( h \). As it can be seen, the location of the origin of coordinate system is chosen at the left end of nanoshell and on middle plane. Within the framework of the first-order shear deformation shell theory in conjunction with von Karman geometrical nonlinearity, the strain–displacement relations for an imperfect nanoshell can be defined as

$$ \begin{aligned} & \varepsilon_{xx} = \varepsilon_{xx}^{0} + z\kappa_{xx} + \varepsilon_{xx}^{E} + \varepsilon_{xx}^{T} , \quad \varepsilon_{yy} = \varepsilon_{yy}^{0} + z\kappa_{yy} + \varepsilon_{yy}^{E} + \varepsilon_{yy}^{T} , \quad \gamma_{xy} = \gamma_{xy}^{0} + z\kappa_{xy} \hfill \\ & \gamma_{xz} = \psi_{x} + w_{,x} , \quad \gamma_{yz} = \psi_{y} + w_{,y} , \hfill \\ \end{aligned} $$
(1)

where the subscripts following a comma represent differentiations. Also, the strain components in mid-plane (\( \varepsilon_{ij}^{0} ; i,j = x,y) \) and curvature components (\( \kappa_{ij} ; i,j = x,y \)) are as follows

$$ \begin{aligned} &\varepsilon_{xx}^{0} = u_{,x} + \frac{1}{2}\left( {w_{,x} } \right)^{2} + w_{,x} w_{,x}^{*} , \quad \varepsilon_{yy}^{0} = v_{,y} - \frac{{w + w^{*} }}{R} + \frac{1}{2}\left( {w_{,y} } \right)^{2} + w_{,w} w_{,x}^{*} \hfill \\ &\gamma_{xy}^{0} = u_{,y} + v_{,x} + w_{,x} w_{,y} + w_{,x} w_{,y}^{*} + w_{,y} w_{,x}^{*} , \kappa_{xx} = \psi_{x,x} \hfill \\ & \kappa_{yy} = \psi_{y,y} , \quad \kappa_{xy} = \psi_{x,y} + \psi_{y,x} , \hfill \\ \end{aligned} $$
(2)

in which \( u \), \( v \) and \( w \) are the displacement components in mid-plane in order along \( x, y \) and \( z \) axis, \( \psi_{x} \) and \( \psi_{y} \) are the rotations of the mid-plane normal about the \( y \)- and \( x \)-axis, respectively. Also \( w^{*} \) stands for the initial geometric imperfection. Additionally, the electrical strain components (\( \varepsilon_{ii}^{E} ; i = x,y) \) and thermal strain components (\( \varepsilon_{ii}^{T} ; i = x,y) \) can be given as

$$ \varepsilon_{xx}^{E} = \frac{{d_{31} {\mathcal{V}}}}{h} , \quad \varepsilon_{yy}^{E} = \frac{{d_{32} {\mathcal{V}}}}{h}, \quad \varepsilon_{xx}^{T} = \varepsilon_{yy}^{T} = \alpha \Delta T, $$
(3)

where \( d_{31} , d_{32} \) denote piezoelectric constants, \( {\mathcal{V}} = E_{z} h \) is the value of voltage related to the applied lateral electric field, \( \alpha \) is thermal expansion coefficient, and \( \Delta T \) represents the temperature change.

Fig. 1
figure 1

Schematic representation of thermo-electro-mechanical excited piezoelectric nanoshell

Full size image

In contrast to the local (classical) continuum theory, in the nonlocal continuum elasticity, the stress at a reference point is dependent on the strain components of all other point of the continuum in addition to that of the reference point. Thereby, the nonlocal constitutive relations of a piezoelectric nanoshell are in the forms as

$$ \left( {1 - e_{0}^{2} \theta^{2} \nabla^{2} } \right)\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ {\sigma_{xz} } \\ {\sigma_{yz} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{21} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{33} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{55} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{33} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{55} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{{\mathcal{V}}}{h}} & 0 \\ 0 & {\frac{{\mathcal{V}}}{h}} \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d_{31} } \\ {d_{32} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{33} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{55} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\alpha \Delta T} \\ {\alpha \Delta T} \\ \end{array} } \right\}, $$
(4)

where \( e_{0} \theta \) denotes the nonlocal parameter in such a way that \( \theta \) is an internal characteristic constant and \( e_{0} \) is a constant related to the selected material. Also, \( \nabla^{2} \) represents the Laplacian operator. The elastic constants can be introduced as below

$$ Q_{11} = Q_{22} = \lambda + 2\mu , \quad Q_{12} = Q_{21} = \lambda ,\quad Q_{33} = Q_{44} = Q_{55} = \mu , $$
(5)

in which \( \lambda = E\nu /\left( {\left( {1 - \nu } \right)(1 + 2\nu )} \right) \), \( \mu = E/\left( {2\left( {1 + \nu } \right)} \right) \) represents Lame’s constants.

By employing the principle of minimum potential energy of system, the nonlinear governing equations for piezoelectric nanoshell are constructed as

$$ N_{xx,x} + N_{xy,y} = 0 , $$
(6a)
$$ N_{xy,x} + N_{yy,y} = 0, $$
(6b)
$$ Q_{x,x} + Q_{y,y} + \frac{{N_{yy} }}{R} + N_{xx} \left( {w_{,xx} + w_{,xx}^{*} } \right) + 2N_{xy} \left( {w_{,xy} + w_{,xy}^{*} } \right) + \mathop {\overline{N} }\limits^{{}}_{yy} \left( {w_{,yy} + w_{,yy}^{*} } \right), $$
(6c)
$$ M_{xx,x} + M_{xy,y} - Q_{x} = 0 , $$
(6d)
$$ M_{xy,x} + M_{yy,y} - Q_{y} = 0 , $$
(6e)

where the nonlocal resultants can be expressed as

$$ \left( {1 - e_{0}^{2} \theta^{2} \nabla^{2} } \right)\left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{yy} } \\ {N_{xy} } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right\}dz = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 \\ {A_{21} } & {A_{22} } & 0 \\ 0 & 0 & {A_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{0} } \\ {\varepsilon_{yy}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 \\ {A_{21} } & {A_{22} } & 0 \\ 0 & 0 & {A_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{E} } \\ {\varepsilon_{yy}^{E} } \\ 0 \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 \\ {A_{21} } & {A_{22} } & 0 \\ 0 & 0 & {A_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{T} } \\ {\varepsilon_{yy}^{T} } \\ 0 \\ \end{array} } \right\}, $$
(7a)
$$ \left( {1 - e_{0}^{2} \theta^{2} \nabla^{2} } \right)\left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{yy} } \\ {M_{xy} } \\ \end{array} } \right\} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right\}zdz = \left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & 0 \\ {D_{21} } & {D_{22} } & 0 \\ 0 & 0 & {D_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\kappa_{xx} } \\ {\kappa_{yy} } \\ {\kappa_{xy} } \\ \end{array} } \right\}, $$
(7b)
$$ \left( {1 - e_{0}^{2} \theta^{2} \nabla^{2} } \right)\left\{ {\begin{array}{*{20}c} {Q_{x} } \\ {Q_{y} } \\ \end{array} } \right\} = k_{s} \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xz} } \\ {\sigma_{yz} } \\ \end{array} } \right\}dz = \left[ {\begin{array}{*{20}c} {A_{44} } & 0 \\ 0 & {A_{55} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\}, $$
(7c)

in which \( A_{ij} \) and \( D_{ij} \) in order are stretching stiffness components and bending stiffness components as below

$$ \begin{aligned} & A_{11} = A_{22} = \left( {\lambda + 2\mu } \right)h, A_{12} = A_{21} = \lambda h, A_{33} = \mu h, A_{44} = A_{55} = k_{s} \mu h \hfill \\ & D_{11} = D_{22} = \frac{{\left( {\lambda + 2\mu } \right)h^{3} }}{12}, D_{12} = D_{21} = \frac{{\lambda h^{3} }}{12}, D_{33} = \frac{{\mu h^{3} }}{12}. \hfill \\ \end{aligned} $$
(8)

Moreover, \( k_{s} \) stands for the shear correction factor (Chroscielewski et al. 2010).

Through definition of Airy stress function \( f\left( {x,y} \right) \) as below, the two first governing Eqs. (6a) and (6b) can be satisfied completely:

$$ N_{xx} = f_{,yy} , N_{yy} = f_{,xx} , N_{xy} = - f_{,xy} . $$
(9)

Furthermore, for an imperfect nanoshell, the compatibility relation corresponding to the mid-plane strain components can be rewritten as

$$ \varepsilon_{xx,yy}^{0} + \varepsilon_{yy,xx}^{0} - \gamma_{xy,xy}^{0} = \left( {w_{,xy} } \right)^{2} - w_{,xx} w_{,yy} + 2w_{,xy} w_{,xy}^{*} - w_{,xx} w_{,yy}^{*} - w_{,yy} w_{,xx}^{*} - \frac{1}{R}w_{,xx} . $$
(10)

Now, by substituting Eq. (9) in the inverse of Eqs. (7) and using Eqs. (6) and (10), the governing differential equations related to nonlocal thermo-electro-mechanic exciting behavior can be extracted as

$$ - D_{11} \psi_{x,xxx} - \left( {D_{12} + 2D_{33} } \right)\psi_{x,xyy} - D_{11} \psi_{y,yyy} - \left( {D_{12} + 2D_{33} } \right)\psi_{y,xxy} - \frac{1}{R}f_{,xx} = \left( {1 - e_{0}^{2} \theta^{2} \nabla^{2} } \right)\left( {\left( {w_{,xx} + w_{,xx}^{*} } \right)f_{,yy} - 2\left( {w_{,xy} + w_{,xy}^{*} } \right)f_{,xy} + \left( {w_{,yy} + w_{,yy}^{*} } \right)f_{,xx} } \right), $$
(11a)
$$ \left( {\frac{{A_{11} }}{{\left( {A_{11} } \right)^{2} - \left( {A_{12} } \right)^{2} }}} \right)f_{,xxxx} + \left( {\frac{1}{{A_{33} }} - \frac{{2A_{12} }}{{\left( {A_{11} } \right)^{2} - \left( {A_{12} } \right)^{2} }}} \right)f_{,xxyy} + \left( {\frac{{A_{11} }}{{\left( {A_{11} } \right)^{2} - \left( {A_{12} } \right)^{2} }}} \right)f_{,yyyy} + \frac{1}{R}w_{,xx} = \left( {w_{,xy} + w_{,xy}^{*} } \right)^{2} - \left( {w_{,xx} + w_{,xx}^{*} } \right)\left( {w_{,yy} + w_{,yy}^{*} } \right) , $$
(11b)
$$ D_{11} \psi_{x,xx} + D_{55} \psi_{x,yy} - A_{44} \left( {\psi_{x} + w_{,x} } \right) + \left( {D_{12} + D_{55} } \right)\psi_{y,xy} = 0, $$
(11c)
$$ D_{11} \psi_{y,yy} + D_{55} \psi_{y,xx} - A_{44} \left( {\psi_{y} + w_{,y} } \right) + \left( {D_{12} + D_{55} } \right)\psi_{x,xy} = 0. $$
(11d)

Regarding the boundary conditions at the left and right ends of piezoelectric nanoshells, the clamped edge supports are considered based on which: \( w = 0 , w_{,x} = 0 \)

Also, the equilibrium satisfaction for loading conditions along \( x \)-axis yields

$$ \mathop \int \limits_{0}^{2\pi R} N_{xx} dy + 2\pi Rh\sigma_{xx} = 0. $$
(12)

For a closed shell-type structure, the periodicity condition results in

$$ \mathop \int \limits_{0}^{2\pi R} v_{,y} dy = 0, $$
(13)

which can be summarized in the following form

$$ \mathop \int \limits_{0}^{2\pi R} \left\{ { - \left( {\frac{{A_{12} }}{{\left( {A_{11} } \right)^{2} - \left( {A_{12} } \right)^{2} }}} \right)f_{,yy} + \left( {\frac{{A_{11} }}{{\left( {A_{11} } \right)^{2} - \left( {A_{12} } \right)^{2} }}} \right)f_{,xx} + \frac{{w + w^{*} }}{R} - \frac{1}{2}\left( {w_{,y} + w_{,y}^{*} } \right)^{2} - w_{,y} w_{,y}^{*} - \frac{{d_{32} {\mathcal{V}}}}{h} - \alpha \Delta T} \right\}dy = 0. $$
(14)

Moreover, the unit shortening associated to the movable ends of thermo-electro-mechanical excited piezoelectric nanoshell can be evaluated by

$$ \frac{{\Delta_{x} }}{L} = - \frac{1}{2\pi RL}\mathop \int \limits_{0}^{2\pi R} \mathop \int \limits_{0}^{L} u_{,x} dxdy = - \frac{1}{2\pi RL}\mathop \int \limits_{0}^{2\pi R} \mathop \int \limits_{0}^{L} \left\{ { - \left( {\frac{{A_{12} }}{{\left( {A_{11} } \right)^{2} - \left( {A_{12} } \right)^{2} }}} \right)f_{,xx} + \left( {\frac{{A_{11} }}{{\left( {A_{11} } \right)^{2} - \left( {A_{12} } \right)^{2} }}} \right)f_{,yy} - \frac{1}{2}\left( {w_{,x} + w_{,x}^{*} } \right)^{2} - w_{,x} w_{,x}^{*} - \frac{{d_{31} {\mathcal{V}}}}{h} - \alpha \Delta T} \right\}dxdy. $$
(15)

3 Solving process for asymptotic solutions

3.1 Boundary layer theory of nonlocal shell buckling

In order to solve the problem in a more general framework, the following dimensionless parameters are supposed

$$ \begin{aligned} & X = \frac{\pi x}{L}, \quad Y = \frac{y}{R}, \quad \beta = \frac{L}{\pi R}, \quad \epsilon = \frac{{\pi^{2} Rh}}{{L^{2} }} \hfill \\ & \left\{ {a_{11}^{*} ,a_{12}^{*} ,a_{33}^{*} ,a_{44}^{*} ,a_{55}^{*} } \right\} = \left\{ {\frac{{A_{11} }}{{A_{110} }},\frac{{A_{12} }}{{A_{110} }},\frac{{A_{33} }}{{A_{110} }}, \frac{{A_{44} }}{{A_{110} }},\frac{{A_{55} }}{{A_{110} }}} \right\} \hfill \\ & \left\{ {d_{11}^{*} ,d_{12}^{*} ,d_{33}^{*} } \right\} = \left\{ {\frac{{D_{11} }}{{A_{110} h^{2} }},\frac{{D_{12} }}{{A_{110} h^{2} }},\frac{{D_{33} }}{{A_{110} h^{2} }}} \right\} \hfill \\ & \left\{ {W,W^{*} } \right\} = \frac{\epsilon }{h}\left\{ {w,w^{*} } \right\} , F = \frac{{\epsilon^{2} f}}{{A_{110} h^{2} }} , \quad \left\{ {\varPsi_{X} , \quad \varPsi_{Y} } \right\} = \frac{{\epsilon^{2} L}}{\pi h}\left\{ {\psi_{x} , \psi_{y} } \right\} \hfill \\ & {\mathcal{P}}_{x} = \frac{{\sigma_{xx} R}}{{2A_{110} }} , \delta_{x} = \frac{{\Delta_{x} R}}{2Lh}\text{ },{ \mathcal{G}} = \frac{{e_{0} \theta }}{L}, \hfill \\ \end{aligned} $$
(16)

in which \( A_{110} = \left( {\lambda + 2\mu } \right)h \). Now, by introducing the derivative operators as presented in Appendix A, the dimensionless form of the nonlocal nonlinear governing differential equations can be rewritten as

$$ - d_{11}^{*} \epsilon \varPsi_{X,XXX} - \left( {d_{12}^{*} + 2d_{33}^{*} } \right)\beta^{2} \epsilon \varPsi_{X,XYY} - d_{11}^{*} \beta^{3} \epsilon \varPsi_{Y,YYY} - \left( {d_{12}^{*} + 2d_{33}^{*} } \right)\beta \epsilon \varPsi_{Y,XXY} - F_{,XX} = \left( {1 - \pi^{2} {\mathcal{G}}^{2} \nabla^{2} } \right)\beta^{2} \left( {\left( {W_{,XX} + W_{,XX}^{*} } \right)F_{,YY} - 2\left( {W_{,XY} + W_{,XY}^{*} } \right)F_{,XY} + \left( {W_{,YY} + W_{,YY}^{*} } \right)F_{,XX} } \right), $$
(17a)
$$ \begin{aligned} & \left( {\frac{{a_{11}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }}} \right)F_{,XXXX} + \left( {\frac{1}{{a_{33}^{*} }} - \frac{{2a_{12}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }}} \right)\beta^{2} F_{,XXYY} + \left( {\frac{{a_{11}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }}} \right)\beta^{4} F_{,YYYY} \\ & \quad + W_{,XX} = \beta^{2} \left( {W_{,XY} + W_{,XY}^{*} } \right)^{2} - \left( {W_{,XX} + W_{,XX}^{*} } \right)\left( {W_{,YY} + W_{,YY}^{*} } \right), \end{aligned} $$
(17b)
$$ d_{11}^{*} \varPsi_{X,XX} + d_{33}^{*} \beta^{2} \varPsi_{X,YY} - a_{44}^{*} \left( {\varPsi_{X} + \epsilon W_{,X} } \right) + \left( {d_{12}^{*} + d_{33}^{*} } \right)\beta \varPsi_{Y,XY} = 0, $$
(17c)
$$ d_{11}^{*} \beta^{2} \varPsi_{Y,YY} + d_{55}^{*} \varPsi_{Y,XX} - a_{44}^{*} \left( {\varPsi_{Y} + \beta \epsilon W_{,Y} } \right) + \left( {d_{12}^{*} + d_{33}^{*} } \right)\beta \varPsi_{X.XY} = 0 . $$
(17d)

Additionally, the dimensionless form of the clamped boundary conditions at the left (\( X = 0 \)) and right (\( X = \pi \)) ends of the piezoelectric nanoshell can be given as \( W = 0, W_{,X} = 0 \).

Also, the boundary layer-type equilibrium requirement for axially loading condition can be expressed as

$$ \frac{1}{2\pi }\mathop \int \limits_{0}^{2\pi } \beta^{2} F_{,YY} dY + 2\epsilon {\mathcal{P}}_{x} = 0. $$
(18)

The dimensionless periodicity condition takes the form as

$$ \mathop \int \limits_{0}^{2\pi R} \left\{ { - \left( {\frac{{a_{12}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }}} \right)\beta^{2} F_{,YY} + \left( {\frac{{a_{11}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }}} \right)F_{,XX} + W + W^{*} - \frac{{\beta^{2} }}{2}\left( {W_{,Y} + W_{,Y}^{*} } \right)^{2} - \beta^{2} W_{,Y} W_{,Y}^{*} - \left( {\frac{{d_{32} R{\mathcal{V}}}}{{h^{2} }} + \frac{\alpha R\Delta T}{h}} \right)\epsilon } \right\}dY = 0 $$
(19)

In addition, the unit shortening of thermo-electro-mechanical excited piezoelectric nanoshell in dimensionless form can be introduced as

$$ \delta_{x} = - \frac{1}{{4\pi^{2} \varepsilon }}\mathop \int \limits_{0}^{2\pi } \mathop \int \limits_{0}^{\pi } \left\{ {\left( {\frac{{a_{11}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }}} \right)\beta^{2} F_{,YY} - \left( {\frac{{a_{12}^{*} }}{{\left( {a_{11}^{*} } \right)^{2} - \left( {a_{12}^{*} } \right)^{2} }}} \right)F_{,XX} - \frac{1}{2}\left( {W_{,X} + W_{,X}^{*} } \right)^{2} - W_{,X} W_{,X}^{*} - \left( {\frac{{d_{31} R{\mathcal{V}}}}{{h^{2} }} + \frac{\alpha R\Delta T}{h}} \right)\varepsilon } \right\}dXdY $$
(20)

3.2 Perturbation-based solution methodology

In the preceding subsection, through definition of \( \epsilon \) namely the small perturbation parameter, the nonlocal governing differential Eqs. (17) were constructed in the form of boundary layer. At this step of the solving process, using the singular perturbation technique (Shen 1998, 2001, 2008; Shen and Li 2002; Sahmani et al. 2016a, b), the independent variables are considered as the summations of the regular and boundary layer solutions as below

$$ W = \mathop {\bar{W}}\limits^{{}} \left( {X,Y,\epsilon } \right) + \mathop {\tilde{W}}\limits^{{}} \left( {X,Y,\epsilon ,\xi } \right) + \mathop {\hat{W}}\limits^{{}} \left( {X,Y,\epsilon ,\varsigma } \right), $$
(21a)
$$ F = \mathop {\bar{F}}\limits^{{}} \left( {X,Y,\epsilon } \right) + \mathop {\tilde{F}}\limits^{{}} \left( {X,Y,\epsilon ,\xi } \right) + \mathop {\hat{F}}\limits^{{}} \left( {X,Y,\epsilon ,\varsigma } \right), $$
(21b)
$$ \varPsi_{X} = \mathop {\bar{\varPsi }}\limits^{{}}_{X} \left( {X,Y,\epsilon } \right) + \mathop {\tilde{\varPsi }}\limits^{{}}_{X} \left( {X,Y,\epsilon ,\xi } \right) + \mathop {\hat{\varPsi }}\limits^{{}}_{X} \left( {X,Y,\epsilon ,\varsigma } \right), $$
(21c)
$$ \varPsi_{Y} = \mathop {\overline{\varPsi } }\limits^{{}}_{Y} \left( {X,Y,\epsilon } \right) + \mathop {\tilde{\varPsi }}\limits^{{}}_{Y} \left( {X,Y,\epsilon ,\xi } \right) + \mathop {\hat{\varPsi }}\limits^{{}}_{Y} \left( {X,Y,\epsilon ,\varsigma } \right), $$
(21d)

where the accent character ˉ represents the regular solution, and the accent characters ~ and ^ denote the boundary layer solutions associated with the left (\( X = 0 \)) and right (\( X = \pi \)) ends of piezoelectric nanoshell, respectively.

Now, each part of the solutions can be altered to the perturbation expansions in the following forms

$$ \begin{aligned} \mathop {\bar{W}}\limits^{{}} \left( {X,Y,\epsilon } \right) &= \mathop \sum \limits_{i = 0} \epsilon^{i/2} \bar{W}_{i/2} (X,Y) , \mathop {\bar{F}}\limits^{{}} \left( {X,Y,\epsilon } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2} \bar{F}_{i/2} \left( {X,Y} \right) \hfill \\ \mathop {\bar{\varPsi }}\nolimits^{{}}_{x} \left( {X,Y,\epsilon } \right) &= \mathop \sum \limits_{i = 1} \epsilon^{i/2} \bar{\varPsi }_{xi/2} \left( {X,Y} \right) , \bar{\varPsi }_{y} \left( {X,Y,\epsilon } \right) = \mathop \sum \limits_{i = 1} \epsilon^{i/2} \bar{\varPsi }_{yi/2} \left( {X,Y} \right) \hfill \\ \mathop {\tilde{W}}\limits^{{}} \left( {X,Y,\epsilon ,\xi } \right) &= \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 1} \tilde{W}_{i/2 + 1} \left( {X,Y,\xi } \right)\varvec{ },\varvec{ }\mathop {\tilde{F}}\limits^{{}} \left( {X,Y,\epsilon ,\xi } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 2} \tilde{F}_{i/2 + 2} \left( {X,Y,\xi } \right) \hfill \\ \mathop {\tilde{\varPsi }}\nolimits^{{}}_{x} \left( {X,Y,\epsilon ,\xi } \right) &= \mathop \sum \limits_{i = 0} \epsilon^{i + 3/2} \tilde{\varPsi }_{xi + 3/2} \left( {X,Y,\xi } \right)\varvec{ },\varvec{ }\tilde{\varPsi }_{y} \left( {X,Y,\epsilon ,\xi } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 2} \tilde{\varPsi }_{yi/2 + 2} \left( {X,Y,\xi } \right) \hfill \\ \mathop {\hat{W}}\limits^{{}} \left( {X,Y,\epsilon ,\varsigma } \right) &= \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 1} \hat{W}_{i/2 + 1} (X,Y,\varsigma ), \mathop {\hat{F}}\limits^{{}} \left( {X,Y,\epsilon ,\varsigma } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 2} \hat{F}_{i/2 + 2} (X,Y,\varsigma ) \hfill \\ \mathop {\hat{\varPsi }}\nolimits^{{}}_{x} \left( {X,Y,\epsilon ,\varsigma } \right) & = \mathop \sum \limits_{i = 0} \epsilon^{i + 3/2} \hat{\varPsi }_{xi + 3/2} (X,Y,\varsigma ) , \hat{\varPsi }_{y} \left( {X,Y,\epsilon ,\varsigma } \right) = \mathop \sum \limits_{i = 0} \epsilon^{i/2 + 2} \hat{\varPsi }_{yi/2 + 2} (X,Y,\varsigma ), \hfill \\ \end{aligned} $$
(22)

where \( \xi \) and \( \varsigma \) represent the boundary layer variables in the following forms

$$ \xi = \frac{X}{\sqrt \epsilon } , \quad \varsigma = \frac{\pi - X}{\sqrt \epsilon }. $$
(23)

Thereafter, by substituting Eqs. (21) and (22) into the nonlocal governing differential Eqs. (17) and then collecting the expressions having the similar order of \( \varepsilon \), the sets of perturbation equations can be extracted for the both regular and boundary layer solutions. This procedure resumes until a maximum order of \( \varepsilon \) corresponding to which the convergence of the solving process is confirmed. For this purpose, a tolerance limit <\( 0.001 \) is supposed and it is indicated that the tolerance limit is achieved up to the forth-order of the small perturbation parameter.

To continue the solution methodology, it needs to define the initial buckling mode shape in conjunction with the initial geometric imperfection for the imperfect piezoelectric nanoshell as follows

$$ \mathop {\bar{W}}\limits^{{}}_{2} \left( {X,Y} \right) = {\mathcal{A}}_{00}^{\left( 2 \right)} + {\mathcal{A}}_{11}^{\left( 2 \right)} \sin \left( {mX} \right)\sin \left( {nY} \right) + {\mathcal{A}}_{02}^{\left( 2 \right)} \cos \left( {2nY} \right), $$
(24)
$$ W^{*} \left( {X,Y,\epsilon } \right) = \varepsilon^{2} {\mathcal{A}}_{11}^{*} \sin \left( {mX} \right)\cos \left( {nY} \right) = \epsilon^{2} \ell {\mathcal{A}}_{11}^{(2)} \sin \left( {mX} \right)\cos \left( {nY} \right), $$
(25)

in which \( \ell \) stands for the imperfection parameter.

Afterwards, through performing some mathematical calculations, the asymptotic solutions can be extracted relevant to each independent variable as given in Appendix A. by inserting them in Eqs. (18) and (20) and rearranging them in accordance with the order of the second perturbation parameter (\( {\mathcal{A}}_{11}^{(2)} \epsilon \)), the explicit expressions for the nonlocal load–deflection and nonlocal load-shortening equilibrium curves are obtained, respectively, as below

$$ {\mathcal{P}}_{x} = \mathop \sum \limits_{i = 0,2,4, \ldots } {\mathcal{P}}_{x}^{\left( i \right)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon } \right)^{i} = {\mathcal{P}}_{x}^{\left( 0 \right)} + {\mathcal{P}}_{x}^{\left( 2 \right)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon } \right)^{2} + {\mathcal{P}}_{x}^{\left( 4 \right)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon } \right)^{4} + \cdots , $$
(26)
$$ \delta_{x} = \mathop \sum \limits_{i = 0,2,4, \ldots } \delta_{x}^{(i)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon } \right)^{i} + \delta_{x}^{T} + \delta_{x}^{E} = \delta_{x}^{(0)} + \delta_{x}^{T} + \delta_{x}^{E} + \delta_{x}^{(2)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon } \right)^{2} + \delta_{x}^{(4)} \left( {{\mathcal{A}}_{11}^{\left( 2 \right)} \epsilon } \right)\varepsilon^{4} + \cdots . $$
(27)

The parameters presented in the above equations are defined in Appendix B. Now, it is supposed that the dimensionless coordinate of the point in which the maximum deflection occurs is in the form as \( \left( {X,Y} \right) = \left( {\pi /2m,\pi /2n} \right) \). So, it yields

$$ {\mathcal{A}}_{11}^{(2)} \epsilon = \frac{{w_{m} }}{h} + {\mathcal{S}}_{2} + {\mathcal{S}}_{1} \left( {\frac{{w_{m} }}{h} + {\mathcal{S}}_{2} } \right)^{2} , $$
(28)

where \( w_{m} \) is the maximum deflection. Also, the symbols \( {\mathcal{S}}_{1} \) and \( {\mathcal{S}}_{2} \) are defined in Appendix B.

4 Results and discussion

Selected numerical results for nonlocal instability of thermo-electro-mechanical excited piezoelectric nanoshell are given corresponding to various parameters. In the preceding presentation of results, the left and right ends of nanoshell is supposed to be clamped and \( R/h = 50 \), \( L = 2R \). The properties are tabulated in Table 1 relevant to PZT-5H piezoelectric material.

Table 1 Material properties of PZT-5H piezoelectric material (Huang and Yu 2006; Yan 2011)
Full size table

The mechanical excitation of piezoelectric nanoshell is demonstrated firstly as in Figs. 2 and 3, the local and nonlocal postbuckling load–deflection curves are displayed for perfect and imperfect piezoelectric nanoshells, respectively, and corresponding to different shell thicknesses. It is revealed that the nonlocality effect leads to decrease the critical axial load and the width of the postbuckling regime, but it increases the minimum load of the postbuckling domain. These anticipations are similar for the cases of in the presence and in the absence of the initial geometric imperfection. Additionally, it is indicated that an increment in the value of shell thickness causes to reduce the nonlocality influence.

Fig. 2
figure 2

Local and nonlocal load–deflection response of perfect piezoelectric nanoshells corresponding to different nonlocal parameters: a \( h = 1 \,{\text{nm}} \), b \( h = 2 \,{\text{nm}} \)

Full size image
Fig. 3
figure 3

Local and nonlocal load–deflection response of imperfect piezoelectric nanoshells corresponding to different nonlocal parameters: a \( h = 1 \;{\text{nm}} \), b \( h = 2\,{\text{nm}} \)

Full size image

Figures 4 and 5 illustrate the local and nonlocal load-shortening curves including the both prebuckling and postbuckling domains for piezoelectric nanoshells with various nonlocal parameters and shell thicknesses in order without and with initial geometric imperfection. The snap-through phenomenon is obvious for the both local and nonlocal models. It is seen that by increasing the value of nonlocal parameter, the gap between the classical and size-dependent shell models increases. Moreover, it can be observed that in addition to the critical buckling load, the critical shortening of nanoshell decreases due to the nonlocality effect.

Fig. 4
figure 4

Local and nonlocal load-shortening response of perfect piezoelectric nanoshells corresponding to different nonlocal parameters: a \( h = 1\, {\text{nm}} \), b \( h = 2 \,{\text{nm}} \)

Full size image
Fig. 5
figure 5

Local and nonlocal load-shortening response of imperfect piezoelectric nanoshells corresponding to different nonlocal parameters: a \( h = 1 \,{\text{nm}} \), b \( h = 2\, {\text{nm}} \)

Full size image

After that, the electro-mechanical response of piezoelectric nanoshell is investigated as in Fig. 6, the nonlinear local and nonlocal postbuckling load–deflection curves are shown for piezoelectric nanoshells subjected to various lateral electric fields. It is found that for the both local and nonlocal models with and without initial geometric imperfection, an electric field coming from a positive applied voltage leads to increase the axial stiffness of piezoelectric nanoshell in such a way that the critical load and width of postbuckling domain increase, but no considerable change occurs in the minimum load of the postbuckling regime. However, it can be seen that an electric field coming from a negative applied voltage leads to reduce the axial stiffness of piezoelectric nanoshell.

Fig. 6
figure 6

Electro-mechanical load–deflection response of piezoelectric nanoshells under various electric fields corresponding to local and nonlocal models: a \( W^{*} = 0 \), b \( W^{*} = 0.1 \)

Full size image

Depicted in Fig. 7 are the local and nonlocal electro-mechanical load-shortening behaviors of piezoelectric nanoshells including the both prebuckling and postbuckling domains corresponding to different external electric fields. It is observed that in the both local and nonlocal shell models, the lateral applied electric fields with positive and negative signs induce, respectively, initial contraction and expansion in the piezoelectric nanoshell which causes in order to increase and decrease the critical shortening relevant to electro-mechanical instability of piezoelectric nanoshell.

Fig. 7
figure 7

Electro-mechanical load-shortening response of piezoelectric nanoshells under various electric fields corresponding to local and nonlocal models: a \( W^{*} = 0 \), b \( W^{*} = 0.1 \)

Full size image

Finally, the thermo-mechanical excitation of piezoelectric nanoshell is studied as in Fig. 8, the nonlinear local and nonlocal postbuckling load–deflection curves are shown for piezoelectric nanoshells subjected to different thermal environments. It is revealed that for the both local and nonlocal models with and without initial geometric imperfection, a temperature increment reduces the buckling load of piezoelectric nanoshell, but a temperature reduction leads to increase it. However, in the both cases, the temperature change has a negligible influence on the value of minimum load of the postbuckling domain.

Fig. 8
figure 8

Thermo-mechanical load–deflection response of piezoelectric nanoshells under various thermal environments corresponding to local and nonlocal models: a \( W^{*} = 0 \), b \( W^{*} = 0.1 \)

Full size image

Figure 9 represents the local and nonlocal thermo-mechanical load-shortening behaviors of piezoelectric nanoshells including the both prebuckling and postbuckling domains corresponding to different thermal environments. It can be seen that in the both local and nonlocal shell models with and without consideration of initial imperfection, increment and reduction of temperature induce, respectively, initial expansion and contraction in the piezoelectric nanoshell which causes in order to decrease and increase the critical shortening relevant to thermo-mechanical instability of piezoelectric nanoshell.

Fig. 9
figure 9

Thermo-mechanical load-shortening response of piezoelectric nanoshells under various thermal environments corresponding to local and nonlocal models: a \( W^{*} = 0 \), b \( W^{*} = 0.1 \)

Full size image

5 Concluding remarks

The prime objective of the current work was to evaluate the nonlocality effect on the nonlinear instability of piezoelectric nanoshells under thermo-electro-mechanical excitation. To capture the size dependency, the nonlocal continuum elasticity theory was put to use within the framework of the first-order shear deformation shell theory. To simulate the large deflection relevant to the postbuckling response, von Karman kinematics nonlinearity was taken into consideration. With the aid of the boundary layer shell-buckling theory in conjunction with a perturbation-based solution methodology, explicit expressions for the nonlocal postbuckling equilibrium paths were constructed.

It was displayed that the nonlocality effect leads to decrease the critical axial load and the width of the postbuckling regime, but it increases the minimum load of the postbuckling domain. Additionally, it was shown that an increment in the value of shell thickness causes to reduce the nonlocality influence. Furthermore, it was seen that in addition to the critical buckling load, the critical shortening of nanoshell decreases due to the nonlocality effect. It was found that for the both local and nonlocal models with and without initial geometric imperfection, an electric field coming from a positive applied voltage leads to increase the axial stiffness of piezoelectric nanoshell in such a way that the critical load and width of postbuckling domain increase, but no considerable change occurs in the minimum load of the postbuckling regime. Also, it was indicated that in the both local and nonlocal shell models with and without consideration of initial imperfection, increment and reduction of temperature induce, respectively, initial expansion and contraction in the piezoelectric nanoshell which causes in order to decrease and increase the critical shortening relevant to thermo-mechanical instability of piezoelectric nanoshell.

6 Applications of piezoelectric nanostructures in micro- and nano-technology

Because of having the capability of converting mechanical deformation into electrical signal, the piezoelectric nanostructures have a wide range of application in micro-electromechanical systems (MEMSs) and nanotechnology. To mention some of these applications, the piezoelectric nanoscaled structures can be used as energy harvesting (Wang and Song 2006), sensing (Wang et al. 2006) and actuation (Pu et al. 2010), micro- and nanogenerator to convert the mechanical energy in our environments to wireless electric systems (Hudak and Amatucci 2008), and strain sensors to produce free-standing nanowires with high sensitivity (Wang 2010).

In order to use piezoelectric nanostructures in a more efficient way, it is essential to predict the size dependency in their mechanical characteristics. Therefore, the numerical results given in the current study may be useful in capturing the desirable efficiency for piezoelectric nanodevices and smart microsystems.