1 Introduction

Resonant micro-accelerometers inherit the properties of quasi-digital output and excellent performances in stability, resolution, and repeatability from the resonant sensing mechanism (Ashwin et al. 2002). Moreover, micromachining processes produce drastic reduction in size, weight, and cost of the accelerometer (Yu and Lan 2001; Eloy and Roussel 2002; Masako 2007; Chuang et al. 2010).

As the core component of the resonant micro-accelerometer, the resonator has a great influence on the performance of the sensor. Design and optimization of the resonator structure has become an important study of resonant micro-accelerometer. Working as the resonator, Double-Ended-Tuning Fork (DETF) with the advantages of simple structure and easy processing is widely used in the resonant micro-accelerometers (Hopkins et al. 2006; Lee et al. 2008). The structure of the DETF resonator is related to the whole structure of the accelerometer and the performances like scaling factor, resolution, and sensitivity (Kim et al. 2005; Su et al. 2006; Seok and Chun 2006; He et al. 2008). Therefore, the design and optimization of the structure of DETF resonator, particularly boundary structure and geometry parameters of DETF resonator, are very important.

In order to obtain better performance, selection of boundary structure of DETF resonator is based on high quality factor (Q value) (Beeby and Tudor 1995; Beeby et al. 2000; Hassanpour et al. 2007). For design and optimization of the DETF geometric parameters, the influence of different structure parameters on the performance should be clear, beside which, the specific adjustment of different geometric parameters can be done. Especially when all the performances can not be achieved optimal at the same time, the necessary trade-offs must be done according to the information of impact of each DETF geometric parameter on the particular performance. Therefore, it is very important to obtain the degree of influence of different structural parameters on different performances, and to obtain the most influential geometric parameter for each certain performance.

A systematic methodology incorporating the parametric uncertainty distribution to analyze the effects of the DETF geometric parameter is necessary. Shi et al. (2014) applied a sample-based stochastic model to investigate the influence of different parameters in design and optimization of an electro-thermal excited MEMS resonant sensor. Peng et al. (2013) applied a sample-based stochastic model to investigate the influence of different uncertain parameters on the solid–liquid–vapor phase change processes in order to find the key parameters that have the dominant effects. The effects of uncertainty in the optical fiber drawing process (Mawardi and Pitchumani 2008; Myers 1989) and in the nonisothermal flow during resin transfer molding (Padmanabhan and Pitchumani 1999) were also investigated with a sampling-based stochastic model. This method can be applied to the design and optimization of the geometric parameters of the DETE resonator to obtain the degree of influence of different geometric parameters on different performances.

In this paper, the theoretical vibration model of the DETF resonator in a micro-accelerometer is established and verified by finite element method to invest the boundary structure and geometry parameters of the DETF resonator. Uncertainty analysis incorporating the parametric uncertainty distribution is conducted by establishing the sample-based stochastic model to systematically investigate the influence of different geometry parameters of the DETF resonator on the natural frequency and the sensitivity of the DETF resonator for design and optimization of the DETF resonator of the micro-accelerometer.

2 Working principle of the resonant micro accelerometer

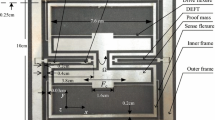
The resonant silicon micro accelerometer is based on the principle of resonance measurement to measure the acceleration. The schematic diagram of the measurement principle is shown in Fig. 1.

Fig. 1
figure 1

a schematic structure and b drive unit structure of resonant micro accelerometer

Full size image

The resonant micro accelerometer mainly comprises a mass block, a supporting beam, a resonator, a driving unit and a detection unit. In this paper, the primary sensitive structure of the resonant accelerometer is composed of the mass block and the supporting beams. When the measured acceleration is along the X axis, the primary sensitive structure transforms the acceleration into the inertial force along the X axis. The DETF resonator is the secondary sensitive structure, which is used to measure the inertial force. When there is an inertial force along the X axis, the natural frequency of the DETF resonator is changed. In order to realize differential measurement, the accelerometer uses two identical DETF resonators to feel the same amount of tension and pressure along the axial direction of the DETF beams, which can eliminate the common mode interference signal in signal processing. The drive unit drives the DETF resonator into vibration and maintains the resonant state. The vibration signal detected by the detection unit, and the closed-loop feedback control circuit controls the drive unit tracking the natural frequency of the DETF resonator. According to the vibration signal detected by the detection unit, the change of the natural frequency can be obtained, and then acceleration can be calculated.

The vibration characteristic of the DETF resonator can be expressed as a single freedom second order system. When there is no axial force, the natural frequency of the resonator is:

$$ \omega_{\text{n}} = \sqrt {k_{\text{eff}}/M_{\text{eff}}}, $$
(1)

where, \( k_{{\text{eff}}} \) is the equivalent stiffness of the DETF resonator without axial force, and \( M_{{\text{eff}}} \) is the equivalent mass of the DETF resonator. The mass block and the supporting beams together transform the acceleration into the inertial force. A part of the inertia force is consumed by the supporting beams of the mass block, and the other part acts on both DETF resonators in the axial direction.

3 Structure design of the DETF resonator

The structure of the DETF resonator is related to the whole structure of the accelerometer and the performances (scaling factor, resolution, and sensitivity). The DETF resonator mainly consists of two identical resonant beams, and the structure design of the DETF resonator focus on boundary structure and geometry parameters of the resonant beam. In order to obtain better performance, selection of the boundary structure of the DETF resonator is based on high quality factor (Q value) (Beeby and Tudor 1995; Beeby et al. 2000; Hassanpour et al. 2007).

In order to select the proper boundary condition and vibration model of the DETF resonators, the DETF resonator is taken as the object of study. Four kinds of DETF resonators with different boundary structures are shown in Fig. 2. Based on the comparison of the boundary structures, the DETF resonator with better performance is selected. And according to the selected boundary structure, four basic mode shapes of the DETF resonator are shown in Fig. 3. In Fig. 3, mode 1 and mode 3 are the in-phase vibration mode, mode 2 and mode 4 are the inverse vibration mode. Compared to mode 3 and mode 4, mode 1 and mode 2 are easily to be implemented from the aspects of the excitation methods and the detection method.

Fig. 2
figure 2

Four kinds of DETF resonators with different boundary structures

Full size image
Fig. 3
figure 3

Basic mode shapes of DETF resonator

Full size image

When the DETF resonator works in the inverse vibration mode (mode 2 or mode 4) as Fig. 3 shown, two resonant beams of the DETF resonator are vibrating with the stress and moment same in magnitude and opposite in direction at the combined place, which lead the stress at the combined place to be eliminated by each other. Meantime, for the inverse vibration mode, the vibrations of two beams offset each other at the end of the merger, and the energy of the DETF transmission from the fixed end to the outside reduces, which lead the DETF resonator to have high Q value and the ability to resist the vibration of surrounding structure. Since the DETF resonator has high Q value, the DETF resonator loses less energy due to damping and can easily keep a more stable vibration by forming a self-excited close-loop system. At the same time, increasing the Q value is helpful to reduce the thermal mechanical noise and improve the resolution of the DETF resonator.

The stress of the fixed end of the DETF resonator determines the Q value. The energy loss is large and the mechanical coupling between the beam and the surrounding structure is serious when the stress of the fixed end of the DETF resonator is large, which makes the Q value is low. Conversely, the Q value is high when the stress of the fixed end of the DETF resonator is small.

Therefore, the inverse vibration mode is ideal operating mode. And, in consideration of the implemented of the excitation methods and the detection method, mode 2 is selected as the operating mode. When one mode is taken as the operating mode, all the other vibration modes are taken as the interference mode. And the interference mode has little influence on the working mode when the difference between the natural frequencies of the operating mode and the interference mode is great.

According to the boundary structure as shown in Fig. 2, four DETF resonators with different boundary structure were analyzed by FEM simulation utilizing the Finite Element program ANSYS. In FEM simulation, all models of DETF resonator with isotropic single crystal silicon material were meshed with Four-node quadrilateral plane stress elements. A group of parameters are used: L = 500 μm, h = 4 μm, b = 40 μm, gap = 10 μm, fsl = 50 μm, s = 2 μm, sl = 50 μm, sw = 10 μm, and the Young’s modulus E = 133 Gpa, the Poisson’s ratio \( \nu = 0. 2 7 8 \), the material density \( \rho = 2329 \) kg m−3. The result is shown in Table 1, and the natural frequencies of the DETF resonators in mode 1(in-phase vibration mode), mode 2 (inverse vibration mode) and the stresses of the fixed end of the DETF resonators with different boundary structure are given.

Table 1 FEM simulation result of DETF resonators with different boundary structure
Full size table

From Table 1, it can be found that the difference of natural frequency between mode 2 (inverse vibration mode) and mode 1 (in-phase vibration mode) of No. 3 and No. 4 boundary structure is larger than that of No. 1 and No. 2 boundary structure. The boundary structure of No. 3 and No. 4 can make the natural frequency of mode 1 far away from the working mode, which reduces the influence of the interference mode.

The Q value is determined by the stress at the fixed end. No. 4 boundary structure has the least stress in four boundary structures. The fixed end stress of the DETF resonator with No. 4 boundary structure is just 0.08 times of the fixed end stress of the DETF resonator with No. 3 boundary structure, and the fixed end stress of the DETF resonator with No. 3 boundary structure is the second least stress in all DETF resonators.

Based on the above simulation results, No. 4 boundary structure is selected. For this boundary structure, two beams of the DETF resonator are vibrating with the same frequency and opposite phase in the XY plane when it working at the working mode (mode 2), and the natural frequency depends only on the geometric parameters of the DETF resonator and the measured acceleration.

4 Vibration analysis of DETF resonator

When the DETF resonator is working at inverse vibration mode (mode 2), the displacement of the fixed end is very small (almost zero). So the two beam of the DETF resonator can be regarded as independent double clamped resonant beams. According to the Euler–Bernoulli beam model (Li et al. 2012), the differential equations of motion for the transverse bending vibration of beam is:

$$ \frac{{\partial^{2} }}{{\partial x^{2} }}\left( {EI\frac{{\partial^{2} w(x,t)}}{{\partial x^{2} }}} \right) + \frac{\partial }{\partial x}\left( {F\frac{\partial w(x,t)}{\partial x}} \right) + \rho bh\frac{{\partial^{2} w(x,t)}}{{\partial t^{2} }} = P(x), $$
(2)

where, \( w(x,t) \) is transversal displacement of a resonance beam, x is the distance along the resonant beam from a clamped end, and t is time. \( b \) is the width of the resonant beam, and \( h \) is the thickness of the resonant beam. \( \rho \) is the material density, and \( E \) is the Young’s modulus of the material. I is the second moment of the beam cross section. F is the axial load caused by the measured acceleration, including the axial inertia force \( N_{\text{a}} \) and the residual internal force of the beam \( N_{\text{r}} \). P is the inertia force caused by the added mass of the comb on the resonant beam.

Boundary conditions of this clamped–clamped resonant beam are:

$$ w(0,t) = w(L,t) = 0\quad \left. {\frac{\partial w}{\partial x}} \right|_{{{\text{x}} = 0}} = \left. {\frac{\partial w}{\partial x}} \right|_{{{\text{x}} = L}} = 0, $$
(3)

where, L is the length of the resonant beam.

The partial differential equation Eq. (2) can be decomposed into a series of ordinary differential equations by means of the mode superposition method. The transversal bending vibration of the beam can be expressed as the sum of an infinite number of mutually orthogonal modes, and \( w(x,t) \) is:

$$ w(x,t) = \sum\limits_{i} {\phi_{\text{i}} (x)} u_{\text{i}} (t), $$
(4)

where, \( \phi_{\text{i}} (x) \) is the i order mode shape function of the resonant beam, and \( u_{\text{i}} (t) \) is the generalized coordinates corresponding to the i order mode. It is assumed that the cross-sectional area, the elastic modulus and the axial force remain constant along the axis of the beam, and arbitrary order mode can be solved by the orthogonality between the modes.

$$ \left( {\int_{0}^{L} {\rho bh\phi_{\text{i}}^{2} {\text{d}}x + } m_{\text{a}} \phi_{\text{i}} (x_{\text{a}} )^{2} } \right)\ddot{u}_{\text{i}} + \left( {\int_{0}^{L} {EI\left( {\frac{{\partial^{2} \phi_{\text{i}} }}{{\partial x^{2} }}} \right)^{2} {\text{d}}x + \int_{0}^{L} {F\left( {\frac{{\partial \phi_{\text{i}} }}{\partial x}} \right)^{2} {\text{d}}x} } } \right)u_{\text{i}} = 0, $$
(5)

where, m a is the added mass of the comb on the resonant beam, and \( x_{\text{a}} \) is the distance of the comb from a clamped end of the beam.

According to the energy method, the Eq. (5) represents a single freedom second order system. The first term is the inertia term and the second term is the stiffness term. And the equivalent mass and equivalent stiffness of resonant beam at a single mode can be expressed as:

$$ \left\{ \begin{aligned} & M_{{\text{eff,i}}} = \int_{0}^{L} {\rho bh\phi_{\text{i}}^{ 2} {\text{d}}x + } m_{\text{a}} \phi_{\text{i}} (x_{\text{a}} )^{ 2} \\ & K_{{\text{eff,i}}} = \int_{0}^{L} {EI\left( {\frac{{\partial^{2} \phi_{\text{i}} }}{{\partial x^{2} }}} \right)^{ 2} {\text{d}}x + \int_{0}^{L} {F\left( {\frac{{\partial \phi_{\text{i}} }}{\partial x}} \right)^{ 2} {\text{d}}x} } \\ \end{aligned} \right.. $$
(6)

The transversal bending vibration of the beam at the i mode can be expressed as:

$$ M_{{\text{eff,i}}} \ddot{u}_{\text{i}} + K_{{\text{eff,i}}} u_{\text{i}} = 0. $$
(7)

Therefore, the natural frequencies of the resonant beam at the i mode are:

$$ \omega_{{\text{n,i}}} = \sqrt {\frac{{K_{{\text{eff,i}}} }}{{M_{{\text{eff,i}}} }}} = \sqrt {\frac{{\int_{0}^{L} {EI\left( {\frac{{\partial^{2} \phi_{\text{i}} }}{{\partial x^{2} }}} \right)^{ 2} {\text{d}}x + \int_{0}^{L} {F\left( {\frac{{\partial \phi_{\text{i}} }}{\partial x}} \right)^{2} {\text{d}}x} } }}{{\int_{0}^{L} {\rho bh\phi_{\text{i}}^{2} {\text{d}}x + } m_{\text{a}} \phi_{\text{i}} (x_{\text{a}} )^{2} }}} . $$
(8)

Based on the above analysis, it is found that the transversal bending vibration of the resonant beam is the sum of the infinitely simple solutions of a second order equation as Eq. (7). Each two order equation corresponds to a mode shape function and its natural frequency.

According to the Eq. (8), the first natural frequency of the DETF resonator under the action of axial force F can be obtained:

$$ f = \frac{\omega_{\text{n,1}}}{( 2 {\pi})}. $$
(9)

According to Eq. (8), the first order natural frequency of resonant beam in DETF resonator depends on the axial load along the beam after the geometric parameters of DETF resonator are determined.

The sensitivity of the DETF resonator is an important performance which determines the scale factor of the accelerometer, and it is the change of the natural frequency caused by unit axial force. In order to improve the performance of accelerometer, the DETF resonator must have high sensitivity.

The frequency change caused by the unit axial force is:

$$ S{ = }\frac{f(F) - f(0)}{F}. $$
(10)

According to Eqs. (8), (9) and (10), the natural frequency and the sensitivity of the DETF resonator depends on the geometric parameters of the DETF resonator, including the length of the resonant beam L, the width of the resonant beam b, the thickness of the resonant beam h, and the added mass of the comb on the resonant beam m a.

Based on the above analysis, the theoretical analysis results were compared with the FEM simulation results obtained by utilizing the Finite Element program ANSYS when the residual stress on the resonant beam is not taken into considered. The compared results are shown in Fig. 4. By comparing the simulation results with the results of theoretical analysis, it is shown that the analysis results of theoretical model are in good agreement with the simulation results, which indicated that the theoretical model has very high accuracy.

Fig. 4
figure 4

The comparison of theoretical values and simulation values. a Theoretical values and simulation values of natural frequencies of beams with different lengths. b Theoretical values and simulation values of natural frequencies of beams with different thicknesses. c Theoretical values and simulation values of natural frequencies of beams with different widths. d Theoretical values and simulation values of natural frequencies of beams with different added mass

Full size image

Through established theoretical model of the DETF resonator, the change trend of the performance with the different geometric structure parameters of the DETF resonator can be obtained. However, the influence degree of each parameter on a particular performance can not be obtained and compared, and it is not clear which parameters have the greatest impact on a particular performance.

5 Uncertainty analysis method

5.1 Sample-based stochastic model

Based on the theoretical vibration model of the DETF resonator, the stochastic modeling is realized. The detailed procedure of the stochastic modeling is given in Fig. 5. Different input parameter combines randomly as a combination, and a number of combinations are selected to evaluate the variability of the output parameters. In order to decide the number of input parameter combinations, stochastic convergence analysis is conducted. The degree to which input parameters vary is quantified, and uncertainties of the input parameters are propagated through the established theoretical vibration model of the DETF resonator, so that the variability of output parameters is quantified according to the results.

Fig. 5
figure 5

Sample-based stochastic model

Full size image

The output parameters of interest in this study include: the natural frequency of the DETF resonator and the sensitivity of the DETF resonator. Firstly, the influence of different uncertain geometric parameters of the DETF resonator, including the length of the resonant beam L, the width of the resonant beam b, the thickness of the resonant beam h, the added mass of the comb on the resonant beam m a, on the output parameters are investigated. Assuming all of these input parameters obey the Gaussian distribution with the mean value \( \mu \) and the standard deviation \( \sigma \). The mean value is considered as the design value of the input parameters here, and the standard deviation shows the uncertainty of the input parameters. The coefficient of variance (COV) \( \sigma /\mu \) is defined to represent the degree of uncertainty of the input parameters, and the COV of the uncertain parameters with high standard deviation and low nominal mean value is high while the COVs of the certain parameters are zero. Monte Carlo sampling (MCS) method is used to randomly select every input parameter from its prescribed Gaussian distribution and combining them together as one sample.

The variability of output parameters is highly dependent on the number of samples (Peng et al. 2013). The mean value and standard deviation of the input parameters converge to the nominal mean value and standard deviation of the Gaussian distribution when the number of samples increases, and meantime the mean values and standard deviations of the output parameters also converge within a certain tolerance (Peng et al. 2013; Mawardi and Pitchumani 2008). By the stochastic convergence analysis, the number of input parameter samples is selected to ensure that the number of input parameter sample is proper and the samples are representative.

For every input sample, the vibration model of the DETF resonator is used to calculate the output parameters after sufficient samples are selected. The effects of the input parameters variability on the uncertainty of output parameters is assessed by obtaining each set of output parameter through this deterministic vibration model of the DETF resonator. The probability distribution is generated from the resulting sets of output parameters.

In order to quantify the uncertainty of the output parameters, the interquartile range (IQR) is defined as the difference between the 25th percentile (P25) and the 75th percentile (P75) (Peng et al. 2013; Mawardi and Pitchumani 2008):

$$ IQR = P75 - P25. $$
(11)

5.2 The stochastic convergence analysis

The properties of the DETF resonator in this paper are: the Young’s modulus E = 133 GPa, the Poisson’s ratio \( \nu = 0. 2 7 8 \), the material density \( \rho = 2329 \) kg m−3, and gap = 10 μm, fsl = 50 μm, s = 2 μm, sl = 50 μm, sw = 10 μm.

According to the uncertain input distributions, the output distributions are obtained by the sample-based stochastic model previously discussed. The stochastic convergence analysis is conducted to identify a minimum quantity of input parameters which can represent the input sample distribution and guarantee steady output distribution. In the process to obtain number of input samples N s , the design values of the input parameters are set as their mean values: L = 500 μm, h = 4 μm, b = 40 μm, \( m_{\text{a}} = 1 \times 10^{ - 10} \) kg. And the COVs of each input parameter are set as 0.04.

The stochastic convergence analysis of the mean values of input parameters L, b, h, m a is conducted. The results are shown in Fig. 6. It can be found that the mean values of the input parameters frequently fluctuate when N s is less than 300. The mean values of the input parameters still oscillate but the changing amplitude is less than 1% at N s  = 300. Therefore, 300 samples are sufficient to ensure that the nominal mean values of input parameters are steady.

Fig. 6
figure 6

Stochastic convergence analysis of the input parameters. a Convergence analysis of mean value of L. b Convergence analysis of mean value of b. c Convergence analysis of mean value of h. d Convergence analysis of mean value of m a

Full size image

The stochastic convergence analysis of the standard deviation of the input parameters is also conducted, and the results are shown in Fig. 7. It can be seen that the standard deviation oscillates significantly even when the number of input parameters N s is more than 300.The reason for this is that the deviation is a higher order moment and converges much more slowly than the mean values (Peng et al. 2013). When the sample number increases to 400, the standard deviation of L, b, h, m a converges within 1.72, 1.29, 1.45 and 0.05%, respectively.

Fig. 7
figure 7

Stochastic convergence analysis of the standard deviation of the input parameters. a Convergence analysis of standard deviation of L. b Convergence analysis of standard deviation of b. c Convergence analysis of standard deviation of h. d Convergence analysis of standard deviation of m a

Full size image

The stochastic convergence analysis of output parameters is shown in Fig. 8. Inputs are L, b, h, m a, and it can be seen that the mean value converges very fast. The mean values of output parameters are within 0.43% for f and 0.46% for S when the number of samples increases beyond 400. The standard deviation converges to be within 1.79% for f and 1.87% for S when 400 samples are used.

Fig. 8
figure 8

Stochastic convergence analysis of the output parameters. a Convergence analysis of mean value of f. b Convergence analysis of mean value of S. c Convergence analysis of standard deviation of f. d Convergence analysis of standard deviation of S

Full size image

According to the above discussion, the minimum number of samples N s  = 400 is obtained and this number of samples will be used to conduct following analysis.

5.3 The result of uncertainty method

The IQRs of f and S is a function of the COVs of the input parameters L, b, h, and m a. When the COV of one input parameter increases from 0.01 to 0.1, the COVs of other parameters are kept constant at 0.01. The IQR analysis of output parameters indicates a different relationship between the IQRs and the COVs of the parameters. The IQRs of f and S are shown in Fig. 9.

Fig. 9
figure 9

The IQR analysis of output parameters when the inherent heat elevation is not taken into account. a IQR of f with different input parameters COV. b IQR of S with different input parameters COV

Full size image

As shown in Fig. 9a, the IQR analysis of the natural frequency of the DETF resonator indicates a strong relationship between the IQR and the COV of parameters L, which indicates that the natural frequency of the DETF resonator greatly depends on the length of the resonant beam L. On the contrary, the effects of the width of the resonant beam b, the thickness of the resonant beam h, and the added mass of the comb on the resonant beam m a on the natural frequency of the DETF resonator are relatively insignificant.

As shown in Fig. 9b, the IQR analysis of the sensitivity of DETF resonator indicates a strong relationship between the IQR and the COV of parameters L and h, and the effects of the COV of b and m a on the IQR are relatively insignificant. This indicates that the sensitivity of the DETF resonator greatly depends on the length of the resonant beam L and the thickness of the resonant beam h. Besides, b, and m a can also affect S greatly, which means that the width of the resonant beam b and the added mass of the comb on the resonant beam m a also have great effect on the sensitivity of the DETF resonator.

According to the above analysis, the influence degree of the length of the resonant beam L, the width of the resonant beam b, the thickness of the resonant beam h, and the added mass of the comb on the resonant beam m a on the natural frequency and the sensitivity of the DETF resonator are obtained and compared. It is clear which parameters have the greatest impact on a particular performance. When it is need to adjust input parameters to change the natural frequency and the sensitivity of the DETF resonator, the length of the resonant beam L is the preferred parameters.

6 Conclusions

In this paper, the boundary structure and geometry parameters of the DETF resonator in a micro-accelerometer are invested. Based on established theoretical vibration model of the DETF resonator which is verified by finite element method, the sample-based stochastic model is established to systematically investigate the influence of different geometry parameters of the DETF resonator on the natural frequency and the sensitivity of the DETF resonator. The results reveal that the length of the resonant beam in the DETF resonator has great influence on the natural frequency and the sensitivity of the DETF resonator. The obtained results can be used as reference for design and optimization of the DETF resonator to improve the performances of the micro-accelerometer.