1 Introduction

In order to increase the storage density of magnetic disk drives, the reduction of the spacing between the slider and the rotating disk is of great importance. If the spacing between the slider and the disk approaches the molecular mean-free path of the gas medium, continuum theory cannot be used anymore (Burgdorfer 1959; Hsia and Domoto 1983; Juang et al. 2007; Liu et al. 2007). In present hard disk drives (HDDs), the minimum spacing under the slider has decreased to the order of several nanometers (<5 nm) (Liu and Zheng 2011; Zheng et al. 2012; Salas and Talke 2013). Under such conditions, gaseous rarefaction effects cannot be neglected and must be taken into account.

In order to account for rarefaction effects, several researchers introduced slip correction models for use in conjunction with the generalized Reynolds equation. Burgdorfer (1959) applied a first-order slip-flow correction to the non-slip continuum boundary condition. Hsia and Domoto (1983) derived a modified Reynolds equation that considers both first and second order slip flow for the velocity boundary conditions. Mitsuya (1993) introduced a 1.5-order slip flow model that uses different order slip boundary conditions for the integration of the isothermal compressible Navier–Stokes equations. The three slip-flow models proposed by Burgdorfer, Hsia and Domoto, and Mitsuya are only valid for large inverse Knudsen numbers, where the Knudsen number is defined as λ/h (λ is the molecular mean-free path of the gas medium and h is the head/disk interface spacing). Gans (1985) derived a lubrication equation using a linearized Boltzmann equation similar to Burgdorfer’s modified first-order Reynolds equation and claimed that the linearized equation is valid for all inverse Knudsen numbers. Fukui and Kaneko (1988) derived a generalized Reynolds equation that includes thermal creep flow. This equation is based on a linearized Boltzmann equation similar to Gans’ equation but implements a different solution method. Fukui and Kaneko (1990) proposed a cubic polynomial curve fitting procedure which creates a function that explicitly expresses the Poseuille flow rate as a function of the inverse Knudsen number. From this expression they developed a Poiseuille flow rate database. Fukui and Kaneko’ model will be referred to as the FK model in this paper. In order to overcome complicated and time-consuming difficulties found in solving the linearized Boltzmann equation, Hwang et al. (1996) proposed an adjustable slip model based on a modified high-order slip-flow velocity distribution. The slip model has three adjustable coefficients which are correlated to the Boltzman model. Li (2002, 2003) developed a complete database of Poiseuille flow rates and Couette flow rates by solving the linearized Boltzmann equation. Peng et al. (2004) investigated the unidirectional flow of rarefied gas between two parallel plates and proposed a nanoscale effect function that describes the influence of space restriction on gas lubrication between the slider and the disk. Using a linearized flow rate model (LFR), Shi and Yang (2010) derived a simplified Reynolds equation for ultra-thin gas film lubrication in HDDs.

In the following two sections, the authors will derive a simplified model of the Reynolds equation. Then the new model will be used to perform error analysis and numerical simulation to validate its accuracy and efficiency. In the second section, based on a Poiseuille flow rate database introduced in the FK model (Fukui and Kaneko 1990), a simplified precise second order (PSO) model is proposed and used to simulate ultra-thin gas film lubrication at the head/disk interface in HDDs. In the third section, the PSO model is evaluated using the finite volume method and the resultant numerical solutions are compared with other models, including the FK model.

2 Reynolds equation and simplified model

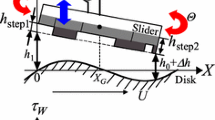
For a two dimension (2D) plane air bearing slider as shown in Fig. 1, the generalized non-dimensional 2D-Reynolds equation based on the FK model (Fukui and Kaneko 1990) is as follows:

Fig. 1
figure 1

Geometry of two dimensional inclined plane slider bearing and coordinate system employed

Full size image
$$\left\{ \begin{gathered} \frac{d}{dX}\left( {QPH^{3} \frac{dP}{dX} - \varLambda_{x} PH} \right) + \frac{d}{dY}\left( {QPH^{3} \frac{dP}{dY} - \varLambda_{y} PH} \right) = 0 \hfill \\ Q = \frac{{Q_{p} (D,\alpha )}}{{Q_{con} (D)}} \hfill \\ \varLambda_{x} = 6\mu UL/(p_{a} h_{1}^{2} ),\begin{array}{*{20}c} {} \\ \end{array} \varLambda_{y} = 6\mu VB/(p_{a} h_{1}^{2} ) \hfill \\ H(X) = 1 + \frac{L}{{h_{1} }}(1 - X)\tan (\theta ) \hfill \\ \end{gathered} \right.$$
(1)

where P and H are the non-dimensional pressure and spacing, respectively. P is normalized by the ambient pressure (p a ) and H is normalized by the minimum spacing at the trailing edge of the slider (h 1). X is the coordinate along the length of the slider and Y is the coordinate along the width of the slider. L and B are the length and width of the slider, respectively. Λ x and Λ y are the bearing numbers in the X and Y directions, respectively. The dynamic viscosity of the gas is given by μ. θ is the pitch angle of the slider, and U and V are the disk velocity in the X and Y direction, respectively. Q is the flow factor accounting for difference between different rarefaction and slip models. Q p (D, α) is the Poiseuille flow rate coefficient, and Q con (D) is the coefficient of continuum flow. Quantities D and α are the inverse Knudsen number and the surface accommodation coefficient, respectively. The definition of D and Q con is as follows:

$$D = D_{0} PH = ph/(\mu/\sqrt{2RT})$$
(2)
$$Q_{con} = D\! /\!6$$
(3)

where, D 0 denotes the inverse Knudsen number of the gas film at the minimum spacing, T is the characteristic temperature, and R is the gas constant.

The flow factor can be calculated from flow rate coefficients that are expressed in the form of a power series. For small inverse Knudsen numbers (D), where the slip flow assumption is reasonably valid, an asymptotic expression for K n  ≫ 1 can be employed. Power series representations for 0.15 ≤ D ≤ 5 and 0.01 ≤ D < 0.15 can be calculated using the least squares method. The Poiseuille flow rate coefficient (Q p ) of the FK model are as follows (Fukui and Kaneko 1990):

$$\left\{ {\begin{array}{*{20}l} {Q_{p} = {D \!/\! 6} + 1.0162 + {{1.0653} \!/\! D} - {{2.1354} \!/\! {D^{2} }}\begin{array}{*{20}c} {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {} & {} \\ \end{array} \begin{array}{*{20}l} {} \hfill \\ \end{array} \left( {5 \le D} \right)} \hfill \\ {Q_{p} = 0.13852D + 1.25087 + {{0.15653} \!/\! D} - {{0.00969} \!/\! {D^{2} }}\begin{array}{*{20}c} {} & {} \\ \end{array} \left( {0.15 \le D \le 5} \right)} \hfill \\ {Q_{p} = - 2.22919D + 2.10673 + {{0.01653} \!/\! D} - {{0.0000694} \!/\! {D^{2} }}\begin{array}{*{20}l} {} \hfill \\ \end{array} \left( {0.01 \le D \le 0.15} \right)} \hfill \\ \end{array} } \right.$$
(4)

Then, the flow factor (Q) can be obtained by using Eqs. 3, 4, and the second equation of Eq. 1:

$$Q = \frac{{Q_{p} \left( {D,\alpha } \right)}}{{Q_{con} \left( D \right)}} = K_{1} + K_{2} \left( {PH} \right)^{ - 1} + K_{3} \left( {PH} \right)^{ - 2} - K_{4} \left( {PH} \right)^{ - 3}$$
(5)

The corresponding coefficients for various inverse Knudsen numbers are shown in Table 1.

Table 1 FK model coefficients for various inverse Knudsen numbers in the FK model
Full size table

Substituting Eq. 5 into the first equation of Eq. 1, one can obtain the following equation:

$$\begin{gathered} \frac{d}{dX}\left[ {(K_{1} PH^{3} + K_{2} H^{2} + K_{3} P^{ - 1} H - K_{4} P^{ - 2} )\frac{dP}{dX} - \varLambda_{x} PH} \right] \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} +\frac{d}{dY}\left[ {(K_{1} PH^{3} + K_{2} H^{2} + K_{3} P^{ - 1} H - K_{4} P^{ - 2} )\frac{dP}{dY} - \varLambda_{y} PH} \right] = 0 \hfill \\ \end{gathered}$$
(6)

Equation (6) is a non-linear differential equation. It is difficult and time-consuming to solve this equation using numerical methods.

The Poiseuille flow rate coefficients can be calculated numerically for various inverse Knudsen numbers (D) and accommodation coefficients (α). In this paper we will only consider the case of α = 1. This corresponds to a case where gas molecules diffusely reflect at all surfaces. A database of the flow rate coefficients corresponding to α = 1 are shown in Table 2 (Fukui and Kaneko 1990).

Table 2 Poiseuille flow database for α = 1
Full size table

In order to further simplify the FK model of the Reynolds equation, the Poiseuille flow rate database is divided into eight intervals. Within each interval ([d i , d j ]) the following continuous function (\(\bar{Q}_{p}\)) is implemented:

$$\bar{Q}_{p} = a + bD + cD^{ - 1} \, d_{i} \le D \le d_{j}$$
(7)

where a, b, and c are unknown coefficients. At each interval, the values of a, b, and c are calculated as shown in Table 3 using the least squares method. Equation 7 has the same mathematical form in the other models including the first-order, second-order, and 1.5-order model.

Table 3 PSO model coefficients for various inverse Knudsen numbers
Full size table

Figure 2 compares Poiseuille flow rates calculated using different models. The flow rate calculated from the Boltzmann equation is included for reference. When compared to the flow rate calculated from the Boltzmann equation over a regime where the inverse Knudsen number varies from D = 0.01 to D = 100, the first-order slip-flow approximation under-estimates the flow rate while the second-order and 1.5th-order slip-flow approximations overestimate the flow rate. Using the model presented in this paper, we find a good approximation that is close to the flow rate calculated from the Boltzmann equation.

Fig. 2
figure 2

Flow rate Q p as function of inverse Knudsen number

Full size image

The flow factor Q of the simplified model is as follows and can be obtained by using Eqs. 3, 7, and the second equation of Eq. 1:

$$Q = A_{1} + A_{2} \frac{{K_{n} }}{PH} + A_{3} \left( {\frac{{K_{n} }}{PH}} \right)^{2}$$
(8)

where A 1, A 2 and A 3 are coefficients based on a, b and c in Eq. 7. K n is the Knudsen number. The values of A 1, A 2, and A 3 are shown in Table 4.

Table 4 Coefficients used in Eqs. 8 and 9 for various inverse Knudsen numbers
Full size table

Substituting Eq. 8 into Eq. 1, one obtains:

$$\begin{gathered} \frac{d}{dX}\left( {\left( {A_{1} PH^{3} + A_{2} K_{n} H^{2} + A_{3} K_{n}^{2} P^{ - 1} H} \right)\frac{dP}{dX} - \varLambda_{x} PH} \right) + \hfill \\ \, \frac{d}{dY}\left( {\left( {A_{1} PH^{3} + A_{2} K_{n} H^{2} + A_{3} K_{n}^{2} P^{ - 1} H} \right)\frac{dP}{dY} - \varLambda_{y} PH} \right) = 0 \hfill \\ \end{gathered}$$
(9)

This simplified model is called the “precise second order model”, or PSO model. It is easy to see that the mathematical formulation of the PSO model is simpler than that of the FK model.

3 Error analysis and numerical examples

3.1 Error analysis

In order to compare the accuracy of the PSO model with the FK model, the relative errors of the two models are compared. The relative error E is defined as:

$$E_{i} = \left( {X_{i} - Y} \right)/Y \times 100\;\% \, \left( {i = 1,2} \right) \,$$
(10)

where X 1 is the Poiseuille flow rate calculated using the FK model and X 2 is the flow rate calculated using the PSO model. Y is the corresponding flow rate from the database.

Figure 3 shows the relative errors of the Poiseuille flow rate for the two models versus the inverse Knudsen number. From Fig. 3, we observe that the relative error of the PSO model is less than that of the FK model and is very small across the whole domain. This indicates that the accuracy of the PSO model is better than that of the FK model.

Fig. 3
figure 3

Relative error of Poiseuille flow rate versus inverse Knudsen number for the PSO and FK model

Full size image

3.2 Numerical examples

The two models, the PSO and FK models, were solved using the finite volume method in order to further compare their accuracy and computational efficiency.

Figure 4 shows pressure distributions for an infinitely long air bearing slider calculated using the PSO and FK models. For the calculation in Fig. 4, a film-thickness ratio H 1 = h 2/h 1 = 2, a Knudsen number K n  = 1.25, and bearing numbers of Λ x  = 61.6 and Λ x  = 123.2 were used. It is easy to see that the pressure distributions of the two models are in very good agreement with each other. The maximum relative errors of the PSO and FK models are 0.0486 and 0.0492 %, respectively.

Fig. 4
figure 4

Comparison of pressure distribution for an infinitely long air bearing slider for the PSO and FK model

Full size image

The pressure distribution of a tri-pad slider is shown in Fig. 5. Figure 6 shows the relative errors of the pressure profiles calculated using the PSO and FK models for the tri-pad slider. The flying attitude parameters of the tri-pad slider are listed in Table 5. The parameters α and β represent the pitch and roll angles, respectively, of the slider about the pivot point where the suspension is attached. δ denotes the skew angle at the radial position and is considered to be fixed.

Fig. 5
figure 5

Non-dimensional pressure profile for typical tri-pad slider

Full size image
Fig. 6
figure 6

Relative error of pressure for the PSO and FK model for typical tri-pad slider

Full size image
Table 5 Flying attitude parameters of tri-pad slider
Full size table

Figure 6 shows that the relative errors of the pressure profiles calculated using the two models are very small for most of the air bearing surface. For the two models, the maximum relative error of the tri-pad slider is less than 3 %.

The computation times of the PSO and FK model for the tri-pad slider are listed in Table 6 for comparison. We can see that the computation time for the PSO model is a little less than that of the FK model. In other words, the PSO model is slightly more computational efficient than the FK model.

Table 6 Comparison of computation time for tri-pad slider using PSO and FK model
Full size table

4 Summary and conclusions

Starting from a Poiseuille flow rate database, we have proposed a simplified precise second order (PSO) model to simulate ultra-thin gas film lubrication at the head/disk interface in hard disk drives (HDDs). The PSO model is solved using the finite volume method. The numerical results are compared with other models, including the first-order model, the second-order model, and the widely used FK model. Numerical results show that the PSO model not only has a simple mathematical formulation, but also possesses good accuracy and is computationally efficient.