1 Introduction

Thermal fly-height control (TFC) and heat-assisted magnetic recording (HAMR) have been proposed as new magnetic recording techniques in order to increase the recording density of hard disk drives (HDDs) (Kurita et al. 2005; Peng et al. 2005; Dahl and Bogy 2014). In addition, He-enclosed HDDs can significantly reduce windage loss, disk flutter, and temperature increase, because He has a lower density and a higher heat conductivity than air (Ohkubo et al. 1989; Liu et al. 2011; Fukui et al. 2014a, b).

In the present paper, using the thermo-molecular gas-film lubrication (t-MGL) equation, we first examine the static and dynamic air-film characteristics of a plane inclined slider by a heat spot (Case 1), and then a step slider flying in either air or He over a running boundary wall with local temperature distributions and thermal deformation (projection) (Case 2) are analyzed. The aims of Cases 1 and 2 are to understand the physics of pressure generation produced by boundary temperature (Case 1) and to examine more realistic flying characteristics in modern HDD (Case 2), respectively. In this paper, the heat transfer at the interface is neglected.

2 Fundamental equations

2.1 Equations of motion

The equations of motion for a slider with two DOF are expressed as:

$$m\ddot{z }+kz = \int_{0}^{b} \int_{0}^{l} {\Delta p }dxdy,$$
(1)
$$J\ddot{\theta } + k_{\theta } \theta = \int_{0}^{b} {\int_{0}^{l} {\Delta p \cdot \left( {x_{G} - x} \right)dx} } dy,$$
(2)

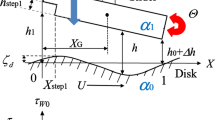
where z and θ are the translational and pitching displacements, respectively, m and J are the mass and the moment of inertia for pitching motion, respectively, l and b are the slider’s length and width, respectively, k and k θ are the translational and pitching stiffnesses of the suspension, respectively, and Δp is the dynamic pressure, as shown in Fig. 1.

Fig. 1
figure 1

Two-DOF model slider with local boundary temperature distribution

Full size image

2.2 Thermo-molecular gas-film lubrication (t-MGL) equation

The thermo-molecular gas-film lubrication (t-MGL) equation with time-dependence to examine dynamic characteristics is given by (Fukui et al. 2001, 2014a, b):

$$\begin{aligned} \; & \left( {\frac{b}{l}} \right)^{2} \frac{\partial }{\partial X}\left\{ {\tilde{Q}_{p} (D)\frac{{PH^{3} }}{{1 + \tau_{W} }}\frac{\partial P}{\partial X} - \tilde{Q}_{T} (D)\frac{{P^{2} H^{3} }}{{\left( {1 + \tau_{W} } \right)^{2} }}\frac{{\partial \tau_{W} }}{\partial X}} \right\} \\ & \quad\quad + \frac{\partial }{\partial Y}\left\{ {\tilde{Q}_{p} (D)\frac{{PH^{3} }}{{1 + \tau_{W} }}\frac{\partial P}{\partial Y} - \tilde{Q}_{T} (D)\frac{{P^{2} H^{3} }}{{\left( {1 + \tau_{W} } \right)^{2} }}\frac{{\partial \tau_{W} }}{\partial Y}} \right\}\\ &\quad= \varLambda_{b} \frac{\partial }{\partial X}\left( {\frac{PH}{{1 + \tau_{W} }}} \right) + \sigma_{b} \frac{\partial }{{\partial \tilde{t}}}\left( {\frac{PH}{{1 + \tau_{W} }}} \right), \\ \end{aligned}$$
(3)

where P (=p/p a , p a ambient pressure) is the non-dimensional pressure, H (=h/h 0, h 0 minimum spacing) is the non-dimensional spacing, \(\tilde{t}\)(=ω 0 t, ω 0 normalizing angular frequency) is the non-dimensional time, X (=x/l) and Y (=y/b) are non-dimensional coordinates, D is the inverse Knudsen number defined as \(D = ph/\mu \sqrt {2RT}\), Λ b (≡6μUb 2/p a h 20 l) is the bearing number, and σ b (≡12μω 0 b 2/p a h 20 ) is the squeeze number. The quantities \(\tilde{Q}_{P} (D)\,\,( {\equiv} Q_{P} /Q_{Pcon} )\) and \(\tilde{Q}_{T} (D)\,\,( {\equiv} Q_{T} /Q_{Pcon} )\) are the pressure flow rate ratio and the thermal creep flow rate ratio, respectively. The relationships between Q p and D and between Q T and D when accommodation coefficients of the slider, α s , and the disk, α d , are both unity (α s  = α d  = 1), that is, molecules reflect diffusely at boundaries, are presented by means of a database in references (Fukui and Kaneko 1990b; Fukui et al. 2014a, b). The non-dimensional temperature τ W (=T/T 0 − 1) in Eq. (3) is defined as the average temperature of the slider surface, τ Ws , and the disk surface, τ Wd , i.e., τ W  = (τ Ws  + τ Wd )/2.

For a different gas, such as helium, the pressure generation can be obtained by solving Eq. (3) using the same database of Q P and Q T values and the corresponding values of viscosity μ and the gas constant R. The mean free path values used in the calculations are \(\lambda_{air} = 64\) nm for air and \(\lambda_{He} = 190\) nm for He, whereas the viscosity values are 1.81 × 10−5 Pa s for air and 1.96 × 10−5 Pa s for He. The gas constants R are 287.03 J/(kg K) for air and 2077.15 J/(kg K) for He.

2.3 Thermal creep flow

When the Knudsen number, K n, is not negligible (or when the molecular mean free path is not negligible compared with the spacing) and temperature gradients exist along the boundary walls, a special type of flow, referred to as thermal creep flow or thermal transpiration flow, is induced from the colder regions to the hotter regions. When the boundary temperature has a symmetric distribution, levitation pressure (force) occurs under the slider (Fukui and Kaneko 1988; Fukui et al. 2001).

Pressure generated by the thermal creep flow is evident when the boundary is stationary or moves very slowly, because the wedge effect is insignificant (Fukui et al. 2014a). In contrast, when the boundary (disk) is running, pressures generated by the wedge effect overwhelm those generated by the thermal creep flow (Fukui et al. 2014b). Therefore, in the latter part of the present study (Case 2), we neglect the thermal creep flow terms:

$$\left( {\frac{b}{l}} \right)^{2} \frac{\partial }{\partial X}\left\{ {\tilde{Q}_{p} \left( D \right)\frac{{PH^{3} }}{{1 + \tau_{W} }}\frac{\partial P}{\partial X}} \right\} + \frac{\partial }{\partial Y}\left\{ {\tilde{Q}_{p} \left( D \right)\frac{{PH^{3} }}{{1 + \tau_{W} }}\frac{\partial P}{\partial Y}} \right\} = \varLambda_{b} \frac{\partial }{\partial X}\left( {\frac{PH}{{1 + \tau_{W} }}} \right) + \sigma_{b} \frac{\partial }{{\partial \tilde{t}}}\left( {\frac{PH}{{1 + \tau_{W} }}} \right).$$
(4)

2.4 Van der Waals (vdW) force equation

The vdW pressure P vdW between the slider and the disk is expressed as (Israelachivili 1992; Matsuoka et al. 2005):

$$P_{\text{vdW}} = {{ - \tilde{A}_{132} } \mathord{\left/ {\vphantom {{ - \tilde{A}_{132} } {6\pi H^{3} }}} \right. \kern-0pt} {6\pi H^{3} }},$$
(5)

where \(\tilde{A}_{132} ( {=} A_{132} /p_{a} h_{0}^{3} )\) is the non-dimensional Hamaker constant determined from the refractive indices of the solids. When both the disk and the slider have diamond-like carbon (DLC) coatings, A132 will be 3.26 × 10−19 J. From this equation, we obtain the static force (attractive pressure) and dynamic pressure (negative stiffness).

3 Analysis method

3.1 Perturbation method

In order to analyze the static and dynamic slider characteristics, we used the perturbation method while assuming that the spacing fluctuation Δh is small compared with the minimum spacing h 0. We obtained the following equation for the static pressure P 0 and the infinitesimal dynamic pressure ψ (=Δp/p a ):

$$P\left( {X,\,\,Y,\,\,\tilde{t}} \right) = P_{0} \left( {X,\,\,Y} \right) + \psi \left( {X,\,Y,\,\,\tilde{t}} \right),\;\quad \psi \ll P_{0} .$$
(6)

The spacing between the slider and the disk, H, consists of the time-independent spacing, H 0, and time-dependent infinitesimal variations, η (=Δh/h 0):

$$H\left( {X,\,Y,\,\,\tilde{t}} \right) = H_{0} \left( {X,\,Y} \right) + \eta \left( {X,\,Y,\,\,\tilde{t}} \right),\quad \eta \ll H_{0} .$$
(7)

By substituting Eqs. (6) and (7) into Eqs. (3) (or Eq. (4)) and (5), we obtain the static equilibrium equation and the linearized dynamic equation.

3.2 Fundamental equation giving dynamic pressure ψ

In order to obtain a simple relationship between σ b and Λ b , the characteristic frequencies are determined to be

$$f_{L} \equiv U/l\quad {\text{and}}\quad \omega_{0} = 2\pi f_{L} ,$$
(8)

where U is the disk speed.

This frequency (f L ) is the frequency that gives the geometric restriction of the spacing fluctuation caused by a running wavy wall. The non-dimensional frequency Ω is given by

$$\varOmega = \omega /\omega_{0} = f/f_{L} .$$
(9)

The relationship between σ b and Λ b , from their definitions and Eq. (9), is expressed as

$$\begin{aligned} \sigma_{b} & = \varLambda_{b} \,(2l\omega_{0} /U) \\ \;\;\;\;\; & = 4\pi \varLambda_{b} . \\ \end{aligned}$$
(10)

For a wavy mode, Ω is equivalent to the slider ratio, R S, which is the ratio of the slider length, l, to the wavelength of a wavy wall, L, i.e.:

$$\varOmega = f/f_{L} = l/L \equiv R_{S} .$$
(11)

The small spacing fluctuation η in Eq. (7) consists of the translational and pitching displacements of the slider, ζ(=z/h 0), Θ(=θl/h 0), and the displacement of the disk surface ζ d :

$$\eta = \zeta + \varTheta \cdot (X_{G} - X) - \zeta_{d} ,$$
(12)

where the disk displacements for a wavy mode are as follows:

$$\zeta_{d} = \tilde{a}\,\sin (2\pi \varOmega X - \varOmega \,\tilde{t}).$$
(13)

Therefore, the dynamic pressure can be divided into components of each displacement and is given by:

$$\psi = G_{1} (X,\,Y) \cdot \zeta (\tilde{t}) + G_{2} (X,\,Y) \cdot \varTheta (\tilde{t}) + G_{3} (X,\,Y) \cdot \tilde{a}\sin (\varOmega \tilde{t}),$$
(14)

where G k (k = 1–3) are the dynamic pressure coefficients generated by the translational displacement, the pitching displacement, and the displacement of the disk surface, respectively. We performed numerical analysis using the finite volume method for a two-dimensional linear differential equation, which gives the dynamic pressure coefficient G k , in the frequency domain (Ono 1975).

Substituting Eq. (14) into Eqs. (1) and (2), the equations of motion are expressed as:

$$\tilde{m}\ddot{\zeta } + \gamma_{11} \dot{\zeta } + \gamma_{12} \dot{\varTheta } + (\kappa_{11} + \tilde{k})\zeta + \kappa_{12} \varTheta = \tilde{a}\,(\delta_{s1} \cdot \sin \varOmega \,\tilde{t} + \delta_{c1} \cdot \cos \varOmega \,\tilde{t})$$
(15)

and

$$\tilde{J}\ddot{\varTheta } + \gamma_{21} \dot{\zeta } + \gamma_{22} \dot{\varTheta } + \kappa_{21} \zeta + (\kappa_{22} + \tilde{k}_{\theta } )\varTheta = \tilde{a}\,(\delta_{s2} \cdot \sin \varOmega \,\tilde{t} + \delta_{c2} \cdot \cos \varOmega \,\tilde{t}) ,$$
(16)

where κ ij and γ ij (i = 1, 2, j = 1,2) are the stiffnesses and damping coefficients obtained from G 1 and G 2, respectively (Fukui et al. 1985).

The real and imaginary parts of quantities −G 1 and −G 2 · (X G  − X) are the stiffnesses and damping coefficients for translational and pitching motions, respectively.

4 Two approximate solutions for limiting cases

4.1 Static and dynamic approximate solutions for an infinite bearing number (Λ b  → ∞)

For a spacing of several nanometers, the conventional bearing number Λ, and, therefore, Λ b and σ b also increase dramatically (see Eq. (10)). For an infinite bearing number, Eq. (3) is expressed as

$$\frac{\partial }{\partial X}\left( {\frac{PH}{{1 + \tau_{W} }}} \right) + 4\pi \frac{\partial }{{\partial \tilde{t}}}\left( {\frac{PH}{{1 + \tau_{W} }}} \right) = 0.$$
(17)

Note that in Eq. (17) for Λ b  → ∞, the temperature distribution τ W is arbitrary.

The static solution of Eq. (17) is as follows:

$$\left. {P_{0} } \right|_{{\varLambda_{b} \to \infty }} = \left( {1 + \tau_{W} } \right) \cdot \left. {P_{0} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} }$$
(18)

where

$$\left. {P_{0} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} } = H_{1} '/H_{0} \quad (H_{1} ' \;{\text{is the inlet spacing}})$$
(19)

The quantity \(\left. {P_{0} } \right|\,_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} }\) is the conventional approximation solution for an infinite bearing number without a local temperature distribution (Fukui and Kaneko 1990a).

The dynamic solutions for Eq. (17) are as follows:

$$\left. {G_{k} } \right|_{{\varLambda_{b} \to \infty }} = \left( {1 + \tau_{W} } \right) \cdot \left. {G_{k} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} } ,\quad k = { 1},{ 2},{ 3}\,$$
(20)

where

$$\begin{aligned} \left. {G_{1} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} } & = \frac{1}{{H_{0} }}\left\{ {\cos \left( {4\pi \varOmega X} \right) - \frac{{H_{1} }}{{H_{0} }}} \right\} - i\frac{1}{{H_{0} }}\sin \left( {4\pi \varOmega X} \right), \\ \left. {G_{2} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} } & = \frac{1}{{H_{0} }}\left\{ {X_{G} \cos \left( {4\pi \varOmega X} \right) - \frac{{H_{1} }}{{H_{0} }}\left( {X_{G} - X} \right)} \right\}\\ &\quad- i\frac{{X_{G} }}{{H_{0} }}\sin \left( {4\pi \varOmega X} \right), \\ \left. {G_{3} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} } & = \frac{1}{{H_{0} }}\left\{ {\cos \left( {4\pi \varOmega X} \right) - \frac{{H_{1} }}{{H_{0} }}\cos \left( {2\pi \varOmega X} \right)} \right\} \\&\quad- i\frac{1}{{H_{0} }}\left\{ {\sin \left( {4\pi \varOmega X} \right) - \frac{{H_{1} }}{{H_{0} }}\sin \left( {2\pi \varOmega X} \right)} \right\}. \\ \end{aligned}$$
(21)

The quantities \(\left. {G_{k} } \right|\,_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} }\) (k = 1–3) shown in Eq. (21) are also conventional approximation solutions for an infinite bearing number without a local temperature distribution (Fukui and Kaneko 1990a).

The static and dynamic pressure increases produced by the boundary temperature for Λ b  → ∞ are as follows:

$$\begin{aligned} \left. {\delta P_{0} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} \end{subarray} } & \equiv \left. {P_{0} } \right|_{{\varLambda_{b} \to \infty }} - \left. {P_{0} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; & = \tau_{W} (X,\;Y) \cdot \left. {P_{0} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} } \\ \end{aligned}$$
(22)
$$\begin{aligned} \left. {\delta G_{k} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} \end{subarray} } & \equiv \left. {G_{k} } \right|_{{\varLambda_{b} \to \infty }} - \left. {P_{0} G_{k} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} } \\ \;\;\;\;\;\;\;\;\;\;\;\;\; & = \tau_{W} (X,\;Y) \cdot \left. {G_{k} } \right|_{\begin{subarray}{l} \varLambda_{b} \to \infty \\ \tau_{W} = 0 \end{subarray} } \quad \left( {k = 1- 3} \right). \\ \end{aligned}$$
(23)

These static and dynamic pressure increases can be the theoretical maximum values produced by the applied temperature.

4.2 Static and dynamic solutions by incompressible short bearing approximation (Λ b  → 0)

This approximation is based on the assumptions that:

  1. 1.

    The slider width b is much smaller than slider length l: b/l ≪ 1.

  2. 2.

    The bearing number is small: Λ b  ≪ 1.

  3. 3.

    Neither the spacing H nor the applied temperature τ W depend on Y:

$$H = H(X,\,\,\tilde{t}\,),\;\;\tau_{W} = \tau_{W} (X).$$

Under these conditions, Eq. (3) is simplified to

$$\left. {\tilde{Q}_{p} } \right|_{0} \frac{{H^{3} }}{{1 + \tau_{W} }}\frac{{\partial^{2} P}}{{\partial Y^{2} }} = \varLambda_{b} \frac{\partial }{\partial X}\left( {\frac{H}{{1 + \tau_{W} }}} \right) + \sigma_{b} \frac{1}{{1 + \tau_{W} }}\frac{\partial H}{{\partial \widetilde{t}}}$$
(24)

where \(\left. {\tilde{Q}_{p} } \right|_{{D_{0} }} = \tilde{Q}_{p} \left( {D_{0} H/\sqrt {1 + \tau_{W} } } \right)\).

The static pressure, P 0, is expressed as;

$$P_{0} = \varLambda_{b} \cdot g_{1} \cdot \frac{d}{dX}\left( {\frac{{H_{0} }}{{1 + \tau_{W} }}} \right) \cdot Y\left( {Y - 1} \right)/2 + 1.$$
(25)

Moreover, the complex dynamic component, G k , is given by

$$G_{k} = \varLambda_{b} \cdot \left\{ {g_{2} F_{k} + g_{1} \frac{d}{dX}\left( {\frac{{F_{k} }}{{1 + \tau_{W} }}} \right) + i \cdot 4\pi \varOmega g_{1} \frac{{F_{k} }}{{1 + \tau_{W} }}} \right\} \cdot Y\left( {Y - 1} \right)/2,\quad \left( {k = 1- 3} \right)$$
(26)

where Ω = f/f 0 and

$$\begin{aligned} F_{1} & = 1{\kern 1pt} ,\quad F_{2} = X_{G} - X,\quad F_{3} = \cos \left( {2\pi \varOmega X} \right) - i \cdot \sin \left( {2\pi \varOmega X} \right) \\ g_{1} & = {{\left( {1 + \tau_{W} } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \tau_{W} } \right)} {\left\{ {\left. {\tilde{Q}_{p} } \right|_{{D_{0} H_{0} }} \cdot H_{0}^{3} } \right\}}}} \right. \kern-0pt} {\left\{ {\left. {\tilde{Q}_{p} } \right|_{{D_{0} H_{0} }} \cdot H_{0}^{3} } \right\}}} \\ g_{2} & = - g_{1}^{2} \left\{ {\left. {\tilde{Q}_{p} } \right|_{{D_{0} H_{0} }} \frac{{3H_{0}^{2} }}{{1 + \tau_{W} }} + \frac{{D_{0} H_{0}^{3} }}{{\left( {1 + \tau_{W} } \right)^{3/2} }}\left. {\frac{{\partial \tilde{Q}_{p} }}{\partial D}} \right|_{{D_{0} H_{0} }} } \right\} \cdot \frac{d}{dX}\left( {\frac{{H_{0} }}{{1 + \tau_{W} }}} \right). \\ \end{aligned}$$
(27)

In the incompressible short bearing approximation, the stiffness κ ij is independent of the frequency and the damping Ωγ ij is proportional to the frequency.

5 Static and dynamic characteristics with local boundary temperature

5.1 Applied temperature

The temperature distributions at the slider or disk surface are considered to be Gaussian distributions, the maximum temperature of which is given by the parameter τ wo, as follows:

$$\tau_{W} \left( {X,Y} \right) = \tau_{W0} \exp \left[ { - \frac{1}{2}\left\{ {\left( {\frac{{X - X_{C} }}{{\sigma_{x} }}} \right)^{2} + \left( {\frac{{Y - Y_{C} }}{{\sigma^{\prime}_{y} }}} \right)^{2} } \right\}} \right]$$
(28)

where σ x and σ ′ y (=(b/l) · σ y ) are the standard deviations and X C and Y C are the centers of the distribution in the x and y directions, respectively. The standard parameters in the temperature distribution are set to be σ x  = σ ′ y  = 0.005 and X C  = 0.98, Y C  = 0.5.

5.2 Fundamental characteristics for a plane inclined slider (Case 1)

We first examine the fundamental air-film characteristics by the heat spot for a plane inclined slider (see Fig. 2).

Fig. 2
figure 2

Plane inclined slider with boundary temperature distribution (Case 1)

Full size image

5.2.1 Static pressure generation in air produced by the heat spot

Figure 3 shows typical pressure distributions in an air atmosphere with a Gaussian heat spot near the trailing edge with a minimum spacing of h 0 = 5 nm, with a corresponding modified bearing number \(\tilde{\varLambda }_{b}\) of 2.2 × 103, and a slider inclination of h 1/h 0 = 2. A pressure spike can be observed near the trailing edge produced by the heat spot (τ W0 = 0.5, which corresponds to a disk temperature increase of 300 K).

Fig. 3
figure 3

Static pressure distributions with temperature distribution (in air). h 0 = 5 nm, U = 10 m/s (\(\tilde{\varLambda }_{b} = 2.2 \times 10^{3}\)), h 1/h 0 = 2, h step1 = h step2 = 0. X c = 0.98, Y c = 0.5, σ x  = σ y ’ = 0.05, l = b = 1 m, \(\tau_{{W_{0} }} = 0.5\)

Full size image

Figure 4a, b show the pressure distributions along the centerline (Y = 0.5) with the maximum temperature τ W0 as a parameter and minimum spacings of h 0 = 5 and 20 nm. Figure 4a shows a general view for X = 0–1, and Fig. 4b shows an enlarged view for X = 0.9–1. For a smaller spacing, say 1 or 2 nm, the pressure distributions approximately coincide to the approximate solutions for Λ b  → ∞ (see Eq. (18)) corresponding to each maximum temperature τ W0.

Fig. 4
figure 4

Static pressure distributions for different spacings (in air). a General view (X = 0–1), b enlarged view (X = 0.9–1)

Full size image

Figure 5a, b show pressure contour plots in an air atmosphere with a Gaussian heat spot near the trailing edge with minimum spacings of h 0 = 5 and 20 nm and the corresponding modified bearing numbers of Λ b  = 2.2 × 103 and 705, respectively. The pressure profile for h 0 = 5 nm is greater and steeper than that for h 0 = 20 nm. Since the modified bearing number \(\tilde{\varLambda }_{b}\) is very large for h 0 = 5 nm, the non-dimensional value of the pressure peak for h 0 = 5 nm is 0.88, which is close to the value of ΔP 0HT (=1), where ΔP 0HT denotes the theoretical maximum value of the additional pressure given by Eq. (A1) (see “Appendix 1”).

Fig. 5
figure 5

Contour plots of additional static pressure produced by the heat spot for different spacings (in air). a h 0 = 5 nm \((\tilde{\varLambda }_{b} = 2.2 \times 10^{3} ,\;\delta P_{0HT} = 1)\), b h 0 = 20 nm \((\tilde{\varLambda }_{b} = 705,\;\delta P_{0HT} = 1)\)

Full size image

Figure 6 shows the relationships between the load carrying capacity, W, and the modified bearing number, \(\tilde{\varLambda }_{b} \,( {=} \varLambda_{b} /\tilde{Q}_{P0} )\), where \(\tilde{Q}_{P0}\) corresponds to the Poiseuille flow rate ratio for the minimum spacing, h 0. For very large \(\tilde{\varLambda }_{b}\), W is approximately constant and coincides with the approximate value for \(\tilde{\varLambda }_{b} \to \infty\) (Eq. (18)). For \(10^{ - 1} < \tilde{\varLambda }_{b} < 10^{2}\), W decreases and approximately coincide with the incompressible short bearing approximation (\(\tilde{\varLambda }_{b} \to 0\), Eq. (25)), which is proportional to \(\tilde{\varLambda }_{b}\). For \(\tilde{\varLambda }_{b} < 10^{ - 1}\), numerical solutions approach constant values, whereas the short bearing approximation (\(\tilde{\varLambda }_{b} \to 0\)) continues to decrease. These differences between the numerical solutions and the short bearing approximation occur because numerical solutions that include the thermal creep flow term yield pressures produced by the thermal-wedge effect. (Fukui et al. 2014a). Note that in the short bearing approximation equation (\(\tilde{\varLambda }_{b} \to 0\)), the thermal creep flow term vanishes automatically.)

Fig. 6
figure 6

Load carrying capacity W vs. modified bearing number \(\tilde{\varLambda }_{b}\) (b/l = 0.1)

Full size image

5.2.2 Dynamic pressure generation in air produced by the heat spot

Figure 7 shows the typical translational stiffness component {−Re(G 1)} for the flying state of Ω = 1 in an air atmosphere with a Gaussian heat spot near the trailing edge with a minimum spacing of h 0 = 5 nm, that corresponds to Fig. 3. Moreover, in Fig. 7, a dynamic pressure spike can be observed near the trailing edge produced by the heat spot. Figure 8a, b show the translational stiffness distributions along the centerline (Y = 0.5) with the maximum temperature τ W0 as a parameter and minimum spacings of h 0 = 5 and 20 nm. Figure 8a shows a general view for X = 0–1, and Fig. 8b shows an enlarged view for X = 0.9–1. For smaller spacings, the pressure distributions approximately coincide with the approximate solutions for Λ b  → ∞ (see Eq. (20)) corresponding to each maximum temperature τ W0.

Fig. 7
figure 7

Translational stiffness component {−Re(G 1)} with temperature distribution (in air). h 0 = 5 nm, U = 10 m/s (\(\tilde{\varLambda }_{b} = 2.2 \times 10^{3}\)), h 1/h 0 = 2, h step1 = h step2 = 0. Gas: Air, Ω = f/f 0 = 1, \(\tau_{{W_{0} }} = 0.5\)

Full size image
Fig. 8
figure 8

Translational stiffness component {−Re(G 1)} for different spacings (in air). a General view (X = 0–1), b enlarged view (X = 0.9–1)

Full size image

Figure 9 shows the translational stiffness contour plots in an air atmosphere with a Gaussian heat spot near the trailing edge with minimum spacings of h 0 = 5 and 20 nm and the corresponding modified bearing numbers of Λ b  = 2.2 × 103 and 705, respectively. The stiffness contours for h 0 = 5 and 20 nm are approximately the same. Since the modified bearing number \(\tilde{\varLambda }_{b}\) is very large for h 0 = 5 nm, the non-dimensional value of the pressure peak for h 0 = 5 nm is 0.55, which is comparable to the value of ΔG 1HT (=1), where ΔG 1HT denotes the theoretical maximum value of the additional pressure given by Eq. (30) (see “Appendix 1”).

Fig. 9
figure 9

Contour plots of additional dynamic pressure {−Re(G 1)} produced by the heat spot for different spacings (in air), \(\tau_{{W_{0} }} = 0.5\). a h 0 = 5 nm \((\tilde{\varLambda }_{b} = 2.2 \times 10^{3} ,\;Q_{TP} = 0.356,\; - \text{Re} [G_{1HT} ] = 0.5)\), b h 0 = 20 nm \((\tilde{\varLambda }_{b} = 705,\;Q_{TP} = 0.290,\; - \text{Re} [G_{1HT} ] = 0.5)\)

Full size image

Figure 10a shows the relationships between translational stiffness, κ 11, and frequency ratio, Ω(=f/f 0), and Fig. 10b shows the relationships between the translational damping coefficient, Ωγ 11, and the frequency ratio, Ω, with minimum spacing h 0 as a parameter. The definitions of stiffness, κ ij , and damping coefficients, Ωγ ij , are shown in “Appendix 2”. The tendency for h 0 = 20 and 5 nm and the infinite bearing number solution (Λ b  → ∞) are approximately the same.

Fig. 10
figure 10

Translational stiffness and damping coefficient for different spacings (in air), \(\tau_{{W_{0} }} = 0.5\). a Translational stiffness, b translational damping coefficient

Full size image

Figure 11 shows the relationships between the translational stiffness, κ 11, and the modified bearing number \(\tilde{\varLambda }_{b} \,( = \varLambda_{b} /\tilde{Q}_{P0} )\). For very large \(\tilde{\varLambda }_{b}\), κ 11 is approximately constant and coincides with the approximate value for \(\tilde{\varLambda }_{b} \to \infty\) (Eq. (20)). For \(10^{ - 2} < \tilde{\varLambda }_{b} < 10^{2}\), κ 11 decreases and approaches the incompressible short bearing approximation (\(\tilde{\varLambda }_{b} \to 0\), Eq. (26)), which is proportional to \(\tilde{\varLambda }_{b}\). For \(\tilde{\varLambda }_{b} < 10^{ - 2}\), the numerical solutions approach constant values, whereas the short bearing approximation (\(\tilde{\varLambda }_{b} \to 0\)) continues to decrease. These differences between the numerical solutions and the short bearing approximation occur because numerical solutions for κ ij that include the thermal creep flow term yield dynamic pressures produced by the thermal-wedge effect. [Note that in the short bearing approximation equation (\(\tilde{\varLambda }_{b} \to 0\)), the thermal creep flow term vanishes automatically.]

Fig. 11
figure 11

Translational stiffness vs. modified bearing number \(\tilde{\varLambda }_{b}\) for different spacings (in air) (b/l = 0.1)

Full size image

5.3 Flying characteristics analysis of a step slider with the TFC effect (Case 2)

Next, we used a slider having steps of two different depths (five-pad negative-pressure slider) with a length l of 1.25 mm, a width b of 1 mm, and step depths h step1 and h step2 of 0.35 and 3 μm, respectively. In addition, the slider is equipped with an embedded heater at the end, as shown in Fig. 12a. When the heater is powered off (heater off), the pressure generated by MGL effects and vdW attractive pressure acts on the slider. On the other hand, when the heater is powered on (heater on), the flying height is finally reduced by the effect of additional repulsive t-MGL pressure and vdW attractive pressure, due to the temperature distribution and the thermal deformation.

Fig. 12
figure 12

Two-step-depth-type slider with thermal flying height (TFC) effect (Case 2) (negative-pressure-type, five-pad slider). a Side view, b bottom view

Full size image

The temperature distribution at the slider surface is considered to be Gaussian with a non-dimensional maximum temperature τ W0 of 0.1 and a maximum thermal deformation (projection) d max of 5.5 nm, as shown in Fig. 12a (standard deviation σ x  = σ’ y  = 0.005, center of distribution X C  = 0.98, Y C  = 0.5). The essential parameter for estimating the pressure generation is the modified bearing number \(\tilde{\varLambda }_{b} = (b/l)^{2} \cdot {\varLambda / {\tilde{Q}_{P0} }}\) (Fukui et al. 1996), where \(\tilde{Q}_{P0}\) is the pressure flow rate ratio in the reference state.

5.3.1 Static flying characteristics

Figure 13 shows the flying heights, h 0 and h min, for a load of w = 9.8 mN and a pressure center of \(\bar{X} = 0.5\) as a function of the disk velocity U. Here, h 0 and h min are, respectively, the spacing at the trailing edge and the minimum spacing with heating, as shown in Fig. 12a. The flying characteristics are examined for the following conditions: (a) with and without laser heating (heater on/off), (b) with and without van der Waals pressure, and (c) in air and He.

Fig. 13
figure 13

Spacings h 0 and h min vs. disk speed U (heater on/off, \(\tau_{{W_{0} }} = 0.1\), in air/He)

Full size image

Table 1 gives the static flying states (h 0 or h min and the inclination of the slider h 1/h 0) of Fig. 13 for U = 30 m/s. Even if we consider the pressure generated by the thermal deformation and the increase in the vdW attractive force, the minimum spacing h min is smaller than the case without heating by the heater, because the slider surface is protruded by the effect of heating (d max = 5.5 nm). When the ambient gas is He, the slider inclination h 1/h 0 is larger than in the case with air.

Table 1 Static flying states for ambient gas (air/He) and heater condition (heater-on/off, \(\tau_{{W_{0} }} = 0.1\))
Full size table

Figure 14a, b show the static pressure for the flying state of Fig. 13 with heating by the heater for U = 30 m/s. Figure 14a shows the static pressure in air corresponding to the symbol, ×, and Fig. 14b shows that in He corresponding to the symbol, ● in red. A pressure spike occurs in the applied temperature area by the effect of heating. Figure 15a, b show the pressure distributions along the centerline (Y = 0.5) with and without the temperature distributions (heater on/off) and in air and He, respectively. Figure 15a shows a general view for X = 0–1, and Fig. 15b shows an enlarged view for X = 0.9–1.

Fig. 14
figure 14

Static pressure distributions corresponding to symbols, times symbol and filled circle in Fig. 13 and Table 1 (heater-on, \(\tau_{{W_{0} }} = 0.1\), in air/He, U = 30 m/s). a In air (h min = 14.21 nm, h 1/h 0 = 13.97, symbol times symbol). b In helium (h min = 1.65 nm, h 1/h 0 = 40.85, symbol filled circle) (color figure online)

Full size image
Fig. 15
figure 15

Cross section (Y = 0.5) of static pressure distributions corresponding to symbols, times symbol, filled circle, filled triangle, and filled square (heater-on/off, \(\tau_{{W_{0} }} = 0.1\), in air/He, U = 30 m/s). a General view (X = 0–1), b enlarged view (X = 0.9–1)

Full size image

5.3.2 Dynamic flying characteristics

Figure 16a, b show the translational stiffness components {−Re(G 1)} for the flying state of the frequency ratio Ω = 1 (f = f 0 = 24 kHz) shown in Fig. 14a, b. Figure 17a, b show the translational stiffness distributions along the centerline (Y = 0.5) with and without temperature distributions (heater on/off) and in air and Helium. Figure 17a shows a general view for X = 0–1, and Fig. 17b shows an enlarged view for X = 0.9–1. A pressure spike also occurs in the dynamic pressure coefficient as a result of heating as well as the static pressure in Fig. 14a, b. Moreover, the effect of the vdW attractive force is remarkable because the minimum spacing decreases locally as a result of thermal deformation due to heating by the heater.

Fig. 16
figure 16

Translational stiffness components {−Re(G 1)} corresponding to symbols, times symbol and filled circle (heater-on, \(\tau_{{W_{0} }} = 0.1\), in air/helium, U = 30 m/s, Ω = 1). a In air (h min = 14.21 nm, h 1/h 0 = 13.97, symbol times symbol). b In helium (h min = 1.65 nm, h 1/h 0 = 40.85, symbol filled square)

Full size image
Fig. 17
figure 17

Cross section (Y = 0.5) of translational stiffness distributions {−Re(G 1)} corresponding to symbols, times symbol, filled circle, filled triangle, and filled square (heater on/off, \(\tau_{{W_{0} }} = 0.1\), in air/He, U = 30 m/s, Ω = 1). a General view (X = 0–1), b enlarged view (X = 0.9–1)

Full size image

Figure 18 shows the relationships between the translational stiffness, κ 11, the translational damping coefficient, Ωγ 11, which are integral values of the dynamic pressure coefficient, G 1, and the frequency ratio, Ω. The curves in Fig. 18 correspond to the symbols ×, ●, ▲, and ■ in Fig. 13 and Table 1. When the ambient gas is replaced with He, Fig. 18 shows that κ 11 and Ωγ 11 decrease compared with the case of air. Figure 19 shows the relationships between the spacing fluctuation ratio |Δh/a| and the frequency ratio Ω (Fukui et al. 1985). By replacing the ambient gas with He, the spacing fluctuation ratio at the trailing edge (X = 1) is reduced compared with the case in air because the inlet-to-outlet spacing ratio (h 1/h 0) increases. In this calculation condition, the influence of the heating on the translational stiffness, κ 11, the translational damping coefficient, Ωγ 11, and the spacing fluctuation ratio, |Δh/a|, is negligible.

Fig. 18
figure 18

Stiffnesses and damping coefficients corresponding to symbols, times symbol, filled circle, filled triangle, and filled square (heater on/off, \(\tau_{{W_{0} }} = 0.1\), in air/He, U = 30 m/s)

Full size image
Fig. 19
figure 19

Spacing fluctuations corresponding to symbols, times symbol, filled circle, filled triangle, and filled square (heater on/off, \(\tau_{{W_{0} }} = 0.1\), in air/He, U = 30 m/s)

Full size image

6 Conclusion

In the present paper, the characteristics of a plane inclined slider (Case 1) and a step slider flying in either air or He (Case 2) over a running boundary wall with local temperature distributions are analyzed using the thermo-molecular gas-film lubrication (t-MGL) equation. For a plane inclined slider (Case 1), the fundamental static and dynamic characteristics are analyzed numerically and are examined through two limiting approximations: the approximation for infinite bearing number and the incompressible short bearing approximation. For a step slider (Case 2), the decreases in the minimum spacing for a slider flying in He are significant because the mean free path of He, λ He , is approximately three times that of air, λ air . The increases in the minimum spacing due to laser heating are negligible in both air and He because the heat spot size is very small. Moreover, the decrease in the minimum spacing produced by thermal deformation (projection height, d max) by laser heating in the thermal fly-height control (TFC) slider is reduced by the total additional pressure of (1) MGL pressures produced by the air-film wedge effect, (2) t-MGL pressures produced by the applied temperature distribution, and (3) van der Waals attractive pressure due to the ultra-small spacing. The spacing fluctuation in He caused by a running wavy disk is smaller than that in air, because the inlet-to-outlet spacing ratio (h 1/h 0) in He is larger than that in air.