1 Introduction

The importance of the control techniques for the Microelectromechanical systems (MEMS) is recognized gradually in recently years. The electrostatic torsional micromirrors (ETMs) have extensive applications in MEMS, such as the projection systems, optical network switches, and optical crossconnects (Bryzek et al. 2003; Borovic et al. 2004; Owusu et al. 2006; Pan et al. 2008) etc. It is similar to the parallel-plate or comb electrostatic actuators, the ETMs systems show the so-called “Pull-In” or “Snap-Through” bifurcation phenomena (Degani et al. 1998) due to the nonlinear characteristics of the dynamics of the systems. In order to overcome the Pull-In limits such that the travel range of electrostatic actuators can exceed the bifurcation point, some research reports can be found in the literatures (Dean et al. 2005; Pons-Nin et al. 2002; Tee and Ge 2009; Maithripala et al. 2005; Zhu et al. 2007, 2008; Li and Liu 2009; Piyabongkarn et al. 2005; Chen et al. 2004; Agudelo et al. 2009; Ma et al. 2011; Pu et al. 2004), of which the parallel-plate electrostatic actuators are in the majority (Pons-Nin et al. 2002; Tee and Ge 2009; Maithripala et al. 2005; Zhu et al. 2007, 2008; Li and Liu 2009), while the researches about the comb electrostatic actuators (Piyabongkarn et al. 2005; He and Geng 2012) or the ETMs are relatively less due to the complexity of the nonlinear dynamics.

The topics with respect to the design (Pu et al. 2004), modeling (Degani et al. 1998) and stability analysis (Zhao et al. 2005; Guo and Zhao 2004, 2006) of the dynamics of the ETMs have been extensively investigated in the past decade. To improve the performances of the ETMs from different aspects, some different design methods were presented in the literatures. For instance, the torsional beam type (Pan et al. 2008), comb drive type (Borovic et al. 2004; Owusu et al. 2006) and sidewall electrodes type (Pu et al. 2004) etc. Although the specific designs have their different merits, such as the comb drive electrostatic actuators can considerably reduce the source voltage since they can provide the relative larger capacitance, the sidewall electrodes type provides a perfect approach for designing multi-degrees of freedom micromirrors, the torsional beam type ETMs are still the primary selection because of the simple structure. For the modeling of the micromirror systems, Degani et al. (1998) and his coworkers gave a fundamental contribution. As to the dynamics analysis of the micromirror systems, Zhao et al. (2005) and Guo and Zhao (2004, 2006) had given some efforts for investigating the complex effects of van der waals force and Casimer force acting on the micro-systems. Comparatively, there are quite a few of researches in literatures with regarding to the control problems of the ETMs. For instance, Chen et al. (2004) proposed a linear voltage control law to enable the operation of the ETMs beyond the pull-in angle. The main problem of the control method is the inferior transient response. Agudelo et al. (2009) proposed a differential flat motion planning method that permits one to design the transient response of the ETMs and had been verified by their experiment system, whereas the suggested control method use a smooth feedbacks such that the settling time of the controller is actually infinite, therefore the bandwidth of the ETMs is not optimized. Similar results are also shown in (Ma et al. 2011), of which two active control methods are proposed based on the simple proportional and derivative (PD) controller.

Motivated by the works (Zhu et al. 2008; Piyabongkarn et al. 2005; Agudelo et al. 2009; Degani et al. 1998), we are interested in the output feedback control and the finite-time stabilization for the ETMs. Finite-time control is based on the finite-time differential equations and Lyapunov’s stability theory, and had been given continuous researches by several scientists for developing this technique in the past last two-decade years. To date, there are two classes of methods can be chosen to design a finite-time control for some classes of nonlinear systems. The first class method is the high order sliding mode control, which had been proposed by Levant (1998, 2001, 2003). This technique utilize the time derivates of the actual inputs to be the virtual input by artificially enhancing the relative degrees of a system, such that the discontinuity only occurs in the virtual input while the actual input is continuous. The main obstacles of applying this kind of finite-time controller design method in practice are the necessary of using faster actuators and the stability of the controller cannot be easily proved. Another class of finite-time controls adopts non-smooth but Hölder continuous feedback. Bhat and Bernstein (1998, 2000), Qian and Lin (2001), Huang and Lin (2005) and Hong et al. (2001) had contributed some important results in this field. The finite-time controllers based on the Hölder continuous feedback preserve the robust stability of the discontinuous feedback control while avoiding the “Chattering” defect of them, and showing appealing transient response from the point of view of engineering since the naturally time-optimal control effect. For the electrostatic microactuators, the uncertainties could be caused by the layout, parastics, structure deformations, and damping system etc., at the same time the microactuators should hold accurate and stable positioning capability and high sensitivity in response. These features of microactuators provide a perfect field for applying the Hölder continuous feedback controller with robust and finite-time stability. Nevertheless, designing a finite-time control is generally a difficult work because of the limited mathematical tools that can be utilized to deal with non-smooth differential equations. Designing an explicit finite-time controller for the general high order nonlinear systems is still an open problem.

In this paper, it is firstly shown that the nonlinear dynamics of the ETMs with electrical uncertain parameters can be exactly transformed into the third order linear systems, and then an output feedback FTS controller is presented for the third order linear system with considering bounded uncertainties by combining a full state FTS observer and a state feedback FTS controller. Even though both the FTS observer and the FTS controller are nonlinear, it is shown that output feedback FTS controller presented in this paper is globally stable. The stability of the presented output feedback controller is directly proved without using the separation principle. Thus the control scheme can considerably reduce the complexity of sensing subsystem, which commonly needs the on-chip implementation for the MEMS devices.

2 The dynamics of the ETM

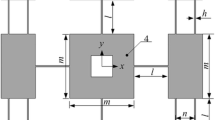
A schematic representation of the ETMs is illustrated in the Fig. 1, where the tilt angle of the micromirror is denoted by \( \theta \), \( d \) the air gap of the electrostatic microactuator, and \( k \) the torsional stiffness of the mechanical system. Assume the top movable electrode is positive and the bottom fixed electrode is connected to the electrical ground, both the two electrodes of the ETMs are rectangular and the length and width of them are \( L \) and \( W \) respectively. Then one can establish a cylindrical coordinate system denoted by \( o - \left( {r,\phi ,z} \right) \), where the origin \( o \) of the coordinate system is at the cross point of the two nonparallel-plates, and the direction with \( \phi = 0 \) is along the length direction \( L \) of the fixed electrode.

Fig. 1
figure 1

A schematic representation of the ETM

Full size image

When the source voltage of the microactuator is not zero, in the cylindrical coordinate system \( o - \left( {r,\varphi ,z} \right) \) the electrostatic potential approximately satisfies the Laplacian (Dean et al. 2005)

$$ \nabla^{2} \varPhi (\varphi ) = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \varPhi }{\partial r}} \right) + \frac{1}{{r^{2} }}\frac{{\partial^{2} \varPhi }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} \varPhi }}{{\partial z^{2} }} = 0 $$
(1)

where the single variable is \( \varphi \) for any point in the air gap of the microactuator, thus Eq. (1) can be simplified as

$$ \nabla^{2} \varPhi (\varphi ) = \frac{{\partial^{2} \varPhi }}{{\partial \varphi^{2} }} = 0 $$
(2)

and the boundary conditions of (2) satisfy \( \left. {\varPhi (\varphi )} \right|_{\varphi = 0} = 0 \) and \( \left. {\varPhi (\varphi )} \right|_{\varphi = \theta } = V_{a} \), where \( V_{a} \) is the actuation voltage of the capacitor of the ETMs. It is obvious that the solution of the second order partial differential Eq. (2) is given by

$$ \varPhi (\varphi ) = \frac{{V_{a} }}{\theta }\varphi . $$
(3)

Then the electrostatic field can be expressed as the negative gradient of the electrostatic potential \( \varPhi (\varphi ) \), and it can be expressed as

$$ E = - \nabla \varPhi = - \left( {e_{r} \frac{\partial \varPhi }{\partial r} + e_{\varphi } \frac{1}{r}\frac{\partial \varPhi }{\partial \varphi } + e_{z} \frac{\partial \varPhi }{\partial z}} \right) $$
(4)

where \( {\text{e}}_{r} \), \( {\text{e}}_{\varphi } \) and \( {\text{e}}_{z} \) denote the identity vectors of coordinates \( r,\varphi \) and \( z \) respectively. Since both the coordinates \( r \) and \( z \) are constants at any point in the air gap of the ETMs, the Eq. (4) can be simplified to

$$ \varvec{E} = - e_{\varphi } \frac{1}{r}\frac{\partial \varPhi }{\partial \varphi } = - e_{\varphi } \frac{{V_{a} }}{r\theta } . $$
(5)

In the electric field \( \varvec{E} \), the electric displacement can be calculated by

$$ \varvec{D} = \varepsilon_{r} \varepsilon_{0}\, \varvec{E} = - e_{\varphi } \frac{{\varepsilon_{r} \varepsilon_{0} V_{a} }}{r\theta } $$
(6)

where \( \varepsilon_{0} = 8.8542 \times 10^{ - 12} \) (F/m) and \( \varepsilon_{r} \) are the permittivity in free-space and the relative dielectric permittivity respectively, and the density of surface charge on the top palate is

$$ \rho = - \left| D \right| = \frac{{\varepsilon_{r} \varepsilon_{0} V_{a} }}{r\theta } . $$
(7)

Thus the total charge on the top plate can be computed by the surface integral

$$ Q_{a} = \int_{0}^{W} {\int_{{r_{1} }}^{{r_{1} + L}} {\rho drdz} } = \frac{{\varepsilon_{r} \varepsilon_{0} W}}{\theta }\ln \left( {\frac{{r_{1} + L}}{{r_{1} }}} \right)V_{a} $$
(8)

and the capacitance of the electrostatic microactuator is

$$ C_{a} = \frac{{Q_{a} }}{{V_{a} }} = \frac{{\varepsilon_{r} \varepsilon_{0} W}}{\theta }\ln \left( {\frac{d}{d - L\sin \theta }} \right) . $$
(9)

Then the electric energy of the electrostatic microactuator can be given by

$$ E_{c} = \frac{1}{2}C_{a} V_{a}^{2} . $$
(10)

By the principle of virtual work (Senturia 2002), the electrostatic torque acting on the micromirror can be calculated by

$$ M_{e} = \frac{{\partial E_{c} }}{\partial \theta } = \frac{{\varepsilon_{r} \varepsilon_{0} W}}{{2\theta^{2} }}\left[ {\frac{L\theta \cos \theta }{d - L\sin \theta } + \ln \left( {\frac{d - L\sin \theta }{d}} \right)} \right]V_{a}^{2} $$
(11)

By the assumption of small tilt angle, then the electrostatic torque (11) can be simplified to

$$ M_{e} = \frac{{\varepsilon_{r} \varepsilon_{0} W}}{{2\theta^{2} }}\left[ {\frac{L\theta }{d - L\theta } + \ln \left( {1 - \frac{L\theta }{d}} \right)} \right]V_{a}^{2} $$
(12)

The electrostatic torque (12) is expressed as a function of the tilt angle \( \theta \) and the actuated voltage \( V_{a} \). This expression is generally used to analyze the pull-in voltage and pull-in angle of micromirrors (Degani et al. 1998). Since the relationship between the charge and the voltage \( Q_{a} = C_{a} V_{a} \), the electrostatic torque (12) can also be expressed by a function of the tilt angle \( \theta \) and the charge \( Q_{a} \), and it is easy to show that

$$ M_{e} = \frac{{\left[ {\frac{L\theta }{d - L\theta } + \ln \left( {1 - \frac{L\theta }{d}} \right)} \right]}}{{2\varepsilon_{r} \varepsilon_{0} W\ln^{2} \left( {1 - \frac{L\theta }{d}} \right)}}Q_{a}^{2} $$
(13)

Therefore, the dynamics of the ETM can be given by

$$ J\ddot{\theta } + b\dot{\theta } + k\theta = M_{e} $$
(14)

where \( J \) the inertia of the movable electrode, \( b \) the viscous damping coefficient, and \( k \) the stiffness of the mechanical torsional spring. In reference (Chen et al. 2004), the motion control for the ETMs is investigated by using the dynamics (14) with electrostatic torque formed as (12). Since the electrical subsystem of the ETM is not considered in (Chen et al. 2004), the uncertainties caused by the electrical subsystem could not be considered in designing the controller. Similar imperfections also occurred in (Ma et al. 2011).

Refer to (He and Geng 2012), the equivalent circuit of the electrostatic microactuators is illustrated in the Fig. 2, where \( R \) is the resistance of the circuit, \( C_{a} \) is the capacitance of the actuated capacitor, \( V_{a} \) is the actuated voltage acting on the microactuators, \( V_{s} \) is the source voltage of the system, and \( I_{s} \) is the source current, \( C_{pp} \) denote the parallel parasitic capacitor and \( C_{sp} \) denote the serial parasitic capacitor.

Fig. 2
figure 2

The ideal equivalent circuit of the ETM

Full size image

According to the equivalent circuit, some electrical equations can be given by

$$ V_{s} = I_{s} R + V_{0} $$
(15)
$$ I_{s} = \dot{Q}_{a} + \dot{Q}_{pp} $$
(16)
$$ Q_{a} = C_{a} V_{a} $$
(17)
$$ V_{0} = \frac{{Q_{pp} }}{{C_{pp} }} = \frac{{Q_{a} }}{{C_{a} }} + \frac{{Q_{a} }}{{C_{sp} }} $$
(18)

The current in the microactuator can be deduced from the Eqs. 15–18, and can be written as

$$ \dot{Q}_{a} = \frac{{V_{s} - \left( {\frac{1}{{C_{a} }} + \frac{1}{{C_{sp} }} - R\frac{{C_{pp} }}{{C_{a}^{2} }}\dot{C}_{a} } \right)Q_{a} }}{{R\left( {1 + \frac{{C_{pp} }}{{C_{sp} }} + \frac{{C_{pp} }}{{C_{a} }}} \right)}} $$
(19)

To describe the relative magnitude of the parasitic capacitances, define

$$ \begin{gathered} \rho_{p} = \frac{{C_{pp} }}{{C_{0} }} \hfill \\ \rho_{s} = \frac{{C_{0} }}{{C_{sp} }} \hfill \\ \end{gathered} $$
(20)

where \( C_{0} \) is the capacitance of the ETM’s normal capacitance at the balance position, and it is given by

$$ C_{0} = \varepsilon_{r} \varepsilon_{0} WL/d $$
(21)

If one defines the state vector \( x = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } \\ \end{array} } \right]^{T} \), where the variables are defined by

$$ \begin{gathered} x_{1} = \theta \hfill \\ x_{2} = \dot{\theta } \hfill \\ x_{3} = Q^{2} \hfill \\ \end{gathered} $$
(22)

then using the Eqs. 13, 14 and 19–22, the nonlinear dynamics of the ETMs in state space can be expressed as

$$ \begin{gathered} \dot{x}_{1} = f_{1} (x_{1} ) + g_{1} (x_{1} )x_{2} \hfill \\ \dot{x}_{2} = f_{2} (x_{1} ,x_{2} ) + g_{2} (x_{1} ,x_{2} )x_{3} \hfill \\ \dot{x}_{3} = f_{3} (\varvec{x}) + g_{3} (\varvec{x})V_{s} \hfill \\ \end{gathered} $$
(23)

where

$$ f_{1} (x_{1} ) = 0,\;g_{1} (x_{1} ) = 1 $$
$$ f_{2} (x_{1} ,x_{2} ) = - \frac{k}{J}x_{1} - \frac{b}{J}x_{2} $$
$$ g_{2} (x_{1} ,x_{2} ) = \frac{1}{{2J\varepsilon_{r} \varepsilon_{0} W}}\left[ {\frac{{Lx_{1} }}{{d - Lx_{1} }}\ln^{ - 2} \left( {1 - \frac{{Lx_{1} }}{d}} \right) + \ln^{ - 1} \left( {1 - \frac{{Lx_{1} }}{d}} \right)} \right] ,$$
$$ f_{3} (x) = - 2x_{3} {{h_{1} (x)} \mathord{\left/ {\vphantom {{h_{1} (x)} {h_{2} (x)}}} \right. \kern-0pt} {h_{2} (x)}} ,$$
$$ g_{3} (x) = 2{{\sqrt {x_{3} } } \mathord{\left/ {\vphantom {{\sqrt {x_{3} } } {h_{2} (x)}}} \right. \kern-0pt} {h_{2} (x)}} ,$$
$$ \begin{gathered} h_{1} (x) = \frac{{x_{1} }}{{\varepsilon_{r} \varepsilon_{0} W}}\ln^{ - 1} \left( {\frac{d}{{d - L\sin x_{1} }}} \right) + \frac{{\rho_{s} d}}{{\varepsilon_{r} \varepsilon_{0} WL}} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} + R\rho_{p} L^{2} x_{2}^{2} \left( {\frac{{d - Lx_{1} }}{d}} \right)\ln^{ - 2} \left( {\frac{d}{{d - L\sin x_{1} }}} \right) \hfill \\ \end{gathered} ,$$
$$ h_{2} (x) = R\left[ {1 + \rho_{s} \rho_{p} + R\rho_{p} \frac{{Lx_{1} }}{d}\ln^{ - 1} \left( {\frac{d}{{d - L\sin x_{1} }}} \right)} \right] .$$

As the special cascade structure in state variables, the nonlinear system (23) belongs to a class of special nonlinear systems with strict feedback normal forms (Krstić et al. 1995). It was proved that a Single Input Single Output (SISO) nonlinear system with strict feedback normal form is differentially flat (Sira-Ramírez and Agrawal 2004). Both in Zhu et al. (2008) and Agudelo et al. (2009) the differentially flat property was utilized for solving the control problem of electrostatic parallel-plate microactuators (Zhu et al. 2008) or torsional micromirrors (Agudelo et al. 2009). Even though a speed observer was integrated in the controller of (Agudelo et al. 2009), charge or voltage sensors were necessary for stabilizing the ETMs. In this paper we aim to design an output feedback finite-time stabilizing controller such that the sensing subsystem of the ETMs can be further simplified. To this end, the Brunovsky’s canonical form of the dynamics of ETM is introduced in the next section for the purpose of simplifying the control design.

3 The normal form of the dynamics of the ETMs

The input–output system of the system (23) can be written as

$$ \begin{gathered} \dot{\varvec{x}} = \varvec{f}(\varvec{x}) + \varvec{g}(\varvec{x})u \hfill \\ y = x_{1} \hfill \\ \end{gathered} $$
(24)

where \( u = V_{s} \) the input of the system, \( y = x_{1} \) is defined to be the output, the vector fields \( \varvec{f}(\varvec{x}) \) and \( \varvec{g}(\varvec{x}) \) are given by, \( \varvec{f}(\varvec{x}) = \left[ \begin{gathered} f_{1} (x_{1} ) + g_{1} (x_{1} )x_{2} \hfill \\ f_{2} (x_{1} ,x_{2} ) + g_{2} (x_{1} ,x_{2} )x_{3} \hfill \\ f_{3} (\varvec{x}) \hfill \\ \end{gathered} \right],\;\varvec{g}(\varvec{x}) = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {g_{3} (\varvec{x})} \\ \end{array} } \right] \)

Then the third order Brunovsky’s canonical form for the nonlinear system (24) can be given by the Proposition 1 on the basis of the exact linearization theory (Isidori 1995, Ch 4).

Proposition 1

(Bronovsky’s canonical form) Suppose \( x_{3} \ne 0 \), and define \( \varvec{z} = \left[ {\begin{array}{*{20}c} {z_{1} } & {z_{2} } & {z_{3} } \\ \end{array} } \right] \) to be a new state vector, then by the coordinates transformation

$$ \left[ {\begin{array}{*{20}c} {z_{1} } & {z_{2} } & {z_{3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} y & {\dot{y}} & {\ddot{y}} \\ \end{array} } \right] $$
(25)

and the input transformation

$$ v = L_{f}^{3} y + \left( {L_{g} L_{f}^{2} y} \right)u $$
(26)

the nonlinear system (24) can be transformed into a linear system with the third order Brunovsky’s canonical form

$$ \begin{gathered} \dot{z}_{1} = z_{2} \hfill \\ \dot{z}_{2} = z_{3} \hfill \\ \dot{z}_{3} = v \hfill \\ \end{gathered} . $$
(27)

Proof

Calculating the first to the third order time derivates of the output \( y = x_{1} \), then it can be shown that \( \dot{y} = L_{f} y + \left( {L_{g} y} \right)u \), \( \ddot{y} = L_{f}^{2} y + \left( {L_{g} L_{f} y} \right)u \) and \( \dddot y = L_{f}^{3} y + \left( {L_{g} L_{f}^{2} y} \right)u \) where \( L_{f}^{{}} y = x_{2} ,\) \( L_{g}^{{}} y = 0 \), \( L_{f}^{2} y = f_{2} + g_{2} x_{3} \), \( L_{g} L_{f} y = 0 \), \( L_{f}^{3} y = \frac{\partial }{\partial x}(f_{2} + g_{2} x_{3} )f(x) \ne 0 \), and \( L_{g} L_{f}^{2} y = \frac{\partial }{\partial x}(f_{2} + g_{2} x_{3} )g(x) \ne 0 \).Thus the Proposition 1 is proved. □

Remark 1

As to the linear systems (27), there exist many different controllers, such as poles point placement (Agudelo et al. 2009), dynamic sliding modes and \( {{H_{2} } \mathord{\left/ {\vphantom {{H_{2} } {H_{\infty } }}} \right. \kern-0pt} {H_{\infty } }} \) robust controls (Li and Liu 2009) etc. Nevertheless, most of the controllers presented for stabilizing the ETMs in literatures applied full/partial state feedback, where still require a complex sensing subsystem. Although the charge and position sensing are realizable (Anderson et al. 2005), the measurement of the angular speed of the ETMs is intractable (Zhu et al. 2008; Agudelo et al. 2009). In the next section, an output feedback controller is presented for stabilizing the linear system (27) with considering some bounded uncertainties.

4 Output feedback finite-time stabilizing controller

Designing an output feedback controller depends on the real-time robust estimations of the higher-order time derivatives of the outputs. Therefore, designing a high performance observer is important for implementing this task. The popular high-gain observer (Atassi and Khalil 1999) can be used in any continuous feedback systems. Whereas, in order to realize the finite-time stabilization in output feedback control, an observer with finite settling time is necessary.

Let’s consider the third order linear system (27), suppose the variable \( z_{1} \) is measureable and the measured value is \( \hat{z}_{1} \), but the variables \( z_{2} \) and \( z_{3} \) are not measurable, and the estimated values are \( \hat{z}_{2} \) and \( \hat{z}_{3} \) respectively. Define the error variables \( e_{1} = \hat{z}_{1} - z_{1} \), \( e_{2} = \hat{z}_{2} - z_{2} \) and \( e_{3} = \hat{z}_{3} - z_{3} \), then the error systems of (27) can be written as

$$ \begin{gathered} \dot{e}_{1} = \dot{\hat{z}}_{1} - \dot{z}_{1} = e_{2} \hfill \\ \dot{e}_{2} = \dot{\hat{z}}_{2} - \dot{z}_{2} = e_{3} \hfill \\ \dot{e}_{3} = \dot{\hat{z}}_{3} - \dot{z}_{3} = w \hfill \\ \end{gathered} $$
(28)

For the errors system (28), a FTS observer can be given by the following Proposition 2.

Proposition 2

(FTS observer) For the third order Brunovsky’s canonical form system (28), there exists positive real numbers \( \lambda_{i} > 0,i = 1,2,3 \), such that the observer

$$ \dot{\hat{z}}_{1} = \beta_{1} ,\;\beta_{1} = - \lambda_{1} \left( {\hat{z}_{1}^{{}} - z_{1} } \right)^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} + \hat{z}_{2} $$
$$ \dot{\hat{z}}_{2} = \beta_{2} ,\;\beta_{2} = - \lambda_{2} \left( {\hat{z}_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \beta_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{3 \mathord{\left/ {\vphantom {3 7}} \right. \kern-0pt} 7}}} + \hat{z}_{3} $$
(29)

\( \dot{\hat{z}}_{3} = \beta_{3} ,\;\beta_{3} = - \lambda_{3} \left( {\hat{z}_{3}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \beta_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0pt} 7}}} \), be globally finite-time stable.

Proof

In reference (He and Geng 2012), a detailed proof was presented for the finite-time stabilizing controller of the third order linear system. The proof of the observer (29) is similar to that for the finite-time stabilizing controller. Thus the proof is not presented here. Whereas, refer to the proof of Proposition 3 in the sequel, the proposition 2 can also be proved without any difficulties. □

Remark 2

The finite-time observer (29) is actually a second order accurate differentiator. If the observer is stable, then after a finite-time transient process, \( \hat{z}_{1} = z_{1} \), \( \dot{\hat{z}}_{1} = \dot{z}_{1} \) and \( \ddot{\hat{z}}_{1} = \ddot{z}_{1} \) are accurately satisfied. Therefore, let \( z_{1} = y(t) \) be a known function of time, then the time derivatives \( \dot{\hat{z}}_{1} = \dot{y}(t) \) and \( \ddot{\hat{z}}_{1} = \ddot{y}(t) \) can be accurately obtained by the observer (29) after a finite settling time.

Remark 3

In references (Levant 2001, 2003), arbitrary order exact robust differentiators were presented on the basis of high order sliding modes. The author proved that the input noises are stable under certain conditions. It is worth noting that the sliding mode controllers are discontinuous, such that the input noises will be considerably enlarged in the higher order time derivatives [higher than the fifth order (Levant 2003)]. Whereas, the differentiators (observers) given by Proposition 2 are continuous, and the order of the differentiators (29) is only three, thus the sensitivity to the input noise is not a problem.

Remark 4

For the purpose of intuition, consider the function \( y(t) = 2\sin t\,{ + }\, 0. 5 {\text{cos(1}} . 5t ) \), by the second order differentiator (29) and let the tunable parameters of it be \( \left( {\lambda_{1} ,\lambda_{2} ,\lambda_{3} } \right) = \left( {3,3,5} \right) \), the numerical simulation result is shown in Fig. 3. One can find that the second order differentiator is finite-time stable, and both the first order differential \( \dot{y}(t) \) and the second order differential \( \ddot{y}(t) \) are accurately recovered by the outputs \( \hat{z}_{2} \) and \( \hat{z}_{3} \) of the observer (29) respectively.

Fig. 3
figure 3

An example for testing the observer’s stability

Full size image

Let’s further consider the robust controller design problem for the system (27) with bounded uncertainties. Suppose \( z_{1}^{d} \), \( z_{2}^{d} \) and \( z_{3}^{d} \) are the desired states of the system (27), and let \( \xi_{1} = z_{1} - z_{1}^{d} ,\xi_{2} = z_{2} - z_{2}^{d} \), and \( \xi_{3} = z_{3} - z_{3}^{d} \) be the errors of the state variables. Then the errors system of (27) can be written as

$$ \begin{gathered} \dot{\xi }_{1} = \xi_{2} + \mu_{1} (\varvec{\xi}) \hfill \\ \dot{\xi }_{2} = \xi_{3} + \mu_{2} (\varvec{\xi}) \hfill \\ \dot{\xi }_{3} = v + \mu_{3} (\varvec{\xi}) \hfill \\ \end{gathered} $$
(30)

where \( \mu_{i} (\varvec{\xi}) \), \( i = 1,2,3 \) be the uncertain terms. For the ETMs systems, the uncertainties could come from the un-modeled errors of the mechanical systems and/or the disturbances of the working circumstance. To stabilize the uncertain linear system (30), the following Proposition 3 can be proved.

Proposition 3

(State feedback FTS controller) For the uncertain linear system (30), suppose \( \left| {\mu_{i} ({\varvec{\upxi}})} \right| \le \mu_{0} \sum\nolimits_{j = 1}^{i} {\left| {\xi_{j} } \right|} \), where \( \mu_{0} > 0 \) be a constant, then there exists a set of positive real number \( k_{i} > 0,i = 1,2,3 \), the following controller

$$ v = - k_{3} {\text{sign}}\left( {\xi_{3}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \alpha_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right)\left| {\xi_{3}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \alpha_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right|^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0pt} 7}}} $$
(31)

where \( \alpha_{1} = - k_{1} {\text{sign}}(\xi_{1} )\left| {\xi_{1} } \right|^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} \) and \( \alpha_{2} = - k_{2} {\text{sign}}(\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} )\left| {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right|^{{{3 \mathord{\left/ {\vphantom {3 7}} \right. \kern-0pt} 7}}} \), renders the origin of the system (30) to globally stabilize in finite settling time.

Proof

By the “adding a power integrator” method presented in (Qian and Lin 2001; Huang and Lin 2005), and following the standard backstepping procedure (Krstić et al. 1995), the proposition 3 can be proved step by step.

Consider the subsystem \( \xi_{1} \) of (30), define a positive definite function \( V_{1} = \frac{1}{2}\xi_{1}^{2} \), the time derivate of the function \( V_{1} \) is given by

$$ \dot{V}_{1} = \xi_{1}^{{}} \alpha_{1} + \xi_{1}^{{}} \left( {\xi_{2} - \alpha_{1} } \right) + \xi_{1}^{2} \mu_{1} (\xi ) $$
(32)

Let the virtual input \( \alpha_{1} \) be

$$ \alpha_{1} = - \hat{k}_{1} \xi_{1}^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} $$
(33)

where \( \hat{k}_{1} > 0 \) is a constant. Since \( \left| {\xi_{1}^{2} \mu_{1} (\xi )} \right| \le \xi_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \left| {\tilde{\mu }_{1} (\xi )} \right| \), then (32) satisfies

$$ \dot{V}_{1} \le - \left( {\hat{k}_{1} - \delta_{0} } \right)\xi_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} + \xi_{1}^{{}} \left( {\xi_{2} - \alpha_{1} } \right) $$
(34)

where \( \delta_{0} > \left| {\tilde{\mu }_{1} (\xi )} \right| > 0 \) is a constant. Further consider the subsystem \( (\xi_{1} ,\xi_{2} ) \), define

$$ V_{2} = V_{1} + W_{1} $$
(35)

where

$$ W_{1} = \int_{{\alpha_{1} }}^{{\xi_{2} }} {\left( {s^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)}^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} ds $$
(36)

Due to the Lemma 3 presented in the Appendix of the paper, the positive definite property of (36) is guaranteed. Then the time-derivate of (35) is given by

$$ \begin{gathered} \dot{V}_{2} = - \left( {k_{1} - \delta_{0} } \right)\xi_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} + \xi_{1}^{{}} \left( {\xi_{2} - \alpha_{1} } \right) \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \quad+ \frac{{\partial W_{1} }}{{\partial \xi_{2} }}\dot{\xi }_{2} + \frac{{\partial W_{1} }}{{\partial \alpha_{1} }}\frac{{\partial \alpha_{1} }}{{\partial \xi_{1} }}\xi_{2} \hfill \\ \end{gathered} $$
(37)

By the Lemma 1 and Lemma 2 that are presented in the Appendix of the paper, it is not difficult to show that the second term of the right hand side of (37) satisfies

$$ \begin{gathered} \left| {\xi_{1}^{{}} \left( {\xi_{2} - \alpha_{1} } \right)} \right| \le \left| {\xi_{1}^{{}} \left( {\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} - \left( {\alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} } \right)} \right| \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {\begin{array}{*{20}c} {} &\quad \quad \quad { \le 2\left| {\xi_{1}^{{}} } \right|\left| {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right|} \\ \end{array} } \\ \end{array}^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {\begin{array}{*{20}c} {} &\quad \quad \quad { \le 2} \\ \end{array} } \\ \end{array} \left[ {\frac{7}{12}\xi_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} + \frac{5}{12}\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} } \right] \hfill \\ \begin{array}{*{20}c} {} & {} & {} & {\begin{array}{*{20}c} {} &\quad \quad \quad { \le \delta_{1} } \\ \end{array} } \\ \end{array} \xi_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} + \delta_{2} \left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \end{gathered} $$
(38)

where \( \delta_{1} > 0 \) and \( \delta_{2} > 0 \) are constants.

The third term of the right hand side of (37) is given by

$$ \frac{{\partial W_{1} }}{{\partial \xi_{2} }}\dot{\xi }_{2} = \left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} \left[ {\xi_{3} + \mu_{2} (\xi )} \right] $$
(39)

The fourth term of the right hand side of (37) can be written as

$$ \begin{gathered} \left| {\frac{{\partial W_{1} }}{{\partial \alpha_{1} }}\frac{{\partial \alpha_{1} }}{{\partial \xi_{1} }}\xi_{2} } \right| = \frac{9}{7}\left| {\left( {\hat{k}_{1} } \right)^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right|\left| {\int_{{\alpha_{1} }}^{{\xi_{2} }} {\left( {s^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)}^{{{2 \mathord{\left/ {\vphantom {2 7}} \right. \kern-0pt} 7}}} ds} \right|\left| {\xi_{2} } \right| \hfill \\ \begin{array}{*{20}c} {} & {} & {} &\qquad \qquad { \le \frac{9}{7}\left| {\left( {\hat{k}_{1} } \right)^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right|\left| {\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{2 \mathord{\left/ {\vphantom {2 7}} \right. \kern-0pt} 7}}} } \right|\left| {\xi_{2} - \alpha_{1} } \right|\left| {\xi_{2} } \right|} \\ \end{array} \hfill \\ \end{gathered} $$
(40)

Using the Lemma 1 and Lemma 2 of the Appendix once more, the inequality (40) follows that

$$ \begin{gathered} \left| {\frac{{\partial W_{1} }}{{\partial \alpha_{1} }}\frac{{\partial \alpha_{1} }}{{\partial \xi_{1} }}\xi_{2} } \right| \le \frac{18}{7}\left| {\left( {\hat{k}_{1} } \right)^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right|\left| {\left( {\xi_{2}^{7/5} - \alpha_{1}^{7/5} } \right)} \right|\left( {\left| {\xi_{2} - \alpha_{1} } \right| + \left| {\alpha_{1} } \right|} \right) \hfill \nonumber\\ \begin{array}{*{20}c} {} & {} & {} & \quad \quad \quad \quad \le \\ \end{array} \delta_{3} \xi_{1}^{12/7} + \delta_{4} \left( {\xi_{2}^{7/5} - \alpha_{1}^{7/5} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \end{gathered} $$
(41)

where \( \delta_{3} > 0 \) and \( \delta_{4} > 0 \) are constants. Substitute (38), (39) and (41) into (37), then (37) can be written as

$$ \begin{gathered} \dot{V}_{2} \le - \left( {k_{1} - \delta_{0} - \delta_{1} - \delta_{3} } \right)\xi_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \quad+ \left( {\delta_{2} + \delta_{4} } \right)\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \quad+ \left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} \left[ {\xi_{3} + \mu_{2} ({\varvec{\upxi}})} \right] \hfill \\ \end{gathered} $$
(42)

Note that \( \alpha_{1} = - \hat{k}_{1} \xi_{1}^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} \) and

$$ \begin{gathered} \left| {\xi_{2} } \right| \le \left| {\xi_{2} - \alpha_{1} } \right| + \left| {\alpha_{1} } \right| \hfill \nonumber\\ \begin{array}{*{20}c} {} & \quad { \le 2\left| {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right|^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} + \left| {\hat{k}_{1} \xi_{1}^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} } \right|} \\ \end{array} \hfill \\ \end{gathered} $$
(43)

Thus the last term of (42) satisfies

$$ \begin{gathered} \left| {\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} \mu_{2} (\xi )} \right| \hfill \nonumber\\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} = \left| {\mu_{2} (\xi )} \right|\left| {\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} } \right|\left( {\left| {\xi_{1} } \right| + \left| {\xi_{2} } \right|} \right) \hfill \\ \end{gathered} $$
(44)

Then using the Lemma 1 and Lemma 2 of the Appendix, it is not difficult to show that

$$ \begin{gathered} \left| {\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} \mu_{2} (\xi )} \right| \hfill \nonumber\\ \begin{array}{*{20}c} {} & { \le \left| {\tilde{\mu }_{2} (\xi )} \right|\left| {\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} } \right|\left( {\left| {\xi_{1} } \right|^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} + \left| {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right|^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} } \right)} \\ \end{array} \hfill \nonumber\\ \begin{array}{*{20}c} {} & { \le \delta_{5} \left| {\xi_{1} } \right|^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} } \\ \end{array} + \delta_{6} \left| {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right|^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \end{gathered} $$
(45)

where \( \delta_{5} > 0 \) and \( \delta_{6} > 0 \) are two constants. Therefore (42) satisfies

$$ \begin{gathered} \dot{V}_{2} \le - \left( {\hat{k}_{1} - \delta_{0} - \delta_{1} - \delta_{3} - \delta_{5} } \right)\xi_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \quad+ \left( {\delta_{2} + \delta_{4} + \delta_{6} } \right)\left( {\xi_{2}^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} - \alpha_{1}^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array}\quad + \left( {\xi_{2}^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} - \alpha_{1}^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} } \right)^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} \left( {\xi_{3} - \alpha_{2} } \right) \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \quad+ \left( {\xi_{2}^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} - \alpha_{1}^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} } \right)^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} \alpha_{2} \hfill \\ \end{gathered} $$
(46)

If define the virtual input \( \alpha_{2} \) to be

$$ \alpha_{2} = - \left( {\hat{k}_{2} + \delta_{2} + \delta_{4} + \delta_{6} } \right)\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{3 \mathord{\left/ {\vphantom {3 7}} \right. \kern-0pt} 7}}} $$
(47)

where \( \hat{k}_{2} > 0 \) is a constant, then (46) follows that

$$ \begin{gathered} \dot{V}_{2} \le - \left( {\hat{k}_{1} - \delta_{0} - \delta_{1} - \delta_{3} - \delta_{5} } \right)\xi_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \qquad- \hat{k}_{2} \left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} + \left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} \left( {\xi_{3} - \alpha_{2} } \right) \hfill \\ \end{gathered} $$
(48)

Along a similar line of the derivations of above, for the system (30), one can define positive definite function

$$ V_{3} = V_{2} + W_{2} $$
(49)

where

$$ W_{2} = \int_{{\alpha_{2} }}^{{\xi_{3} }} {\left( {s^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \alpha_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right)}^{{{{11} \mathord{\left/ {\vphantom {{11} 7}} \right. \kern-0pt} 7}}} ds $$
(50)

Then the controller

$$ u = - \left( {\hat{k}_{3} + \delta_{1}^{*} } \right)\left( {\xi_{3}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \alpha_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0pt} 7}}} $$
(51)

where \( \hat{k}_{3} > 0 \) and \( \delta_{1}^{*} > 0 \) are constants, renders the time derivate of (49) to satisfy

$$ \begin{gathered} \dot{V}_{3} \le - \left( {\hat{k}_{1} - \delta_{0} - \delta_{1} - \delta_{3} - \delta_{5} } \right)\xi_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \quad- \hat{k}_{2} \left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \quad- \hat{k}_{3} \left( {\xi_{3}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \alpha_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} \hfill \\ \end{gathered} $$
(52)

On the other hand, since the function \( V_{3} \) in (49) is defined to be

$$ \begin{gathered} V_{3} = V_{1} + W_{1} + W_{2} \hfill \\ \begin{array}{*{20}c} {} &\,\,\,{ \le 2\xi_{1}^{2} } \\ \end{array} + 2\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{2} \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \quad+ 2\left( {\xi_{3}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \alpha_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right)^{2} \hfill \\ \end{gathered} $$
(53)

Thus, there exists a sufficiently large constant \( k > 0, \) such that \( \dot{V}_{3} \le - kV_{3}^{{{6 \mathord{\left/ {\vphantom {6 7}} \right. \kern-0pt} 7}}} \). Then according to the Lemma 4 of the Appendix in this paper, the Propostion 3 can be proved. □

Remark 5

In this paper, we extend the controller design method presented in (Qian and Lin 2001; Huang and Lin 2005; Hong et al. 2001; He and Geng 2012) to a class of uncertain nonlinear systems, and the results presented in this paper clearly demonstrate the robust stability of the finite-time controllers based on the Hölder continuous non-smooth feedback. For the general nth order uncertain linear systems, the corresponding finite-time controller can also be given as that shown in the Remark 3 of the reference (He and Geng 2012).

Remark 6

Refer to the state Eq. (23), one can find that \( x_{3} = Q^{2} = 0 \) is a singular point, where \( g_{3} = 0 \) is satisfied and the system is not controllable at that point. In practice, the singular point can be avoided by applying a small bias voltage to keep the operational point away from the uncontrollable point (Agudelo et al. 2009).

Now let’s consider the output feedback control problem for the ETMs. On the basis of the FTS observer (29) and the FTS controller (31), the following proposition can be proved.

Propostion 4

(Output feedback FTS controller) The output feedback controller that is composed of the finite-time stabilizing observer (29) and the state feedback finite-time stabilizing control (31), globally stabilize the uncertain linear system (30) in finite settling time if the parameters \( \lambda_{i} > 0,i = 1,2,3 \) and \( k_{i} > 0,i = 1,2,3 \) are properly chosen.

Proof

Using the outputs of the observer (29), then the errors variables of the uncertain linear system (30) can be redefined to be

$$ \begin{gathered} \xi_{1} = z_{1} - \left( {\hat{z}_{1}^{{}} - e_{1} } \right) \hfill \\ \xi_{2} = z_{2} - \left( {\hat{z}_{2}^{{}} - e_{2} } \right) \hfill \\ \xi_{3} = z_{3} - \left( {\hat{z}_{3}^{{}} - e_{3} } \right) \hfill \\ \end{gathered} $$
(54)

According to the Proposition 2, the observer (29) is stable in finite settling time, thus there exists a constant \( e_{0} > 0,\) such that for all \( t \in \left[ {0, + \infty } \right) \), the errors variables of the observer (29) are bounded, namely

$$ \hbox{max} \left\{ {\left| {e_{i} (t)} \right|,i = 1,2,3} \right\} \le e_{0} $$
(55)

and one can define a positive definite function as follows for the errors dynamics of the observer

$$ U(\varvec{e}) = \frac{1}{2}e_{1}^{2} + \int_{{\beta_{1} }}^{{e_{2} }} {\left( {s^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \hat{\beta }_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)}^{{{9 \mathord{\left/ {\vphantom {9 7}} \right. \kern-0pt} 7}}} ds + \int_{{\beta_{2} }}^{{e_{3} }} {\left( {s^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \hat{\beta }_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right)}^{{{{11} \mathord{\left/ {\vphantom {{11} 7}} \right. \kern-0pt} 7}}} ds $$
(56)

where \( \hat{\beta }_{1} = - \lambda_{1} e_{1}^{{{5 \mathord{\left/ {\vphantom {5 7}} \right. \kern-0pt} 7}}} \),\( \hat{\beta }_{2} = - \lambda_{2} \left( {e_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \hat{\beta }_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{3 \mathord{\left/ {\vphantom {3 7}} \right. \kern-0pt} 7}}} \) and the feedback of the FTS observer is given by \( \hat{\beta }_{3} = - \lambda_{3} \left( {e_{3}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \hat{\beta }_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0pt} 7}}} \), and \( \hat{\lambda }_{i} > 0 \), \( i = 1,2,3 \) are constants,then there exist a constant \( \lambda \ge \hbox{max} \left\{ {\lambda_{i} ,i = 1,2,3} \right\} \), such that the time derivate of (56) satisfies

$$ \dot{U}(\varvec{e}) \le - \lambda \left[ {e_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} + \left( {e_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \hat{\beta }_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} + \left( {e_{3}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \hat{\beta }_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} } \right] $$
(57)

On the other hand, according to the Proposition 3, for any bounded errors \( \mu_{i} (\varvec{\xi},\varvec{e}) \), \( i = 1,2,3 \), there exist sufficiently large constant \( k > 0 \), such that (52) satisfies the inequality

$$ \dot{V}_{3} \le - k\xi_{1}^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} - k\left( {\xi_{2}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} - \alpha_{1}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0pt} 5}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} - k\left( {\xi_{3}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} - \alpha_{2}^{{{7 \mathord{\left/ {\vphantom {7 3}} \right. \kern-0pt} 3}}} } \right)^{{{{12} \mathord{\left/ {\vphantom {{12} 7}} \right. \kern-0pt} 7}}} $$
(58)

Then, if one defines a positive definite function as follows for the closed-loop system

$$ V = V_{3} (\varvec{\xi}) + U(\varvec{e}) $$
(59)

there always exist a sufficiently large constant \( \eta > 0 \), such that the time derivate of (59) satisfies the inequality

$$ \dot{V} = \dot{V}_{3} (\varvec{\xi}) + \dot{U}(\varvec{e}) \le - \eta V^{{{6 \mathord{\left/ {\vphantom {6 7}} \right. \kern-0pt} 7}}} $$
(60)

According to the Lemma 4 of the Appendix in this paper, then the Proposition 4 can be proved. □

Remark 7

Both of the observer (29) and the controller (31) are continuous in Hölder sense, thus the outputs of the observer are bounded, and then the conditions of the separation principle presented in (Atassi and Khalil 1999) are satisfied. The separation principle means that a controller and an observer can be designed separately under certain conditions, and the output feedback combined observer-controller preserve the main properties of the full state feedback controllers (Levant 2003). In reference (Atassi and Khalil 1999), the separation principle was proved for the autonomous systems with high-gain observers and asymptotic continuous feedback. The output feedback controller given by (31) with observer (29) is Hölder continuous, thus the stability of the presented output feedback controller is also ensured by the separation principle even though the stability of the Proposition is directly proved in this paper.

5 Numerical simulations

In the simulations of this section, the physical parameters of the ETMs are listed in the Table 1. One can find that the tilt angle of the movable electrode is limited to \( \theta_{\hbox{max} } = {\text{asin(}}{d \mathord{\left/ {\vphantom {d L}} \right. \kern-0pt} L} )\approx \) \( 0.05({\text{rad}})\,\,\, \approx 2.85 ( {\text{deg}}) \), which is rather small for the purpose of reducing the source voltage as commonly do in the relative literatures (Chen et al. 2004; Agudelo et al. 2009; Ma et al. 2011).

Table 1 The physical parameters of the ETM
Full size table

When the target positions are set to 0.5°, 1.5° and 2.5° respectively, using the output feedback controller given by (31)–(29) with the definition of errors variables (54). The stabilization results are shown in Fig. 4, of which the same set of tunable parameters is used and the coefficients of the parasitic capacitances are given to be \( \rho_{p} = \rho_{s} = 0.5 \). One can find that the source voltage holds the maximum from the Fig. 4d. If the tilt angle is larger than a given value, the source voltage in the stable state is smaller than that for a smaller stable tilt angle. This phenomenon is caused by the existence of the well-known pull-in bifurcation point in the travel range of the electrostatic microactuators.

Fig. 4
figure 4

The responses of the ETM for different positions control. a The response of the tilt angle. b The responses of the electrostatic torques and mechanical torques. c The variations of the charges. d The variations of the source voltages

Full size image

The Fig. 5 illustrates the curves of electrostatic torques with different source voltages and the mechanical torque about the variations of the tilt angle. Since the electrostatic torque should balance the mechanical torque at the stable state of the system (Fig. 4b), it is obvious that the maximum of source voltage happens to be the pull-in voltage when the overshoot is absent in the transient response.

Fig. 5
figure 5

The electrostatic torques with different actuated voltages and the mechanical torque with respect to the variations of the tilt angle

Full size image

6 Conclusions

For the purpose of simplifying the sensing subsystem of the ETMs, it is shown that the output feedback controllers can be applied to realize this end in this paper. It is the first time find that the highly nonlinear dynamics of the ETMs with considering the uncertainties of the electrical parameters can be exactly transformed into the third order linear system. For the uncertain linear systems, an output feedback control scheme that is composed of a FTS observer and a state feedback FTS controller for the third order Brunovsky’s canonical form systems is proposed in this paper. Both the controller and the observer are proved to be globally stable in finite settling time, thus the angular speed and angular acceleration of the ETMs can be accurately estimated by the observer. The stability of the output feedback controller based on the nonlinear observer is also directly proved. Therefore, the proposed controller permits the least necessary to stabilize the ETMs in its full operational range, and can be applied to control many nonlinear systems that are exactly linearizable or linear systems with bounded uncertainties, such as the full-actuated nonlinear systems and the underactuated systems with differentially flat property.