1 Introduction

Flexure based compliant manipulator transmits motion and force through its own elastic deformations, which provides the advantages such as no backlash, no friction and vacuum compatibility (Yong et al. 2009; Tang and Li 2015). Thus, compliant manipulator is preferred over the traditional manipulator in high precision applications, such as atomic force microscopy (Peng et al. 2011), optical fiber alignment (Qu et al. 2015; Zhao et al. 2012), microsurgery (Yang et al. 2012) and biomedical cell manipulation (Zhang et al. 2009). With the emergence of different specific applications, complaint manipulators with compact size and large stroke are highly desired, which raises a challenge to the mechanical design of the manipulator.

At present, the structure of the complaint manipulator for 2-DOF micro/nano positioning can be divided into two categories. One is serial structure, the other is parallel structure (Akbari and Pirbodaghi 2016; Li and Xu 2011). Serial structure is always implemented by stacking two 1-DOF mechanisms together. Though this configuration is easy to realize kinematic decoupling, it will lead to different dynamic characteristic of the two axes. At the same time, the accumulation of the positioning error is inevitable. Parallel structure is drawing more and more attention due to its advantages of high stiffness, high accuracy and high load capability (Tian et al. 2010).

Besides, decoupling design is a hot topic in this field. Decoupled mechanism is easy to control, which will reduce the difficulty of controller design. In addition, it can isolate and protect the actuators (Yue et al. 2010). So decoupling performances in terms of input decoupling and output decoupling are pursued during the design of the 2-DOF parallel compliant manipulator. Another issue is how to achieve a large motion range. Except for the mechanical structure, actuator is the primary determinant of motion ability of the manipulator. Since piezoelectric actuator (PZT) can only provide a small stroke (usually less than \({100\,\upmu {\mathrm{m}}}\)), actuators based on electromagnetic principle such as electromagnetic actuators and voice coil actuators are introduced (Tang and Chen 2006). Besides, magnetic levitation technology is also employed to develop a large stroke manipulator (Ding et al. 2012; Verma et al. 2004).

Based on the above considerations, many decoupled large stroke 2-DOF manipulators have been proposed. Awtar (2004) synthesized a family of XY flexure mechanisms with a large motion of range. Choi and Kim (2006) presented a monolithic parallel linear compliant mechanism for two axes ultraprecision linear motion. Li et al. (2012) proposed a totally decoupled compliant parallel XY micromotion stage. Xiao and Li (2013) introduced a XY micro-positioning stage that was driven by electromagnetic actuators.

In these designs, double parallelogram and symmetric layout with 2-PP or 4-PP (P for prismatic joint) configurations are adopted, which becomes the design principle of the decoupled large stroke compliant mechanisms. Based on above advances and our previous research, symmetrical double layer leaf spring flexures based compliant P joints and single layer leaf spring flexure based compliant P joints are introduced as the active P joints and passive P joints to form a 4-PP configuration in this paper. What is more, contact surface deformations of the flexures and parasitic motion are taken into consideration (Gong et al. 2013). In consequence, a novel decoupled 2-DOF manipulator that actuated by electromagnetic actuators is proposed.

In the rests of the paper, mechanical design of the manipulator is demonstrated in Sect. 2. In Sects. 3 and 4, mathematical models of the proposed micromanipulator are derived. Afterwards, FEA verifications of the mathematical models are performed in Sect. 5. System dynamic modeling and controller design are depicted in Sect. 6. And in Sect. 7, experimental tests are conducted to verify the performances of the propose manipulator. Finally, conclusion and future works are presented in Sect. 8.

2 Conceptual design of the manipulator

2.1 Original design

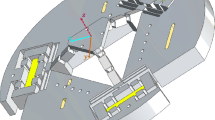
As shown in Fig. 1, the micromanipulator consists of six compliant P joints. That is, four identical symmetrical double-layer-leaf-spring-flexure compliant P joints (DCP joint) and two identical single-layer-leaf-spring-flexure compliant P joints (SCP joint). The six compliant P joints can be divided into two groups to form two branches. The two branches are orthogonally arranged along the x and y axes, respectively. Each branch is composed of two DCP joints and one SCP joint by serial connection. The symmetrical arrangement is employed to eliminate the parasitic motions caused by the single layer leaf spring flexures.

The working principle of the proposed manipulator is illustrated in Fig. 2. The manipulator is a decoupled 2-DOF translational planer mechanism. At any moment, only one DCP joint in each branch is actuated. So except for the two active P joints along the working directions, other P joints are passive P joints.

Fig. 1
figure 1

Original structure of the manipulator. 1 Fixed support, 2 compliant P module, 3 leaf spring flexure, 4 platform

Full size image

Considering the piezoelectric actuator can only produce pushing force, the workspace of the manipulator will only cover quadrant of the coordinate system. While the electromagnetic actuator can produce both pulling and pushing forces, and most importantly, it provides a non-contact actuation mode. So four electromagnetic actuators can be adopted to actuate the manipulator. The workspace will be four times the size of the piezoelectric actuated micromanipulator.

Compliant mechanism transmits forces and displacements by the elastic deformations of the flexures, which makes it preferred over the rigid mechanisms in high precision applications. From this point of view, we should make full use of elastic deformations. However, some elastic deformations in the mechanism are adverse to the performances of the manipulator. For instance, due to the single layer leaf spring flexures, totally kinematics decoupling is only valid in theory. At the same time, tensile and compression deformations of the single layer leaf spring flexures along the working direction will lead to motion loss. In addition, the deformations of the contact surfaces of the leaf spring flexures that caused by the inner forces will decrease the positioning accuracy of the micromanipulator.

To overcome the above mentioned drawbacks, some improvements aimed at improving the performances of the manipulator are made in the following section.

Fig. 2
figure 2

Working principle of the micromanipulator

Full size image

2.2 Improved design

The contact surfaces are usually considered to be rigid, so the deformations of the surfaces are ignored. But for nano/micro applications, anything that may influence the performances of the micro manipulator should be taken into consideration. Since it is difficult to establish an accurate mathematical model for the deformation. FEA simulation method is adopted in this section to fulfill an approximate optimization. As a result, a modified compliant P joint is proposed, as shown in Fig. 3.

Fig. 3
figure 3

A modified compliant P joint

Full size image

Compared with the compliant P joints introduced in Fig. 1, notches are added around the contact surfaces. FEA comparison of the normal compliant P joint and the modified compliant P joint is illustrated in Figs. 4 and 5.

Fig. 4
figure 4

Equivalent stress of the normal compliant P joint

Full size image
Fig. 5
figure 5

Equivalent stress of the modified compliant P joint

Full size image

It is observed that the stress area and the max equivalent stress of the modified compliant P joint are smaller than those of the normal compliant P joint, which indicate the notches are effective to reduce the elastic deformation of the contact surfaces.

Another benefit of the notches is that the length of the flexures can be enlarged without changing the dimension of the micromanipulator.

In order to eliminate the parasitic motion, passive DCP joints are introduced to form a symmetrical structure in this design. However, the passive DCP joint will exert a reaction force to the platform, which will decrease the output displacement of the platform. Based on the above consideration, a rigid bridge is employed to compensate the lost motion, as shown in Fig. 6.

Fig. 6
figure 6

Improved micromanipulator with rigid bridge

Full size image

The rigid bridge is fixed on the platforms of the DCP joints and has no connection with the single layer leaf spring flexures and the platform. Due to the rigid bridge, the two DCP joints in each branch will be actuated by the actuation force simultaneously, and moreover, the displacements of the two DCP joints are equal.

3 Stiffness modeling of the micromanipulator

For convenience of the analysis, the micromanipulator is divided into four identical chains and a platform, as shown in Fig. 7. Each chain consists of a DCP joint and a single layer leaf spring flexure. Due to the symmetric property, we can select one quarter of the manipulator (chain A) for the stiffness modeling.

As shown in Fig. 7, chain A is divided into 6 elements. Among which, elements ①, ②, ③, ④ and ⑥ are leaf spring flexures. Element ⑤ is rigid part of the DCP joint. The elements connect to each other by node \({{n_i}}\). Let \({{\varvec{F}_{i}}}\) and \({{\varvec{U}_{i}}}\) denote the force vectors and the corresponding displacement vectors of the node \({n_{i}}\), respectively. Without loss of generality, both the force and displacement are treated as \({6 \times \ 1}\) vectors in this study.

According to the element stiffness equation, the stiffness model of elements ① and ② can be represented as

$$\begin{aligned} {\varvec{F}}_{1}={\varvec{K}}{\varvec{U}}_{1} \end{aligned}$$
(1)
$$\begin{aligned} {\varvec{F}}_{2}={\varvec{K}}{\varvec{U}}_{2} \end{aligned}$$
(2)

where \({{\varvec{K}}}\) is the element stiffness matrix of the leaf spring flexure, which can be expressed as

$$\begin{aligned} {\varvec{K}} = \left[ {\begin{array}{lllllll} {\frac{{EA}}{l}} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} {\frac{{12EI_1}}{{{l^3}}}} &{} 0 &{} 0 &{} 0 &{} -{\frac{{6EI_1}}{{{l^2}}}} \\ 0 &{} 0 &{} {\frac{{12EI_2}}{{{l^3}}}} &{} 0 &{} { \frac{{6EI_2}}{{{l^2}}}} &{} 0 \\ 0 &{} 0 &{} 0 &{} {\frac{{G{I_P}}}{l}} &{} 0 &{} 0 \\ 0 &{} 0 &{} { \frac{{6EI_1}}{{{l^2}}}} &{} 0 &{} {\frac{{4EI_1}}{l}} &{} 0 \\ 0 &{} -{\frac{{6EI_2}}{{{l^2}}}} &{} 0 &{} 0 &{} 0 &{} {\frac{{4EI_2}}{l}} \\ \end{array}} \right] \end{aligned}$$

where E and G denote the Young’s modulus and shear modulus of the material, respectively. A and l denote the cross-section area and length of the leaf spring flexures, respectively. \({I_1}\), \({I_2}\) and \({I_p}\) denote the moment of inertia and polar moment of inertia, respectively.

Fig. 7
figure 7

Division of the micromanipulator

Full size image

Under the same coordinate system, the stiffness models of the elements ③ and ④ can be obtained by coordinate transformation. That is

$$\begin{aligned} {\varvec{F}}_{3}={{\varvec{U}}^{-1}_{1}}{\varvec{K}}{{\varvec{U}}_{1}}{{\varvec{U}}_{3}} \end{aligned}$$
(3)
$$\begin{aligned} {\varvec{F}}_{4}={{\varvec{U}}^{-1}_{1}}{\varvec{K}}{{\varvec{U}}_{1}}{{\varvec{U}}_{4}} \end{aligned}$$
(4)

where \({{{\varvec{U}}_{1}}}\) is the transformation matrix. It can be obtained by rotating the local coordinate system by 180\(^{\circ }\) about its z axis.

Considering the rigid part (elements ⑤) of the DCP joint in chain A, the following force equilibrium equation and displacement compatibility equation can be derived

$$\begin{aligned} {\varvec{F}} = \sum \limits _{n = 1}^4 {{{\varvec{f}}_n}{{\varvec{F}}_n}} \end{aligned}$$
(5)
$$\begin{aligned} {{\varvec{U}}_n} = {{\varvec{\lambda }} _n}{\varvec{U}}\begin{array}{ll} {} &{} {\left( {n = 1,2,3,4} \right) } \\ \end{array} \end{aligned}$$
(6)

where \({{\varvec{F}}}\) denotes the external force applied on elements ⑤ and \({{\varvec{U}}}\) denotes the corresponding displacement. \({{\varvec{f}}_{n}}\) and \({{\varvec{\lambda }}_{n}}\) denote the force equilibrium matrix and deformation compatibility matrix, respectively.

Substituting Eqs. (1)–(4) and (6) into (5), we can get

$$\begin{aligned} {\varvec{F}}={\varvec{K}}_{p}{\varvec{U}} \end{aligned}$$
(7)

where \({{\varvec{K}}_{p}}\) is the stiffness matrix of the DCP joint, and

$$\begin{aligned} {{\varvec{K}}_p} = {{\varvec{f}}_1}{\varvec{K}}{{\varvec{\lambda }} _1} + {{\varvec{f}}_2}{\varvec{K}}{{\varvec{\lambda }} _2} + {{\varvec{f}}_3}{{{\varvec{U}}}^{-1}_{1}{\varvec{K}}{{\varvec{U}}}_{1}}{{\varvec{\lambda }} _3} + {{\varvec{f}}_4}{{{\varvec{U}}}^{-1}_{1}{\varvec{K}}{{\varvec{U}}}_{1}}{{\varvec{\lambda }} _4} \end{aligned}$$

It can be observed that both ends of the element ⑥ will experience a displacement. This situation is much more complicated than that of elements ①–④ since both ends of element ① are loaded. When node \({n_5}\) is fixed and node n6 is free, the stiffness matrix of element ⑥ can be derived by

$$\begin{aligned} {\varvec{K}}_{1}={{\varvec{U}}}^{-1}_{2}{\varvec{K}}{{\varvec{U}}}_{2} \end{aligned}$$
(8)

where \({{{\varvec{U}}_{2}}}\) is the transformation matrix.

When both ends of element ⑥ are free, the stiffness model can be written as

$$\begin{aligned} {{\varvec{F}}_6} = {{\varvec{K}}_1}{{\varvec{U}}_6} - {\varvec{f}}{{\varvec{U}}}_3^{ - 1}{{\varvec{K}}_1}{{{\varvec{U}}}_3}{{\varvec{U}}_5} \end{aligned}$$
(9)

where \({{\varvec{f}}}\) and \({{{\varvec{U}}}_3}\) denote the force equilibrium matrix and coordinate transformation matrix, respectively. \({{\varvec{f}}}\) can be calculated by the following force equilibrium equation.

$$\begin{aligned} {{\varvec{F}}_6} + {\varvec{f}} { {{\varvec{F}}_5}} = 0 \end{aligned}$$
(10)

where \({{\varvec{F}}_{5}}\) is the internal force between the element ⑤ and element ⑥.

In view of the fact that the DCP joint in each chain is either an active P joint or a passive P joint, the stiffness model of the chain can be classified into two categories.

  1. 1.

    When chain A is an active chain, we have

    $$\begin{aligned} {\varvec{F}}_{y}+\left( - {\varvec{F}}_{5} \right) ={\varvec{k}}_{p}{\varvec{U}}_{5} \end{aligned}$$
    (11)

    Substituting Eqs. (10) and (11) into (9) will yield to

    $$\begin{aligned} {\varvec{n}}_{1}{\varvec{F}}_{y}+{\varvec{n}}_{2}{\varvec{F}}_{6}={\varvec{K}}_{1}{\varvec{U}}_{6} \end{aligned}$$
    (12)

    where

    $$\begin{aligned} {{\varvec{n}}_1} = {\varvec{f}}{{\varvec{U}}}_3^{ - 1}{{\varvec{K}}_1}{{{\varvec{U}}}_3}{\varvec{K}}_p^{ - 1} \end{aligned}$$
    $$\begin{aligned} {{\varvec{n}}_2} = {\varvec{E}} + {\varvec{f}}{{\varvec{U}}}_3^{ - 1}{{\varvec{K}}_1}{{{\varvec{U}}}_3}{\varvec{K}}_p^{ - 1}{{\varvec{f}}^{ - 1}} \end{aligned}$$
  2. 2.

    When chain A is a passive chain, there is no external force applied on element ⑤. Then according to Eq. (12) we can get

    $$\begin{aligned} {{\varvec{F}}_6} ={\varvec{n}}_{2}^{-1}{\varvec{K}}_{1}{{\varvec{U}}_6} \end{aligned}$$
    (13)

    As shown in Fig. 3, chain A and chain B are assumed as active chains. Based on Eqs. (12) and (13), the stiffness model of the other three chains can be derived by

    $$\begin{aligned} {{{\varvec{U}}}_B}{{\varvec{F}}_7} = {\varvec{n}}_2^{ - 1}{{\varvec{K}}_1}{{{\varvec{U}}}_B}{{\varvec{U}}_7} \end{aligned}$$
    (14)
    $$\begin{aligned} {{{\varvec{U}}}_C}{{\varvec{F}}_8} = {\varvec{n}}_2^{ - 1}{{\varvec{K}}_1}{{{\varvec{U}}}_C}{{\varvec{U}}_8} \end{aligned}$$
    (15)
    $$\begin{aligned} {{\varvec{n}}_1}{{{\varvec{U}}}_D}{{\varvec{F}}_x} + {{\varvec{n}}_2}{{{\varvec{U}}}_D}{{\varvec{F}}_9} = {{\varvec{K}}_1}{{{\varvec{U}}}_D}{{\varvec{U}}_9} \end{aligned}$$
    (16)

    where \({{{\varvec{U}}}_{B}}\), \({{{\varvec{U}}}_{C}}\) and \({{{\varvec{U}}}_{D}}\) are transformation matrices of chain B, chain C and chain D, respectively. Considering that external force acting on the platform can be ignored, the following force equilibrium equation and displacement compatibility equation can be obtained by

    $$\begin{aligned} \sum \limits _{j = 6}^9 {{{\varvec{f}}_j}{{\varvec{F}}_j}} = 0 \end{aligned}$$
    (17)
    $$\begin{aligned} {{\varvec{U}}_j} = {{\varvec{\lambda }} _j}{{\varvec{U}}_p} \begin{array}{ll} {} &{} {\left( {j = 6,7,8,9} \right) } \\ \end{array} \end{aligned}$$
    (18)

    where \({{\varvec{U}}_{p}}\) is the displacement of the platform. Besides, the two driving forces can be integrated into one force by

    $$\begin{aligned} {{{\varvec{F}}_x} = {{\varvec{a}}_1}{{\varvec{F}}_{IN}}}&{{{\varvec{F}}_y} = {{\varvec{a}}_2}{{\varvec{F}}_{IN}}} \end{aligned}$$
    (19)

    where \({{\varvec{a}}_{1}}\) and \({{\varvec{a}}_{2}}\) are force transformation matrices, \({{\varvec{F}}_{IN}}\) is the integrated external input force. Combining Eqs. (12) and (14)–(19), the stiffness model of the manipulator can be derived as

    $$\begin{aligned} {{\varvec{F}}_{IN}} = {{\varvec{K}}_m}{{\varvec{U}}_p} \end{aligned}$$
    (20)

    where

    $$\begin{aligned} {{\varvec{K}}_m} = {{\varvec{P}}^{ - 1}}{\varvec{Q}} \end{aligned}$$
    $$\begin{aligned} {\varvec{P}} = {{\varvec{f}}_6}{\varvec{n}}_2^{ - 1}{{\varvec{n}}_1}{{\varvec{a}}_2} + {{\varvec{f}}_9}{\left( {{{\varvec{n}}_2}{{{\varvec{U}}}_D}} \right) ^{ - 1}}{{\varvec{n}}_1}{{{\varvec{U}}}_D}{{\varvec{a}}_1} \end{aligned}$$
    $$\begin{aligned} \begin{array}{l} {\varvec{Q}} = {{\varvec{f}}_6}{\varvec{n}}_2^{ - 1}{{\varvec{K}}_1}{{\varvec{\lambda }} _6} + {{\varvec{f}}_7}{{\varvec{U}}}_B^{ - 1}{\varvec{n}}_2^{ - 1}{{\varvec{K}}_1}{{{\varvec{U}}}_B}{{\varvec{\lambda }} _7} + \\ {{\varvec{f}}_8}{{\varvec{U}}}_C^{ - 1}{\varvec{n}}_2^{ - 1}{{\varvec{K}}_1}{{{\varvec{U}}}_C}{{\varvec{\lambda }} _8} + {{\varvec{f}}_9}{\left( {{{\varvec{n}}_2}{{{\varvec{U}}}_D}} \right) ^{ - 1}}{{\varvec{K}}_1}{{{\varvec{U}}}_D}{{\varvec{\lambda }} _9} \\ \end{array} \end{aligned}$$

4 Kinematics of the micromanipulator

Equation (20) indicates the relationship of input force and output displacement. The displacement of the manipulator can be calculated when driving force is given. But it is difficult to accurately control the output force of piezoelectric actuators. So stiffness model is unsuitable for control purpose for piezoelectric actuated manipulators.

Kinematics is the relationship of input displacement and output displacement, which can be served as a control law or a reference of the controller design. Moreover, it is the basis of workspace and velocity analyses. Owing to the flexible connections, the kinematics of the flexure-based manipulators can not be derived by pseudo rigid body model. To address this issue, a new kinematics analysis method is proposed in this section.

Based on Eqs. (9)–(11), the following displacement equation can be derived

$$\begin{aligned} {\varvec{U}}_{5}={\varvec{B}}_{1}{\varvec{F}}_{y}+{\varvec{B}}_{2}{\varvec{U}}_{6} \end{aligned}$$
(21)

where

$$\begin{aligned} {{\varvec{B}}_1}={\left( {{{\varvec{U}}}_3^{{{ - }}1}{{\varvec{K}}_1}{{{\varvec{U}}}_3} + {{\varvec{K}}_p}} \right) ^{ - 1}} \end{aligned}$$
$$\begin{aligned} {{\varvec{B}}_2}={\left( {{{\varvec{U}}}_3^{{{- }}1}{{\varvec{K}}_1}{{{\varvec{U}}}_3} + {{\varvec{K}}_p}} \right) ^{ - 1}}{{\varvec{f}}^{ - 1}}{{\varvec{K}}_{1}} \end{aligned}$$

When the chain A is a passive chain, \({{\varvec{F}}_{y}=0}\). Equation (21) can be rewritten as

$$\begin{aligned} {\varvec{U}}_{5}={\varvec{B}}_{2}{\varvec{U}}_{6} \end{aligned}$$
(22)

Similarly, displacement equations for the other three chains can be obtained by coordinate transformation

$$\begin{aligned} {{\varvec{U}}}_{B}{\varvec{U}}_{B}={\varvec{B}}_{2}{{\varvec{U}}}_{B}{\varvec{U}}_{7} \end{aligned}$$
(23)
$$\begin{aligned} {{\varvec{U}}}_{C}{\varvec{U}}_{C}={\varvec{B}}_{2}{{\varvec{U}}}_{C}{\varvec{U}}_{8} \end{aligned}$$
(24)
$$\begin{aligned} {{\varvec{U}}}_{D}{\varvec{U}}_{D}={\varvec{B}}_{1}{{\varvec{U}}}_{D}{\varvec{F}}_{x}+{\varvec{B}}_{2}{{\varvec{U}}}_{D}{\varvec{U}}_{9} \end{aligned}$$
(25)

where \({{\varvec{U}}_{B}}\), \({{\varvec{U}}_{C}}\) and \({{\varvec{U}}_{D}}\) denote the displacement of DCP joints of chain B, chain C and chain D, respectively.

Combining Eqs. (18)–(21), we can get

$$\begin{aligned} {{\varvec{U}}_5} = \left( {{{\varvec{B}}_1}{{\varvec{a}}_2}{{\varvec{K}}_m} + {{\varvec{B}}_2}{{\varvec{\lambda }} _6}} \right) {{\varvec{U}}_p} \end{aligned}$$
(26)

Again, combining Eqs. (18)–(20) and (25), we can have

$$\begin{aligned} {{\varvec{U}}_D} = \left( {{{\varvec{U}}}_D^{ - 1}{{\varvec{B}}_1}{{{\varvec{U}}}_D}{{\varvec{a}}_1}{{\varvec{K}}_m} + {{\varvec{U}}}_D^{ - 1}{{\varvec{B}}_2}{{{\varvec{U}}}_D}{{\varvec{\lambda }} _9}} \right) {{\varvec{U}}_p} \end{aligned}$$
(27)

Similar to Eq. (19), \({{\varvec{U}}_{5}}\) and \({{\varvec{U}}_{D}}\) can be integrated by

$$\begin{aligned} {{{\varvec{U}}_D} = {{\varvec{a}}_1}{{\varvec{U}}_{in}}}&{{{\varvec{U}}_5} = {{\varvec{a}}_2}{{\varvec{U}}_{in}}} \end{aligned}$$
(28)

According to Eqs. (26)–(28), we can get

$$\begin{aligned} {{\varvec{U}}_{in}} = {\varvec{J}}{{\varvec{U}}_{p}} \end{aligned}$$
(29)

where

$$\begin{aligned} {\varvec{J}} &= {\left( {{{\varvec{a}}_1} + {{\varvec{a}}_2}} \right) ^{ - 1}}\left( {\left( {{{\varvec{B}}_1}{{\varvec{a}}_2}{{\varvec{K}}_m} + {{\varvec{B}}_2}{{\varvec{\lambda }} _6}} \right) } \right. \\ &\quad\left. +{\left( {{{\varvec{U}}}_D^{ - 1}{{\varvec{B}}_1}{{{\varvec{U}}}_D}{{\varvec{a}}_1}{{\varvec{K}}_m} + {{\varvec{U}}}_D^{ - 1}{{\varvec{B}}_2}{{{\varvec{U}}}_D}{{\varvec{\lambda }} _9}} \right) } \right) \end{aligned}$$

Equation (29) is the kinematics model of the manipulator. \({{\varvec{U}}_{in}}\) is the input displacement.

Besides, Eqs. (23) and (24) can be rewritten as

$$\begin{aligned} {{\varvec{U}}_B} = {{\varvec{U}}}_B^{ - 1}{{\varvec{B}}_2}{{{\varvec{U}}}_B}{{\varvec{\lambda }} _7}{{\varvec{U}}_p} \end{aligned}$$
(30)
$$\begin{aligned} {{\varvec{U}}_C} = {{\varvec{U}}}_C^{ - 1}{{\varvec{B}}_2}{{{\varvec{U}}}_C}{{\varvec{\lambda }} _8}{{\varvec{U}}_p} \end{aligned}$$
(31)

It is noticeable that when giving the output displacement of the platform, the displacements of the active P joints (input displacement) and the passive P joints can be easily calculated.

5 Model evaluation

In order to validate the derived stiffness model and kinematics model, evaluations with MATLAB and ANSYS softwares are carried out in this section. Aluminum alloy 7075 is adopted as the material of the manipulator and a set of structural parameters are given in Table 1.

Table 1 Structural parameters
Full size table

During the static FEA simulation, a force of 1N is separately exerted along the x and y axes. The results are depicted in Figs. 8 and 9, which indicate the micromanipulator is decoupled and isotropic.

Fig. 8
figure 8

Total deformation when \({{{\varvec{F}}_{IN}} = {\left[ {1,0,0,0,0,0} \right] ^T}}\)

Full size image
Fig. 9
figure 9

Total deformation when \({{{\varvec{F}}_{IN}} = {\left[ {0,1,0,0,0,0} \right] ^T}}\)

Full size image

The comparison of static FEA simulation and MATLAB numerical calculation is shown in Tables 2 and 3, respectively. Due to the symmetrical structure, only y direction is selected to evaluate the kinematics model. Furthermore, the natural frequency of the manipulator is also obtained and the first four modes are illustrated in Table 4.

Table 2 Stiffness model evaluation
Full size table
Table 3 Kinematics model evaluation (y-direction)
Full size table
Table 4 Natural frequency of the improved design
Full size table

It is observed that the results are agreeable with each other within a low error, which indicate the correctness of the derived mathematical models, especially for the kinematics model.

Since the manipulator is directly driven by the actuators, the workspace of the manipulator is determined by the output ability of the actuators. If PZTs are selected as the actuators, the workspace of the manipulator depends on the stroke of the PZTs. While when electromagnetic actuators are utilized, the workspace depends on the rated output force. For example, when four electromagnetic actuators whose rated force is 180N are employed as the actuators, the workspace of the micromanipulator can be calculated as \({1344\, \upmu {\mathrm{m}} \times 1344 \,\upmu {\mathrm{m}}}\) in theory.

6 Controller design

6.1 System dynamic model

The force generated by the electromagnetic actuator can be modeled by (Xiao and Li 2016):

$$\begin{aligned} {F_m} = c{\left( {\frac{i}{{y_a + a}}} \right) ^2} \end{aligned}$$
(32)

where a and c are constant parameters that related to the structure of the electromagnetic actuator. i is the exciting current, and \(y_a\) is the air gap between the armature and the pole surface of the actuator.

Because the electromagnetic actuator is controlled by voltage, so the electrical equation can be written as

$$\begin{aligned} e = Ri + \frac{d}{{dt}}\left( {Li} \right) \end{aligned}$$
(33)

where e is the input voltage, R and L are the resistance and inductance of the coil, respectively.

As indicated by the experiment, the inductance of the coil changes with the position of the armature, which can be expressed as

$$\begin{aligned} L= {L_1} + \frac{{a{L_0}}}{{y_a + a}} \end{aligned}$$
(34)

where \(L_1\) is the inductance when the air gap is \(\infty\), and \(L_0\) is the incremental inductance when the air gap is zero.

At any time, only one electromagnetic actuator is activated. So the motion differential equation of the system can be established as

$$\begin{aligned} m\frac{{{d^2}y_a}}{{d{t^2}}} + \omega \dot{y}_a + k\left( {{\delta _0} - y_a} \right) ={F_m} \end{aligned}$$
(35)

where m is the total mass of the moving part, including the platforms, rigid bridges and the four armatures. \(\omega\) is the damping coefficient, and k is the stiffness along the motion direction. \(\delta _0\) is the initial air gap.

Let the state variables be \(x_1=y_a\), \({x_2}= \dot{y}_a\), \(x_3=i\), and the control input be \(u=e\). Then the state-space model of the system can be written as

$$\begin{aligned} {\dot{x}_1}&= {x_2}&\nonumber \\ {\dot{x}_2}&= \frac{c}{m}{\left( {\frac{{{x_3}}}{{{x_1} + a}}} \right) ^2} - \frac{\omega }{m} x_2 - \frac{k}{m}\left( {{\delta _0} - {x_1}} \right)&\nonumber \\ {\dot{x}_3}&= \frac{1}{L}\left( { - R{x_3} + \frac{{{L_0}a{x_2}{x_3}}}{{{{\left( {{x_1} + a} \right) }^2}}} + u} \right)&\end{aligned}$$
(36)

The system is nonlinear and open-loop unstable due to the nonlinearities of the electromagnetic dynamics, which poses a great challenge for the controller design. Although mathematical model of the system is established, there are several model parameters that should be identified. At the same time, it is usually difficult to derive the control law, which makes model-based control particularly complex. To solve these problems, a model-free control method is introduced in this paper.

6.2 Repetitive control

In order to evaluate the performances of the manipulator, a high precision PID controller based on repetitive control compensation is implemented in this paper (Chao et al. 2009; Moon et al. 1998).

The block diagram is illustrated in Fig. 10, in which \({r\left( t \right) }\) is the input signals, e is the deviation of the input and output, u is the combination output of the two controllers, \({y\left( t \right) }\) is the system output signals. The PID controller is used for real-time control of the deviation, so as to decrease the uncertainty disturbances. While the repetitive controller is used for tracking the periodic input signals and restraining the periodic disturbance. A low pass filter \({Q\left( s \right) }\) is adopted to guarantee the system stability. The time constant of the filter should be properly chosen so that the system will keep stable when good tracking performance is obtained.

Fig. 10
figure 10

Block diagram of the high precision PID controller

Full size image

The combination of the traditional PID controller and the repetitive controller has the following advantages: (1) High dynamic response speed and high output signal tracking precision will be obtained based on the compound controller; (2) The periodic tracking error will be eliminated and the uncertainty disturbances will be resisted by using the compound controller.

7 Experimentation

7.1 Experimental setup

As shown in Fig. 11, a prototype of the proposed micromanipulator with optimized parameters is fabricated by using wire cut electrical discharge machining (WEDM) and other precision machining techniques. In which, aluminum alloy 7075 and pure iron DT4 are selected as materials of the micro manipulator and the armatures, respectively. A dSPACE rapid prototyping system (consists of a DS1005 DSP board, a DS2001 A/D conversion board and a DS2102 D/A conversion board) together with an industrial PC is employed as the real-time control unit. A 4-channel power amplifier based on OPA548 is designed to drive the electromagnetic actuators (model: ZYE1-P34/18 from Yueqing Zhengyong Electrical, Inc. Rated voltage 12v. Rated force 180N.). And two high speed laser displacement sensors (model: LTC-025-02 from MTI, Inc.) are adopted to measure the output displacement of the manipulator. In order to avoid the influence of external vibrations, the micromanipulator and the laser sensors are mounted on an active vibration isolation table (from Newport, Inc.). Additionally, a digital microscope (model: Supereyes T004 from D&F Co., Ltd) with a variable magnification of 0.7-4.5X for the objective is employed to monitor the motion of the micromanipulator.

Fig. 11
figure 11

Experimental setup: 1 Laser sensor controller, 2 industrial computer, 3 dSPACE control system, 4 digital microscope, 5 electromagnetic actuator amplifier, 6 x-laser displacement sensor, 7 active vibration isolation mount, 8 y-laser displacement sensor, 9 micromanipulator

Full size image

7.2 Preliminary experiments

7.2.1 Unidirectional open-loop test

Equation (32) demonstrates a negative correlation between the electromagnetic force and the air gap. It can be concluded that the smaller the air gap is, the larger the force will be generated. While in our application, air gap should be always guaranteed to provide enough space for the motion of the platform and prevent the armature from getting sucked by the actuator. Thus, the actuation voltage, the stroke and the initial air gap should be pre-determined so as to make the micromanipulator achieve optimal performances.

Calibrations are carried out to record pull-in voltage and maximum stroke for each actuator, in which feeler gauge and laser sensor are applied to set the initial air gap and detect the displacement of the platform of the micromanipulator. For a pre-set stroke, the needed actuation voltage is closely related to the initial air gap. Considering that the armature get sucked will cause vibration and chattering, initial air gap should be set relatively large. But a large air gap requires large actuation voltage. What is more, the electromagnetic force generated under rated voltage is limited, and achievable stroke is small in this circumstance. Experiments indicate that the initial air gap is appropriate to be set as 400 \({\upmu }\)m. Due to manufacturing and assembling tolerances, the actual air gap usually deviates from the nominal value. Open-loop tests are carried out to separately test the four actuators, in which a sine wave signal (0–12 v) is applied as the test signal. The actual air gap is obtained when the armature is actuated to the limit position, and the maximum actuation voltage that without causing suction is defined as safety voltage, the corresponding maximum displacement is defined as the stroke. The experimental results are shown in Table 5.

Due to the nonlinear characteristics of the electromagnetic actuator, it is difficult to accurately control the displacement of the armature in open-loop condition. Experiments show that the stroke can be significantly improved by using closed-loop control, which will be illustrated in the next section.

Table 5 Actuation voltage and stroke test
Full size table

7.2.2 Unidirectional closed-loop test

In this section, single axis closed-loop tests are carried out to verify the closed-loop stroke of each axis. The four actuators are separately driven to track a periodic sine wave signal (0.125 Hz, 0–180 \(\upmu\)m). The results are illustrated in Figs. 12 and 13. Figures 12 and 13 are closed-loop control of positive direction and negative direction of the x and y axis, respectively. It can be observed that satisfactory tracking results are obtained, the positioning errors fluctuate within ±0.5 \(\upmu\)m. Maximum error occurs near zero points (see the magnified views), which are resulted from sudden changes of acceleration and direction of the motion. Nevertheless, the consistency of the four independent tests demonstrates the isotropic characteristic of the proposed micromanipulator.

Fig. 12
figure 12

Closed-loop control of positive direction

Full size image
Fig. 13
figure 13

Closed-loop control of negative direction

Full size image

7.2.3 Bidirectional closed-loop test

Further, bidirectional closed-loop test is accomplished to demonstrate the decoupling characteristic of the micromanipulator. The two axes are controlled to synchronously track a sine wave trajectory (0.125 Hz, −80 to 80 \(\upmu\)m). The motion of the two axes are independent. As shown in Fig. 14, both axes track the desired position with very good performance, and the deviations are within ±0.6 \(\upmu\)m, which indicates that the micromanipulator posses a good decoupling performance. Therefore, we can design two single input single output (SISO) controllers to separately control the two axes without considering cross coupling.

Fig. 14
figure 14

Bi-axial synchronizing control

Full size image

7.3 Planar trajectory tracking experiments

To further illustrate the planar motion ability of the proposed micromanipulator, two more complex curve tracking experiments are conducted. In which, archimedean spiral and square spiral are selected as the target tracking trajectories due to their continuity and plane coverage ability. The tracking results are shown in Figs. 15 and 16.

As shown in Fig. 15, the micromanipulator is controlled to track a archimedean spiral with variable amplitude from the start point (3,0)\(\upmu\)m to the end point in four cycles (T = 8s). The tracking errors are shown in the sub-figure, where both x and y axes tracking errors are demonstrated. The same as the above mentioned experiments, maximum errors also occur at the switching points, specifically, when the motion switches between positive axis and negative axis. Because positive and negative direction movements of each axis are driven by different actuator respectively. In addition, the errors get larger as the velocity increases. While the deviations of both axes are within ±0.8 \(\upmu\)m.

Fig. 15
figure 15

Archimedean spiral tracking result

Full size image
Fig. 16
figure 16

Square spiral tracking result: a v = 8 \(\upmu\)m/s, b v = 16 \(\upmu\)m/s, c v = 20 \(\upmu\)m/s, d v = 30 \(\upmu\)m/s

Full size image

Then, the micromanipulator is controlled to track a square spiral curve with varied velocity, as shown in Fig. 16. The maximum switching errors are recorded as 1.5, 2.5, 3 and 5 \(\upmu\)m, respectively. While the peak to peak error during tracking process without switching points is less than 0.6 \(\upmu\)m. So it can be concluded that the influences from the velocity are much smaller than that of the switching points. In order to further improve the tracking performances of the micromanipulator, solutions should be put forward to reduce the switching errors, which becomes the primary work in our future research. Nevertheless, in view of the obtained results, the performances of the micromanipulator is evaluated. Meanwhile, the feasibility of the electromagnetic actuator in micro/nano positioning applications is verified.

8 Conclusion and future work

This paper presents the design, analysis and control of a novel decoupled large stroke 2-DOF micromanipulator. Firstly, the design process of the proposed manipulator is described. Then the stiffness model and kinematics model of the manipulator are derived and validated by using ANSYS and MATLAB softwares. Simulation results indicate that the micromanipulator posses a good decoupling and isotropy characteristics. The first two natural frequencies of the micromanipulator are obtained as 354.8 and 355.4 Hz, respectively. Based on the decoupling property, two high precision PID repetitive controllers are designed to separately control the motion of x and y axes. Finally, a prototype is fabricated and experimental setup is established. Both open-loop and closed-loop tests are carried out. The closed-loop stroke of each axis is ±180 \(\upmu\)m. Positioning accuracy is better than 0.8 \(\upmu\)m irrespective of switching point error. Experimental results indicate that maximum errors always occur at the switching points, so possible solution should be proposed to eliminate or reduce the switching error in our future work, meanwhile automatic bio-manipulation experiments will be conducted.