Abstract
An effective model is identified for thin perfectly plastic plates whose microstructure consists of the periodic assembling of two elastoplastic phases, as the periodicity parameter converges to zero. Assuming that the thickness of the plates and the periodicity of the microstructure are comparably small, a limiting description is obtained in the quasistatic regime via simultaneous homogenization and dimension reduction by means of evolutionary \(\Gamma \)-convergence, two-scale convergence, and periodic unfolding.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With this paper, we begin the task of identifying reduced models for thin composite elastoplastic plates with periodic microstructure. We focus here on the case in which the thickness h of the plates and their microstructure width \(\varepsilon _h\) are asymptotically comparable, namely, we assume the existence of the limit
This corresponds, roughly speaking, to the situation in which homogenization and dimension reduction occur somewhat simultaneously and a strong interaction between vanishing thickness and periodicity comes into play. Different scalings of \(\gamma \) (i.e., \(\gamma =0\) and \(\gamma =+\infty \)) will be the subject of a forthcoming companion paper.
Finding lower dimensional models for thin three-dimensional structures is a classical task in the Mathematics of Continuum Mechanics. A rigorous identification of a reduced model for perfectly plastic plates in the quasistatic regime has been undertaken in [13]. An additional regularity result for the associated stress has been established in [19]. The case of dynamic perfect plasticity is the subject of [28, 38], whereas the setting of shallow shells has been tackled in [37]. A parallel analysis in the presence of hardening has been performed in [35, 36] We further mention the two works [14, 15] in the purview of finite plasticity.
The study of composite elastoplastic materials is a challenging endeavour. In the small strain regime, limit plasticity equations have been identified in [31, 32, 42] both in the periodic and in the aperiodic and stochastic settings. The Fleck and Willis model is the subject of [25, 27], whereas gradient plasticity has been studied in [30]. For completeness, we also mention [9, 10, 16, 18] for an analysis of large-strain stratified composites in crystal plasticity and [17] for a static result in the finitely plastic setting. The characterization of inhomogeneous perfectly plastic materials and a subsequent periodic homogenization have been undertaken in [23, 24].
The novelty of the present contribution consists in the fact that we combine both dimension reduction and periodic homogenization in order to deduce a limiting description, as the two smallness scales (thickness and width of the microstructure) converge to zero, for perfectly plastic thin plates.
To complete our literature overview, we briefly recall the main mathematical contributions on simultaneous homogenization and dimension reduction. In [6], the author derives a limiting plate model starting from 3d linearized elasticity, while assuming the material to be isotropic and the microstructure to be periodic. In [12], the case of linear elastic plates with possible aperiodic microstructure is tackled by relying on material (planar) symmetries of the elasticity tensor, and by introducing the notion of H-convergence adapted to dimension reduction. In [4] an effective plate model is identified in the general case (without further periodicity or material-symmetries assumptions) by means of \(\Gamma \)-convergence (the analysis presented there also covers some non-linear models). We also mention the book [41] where linear rod and plate models are obtained by simultaneous homogenization and dimension reduction, and appropriate estimates are also provided, as well as the recent work [5] on high-contrast elastic plates. Different non-linear elastic plate models obtained by \(\Gamma \)-convergence are discussed in [3, 8, 33, 40, 45].
To the Authors’ knowledge, this manuscript represents instead the first work on effective theories for plates undergoing inelastic deformations.
We conclude this introduction by briefly presenting our results. First, after establishing a general disintegration result for measures in the image of suitable first-order differential operators, cf. Proposition 4.2, and relying on an auxiliary result related to De Rham cohomology, cf. Proposition 4.11, in Theorem 4.14, we identify two-scale limits of rescaled strains. We point out that the intermediate results in Proposition 4.2 are of independent interest and apply to a more general setting than that investigated in this contribution. We have chosen to pursue this avenue because these tools will also be instrumental for the analysis of further regimes of plastic thin-plates homogenization. We emphasize that for identifying two-scale limits of rescaled strains we could not rely on the results obtained in the context of elasticity (see, e.g. [4]), since these results relied on Korn inequalities which are not available in the plastic setting, hence a new approach needed to be developed.
For a given boundary datum w, the limiting model that we identify is finite on triples \((u,E,P) \in \mathcal {A}^{hom}_{\gamma }(w)\), where the latter denotes the set of limits of plastic triples given by displacements, elastic, and plastic strains in the sense of two-scale convergence for measures, cf. Definition 3.9. We refer to Definition 5.7 and to Sect. 5.2 for the precise definition and main disintegration properties of the class \(\mathcal {A}^{hom}_{\gamma }(w)\). On such triples, the effective elastic energy and dissipation potential are homogenized densities depending only on the limiting two-scale elastic and plastic strain, respectively. Our analysis stems from adapting the approach of [23] to the setting of dimension reduction problems for composite plates. This is, however, a non-trivial task: a first hurdle consists in the already mentioned compactness result for rescaled strains, see Sect. 4.3. Further difficulties originate from the fact that the limit problem is of fourth order, see Sect. 5. Further, analogously to [13], the limiting description is truly three-dimensional. We refer to [19, Section 5] for a discussion of this issue and an example. Our effective model is completely characterized in Sect. 5.5. After introducing a suitable notion of stress–strain duality, in Theorem 5.15 we prove a two-scale limiting Hill’s principle. The lower semicontinuity of the effective energy and dissipation functionals is proven in Theorem 5.17. Key tools are an adaptation of unfolding techniques for dimension reduction (see Proposition 4.17), as well as a technical rank-one decomposition characterization (see Lemma 4.18). Finally, with Theorem 6.2 we prove the main result of this contribution, showing via evolutionary \(\Gamma \)-convergence, cf. [39] the convergence of three-dimensional inhomogeneous quasistatic evolutions to energetic solutions for our two-scale reduced model.
The paper is organized as follows. Section 2 contains some preliminary results on two-scale convergence, disintegration of Radon measures, BD and BH functions, as well as some auxiliary claims about stress tensors. In Sect. 3 we specify the setting of the problem and the main assumptions. We additionally recall the existence results for quasistatic evolution for general multi-phase materials. The characterization of limiting triples in the sense of two-scale convergence for Radon measures is the focus of Sect. 4. The effective stress–strain duality is analyzed in Sect. 5, whereas the convergence of quasistatic evolutions is proven in Sect. 6.
2 Preliminaries
In this section we specify our notation and collect a few preliminary results.
2.1 Notation
We will write any point \(x \in \mathbb {R}^3\) as a pair \((x',x_3)\), with \(x' \in \mathbb {R}^2\) and \(x_3 \in \mathbb {R}\), and we will use the notation \(\nabla _{x'}\) to denote the gradient with respect to \(x'\). We denote by \(y \in \mathcal {Y}\) the points on a flat 2-dimensional torus (\(\mathcal {Y}=\mathbb {R}^2/\mathbb {Z}^2\) with quotient topology). We denote by I the open interval \(I:= \left( -\frac{1}{2}, \frac{1}{2}\right) \). In what follows we will also adopt the following notation for scaled gradients and symmetrized scaled gradients:
where \(h,\gamma >0\) and v is a function on the appropriate domain. The scaled divergence operators \(\textrm{div}_h\) and \({\widetilde{\textrm{div}}}_{\gamma }\) are defined in the following way:
Analogously, we define the operator \({\widetilde{{{\,\textrm{curl}\,}}}}_{\gamma }\), for functions taking values in \(\mathbb {R}^3\) (see (4.21)–(4.23) below). Note that the operators \({\widetilde{\nabla }}_{\gamma }\), \({\widetilde{\textrm{div}}}_{\gamma }\), \({\widetilde{{{\,\textrm{curl}\,}}}}_{\gamma }\) act on functions that have as (part of) their domain \(I \times \mathcal {Y}\) (with a slight abuse of notation we write this domain with I on the first place, despite the fact that the associated differential operators are defined as above). Furthermore, if \(\gamma = 1\) we will use the shorter notation \({\widetilde{E}}\), \({\widetilde{\nabla }}\), \({\widetilde{\textrm{div}}}\), \({\widetilde{{{\,\textrm{curl}\,}}}}\) for the corresponding differential operators.
If \(a, b \in \mathbb {R}^N\), we write \(a \cdot b\) for the Euclidean scalar product, and we denote by \(|a|:= \sqrt{a \cdot a}\) the Euclidean norm. We write \(\mathbb {M}^{N \times N}\) for the set of real \(N \times N\) matrices. If \(A, B \in \mathbb {M}^{N \times N}\), we use the Frobenius scalar product \(A: B:= \sum _{i,j}A_{ij}\,B_{ij}\) and the associated norm \(|A|:= \sqrt{A:A}\). We denote by \(\mathbb {M}^{N \times N}_{{{\,\textrm{sym}\,}}}\) the space of real symmetric \(N \times N\) matrices, and by \(\mathbb {M}^{N \times N}_{{{\,\textrm{dev}\,}}}\) the set of real deviatoric matrices, respectively, i.e. the subset of \(\mathbb {M}^{N \times N}_{{{\,\textrm{sym}\,}}}\) given by matrices having null trace. For every matrix \(A \in \mathbb {M}^{N \times N}\) we denote its trace by \(\textrm{tr}{A}\), and its deviatoric part by \(A_{{{\,\textrm{dev}\,}}}\) will be given by
The symmetrized tensor product \(a \odot b\) of two vector \(a, b \in \mathbb {R}^N\) is the symmetric matrix with entries \((a \odot b)_{ij}:= \frac{a_i b_j + a_j b_i}{2}\). Note that \(\textrm{tr}{\left( a \odot b\right) } = a \cdot b\), and that \(|a \odot b|^2 = \frac{1}{2}|a|^2|b|^2 + \frac{1}{2}(a \cdot b)^2\), so that
Given a vector \(v \in \mathbb {R}^3\), we will use the notation \(v^{\prime }\) to denote the vector
The Lebesgue measure in \(\mathbb {R}^N\) and the \((N-1)\)-dimensional Hausdorff measure are denoted by \(\mathcal {L}^N\) and \(\mathcal {H}^{N-1}\), respectively. For \(U \subset \mathbb {R}^N\), \(\overline{U}\) denotes its closure. Given an open subset \(U \subset \mathbb {R}^N\) and a finite dimensional Euclidean space E, we use standard notations for Lebesgue spaces \(L^p(U;E)\) and Sobolev spaces \(H^1(U;E)\) or \(W^{1,p}(U;E)\). The characteristic function of U will be given by \(\mathbb {1}_{U}\).
We will write \(C^k(U;E)\) for the space of k-times continuously differentiable functions \(\varphi : U\rightarrow E\) and \(C^{\infty }(U;E):= \bigcap _{k=0}^{\infty } C^k(U;E)\) for the space of infinitely differentiable function. We will distinguish between the spaces \(C_c^k(U;E)\) (\(C^k\) functions with compact support contained in \(U\)) and \(C_0^k(U;E)\) (\(C^k\) functions “vanishing on \(\partial {U}\)"). We will write \(C(\mathcal {Y};E)\) to denote the space of all continuous functions which are \([0,1]^2\)-periodic, and set \(C^k(\mathcal {Y};E):= C^k(\mathbb {R}^2;E) \cap C(\mathcal {Y};E)\). We will identify \(C^k(\mathcal {Y};E)\) with the space of all \(C^k\) functions on the 2-dimensional torus.
We will frequently make use of the standard mollifier \(\rho \in C^{\infty }(\mathbb {R}^N)\), defined by
where the constant \(C > 0\) is selected so that \(\int _{\mathbb {R}^N} \rho (x) \,dx = 1\), and the associated family \(\{\rho _\epsilon \}_{\epsilon >0} \subset C^{\infty }(\mathbb {R}^N)\) with
Throughout the text, the letter C stands for generic constants which may vary from line to line.
2.2 Measures
We first recall some basic notions from measure theory that we will use throughout the paper (see, e.g. [22]).
Given a Borel set \(U\subset \mathbb {R}^N\) and a finite dimensional Hilbert space X, we denote by \(\mathcal {M}_b(U;X)\) the space of bounded Borel measures on \(U\) taking values in X, and endowed with the norm \(\Vert \mu \Vert _{\mathcal {M}_b(U;X)}:= |\mu |(U)\), where \(|\mu | \in \mathcal {M}_b(U;\mathbb {R})\) is the total variation of the measure \(\mu \). For every \(\mu \in \mathcal {M}_b(U;X)\) we consider the Lebesgue decomposition \(\mu = \mu ^a + \mu ^s\), where \(\mu ^a\) is absolutely continuous with respect to the Lebesgue measure \(\mathcal {L}^N\) and \(\mu ^s\) is singular with respect to \(\mathcal {L}^N\). If \(\mu ^s = 0\), we always identify \(\mu \) with its density with respect to \(\mathcal {L}^N\), which is a function in \(L^1(U;X)\). With a slight abuse of notation, we will write \(\mathcal {M}_b(U;\mathbb {R})=\mathcal {M}_b(U)\) and \(\mathcal {M}_b(U;{[0,+\infty )})=\mathcal {M}_b^+(U)\).
If the relative topology of \(U\) is locally compact, by Riesz representation theorem the space \(\mathcal {M}_b(U;X)\) can be identified with the dual of \(C_0(U;X)\), which is the space of all continuous functions \(\varphi : U\rightarrow X\) such that the set \(\{|\varphi |\ge \delta \}\) is compact for every \(\delta > 0\). The weak* topology on \(\mathcal {M}_b(U;X)\) is defined using this duality.
The restriction of \(\mu \in \mathcal {M}_b(U;X)\) to a subset \(E \subset U\) is the measure \(\mu \lfloor {E} \in \mathcal {M}_b(E;X)\) defined by
Given two real-valued measures \(\mu _1,\, \mu _2 \in \mathcal {M}_b(U)\) we write \(\mu _1 \ge \mu _2\) if \(\mu _1(B) \ge \mu _2(B)\) for every Borel set \(B \subset U\).
2.2.1 Convex functions of measures
Let U be an open set of \(\mathbb {R}^N\). For every \(\mu \in \mathcal {M}_b(U;X)\) let \(\frac{d\mu }{d|\mu |}\) be the Radon-Nikodym derivative of \(\mu \) with respect to its variation \(|\mu |\). Let \(H: X \rightarrow [0,+\infty )\) be a convex and positively one-homogeneous function such that
where r and R are two constants, with \(0 < r \le R\).
Using the theory of convex functions of measures, developed in [21, 29], we introduce the nonnegative Radon measure \(H(\mu ) \in \mathcal {M}_b^+(U)\) defined by
for every Borel set \(A \subset U\). We also consider the functional \(\mathcal {H}: \mathcal {M}_b(U;X) \rightarrow [0,+\infty )\) defined by
One can prove that \(\mathcal {H}\) is lower semicontinuous on \(\mathcal {M}_b(U;X)\) with respect to weak* convergence (see, e.g., [1, Theorem 2.38]).
Let \(a,\, b \in [0,T]\) with \(a \le b\). The total variation of a function \(\mu : [0,T] \rightarrow \mathcal {M}_b(U;X)\) on [a, b] is defined by
Analogously, we define the \(\mathcal {H}\)-variation of a function \(\mu : [0,T] \rightarrow \mathcal {M}_b(U;X)\) on [a, b] as
From (2.2) it follows that
2.2.2 Disintegration of a measure
Let S and T be measurable spaces and let \(\mu \) be a measure on S. Given a measurable function \(f: S \rightarrow T\), we denote by \(f_{\#}\mu \) the push-forward of \(\mu \) under the map f, defined by
In particular, for any measurable function \(g: T \rightarrow {\overline{\mathbb {R}}}\) we have
Note that in the previous formula \(S = f^{-1}(T)\).
Let \(S_1 \subset \mathbb {R}^{N_1}\), \(S_2 \subset \mathbb {R}^{N_2}\), for some \(N_1,N_2 \in \mathbb {N}\), be open sets, and let \(\eta \in \mathcal {M}_b^+(S_1)\). We say that a function \(x_1 \in S_1 \mapsto \mu _{x_1} \in \mathcal {M}_b(S_2;\mathbb {R}^M)\) is \(\eta \)-measurable if \(x_1 \in S_1 \mapsto \mu _{x_1}(B)\) is \(\eta \)-measurable for every Borel set \(B \subseteq S_2\).
Given a \(\eta \)-measurable function \(x_1 \mapsto \mu _{x_1}\) such that \(\int _{S_1}|\mu _{x_1}|\,d\eta <+\infty \), then the generalized product \(\eta {\mathop {\otimes }\limits ^{\text {gen.}}}\mu _{x_1}\) satisfies \(\eta {\mathop {\otimes }\limits ^{\text {gen.}}}\mu _{x_1} \in \mathcal {M}_b(S_1 \times S_2;\mathbb {R}^M)\) and is such that
for every bounded Borel function \(\varphi : S_1 \times S_2 \rightarrow \mathbb {R}\).
Moreover, the following disintegration result holds (c.f. [1, Theorem 2.28 and Corollary 2.29]):
Theorem 2.1
Let \(\mu \in \mathcal {M}_b(S_1 \times S_2;\mathbb {R}^M)\) and let \(proj: S_1 \times S_2 \rightarrow S_1\) be the projection on the first factor. Denote by \(\eta \) the push-forward measure \(\eta := proj_{\#}|\mu | \in \mathcal {M}_b^+(S_1)\). Then there exists a unique family of bounded Radon measures \(\{\mu _{x_1}\}_{x_1 \in S_1} \subset \mathcal {M}_b(S_2;\mathbb {R}^M)\) such that \(x_1 \rightarrow \mu _{x_1}\) is \(\eta \)-measurable, and
For every \(\varphi \in L^1(S_1 \times S_2, d|\mu |)\) we have
Furthermore,
Arguing as in [23, Remark 5.5], we have the following:
Proposition 2.2
With the same notation as in Theorem 2.1, for \(\eta \)-a.e. \(x_1 \in S_1\)
Proof
Since \(\frac{d\mu }{d|\mu |} \in L^1(S_1 \times S_2, d|\mu |)\), from Theorem 2.1 we have \(\frac{d\mu }{d|\mu |}(x_1,\cdot ) \in L^1(S_2,d|\mu _{x_1}|)\) for \(\eta \)-a.e. \(x_1 \in S_1\). Thus,
from which we have the claim. \(\square \)
2.3 BD and BH functions
2.3.1 Functions with bounded deformation
Let U be an open set of \(\mathbb {R}^N\). The space BD(U) of functions with bounded deformation is the space of all functions \(u \in L^1(U;\mathbb {R}^N)\) whose symmetric gradient \(Eu:={{\,\textrm{sym}\,}}\, Du\) (in the sense of distributions) satisfies \(Eu \in \mathcal {M}_b(U;{\mathbb {M}}^{N \times N}_{sym})\). We point out that BD(U) is a Banach space endowed with the norm
We say that a sequence \(\{u^k\}_k\) converges to u weakly* in BD(U) if \(u^k\rightharpoonup u\) weakly in \(L^1(U;\mathbb {R}^N)\) and \(Eu^k\rightharpoonup Eu\) weakly* in \(\mathcal {M}_b(U;{\mathbb {M}}^{N \times N}_{sym})\). As a consequence of compactness, then necessarily \(\{u^k\}_k\) converges to u strongly in \(L^1\). Every bounded sequence in BD(U) has a weakly* converging subsequence. If U is bounded and has a Lipschitz boundary, BD(U) can be embedded into \(L^{N/(N-1)}(U;\mathbb {R}^N)\) (the embedding is compact in \(L^p\), for \(1 \le p<N/(N-1)\)) and every function \(u \in BD(U)\) has a trace, still denoted by u, which belongs to \(L^1(\partial U;\mathbb {R}^N)\). If \(\Gamma \) is a nonempty open subset of \(\partial U\), there exists a constant \(C>0\), depending on U and \(\Gamma \), such that
(see [43, Chapter II, Proposition 2.4 and Remark 2.5]). For the general properties of the space BD(U) we refer to [43].
2.3.2 Functions with bounded Hessian
The space BH(U) of functions with bounded Hessian is the space of all functions \(u \in W^{1,1}(U)\) whose Hessian \(D^2u\) (in the sense of distributions) belongs to \(\mathcal {M}_b(U;{\mathbb {M}}^{N \times N}_{\textrm{sym}})\). It is a Banach space endowed with the norm
If U has the cone property, then BH(U) coincides with the space of functions in \(L^1(U)\) whose Hessian belongs to \(\mathcal {M}_b(U;\mathbb M^{N \times N}_{sym})\). If U is bounded and has a Lipschitz boundary, BH(U) can be embedded into \(W^{1,N/(N-1)}(U)\). If U is bounded and has a \(C^2\) boundary, then for every function \(u \in BH(U)\) one can define the traces of u and of \(\nabla u\), still denoted by u and \(\nabla u\); they satisfy \(u \in W^{1,1}(\partial U)\), \(\nabla u \in L^1(\partial U;\mathbb {R}^N)\), and \(\frac{\partial u}{\partial \tau }=\nabla u\cdot \tau \) in \(L^1(\partial U)\), where \(\tau \) is any tangent vector to \(\partial U\). If, in addition, \(N=2\), then BH(U) embeds into \(C({\overline{U}})\), which is the space of all continuous functions on \({\overline{U}}\). The general properties of the space BH(U) can be found in [20].
2.4 Auxiliary claims about stress tensors
2.4.1 Traces of stresses
We suppose here that \(U\) is an open bounded set of class \(C^2\) in \(\mathbb {R}^N\). If \(\sigma \in L^2(U;\mathbb {M}^{N \times N}_{{{\,\textrm{sym}\,}}})\) and \(\textrm{div}\sigma \in L^2(U;\mathbb {R}^N)\), then we can define a distribution \([ \sigma \nu ]\) on \(\partial {U}\) by
for every \(\psi \in H^1(U;\mathbb {R}^N)\). It follows that \([ \sigma \nu ] \in H^{-1/2}(\partial {U};\mathbb {R}^N)\) (see, e.g., [44, Chapter 1, Theorem 1.2]). If, in addition, \(\sigma \in L^{\infty }(U;\mathbb {M}^{N \times N}_{{{\,\textrm{sym}\,}}})\) and \(\textrm{div}\sigma \in L^N(U;\mathbb {R}^N)\), then (2.5) holds for \(\psi \in W^{1,1}(U;\mathbb {R}^N)\). By Gagliardo’s extension theorem [26, Theorem 1.II], in this case we have \([ \sigma \nu ] \in L^{\infty }(\partial {U};\mathbb {R}^N)\), and

whenever  and
and  weakly in \(L^N(U;\mathbb {R}^N)\).
weakly in \(L^N(U;\mathbb {R}^N)\).
We will consider the normal and tangential parts of \([ \sigma \nu ]\), defined by
Since \(\nu \in C^1(\partial {U};\mathbb {R}^N)\), we have that \([ \sigma \nu ]_\nu ,\, [ \sigma \nu ]_\nu ^\perp \in H^{-1/2}(\partial {U};\mathbb {R}^N)\). If, in addition, \(\sigma _{{{\,\textrm{dev}\,}}} \in L^{\infty }(U;\mathbb {M}^{N \times N}_{{{\,\textrm{dev}\,}}})\), then it was proved in [34, Lemma 2.4] that \([ \sigma \nu ]_\nu ^\perp \in L^{\infty }(\partial {U};\mathbb {R}^N)\) and
More generally, if \(U\) has Lipschitz boundary and is such that there exists a compact set \(S \subset \partial {U}\) with \(\mathcal {H}^{N-1}(S) = 0\) such that \(\partial {U} {\setminus } S\) is a \(C^2\)-hypersurface, then arguing as in [24, Section 1.2] we can uniquely determine \([ \sigma \nu ]_\nu ^\perp \) as an element of \(L^{\infty }(\partial {U};\mathbb {R}^N)\) through any approximating sequence \(\{\sigma _n\} \subset C^{\infty }(\overline{U};\mathbb {M}^{N \times N}_{{{\,\textrm{sym}\,}}})\) such that
2.4.2 \(L^p\) regularity
We recall the following proposition from [24] (see also [34]).
Proposition 2.3
Let \(U\subset \mathbb {R}^N\) be an open, bounded set with Lipschitz boundary. The set
is a subset of \(L^p(U;\mathbb {M}^{N \times N}_{{{\,\textrm{sym}\,}}})\) for every \(1 \le p < \infty \), and
3 Setting of the problem
We describe here our modeling assumptions and recall a few associated instrumental results. Unless otherwise stated, \(\omega \subset \mathbb {R}^2\) is a bounded, connected, and open set with \(C^2\) boundary. Given a small positive number \(h > 0\), we assume that the set
is the reference configuration of a linearly elastic and perfectly plastic plate.
We consider a non-zero Dirichlet boundary condition on the whole lateral surface, i.e. the Dirichlet boundary of \(\Omega ^h\) is given by \(\Gamma _D^h:= \partial \omega \times (h I)\).
We work under the assumption that the body is only submitted to a hard device on \(\Gamma _D^h\) and that there are no applied loads, i.e. the evolution is only driven by time-dependent boundary conditions. More general boundary conditions, together with volume and surface forces have been considered, e.g., in [11, 13, 24] but will, for simplicity of exposition, be neglected in this analysis.
3.1 Phase decomposition
We recall here some basic notation and assumptions from [23].
Recall that \(\mathcal {Y}= \mathbb {R}^2/\mathbb {Z}^2\) is the 2-dimensional torus, let \(Y:= [0, 1)^2\) be its associated periodicity cell, and denote by \(\mathcal {I}: \mathcal {Y}\rightarrow Y\) their canonical identification. We denote by \(\mathcal {C}\) the set
For any \(\mathcal {Z}\subset \mathcal {Y}\), we define
and to every function \(F: \mathcal {Y}\rightarrow X\) we associate the \(\varepsilon \)-periodic function \(F_\varepsilon : \mathbb {R}^2 \rightarrow X\), given by
With a slight abuse of notation we will also write \(F_\varepsilon (x) = F\left( \frac{x}{\varepsilon }\right) \).
The torus \(\mathcal {Y}\) is assumed to be made up of finitely many phases \(\mathcal {Y}_i\) together with their interfaces. We assume that those phases are pairwise disjoint open sets with Lipschitz boundary. Then we have \(\mathcal {Y}= \bigcup _{i} \overline{\mathcal {Y}}_i\) and we denote the interfaces by
Furthermore, the interfaces are assumed to have a negligible intersection with the set \(\mathcal {C}\), i.e. for every i
We will write
where \(\Gamma _{ij}\) stands for the interface between \(\mathcal {Y}_i\) and \(\mathcal {Y}_j\).
We assume that \(\omega \) is composed of the finitely many phases \((\mathcal {Y}_i)_\varepsilon \), and that \(\Omega ^h \cup \Gamma _D^h\) is a geometrically admissible multi-phase domain in the sense of [24, Subsection 1.2]. Additionally, we assume that \(\Omega ^h\) is a specimen of an elasto-perfectly plastic material having periodic elasticity tensor and dissipation potential.
We are interested in the situation when the period \(\varepsilon \) is a function of the thickness h, i.e. \(\varepsilon = {\varepsilon _h}\), and we assume that the limit
exists in \((0, +\infty )\). We additionally require that \(\Gamma \) satisfies the following: there exists a compact set \(S \subset \Gamma \) with \(\mathcal {H}^1(S) = 0\) such that \(\Gamma {\setminus } S\) is a \(C^2\)-hypersurface.
We say that a multi-phase torus \(\mathcal {Y}\) is geometrically admissible if it satisfies the above assumptions.
Remark 3.1
We point out that we assume greater regularity than that in [23], where the interface \(\Gamma {\setminus } S\) was allowed to be a \(C^1\)-hypersurface. Under such weaker assumptions, in fact, the tangential part of the trace of an admissible stress \([ \sigma \nu ]_\nu ^\perp \) at a point x on \(\Gamma \setminus S\) would not be defined independently of the considered approximating sequence. By requiring a higher regularity of \(\Gamma \setminus S\), we will avoid dealing with this situation.
The set of admissible stresses.
We assume there exist convex compact sets \(K_i \in \mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}}\) associated to each phase \(\mathcal {Y}_i\). We work under the assumption that there exist two constants \(r_K\) and \(R_K\), with \(0 < r_K \le R_K\), such that for every i
Finally, we define
The elasticity tensor.
For every i, let \((\mathbb {C}_{\textrm{dev}})_i\) and \(k_i\) be a symmetric positive definite tensor on \(\mathbb {M}^{3\times 3}_{\textrm{dev}}\) and a positive constant, respectively, such that there exist two constants \(r_c\) and \(R_c\), with \(0 < r_c \le R_c\), satisfying
Let \(\mathbb {C}\) be the elasticity tensor, considered as a map from \(\mathcal {Y}\) taking values in the set of symmetric positive definite linear operators, \(\mathbb {C}: \mathcal {Y}\times \mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}} \rightarrow \mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}\), defined as
where \(\mathbb {C}_{{{\,\textrm{dev}\,}}}(y)=(\mathbb {C}_{{{\,\textrm{dev}\,}}})_i\) and \(k(y) = k_i\) for every \(y \in \mathcal {Y}_i\).
Let \(Q:\mathcal {Y}\times \mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}\rightarrow [0,+\infty )\) be the quadratic form associated with \(\mathbb {C}\), and given by
It follows that Q satisfies
The dissipation potential.
For each i, let \(H_i: \mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}} \rightarrow [0,+\infty )\) be the support function of the set \(K_i\), i.e
It follows that \(H_i\) is convex, positively 1-homogeneous, and satisfies
Then we define the dissipation potential \(H: \mathcal {Y}\times \mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}} \rightarrow [0,+\infty ]\) as follows:
-
i
For every \(y \in \mathcal {Y}_i\), we take
$$\begin{aligned} H(y, \xi ):= H_i(\xi ). \end{aligned}$$ -
ii
For a point \(y \in \Gamma \setminus S\) on the interface between \(\mathcal {Y}_i\) and \(\mathcal {Y}_j\), such that the associated normal \(\nu (y)\) points from \(\mathcal {Y}_j {\times I}\) to \(\mathcal {Y}_i {\times I}\), we set
$$\begin{aligned} H(y, \xi ):= {\left\{ \begin{array}{ll} H_{ij}(a, \nu (y)) &{} \ \text { if } \xi = a \odot \nu (y) \in \mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}},\\ +\infty &{} \ \text { otherwise on }\mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}}, \end{array}\right. } \end{aligned}$$where for \(a \in \mathbb {R}^3\) and \(\nu \perp a \in \mathbb {S}^2\),
$$\begin{aligned} H_{ij}(a, \nu ) := \inf \Big \{&H_i( a_i \odot \nu ) + H_j( -a_j \odot \nu ) :\\&a = a_i - a_j,\ a_i \perp \nu ,\ a_j \perp \nu \Big \}. \end{aligned}$$ -
iii
For \(y \in S\), we define H arbitrarily (e.g. \(H(y, \xi ):= r_k\,|\xi |\)).
Remark 3.2
We point out that H is a Borel function on \(\mathcal {Y}\times \mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}}\). Furthermore, for each \(y \in \mathcal {Y}\), the function \(\xi \mapsto H(y, \xi )\) is positively 1-homogeneous and convex. However, the function \((y, \xi ) \mapsto H(y, \xi )\) is not necessarily lower semicontinous. This creates additional difficulties in proving lower semicontinuity of dissipation functional given in Theorem 5.17, see also [23, Theorem 5.7].
Admissible triples and energy.
On \(\Gamma _D^h\) we prescribe a boundary datum being the trace of a map \(w^h \in H^1(\Omega ^h;\mathbb {R}^3)\) of the following form:
where \({\bar{w}}_\alpha \in H^1(\omega )\), \(\alpha =1,2\), and \({\bar{w}}_3 \in H^2(\omega )\). The set of admissible displacements and strains for the boundary datum \(w^h\) is denoted by \(\mathcal {A}(\Omega ^h, w^h)\) and is defined as the class of all triples \((v,f,q) \in BD(\Omega ^h) \times L^2(\Omega ^h;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}) \times \mathcal {M}_b(\Omega ^h;\mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}})\) satisfying
The function v represents the displacement of the plate, while f and q are called the elastic and plastic strain, respectively.
For every admissible triple \((v,f,q) \in \mathcal {A}(\Omega ^h, w^h)\) we define the associated energy as
The first term represents the elastic energy, while the second term accounts for plastic dissipation.
3.2 The rescaled problem
As usual in dimension reduction problems, it is convenient to perform a change of variables in such a way to rewrite the system on a fixed domain independent of h. To this purpose, we consider the open interval \(I = \left( -\frac{1}{2}, \frac{1}{2}\right) \) and set
We consider the change of variables \(\psi _h: \overline{\Omega } \rightarrow \overline{\Omega ^h}\), defined as
and the linear operator \(\Lambda _h: \mathbb {M}_{{{\,\textrm{sym}\,}}}^{3 \times 3} \rightarrow \mathbb {M}_{{{\,\textrm{sym}\,}}}^{3 \times 3}\) given by
To any triple \((v,f,q) \in \mathcal {A}(\Omega ^h, w^h)\) we associate a triple \((u,e,p) \in BD(\Omega ) \times L^2(\Omega ;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}) \times \mathcal {M}_b(\Omega \cup \Gamma _D;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) defined as follows:
Here the measure \(\psi _h^{\#}(q) \in \mathcal {M}_b(\Omega ;\mathbb {M}^{3 \times 3})\) is the pull-back measure of q, satisfying
According to this change of variable we have
where
and
We also introduce the scaled Dirichlet boundary datum \(w \in H^1(\Omega ;\mathbb {R}^3)\), given by
By the definition of the class \(\mathcal {A}(\Omega ^h, w^h)\) it follows that the scaled triple (u, e, p) satisfies the equalities
We are thus led to introduce the class \(\mathcal {A}_h(w)\) of all triples \((u,e,p) \in BD(\Omega ) \times L^2(\Omega ;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}) \times \mathcal {M}_b(\Omega \cup \Gamma _D;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) satisfying (3.13)–(3.15), and to define the functional
for every \((u,e,p) \in {\mathcal {A}}_h(w)\). In the following we will study the asymptotic behaviour of the quasistatic evolution associated with \(\mathcal {J}_{h}\), as \(h \rightarrow 0\) and \(\varepsilon _h \rightarrow 0\).
Notice that if \({\bar{w}}_\alpha \in H^1(\widetilde{\omega })\), \(\alpha =1,2\), and \({\bar{w}}_3 \in H^2(\widetilde{\omega })\), where \(\omega \subset \widetilde{\omega }\), then we can trivially extend the triple (u, e, p) to \(\widetilde{\Omega }:= \widetilde{\omega } \times I\) by
In the following we will always denote this extension also by (u, e, p), whenever such an extension procedure is needed.
Kirchhoff-Love admissible triples and limit energy.
We consider the set of Kirchhoff-Love displacements, defined as
We note that \(u \in KL(\Omega )\) if and only if \(u_3\in BH(\omega )\) and there exists \({\bar{u}}\in BD(\omega )\) such that
In particular, if \(u \in KL(\Omega )\), then
If, in addition, \(u \in W^{1,p}(\Omega ;\mathbb {R}^3)\) for some \(1 \le p \le \infty \), then \({\bar{u}}\in W^{1,p}(\omega ;\mathbb {R}^2)\) and \(u_3\in W^{2,p}(\omega )\). We call \({\bar{u}}, u_3\) the Kirchhoff-Love components of u.
For every \(w\in H^1(\Omega ;\mathbb {R}^3) \cap KL(\Omega )\) we define the class \(\mathcal {A}_{KL}(w)\) of Kirchhoff-Love admissible triples for the boundary datum w as the set of all triples \((u,e,p) \in KL(\Omega ) \times L^2(\Omega ;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}) \times \mathcal {M}_b(\Omega \cup \Gamma _D;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) satisfying
Note that the space
is canonically isomorphic to \(\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}}\). Therefore, in the following, given a triple \((u,e,p) \in \mathcal {A}_{KL}(w)\) we will usually identify e with a function in \(L^2(\Omega ;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\) and p with a measure in \(\mathcal {M}_b(\Omega \cup \Gamma _D;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\). Note also that the class \(\mathcal {A}_{KL}(w)\) is always nonempty as it contains the triple (w, Ew, 0).
To provide a useful characterization of admissible triplets in \(\mathcal {A}_{KL}(w)\), let us first recall the definition of zero-th and first order moments of functions.
Definition 3.3
For \(f \in L^2(\Omega ;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\) we denote by \({\bar{f}}\), \({\hat{f}} \in L^2(\omega ;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\) and \(f^\perp \in L^2(\Omega ;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\) the following orthogonal components (with respect to the scalar product of \(L^2(\Omega ;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\)) of f:
for a.e. \(x' \in \omega \), and
for a.e. \(x \in \Omega \). We name \({\bar{f}}\) the zero-th order moment of f and \({\hat{f}}\) the first order moment of f.
The coefficient in the definition of \({\hat{f}}\) is chosen from the computation \(\int _{I} x_3^2 \,dx_3 = \frac{1}{12}\). It ensures that if f is of the form \(f(x) = x_3 g(x')\), for some \(g \in L^2(\omega ;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\), then \({\hat{f}} = g\).
Analogously, we have the following definition of zero-th and first order moments of measures.
Definition 3.4
For \(\mu \in \mathcal {M}_b(\Omega \cup \Gamma _D;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\) we define \({\bar{\mu }}\), \({\hat{\mu }} \in \mathcal {M}_b(\omega \cup \gamma _D;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\) and \(\mu ^\perp \in \mathcal {M}_b(\Omega \cup \Gamma _D;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\) as follows:
for every \(\varphi \in C_0(\omega \cup \gamma _D;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\), and
where \(\otimes \) is the usual product of measures, and \(\mathcal {L}^{1}_{x_3}\) is the Lebesgue measure restricted to the third component of \(\mathbb {R}^3\). We name \({\bar{\mu }}\) the zero-th order moment of \(\mu \) and \({\hat{\mu }}\) the first order moment of \(\mu \).
Remark 3.5
More generally, for any function f which is integrable over I, we will use the short-hand notation
We are now ready to recall the following characterization of \(\mathcal {A}_{KL}(w)\), given in [13, Proposition 4.3].
Proposition 3.6
Let \(w \in H^1(\Omega ;\mathbb {R}^3) \cap KL(\Omega )\) and let \((u,e,p) \in {KL}(\Omega ) \times L^2(\Omega ;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}) \times \mathcal {M}_b(\Omega \cup \Gamma _D;\mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}})\). Then \((u,e,p) \in \mathcal {A}_{KL}(w)\) if and only if the following three conditions are satisfied:
-
1.
\(E{\bar{u}} = {\bar{e}}+{\bar{p}}\) in \(\omega \) and \({\bar{p}} = ({\bar{w}}-{\bar{u}}) \odot \nu _{\partial \omega } \mathcal {H}^1\) on \(\gamma _D\);
-
2.
\(D^2u_3 = - ({\hat{e}}+{\hat{p}})\) in \(\omega \), \(u_3 = w_3\) on \(\gamma _D\), and \({\hat{p}} = (\nabla u_3-\nabla w_3) \odot \nu _{\partial \omega } \mathcal {H}^1\) on \(\gamma _D\);
-
3.
\(p^\perp = - e^\perp \) in \(\Omega \) and \(p^\perp = 0\) on \(\Gamma _D\).
3.3 Definition of quasistatic evolutions
Recalling Sect. 2.2, the \(\mathcal {H}_h\)-variation of a map \(\mu : [0,T] \rightarrow \mathcal {M}_b(\Omega \cup \Gamma _D;\mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}})\) on [a, b] is defined as
For every \(t \in [0, T]\) we prescribe a boundary datum \(w(t) \in H^1(\Omega ;\mathbb {R}^3) \cap KL(\Omega )\) and we assume the map \(t\mapsto w(t)\) to be absolutely continuous from [0, T] into \(H^1(\Omega ;\mathbb {R}^3)\).
Definition 3.7
Let \(h > 0\). An h-quasistatic evolution for the boundary datum w(t) is a function \(t \mapsto (u^h(t), e^h(t), p^h(t))\) from [0, T] into \(BD(\Omega ) \times L^2(\Omega ;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}) \times \mathcal {M}_b(\Omega \cup \Gamma _D;\mathbb {M}^{3 \times 3}_{{{{\,\textrm{sym}\,}}}})\) that satisfies the following conditions:
- \((qs1)_{h}\):
-
for every \(t \in [0,T]\) we have \((u^h(t), e^h(t), p^h(t)) \in \mathcal {A}_h(w(t))\) and
$$\begin{aligned} \mathcal {Q}_h(\Lambda _h e^h(t)) \le \mathcal {Q}_h(\Lambda _h \eta ) + \mathcal {H}_h(\Lambda _h \pi -\Lambda _h p^h(t)), \end{aligned}$$for every \((\upsilon ,\eta ,\pi ) \in \mathcal {A}_h(w(t))\).
- \((qs2)_{h}\):
-
the function \(t \mapsto p^h(t)\) from [0, T] into \(\mathcal {M}_b(\Omega \cup \Gamma _D;\mathbb {M}^{3 \times 3}_{{{{\,\textrm{sym}\,}}}})\) has bounded variation and for every \(t \in [0, T]\)
$$\begin{aligned} \mathcal {Q}_h(\Lambda _h e^h(t)) + \mathcal {D}_{\mathcal {H}_h}(\Lambda _h p^h; 0, t){} & {} = \mathcal {Q}_h(\Lambda _h e^h(0))\\{} & {} \quad \ + \int _0^t \int _{\Omega } \mathbb {C}\left( \tfrac{x'}{{\varepsilon _h}}\right) \Lambda _h e^h(s): E{\dot{w}}(s) \,dx ds. \end{aligned}$$
The following existence result of a quasistatic evolution for a general multi-phase material can be found in [24, Theorem 2.7].
Theorem 3.8
Assume (3.4), (3.5), and (3.7). Let \(h > 0\) and let \((u^h_0, e^h_0, p^h_0) \in \mathcal {A}_h(w(0))\) satisfy the global stability condition \((qs1)_{h}\). Then, there exists a two-scale quasistatic evolution \(t \mapsto (u^h(t), e^h(t), p^h(t))\) for the boundary datum w(t) such that \(u^h(0) = u_0\), \(e^h(0) = e^h_0\), and \(p^h(0) = p^h_0\).
Our goal is to study the asymptotics of the quasistatic evolution when h goes to zero. The main result is given by Theorem 6.2.
3.4 Two-scale convergence adapted to dimension reduction
We briefly recall some results and definitions from [23].
Definition 3.9
Let \(\Omega \subset \mathbb {R}^3\) be an open set. Let \(\{\mu ^h\}_{h>0}\) be a family in \(\mathcal {M}_b(\Omega )\) and consider \(\mu \in \mathcal {M}_b(\Omega \times \mathcal {Y})\). We say that

if for every \(\chi \in C_0(\Omega \times \mathcal {Y})\)
The convergence above is called two-scale weak* convergence.
Remark 3.10
Notice that the family \(\{\mu ^h\}_{h>0}\) determines the family of measures \(\{\nu ^h\}_{h>0} \subset \mathcal {M}_b(\Omega \times \mathcal {Y})\) obtained by setting
for every \(\chi \in C_0^0(\Omega \times \mathcal {Y})\). Thus \(\mu \) is simply the weak* limit in \(\mathcal {M}_b(\Omega \times \mathcal {Y})\) of \(\{\nu ^h\}_{h>0}\).
We collect some basic properties of two-scale convergence below:
Proposition 3.11
-
(i)
Any sequence that is bounded in \(\mathcal {M}_b(\Omega )\) admits a two-scale weakly* convergent subsequence.
-
(ii)
Let \(\mathcal {D}\subset \mathcal {Y}\) and assume that \({{\,\textrm{supp}\,}}(\mu ^h) \subset \Omega \cap (\mathcal {D}_{\varepsilon _h}\times I)\). If
 two-scale weakly* in \(\mathcal {M}_b(\Omega \times \mathcal {Y})\), then \({{\,\textrm{supp}\,}}(\mu ) \subset \Omega \times \overline{\mathcal {D}}\).
two-scale weakly* in \(\mathcal {M}_b(\Omega \times \mathcal {Y})\), then \({{\,\textrm{supp}\,}}(\mu ) \subset \Omega \times \overline{\mathcal {D}}\).
4 Compactness results
In this section, we provide a characterization of two-scale limits of symmetrized scaled gradients. We will consider sequences of deformations \(\{v^h\}\) such that \(v^h \in BD(\Omega ^h)\) for every \(h > 0\), their \(L^1\)-norms are uniformly bounded (up to rescaling), and their symmetrized gradients \(E v^h\) form a sequence of uniformly bounded Radon measures (again, up to rescaling). As already explained in Sect. 3.2, we associate to the sequence \(\{v^h\}\) above a rescaled sequence of maps \(\{u^h\} \subset BD(\Omega )\), defined as
where \(\psi _h\) is defined in (3.9). The symmetric gradients of the maps \(\{v^h\}\) and \(\{u^h\}\) are related as follows
The boundedness of \(\frac{1}{h}\Vert Ev^h\Vert _{\mathcal {M}_b(\Omega ^h;{\mathbb {M}}^{3 \times 3}_{sym}) } \) is equivalent to the boundedness of \(\Vert \Lambda _h Eu^h\Vert _{\mathcal {M}_b(\Omega ;{\mathbb {M}}^{3 \times 3}_{sym}) } \). We will express our compactness result with respect to the sequence \(\{u^h\}_{h>0}\).
We first recall a compactness result for sequences of non-oscillating fields (see [13]).
Proposition 4.1
Let \(\{u^h\}_{h>0} \subset BD(\Omega )\) be a sequence such that there exists a constant \(C>0\) for which
Then, there exist functions \({\bar{u}} = ({\bar{u}}_1, {\bar{u}}_2) \in BD(\omega )\) and \(u_3 \in BH(\omega )\) such that, up to subsequences, there holds

Now we turn to identifying the two-scale limits of the sequence \(\Lambda _h E u^h\).
4.1 Corrector properties and duality results
In order to define and analyze the space of measures which arise as two-scale limits of scaled symmetrized gradients of BD functions, we will consider the following general framework (see also [2]).
Let V and W be finite-dimensional Euclidean spaces of dimensions N and M, respectively. We will consider kth order linear homogeneous partial differential operators with constant coefficients \(\mathcal {A}: C_c^{\infty }(\mathbb {R}^n;V) \rightarrow C_c^{\infty }(\mathbb {R}^n;W)\). More precisely, the operator \(\mathcal {A}\) acts on functions \(u: \mathbb {R}^n \rightarrow V\) as
where the coefficients \(A_\alpha \in W \otimes V^* \cong \textrm{Lin}(V;W)\) are constant tensors, \(\alpha = (\alpha _1, \dots , \alpha _n) \in \mathbb {N}_0^n\) is a multi-index and \(\partial ^\alpha := \partial _1^{\alpha _1} \cdots \partial _n^{\alpha _n}\) denotes the distributional partial derivative of order \(|\alpha | = \alpha _1 + \cdots + \alpha _n\).
We define the space
of functions with bounded \(\mathcal {A}\)-variations on an open subset U of \(\mathbb {R}^n\). This is a Banach space endowed with the norm
Here, the distributional \(\mathcal {A}\)-gradient is defined and extended to distributions via the duality
where \(\mathcal {A}^*: C_c^{\infty }(\mathbb {R}^n;W^*) \rightarrow C_c^{\infty }(\mathbb {R}^n;V^*)\) is the formal \(L^2\)-adjoint operator of \(\mathcal {A}\)
The total \(\mathcal {A}\)-variation of \(u \in L^1_{loc}(U;V)\) is defined as
Let \(\{u_n\} \subset BV^{\mathcal {A}}(U)\) and \(u \in BV^{\mathcal {A}}(U)\). We say that \(\{u_n\}\) converges weakly* to u in \(BV^{\mathcal {A}}\) if \(u_n \rightarrow u \;\text { in } L^1(U;V)\) and  .
.
In order to characterize the two-scale weak* limit of scaled symmetrized gradients, we will generally consider two domains \(\Omega _1 \subset \mathbb {R}^{{n_1}}\), \(\Omega _2 \subset \mathbb {R}^{{n_2}}\), for some \({n_1}, {n_2} \in \mathbb {N}\), and we will (just for the purposes of this subsection) denote their points by \(x_1 \in \Omega _1\), \(x_2 \in \Omega _2\). We will assume that the operator \(\mathcal {A}_{x_2}\) is defined through partial derivatives only with respect to the entries of the \(n_2\)-tuple \(x_2\). In the spirit of [23, Section 4.2], we will define the space
We will assume that \(BV^{\mathcal {A}_{x_2}}(\Omega _2)\) satisfies the following weak* compactness property:
Assumption 1
If \(\{u_n\} \subset BV^{\mathcal {A}_{x_2}}(\Omega _2)\) is uniformly bounded in the \(BV^{\mathcal {A}_{x_2}}\)-norm, then there exists a subsequence \(\{u_m\} \subseteq \{u_n\}\) and a function \(u \in BV^{\mathcal {A}_{x_2}}(\Omega _2)\) such that \(\{u_m\}\) converges weakly* to u in \(BV^{\mathcal {A}_{x_2}}(\Omega _2)\), i.e.

Furthermore, there exists a countable collection \(\{U^k\}\) of open subsets of \(\mathbb {R}^{n_2}\) that increases to \(\Omega _2\) (i.e. \(\overline{U^k} \subset U^{k+1}\) for every \(k\in \mathbb {N}\), and \(\Omega _2 = \bigcup _{k} U^k\)) such that \(BV^{\mathcal {A}_{x_2}}(U^k)\) satisfies the weak* compactness property above for every \(k\in \mathbb {N}\).
The following theorem is our main disintegration result for measures in \(\mathcal {X}^{{\mathcal {A}_{x_2}}}({\Omega _1})\), which will be instrumental to define a notion of duality for admissible two-scale configurations. The proof is an adaptation of the arguments in [23, Proposition 4.7].
Proposition 4.2
Let Assumption 1 be satisfied. Let \(\mu \in \mathcal {X}^{{\mathcal {A}_{x_2}}}({\Omega _1})\). Then there exist \(\eta \in \mathcal {M}_b^+(\Omega _1)\) and a Borel map \((x_1,x_2) \in \Omega _1 \times \Omega _2 \mapsto \mu _{x_1}(x_2) \in V\) such that, for \(\eta \)-a.e. \(x_1 \in \Omega _1\),
and
Moreover, the map \(x_1 \mapsto \mathcal {A}_{x_2}\mu _{x_1} \in \mathcal {M}_b(\Omega _2;W)\) is \(\eta \)-measurable and
Proof
By assumption, we have \(\mu \in \mathcal {M}_b(\Omega _1 \times \Omega _2;V)\) and \(\lambda := \mathcal {A}_{x_2}\mu \in \mathcal {M}_b(\Omega _1 \times \Omega _2;W)\). Setting
where \(proj_{\#}\) is the push-forward by the projection of \(\Omega _1 \times \Omega _2\) on \(\Omega _1\), we obtain as a consequence of Theorem 2.1:
with \(\mu _{x_1} \in \mathcal {M}_b(\Omega _2;V)\) and \(\lambda _{x_1} \in \mathcal {M}_b(\Omega _2;W)\). Further, if we set \(S:= \{x_1 \in \Omega _1: |\lambda _{x_1}|(\Omega _2) \ne 0\}\), then \(\lambda = \eta \lfloor {S} {\mathop {\otimes }\limits ^{\text {gen.}}}\lambda _{x_1}\).
For every \(\varphi ^{(1)} \in C_c^{\infty }(\Omega _1)\) and \(\varphi ^{(2)} \in C_c^{\infty }(\Omega _2;W^*)\) we have
From this we infer that for \(\eta \)-a.e. \(x_1 \in \Omega _1\) and for every \(\varphi \in C_c^{\infty }(\Omega _2;W^*)\)
We can consider \(\mu _{x_1}\) and \(\lambda _{x_1}\) as measures on \(\mathbb {R}^{n_2}\) if we extend the measure \(\mu \) by zero on the complement of \(\Omega _2\). Then, using the standard mollifiers \(\{\rho _\epsilon \}_{\epsilon >0}\) on \(\mathbb {R}^{n_2}\), we define the functions \(\mu _{x_1}^\epsilon := \mu _{x_1} *\rho _\epsilon \) and \(\lambda _{x_1}^\epsilon := \lambda _{x_1} *\rho _\epsilon \), which are smooth and uniformly bounded in \(L^1(\Omega _2;V)\) and \(L^1(\Omega _2;W)\), respectively. For every \(\varphi \in C_c^{{m}}(\Omega _2;W^*)\) (where m is taken to be the order of the partial differential operator \(\mathcal {A}_{x_2}^*\)), \({{\,\textrm{supp}\,}}(\varphi ) \subset U^k\) for k large enough. Furthermore, the support of \(\varphi *\rho _\epsilon \) is contained in \(\Omega _2\) provided \(\epsilon \) is sufficiently small (smallness depending only on k), and thus from (4.5) we have
Hence, for \(\eta \)-a.e. \(x_1 \in \Omega _1\) the sequence \(\{\mu _{x_1}^\epsilon \}\) is eventually bounded in \(BV^{\mathcal {A}_{x_2}}(U^k)\). By Assumption 1, this implies strong convergence in \(L^1(U^k;V)\) up to a subsequence. As \(\epsilon \rightarrow 0\), we have both \(\varphi *\rho _\epsilon \rightarrow \varphi \) and \(\mathcal {A}_{x_2}^*\varphi *\rho _\epsilon \rightarrow \mathcal {A}_{x_2}^*\varphi \) uniformly, so by the Lebesgue’s dominated convergence theorem we obtain, for \(\eta \)-a.e. \(x_1 \in \Omega _1\),
From the convergence above, we conclude for \(\eta \)-a.e. \(x_1 \in \Omega _1\) that \(\mu _{x_1}^\epsilon \rightarrow \mu _{x_1}\) strongly in \(L^1(U^k;V)\) (the convergence holds for the whole sequence since every subsequence has a subsequence converging in n \(L^1\) to the same limit). Since \(\mu _{x_1}\) has bounded total variation, we have that \(\mu _{x_1} \in L^1(\Omega _2;V)\) for \(\eta \)-a.e. \(x_1 \in \Omega _1\). This, together with (4.5), implies
From (4.4) we now have that \(\mu \) is absolutely continuous with respect to \(\eta \otimes \mathcal {L}^{n_2}_{x_2}\). Consequently, for \(\eta \)-a.e. \(x_1 \in \Omega _1\) there exists a Borel measurable function which is equal to \(\mu _{x_1}\) for \(\mathcal {L}^{n_2}_{x_2}\)-a.e. \(x_2 \in \Omega _2\), so that (4.3) immediately follows.
Finally, since \(\mu (F \times \Omega _2) = 0\) for every Borel set \(F \subseteq \Omega _1\), we have
for every \(f \in C_c(\Omega _1)\), from which we obtain the second claim in (4.2). This concludes the proof. \(\square \)
Lastly, we give a necessary and sufficient condition with which we can characterize the \(\mathcal {A}_{x_2}\)-gradient of a measure, under the following two assumptions.
Assumption 2
For every \(\chi \in C_0(\Omega _1 \times \Omega _2;W)\) with \(\mathcal {A}_{x_2}^*\chi = 0\) (in the sense of distributions), there exists a sequence of smooth functions \(\{\chi _n\} \subset C_c^{\infty }(\Omega _1 \times \Omega _2;W)\) such that \(\mathcal {A}_{x_2}^*\chi _n = 0\) for every n, and \(\chi _n \rightarrow \chi \) in \(L^{\infty }(\Omega _1 \times \Omega _2;W)\).
Assumption 3
The following Poincaré-Korn type inequality holds in \(BV^{\mathcal {A}_{x_2}}(\Omega _2)\):
Proposition 4.3
Let Assumption 1, 2 and 3 be satisfied. Let \(\lambda \in \mathcal {M}_b(\Omega _1 \times \Omega _2;W)\). Then, the following items are equivalent:
-
(i)
For every \(\chi \in C_0(\Omega _1 \times \Omega _2;W)\) with \(\mathcal {A}_{x_2}^*\chi = 0\) (in the sense of distributions) we have
$$\begin{aligned} \int _{\Omega _1 \times \Omega _2} \chi (x_1,x_2) \cdot d\lambda (x_1,x_2) = 0. \end{aligned}$$ -
(ii)
There exists \(\mu \in \mathcal {X}^{{\mathcal {A}_{x_2}}}({\Omega _1})\) such that \(\lambda = \mathcal {A}_{x_2}\mu \).
Proof
Let \(\chi \in C_0(\Omega _1 \times \Omega _2;W)\) with \(\mathcal {A}_{x_2}^*\chi = 0\) (in the sense of distributions) and let \(\{\chi _n\}\) be an approximating sequence of \(\chi \) as in Assumption 2. Assume that i holds. Then, we have
So we have i.
Let us prove that the space
is weakly* closed in \(\mathcal {M}_b(\Omega _1 \times \Omega _2;W)\). By the Krein-Šmulian theorem it is enough to show that the intersection of \(\mathcal {E}^{\mathcal {A}_{x_2}}\) with every closed ball in \(\mathcal {M}_b(\Omega _1 \times \Omega _2;W)\) is weakly* closed. This implies, since the weak* topology is metrizable on any closed ball of \(\mathcal {M}_b(\Omega _1 \times \Omega _2;W)\), that it is enough to prove that \(\mathcal {E}^{\mathcal {A}_{x_2}}\) is sequentially weakly* closed.
Let \(\{\lambda _n\}_{n\in \mathbb {N}} \subset \mathcal {E}^{\mathcal {A}_{x_2}}\) and \(\lambda \in \mathcal {M}_b(\Omega _1 \times \Omega _2;W)\) be such that

By the definition of the space \(\mathcal {E}^{\mathcal {A}_{x_2}}\), there exist measures \(\mu _n \in \mathcal {M}_b(\Omega _1 \times \Omega _2;V)\) such that \(\lambda _n = \mathcal {A}_{x_2}\mu _n\). By Proposition 4.2, for every \(n \in \mathbb {N}\) we have that there exist \(\eta _n \in \mathcal {M}_b^+(\Omega _1)\) and \(\mu ^n_{x_1} \in BV^{\mathcal {A}_{x_2}}(\Omega _2)\) such that, for \(\eta _n\)-a.e. \(x_1 \in \Omega _1\),
Additionally, \(\mu ^n_{x_1}\) satisfies \(\int _{\Omega _2} \mu ^n_{x_1}(x_2) \,dx_2 = 0\) for every \(n\in \mathbb {N}\). Then, by Assumption 3, there is a constant C independent of n such that
Hence there exists a subsequence of \(\{ \mu _n \}\), not relabeled, and an element \(\mu \in \mathcal {M}_b(\Omega _1 \times \Omega _2;V)\) such that

Then, for every \(\varphi \in C_c^{\infty }(\Omega _1 \times \Omega _2;W^*)\) we have
From the convergence above we deduce that \(\lambda = \mathcal {A}_{x_2}\mu \in \mathcal {E}^{\mathcal {A}_{x_2}}\). This implies that \(\mathcal {E}^{\mathcal {A}_{x_2}}\) is weakly* closed in \(\mathcal {M}_b(\Omega _1 \times \Omega _2;W) = \left( C_0(\Omega _1 \times \Omega _2;W^*) \right) '\).
Assume now that i holds. If \(\lambda \notin \mathcal {E}^{\mathcal {A}_{x_2}}\), by Hahn-Banach’s theorem, there exists \(\chi \in C_0(\Omega _1 \times \Omega _2;W^*)\) such that
and, for every \(u \in BV^{\mathcal {A}_{x_2}}(\Omega _1 \times \Omega _2)\),
In particular, choosing u to be a smooth function, (4.7) implies that \(\mathcal {A}_{x_2}^*\chi = 0\) (in the sense of distributions). As a consequence, (4.6) contradicts i. Thus, \(\lambda \in \mathcal {E}^{\mathcal {A}_{x_2}}\). \(\square \)
4.1.1 Compactness result for scaled maps with finite energy
If we consider \(\mathcal {A}_{x_2}= {\widetilde{E}}_{\gamma }\), \(\mathcal {A}_{x_2}^* = {\widetilde{\textrm{div}}}_{\gamma }\), \(\Omega _1 = \omega \) with points \(x_1 = x'\), and \(\Omega _2 = I \times \mathcal {Y}\) with points \(x_2 = (x_3,y)\), then we denote the associated spaces from the previous section by:
Despite the fact that \(\mathcal {Y}\) is a flat torus, Proposition 4.2 and Proposition 4.3 are satisfied if we establish the validity of Assumption 1, 2 and 3, which will be done below.
Remark 4.4
To each \(u \in BD_\gamma (I \times \mathcal {Y})\), we can associate a function
Then
from which we can see that \(v \in BD(I \times \mathcal {Y})\). Here \(E_yu'\) denotes the symmetrized gradient in y of the field \(u'\), which is a \(2 \times 2\) matrix. Furthermore, the \(L^1\)-norms of u and v are always within a constant factor of one another, whose magnitude depends on a fixed estimate of \(\gamma \) and \(\frac{1}{\gamma }\). The same holds true for the \(\mathcal {M}_b\)-norms of \({\widetilde{E}}_{\gamma } u\) and Ev.
Alternatively, we can define the change of variables \(\psi : (\gamma I) \times \mathcal {Y}\rightarrow I \times \mathcal {Y}\) given by \(\psi (x_3,y):= \left( \tfrac{1}{\gamma }x_3,y\right) \) and consider the function \(w:= u \circ \psi \). Then \(w \in BD((\gamma I) \times \mathcal {Y})\) and we have
Using any one of these scalings, we obtain that \(BD_\gamma (I \times \mathcal {Y})\) satisfies the weak* compactness property Assumption 1.
The following lemma establishes the validity of Assumption 2.
Lemma 4.5
For any \(\chi \in C_0(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) with \({\widetilde{\textrm{div}}}_{\gamma }\chi (x,y) = 0\) (in the sense of distributions), we can construct an approximating sequence which satisfies Assumption 2.
Proof
We take \(\chi \in C_0(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\), extend it by zero outside \(\Omega \) and define
where \(\Lambda _{1+\epsilon }\) is the linear operator described in (3.10), and \(\varphi ^{\epsilon }: \omega \rightarrow [0,1]\) is a continuous function that is zero in a neighbourhood of \(\partial \omega \) and equal to 1 for \(x' \in \omega \) such that \({{\,\textrm{dist}\,}}(x',\partial \omega ) \ge \epsilon \). Notice that \({\tilde{\chi }}^{\epsilon } \in C_c(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\), \({\tilde{\chi }}^{\epsilon } \rightarrow \chi \) as \(\epsilon \rightarrow 0\) in \(L^{\infty }\) and \({\widetilde{\textrm{div}}}_{\gamma }{\tilde{\chi }}^{\epsilon } = 0\) (in the sense of distributions). The \(C^\infty \)-regularity of the approximating sequence follows by convolving \(\{{\tilde{\chi }}^{\epsilon }\}\) with a standard sequence of mollifiers. \(\square \)
The following claim establishes the validity of Assumption 3.
Theorem 4.6
There exists a constant \(C > 0\) such that
for each function \(u \in BD_{\gamma } (I \times \mathcal {Y})\). The constant C can be chosen uniformly in \(\gamma \) in a fixed interval \([\gamma _1,\gamma _2]\), for \(0<\gamma _1<\gamma _2<\infty \) (depending then on \(\gamma _1,\gamma _2\)).
Proof
In view of the first part Remark 4.4, it is enough to show the claim for the case \(\gamma = 1\). Namely, if we prove it for arbitrary u and \(\gamma =1\) by applying it to v defined by (4.8) and \(\gamma \in [\gamma _1,\gamma _2]\), we obtain the claim. In order to prove the claim for \(\gamma =1\), we argue by contradiction. If the thesis does not hold, then there exists a sequence \(\{u_n\}_n \subset BD(I \times \mathcal {Y})\) such that
We can normalize the sequence such that
In particular the sequence \(\{u_n\}\) is bounded in \(BD(I \times \mathcal {Y})\).
By Assumption 1, there exists a subsequence \(\{u_m\} \subseteq \{u_n\}\) and a function \(u \in BD(I \times \mathcal {Y})\) such that \(\{u_m\}\) converges weakly* to u in \(BD(I \times \mathcal {Y})\), i.e.

It’s clear that the limit satisfies
Also, by the weak* lower semicontinuity of the total variation of measures, we have
which implies \({\widetilde{E}} u = 0\). As a result, the limit u is a rigid deformation, i.e. is of the form
Further, (4.10) implies that u has no jumps along \(C^1\) hypersurfaces contained in \(I \times \mathcal {Y}\). Thus u should be \([0,1]^2\)-periodic in the y variable, and a simple calculation shows that the only function of the above form must satisfy \(A \equiv 0\). Hence, u must be a constant vector. However, this contradicts with (4.9). \(\square \)
Remark 4.7
If one doesn’t assume periodicity, then the following version of the Poincaré-Korn inequality can be proved, using the arguments in the proof of Assumption 4.6: There exists a constant \(C > 0\) such that
for each function \(u \in BD_{\gamma } ((0,1)^2 \times I)\) and suitably chosen \( A \in \mathbb {M}_{{{\,\textrm{skew}\,}}}^{3 \times 3}\), \(b \in \mathbb {R}^3\), depending on u. Again, the constant C can be chosen independently of \(\gamma \) in a fixed interval \([\gamma _1,\gamma _2]\), for \(0<\gamma _1<\gamma _2<\infty \).
The following two propositions are now a consequence of Proposition 4.2 and Proposition 4.3, respectively.
Proposition 4.8
Let \(\mu \in \mathcal {X}_{\gamma }({\omega })\). Then there exist \(\eta \in \mathcal {M}_b^+(\omega )\) and a Borel map \((x',x_3,y) \in \Omega \times \mathcal {Y}\mapsto \mu _{x'}(x_3,y) \in \mathbb {R}^3\) such that, for \(\eta \)-a.e. \(x' \in \omega \),
and
Moreover, the map \(x' \mapsto {\widetilde{E}}_{\gamma }\mu _{x'} \in \mathcal {M}_b(I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) is \(\eta \)-measurable and
Proposition 4.9
Let \(\lambda \in \mathcal {M}_b(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\). The following items are equivalent:
-
(i)
For every \(\chi \in C_0(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) with \({\widetilde{\textrm{div}}}_{\gamma }\chi (x,y) = 0\) (in the sense of distributions) we have
$$\begin{aligned} \int _{\Omega \times \mathcal {Y}} \chi (x,y): d\lambda (x,y) = 0. \end{aligned}$$ -
(ii)
There exists \(\mu \in \mathcal {X}_{\gamma }({\omega })\) such that \(\lambda = {\widetilde{E}}_{\gamma }\mu \).
Additionally, we state the following property, which will be used in the proof of Lemma 4.18. The proof is analogous to [23, Proposition 4.7. item (b)].
Proposition 4.10
Let \(\mu \in \mathcal {X}_{\gamma }({\omega })\). For any \(C^1\)-hypersurface \(\mathcal {D}\subseteq \mathcal {Y}\), if \(\nu \) denotes a continuous unit normal vector field to \(\mathcal {D}\), then
where \(a: \Omega \times \mathcal {D}\mapsto \mathbb {R}^3\) is a Borel function.
4.2 Auxiliary results
We will need the following result, which is connected with the compactly supported De Rham cohomology. Recall the definitions of \({\widetilde{\nabla }}_\gamma \), \({\widetilde{\textrm{div}}}_\gamma \), and \({\widetilde{{{\,\textrm{curl}\,}}}}_\gamma \). In the next proposition, we will consider the case \(\gamma =1\).
Proposition 4.11
-
(a)
Let \(\mathcal {Y}^{(3)}\) be a flat torus in \(\mathbb {R}^3\) and let \(\chi \in C^{\infty }(\mathcal {Y}^{(3)};\mathbb {R}^3)\) be such that \(\textrm{div}\chi = 0\) and \(\int _{\mathcal {Y}^{(3)}} \chi = 0\). Then there exists \(F \in C^{\infty }(\mathcal {Y}^{(3)};\mathbb {R}^3)\) such that \({{\,\textrm{curl}\,}}F = \chi \).
-
(b)
Let \(\mathcal {Y}\) be a flat torus in \(\mathbb {R}^2\) and let \(\chi \in C_c^{\infty }(I \times \mathcal {Y};\mathbb {R}^3)\) be such that \({\widetilde{\textrm{div}}}\, \chi = 0\) and \(\int _{I \times \mathcal {Y}} \chi = 0\). Then there exists \(F \in C_c^{\infty }(I \times \mathcal {Y};\mathbb {R}^3)\) such that
$$\begin{aligned} {\widetilde{{{\,\textrm{curl}\,}}}}\, F = \chi . \end{aligned}$$
Proof
The first claim is standard and can be easily proved by, e.g. Fourier transforms. For the second claim, observing that \(\chi \) is also periodic on \(\mathcal {Y}^{(3)}\), by the first part of the statement we obtain \({\tilde{F}} \in C^{\infty }(\mathcal {Y}^{(3)};\mathbb {R}^3)\) such that \({{\,\textrm{curl}\,}}{\tilde{F}} = \chi \) on \(\mathcal {Y}^{(3)}\). Since \(\chi \) has compact support in \(I \times \mathcal {Y}\), there exists \(0< \delta < \frac{1}{2}\) such that \({\widetilde{{{\,\textrm{curl}\,}}}}\, {\tilde{F}} = 0\) on \(\tilde{I}_{\delta } \times \mathcal {Y}\), where \({{\tilde{I}}}_{\delta } = \{ (\frac{1}{2}-\delta , \frac{1}{2}) \cup (-\frac{1}{2}, -\frac{1}{2}+\delta ) \}\). Let now \({\tilde{\varphi }} \in C^{\infty }(S_{\delta })\), where \(S_{\delta } = {{\tilde{I}}}_{\delta } \times (0,1)^2 \), be such that \({\tilde{F}} = {\widetilde{\nabla }} {\tilde{\varphi }}\) on \(S_{\delta }\). For \(\alpha \in \{1,2\}\), let
be the exponential Fourier series of \({\tilde{F}}_\alpha = \partial _{y_\alpha }{\tilde{\varphi }}\) with respect to the variable \(y_1\). Note that the coefficients \(\{a^{\alpha }_k(x_3,y_2)\}_{k \in \mathbb {Z}}\) are smooth functions and periodic with respect to the variable \(y_2\) and \(x_3\). Additionally, the Fourier series of smooth functions converges uniformly, and the result of differentiating or integrating the series term by term will converge to the derivative or integral of the original series. Hence, we infer that
for a suitable smooth function \(b^1(x_3,y_2)\). Then, differentiating with respect to \(y_1\) and \(y_2\), we have that
However, since
by the uniqueness of the Fourier expansion we have that \(\partial _{y_2}a^{1}_0(x_3,y_2) = 0\), i.e.
for some \(c_1 \in C^{\infty }({{\tilde{I}}}_\delta )\). Further, differentiating (4.13) with respect to \(y_2\), we have that
Since \(\partial _{y_2}{\tilde{\varphi }} = {\tilde{F}}_2\) is periodic, we conclude that \(\partial _{y_2}b^1\) is also periodic with respect to the variable \(y_2\) and we can consider its Fourier series. Let \(c_2 \in C^{\infty }({{\tilde{I}}}_\delta )\) be the corresponding zero-th term. Then the antiderivative of \(\partial _{y_2}b^1 - c_2 \) with respect to \(y_2\) is a periodic function. Combining this fact with (4.13) and (4.14), we deduce that there exists a smooth function \({\hat{\varphi }} \in C^{\infty }({{\tilde{I}}}_{\delta };C^{\infty }(\mathcal {Y}))\) such that \({\tilde{\varphi }}\) can be rewritten as
From this, differentiating with respect to \(x_3\), we have that
As a consequence of the periodicity of \({\tilde{F}}_3\) and \(\partial _{x_3}{\hat{\varphi }}\) in the variables \(y_1\) and \(y_2\), we conclude that \(c_1' = 0\) and \(c_2' = 0\). Since \( {{\tilde{I}}}_{\delta } \times \mathcal {Y}\) is a union of two disjoint open sets, we have that \(c_1, c_2\) are constant on each connected component. Using the fact that, for \(\alpha \in \{1,2\}\),
the periodicity of \({\tilde{F}}_\alpha = \partial _{y_\alpha }{\tilde{\varphi }}\) implies that \(c_1, c_2\) are in fact constant. This can be seen by integrating the equation (4.15) over the plane \(x_3 = -\frac{1}{2}\) and \(x_3 = \frac{1}{2}\). Thus we conclude that
Consider now the exponential Fourier series of \({\tilde{F}}_3\) with respect to the \(x_3\) variable, such that
Integrating the third component in (4.16) with respect to \(x_3\), we have that there exists a smooth function \(b^3(x_3,y)\), which has values \(b^3_{+}(y)\) and \(b^3_{-}(y)\) on each of the two parts of \({{\tilde{I}}}_{\delta } \times \mathcal {Y}\), such that
From this and (4.15) we have, for \(\alpha \in \{1,2\}\),
Considering the continuity and periodicity in \(x_3\) of the above terms, evaluating in \(x_3 = -\frac{1}{2}\) and \(x_3 = \frac{1}{2}\) gives \(\partial _{y_\alpha }a^{3}_0(y) = \partial _{y_\alpha }b^3_{-}(y) - \partial _{y_\alpha }b^3_{+}(y)\). From this we have that there exists a constant \(c_3\) and a map \(\varphi \in C^{\infty }(\mathcal {Y}\times {{\tilde{I}}}_{\delta })\) such that \(\varphi \) and all its derivatives are periodic in the \(x_3\) variable, and for which
From this and (4.16) we conclude that
Finally, we consider a smooth function \(k: I \rightarrow \mathbb {R}\) that is zero on the set \(\left[ -\frac{1}{2}+\delta , \frac{1}{2}-\delta \right] \) and one in a neighbourhood of \(x_3 = -\frac{1}{2}\), \(x_3 = \frac{1}{2}\). By taking
we have the claim. \(\square \)
Remark 4.12
By considering functions scaled by \(\gamma \) in the third component and by \(\frac{1}{\gamma }\) in the direction \(x_3\), one can apply the proof item (b) in Proposition 4.11 so that the statement is valid for maps in the space \(C_c^{\infty }((\gamma I) \times \mathcal {Y};\mathbb {R}^3)\).
Consequently, for \(\chi \in C_c^{\infty }(I \times \mathcal {Y};\mathbb {R}^3)\) such that \({\widetilde{\textrm{div}}}_{\gamma }\chi = 0\) and \(\int _{I \times \mathcal {Y}} \chi = 0\) there exists \(F \in C_c^{\infty }(I \times \mathcal {Y};\mathbb {R}^3)\) such that \({\widetilde{{{\,\textrm{curl}\,}}}}_{\gamma } F = \chi \), which can be easily seen by rescaling in the direction \(x_3\).
Remark 4.13
If \(\chi \in C_c^{\infty }(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) is such that \({\widetilde{\textrm{div}}}_{\gamma }\chi = 0\), then for a.e. \(x' \in \omega \)
Indeed, by putting
for \(c \in C_c^{\infty }(\omega ;\mathbb {R}^3)\), we infer that
and the conclusion results from testing \(\chi \) with \({\widetilde{E}}_{\gamma }\varphi \) on \(I \times \mathcal {Y}\), and by the arbitrariness of the maps \(c_i\), \(i = 1, 2, 3\).
4.3 Two-scale limits of scaled symmetrized gradients
We are now ready to prove the first main result of this section.
Theorem 4.14
Let \(\{u^h\}_{h>0} \subset BD(\Omega )\) be a sequence such that there exists a constant \(C>0\) for which
Then there exist \({\bar{u}} = ({\bar{u}}_1, {\bar{u}}_2) \in BD(\omega )\), \(u_3 \in BH(\omega )\), \(\mu \in \mathcal {X}_{\gamma }({\omega })\), and a subsequence of \(\{u^h\}_{h>0}\), not relabeled, which satisfy:

Proof
Owing to [43, Chapter II, Remark 3.3], we can assume without loss of generality that the maps \(u^h\) are smooth functions for every \(h > 0\). Further, the uniform boundedness of the sequence \(\{Ev^h\}\) implies that
In the following, we will consider \(\lambda \in \mathcal {M}_b(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) such that

By using Proposition 4.1 we have that there exist \(({\bar{u}}_1, {\bar{u}}_2) \in BD(\omega )\), \(u_3 \in BH(\omega )\) such that

Let \(\chi \in C_c^{\infty }(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) be such that \({\widetilde{\textrm{div}}}_{\gamma }\chi = 0\). We have
where in the last equality we used that \(\frac{1}{{\varepsilon _h}}\partial _{y_1}\chi _{i1}+\frac{1}{{\varepsilon _h}}\partial _{y_2}\chi _{i2}+\frac{1}{h}\partial _{x_3}\chi _{i3} = \left( \frac{1}{h}-\frac{1}{{\varepsilon _h}\gamma }\right) \partial _{x_3}\chi _{i3}\).
From Proposition 4.1 we know that we have the following convergences:
Notice that
Next, in view of Remark 4.13, we can use item b in Proposition 4.11, i.e. Remark 4.12 to conclude that there exists \(F \in C_c^{\infty }(\Omega \times \mathcal {Y};\mathbb {R}^3)\) such that \({\widetilde{{{\,\textrm{curl}\,}}}}_{\gamma } F= (\chi _{3i})_{i=1,2,3}\). Thus we have
Next we compute
Notice that
Recalling (4.17), we find
From (4.24), (4.25), (4.26) we infer
In a similar way for \(u^h_3\) (recalling (4.18)), we deduce
From (4.21), (4.27), (4.28) we conclude that
Analogously, we obtain
Lastly, using similar arguments as above, we compute
From (4.19), (4.20), (4.29), (4.30), (4.31) we have that
From this and Proposition 4.9 we find that there exists \(\mu \in \mathcal {X}_{\gamma }({\omega })\) such that
This, in turn, yields the claim. \(\square \)
4.4 Unfolding adapted to dimension reduction
We proceed along the lines of [23, Section 4.3].
For every \(\varepsilon > 0\) and \(i \in \mathbb {Z}^2\), let
Given an open set \(\omega \subseteq \mathbb {R}^2\), we will set
Given \(\mu _\varepsilon \in \mathcal {M}_b(\omega \times I)\) and \(Q_\varepsilon ^i \subset \omega \), we define \(\mu _\varepsilon ^i \in \mathcal {M}_b(I \times \mathcal {Y})\) such that
Definition 4.15
For every \(\varepsilon > 0\), the unfolding measure associated with \(\mu _\varepsilon \) is the measure \({\tilde{\lambda }}_\varepsilon \in \mathcal {M}_b(\omega \times I \times \mathcal {Y})\) defined by
The following proposition provides the relationship between the two-scale weak* convergence and unfolding measures. The proof is analogous to [23, Proposition 4.11.].
Proposition 4.16
Let \(\omega \subseteq \mathbb {R}^2\) be an open set and let \(\{\mu _\varepsilon \} \subset \mathcal {M}_b(\omega \times I)\) be a bounded family such that

Let \(\{{\tilde{\lambda }}_\varepsilon \} \subset \mathcal {M}_b(\omega \times I \times \mathcal {Y})\) be the family of unfolding measures associated with \(\{\mu _\varepsilon \}\). Then

To analyze the sequences of symmetrized scaled gradients of BD functions in the context of unfolding, we will need to consider the following auxiliary spaces
where \({\widetilde{E}}_{\frac{h}{\varepsilon }}\) and \(E_{\frac{h}{\varepsilon }}\) denote the distributional symmetrized scaled gradients, cf. (2.1). Similarly as in Remark 4.4, scaling in the the first two components shows that these auxiliary spaces are equivalent to the usual BD space on the appropriate domain.
Proposition 4.17
Let \(\omega \subseteq \mathbb {R}^2\) be an open set and let \(\mathcal {B}\subseteq \mathcal {Y}\) be an open set with Lipschitz boundary. Let \(\gamma _0 \in (0,1]\) and let \(h,\, \varepsilon > 0\) be such that
If \(u_\varepsilon \in BD(\omega \times I)\), the unfolding measure associated with \(\Lambda _h Eu_\varepsilon \lfloor {(\mathcal {B}_\varepsilon {\setminus } \mathcal {C}_\varepsilon ) \times I}\) is given by
where \(\mathcal {C}\) has been introduced in (3.1) and \({\hat{u}}_{h,\varepsilon }^i \in BD_{\frac{h}{\varepsilon }}(I \times \mathcal {Y})\) is such that
for some constant C independent of i, h and \(\varepsilon \).
Proof
Since \(\mathcal {B}_\varepsilon \) has Lipschitz boundary, \(u_\varepsilon \mathbb {1}_{\mathcal {B}_\varepsilon \times I} \in BD_{loc}(\omega \times I)\) with
where \(u_\varepsilon \lfloor {\partial \mathcal {B}_\varepsilon \times I}\) denotes the trace of \(u_\varepsilon \mathbb {1}_{\mathcal {B}_\varepsilon \times I}\) on \(\partial \mathcal {B}_\varepsilon \times I\), while \(\nu \) is the exterior normal to \(\partial \mathcal {B}_\varepsilon \times I\). We note that the third component of \(\nu \) is equal to zero.
Remark that \(\mathcal {C}_\varepsilon = \left( \cup _i \partial Q_\varepsilon ^i\right) \cap \omega \). Accordingly, for \(i \in I_\varepsilon (\omega )\) and \(\psi \in C^1(I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\),
We set \(v_{h,\varepsilon }^i(x):= {{\,\textrm{diag}\,}}\left( 1,1,\frac{1}{h}\right) \,u_\varepsilon (\varepsilon i+\varepsilon x', x_3)\) for \(x\in (0, 1)^2 \times I\). Then \(v_{h,\varepsilon }^i \in BD_{\frac{h}{\varepsilon }}\left( (0, 1)^2 \times I\right) \), and \(E_{\frac{h}{\varepsilon }}v_{h,\varepsilon }^i(x) = \varepsilon \Lambda _h Eu_\varepsilon (\varepsilon i+\varepsilon x', x_3)\). Performing a change of variables, we find
Notice that we can assume that
for some constant C independent of i, h and \(\varepsilon \). This can be achieved by using Remark 4.7 since subtracting a rigid deformation to \(u_\varepsilon \) on \(Q_\varepsilon ^i \times I\) corresponds to subtracting an element of the kernel of \(E_{\frac{h}{\varepsilon }}\) to \(v_{h,\varepsilon }^i\), which does not modify the calculations done thus far. Hence, by the trace theorem and Poincaré-Korn’s inequality in \(BD\left( (0, 1)^2 \times I\right) \), we get the desired inequality.
Defining \({\hat{u}}_{h,\varepsilon }^i(x_3,y):= \frac{1}{\varepsilon } v_{h,\varepsilon }^i\left( \mathcal {I}(y),x_3\right) \), we obtain
Furthermore,
and
So we have
from which (4.32) follows. It remains to prove (4.33). Again, up to adding an affine transformation to \({\hat{u}}_{h,\varepsilon }^i\) (cf. Remark 4.7) on \(I \times \mathcal {B}\), we can assume
This concludes the proof of the theorem. \(\square \)
As a consequence of Proposition 4.17, we deduce the following lemma, which in turn will be used in the proof of the lower semicontinuity of \(\mathcal {H}^{hom}\) in Sect. 5.5.
Lemma 4.18
Let \(\mathcal {B}\subseteq \mathcal {Y}\) be an open set with Lipschitz boundary, such that \(\partial \mathcal {B}\setminus \mathcal {T}\) is a \(C^1\)-hypersurface, for some compact set \(\mathcal {T}\) with \(\mathcal {H}^{1}(\mathcal {T}) = 0\). Additionally, assume that \(\partial \mathcal {B}\cap \mathcal {C}\subseteq \mathcal {T}\). Let \(v^h \in BD({{\Omega }})\) be such that

and

Then \(\pi \) is supported in \({{\Omega }} \times {\bar{\mathcal {B}}}\) and
where \(\zeta \in \mathcal {M}_b^+ ({{\Omega }} \times (\partial \mathcal {B}{\setminus } \mathcal {T}))\), \(a: {{\Omega }} \times (\partial \mathcal {B}{\setminus } \mathcal {T}) \rightarrow \mathbb {R}^3\) is a Borel map, and \(\nu \) is the exterior normal to \(\partial \mathcal {B}\).
Proof
Denote by \({\tilde{\pi }} \in \mathcal {M}_b({{\Omega }} \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) the two-scale weak* limit (up to a subsequence) of
Then it is enough to prove the analogue of (4.34) for \({\tilde{\pi }}\). Indeed, the two-scale weak* limit (up to a subsequence) of
is supported on \({{\Omega }} \times \overline{\mathcal {B}\cap \mathcal {C}}\). Since by assumption \(\partial \mathcal {B}\cap \mathcal {C}\subseteq \mathcal {T}\), we have that \(\partial \mathcal {B}{\setminus } \mathcal {T}\) and \(\overline{\mathcal {B}\cap \mathcal {C}}\) are disjoint sets, which implies
By Proposition 4.17, the unfolding measure associated with \(\Lambda _h Ev^h\lfloor {(\mathcal {B}_{\varepsilon _h}{\setminus } \mathcal {C}_{\varepsilon _h}) \times I}\) is given by
where \({\hat{v}}_{{\varepsilon _h}}^i \in BD(I \times \mathcal {Y})\) is such that
Further, by Proposition 4.16, the family of associated measures in (4.35) converge weakly* to \({\tilde{\pi }}\) in \(\mathcal {M}_b({{\Omega }} \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\). Then, for every \(\chi \in C_c^{\infty }({{\Omega }} \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) with \({\widetilde{\textrm{div}}}_{\gamma }\chi (x,y) = 0\), we get
By the integration by parts formula for BD functions over \(I \times \mathcal {B}\) we have
Owing to (4.36), we conclude that the the sum
is finite. Further, in view of (4.36) we can rewrite the above limit as
with \(\lambda ^h_1,\, \lambda ^h_2 \in \mathcal {M}_b({{\Omega }} \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\), such that (up to a subsequence)

for suitable \(\lambda _1, \lambda _2 \in \mathcal {M}_b({{\Omega }} \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\). Then, we have \({{\,\textrm{supp}\,}}(\lambda _1) \subseteq {{\Omega }} \times \partial \mathcal {B}\) and \({{\,\textrm{supp}\,}}(\lambda _2) \subseteq {{\Omega }} \times (\overline{\mathcal {B}\cap \mathcal {C}})\).
By the density argument described in Lemma 4.5, we conclude that (4.38) holds for every \(\chi \in C_0({{\Omega }} \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) with \({\widetilde{\textrm{div}}}_{\gamma }\chi = 0\). The definition of \(\lambda _1\) and \(\lambda _2\) then yields
Thus, from Proposition 4.9 we conclude that there exists \(\mu \in \mathcal {X}_{\gamma }({{{\omega }}})\) such that
Recalling the assumption that \(\partial \mathcal {B}\cap \mathcal {C}\subseteq \mathcal {T}\) and using the same argument as above, we obtain
In view of Proposition 4.10 and recalling the assumption that \(\partial \mathcal {B}\setminus \mathcal {T}\) is a \(C^1\)-hypersurface, we are left to prove the analogue of (4.34) for \(\lambda _1\).
We consider
so that \(\lambda ^h_1(x,y) = \left[ {\hat{v}}^h(x_3,y) \odot \nu \right] \mathcal {L}_{x'}^2 \otimes (\mathcal {H}^{2}_{x_3,y}\lfloor {I \times \partial \mathcal {B}})\). Then \(\{{\hat{v}}^h\}\) is bounded in \(L^1({{\Omega }} \times \partial \mathcal {B};\mathbb {R}^3)\) by (4.36). Up to a subsequence,

for a suitable \(\eta \in \mathcal {M}_b({{\Omega }} \times \partial \mathcal {B};\mathbb {R}^3)\). Since \(\nu \) is continuous on \(\partial \mathcal {B}\setminus \mathcal {T}\), we infer
which concludes the proof, since \(\frac{\eta }{|\eta |}\) is a Borel function. \(\square \)
5 Two-scale statics and duality
In this section we define a notion of stress–strain duality and analyze the two-scale behavior of our functionals.
5.1 Stress-plastic strain duality on the cell
Definition 5.1
Let \(\gamma \in (0,+\infty )\). The set \(\mathcal {K}_{\gamma }\) of admissible stresses is defined as the set of all elements \(\Sigma \in L^2(I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) satisfying:
-
(i)
\({\widetilde{\textrm{div}}}_{\gamma }\Sigma = 0 \text { in } I \times \mathcal {Y}\),
-
(ii)
\(\Sigma \,\textbf{e}_3 = 0 \text { on } \partial {I} \times \mathcal {Y}\),
-
(iii)
\(\Sigma _{{{\,\textrm{dev}\,}}}(x_3,y) \in K(y) \,\text { for } \mathcal {L}^{1}_{x_3} \otimes \mathcal {L}^{2}_{y}\text {-a.e. } (x_3,y) \in I \times \mathcal {Y}\).
Since condition iii implies that \(\Sigma _{{{\,\textrm{dev}\,}}} \in L^{\infty }(I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\), for every \(\Sigma \in \mathcal {K}_{\gamma }\) we deduce from Proposition 2.3 that \(\Sigma \in L^p(I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) for every \(1 \le p < \infty \).
Definition 5.2
Let \(\gamma \in (0,+\infty )\). The family \(\mathcal {A}_{\gamma }\) of admissible configurations is given by the set of triplets
such that
Definition 5.3
Let \(\Sigma \in \mathcal {K}_{\gamma }\) and let \((u, E, P) \in \mathcal {A}_{\gamma }\). We define the distribution \([ \Sigma _{{{\,\textrm{dev}\,}}}: P ]\) on \(\mathbb {R}\times \mathcal {Y}\) by
for every \(\varphi \in C_c^{\infty }(\mathbb {R}\times \mathcal {Y})\).
Remark 5.4
Note that the second integral in (5.1) is well defined since \(BD(I \times \mathcal {Y})\) is embedded into \(L^{3/2}(I \times \mathcal {Y};\mathbb {R}^3)\). Moreover, the definition of \([ \Sigma _{{{\,\textrm{dev}\,}}}: P ]\) is independent of the choice of (u, E), so (5.1) defines a meaningful distribution on \(\mathbb {R}\times \mathcal {Y}\).
The following results can be established from the proofs of [24, Theorem 6.2] and [24, Proposition 3.9] respectively, by treating the relative boundary of the “Dirichlet” part as empty, the “Neumann” part as \(\partial {I} \times \mathcal {Y}\), and considering approximating sequences which must be periodic in \(\mathcal {Y}\).
Proposition 5.5
Let \(\Sigma \in \mathcal {K}_{\gamma }\) and \((u, E, P) \in \mathcal {A}_{\gamma }\). Then \([ \Sigma _{{{\,\textrm{dev}\,}}}: P ]\) can be extended to a bounded Radon measure on \(\mathbb {R}\times \mathcal {Y}\), whose variation satisfies
Proposition 5.6
Let \(\Sigma \in \mathcal {K}_{\gamma }\) and \((u, E, P) \in \mathcal {A}_{\gamma }\). If \(\mathcal {Y}\) is a geometrically admissible multi-phase torus, then
5.2 Disintegration of admissible configurations
Let \(\widetilde{\omega } \subseteq \mathbb {R}^2\) be an open and bounded set such that \(\omega \subset \widetilde{\omega }\) and \(\widetilde{\omega } \cap \partial {\omega } = \gamma _D\). We also denote by \(\widetilde{\Omega } = \widetilde{\omega } \times I\) the associated reference domain.
In order to make sense of the duality between the two-scale limits of stresses and plastic strains, we will need to disintegrate the two-scale limits of the kinematically admissible fields in such a way to obtain elements of \(\mathcal {A}_{\gamma }\), for \(\gamma \in (0,+\infty )\).
Definition 5.7
Let \(w \in H^1(\widetilde{\Omega };\mathbb {R}^3) \cap KL(\widetilde{\Omega })\). We define the class \(\mathcal {A}^{hom}_{\gamma }(w)\) of admissible two-scale configurations relative to the boundary datum w as the set of triplets (u, E, P) with
such that
and also such that there exists \(\mu \in \mathcal {X}_{\gamma }({\widetilde{\omega }})\) with
Lemma 5.8
Let \((u,E,P) \in \mathcal {A}^{hom}_{\gamma }(w)\) with the associated \(\mu \in \mathcal {X}_{\gamma }({\widetilde{\omega }})\), and let \({\bar{u}} \in BD(\widetilde{\omega })\) and \(u_3 \in BH(\widetilde{\omega })\) be the Kirchhoff-Love components of u. Set
Then the following disintegrations hold true:
Above, \(A_1, A_2: \widetilde{\omega } \rightarrow \mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}}\) and \(C: \widetilde{\omega } \rightarrow [0, +\infty ]\) are Radon-Nikodym derivatives of \(E{\bar{u}}\), \(-D^2u_3\) and \(\mathcal {L}^{2}_{x'}\) with respect to \(\eta \), E(x, y) is a Borel representative of E, and \(P_{x'} \in \mathcal {M}_b(I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}})\) for \(\eta \)-a.e. \(x' \in \widetilde{\omega }\).
Furthermore, we can choose a Borel map \((x',x_3,y) \in \widetilde{\Omega } \times \mathcal {Y}\mapsto \mu _{x'}(x_3,y) \in \mathbb {R}^3\) such that, for \(\eta \)-a.e. \(x' \in \widetilde{\omega }\),
where \(\mu _{x'} \in BD_\gamma (I \times \mathcal {Y})\), \(\int _{I \times \mathcal {Y}} \mu _{x'}(x_3,y) \,dx_3 dy = 0\).
Proof
The proof is analogous to [23, Lemma 5.4]. The only difference is the statement and argument for the disintegration of \(Eu \otimes \mathcal {L}^{2}_{y}\), that we detail below.
First we note that \(proj_{\#}\left( {\widetilde{E}}_{\gamma }\mu \right) _{\alpha \beta } = proj_{\#}\left( E_{y}\mu \right) _{\alpha \beta } = 0\) for \(\alpha ,\beta =1,2\). Then, from (5.2) we get
where we set \(e^{(1)}:=\int _{I \times \mathcal {Y}} |E(\cdot ,x_3,y)| \,dx_3 dy + (proj_{\#}|P|)^a \in L^2(\widetilde{\omega };\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\). Similarly, after multiplying equation (5.2) by \(x_3\), we have that
where we set \(e^{(2)}:= \frac{1}{12}\,\int _{I \times \mathcal {Y}} |x_3 E(\cdot ,x_3,y) | \,dx_3 dy + \frac{1}{12}\,(proj_{\#}|x_3 P|)^a \in L^2(\widetilde{\omega };\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\). Consequently, the measures \(E{\bar{u}}\) and \(-D^2u_3\) are absolutely continuous with respect to \(\eta \), so we find
for suitable \(A_1, A_2: \widetilde{\omega } \rightarrow \mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}}\) such that (5.3) hold true. \(\square \)
Remark 5.9
From the above disintegration, we have that, for \(\eta \)-a.e. \(x' \in \widetilde{\omega }\),
Thus, the triple
is an element of \(\mathcal {A}_{\gamma }\).
5.3 Admissible stress configurations and approximations
For every \(e^h \in L^2(\Omega ;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) we define \(\sigma ^h(x):= \mathbb {C}\left( \frac{x'}{{\varepsilon _h}}\right) \Lambda _h e^h(x)\). Then, in view of [24, Theorem 3.6], we introduce the set
which is the set of stresses for the rescaled h problems. Next we introduce the set of two-scale limiting stresses.
Definition 5.10
The set \(\mathcal {K}^{hom}_{\gamma }\) is the set of all elements \(\Sigma \in L^2(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) satisfying:
-
(i)
\({\widetilde{\textrm{div}}}_{\gamma }\Sigma (x',\cdot ) = 0 \text { in } I \times \mathcal {Y}\,\text { for a.e. } x' \in \omega \),
-
(ii)
\(\Sigma (x',\cdot )\,\textbf{e}_3 = 0 \text { on } \partial {I} \times \mathcal {Y}\,\text { for a.e. } x' \in \omega \),
-
(iii)
\(\Sigma _{{{\,\textrm{dev}\,}}}(x,y) \in K(y) \,\text { for } \mathcal {L}^{3}_{x} \otimes \mathcal {L}^{2}_{y}\text {-a.e. } (x,y) \in \Omega \times \mathcal {Y}\),
-
(iv)
\(\sigma _{i3}(x) = 0 \,\text { for } i=1,2,3\),
-
(v)
\(\textrm{div}_{x'}{\bar{\sigma }} = 0 \text { in } \omega \),
-
(vi)
\(\textrm{div}_{x'}\textrm{div}_{x'}{\hat{\sigma }} = 0 \text { in } \omega \),
where \(\sigma := \int _{\mathcal {Y}} \Sigma (\cdot ,y) \,dy\), and \({\bar{\sigma }},\, {\hat{\sigma }} \in L^2(\omega ;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\) are the zero-th and first order moments of the \(2 \times 2\) minor of \(\sigma \).
Remark 5.11
Notice that as a consequence of the properties (iii) and (iv) in the Definition 5.10 we can actually conclude that \({\bar{\sigma }},\, {\hat{\sigma }} \in L^\infty (\omega ;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\). Namely, the uniform boundedness of sets K(y) implies that the deviatoric part of the weak limit, i.e. \(\sigma _{{{\,\textrm{dev}\,}}} = \sigma - \frac{1}{3} {{\,\textrm{tr}\,}}{\sigma } I_{3 \times 3}\), is bounded in \(L^\infty (\Omega ;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\). Thus we have that
Hence, the components \(\sigma _{\alpha \beta }\) are all bounded in \(L^\infty (\Omega )\).
In the following proposition we show that the set \(\mathcal {K}_\gamma ^\textrm{hom}\) characterizes weak two-scale limits of sequences of elastic stresses \(\{\sigma ^h\}\).
Proposition 5.12
Let \(\{\sigma ^h\}\) be a bounded family in \(L^2(\Omega ;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) such that \(\sigma ^h \in \mathcal {K}_h\) for every h, and

Then \(\Sigma \in \mathcal {K}^{hom}_{\gamma }\).
Proof
Consider a sequence \(\{\sigma ^h\} \subset L^2(\Omega ;\mathbb {M}^{3\times 3}_{\textrm{sym}})\) such that \(\sigma _h \in \mathcal {K}_h\) for every h, and assume that \(\sigma ^h \rightharpoonup \sigma \) weakly in \(L^2(\Omega ;\mathbb {M}^{3\times 3}_{\textrm{sym}})\). We first establish the macroscopic properties (iv), (v), (vi). To obtain (iv), let \(v \in C_c^{\infty }(\Omega ;\mathbb {R}^3)\) and \(V \in C^{\infty }(\overline{\Omega };\mathbb {R}^3)\) be defined by
From the condition \(\textrm{div}_{h}\sigma ^h = 0 \text { in } \Omega \), for every \(\varphi \in H^1(\Omega ;\mathbb {R}^3)\) with \(\varphi = 0\) on \(\Gamma _D\) we have
Setting
and passing to the limit as \(h\rightarrow 0\), we find
Consequently, from the arbitrariness of v, we infer that \(\sigma _{i3} = 0\).
To obtain (iv) and (v) let \({{\bar{\varphi }}} \in C_c^{\infty }(\omega ;\mathbb {R}^3)\) and choose the test function
We deduce from (5.7) that
Passing to the limit, we conclude that
Next we prove the microscopic properties (i), (ii) and (iii). Consider test functions \({\varepsilon _h}\,\phi \left( x,\frac{x'}{{\varepsilon _h}}\right) \), for \(\phi \in C_c^{\infty }(\omega ;C^{\infty }(\overline{I} \times \mathcal {Y};\mathbb {R}^3))\) in (5.7). We first observe that the sequence
converges strongly two-scale in \(L^2(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3})\). Hence, passing to the limit as \(h\rightarrow 0\), we find
Suppose now that \(\phi \left( x,y\right) = \psi ^{(1)}(x')\,\psi ^{(2)}(x_3,y)\) for \(\psi ^{(1)} \in C_c^{\infty }(\omega )\) and \(\psi ^{(2)} \in C^{\infty }(\overline{I} \times \mathcal {Y};\mathbb {R}^3)\). Then
Thus, for a.e. \(x' \in \omega \),
from which we infer \({\widetilde{\textrm{div}}}_{\gamma }\Sigma (x',\cdot ) = 0 \text { in } I \times \mathcal {Y}\) and \(\Sigma (x',\cdot )\,\textbf{e}_3 = 0 \text { on } \partial {I} \times \mathcal {Y}\).
Finally, we define
and consider the set
The construction of \(\Sigma ^h\) from \(\sigma ^h \in \mathcal {K}_h\) ensures that \(\Sigma ^h \in S\) and that  . Since the compactness of K(y) implies that S is is convex and weakly closed in \(L^2(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\), we have that \(\Sigma \in S\), which concludes the proof. \(\square \)
. Since the compactness of K(y) implies that S is is convex and weakly closed in \(L^2(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\), we have that \(\Sigma \in S\), which concludes the proof. \(\square \)
Conversely, under additional star-shapedness assumptions on \(\omega \), we now provide an approximation result for elements of \(\mathcal {K}_\gamma ^{\textrm{hom}}\).
Lemma 5.13
Let \(\omega \subset \mathbb {R}^2\) be an open bounded set that is star-shaped with respect to one of its points and let \(\Sigma \in \mathcal {K}^{hom}_{\gamma }\). Then, there exists a sequence \(\Sigma _n \in L^2(\mathbb {R}^2 \times I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) such that the following holds:
-
(a)
\(\Sigma _n \in C^\infty (\mathbb {R}^2;L^2(I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}))\) and \(\Sigma _n \rightarrow \Sigma \) strongly in \(L^2(\omega \times I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\),
-
(b)
\({\widetilde{\textrm{div}}}_{\gamma }\Sigma _n(x',\cdot ) = 0 \text { on } I \times \mathcal {Y}\) for every \(x' \in \mathbb {R}^2\),
-
(c)
\(\Sigma _n(x',\cdot )\,\textbf{e}_3 = 0 \text { on } \partial {I} \times \mathcal {Y}\) for every \(x' \in \mathbb {R}^2\),
-
(d)
\((\Sigma _n(x,y))_{{{\,\textrm{dev}\,}}} \in K(y) \,\text { for every } x' \in \mathbb {R}^2 \text { and } \mathcal {L}^{1}_{x_3} \otimes \mathcal {L}^{2}_{y}\text {-a.e. } (x_3,y) \in I \times \mathcal {Y}\).
Further, if we set \(\sigma _n(x):= \int _{\mathcal {Y}} \Sigma _n(x,y) \,dy\), and \({\bar{\sigma }}_n,\, {\hat{\sigma }}_n \in L^2(\omega ;\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\) are the zero-th and first order moments of the \(2 \times 2\) minor of \(\sigma _n\), then:
-
(e)
\(\sigma _n \in C^\infty (\mathbb {R}^2 \times I;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) and \(\sigma _n \rightarrow \sigma \) strongly in \(L^2(\omega \times I;\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\),
-
(f)
\(\textrm{div}_{x'}{\bar{\sigma }}_n = 0 \text { in } \omega \),
-
(g)
\(\textrm{div}_{x'}\textrm{div}_{x'}{\hat{\sigma }}_n = 0 \text { in } \omega \).
Proof
After a translation we may assume that \(\omega \) is star-shaped with respect to the origin.
Thus, in particular,
We extend \(\Sigma \) to \(\mathbb {R}^2 \times I \times \mathcal {Y}\) by setting \(\Sigma = 0\) outside \(\Omega \times \mathcal {Y}\). Let \(\rho \) be the standard mollifier on \(\mathbb {R}^2\) and define the planar dilation \(d_n(x') = \left( \tfrac{n}{n+1}x'\right) \), for every \(n \in \mathbb {N}\). Owing to (5.9), there exists a vanishing sequence \(\epsilon _n > 0\) such that for every map \(\varphi \in C_c^{\infty }(\omega ;\mathbb {R}^2)\)
We then set
With a slight abuse of notation, we have
Items a and e are immediate consequences of the above construction, while item d follows from Jensen’s inequality since K(y) is convex. Next, for \(x' \in \mathbb {R}^2\)
which proves item b.
To prove item f, we observe that, for every map \(\varphi \in C_c^{\infty }(\omega ;\mathbb {R}^2)\) there holds
where in last equation we used that \(\textrm{div}_{x'}{\bar{\sigma }} = 0 \text { in } \omega \) and (5.10).
Similarly for item g, for every map \(\varphi \in C_c^{\infty }(\omega )\) we have
where in last equation we used that \(\textrm{div}_{x'}\textrm{div}_{x'}{\hat{\sigma }} = 0 \text { in } \omega \) and (5.10). \(\square \)
5.4 The principle of maximum plastic work
The aim of this subsection is to prove an inequality between two-scale dissipation and plastic work, which in turn will be essential to prove the global stability condition of two-scale quasistatic evolutions. The claim is given in Corollary 5.16 below.
The proof of the following proposition and consequently Theorem 5.15 relies on the approximation argument given in Lemma 5.13 and on two-scale duality, which can be established only for smooth stresses by disintegration and Definition 5.3, see also [23, Proposition 5.11]. The problem is that the measure \(\eta \) defined in Lemma 5.8 can concentrate on the points where the stress (which is only in \(L^2\)) is not well-defined. The difference with respect to [23, Proposition 5.11] is that one can rely only on the approximation given by Lemma 5.13 which is given for star-shaped domains. To prove it for general domains we use the localization argument (see the proof of Step 2 of Proposition 5.14 and the proof of Theorem 5.15).
Proposition 5.14
Let \(\Sigma \in \mathcal {K}^{hom}_{\gamma }\) and \((u,E,P) \in \mathcal {A}^{hom}_{\gamma }(w)\) with the associated \(\mu \in \mathcal {X}_{\gamma }({\widetilde{\omega }})\). There exists an element \(\lambda \in \mathcal {M}_b(\widetilde{\Omega } \times \mathcal {Y})\) such that for every \(\varphi \in C_c^2(\widetilde{\omega })\)
Furthermore, the mass of \(\lambda \) is given by
Proof
The proof is subdivided into two steps.
Step 1. Suppose that \(\omega \) is star-shaped with respect to one of its points.
Let \(\{ \Sigma _n \} \subset C^\infty (\mathbb {R}^2;L^2(I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}))\) be the sequence given by Lemma 5.13. We set
where the duality \([ (\Sigma _n)_{{{\,\textrm{dev}\,}}}(x',\cdot ): P_{x'} ]\) is a well defined bounded measure on \(I \times \mathcal {Y}\) for \(\eta \)-a.e. \(x' \in \widetilde{\omega }\) and \(\eta \) is defined in Lemma 5.8. Further, in view of Remark 5.9, Definition 5.3 gives
for every \(\psi \in C^1(\mathbb {R}\times \mathcal {Y})\), and
where the last inequality stems from item d in Lemma 5.13. This in turn implies that
from which we conclude that \(\{ \lambda _n \}\) is a bounded sequence.
Let now \(\widetilde{I} \supset I\) be an open set which compactly contains I. Let \(\xi \) be a smooth cut-off function with \(\xi \equiv 1\) on I, and with support contained in \(\widetilde{I}\). Finally, consider a test function \(\phi (x,y):= \varphi (x')\xi (x_3)\), for \(\varphi \in C_c^{\infty }(\widetilde{\omega })\). Since \({\widetilde{\nabla }}_{\gamma }\phi (x,y) = 0\), we have
Since \(u \in KL(\widetilde{\Omega })\), we infer
where \({\bar{u}} \in BD(\widetilde{\omega })\) and \(u_3 \in BH(\widetilde{\omega })\) are the Kirchhoff-Love components of u. From the characterization given in Proposition 3.6, we can thus conclude that
where in the last equality we used that \({\bar{\sigma }}_n\) and \({\hat{\sigma }}_n\) are smooth functions. Notice that, since \({\bar{p}} \equiv 0\) and \({\hat{p}} \equiv 0\) outside of \(\omega \cup \gamma _D\), there holds
Since \(e = E = E{\bar{w}} - x_3 D^2w_3\) on \(\widetilde{\Omega } {\setminus } \Omega \), we deduce, using (5.13)-(5.15),that
Using that \(\textrm{div}_{x'}{\bar{\sigma }}_n = 0 \text { in } \omega \), by applying an integration by parts (see also [13, Proposition 7.2]) we obtain for every \(\varphi \in C^1(\overline{\omega })\)
Likewise in view of the fact that \(\textrm{div}_{x'}\textrm{div}_{x'}{\hat{\sigma }}_n = 0 \text { in } \omega \) and \(u_3 = w_3 \text { on } \gamma _D\), by integration by parts (see also [13, Proposition 7.6]) we find that for every \(\varphi \in C^2(\overline{\omega })\)
Let now \(\lambda \in \mathcal {M}_b(\widetilde{\Omega } \times \mathcal {Y})\) be such that (up to a subsequence)

By items a and e in Lemma 5.13, owing to (5.16)-(5.18) we obtain
Taking \(\varphi \nearrow \mathbb {1}_{\widetilde{\omega }}\), we deduce (5.12).
Step 2. If \(\omega \) is not star-shaped, then since \(\omega \) is a bounded \(C^2\) domain (in particular, with Lipschitz boundary) by [7, Proposition 2.5.4] there exists a finite open covering \(\{U_i\}\) of \(\overline{\omega }\) such that \(\omega \cap U_i\) is (strongly) star-shaped with Lipschitz boundary.
Let \(\{\psi _i\}\) be a smooth partition of unity subordinate to the covering \(\{U_i\}\), i.e. \(\psi _i \in C^{\infty }(\overline{\omega })\), with \(0 \le \psi _i \le 1\), such that \({{\,\textrm{supp}\,}}(\psi _i) \subset U_i\) and \(\sum _{i} \psi _i = 1\) on \(\overline{\omega }\).
For each i, let
Since \(\Sigma ^i \in \mathcal {K}^{hom}_{\gamma }\), the construction in Step 1 yields that there exist sequences \(\{ \Sigma ^i_n \} \subset C^\infty (\mathbb {R}^2;L^2(I \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}))\) and
where again \(\eta \) is defined in Lemma 5.8 such that

with
for every \(\varphi \in C_c^2(\overline{\omega } \cap U_i)\). This allows us to define measures on \(\widetilde{\Omega } \times \mathcal {Y}\) by letting, for every \(\phi \in C_0(\widetilde{\Omega } \times \mathcal {Y})\),
and
From the above computations,  weakly* in \(\mathcal {M}_b(\widetilde{\Omega } \times \mathcal {Y})\), and \(\lambda \) satisfies all the required properties. \(\square \)
weakly* in \(\mathcal {M}_b(\widetilde{\Omega } \times \mathcal {Y})\), and \(\lambda \) satisfies all the required properties. \(\square \)
The next theorem allows us to compare the density of the dissipation due to the limiting two-scale plastic strain and that of the measure \(\lambda \).
Theorem 5.15
Let \(\Sigma \in \mathcal {K}^{hom}_{\gamma }\) and \((u,E,P) \in \mathcal {A}^{hom}_{\gamma }(w)\) with the associated \(\mu \in \mathcal {X}_{\gamma }({\widetilde{\omega }})\). Then
where \(\lambda \in \mathcal {M}_b(\widetilde{\Omega } \times \mathcal {Y})\) is given by Proposition 5.14.
Proof
Let \(\{\Sigma ^i_n\}\), \(\{\lambda ^i_n\}\) and \(\lambda ^i\) be defined as in Step 2 of the proof of Proposition 5.14. Item d in Lemma 5.13 implies that
By Proposition 5.6, we have for \(\eta \)-a.e. \(x' \in \widetilde{\omega }\)
Since \(\frac{dP}{d|P|}(x,y) = \frac{dP_{x'}}{d|P_{x'}|}(x_3,y)\) for \(|P_{x'}|\)-a.e. \((x_3,y) \in I \times \mathcal {Y}\) by Proposition 2.2, we can conclude that
By passing to the limit, we have the desired inequality. \(\square \)
As a direct consequence of the previous theorem and (5.12), we are now in a position to state a principle of maximum plastic work in our setting. For \((u,E,P) \in \mathcal {A}^{hom}_{\gamma }(w)\) we now define
and
Corollary 5.16
Let \(\gamma \in (0, +\infty )\). Then
for every \(\Sigma \in \mathcal {K}^{hom}_{\gamma }\) and \((u,E,P) \in \mathcal {A}^{hom}_{\gamma }(w)\).
5.5 Liminf inequalities under weak two-scale convergence
For \((u,e,p) \in \mathcal {A}_h(w)\), we recall the definition of energy functionals \(\mathcal {Q}_h\) and \(\mathcal {H}_h\) given in (3.11) and (3.12). The next result shows that \(\mathcal {Q}^{hom}\) and \(\mathcal {H}^{hom}\) provide lower bounds for the asymptotic behavior of our elastic energies and dissipation potential with respect to weak two-scale convergence of elastic and plastic stresses.
Theorem 5.17
Let \(\gamma \in (0,+\infty )\). Let \((u^h,e^h,p^h) \in \mathcal {A}_h(w)\) be such that



with \((u,E,P) \in \mathcal {A}^{hom}_{\gamma }(w)\). Then,
and
Proof
Let \(\varphi \in C_c^{\infty }(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\). From the coercivity condition on the quadratic form \(\mathcal {Q}_h\) we obtain
Since  weakly two-scale in \(L^2(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\), we can apply the \(\liminf \) to the above inequality and we find
weakly two-scale in \(L^2(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\), we can apply the \(\liminf \) to the above inequality and we find
Choosing \(\varphi \) such that \(\varphi \rightarrow E\) strongly in \(L^2(\Omega \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})\) yields (5.24).
To prove (5.25), we can assume without loss of generality that
We write
where \(p^h_{i}:= p^h\lfloor {\Omega \cap ((\mathcal {Y}_i)_{\varepsilon _h}\times I)}\) and \(p^h_{ij}:= p^h\lfloor {\widetilde{\Omega } \cap ((\Gamma _{ij} {\setminus } S)_{\varepsilon _h}\times I)}\). Up to a subsequence,

Clearly,
with \({{\,\textrm{supp}\,}}(P_{i}) \subseteq \widetilde{\Omega } \times \overline{\mathcal {Y}}_i\) and \({{\,\textrm{supp}\,}}(P_{ij}) \subseteq \widetilde{\Omega } \times \Gamma _{ij}\). In view of (5.22), we infer

Recalling (3.3), we can additionally assume that \(\Gamma _{ij} \cap \mathcal {C}\subseteq S\). Then, with a normal \(\nu \) on \(\Gamma _{ij}\) that points from \(\mathcal {Y}_j\) to \(\mathcal {Y}_i\) for every \(j \ne i\), Lemma 4.18 implies that
for suitable \(\eta _{ij} \in \mathcal {M}_b^+ (\widetilde{\Omega } \times (\Gamma _{ij} {\setminus } S))\) and a Borel map \(a_{ij}: \widetilde{\Omega } \times (\Gamma _{ij} {\setminus } S) \rightarrow \mathbb {R}^3\) such that \(a_{ij} \perp \nu \) for \(\eta _{ij}\)-a.e. \((x,y) \in \widetilde{\Omega } \times (\Gamma _{ij} {\setminus } S)\).
Using a version of Reshetnyak’s lower semicontinuity theorem adapted for two-scale convergence (see [23, Lemma 4.6]), we deduce
Next, we have
where \(u^h_i\) and \(u^h_j\) are the traces on \(\widetilde{\Omega } \cap ((\Gamma _{ij} {\setminus } S)_{\varepsilon _h}\times I)\) of the restrictions of \(u^h\) to \((\mathcal {Y}_i)_{\varepsilon _h}\times I\) and \((\mathcal {Y}_j)_{\varepsilon _h}\times I\) respectively, such that \(u^h_i - u^h_j\) is perpendicular to \(\nu \). Then, since the infimum in the inf-convolution definition of H on \(\Gamma \setminus S\) is actually a minimum, we obtain
for suitable Borel functions \(b^{h,ij}_i, b^{h,ij}_j: \widetilde{\Omega } \cap ((\Gamma _{ij} {\setminus } S)_{\varepsilon _h}\times I) \rightarrow \mathbb {R}^3\) which are orthogonal to \(\nu \) for \(\mathcal {H}^{2}\)-a.e. \(x \in (\Gamma _{ij} {\setminus } S)_{\varepsilon _h}\times I\) and such that
From the coercivity condition of the dissipation potential H and (5.26), we conclude that
for some constant \(C > 0\), which implies the boundedness of \(b^{h,ij}_i\) and \(b^{h,ij}_j\) in \(L^1\). We can now argue as in Step 2 of the proof of [23, Theorem 5.7] or [24, Proposition 2.3], using also (5.28), and infer the existence of suitable measures \(\zeta _{ij} \in \mathcal {M}_b^+(\widetilde{\Omega } \times (\Gamma _{ij} {\setminus } S))\), and Borel functions \(c^i, c^j: \widetilde{\Omega } \times (\Gamma _{ij} {\setminus } S) \rightarrow \mathbb {R}^3\) which are orthogonal to \(\nu \) for \(\zeta _{ij}\)-a.e. \((x,y) \in \widetilde{\Omega } \times (\Gamma _{ij} {\setminus } S)\), and such that
Thus, by (5.29), we have
which in turn concludes the proof. \(\square \)
6 Two-scale quasistatic evolutions
We recall the definition of energy functionals \(\mathcal {Q}^{hom}\) and \(\mathcal {H}^{hom}\) given in (5.19) and (5.20). The associated \(\mathcal {H}^{hom}\)-variation of a function \(P: [0,T] \rightarrow \mathcal {M}_b(\widetilde{\Omega } \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}})\) on [a, b] is then defined as
In this section we prescribe for every \(t \in [0, T]\) a boundary datum \(w(t) \in H^1(\widetilde{\Omega };\mathbb {R}^3) \cap KL(\widetilde{\Omega })\) and we assume the map \(t\mapsto w(t)\) to be absolutely continuous over [0, T] with respect to the \(H^1\)-norm.
We now give the notion of the limiting quasistatic elasto-plastic evolution.
Definition 6.1
A two-scale quasistatic evolution for the boundary datum w is a function \(t \mapsto (u(t), E(t), P(t))\) from [0, T] into \(KL(\widetilde{\Omega }) \times L^2(\widetilde{\Omega } \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}) \times \mathcal {M}_b(\widetilde{\Omega } \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}})\) which satisfies the following conditions:
- \((qs1)^{hom}_{\gamma }\):
-
for every \(t \in [0,T]\) we have \((u(t), E(t), P(t)) \in \mathcal {A}^{hom}_{\gamma }(w(t))\) and
$$\begin{aligned} \mathcal {Q}^{hom}(E(t)) \le \mathcal {Q}^{hom}(H) + \mathcal {H}^{hom}(\Pi -P(t)), \end{aligned}$$for every \((\upsilon ,H,\Pi ) \in \mathcal {A}^{hom}_{\gamma }(w(t))\).
- \((qs2)^{hom}_{\gamma }\):
-
the function \(t \mapsto P(t)\) from [0, T] into \(\mathcal {M}_b(\widetilde{\Omega } \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}})\) has bounded variation and for every \(t \in [0, T]\)
$$\begin{aligned} \mathcal {Q}^{hom}(E(t)) + \mathcal {D}_{\mathcal {H}^{hom}}(P; 0, t) = \mathcal {Q}^{hom}(E(0)) + \int _0^t \int _{\Omega \times \mathcal {Y}} \mathbb {C}(y) E(s): E{\dot{w}}(s) \,dx dy ds. \end{aligned}$$
Recalling the definition of h-quasistatic evolution for the boundary datum w(t) given in Definition 3.7, we are in a position to formulate the main result of the paper.
Theorem 6.2
Let \(t \mapsto w(t)\) be absolutely continuous from [0, T] into \(H^1(\widetilde{\Omega };\mathbb {R}^3) \cap KL(\widetilde{\Omega })\). Assume (3.4) and (3.6) and that there exists a sequence of triples \((u^h_0, e^h_0, p^h_0) \in \mathcal {A}_h(w(0))\) such that



for \((u_0,E_0,P_0) \in \mathcal {A}^{hom}_{\gamma }(w(0))\). For every \(h > 0\), let
be a h-quasistatic evolution in the sense of Definition 3.7 for the boundary datum w such that \(u^h(0) = u^h_0\), \(e^h(0) = e^h_0\), and \(p^h(0) = p^h_0\). Then, there exists a two-scale quasistatic evolution
for the boundary datum w such that \(u(0) = u_0\), \(E(0) = E_0\), and \(P(0) = P_0\), and such that (up to subsequences) for every \(t \in [0,T]\)



Proof
The proof is subdivided into three steps, in the spirit of evolutionary \(\Gamma \)-convergence.
Step 1: Compactness.
We first prove that there exists a constant C, depending only on the initial and boundary data, such that
for every \(h>0\). Indeed, the energy balance of the h-quasistatic evolution \((qs2)_{h}\) and (3.6) imply
where the last integral is well defined as \(t \mapsto E{\dot{w}}(t)\) belongs to \(L^1([0,T];L^2(\widetilde{\Omega };\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}}))\). In view of the boundedness of \(\Lambda _h e^h_0\) that is implied by (6.2), property (6.7) now follows by the Cauchy-Schwarz inequality.
From (6.7) and (3.7), we infer that
for every \(t \in [0,T]\), which together with (6.3) implies
Next, we note that \(\left\| \cdot \right\| _{L^1(\widetilde{\Omega } {\setminus } \overline{\Omega };\mathbb {M}^{3 \times 3}_{{{\,\textrm{sym}\,}}})}\) is a continuous seminorm on \(BD(\widetilde{\Omega })\) which is also a norm on the set of rigid motions. Then, using a variant of Poincaré-Korn’s inequality (see [43, Chapter II, Proposition 2.4]) and the fact that \((u^h(t), e^h(t), p^h(t)) \in \mathcal {A}_h(w(t))\), we conclude that, for every \(h > 0\) and \(t \in [0,T]\),
In view of the assumption on w, from (6.8) and the former inequality in (6.7) it follows that the sequences \(\{u^h(t)\}\) are bounded in \(BD(\widetilde{\Omega })\) uniformly with respect to t.
Owing to (2.3), we obtain that \(\mathcal {D}_{\mathcal {H}_h}\) and \(\mathcal {V}\) are equivalent norms, which immediately implies
for every \(h>0\). Hence, by a generalized version of Helly’s selection theorem (see [11, Lemma 7.2]) and Remark 3.10, there exists a (not relabeled) subsequence, independent of t, and \(P \in BV(0,T;\mathcal {M}_b(\widetilde{\Omega } \times \mathcal {Y};\mathbb {M}^{3 \times 3}_{{{\,\textrm{dev}\,}}}))\) such that

for every \(t \in [0,T]\), and \(\mathcal {V}(P; 0, T) \le C\). By extracting a further subsequence (possibly depending on t),

for every \(t \in [0,T]\). From Proposition 4.1, we conclude that \(u(t) \in KL(\widetilde{\Omega })\) for every \(t \in [0,T]\). According to Proposition 4.14, the above subsequence can be chosen so that there exists \(\mu (t) \in \mathcal {X}_{\gamma }({\widetilde{\omega }})\) for which

Since, \(\Lambda _{h_t} Eu^{h_t}(t) = \Lambda _{h_t} e^{h_t}(t) + \Lambda _{h_t} p^{h_t}(t)\) in \(\widetilde{\Omega }\) for every \(h > 0\) and \(t \in [0,T]\), we deduce that \((u(t),E(t),P(t)) \in \mathcal {A}^{hom}_{\gamma }(w(t))\).
Consider now for every \(t \in [0,T]\) the maps
For a (not relabeled) subsequence, we have

where \(\Sigma (t):= \mathbb {C}(y) E(t)\). Since \(\sigma ^{h_t}(t) \in \mathcal {K}_{h_t}\) for every \(t \in [0,T]\), by Proposition 5.12 we obtain that \(\Sigma (t) \in \mathcal {K}^{hom}_{\gamma }\) for every \(t\in [0,T]\).
Step 2: Global stability.
Since from Step 1 we have \((u(t),E(t),P(t)) \in \mathcal {A}^{hom}_{\gamma }(w(t))\) with the associated \(\mu (t) \in \mathcal {X}_{\gamma }({\widetilde{\omega }})\), then for every \((\upsilon ,H,\Pi ) \in \mathcal {A}^{hom}_{\gamma }(w(t))\) with the associated \(\nu \in \mathcal {X}_{\gamma }({\widetilde{\omega }})\) we have
From the inclusion \(\mathbb {C}(y) E(t) \in \mathcal {K}^{hom}_{\gamma }\), by Corollary 5.16 we infer
Thus,
hence we deduce \((qs1)^{hom}_{\gamma }\).
Now we can prove that limit functions u(t) and E(t) do not depend on the subsequence. Assume that \((\upsilon (t),H(t),P(t)) \in \mathcal {A}^{hom}_{\gamma }(w(t))\) with the associated \(\nu (t) \in \mathcal {X}_{\gamma }({\widetilde{\omega }})\) also satisfy the global stability condition in the definition of the two-scale quasistatic evolution. By the strict convexity of \(\mathcal {Q}^{hom}\), we find
Then, by (5.2),
Identifying Eu(t) and \(E\upsilon (t)\) with elements of \(\mathcal {M}_b(\widetilde{\Omega };\mathbb {M}^{2 \times 2}_{{{\,\textrm{sym}\,}}})\) and integrating over \(\mathcal {Y}\), we obtain
Using the variant of Poincaré-Korn inequality in Step 1, we infer that \(\upsilon (t) = u(t)\) on \(\widetilde{\Omega }\).
This implies that the whole sequences converges without need to extract further t-dependent subsequences, i.e.

Step 3: Energy balance.
In order to prove \((qs2)^{hom}_{\gamma }\), it is enough (by arguing as in, e.g. [11, Theorem 4.7] and [24, Theorem 2.7]) to prove the energy inequality
For a fixed \(t \in [0,T]\), consider a subdivision \(0 = t_1< t_2< \ldots < t_n = t\) of [0, t]. In view of the lower semicontinuity of \(\mathcal {Q}^{hom}\) and \(\mathcal {H}^{hom}\) (see (5.24) and (5.25)), from \((qs2)_{h}\) we have
By the strong convergence assumed in (6.2) and (6.10), owing to the Lebesgue’s dominated convergence theorem we obtain
Hence, we have
Taking the supremum over all partitions of [0, t] yields (6.11), which concludes the proof. \(\square \)
Remark 6.3
We point out that as a Corollary of Theorem 6.2 and of the fact that the limiting model satisfies an energy equality, we find that strong two-scale convergence in the \(L^2\)-topology of the scaled initial elastic strains and weak two-scale convergence in measure of the scaled initial plastic strains are enough to guarantee the strong two-scale convergence of the rescaled elastic strains in the \(L^2\)-topology to the effective one, as well as the convergence of rescaled dissipations to the limiting one.
Data Availibility Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Courier Corporation, New York (2000)
Breit, D., Diening, L., Gmeineder, F.: On the trace operator for functions of bounded \(\mathbb{A} \)-variation. Anal. PDE 13(2), 559–594 (2020)
Bufford, L., Davoli, E., Fonseca, I.: Multiscale homogenization in Kirchhoff’s nonlinear plate theory. Math. Models Methods Appl. Sci. 25(09), 1765–1812 (2015)
Bukal, M., Velčić, I.: On the simultaneous homogenization and dimension reduction in elasticity and locality of \(\Gamma \)-closure. Calc. Var. Partial Differ. Equ. 56(3), 1–41 (2017)
Bužančić, M., Cherednichenko, K., Velčić, I., Žubrinić, J.: Spectral and evolution analysis of composite elastic plates with high contrast. J. Elast. 152(1–2), 79–177 (2022)
Caillerie, D.: Thin elastic and periodic plates. Math. Methods Appl. Sci. 6(2), 159–191 (1984)
Carbone, L., De Arcangelis, R.: Unbounded Functionals in the Calculus of Variations: Representation, Relaxation, and Homogenization. Chapman and Hall/CRC, New York (2019)
Cherdantsev, M., Cherednichenko, K.: Bending of thin periodic plates. Calc. Var. Partial Differ. Equ. 54(4), 4079–4117 (2015)
Christowiak, F., Kreisbeck, C.: Asymptotic rigidity of layered structures and its application in homogenization theory. Arch. Ration. Mech. Anal. 235(1), 51–98 (2020)
Christowiak, F., Kreisbeck, C.: Homogenization of layered materials with rigid components in single-slip finite crystal plasticity. Calc. Var. Partial Differ. Equ. 56(3), 75 (2017)
Dal Maso, G., DeSimone, A., Mora, M.: Quasistatic evolution problems for linearly elastic-perfectly plastic materials. Arch. Ration. Mech. Anal. 180, 237–291 (2006)
Damlamian, A., Vogelius, M.: Homogenization limits of the equations of elasticity in thin domains. SIAM J. Math. Anal. 18(2), 435–451 (1987)
Davoli, E., Mora, M.: A quasistatic evolution model for perfectly plastic plates derived by \(\Gamma \)-convergence. Ann. Inst. H. Poincar é Anal Non Lin é aire 30, 615–660 (2013)
Davoli, E.: Linearized plastic plate models as its of 3D finite elastoplasticity. ESAIM COCV 20(3), 725–747 (2014)
Davoli, E.: Quasistatic evolution models for thin plates arising as low energy \(\Gamma \)-limits of finite plasticity. Math. Models Methods Appl. Sci. 24(10), 2085–2153 (2014)
Davoli, E., Ferreira, R., Kreisbeck, C.: Homogenization in BV of a model for layered composites in finite crystal plasticity. Adv. Calc. Var. 14(3), 441–473 (2021)
Davoli, E., Gavioli, C., Pagliari, V.: A homogenization result in finite plasticity. arXiv:2204.09084 (2022)
Davoli, E., Kreisbeck, C.: On static and evolutionary homogenization in crystal plasticity for stratified composites. In: Espa, M.I., Lewicka, N.M., Scardia, L., Schlömerkemper, A. (eds.) Research in Mathematics of Materials Science, pp. 159–183. Springer, Cham (2022)
Davoli, E., Mora, M.G.: Stress regularity for a new quasistatic evolution model of perfectly plastic plates. Calc. Var. Partial Differ. Equ. 54(3), 2581–2614 (2015)
Demengel, F.: Fonctions à hessien borné. Ann. Inst. Fourier (Grenoble) 34, 155–190 (1984)
Demengel, F., Temam, R.: Convex functions of a measure and applications. Indiana Univ. Math. J. 33(5), 673–709 (1984)
Fonseca, I., Leoni, G.: Modern Methods in the Calculus of Variations: \(L^p\) Spaces. Springer, Berlin (2007)
Eur, J., Francfort, G., Giacomini, A.: On periodic homogenization in perfect elasto-plasticity. Math. Soc. (JEMS) 16, 409–461 (2014)
Francfort, G., Giacomini, A.: Small-strain heterogeneous elastoplasticity revisited. Commun. Pure Appl. Math. 65, 1185–1241 (2012)
Francfort, G.A., Giacomini, A., Musesti, A.: On the Fleck and Willis homogenization procedure in strain gradient plasticity. Discrete. Contin. Dyn. Syst. Ser. S 6(1), 43–62 (2013)
Gagliardo, E.: Caratterizzazioni delle tracce sulla frontiera relative ad alcune classi di funzioni in \( n \) variabili. Rendiconti del seminario matematico della universita di Padova 27, 284–305 (1957)
Giacomini, A., Musesti, A.: Two-scale homogenization for a model in strain gradient plasticity. ESAIM Control Optim. Calc. Var. 17(4), 1035–1065 (2011)
Gidoni, P., Maggiani, G.B., Scala, R.: Existence and regularity of solutions for an evolution model of perfectly plastic plates. Commun. Pure Appl. Anal. 18(4), 1783–1826 (2019)
Goffman, C., Serrin, J.: Sublinear functions of measures and variational integrals. Duke Math. J. 31(1), 159–178 (1964)
Hanke, H.: Homgenization in gradient plasticity. Math. Models Methods Appl. Sci. 21(8), 1651–1684 (2011)
Heida, M., Schweizer, B.: Non-periodic homogenization of infinitesimal strain plasticity equations. ZAMM Z. Angew. Math. Mech. 96(1), 5–23 (2016)
Heida, M., Schweizer, B.: Stochastic homogenization of plasticity equations. ESAIM COCV 24(1), 153–176 (2018)
Hornung, P., Neukamm, S., Velčić, I.: Derivation of a homogenized nonlinear plate theory from 3d elasticity. Calc. Var. Partial Differ. Equ. 51(3), 677–699 (2014)
Kohn, R., Temam, R.: Dual spaces of stresses and strains, with applications to Hencky plasticity. Appl. Math. Optim. 10, 1–35 (1983)
Liero, M., Mielke, A.: An evolutionary elastoplastic plate model derived via \(\Gamma \)-convergence. Math. Models Methods Appl. Sci. 21(09), 1961–1986 (2011)
Liero, M., Roche, T.: Rigorous derivation of a plate theory in linear elastoplasticity via \(\Gamma \)-convergence. Nonlinear Differ. Equ. Appl. NoDEA 19(4), 437–457 (2012)
Maggiani, G.B., Mora, M.G.: Quasistatic evolution of perfectly plastic shallow shells: a rigorous variational derivation. Annali di Matematica Pura ed Applicata (1923-) 197(3), 775–815 (2018)
Maggiani, G.B., Mora, M.G.: A dynamic evolution model for perfectly plastic plates. Math. Models Methods Appl. Sci. 26(10), 1825–1864 (2016)
Mielke, A., Roubíček, T., Stefanelli, U.: \(\Gamma \)-limits and relaxations for rate-independent evolutionary problems. Calc. Var. Partial Differ. Equ. 31(3), 387–416 (2008)
Neukamm, S., Velčić, I.: Derivation of a homogenized von-Kármán plate theory from 3D nonlinear elasticity. Math. Models Methods Appl. Sci. 23(14), 2701–2748 (2013)
Panasenko, G.: Multi-scale Modelling for Structures and Composites, p. xiv+398. Springer, Dordrecht (2005)
Schweizer, B., Veneroni, M.: Homogenization of plasticity equations with two-scale convergence methods. Appl. Anal. 94(2), 375–398 (2015)
Temam, R.: Mathematical Problems in Plasticity. Gauthier-Villars, Paris (1985)
Temam, R.: Navier–Stokes Equations: Theory and Numerical Analysis, p. 343. American Mathematical Society, New York (2001)
Velčić, I.: On the derivation of homogenized bending plate model. Calc. Var. Partial Differ. Equ. 53(3–4), 561–586 (2015)
Acknowledgements
M. Bužančić and I. Velčić were supported by the Croatian Science Foundation under Grant Agreement no. IP-2018-01-8904 (Homdirestroptcm) and under Grant agreement No. IP-2022-10-5181 (HOMeOS). The research of E. Davoli was supported by the Austrian Science Fund (FWF) projects 10.55776/F65, 10.55776/V 662, 10.55776/Y1292, and 10.55776/I 4052. All authors are thankful for the support from the OeAD-WTZ project HR 08/2020.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Andrea Mondino.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Bužančić, M., Davoli, E. & Velčić, I. Effective quasistatic evolution models for perfectly plastic plates with periodic microstructure. Calc. Var. 63, 93 (2024). https://doi.org/10.1007/s00526-024-02693-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-024-02693-w



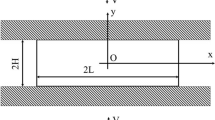
 two-scale weakly* in
two-scale weakly* in