Stress regularity for a new quasistatic evolution model of perfectly plastic plates

Abstract

We study some properties of solutions to a quasistatic evolution problem for perfectly plastic plates, that has been recently derived from three-dimensional Prandtl–Reuss plasticity. We prove that the stress tensor has locally square-integrable first derivatives with respect to the space variables. We also exhibit an example showing that the model under consideration has in general a genuinely three-dimensional nature and cannot be reduced to a two-dimensional setting.

1 Introduction

In this paper we continue the study of the quasistatic evolution model for perfectly plastic plates, that has been derived in [5] starting from three-dimensional Prandtl–Reuss plasticity. Under suitable regularity assumptions for the applied body forces, we prove $W^{1,2}_{loc}$ regularity of the stress with respect to the space variables.

Let $\omega$ be a bounded domain in $\mathbb {R}^2$ with a $C^2$ boundary. The set $\varOmega :=\omega {\times }(-\frac{1}{2},\frac{1}{2})$ represents the reference configuration of a three-dimensional plate. The current configuration of the plate at time t is described by a triple (u(t), e(t), p(t)), where u(t) is the displacement, e(t) is the elastic strain tensor, and p(t) is the plastic strain tensor, satisfying the following conditions:

• (sf1) kinematic admissibility: $Eu(t)=e(t)+p(t)$ in $\varOmega$, $u(t)=w(t)$ on $\varGamma _d$, and $e_{i3}(t)=p_{i3}(t)=0$ in $\varOmega$ for $i=1,2,3$.

Here Eu(t) denotes the infinitesimal strain tensor, given by the symmetric part of D u(t), while w(t) is a prescribed boundary condition on $\varGamma _d:=\gamma _d{\times }(-\frac{1}{2},\frac{1}{2})$, $\gamma _d$ being a subset of $\partial \omega$. These conditions imply that u(t) is a Kirchhoff–Love displacement, that is, the vertical displacement $u_3(t)$ is independent of the out-of-plane variable $x_3$ and the horizontal displacement takes the form

$$\begin{aligned} u_\alpha (t,x)=\bar{u}_\alpha (t,x')- x_3\partial _\alpha u_3(t, x') \quad \text {for }x=(x',x_3)\in \varOmega , \ \alpha =1,2. \end{aligned}$$

(1.1)

In particular, for $\alpha ,\beta =1,2$

$$\begin{aligned} (Eu)_{\alpha \beta }(t,x)= (E\bar{u})_{\alpha \beta }(t,x')-x_3 \partial ^2_{\alpha \beta } u_3(t,x') \quad \text {for }x=(x',x_3)\in \varOmega . \end{aligned}$$

From a mechanical point of view this structure guarantees that straight fibers that are normal to the mid-surface of the plate in the reference configuration, stay straight and normal after the deformation, within the first order (see, e.g. [3]).

Condition (sf1) does not imply, in general, that e(t) and p(t) are affine with respect to $x_3$. However, one can prove (see Proposition 1) that e(t) and p(t) admit the following decomposition:

$$\begin{aligned} e(t,x)=\bar{e}(t,x')+x_3\hat{e}(t,x')+e_\perp (t,x), \quad p(t,x)=\bar{p}(t,x')+x_3 \hat{p}(t,x') -e_\perp (t,x), \end{aligned}$$

where the zero-th order moments $\bar{e}(t)$ and $\bar{p}(t)$ satisfy

$$\begin{aligned} E\bar{u}(t)=\bar{e}(t)+\bar{p}(t) \quad \text { in }\omega \end{aligned}$$

while the first order moments $\hat{e}(t)$ and $\hat{p}(t)$ are such that

$$\begin{aligned} -D^2 u_3(t)=\hat{e}(t)+\hat{p}(t) \quad \text { in }\omega . \end{aligned}$$

In the above identities and in the following we identify e(t), p(t), and their moments with functions taking values in $\mathbb {M}^{2\times 2}_{sym}$, since their third row and column are zero by condition (sf1).

The strong formulation of the quasistatic evolution problem on a time interval [0, T] consists in finding u(t), e(t), and p(t) such that for every $t\in [0,T]$ equation (sf1) is satisfied, together with the following conditions:

• (sf2) constitutive equation: $\sigma (t)=\mathbb {C}_re(t)$ in $\varOmega$, where $\mathbb {C}_r$ is the elasticity tensor;

• (sf3) equilibrium: $-\mathrm {div}_{x'}\bar{\sigma }(t)=f(t)$ and $-\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }(t)=g(t)$ in $\omega$, together with suitable Neumann boundary conditions on $\partial \omega \setminus \gamma _d$;

• (sf4) stress constraint: $\sigma (t)\in K_r$, where $K_r$ is a given convex and compact set, representing the set of admissible stresses;

• (sf5) flow rule: $\dot{p}(t)=0$ if $\sigma (t)\in \mathrm {int}\, K_r$, while $\dot{p}(t)$ belongs to the normal cone to $K_r$ at $\sigma (t)$ if $\sigma (t)\in \partial K_r$.

Here $f(t):\omega \rightarrow \mathbb {R}^2$ and $g(t):\omega \rightarrow \mathbb {R}$ represent the applied body forces at time t, while $\bar{\sigma }(t):=\mathbb {C}_r\bar{e}(t)$ and $\hat{\sigma }(t):=\mathbb {C}_r\hat{e}(t)$ are the stretching and bending components of the stress, respectively. Condition (sf5) can also be written in the equivalent form:

(sf5$'$):

maximum dissipation principle: $H_r(\dot{p}(t))=\sigma (t){\,:\,}\dot{p}(t)$, where $H_r$ is the support function of $K_r$, i.e., $H_r(p):=\sup \{\sigma {\,:\,} p\, :\ \sigma \in K_r\}$,

or alternatively,

(sf5$''$):

maximum plastic work condition: $(\theta -\sigma (t)){\,:\,}\dot{p}(t)\le 0$ for every $\theta \in K_r$.

In [5] this model has been rigorously justified via $\varGamma$-convergence techniques, starting from the three-dimensional Prandtl–Reuss quasistatic evolution model. In other words the system (sf1)–(sf5) describes (up to a suitable scaling) the asymptotic behaviour of the quasistatic evolutions in a three-dimensional plate, when the plate thickness approaches zero.

We note that the equilibrium conditions are purely two-dimensional, while the stress constraint and the flow rule (which are the main ingredients of the plastic response) involve the whole stress $\sigma (t)$, whose dependence on the thickness variable $x_3$ may be not trivial (because of the component $\sigma _\perp (t):=\mathbb {C}_re_\perp (t)$). Thus, the problem has in general a genuinely three-dimensional nature and differs from the classical two-dimensional plastic plate model that has been extensively studied in the literature [2, 6, 9, 10]. This comparison is discussed in the last section of the paper, where an explicit solution to (sf1)–(sf5) is shown for a specific choice of data.

Existence of a solution to (sf1)–(sf5) can be proved by setting the problem within the variational framework for rate-independent processes, developed in [14]. This accounts to approximating the problem by time discretization: the interval [0, T] is subdivided into k subintervals by means of points

$$\begin{aligned} 0=t_k^0<t_k^1<\dots <t_k^{k-1}<t_k^{k}=T\,, \end{aligned}$$

and the approximate solution $u^i_k$, $e^i_k$, $p^i_k$ at time $t^i_k$ is defined by induction as a minimizer of the energy functional

$$\begin{aligned} \frac{1}{2} \int _{\varOmega } \mathbb {C}_re{\,:\,}e\,dx +\int _{\varOmega } H_r(p-p^{i-1}_k)\, dx - \langle {\mathcal {L}}(t^i_k),u\rangle \end{aligned}$$

(1.2)

among all triples (u, e, p) that are kinematically admissible at time $t^i_k$, where

$$\begin{aligned} \langle {\mathcal {L}}(t),u\rangle :=\int _\omega f(t){\,\cdot \,}\bar{u}\, dx' -\frac{1}{12}\int _\omega g(t)u_3\, dx'. \end{aligned}$$

Because of the linear growth of $H_r$, the energy functional in (1.2) is not coercive in any Sobolev norm. The natural setting for a weak formulation is the space $BD(\varOmega )$ of functions with bounded deformation in $\varOmega$ for the displacement u(t) and the space $M_b(\varOmega \cup \varGamma _d;\mathbb {M}^{2\times 2}_{sym})$ of bounded Borel measures on $\varOmega \cup \varGamma _d$ for the plastic strain p(t). This is also natural from a mechanical point of view, because it is well known that in the absence of hardening displacements may develop jump discontinuities along so-called slip surfaces, on which plastic strain concentrates.

Since $p(t)\in M_b(\varOmega \cup \varGamma _d;\mathbb {M}^{2\times 2}_{sym})$, the functional

$$\begin{aligned} \int _{\varOmega } H_r(p(t))\, dx \end{aligned}$$

has to be interpreted according to the theory of convex functions of measures, developed in [12, 15] (see also Sect. 2), as

$$\begin{aligned} \mathcal {H}_r(p(t)):=\int _{\varOmega \cup \varGamma _d} H_r\left( \frac{dp(t)}{d|p(t)|}\right) \, d|p(t)|, \end{aligned}$$

where dp(t) / d|p(t)| is the Radon–Nikodým derivative of p(t) with respect to its total variation |p(t)|. Moreover, the boundary condition is relaxed by requiring that

$$\begin{aligned} p(t)=(w(t)-u(t))\odot \nu _{\partial \varOmega } {\mathcal {H}}^2\quad \text {on }\varGamma _d, \end{aligned}$$

(1.3)

where the symbol $\odot$ denotes the symmetrized tensor product and ${\mathcal {H}}^2$ is the two-dimensional Hausdorff measure. The mechanical interpretation of (1.3) is that u(t) may not attain the boundary condition: in this case a plastic slip is developed along $\varGamma _d$, whose amount is proportional to the difference between the prescribed boundary value and the actual value.

Combining these remarks with the kinematic admissibility condition (sf1), we see that u(t) is a Kirchhoff–Love displacement in $BD(\varOmega )$, that is, $u_3(t)$ belongs to the space $BH(\omega )$ of functions with bounded Hessian in $\omega$ and the averaged tangential displacement $\bar{u}(t)$ in (1.1) belongs to $BD(\omega )$. Therefore, $\bar{u}(t)$ may exhibit jump discontinuities, while, because of the embedding of $BH(\omega )$ into $C(\overline{\omega })$, the normal displacement $u_3(t)$ is continuous, but its gradient may have jump discontinuities. Since the dependence of u on $x_3$ is affine, we can conclude that slip surfaces are vertical surfaces whose projection on $\omega$ is the union of the jump set of $\bar{u}$ and the jump set of $\nabla u_3$.

Moreover, writing condition (1.3) in terms of moments yields

$$\begin{aligned} \begin{array}{c} \bar{p}(t)=(\bar{w}(t)-\bar{u}(t))\odot \nu _{\partial \omega }\mathcal {H}^1 \quad \text { on }\gamma _d,\\ u_3(t)=w_3(t), \qquad \hat{p}(t)=(\nabla u_3(t)-\nabla w_3(t))\odot \nu _{\partial \omega }\mathcal {H}^1 \quad \text { on }\gamma _d. \end{array} \end{aligned}$$

In this setting the flow rule is proved to hold in the form

$$\begin{aligned} \mathcal {H}_r(\dot{p}(t))=\langle \sigma (t),\dot{p}(t) \rangle , \end{aligned}$$

where the product at the right-hand side is meant in the sense of the stress–strain duality introduced in [5] (see also Sect. 3).

In this paper we focus on the spatial regularity of the stress component $\sigma (t)$ for solutions of the quasistatic evolution problem (sf1)–(sf5) in its weak formulation. We restrict to the case where the yield criterion in the fully three-dimensional Prandtl–Reuss problem is that of von Mises, often used for metals (see [13]). In other words, the set of admissible stresses for the fully three-dimensional Prandtl–Reuss problem is a cylinder $B_{\alpha _0}+\mathbb {R}I_{3\times 3}$, where $B_{\alpha _0}$ is a ball of radius $\alpha _0$ in the space of trace-free $\mathbb {M}^{3\times 3}_{sym}$ matrices and $I_{3\times 3}$ is the identity matrix in $\mathbb {M}^{3\times 3}_{sym}$. By the characterization in [5] this implies that the set $K_r$ is an ellipsoid of the form

$$\begin{aligned} K_r=\{\xi \in \mathbb {M}^{2\times 2}_{sym}: \ |\xi |_r\le \alpha _0\}, \end{aligned}$$

where

$$\begin{aligned} |\xi |_r^2:=\frac{1}{6}(\xi _{11}+\xi _{22})^2+\frac{1}{2} (\xi _{11}-\xi _{22})^2 +2\xi _{12}^2 = |\xi |^2-\frac{1}{3} ({\mathrm {tr}}\,\xi )^2. \end{aligned}$$

Our main result is that for the solutions of the quasistatic evolution problem under consideration the stress component is locally $W^{1,2}$ with respect to space variables (Theorem 2). More precisely, we show that for every open set $\omega '$ compactly contained in $\omega$ there exists a positive constant $C_1(\omega ')$ such that

$$\begin{aligned} \sup _{t\in [0,T]} \Vert D_\alpha \sigma (t)\Vert _{L^2(\omega '\times (-\frac{1}{2},\frac{1}{2});\,\mathbb {M}^{2\times 2}_{sym})}\le C_1(\omega ') \quad \text { for } \alpha =1,2 \end{aligned}$$

(1.4)

and for every open set $\varOmega '$ compactly contained in $\varOmega$ there exists a positive constant $C_2(\varOmega ')$ such that

$$\begin{aligned} \sup _{t\in [0,T]} \Vert D_3 \sigma (t)\Vert _{L^2(\varOmega ';\,\mathbb {M}^{2\times 2}_{sym})}\le C_2(\varOmega '). \end{aligned}$$

(1.5)

This implies in particular that the stretching component $\bar{\sigma }$ and the bending component $\hat{\sigma }$ are both in $L^\infty (0,T; W^{1,2}_{loc}(\omega ;\mathbb {M}^{2\times 2}_{sym}))$, while the component $\sigma _\perp$ is in $L^\infty (0,T; W^{1,2}_{loc}(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$.

Local regularity of stresses in the fully three-dimensional Prandtl–Reuss plasticity has been proved in [1, 8], see also [11] for a recent global regularity result for the stress velocity. For the classical two-dimensional plastic plate model local regularity has been established in [10], using different techniques and assuming $K_r$ to be a ball, $\mathbb {C}_r$ to be the identity tensor, and $\gamma _d=\partial \omega$.

The strategy of our proof is inspired by that of [1]. We consider an equivalent formulation of problem (sf1)–(sf5) in terms of a parabolic variational inequality for the stress variable and we construct some approximating problems of Norton–Hoff type, where the constraint (sf4) is replaced by a penalization term. These approximating problems involve a monotone differential equation in the stress variable; the displacement and the plastic strain are then indirectly recovered a posteriori. We first establish regularity for the approximating problems with uniform estimates with respect to the approximation parameter and then prove convergence to the parabolic variational inequality formulation.

The main novelty with respect to [1] is that in the approximating model the equilibrium equations are expressed in terms of the moments $\bar{\sigma }$ and $\hat{\sigma }$, while the nonlinearity in the monotone operator involves the whole stress $\sigma$. For this reason we obtain a slightly better regularity of the stress with respect to the in-plane variables: the regularity estimate (1.4) is indeed global in the out-of-plane direction $x_3$, whereas (1.5) is local with respect to both in-plane and out-of-plane variables. In particular, we observe that (1.4) cannot be deduced from the regularity estimates in [1] for the fully three-dimensional Prandtl–Reuss problem, using the convergence result of [5]; indeed, the estimates of [1] (whose dependence on the domain should be explicited if one wished to pass to the limit as the thickness of the plate tends to zero) are local in all directions.

The plan of the paper is as follows. In Sect. 2 we recall some mathematical preliminaries. The setting of the problem is detailed in Sect. 3. The existence and regularity results are the subject of Sect. 4. In Sect. 5 an explicit example is discussed.

2 Mathematical preliminaries

In this section we recall some notions from measure theory that we will use throughout the article.

Measures. Given a Borel set $B\subset \mathbb {R}^n$ and a finite dimensional Hilbert space X, $M_b(B;X)$ denotes the space of all bounded Borel measures on B with values in X, endowed with the norm $\Vert \mu \Vert _{M_b}:=|\mu |(B)$, where $|\mu |\in M_b(B;\mathbb {R})$ is the variation of the measure $\mu$. If $\mu$ is absolutely continuous with respect to the Lebesgue measure $\mathcal {L}^n$, we always identify $\mu$ with its density with respect to $\mathcal {L}^n$, which is a function in $L^1(B;X)$.

If the relative topology of B is locally compact, by the Riesz representation Theorem the space $M_b(B;X)$ can be identified with the dual of $C_0(B;X)$, which is the space of all continuous functions $\varphi :B\rightarrow X$ such that the set $\{|\varphi |\ge \delta \}$ is compact for every $\delta >0$. The weak* topology on $M_b(B;X)$ is defined using this duality.

Convex functions of measures. For every $\mu \in M_b(B;X)$ let $d\mu /d|\mu |$ be the Radon–Nikodým derivative of $\mu$ with respect to its variation $|\mu |$. Let $H:X\rightarrow [0,+\infty )$ be a convex and positively one-homogeneous function such that

$$\begin{aligned} \alpha _H|\xi |\le H(\xi )\le \beta _H|\xi | \quad \text {for every }\xi \in X, \end{aligned}$$

where $\alpha _H$ and $\beta _H$ are two constants, with $0<\alpha _H\le \beta _H$. According to the theory of convex functions of measures, developed in [12], we introduce the nonnegative Radon measure $H(\mu )\in M_b(B)$ defined by

$$\begin{aligned} H(\mu )(A):=\int _A H\left( \frac{d\mu }{d|\mu |}\right) \, d|\mu | \end{aligned}$$

for every Borel set $A\subset B$. We also consider the functional $\mathcal {H}:M_b(B;X)\rightarrow [0,+\infty )$ defined by

$$\begin{aligned} \mathcal {H}(\mu ):=H(\mu )(B)=\int _B H\left( \frac{d\mu }{d|\mu |}\right) \, d|\mu | \end{aligned}$$

for every $\mu \in M_b(B;X)$. One can prove that $H(\mu )$ coincides with the measure studied in [15, Chapter II, Sect. 4]. Hence,

$$\begin{aligned} \mathcal {H}(\mu )=\sup \left\{ \int _B \varphi {\,:\,} d\mu \,: \ \varphi \in C_0(B;X), \ \varphi (x)\in K \text { for every } x\in B \right\} , \end{aligned}$$

(2.1)

where $K:=\partial H(0)$ is the subdifferential of H at 0. Moreover, $\mathcal {H}$ is lower semicontinuous on $M_b(B;X)$ with respect to weak* convergence.

Functions with bounded deformation. Let U be an open set of $\mathbb {R}^n$. The space BD(U) of functions with bounded deformation is the space of all functions $u\in L^1(U;\mathbb {R}^n)$ whose symmetric gradient $Eu:=\mathrm {sym}\, Du$ (in the sense of distributions) belongs to $M_b(U;{\mathbb {M}}^{n\times n}_{sym})$. It is easy to see that BD(U) is a Banach space endowed with the norm

$$\begin{aligned} \Vert u\Vert _{BD}:=\Vert u\Vert _{L^1} +\Vert Eu\Vert _{M_b}. \end{aligned}$$

We say that a sequence $(u^k)$ converges to u weakly* in BD(U) if $u^k\rightharpoonup u$ weakly in $L^1(U;\mathbb {R}^n)$ and $Eu^k\rightharpoonup Eu$ weakly* in $M_b(U;{\mathbb {M}}^{n\times n}_{sym})$. Every bounded sequence in BD(U) has a weakly* converging subsequence. If U is bounded and has a Lipschitz boundary, BD(U) can be embedded into $L^{n/(n-1)}(U;\mathbb {R}^n)$ and every function $u\in BD(U)$ has a trace, still denoted by u, which belongs to $L^1(\partial U;\mathbb {R}^n)$. Moreover, if $\varGamma$ is a nonempty open subset of $\partial U$, there exists a constant $C>0$, depending on U and $\varGamma$, such that

$$\begin{aligned} \Vert u\Vert _{L^1(\varOmega )}\le C\Vert u\Vert _{L^1(\varGamma )}+C\Vert Eu\Vert _{M_b} \end{aligned}$$

(2.2)

(see [15, Chapter II, Proposition 2.4 and Remark 2.5]). For the general properties of the space BD(U) we refer to [15].

Functions with bounded Hessian. The space BH(U) of functions with bounded Hessian is the space of all functions $u\in W^{1,1}(U)$ whose Hessian $D^2u$ (in the sense of distributions) belongs to $M_b(U;{\mathbb {M}}^{n\times n}_{sym})$. It is easy to see that BH(U) is a Banach space endowed with the norm

$$\begin{aligned} \Vert u\Vert _{BH}:=\Vert u\Vert _{L^1} +\Vert \nabla u\Vert _{L^1}+\Vert D^2u\Vert _{M_b}. \end{aligned}$$

If U has the cone property, then BH(U) coincides with the space of functions in $L^1(U)$ whose Hessian belongs to $M_b(U;{\mathbb {M}}^{n\times n}_{sym})$. If U is bounded and has a Lipschitz boundary, BH(U) can be embedded into $W^{1,n/(n-1)}(U)$. If U is bounded and has a $C^2$ boundary, then for every function $u\in BH(U)$ one can define the traces of u and of $\nabla u$, still denoted by u and $\nabla u$; they satisfy $u\in W^{1,1}(\partial U)$, $\nabla u\in L^1(\partial U;\mathbb {R}^n)$, and $\frac{\partial u}{\partial \tau }=\nabla u\cdot \tau$ in $L^1(\partial U)$, where $\tau$ is any tangent vector to $\partial U$. If, in addition, $n=2$, then BH(U) embeds into $C(\overline{U})$, which is the space of all continuous functions on $\overline{U}$. For the general properties of the space BH(U) we refer to [7].

Notation. The symmetrized tensor product $a\odot b$ of two vectors $a,b\in \mathbb {R}^n$ is the symmetric matrix with entries $(a_ib_j + a_jb_i)/2$. The symbol $I_{n\times n}$ denotes the identity matrix in $\mathbb {M}^{n\times n}_{sym}$. The brackets $\langle \cdot ,\cdot \rangle$ denote the duality pairing between conjugate $L^p$ spaces, as well as between other pairs of spaces, according to the context.

3 Setting of the problem

Throughout the paper $\varOmega$ is an open subset of $\mathbb {R}^3$ of the form $\varOmega =\omega \times (-\frac{1}{2},\frac{1}{2})$, where $\omega$ is a bounded and connected open set of $\mathbb {R}^2$ with a $C^2$ boundary. We suppose that the boundary $\partial \omega$ is partitioned into two disjoint open subsets $\gamma _d$, $\gamma _n$ and their common boundary $\partial \lfloor _{\partial \omega }\gamma _d= \partial \lfloor _{\partial \omega }\gamma _n$ (topological notions refer here to the relative topology of $\partial \omega$). We assume that $\gamma _d\ne \emptyset$ and that $\partial \lfloor _{\partial \omega }\gamma _d$ is made of two points in $\partial \omega$. The outer unit normal to $\partial \omega$ is denoted by $\nu _{\partial \omega }$ and the outer unit normal to $\partial \varOmega$ by $\nu _{\partial \varOmega }$. Moreover, we set $\varGamma _d:=\gamma _d\times (-\frac{1}{2},\frac{1}{2})$.

The elasticity tensor and its inverse. Let $\mathbb {C}_r$ be the elasticity tensor, considered as a symmetric positive definite linear operator $\mathbb {C}_r:\mathbb {M}^{2\times 2}_{sym}\rightarrow \mathbb {M}^{2\times 2}_{sym}$ and let ${\mathbb {A}}_r:\mathbb {M}^{2\times 2}_{sym}\rightarrow \mathbb {M}^{2\times 2}_{sym}$ be its inverse ${\mathbb {A}}_r:=\mathbb {C}_r^{-1}$. It follows that there exist two constants $\alpha _\mathbb {A}$ and $\beta _\mathbb {A}$, with $0<\alpha _\mathbb {A}\le \beta _\mathbb {A}$, such that

$$\begin{aligned} \alpha _\mathbb {A}|\xi |^2 \le \tfrac{1}{2} {\mathbb {A}}_r\xi {\,:\,}\xi \le \beta _\mathbb {A}|\xi |^2 \quad \text {for every }\xi \in \mathbb {M}^{2\times 2}_{sym}. \end{aligned}$$

(3.1)

These inequalities imply

$$\begin{aligned} |{\mathbb {A}}_r\xi |\le 2\beta _\mathbb {A}|\xi | \quad \text {for every }\xi \in \mathbb {M}^{2\times 2}_{sym}. \end{aligned}$$

(3.2)

The set of admissible stresses. Let $K_r$ be a closed convex set of $\mathbb {M}^{2\times 2}_{sym}$ such that there exist two constants $\alpha _H$ and $\beta _H$, with $0<\alpha _H\le \beta _H$, such that

$$\begin{aligned} \{\xi \in \mathbb {M}^{2\times 2}_{sym}:\ |\xi |\le \alpha _H\}\subset K_r\subset \{\xi \in \mathbb {M}^{2\times 2}_{sym}:\ |\xi |\le \beta _H\}. \end{aligned}$$

The boundary of $K_r$ is interpreted as the yield surface. We define the set

$$\begin{aligned} \mathcal {K}_r(\varOmega ):=\{\sigma \in L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}):\ \sigma (x)\in K_r\text { for a.e. } x\in \varOmega \}. \end{aligned}$$

The plastic dissipation potential is given by the support function $H_r:\mathbb {M}^{2\times 2}_{sym}\rightarrow [0,+\infty )$ of $K_r$, defined as

$$\begin{aligned} H_r(\xi ):=\sup _{\sigma \in K_r}\sigma {\,:\,}\xi \quad \text {for every }\xi \in \mathbb {M}^{2\times 2}_{sym}. \end{aligned}$$

It follows that $H_r$ is a convex and positively one-homogeneous function such that

$$\begin{aligned} \alpha _H|\xi |\le H_r(\xi )\le \beta _H|\xi | \quad \text {for every }\xi \in \mathbb {M}^{2\times 2}_{sym}. \end{aligned}$$

(3.3)

In particular, $H_r$ satisfies the triangle inequality

$$\begin{aligned} H_r(\xi +\zeta )\le H_r(\xi )+H_r(\zeta )\quad \text {for every } \xi ,\zeta \in \mathbb {M}^{2\times 2}_{sym}. \end{aligned}$$

(3.4)

In [5] it is proved that, if $K\subset \mathbb {M}^{3\times 3}_{sym}$ is the convex set of admissible stresses for the three-dimensional Prandtl–Reuss plasticity problem, then $K_r$ can be characterized as follows:

$$\begin{aligned} \xi \in K_r\quad \Leftrightarrow \quad \begin{pmatrix} \xi _{11} &{}\quad \xi _{12} &{}\quad 0\\ \xi _{12} &{}\quad \xi _{22} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \end{pmatrix} -\frac{1}{3}({\mathrm {tr}}\,\xi )\, I_{3\times 3}\in K. \end{aligned}$$

(3.5)

Thus, in particular, if

$$\begin{aligned} K=\left\{ \xi \in \mathbb {M}^{3\times 3}_{sym}: \ \left| \xi -\frac{1}{3} (\mathrm{tr}\,\xi )\, I_{3\times 3}\right| \le \alpha _0\right\} \end{aligned}$$

for some $\alpha _0>0$, then (3.5) implies that

$$\begin{aligned} K_r=\{\xi \in \mathbb {M}^{2\times 2}_{sym}: \ |\xi |_r\le \alpha _0\} \end{aligned}$$

(3.6)

and

$$\begin{aligned} H_r(\xi )=\alpha _0\, |\xi +({\mathrm {tr}}\,\xi )I_{2\times 2}|_r \quad \text {for every }\xi \in \mathbb {M}^{2\times 2}_{sym}, \end{aligned}$$

where

$$\begin{aligned} |\xi |_r^2:=\frac{1}{6}(\xi _{11}+\xi _{22})^2+\frac{1}{2} (\xi _{11}-\xi _{22})^2 +2\xi _{12}^2 = |\xi |^2-\frac{1}{3} ({\mathrm {tr}}\,\xi )^2. \end{aligned}$$

(3.7)

Zero-th and first order moments. For $f\in L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ we denote by $\bar{f},\hat{f}\in L^2(\omega ;\mathbb {M}^{2\times 2}_{sym})$ and by $f_\perp \in L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ the following orthogonal components (in the sense of $L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$) of f:

$$\begin{aligned} \bar{f}(x'):=\int _{-\frac{1}{2}}^\frac{1}{2} f(x', x_3)\, dx_3,\qquad \hat{f}(x'):=12\int _{-\frac{1}{2}}^\frac{1}{2} x_3f(x',x_3)\, dx_3 \end{aligned}$$

for a.e. $x'\in \omega$, and

$$\begin{aligned} f_\perp (x):= f(x)-\bar{f}(x') -x_3 \hat{f}(x') \end{aligned}$$

for a.e. $x\in \varOmega$. The component $\bar{f}$ is called the zero-th order moment of f, while $\hat{f}$ is called the first order moment of f. The coefficient 12 in the definition of $\hat{f}$ is a normalization factor, coming from the computation

$$\begin{aligned} \int _{-\frac{1}{2}}^{\frac{1}{2}}x_3^2\,dx_3=\frac{1}{12}. \end{aligned}$$

It guarantees that, if f is of the form $f(x)=x_3g(x')$ for some $g\in L^2(\omega ;\mathbb {M}^{2\times 2}_{sym})$, then $\hat{f}=g$. Moreover, it ensures the orthogonality of the decomposition of f in terms of the moments $\bar{f}$, $\hat{f}$, and $f_\perp$.

Analogously, if $q\in M_b(\varOmega \cup \varGamma _d;\mathbb {M}^{2\times 2}_{sym})$, the zero-th order moment of q is the measure $\bar{q}\in M_b(\omega \cup \gamma _d;\mathbb {M}^{2\times 2}_{sym})$ defined by

$$\begin{aligned} \int _{\omega \cup \gamma _d}\varphi {\,:\,} d\bar{q}:=\int _{\varOmega \cup \varGamma _d} \varphi {\,:\,} dq \end{aligned}$$

for every $\varphi \in C_0(\omega \cup \gamma _d;\mathbb {M}^{2\times 2}_{sym})$, while the first order moment of q is the measure $\hat{q}\in M_b(\omega \cup \gamma _d;\mathbb {M}^{2\times 2}_{sym})$ defined by

$$\begin{aligned} \int _{\omega \cup \gamma _d} \varphi {\,:\,} d\hat{q}:=12\int _{\varOmega \cup \varGamma _d} x_3\varphi {\,:\,} dq \end{aligned}$$

for every $\varphi \in C_0(\omega \cup \gamma _d;\mathbb {M}^{2\times 2}_{sym})$. We also define $q_\perp \in M_b(\varOmega \cup \varGamma _d;\mathbb {M}^{2\times 2}_{sym})$ as the measure given by

$$\begin{aligned} q_\perp :=q-\bar{q}\otimes {\mathcal {L}}^1 -\hat{q}\otimes x_3{\mathcal {L}}^1, \end{aligned}$$

where the symbol $\otimes$ denotes the usual product of measures.

Kirchhoff–Love admissible triples. We introduce the set of Kirchhoff–Love displacements, defined as

$$\begin{aligned} KL(\varOmega ):= \{u\in BD(\varOmega ): \ (Eu)_{i3}=0 \quad \text {for } i=1,2,3\}. \end{aligned}$$

We note that $u\in KL(\varOmega )$ if and only if $u_3\in BH(\omega )$ and there exists $\bar{u}\in BD(\omega )$ such that

$$\begin{aligned} u_{\alpha }=\bar{u}_{\alpha }-x_3\partial _{\alpha }u_3,\quad \alpha =1,2. \end{aligned}$$

(3.8)

In particular, if $u\in KL(\varOmega )$, then Eu can be identified with a $2{\,\times \,}2$ matrix and $(Eu)_{\alpha \beta }=(E\bar{u})_{\alpha \beta }-x_3\partial ^2_{\alpha \beta } u_3$ for $\alpha ,\beta =1,2$. If, in addition, $u\in W^{1,p}(\varOmega ;\mathbb {R}^3)$, then $\bar{u}\in W^{1,p}(\omega ;\mathbb {R}^2)$ and $u_3\in W^{2,p}(\omega )$. We call $\bar{u}, u_3$ the Kirchhoff–Love components of u.

For every $w\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$ we define the class ${\mathcal {A}}_{KL}(w)$ of Kirchhoff–Love admissible triples for the boundary datum w as the set of all triples $(u,e,p)\in KL(\varOmega )\times L^2(\varOmega ;\mathbb {M}^{3\times 3}_{sym})\times M_b(\varOmega \cup \varGamma _d; \mathbb {M}^{3\times 3}_{sym})$ satisfying

$$\begin{aligned} \begin{array}{c} Eu=e+p \quad \text {in }\varOmega , \qquad p=(w-u)\odot \nu _{\partial \varOmega }\mathcal {H}^2 \quad \text {on }\varGamma _d, \\ e_{i3}=0 \quad \text {in }\varOmega , \quad p_{i3}=0 \quad \text {in }\varOmega \cup \varGamma _d, \quad i=1,2,3, \end{array} \end{aligned}$$

(3.9)

where $\mathcal {H}^2$ is the two-dimensional Hausdorff measure. Note that the space

$$\begin{aligned} \{\xi \in \mathbb {M}^{3\times 3}_{sym}: \ \xi _{i3}=0 \text { for }i=1,2,3\} \end{aligned}$$

is canonically isomorphic to $\mathbb {M}^{2\times 2}_{sym}$. Therefore, in the following, given a triple $(u,e,p)\in {\mathcal {A}}_{KL}(w)$ we will always identify e with a function in $L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ and p with a measure in $M_b(\varOmega \cup \varGamma _d;\mathbb {M}^{2\times 2}_{sym})$. Note also that the class ${\mathcal {A}}_{KL}(w)$ is always nonempty as it contains the triple (w, Ew, 0).

Let $(u,e,p)\in {\mathcal {A}}_{KL}(w)$. By definition u is a Kirchhoff–Love displacement, hence $u_3\in BH(\omega )$ and $u_\alpha$, $\alpha =1,2$, is affine in the $x_3$ variable (see (3.8)). In general, one cannot conclude that e and p are affine in $x_3$, too. However, some conditions on the structure of e and p can be deduced.

Proposition 1

Let $w\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$ and $(u,e,p)\in KL(\varOmega )\times L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})\times M_b(\varOmega \cup \varGamma _d; \mathbb {M}^{2\times 2}_{sym})$. Let $\bar{u}\in BD(\omega )$, $u_3\in BH(\omega )$, and $\bar{w}\in W^{1,2}(\omega ;\mathbb {R}^2)$, $w_3\in W^{2,2}(\omega )$ be the Kirchhoff–Love components of u and w, respectively. Finally, let $\bar{e},\hat{e}\in L^2(\omega ;\mathbb {M}^{2\times 2}_{sym})$, $e_\perp \in L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$, $\bar{p},\hat{p}\in M_b(\omega \cup \gamma _d;\mathbb {M}^{2\times 2}_{sym})$, and $p_\perp \in M_b(\varOmega \cup \varGamma _d;\mathbb {M}^{2\times 2}_{sym})$ be the moments of e and p. Then $(u,e,p)\in \mathcal A_{KL}(w)$ if and only if the following three conditions are satisfied:

• (i) $E\bar{u}=\bar{e}+\bar{p}$ in $\omega$ and $\bar{p}=(\bar{w}-\bar{u})\odot \nu _{\partial \omega }\mathcal {H}^1$ on $\gamma _d$;

• (ii) $D^2 u_3=-(\hat{e}+\hat{p})$ in $\omega$, $u_3=w_3$ on $\gamma _d$, and $\hat{p}=(\nabla u_3-\nabla w_3)\odot \nu _{\partial \omega }\mathcal {H}^1$ on $\gamma _d$;

• (iii) $p_\perp =-e_\perp$ in $\varOmega$ and $p_\perp =0$ on $\varGamma _d$,

where $\mathcal {H}^1$ is the one-dimensional Hausdorff measure.

Proof

The statement easily follows from the definition of moments and from the formula $(Eu)_{\alpha \beta }=(E\bar{u})_{\alpha \beta }-x_3\partial ^2_{\alpha \beta } u_3$ for $\alpha ,\beta =1,2$. $\square$

Spaces of stresses. We will also use the set

$$\begin{aligned} \varSigma (\varOmega ):=\{\sigma \in L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}): \ \mathrm {div}_{x'}\bar{\sigma }\in L^2(\omega ;\mathbb {R}^2), \ \mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }\in L^2(\omega )\}, \end{aligned}$$

where $\bar{\sigma },\hat{\sigma }\in L^2(\omega ;\mathbb {M}^{2\times 2}_{sym})$ are the zero-th and first order moments of $\sigma$.

For every $\sigma \in \varSigma (\varOmega )$ we can define the trace $[\bar{\sigma }\nu _{\partial \omega }]\in H^{-\frac{1}{2}}(\partial \omega ;\mathbb {R}^2)$ of its zero-th order moment $\bar{\sigma }$ through the formula

$$\begin{aligned} \langle [\bar{\sigma }\nu _{\partial \omega }],\varphi \rangle := \int _{\omega }\mathrm {div}_{x'}\bar{\sigma }{\,\cdot \,}\varphi \,dx' +\int _{\omega }\bar{\sigma }{\,:\,} E\varphi \,dx' \end{aligned}$$

(3.10)

for every $\varphi \in W^{1,2}(\omega ;\mathbb {R}^2)$. Note that, if $\sigma \in \varSigma (\varOmega )\cap L^\infty (\varOmega ;\mathbb {M}^{2\times 2}_{sym})$, then $\bar{\sigma }\in L^\infty (\omega ;\mathbb {M}^{2\times 2}_{sym})$ and Eq. (3.10) makes sense for every $\varphi \in W^{1,1}(\omega ;\mathbb {R}^2)$ (since by Sobolev embedding any such $\varphi$ belongs to $L^2(\omega ;\mathbb {R}^2)$), so that $[\bar{\sigma }\nu _{\partial \omega }]$ can be identified in this case with an element of $L^\infty (\partial \omega ;\mathbb {R}^2)$.

We can also give a meaning to the traces of the first order moments of elements in $\varSigma (\varOmega )$. More precisely, for every $\sigma \in \varSigma (\varOmega )$ there exist $b_0(\hat{\sigma })\in H^{-\frac{3}{2}}(\partial \omega )$ and $b_1(\hat{\sigma })\in H^{-\frac{1}{2}}(\partial \omega )$ such that

$$\begin{aligned} -\langle b_0(\hat{\sigma }),\psi \rangle + \left\langle b_1(\hat{\sigma }),\frac{\partial \psi }{\partial \nu _{\partial \omega }}\right\rangle =\int _{\omega }\hat{\sigma }{\,:\,} D^2 \psi \,dx' - \int _{\omega }\psi \,\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }\, dx' \end{aligned}$$

(3.11)

for every $\psi \in W^{2,2}(\omega )$. Moreover, if $\hat{\sigma }\in C^2(\overline{\omega };\mathbb {M}^{2\times 2}_{sym})$, then

$$\begin{aligned}&b_0(\hat{\sigma })=\mathrm {div}_{x'}\hat{\sigma }\cdot \nu _{\partial \omega } +\frac{\partial }{\partial \tau _{\partial \omega }} (\hat{\sigma }\nu _{\partial \omega }\cdot \tau _{\partial \omega }),\\&b_1(\hat{\sigma })=\hat{\sigma }\nu _{\partial \omega }\cdot \nu _{\partial \omega }, \end{aligned}$$

where $\tau _{\partial \omega }$ is the tangent vector to $\partial \omega$ (see, e.g. [6, Théorème 2.1]). Note that, if $\sigma \in \varSigma (\varOmega )\cap L^\infty (\varOmega ;\mathbb {M}^{2\times 2}_{sym})$, then $\hat{\sigma }\in L^\infty (\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ and the right-hand side of (3.11) makes sense for every $\psi \in W^{2,1}(\omega )$, so that $b_0(\hat{\sigma })$ can be identified in this case with an element of $(T(W^{2,1}(\omega )))'$, the dual of the space of traces of $W^{2,1}(\omega )$ functions, and $b_1(\hat{\sigma })$ with an element of $L^\infty (\partial \omega )$ (see [6, Théorèm 2.3]).

Using these notions of trace we can give a meaning to (non-homogeneous) Neumann boundary conditions on $\gamma _n$ for stresses in $\varSigma (\varOmega )$, according to the following definition. We recall that $\partial \omega$ is partitioned into the two disjoint open subsets $\gamma _d$, $\gamma _n$ and their common boundary.

Definition 1

Let $h\in H^{-\frac{1}{2}}(\partial \omega ;\mathbb {R}^2)$ and let $m=(m_0,m_1)\in H^{-\frac{3}{2}}(\partial \omega )\times H^{-\frac{1}{2}}(\partial \omega )$. We define $\varTheta (\gamma _n,h,m)$ as the class of all $\sigma \in \varSigma (\varOmega )$ such that

$$\begin{aligned} \langle [\bar{\sigma }\nu _{\partial \omega }]-h,\varphi \rangle =0 \end{aligned}$$

(3.12)

for every $\varphi \in H^{\frac{1}{2}}(\partial \omega ;\mathbb {R}^2)$ satisfying $\varphi =0$ on $\gamma _d$, and

$$\begin{aligned} \langle b_0(\hat{\sigma })-m_0,\psi _0\rangle =\langle b_1(\hat{\sigma })-m_1,\psi _1\rangle =0 \end{aligned}$$

(3.13)

for every $\psi _0\in H^{\frac{3}{2}}(\partial \omega )$ satisfying $\psi _0=0$ on $\gamma _d$ and every $\psi _1\in H^{\frac{1}{2}}(\partial \omega )$ satisfying $\psi _1=0$ on $\gamma _d$.

In the next proposition we prove that the class $\varTheta (\gamma _n,h,m)$ is closed with respect to weak convergence.

Proposition 2

Let $h\in H^{-\frac{1}{2}}(\partial \omega ;\mathbb {R}^2)$ and let $m=(m_0,m_1)\in H^{-\frac{3}{2}}(\partial \omega )\times H^{-\frac{1}{2}}(\partial \omega )$. Let $(\sigma ^k)_k$ be a sequence in $\varTheta (\gamma _n,h,m)$ such that $\sigma ^k\rightharpoonup \sigma$ weakly in $L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$, $\mathrm {div}_{x'}\bar{\sigma }^k\rightharpoonup f$ weakly in $L^2(\omega ;\mathbb {R}^2)$, and $\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }^k\rightharpoonup g$ weakly in $L^2(\omega )$, as $k\rightarrow \infty$. Then $\sigma \in \varTheta (\gamma _n,h,m)$ and $\mathrm {div}_{x'}\bar{\sigma }=f$, $\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }=g$ in $\omega$.

Proof

It is immediate to see that $\sigma \in \varSigma (\varOmega )$ and $\mathrm {div}_{x'}\bar{\sigma }=f$, $\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }=g$ in $\omega$. Passing to the limit in (3.10), we deduce that $[\bar{\sigma }^k\nu _{\partial \omega }]\rightharpoonup [\bar{\sigma }\nu _{\partial \omega }]$ weakly in $H^{-\frac{1}{2}}(\partial \omega ;\mathbb {R}^2)$. Therefore, (3.12) is satisfied.

For every $\psi _0\in H^{\frac{3}{2}}(\partial \omega )$ we can construct $\psi \in W^{2,2}(\omega )$ such that $\psi =\psi _0$ on $\partial \omega$ and $\partial \psi /\partial \nu _{\partial \omega }=0$ on $\partial \omega$. Passing to the limit in (3.11) with this choice of $\psi$, we obtain

$$\begin{aligned} \langle b_0(\hat{\sigma }^k),\psi _0\rangle \rightarrow \langle b_0(\hat{\sigma }),\psi _0\rangle \end{aligned}$$

for every $\psi _0\in H^{\frac{3}{2}}(\partial \omega )$. Arguing analogously, we can prove that

$$\begin{aligned} \langle b_1(\hat{\sigma }^k),\psi _1\rangle \rightarrow \langle b_1(\hat{\sigma }),\psi _1\rangle \end{aligned}$$

for every $\psi _1\in H^{\frac{1}{2}}(\partial \omega )$. Therefore, (3.13) is satisfied. $\square$

We also have the following characterization.

Proposition 3

Let $\sigma \in L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$. Then

$$\begin{aligned} \int _\varOmega \sigma {\,:\,}Ev\, dx=0 \end{aligned}$$

(3.14)

for every $v\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$ such that $v=0$ on $\varGamma _d$ if and only if $\sigma \in \varTheta (\gamma _n,0,0)$ and $\mathrm {div}_{x'}\bar{\sigma }=0$, $\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }=0$ in $\omega$.

Proof

Since

$$\begin{aligned} \int _\varOmega \sigma {\,:\,}Ev\, dx = \int _\omega \bar{\sigma }{\,:\,}E\bar{v}\, dx'-\frac{1}{12}\int _\omega \hat{\sigma }{\,:\,}D^2v_3\, dx' \end{aligned}$$

for every $v\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$, condition (3.14) is equivalent to the two following conditions:

• (a) for every $\varphi \in W^{1,2}(\omega ;\mathbb {R}^2)$ with $\varphi =0$ on $\gamma _d$

  $$\begin{aligned} \int _\omega \bar{\sigma }{\,:\,}E\varphi \, dx'=0; \end{aligned}$$

• (b) for every $\psi \in W^{2,2}(\omega )$ with $\psi =0$ and $\nabla \psi =0$ on $\gamma _d$

  $$\begin{aligned} \int _\omega \hat{\sigma }{\,:\,}D^2\psi \, dx'=0. \end{aligned}$$

By (3.10) condition (a) is equivalent to $\mathrm {div}_{x'}\bar{\sigma }=0$ in $\omega$ and $\langle [\bar{\sigma }\nu _{\partial \omega }],\varphi \rangle =0$ for every $\varphi \in H^{\frac{1}{2}}(\partial \omega ;\mathbb {R}^2)$ satisfying $\varphi =0$ on $\gamma _d$. Similarly, by (3.11) condition (b) is equivalent to $\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }=0$ in $\omega$ and

$$\begin{aligned} \langle b_0(\hat{\sigma }),\psi \rangle - \left\langle b_1(\hat{\sigma }),\frac{\partial \psi }{\partial \nu _{\partial \omega }}\right\rangle =0 \end{aligned}$$

(3.15)

for every $\psi \in W^{2,2}(\omega )$ with $\psi =0$ and $\nabla \psi =0$ on $\gamma _d$. Since for every $\psi _0\in H^{\frac{3}{2}}(\partial \omega )$ there exists $\psi \in W^{2,2}(\omega )$ such that $\psi =\psi _0$ and $\partial \psi /\partial \nu _{\partial \omega }=0$ on $\partial \omega$ and for every $\psi _1\in H^{\frac{1}{2}}(\partial \omega )$ there exists $\psi \in W^{2,2}(\omega )$ such that $\psi =0$ and $\partial \psi /\partial \nu _{\partial \omega }=\psi _1$ on $\partial \omega$, condition (3.15) is in turn equivalent to

$$\begin{aligned} \langle b_0(\hat{\sigma }),\psi _0\rangle =\langle b_1(\hat{\sigma }),\psi _1\rangle =0 \end{aligned}$$

for every $\psi _0\in H^{\frac{3}{2}}(\partial \omega )$ satisfying $\psi _0=0$ on $\gamma _d$ and every $\psi _1\in H^{\frac{1}{2}}(\partial \omega )$ satisfying $\psi _1=0$ on $\gamma _d$. $\square$

Remark 1

Let $\sigma \in \varTheta (\gamma _n,0,0)\cap L^p(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ for some $2\le p\le \infty$. Then

$$\begin{aligned} \int _\varOmega \sigma {\,:\,}Ev\, dx=-\int _\omega \mathrm {div}_{x'}\bar{\sigma }\cdot \bar{v}\, dx'+\frac{1}{12}\int _\omega v_3\,\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }\, dx' \end{aligned}$$

(3.16)

for every $v\in W^{1,p'}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$ such that $v=0$ on $\varGamma _d$, where $p'$ is the conjugate exponent of p. Note that the right-hand side is well defined for such a regularity of v, since $\bar{v}\in L^2(\omega ;\mathbb {R}^2)$ and $v_3\in W^{1,2}(\omega )$ by Sobolev embedding.

Equation (3.16) clearly holds for every $v\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$ such that $v=0$ on $\varGamma _d$ by the definition of $\varTheta (\gamma _n,0,0)$ and can be extended to functions v of $W^{1,p'}$ regularity by approximation (see, e.g. [5, Lemma 7.10]).

Stress–strain duality. In the following we will consider the space $\varPi _{\varGamma _d}(\varOmega )$ of admissible plastic strains, defined as the class of all $p\in M_b(\varOmega \cup \varGamma _d;\mathbb {M}^{2\times 2}_{sym})$ for which there exist $u\in BD(\varOmega )$, $e\in L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$, and $w\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$ such that $(u,e,p)\in {\mathcal {A}}_{KL}(w)$. Following [5, Sect. 7.1], for every $p\in \varPi _{\varGamma _d}(\varOmega )$ and $\sigma \in \varSigma (\varOmega )\cap L^\infty (\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ we can give a meaning to the product $[\sigma {\,:\,}p]$ as a measure in $M_b(\varOmega \cup \varGamma _d)$. We refer to [5, Sect. 7.1] for the precise definition and the main properties of this duality product. Here we just note that, if $\sigma \in \varSigma (\varOmega )\cap L^\infty (\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ is such that $\bar{\sigma },\hat{\sigma }\in C(\overline{\omega };\mathbb {M}^{2\times 2}_{sym})$, then

$$\begin{aligned} \int _{\varOmega \cup \varGamma _d} \varphi \, d[\sigma {\,:\,}p] = \int _{\omega \cup \gamma _d} \varphi \bar{\sigma }{\,:\,}d\bar{p}+\frac{1}{12} \int _{\omega \cup \gamma _d} \varphi \hat{\sigma }{\,:\,}d\hat{p}+ \int _{\varOmega } \varphi \sigma _\perp {\,:\,}p_\perp \, dx \end{aligned}$$

for every $\varphi \in C(\overline{\omega })$. The last integral makes sense since $p_\perp \in L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ by Proposition 1-(iii).

For every $p\in \varPi _{\varGamma _d}(\varOmega )$ and $\sigma \in \varSigma (\varOmega )\cap L^\infty (\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ the duality product $\langle \sigma , p \rangle$ is defined as

$$\begin{aligned} \langle \sigma , p \rangle := [\sigma {\,:\,}p](\varOmega \cup \varGamma _d). \end{aligned}$$

Using this notion of duality, a variant of equality (2.1) can be proved. More precisely, by [5, Proposition 7.8] we have that for every $p\in \varPi _{\varGamma _d}(\varOmega )$

$$\begin{aligned} \mathcal {H}_r(p)=\sup \{ \langle \sigma , p\rangle : \ \sigma \in \varSigma (\varOmega )\cap \mathcal {K}_r(\varOmega )\}. \end{aligned}$$

(3.17)

Moreover, the following integration by parts formula holds.

Proposition 4

Let $\sigma \in \varSigma (\varOmega )\cap L^\infty (\varOmega ;\mathbb {M}^{2\times 2}_{sym})$, $w\in W^{1,2}(\varOmega ;\mathbb {R}^2)\cap KL(\varOmega )$, and $(u,e,p)\in {\mathcal {A}}_{KL}(w)$. Then

$$\begin{aligned}&{\int _{\varOmega \cup \varGamma _d} \varphi \, d[\sigma {\,:\,}p] +\int _\varOmega \varphi \, \sigma {\,:\,}(e-Ew)\, dx} \nonumber \\&\quad = -\int _\omega \bar{\sigma }{\,:\,} (\nabla \varphi {\,\odot \,}(\bar{u}-\bar{w})) \,dx' -\int _\omega \mathrm {div}_{x'}\bar{\sigma }{\,\cdot \,} \varphi \,(\bar{u}-\bar{w}) \,dx' \nonumber \\&\qquad +\int _{\gamma _n} [\bar{\sigma }\nu _{\partial \omega }]{\,\cdot \,} \varphi \,(\bar{u}-\bar{w}) \, d\mathcal {H}^1 +\frac{1}{12} \int _\omega \hat{\sigma }{\,:\,} (u_3-w_3) D^2\varphi \, dx' \nonumber \\&\qquad +\frac{1}{6} \int _\omega \hat{\sigma }{\,:\,} ( \nabla \varphi {\,\odot \,}(\nabla u_3-\nabla w_3))\, dx' -\frac{1}{12}\int _\omega (u_3-w_3) \varphi \,\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }\, dx' \nonumber \\&\qquad +\frac{1}{12}\langle b_0(\hat{\sigma }),\varphi (u_3-w_3)\rangle -\frac{1}{12}\int _{\gamma _n} b_1(\hat{\sigma })\frac{\partial (\varphi (u_3-w_3))}{\partial \nu _{\partial \omega }}\, d\mathcal {H}^1 \end{aligned}$$

(3.18)

for every $\varphi \in C^2(\overline{\omega })$.

Proof

Note that the duality product on the right-hand side of (3.18) is well defined since $T(W^{2,1}(\omega ))=T(BH(\omega ))$ (see, e.g. [7, Sect. 2]). For the proof we refer to [5, Propositions 7.2  and 7.6]. $\square$

4 The quasistatic evolution problem: regularity

In this section we describe the quasistatic evolution problem and prove local regularity of the stress. The data of the problem are the prescribed boundary displacement and the applied forces. More precisely, for every $t\in [0,T]$ we prescribe a boundary displacement $w(t)\in KL(\varOmega )\cap W^{1,2}(\varOmega ;\mathbb {R}^3)$ on $\varGamma _d$. We assume that $t\mapsto w(t)$ is a $W^{1,2}$-map from [0, T] into $W^{1,2}(\varOmega ;\mathbb {R}^3)$. For every $t\in [0,T]$ we consider a body force $(f(t),g(t))\in L^2(\omega ;\mathbb {R}^2)\times L^2(\omega )$ and surface forces $h(t)\in L^\infty (\partial \omega ;\mathbb {R}^2)$ and $m(t)=(m_0(t),m_1(t))\in (T(W^{2,1}(\omega ))'\times L^\infty (\partial \omega )$. We assume that $t\mapsto (f(t),g(t))$, $t\mapsto h(t)$, and $t\mapsto m(t)$ are $W^{1,2}$-maps from [0, T] into their respective spaces. Moreover, the following uniform safe-load condition is assumed: there exist a map $\varrho \in W^{1,2}(0,T;L^\infty (\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$ and a constant $\alpha _1>0$ such that for every $t\in [0,T]$

$$\begin{aligned} \begin{array}{c} -\mathrm {div}_{x'}\bar{\varrho }(t)= f(t), \quad - \mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\varrho }(t)=g(t) \quad \text {in }\omega ,\\ \varrho (t)\in \varTheta (\gamma _n,h(t),m(t)), \end{array} \end{aligned}$$

(4.1)

and

$$\begin{aligned} \varrho (t,x)+\xi \in K_r\end{aligned}$$

(4.2)

for a.e. $x\in \varOmega$ and every $\xi \in \mathbb {M}^{2\times 2}_{sym}$ with $|\xi |_r\le \alpha _1$. Conditions (4.1)–(4.2) ensure that the applied body and surface loads are compatible with the stress admissibility constraint, in the sense that there exists a stress distribution $\varrho (t)$ balancing the loads and strictly below the yield threshold.

Definition 2

Let $t\mapsto (u(t),e(t),p(t))$ be a function from [0, T] into $BD(\varOmega )\times L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})\times M_b(\varOmega \cup \varGamma _d;\mathbb {M}^{2\times 2}_{sym})$ and let $\sigma (t):=\mathbb {C}_re(t)$. We say that $t\mapsto (u(t),e(t),p(t))$ is a quasistatic evolution if the following three conditions are satisfied:

• (qs1) regularity: $t\mapsto (u(t),e(t),p(t))$ is absolutely continuous;

• (qs2) equilibrium: for every $t\in [0,T]$ we have $(u(t),e(t),p(t))\in {\mathcal A}_{KL}(w(t))$,

  $$\begin{aligned} \begin{array}{c} \sigma (t)\in \mathcal {K}_r(\varOmega )\cap \varTheta (\gamma _n,h(t),m(t)),\\ -\mathrm {div}_{x'}\bar{\sigma }(t)= f(t), \quad -\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }(t)=g(t) \text { in }\omega ; \end{array} \end{aligned}$$

• (qs3) flow rule: for a.e. $t\in [0,T]$ there holds

  $$\begin{aligned} \mathcal {H}_r(\dot{p}(t))=\langle \sigma (t),\dot{p}(t) \rangle . \end{aligned}$$

In the previous definition $\varTheta (\gamma _n,h(t),m(t))$ is the set of stresses satisfying the Neumann boundary condition (see Definition 1), while the duality pairing at the right-hand side of the flow rule is intended in the sense of the stress–strain duality defined in Sect. 3. We observe that by (3.17) the flow rule is equivalent to the following maximum plastic work condition: for a.e. $t\in [0,T]$

$$\begin{aligned} \langle \vartheta -\sigma (t), \dot{p}(t) \rangle \le 0 \end{aligned}$$

(4.3)

for every $\vartheta \in \mathcal {K}_r(\varOmega )\cap \varSigma (\varOmega )$.

In [5] existence of a quasistatic evolution is proved assuming the body and surface forces to be zero. Under the assumptions (4.1)–(4.2), existence of a quasistatic evolution in presence of applied forces can be proved by applying the abstract method for rate-independent processes [14], namely by discretizing time and by solving suitable incremental minimum problems. This method leads to a weaker notion of quasistatic evolution, which can be proved to be equivalent to that of Definition 2 arguing as in [4, Sect. 5  and 6]. The safe-load condition (4.1)–(4.2), which is trivially satisfied for zero applied forces, is a crucial assumption in proving the existence of quasistatic evolutions: it guarantees coercivity of the energy in the variational formulation.

In this paper we focus on the spatial regularity for quasistatic evolutions in case of smooth applied forces, under the additional assumption that the set $K_r$ of admissible stresses is of the form (3.6)–(3.7). We note that $|\cdot |_r$ is an anisotropic norm on $\mathbb {M}^{2\times 2}_{sym}$ satisfying

$$\begin{aligned} \frac{1}{\sqrt{3}}\,|\xi |\le |\xi |_r \le |\xi | \quad \text {for every } \xi \in \mathbb {M}^{2\times 2}_{sym}. \end{aligned}$$

(4.4)

We also consider the inner product associated with this norm:

$$\begin{aligned} (\xi ,\zeta )_r:=\xi {\,:\,}\zeta -\frac{1}{3} {\mathrm {tr}}\,\xi \, {\mathrm {tr}}\,\zeta \quad \text {for every } \xi ,\zeta \in \mathbb {M}^{2\times 2}_{sym}. \end{aligned}$$

We now introduce some approximating problems of (qs1)–(qs3). Let $N\in \mathbb {N}$, $N\ge 4$ be a fixed parameter. We consider the function $\phi _N:\mathbb {M}^{2\times 2}_{sym}\rightarrow [0,+\infty )$ defined by

$$\begin{aligned} \phi _N(\xi ):=\frac{1}{N\alpha _0^{N-1}}|\xi |_r^N \quad \text {for every } \xi \in \mathbb {M}^{2\times 2}_{sym}, \end{aligned}$$

where $\alpha _0$ is the radius of $K_r$ (see (3.6)). The function $\phi _N$ is clearly convex and continuously differentiable with differential

$$\begin{aligned} D\phi _N(\xi )= \frac{1}{\alpha _0^{N-1}}|\xi |_r^{N-2}\left( \xi -\frac{1}{3}({\mathrm {tr}}\,\xi )\, I_{2\times 2}\right) \quad \text {for every } \xi \in \mathbb {M}^{2\times 2}_{sym}. \end{aligned}$$

Moreover, we have that

$$\begin{aligned} D\phi _N(\xi ):\xi =\frac{1}{\alpha _0^{N-1}}|\xi |_r^N \quad \text {for every } \xi \in \mathbb {M}^{2\times 2}_{sym}. \end{aligned}$$

(4.5)

Through $\phi _N$ we define an approximating problem of Norton–Hoff type, for which existence of solutions is proved in the following theorem. In this auxiliary problem the flow rule and the stress constraint are replaced by an ordinary differential equation in time for the stress variable $\sigma (t)$. The term $D\phi _N(\sigma (t))$ in the equation acts as a penalization term and will lead to the stress constraint $\sigma (t)\in \mathcal {K}_r$ when passing to the limit as $N\rightarrow \infty$.

Theorem 1

Let $K_r$ be of the form (3.6)– (3.7). Let

$$\begin{aligned} \begin{array}{c} w\in W^{1,2}(0,T;W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )),\\ f\in W^{1,2}(0,T;L^2(\omega ;\mathbb {R}^2)), \quad g\in W^{1,2}(0,T;L^2(\omega )),\\ h\in W^{1,2}(0,T;L^\infty (\partial \omega ;\mathbb {R}^2)), \quad m\in W^{1,2}(0,T;(T(W^{2,1}(\omega ))'\times L^\infty (\partial \omega )). \end{array} \end{aligned}$$

Assume conditions (4.1) and (4.2) with $\varrho \in W^{1,\infty }(0,T;L^\infty (\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$. Let $\sigma _0\in L^{\infty }(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ be such that

$$\begin{aligned} \begin{array}{c} -\mathrm {div}_{x'}\bar{\sigma }_0=f(0), \quad -\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }_0=g(0) \quad \text {in }\omega ,\\ \sigma _0\in \mathcal {K}_r(\varOmega )\cap \varTheta (\gamma _n,h(0),m(0)). \end{array} \end{aligned}$$

Then for every $N\in \mathbb {N}$, $N\ge 4$, the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {A}}_r\dot{\sigma }(t)+D\phi _N(\sigma (t))=E v(t) &{} \text { in }\varOmega ,\\ -\mathrm {div}_{x'}\bar{\sigma }(t)= f(t),\quad -\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }(t)=g(t) &{} \text { in }\omega ,\\ \sigma (t)\in \varTheta (\gamma _n,h(t),m(t)), &{}\\ v(t)=\dot{w}(t) &{}\text { on }\varGamma _d, \end{array}\right. } \end{aligned}$$

(4.6)

has one and only one solution $(\sigma ^N, v^N)$ with

$$\begin{aligned}&\sigma ^N\in W^{1,2}(0,T;L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))\cap L^\infty (0,T;L^N(\varOmega ;\mathbb {M}^{2\times 2}_{sym})),\\&\quad v^N\in L^{N/(N-1)}(0,T;W^{1,N/(N-1)}(\varOmega ;\mathbb {R}^2)\cap KL(\varOmega )) \end{aligned}$$

and satisfying $\sigma ^N(0)=\sigma _0$.

Moreover, the following estimates hold:

$$\begin{aligned}&\sup _{t\in [0,T]} \Vert \sigma ^N(t)\Vert _{L^2}\le C, \quad \int _0^T \Vert \dot{\sigma }^N(t)\Vert ^2_{L^2}\, dt \le C, \end{aligned}$$

(4.7)

$$\begin{aligned}&\sup _{t\in [0,T]}\int _\varOmega |\sigma ^N(t)|_r^N \, dx \le CN\alpha _0^{N-1}, \quad \int _0^T\int _\varOmega |\sigma ^N(t)|_r^N \, dx\, dt \le C\alpha _0^{N-1}, \end{aligned}$$

(4.8)

and

$$\begin{aligned} \Vert v^N\Vert _{L^2(0,T;BD(\varOmega ))} \le C, \end{aligned}$$

(4.9)

where C is a constant independent of N.

Proof

Let us fix $N\in \mathbb {N}$, $N\ge 4$. To prove existence of solutions to problem (4.6), we first consider an auxiliary problem where the penalization term is given in terms of a regularization $\psi _\lambda$ of $\phi _N$. Since $D\psi _\lambda$ is Lipschitz continuous, the auxiliary problem can be solved by applying the Cauchy-Lipschitz Theorem. To conclude, we will then prove uniform estimates of these auxiliary solutions with respect to the regularization parameter $\lambda$.

For every $\lambda >0$ we introduce the functions $\psi _\lambda :\mathbb {M}^{2\times 2}_{sym}\rightarrow [0,+\infty )$ defined by

$$\begin{aligned} \psi _\lambda (\xi ):= \frac{1}{N\alpha _0^{N-1}} (|\xi |_r^N {\,\wedge \,} \lambda ^N) + \frac{1}{2\alpha _0^{N-1}} \lambda ^{N-2} (|\xi |_r^2 -\lambda ^2)^+ \end{aligned}$$

for every $\xi \in \mathbb {M}^{2\times 2}_{sym}$. Note that $\psi _\lambda$ is strictly convex and $C^1$. Moreover, we have that

$$\begin{aligned} D\psi _\lambda (\xi )= \frac{1}{\alpha _0^{N-1}}(|\xi |_r^{N-2}{\,\wedge \,}\lambda ^{N-2}) \left( \xi -\frac{1}{3}({\mathrm {tr}}\,\xi )\, I_{2\times 2}\right) \end{aligned}$$

for every $\xi \in \mathbb {M}^{2\times 2}_{sym}$, hence

$$\begin{aligned}&\displaystyle D\psi _\lambda (\xi ){\,:\,}\zeta = \frac{1}{\alpha _0^{N-1}} (|\xi |_r^{N-2}{\,\wedge \,}\lambda ^{N-2})\, (\xi ,\zeta )_r , \end{aligned}$$

(4.10)

$$\begin{aligned}&\displaystyle |D\psi _\lambda (\xi )|^{N/(N-1)}\le \frac{1}{\alpha _0} D\psi _\lambda (\xi ){\,:\,}\xi , \end{aligned}$$

(4.11)

for every $\xi ,\zeta \in \mathbb {M}^{2\times 2}_{sym}$. Finally, we observe that the functions $D\psi _\lambda$ are Lipschitz continuous on $\mathbb {M}^{2\times 2}_{sym}$ with

$$\begin{aligned} |D^2\psi _\lambda (\xi )|\le \frac{N+1}{\alpha _0^{N-1}} \lambda ^{N-2} \end{aligned}$$

(4.12)

for a.e. $\xi \in \mathbb {M}^{2\times 2}_{sym}$.

In view of the regularity of $D\psi _\lambda$, we can apply Lemma 1 below with $\varPsi =D\psi _\lambda$. This guarantees that for every $\lambda >0$ there exists a unique pair

$$\begin{aligned} (\sigma ^\lambda , v^\lambda )\in W^{1,2}(0,T; L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))\times L^2(0,T; W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )) \end{aligned}$$

satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {A}}_r\dot{\sigma }^\lambda (t)+D\psi _\lambda (\sigma ^\lambda (t))=Ev^\lambda (t) &{} \text { in }\varOmega , \\ -\mathrm {div}_{x'}\bar{\sigma }^\lambda (t)=f(t),\quad -\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }^\lambda (t)=g(t) &{} \text { in }\omega , \\ \sigma ^\lambda (t)\in \varTheta (\gamma _n,h(t), m(t)), &{} \\ v^\lambda (t)=\dot{w}(t) &{}\text { on }\varGamma _d, \\ \sigma ^\lambda (0)=\sigma _0. \end{array}\right. } \end{aligned}$$

(4.13)

We now want to pass to the limit in (4.13), as $\lambda \rightarrow +\infty$. This will provide us with a solution to problem (4.6). In the following estimates we will stress the dependence of the involved constants on the parameters $\lambda$ and N. Unless otherwise stated, C denotes a positive constant independent of $\lambda$ and N.

Multiplying the first equation in (4.13) by $\sigma ^\lambda (t)-\varrho (t)$ and integrating over $\varOmega$ yield

$$\begin{aligned}&\langle {\mathbb {A}}_r\dot{\sigma }^\lambda (t),\sigma ^\lambda (t)-\varrho (t)\rangle + \langle D\psi _\lambda (\sigma ^\lambda (t)), \sigma ^\lambda (t)-\varrho (t)\rangle \nonumber \\&\quad = \langle E\dot{w}(t),\sigma ^\lambda (t)-\varrho (t)\rangle , \end{aligned}$$

(4.14)

where the brackets $\langle \cdot ,\cdot \rangle$ denote the scalar product in $L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ and we used that

$$\begin{aligned} \langle Ev^\lambda (t),\sigma ^\lambda (t)-\varrho (t)\rangle =\langle E\dot{w}(t),\sigma ^\lambda (t)-\varrho (t)\rangle \end{aligned}$$

by Proposition 3 (with the choices $v=v^\lambda (t)-\dot{w}(t)$ and $\sigma =\sigma ^\lambda (t)-\varrho (t)$), taking into account (4.1) and (4.13). Integrating with respect to time, (4.14) implies that

$$\begin{aligned}&\frac{1}{2} \langle {\mathbb {A}}_r(\sigma ^\lambda (t)-\varrho (t)),\sigma ^\lambda (t) -\varrho (t)\rangle +\int _0^t \langle D\psi _\lambda (\sigma ^\lambda (s)),\sigma ^\lambda (s)-\varrho (s)\rangle \,ds \nonumber \\&\quad = \frac{1}{2} \langle {\mathbb {A}}_r(\sigma _0-\varrho (0)),\sigma _0-\varrho (0)\rangle +\int _0^t \langle E\dot{w}(s)-{\mathbb {A}}_r\dot{\varrho }(s),\sigma ^\lambda (s)-\varrho (s)\rangle \,ds.\qquad \end{aligned}$$

(4.15)

Since $\psi _\lambda$ is convex, we have

$$\begin{aligned} (D\psi _\lambda (\xi )-D\psi _\lambda (\zeta )){\,:\,}(\xi -\zeta )\ge 0 \quad \text {for every }\xi ,\zeta \in \mathbb {M}^{2\times 2}_{sym}. \end{aligned}$$

(4.16)

Therefore, we infer

$$\begin{aligned}&\frac{1}{2} \langle {\mathbb {A}}_r(\sigma ^\lambda (t)-\varrho (t)),\sigma ^\lambda (t)-\varrho (t)\rangle \le \frac{1}{2} \langle {\mathbb {A}}_r(\sigma _0-\varrho (0)),\sigma _0-\varrho (0)\rangle \\&\quad +\int _0^t \langle E\dot{w}(s)-{\mathbb {A}}_r\dot{\varrho }(s)- D\psi _\lambda (\varrho (s)),\sigma ^\lambda (s)-\varrho (s)\rangle \,ds. \end{aligned}$$

Note that, by (4.2), the term $D\psi _\lambda (\varrho (s))$ is uniformly bounded independently of $\lambda$ and N for $\lambda \ge \alpha _0$. Thus, by the Cauchy inequality, (3.1), and the regularity assumptions on $\varrho$, $\dot{\varrho }$, and $\dot{w}$, we deduce

$$\begin{aligned} \sup _{t\in [0,T]}\Vert \sigma ^\lambda (t)\Vert _{L^2}\le C \quad \text {and} \quad \int _0^T \langle D\psi _\lambda (\sigma ^\lambda (t)),\sigma ^\lambda (t)-\varrho (t) \rangle \,dt\le C. \end{aligned}$$

(4.17)

From the second estimate above and (4.10), it follows

$$\begin{aligned} \frac{1}{\alpha _0^{N-1}} \int _0^T \int _\varOmega (|\sigma ^\lambda (t)|_r^{N-1}{\,\wedge \,}\lambda ^{N-2} |\sigma ^\lambda (t)|_r)\, \left( |\sigma ^\lambda (t)|_r - |\varrho (t)|_r \right) \, dx \, dt \le C, \end{aligned}$$

(4.18)

where we also used the inequality

$$\begin{aligned} (\sigma ^\lambda (t), \sigma ^\lambda (t)-\varrho (t))_r\ge |\sigma ^\lambda (t)|^2_r -|\sigma ^\lambda (t)|_r |\varrho (t)|_r. \end{aligned}$$

Let now $A_\lambda (t):=\{x\in \varOmega :\ |\sigma ^\lambda (t,x)|_r\ge \alpha _0\}$. Condition (4.2) guarantees that $|\sigma ^\lambda (t)|_r -|\varrho (t)|_r\ge \alpha _1$ on $A_\lambda (t)$: indeed, choosing $\xi =\alpha _1\varrho (t)/|\varrho (t)|_r$ in (4.2), we have

$$\begin{aligned} |\varrho (t)|_r+\alpha _1= | \varrho (t)+ \frac{\alpha _1}{|\varrho (t)|_r}\varrho (t)|_r\le \alpha _0\le |\sigma ^\lambda (t)|_r. \end{aligned}$$

Thus, since the integrand in (4.18) is uniformly bounded from below on $\varOmega \setminus A_\lambda (t)$, we have

$$\begin{aligned} \frac{\alpha _1}{\alpha _0^{N-1}} \int _0^T \int _{A_\lambda (t)} (|\sigma ^\lambda (t)|_r^{N-1}{\,\wedge \,}\lambda ^{N-2} |\sigma ^\lambda (t)|_r) \, dx \, dt \le C. \end{aligned}$$

(4.19)

Combining this inequality with (4.18) and the fact that $|\varrho (t)|_r\le \alpha _0$, we obtain

$$\begin{aligned} \frac{1}{\alpha _0^{N-1}} \int _0^T \int _{A_\lambda (t)} (|\sigma ^\lambda (t)|_r^N{\,\wedge \,}\lambda ^{N-2} |\sigma ^\lambda (t)|_r^2) \, dx \, dt \le C. \end{aligned}$$

By definition of $A_\lambda (t)$ the integrand is clearly bounded on the complement of $A_\lambda (t)$; thus, we conclude that

$$\begin{aligned} \frac{1}{\alpha _0^{N-1}} \int _0^T \int _\varOmega (|\sigma ^\lambda (t)|_r^N{\,\wedge \,}\lambda ^{N-2} |\sigma ^\lambda (t)|_r^2)\, dx \, dt \le C. \end{aligned}$$

(4.20)

We now derive a bound on $\dot{\sigma }^\lambda$. We test the first equation in (4.13) with the map $\dot{\sigma }^\lambda (t)-\dot{\varrho }(t)$:

$$\begin{aligned} \langle {\mathbb {A}}_r\dot{\sigma }^\lambda (t), \dot{\sigma }^\lambda (t)-\dot{\varrho }(t) \rangle +\langle D\psi _\lambda (\sigma ^\lambda (t)), \dot{\sigma }^\lambda (t)-\dot{\varrho }(t) \rangle = \langle E\dot{w}(t), \dot{\sigma }^\lambda (t)-\dot{\varrho }(t)\rangle . \end{aligned}$$

Integrating with respect to time, we obtain

$$\begin{aligned}&\int _0^t \langle {\mathbb {A}}_r(\dot{\sigma }^\lambda (s)-\dot{\varrho }(s)), \dot{\sigma }^\lambda (s)-\dot{\varrho }(s) \rangle \, ds + \int _\varOmega \psi _\lambda (\sigma ^\lambda (t))\, dx \nonumber \\&\quad = \int _\varOmega \psi _\lambda (\sigma _0) \, dx +\int _0^t \langle D\psi _\lambda (\sigma ^\lambda (s)), \dot{\varrho }(s)\rangle \, ds \nonumber \\&\qquad +\int _0^t \langle E\dot{w}(s)-{\mathbb {A}}_r\dot{\varrho }(s), \dot{\sigma }^\lambda (s)- \dot{\varrho }(s)\rangle \, ds. \end{aligned}$$

(4.21)

Note that, since $\sigma _0\in K_r$ a.e. in $\varOmega$, for $\lambda \ge \alpha _0$ the first term on the right-hand side is uniformly bounded independently of $\lambda$ and N. Moreover, from (4.10) and (4.11) it follows immediately that

$$\begin{aligned} \int _\varOmega |D\psi _\lambda (\sigma ^\lambda (t))|^{N/(N-1)} \, dx \le \frac{1}{\alpha _0^N} \int _\varOmega (|\sigma ^\lambda (t)|_r^N{\,\wedge \,}\lambda ^{N-2} |\sigma ^\lambda (t)|_r^2) \,dx, \end{aligned}$$

so that (4.20) implies that the sequence $(D\psi _\lambda (\sigma ^\lambda ))$ is uniformly bounded with respect to $\lambda$ in $L^{N/(N-1)}(0,T;L^{N/(N-1)}(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$. This fact, together with the assumption that $\dot{\varrho }\in L^\infty ((0,T)\times \varOmega ;\mathbb {M}^{2\times 2}_{sym})$, guarantees that the second term on the right-hand side of (4.21) is uniformly bounded, as well. Thus, by the Cauchy inequality and the regularity assumptions on $\dot{w}$ and $\dot{\varrho }$, we have

$$\begin{aligned} \int _0^T \Vert \dot{\sigma }^\lambda (t)\Vert _{L^2}^2\, dt\le C \quad \text { and } \quad \sup _{t\in [0,T]} \int _\varOmega \psi _\lambda (\sigma ^\lambda (t))\, dx\le C. \end{aligned}$$

(4.22)

By the Ascoli–Arzelà Theorem we deduce from the first estimates in (4.17) and (4.22) that there exists a subsequence (not relabelled) and a function $\sigma ^N\in W^{1,2}(0,T;L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$ such that

$$\begin{aligned} \sigma ^\lambda (t)\rightharpoonup \sigma ^N(t) \quad \text {weakly in } L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}), \end{aligned}$$

(4.23)

as $\lambda \rightarrow +\infty$, for every $t\in [0,T]$ and

$$\begin{aligned} \sigma ^\lambda \rightharpoonup \sigma ^N \quad \text {weakly in } W^{1,2}(0,T;L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})), \end{aligned}$$

(4.24)

as $\lambda \rightarrow +\infty$. By (4.23) it is clear that $\sigma ^N(0)=\sigma _0$ and, in view of Proposition 2, that $-\mathrm {div}_{x'}\bar{\sigma }^N(t)=f(t)$, $-\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }^N(t)=g(t)$ in $\omega$, and $\sigma ^N(t)\in \varTheta (\gamma _n,h(t), m(t))$ for every $t\in [0,T]$.

We set $\tau ^\lambda (t):= \chi _{\{|\sigma ^\lambda (t)|_r\le \lambda \}}\sigma ^\lambda (t)$, where $\chi _{\{|\sigma ^\lambda (t)|_r\le \lambda \}}$ is the characteristic function of the set $\{x\in \varOmega : \ |\sigma ^\lambda (t,x)|_r\le \lambda \}$. The second estimate in (4.22) yields

$$\begin{aligned} \sup _{t\in [0,T]}\int _\varOmega |\tau ^\lambda (t)|_r^N \, dx \le CN\alpha _0^{N-1}, \end{aligned}$$

(4.25)

while by (4.20) we have

$$\begin{aligned} \int _0^T \int _\varOmega |\sigma ^\lambda (t)-\tau ^\lambda (t)|_r^2 \, dx \le C \frac{\alpha _0^{N-1}}{\lambda ^{N-2}}. \end{aligned}$$

(4.26)

Therefore, $\sigma ^\lambda -\tau ^\lambda \rightarrow 0$ strongly in $L^2(0,T;L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$, as $\lambda \rightarrow +\infty$. Together with (4.25) and (4.24), this implies that $\sigma ^N\in L^\infty (0,T;L^N(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$, the first inequality in (4.8) is satisfied, and

$$\begin{aligned} \tau ^\lambda \rightharpoonup \sigma ^N \quad \text {weakly} ^* \text {in } L^\infty (0,T;L^N(\varOmega ;\mathbb {M}^{2\times 2}_{sym})), \end{aligned}$$

(4.27)

as $\lambda \rightarrow +\infty$. Moreover, by (4.20) we deduce the second inequality in (4.8).

Finally, since $(D\psi _\lambda (\sigma ^\lambda ))$ is uniformly bounded, with respect to $\lambda$, in the space $L^{N/(N-1)}(0,T;L^{N/(N-1)}(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$, we have that, up to subsequences,

$$\begin{aligned} D\psi _\lambda (\sigma ^\lambda )\rightharpoonup \gamma ^N \quad \text {weakly in } L^{N/(N-1)}(0,T;L^{N/(N-1)}(\varOmega ;\mathbb {M}^{2\times 2}_{sym})), \end{aligned}$$

(4.28)

as $\lambda \rightarrow \infty$, for some function $\gamma ^N\in L^{N/(N-1)}(0,T;L^{N/(N-1)}(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$.

We now want to prove that $\gamma ^N=D\phi _N(\sigma ^N)$. To this purpose we proceed as follows. We multiply the first equation in (4.13) by $\sigma ^N(t)-\varrho (t)$. Integration in space and time, together with Proposition 3, yields

$$\begin{aligned}&\int _0^T \langle {\mathbb {A}}_r\dot{\sigma }^\lambda (t), \sigma ^N(t)-\varrho (t)\rangle \, dt +\int _0^T \langle D\psi _\lambda (\sigma ^\lambda (t)),\sigma ^N(t)-\varrho (t)\rangle \, dt\\&\quad = \int _0^T\langle E\dot{w}(t),\sigma ^N(t)-\varrho (t)\rangle \, dt. \end{aligned}$$

Passing to the limit as $\lambda \rightarrow +\infty$, we deduce

$$\begin{aligned}&\int _0^T \langle {\mathbb {A}}_r\dot{\sigma }^N(t),\sigma ^N(t)-\varrho (t)\rangle \, dt +\int _0^T\langle \gamma ^N(t),\sigma ^N(t)-\varrho (t)\rangle \, dt\nonumber \\&\quad = \int _0^T\langle E\dot{w}(t),\sigma ^N(t)-\varrho (t)\rangle \, dt. \end{aligned}$$

(4.29)

We now go back to identity (4.15) for $t=T$ and observe that by (4.24) the right-hand side of (4.15) converges, as $\lambda \rightarrow +\infty$, to

$$\begin{aligned} \frac{1}{2} \langle {\mathbb {A}}_r(\sigma _0-\varrho (0)),\sigma _0-\varrho (0)\rangle +\int _0^T \langle E\dot{w}(s)-{\mathbb {A}}_r\dot{\varrho }(s),\sigma ^N(s)-\varrho (s)\rangle \,ds. \end{aligned}$$

Thus, we deduce

$$\begin{aligned}&\limsup _{\lambda \rightarrow +\infty }\int _0^T\langle D\psi _\lambda (\sigma ^\lambda (s)),\sigma ^\lambda (s)-\varrho (s)\rangle \, ds\\&\quad \le \frac{1}{2}\langle {\mathbb {A}}_r(\sigma _0-\varrho (0)),\sigma _0-\varrho (0) \rangle -\liminf _{\lambda \rightarrow +\infty }\frac{1}{2}\langle {\mathbb {A}}_r(\sigma ^\lambda (T) -\varrho (T)),\sigma ^\lambda (T)-\varrho (T)\rangle \\&\qquad +\int _0^T\langle E\dot{w}(s)-{\mathbb {A}}_r\dot{\varrho }(s),\sigma ^N(s)-\varrho (s)\rangle \, ds. \end{aligned}$$

On the other hand, by (4.23) we obtain

$$\begin{aligned}&{-\liminf _{\lambda \rightarrow +\infty }\frac{1}{2}\langle {\mathbb {A}}_r(\sigma ^\lambda (T)-\varrho (T)),\sigma ^\lambda (T)-\varrho (T)\rangle }\\&\quad \le - \frac{1}{2}\langle {\mathbb {A}}_r(\sigma ^N(T)-\varrho (T)),\sigma ^N(T) -\varrho (T)\rangle \\&\quad = - \frac{1}{2}\langle {\mathbb {A}}_r(\sigma _0-\varrho (0)),\sigma _0-\varrho (0)\rangle -\int _0^T \langle {\mathbb {A}}_r(\dot{\sigma }^N(s)- \dot{\varrho }(s)),\sigma ^N(s)-\varrho (s)\rangle \, ds. \end{aligned}$$

Combining the two previous inequalities with (4.29), we conclude that

$$\begin{aligned}&{\limsup _{\lambda \rightarrow +\infty }\int _0^T\langle D\psi _\lambda (\sigma ^\lambda (s)),\sigma ^\lambda (s)-\varrho (s)\rangle \, ds } \nonumber \\&\quad \le -\int _0^T \langle {\mathbb {A}}_r\dot{\sigma }^N(s),\sigma ^N(s)-\varrho (s)\rangle \, ds +\int _0^T\langle E\dot{w}(s),\sigma ^N(s)-\varrho (s)\rangle \, dt \nonumber \\&\quad = \int _0^T \langle \gamma ^N(s),\sigma ^N(s)-\varrho (s)\rangle \, ds. \end{aligned}$$

(4.30)

Let now $\tau \in L^\infty ((0,T)\times \varOmega ;\mathbb {M}^{2\times 2}_{sym})$. By (4.16) we have

$$\begin{aligned} \int _0^T\langle D\psi _\lambda (\sigma ^\lambda (t))- D\psi _\lambda (\tau (t)),\sigma ^\lambda (t)-\tau (t)\rangle \, dt\ge 0, \end{aligned}$$

hence, using the fact that $D\psi _\lambda (\tau (t))=D\phi _N(\tau (t))$ for $\lambda >\Vert \tau \Vert _{L^\infty }$,

$$\begin{aligned}&\liminf _{\lambda \rightarrow +\infty }\int _0^T\langle D\psi _\lambda (\sigma ^\lambda (t)),\sigma ^\lambda (t)\rangle \, dt\\&\quad \ge \int _0^T \langle \gamma ^N(t), \tau (t)\rangle \, dt + \int _0^T \langle D\phi _N(\tau (t)),\sigma ^N(t)-\tau (t)\rangle \, dt. \end{aligned}$$

Combining this inequality with (4.30), we conclude that

$$\begin{aligned} \int _0^T\langle \gamma ^N(t)- D\phi _N(\tau (t)),\sigma ^N(t)-\tau (t)\rangle \, dt\ge 0 \end{aligned}$$

for every $\tau \in L^\infty ((0,T)\times \varOmega ;\mathbb {M}^{2\times 2}_{sym})$, hence $\gamma ^N(t)= D\phi _N(\sigma ^N(t))$.

Finally, we establish some compactness for the sequence $(v^\lambda )$. From the first equation in (4.13), combined with (4.22) and (4.28), it follows that the sequence $(v^\lambda )$ is uniformly bounded in $L^{N/(N-1)}(0,T;W^{1,N/(N-1)}(\varOmega ;\mathbb {R}^3))$, hence

$$\begin{aligned} v^\lambda \rightharpoonup v^N \quad \text { weakly in }L^{N/(N-1)}(0,T;W^{1,N/(N-1)}(\varOmega ;\mathbb {R}^3)), \end{aligned}$$

for some $v^N\in L^{N/(N-1)}(0,T;W^{1,N/(N-1)}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega ))$. It is easy to check that $v^N$ satisfies the boundary condition on $\varGamma _d$. This allows us to pass to the limit in the first equation of (4.13) and thus establish the existence of a solution to (4.6).

It remains to prove (4.9). This will follow from the first equation in (4.6) and from (4.7), once we show that the sequence $(D\phi _N(\sigma ^N))$ is bounded in $L^2(0,T;L^1(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$. Multiplying the first equation in (4.6) by $\sigma ^N(t)-\varrho (t)$, integrating over $\varOmega$, and using the first estimate in (4.7) yield

$$\begin{aligned} \langle D\phi _N(\sigma ^N(t)), \sigma ^N(t)-\varrho (t)\rangle \le C( \Vert E\dot{w}(t)\Vert _{L^2}+\Vert \dot{\sigma }^N(t)\Vert _{L^2}) \end{aligned}$$

for a.e. $t\in [0,T]$. On the other hand, setting $A_N(t):=\{x\in \varOmega :\ |\sigma ^N(t,x)|_r\ge \alpha _0\}$ and arguing as in the proof of (4.19), we obtain

$$\begin{aligned}&{\int _{A_N(t)} D\phi _N(\sigma ^N(t)){\,:\,} (\sigma ^N(t)-\varrho (t))\, dx}\\&\quad \ge \frac{1}{\alpha _0^{N-1}} \int _{A_N(t)} |\sigma ^N(t)|_r^{N-1} (|\sigma ^N(t)|_r - |\varrho (t)|_r) \, dx\\&\quad \ge \frac{\alpha _1}{\alpha _0^{N-1}} \int _{A_N(t)} |\sigma ^N(t)|_r^{N-1} \, dx\\&\quad \ge \alpha _1\int _{A_N(t)}|D\phi _N(\sigma ^N(t))|\,dx, \end{aligned}$$

where we used the expression of $D\phi _N$ and (4.2). Moreover, we have

$$\begin{aligned}&\int _{\varOmega \setminus A_N(t)} D\phi _N(\sigma ^N(t)){\,:\,} (\sigma ^N(t)-\varrho (t))\, dx\\&\quad \ge -\int _{\varOmega \setminus A_N(t)} |D\phi _N(\sigma ^N(t))|\, |\varrho (t)|\, dx \ge - C \alpha _0. \end{aligned}$$

Therefore, combining the previous estimates, we deduce that

$$\begin{aligned} \alpha _1\int _{A_N(t)}|D\phi _N(\sigma ^N(t))|\,dx \le C( \Vert E\dot{w}(t)\Vert _{L^2}+\Vert \dot{\sigma }^N(t)\Vert _{L^2} +1). \end{aligned}$$

Since $|D\phi _N(\sigma ^N(t))|\le 1$ on $\varOmega \setminus A_N(t)$, we conclude that

$$\begin{aligned} \int _\varOmega |D\phi _N(\sigma ^N(t))|\,dx \le C(\Vert E\dot{w}(t)\Vert _{L^2}+\Vert \dot{\sigma }^N(t)\Vert _{L^2} +1), \end{aligned}$$

thus, the second inequality in (4.7) implies that the sequence $(D\phi _N(\sigma ^N))$ is bounded in $L^2(0,T;L^1(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$, as claimed.

We now prove uniqueness of solutions. Let $(\sigma ^N, v^N)$ and $(\tau ^N, u^N)$ be solutions of (4.6) with the same initial datum $\sigma ^N(0)=\tau ^N(0)=\sigma _0$. We test the first equation in (4.6) for $(\sigma ^N, v^N)$ and $(\tau ^N, u^N)$ with $\sigma ^N-\tau ^N$ and take the difference:

$$\begin{aligned}&\langle {\mathbb {A}}_r(\dot{\sigma }^N(t)-\dot{\tau }^N(t)), \sigma ^N(t)-\tau ^N(t)\rangle \\&\qquad + \langle D\phi _N(\sigma ^N(t)) - D\phi _N(\tau ^N(t)), \sigma ^N(t)-\tau ^N(t)\rangle \\&\quad = \langle Ev^N-Eu^N, \sigma ^N(t)-\tau ^N(t)\rangle . \end{aligned}$$

Integrating by parts the right-hand side and using the convexity of $\phi _N$ yield

$$\begin{aligned} \langle {\mathbb {A}}_r(\dot{\sigma }^N(t)-\dot{\tau }^N(t)), \sigma ^N(t)-\tau ^N(t)\rangle \le 0. \end{aligned}$$

Owing to the initial condition, this implies

$$\begin{aligned} \frac{1}{2} \langle {\mathbb {A}}_r(\sigma ^N(t)-\tau ^N(t)), \sigma ^N(t)-\tau ^N(t)\rangle \le 0, \end{aligned}$$

hence $\sigma ^N(t)=\tau ^N(t)$ for every $t\in [0,T]$. From the first equation in (4.6) we deduce that $Ev^N(t)=Eu^N(t)$, hence by the boundary condition on $\varGamma _d$ we conclude that $v^N(t)=u^N(t)$ for every $t\in [0,T]$. $\square$

We now prove two lemmas, that were used in the proof of Theorem 1.

Lemma 1

Let

$$\begin{aligned} \begin{array}{c} w\in W^{1,2}(0,T;W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )),\\ f\in W^{1,2}(0,T;L^2(\omega ;\mathbb {R}^2)), \quad g\in W^{1,2}(0,T;L^2(\omega )), \\ h\in W^{1,2}(0,T;H^{-\frac{1}{2}}(\omega ;\mathbb {R}^2)), \quad m\in W^{1,2}(0,T;H^{-\frac{1}{2}}(\omega )\times H^{-\frac{3}{2}}(\omega )). \end{array} \end{aligned}$$

Assume (4.1) with $\varrho \in W^{1,2}(0,T;L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$. Let $\sigma _0\in \varTheta (\gamma _n,h(0),m(0))$ be such that $-\mathrm {div}_{x'}\bar{\sigma }_0=f(0)$, $-\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }_0=g(0)$ in $\omega$. Finally, let $\varPsi :\mathbb {M}^{2\times 2}_{sym}\rightarrow \mathbb {M}^{2\times 2}_{sym}$ be a Lipschitz continuous function. Then the problem

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathbb {A}}_r\dot{\sigma } (t)+\varPsi (\sigma (t))=Ev(t) &{} \text { in }\varOmega ,\\ -\mathrm {div}_{x'}\bar{\sigma }(t)=f(t),\quad -\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }(t)=g(t) &{} \text { in }\omega ,\\ \sigma (t)\in \varTheta (\gamma _n,h(t),m(t)), &{}\\ v(t)=\dot{w}(t) &{}\text { on }\varGamma _d,\\ \sigma (0)=\sigma _0 \end{array}\right. } \end{aligned}$$

(4.31)

has a unique solution

$$\begin{aligned} (\sigma , v)\in W^{1,2}(0,T; L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))\times L^2(0,T; W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )). \end{aligned}$$

Proof

On $L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ we consider the scalar product

$$\begin{aligned} \langle \sigma ,\tau \rangle _{{\mathbb {A}}_r}:=\langle {\mathbb {A}}_r\sigma ,\tau \rangle \quad \text {for every }\sigma ,\tau \in L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}), \end{aligned}$$

(4.32)

which is topologically equivalent to the standard scalar product, owing to (3.1). We introduce the set

$$\begin{aligned} \varSigma ^*:=\{ \sigma \in \varTheta (\gamma _n,0,0) :\ \mathrm {div}_{x'}\bar{\sigma }=0,\ \mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }=0 \text { in } \omega \}, \end{aligned}$$

which is a closed subspace of $L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$, and we denote the projection onto $\varSigma ^*$ with respect to the scalar product (4.32) by $P_*$.

We consider the following problem: to find $\theta \in W^{1,2}(0,T; \varSigma ^*)$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\theta }(t)+ P_*({\mathbb {A}}_r^{-1}\varPsi (\theta (t)+\varrho (t)))=P_*\left( {\mathbb {A}}_r^{-1}E\dot{w}(t)-\dot{\varrho }(t)\right) &{} \text { in }\varSigma ^*, \\ \theta (0)=\sigma _0-\varrho (0). \end{array}\right. } \end{aligned}$$

(4.33)

Let

$$\begin{aligned} \varLambda :[0,T]\times \varSigma ^*\rightarrow \varSigma ^*: (t,\theta )\mapsto P_*({\mathbb {A}}_r^{-1}\varPsi (\theta +\varrho (t)))-P_*({\mathbb {A}}_r^{-1}E\dot{w}(t)-\dot{\varrho }(t)). \end{aligned}$$

Since $\varLambda (t,\cdot )$ is Lipschitz continuous for a.e. $t\in [0,T]$ and $\varLambda (\cdot , \theta )\in L^2(0,T;\varSigma ^*)$ for every $\theta \in \varSigma ^*$, existence and uniqueness of solutions to problem (4.33) follow from the Cauchy–Lipschitz Theorem. Now, the first equation in (4.33) implies that

$$\begin{aligned} \langle \dot{\theta }(t),\tau \rangle _{{\mathbb {A}}_r} +\langle {\mathbb {A}}_r^{-1}\varPsi (\theta (t)+\varrho (t)), \tau \rangle _{{\mathbb {A}}_r} = \langle {\mathbb {A}}_r^{-1} E\dot{w}(t)-\dot{\varrho }(t), \tau \rangle _{{\mathbb {A}}_r} \end{aligned}$$

for every $\tau \in \varSigma ^*$, that is,

$$\begin{aligned} \langle {\mathbb {A}}_r\dot{\theta }(t),\tau \rangle +\langle \varPsi (\theta (t)+\varrho (t)), \tau \rangle = \langle E\dot{w}(t)-{\mathbb {A}}_r\dot{\varrho }(t), \tau \rangle \end{aligned}$$

for every $\tau \in \varSigma ^*$. By Lemma 2 below for a.e. $t\in [0,T]$ there exists $z(t)\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$ such that $z(t)=0$ on $\varGamma _d$ and

$$\begin{aligned} {\mathbb {A}}_r\dot{\theta }(t)+ \varPsi (\theta (t)+\varrho (t)) - E\dot{w}(t) +{\mathbb {A}}_r\dot{\varrho }(t) = Ez(t). \end{aligned}$$

We set $\sigma (t):=\theta (t)+\varrho (t)$ and $v(t):= z(t)+\dot{w}(t)$. We observe that $v\in L^2(0,T; W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega ))$ by construction. Thus, we have found a pair $(\sigma , v)$ satisfying (4.31).

On the other hand, if $(\sigma , v)$ is a solution to (4.31), then $\theta (t):=\sigma (t)-\varrho (t)$ satisfies (4.33) and is therefore uniquely determined. Uniqueness of v follows from Lemma 2. $\square$

Lemma 2

Let $\sigma \in L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ be such that

$$\begin{aligned} \int _\varOmega \sigma :\tau \, dx =0 \quad \text {for every } \tau \in \varSigma ^*, \end{aligned}$$

(4.34)

where $\varSigma ^*:=\{ \tau \in \varTheta (\gamma _n,0,0):\ \mathrm {div}_{x'}\bar{\tau }=0, \ \mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\tau }=0 \text { in }\omega \}$. Then there exists a unique function $u\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$ such that $u=0$ on $\varGamma _d$ and $\sigma =Eu$ in $\varOmega$.

Proof

We consider the set

$$\begin{aligned} E_0:=\{ Ev:\ v\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega ), \ v=0 \text { on } \varGamma _d\}, \end{aligned}$$

which is a closed subspace of $L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$, owing to the Korn–Poincaré inequality. Let $P_0$ be the orthogonal projection onto $E_0$ and let $Eu:=P_0(\sigma )$. By definition u satisfies

$$\begin{aligned} \int _\varOmega Eu{\,:\,}Ev \, dx =\int _\varOmega \sigma {\,:\,}Ev\, dx \end{aligned}$$

(4.35)

for every $v\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$ with $v=0$ on $\varGamma _d$.

We now set $\theta :=\sigma -Eu$. From (4.35) it follows that

$$\begin{aligned} \int _\varOmega \theta {\,:\,}Ev \, dx=0 \end{aligned}$$

for every $v\in W^{1,2}(\varOmega ;\mathbb {R}^3)\cap KL(\varOmega )$ with $v=0$ on $\varGamma _d$. By Proposition 3 we deduce that $\theta \in \varSigma ^*$. On the other hand, since $u=0$ on $\varGamma _d$, integration by parts yields

$$\begin{aligned} \int _\varOmega Eu:\tau \, dx =0 \end{aligned}$$

for every $\tau \in \varSigma ^*$. Therefore, we have by (4.34) that

$$\begin{aligned} \int _\varOmega \theta :\tau \, dx =0 \quad \text {for every } \tau \in \varSigma ^*. \end{aligned}$$

We conclude that $\theta =0$, hence $\sigma =Eu$.

Uniqueness of u is straightforward. $\square$

We now prove additional regularity of $\sigma ^N$.

Proposition 5

In addition to the assumptions of Theorem 1, suppose that $\sigma _0 \!\in \! W^{1,2}(\varOmega ;\mathbb {M}^{2\times 2}_{sym})$ and that

$$\begin{aligned} \mathrm {div}_{x'}\bar{\varrho }\in L^\infty (0,T;W^{2,2}(\varOmega ;\mathbb {R}^2)), \quad \mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\varrho }\in L^\infty (0,T;W^{1,2}(\varOmega )). \end{aligned}$$

(4.36)

For every $N\in \mathbb {N}$, $N\ge 4$, let $\sigma ^N$ be the stress component of the solution of (4.6). Then the following estimates are satisfied:

• for every open set $\omega '$ compactly contained in $\omega$ there exists a constant $C_1(\omega ')>0$, depending on $\omega '$ but independent of N, such that for $\alpha =1,2$

  $$\begin{aligned} \sup _{t\in [0,T]}\Vert D_\alpha \sigma ^N(t)\Vert _{L^2(\omega '\times (-\frac{1}{2},\frac{1}{2});\,\mathbb {M}^{2\times 2}_{sym})}\le C_1; \end{aligned}$$

  (4.37)

• for every open set $\varOmega '$ compactly contained in $\varOmega$ there exists a constant $C_2(\varOmega ')>0$, depending on $\varOmega '$ but independent of N, such that

  $$\begin{aligned} \sup _{t\in [0,T]}\Vert D_3\sigma ^N(t)\Vert _{L^2(\varOmega ';\,\mathbb {M}^{2\times 2}_{sym})}\le C_2. \end{aligned}$$

  (4.38)

Proof

Let $N\in \mathbb {N}$, $N\ge 4$. We first prove higher regularity for $\sigma ^\lambda$, where $\sigma ^\lambda$ is the solution to the auxiliary problem (4.13), constructed in the proof of Theorem 1.

For $i=1,2,3$ let $D_i^h$ be the difference quotient operator defined by

$$\begin{aligned} D_i^h \tau (x)=\frac{1}{h}(\tau (x+he_i)-\tau (x)) \end{aligned}$$

for every function $\tau :\mathbb {R}^3\rightarrow \mathbb {M}^{2\times 2}_{sym}$.

Let $\alpha =1,2$ and let $\varphi \in C^\infty _c(\omega )$. Multiplying the first equation in (4.13) by the term $D_\alpha ^{-h}(\varphi ^2D_\alpha ^h \sigma ^\lambda (t))$, we obtain

$$\begin{aligned}&\langle \varphi ^2 {\mathbb {A}}_rD_\alpha ^h\dot{\sigma }^\lambda (t), D_\alpha ^h\sigma ^\lambda (t)\rangle + \langle \varphi ^2 D_\alpha ^h(D\psi _\lambda (\sigma ^\lambda (t))), D_\alpha ^h\sigma ^\lambda (t)\rangle \\&\quad = \langle \varphi ^2 D_\alpha ^hEv^\lambda (t), D_\alpha ^h\sigma ^\lambda (t)\rangle . \end{aligned}$$

Integrating this equation with respect to time and using (3.1), we deduce

$$\begin{aligned}&{\alpha _\mathbb {A}\int _\varOmega \varphi ^2 | D_\alpha ^h \sigma ^\lambda (t)|^2\, dx- \beta _\mathbb {A}\int _\varOmega \varphi ^2 | D_\alpha ^h \sigma _0|^2\, dx} \nonumber \\&\qquad + \int _0^t \int _\varOmega \int _0^1 \varphi ^2 D^2\psi _\lambda (\sigma ^\lambda (s)+r h D^h_\alpha \sigma ^\lambda (s))\, D_\alpha ^h\sigma ^\lambda (s) {\,:\,}D_\alpha ^h\sigma ^\lambda (s)\, dr\,dx\,ds \nonumber \\&\quad \le \int _0^t \langle \varphi ^2 D_\alpha ^hEv^\lambda (s), D_\alpha ^h\sigma ^\lambda (s)\rangle \, ds. \end{aligned}$$

(4.39)

Note that in the third integral on the left-hand side we used the chain rule, which holds since $D\psi _\lambda$ is a composition of smooth functions with a truncation.

Let us focus on the right-hand side of (4.39). We express it in terms of the Kirchhoff–Love components of $v^\lambda$ and use integration by parts, together with the fact that $\mathrm {div}_{x'}\bar{\sigma }^\lambda (s)=\mathrm {div}_{x'}\bar{\varrho }(s)$ and $\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }^\lambda (s)=\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\varrho }(s)$ in $\omega$. In this way for the zero-th order moment $\bar{\sigma }^\lambda (s)$ and the horizontal displacement $\bar{v}^\lambda (s)$ we obtain the following chain of equalities:

$$\begin{aligned}&{\langle \varphi ^2 D_\alpha ^hE\bar{v}^\lambda (s), D_\alpha ^h\bar{\sigma }^\lambda (s)\rangle }\\&\quad =- \sum _{\beta ,\gamma } \int _\omega \int _0^1 D_\beta \varphi ^2(x')\, D_\alpha \bar{v}^\lambda _\gamma (s, x'+r he_\alpha )\, D_\alpha ^h\bar{\sigma }^\lambda _{\beta \gamma }(s,x')\, dr\, dx'\\&\qquad - \sum _{\beta ,\gamma } \langle \varphi ^2 \,D_\alpha ^{h}\bar{v}^\lambda _\gamma (s), D_\alpha ^hD_\beta \bar{\varrho }_{\beta \gamma }(s) \rangle \\&\quad =- 2\sum _{\beta ,\gamma } \int _\omega \int _0^1 D_\beta \varphi ^2(x')\, (E\bar{v}^\lambda )_{\alpha \gamma }(s, x'+r he_\alpha )\, D_\alpha ^h\bar{\sigma }^\lambda _{\beta \gamma }(s,x')\, dr\, dx' \\&\qquad + \sum _{\beta ,\gamma } \int _\omega \int _0^1 D_\beta \varphi ^2(x')\, D_\gamma \bar{v}^\lambda _\alpha (s, x'+r he_\alpha )\, D_\alpha ^h\bar{\sigma }^\lambda _{\beta \gamma }(s,x')\, dr\, dx'\\&\qquad + \sum _{\beta ,\gamma } \langle D_\alpha ^{-h}\varphi ^2 \,\bar{v}^\lambda _\gamma (s), D_\alpha ^hD_\beta \bar{\varrho }_{\beta \gamma }(s) \rangle +\sum _{\beta ,\gamma } \langle \varphi ^2 \bar{v}^\lambda _\gamma (s), D_\alpha ^{-h}D_\alpha ^hD_\beta \bar{\varrho }_{\beta \gamma }(s) \rangle \end{aligned}$$

for a.e. $s\in [0,T]$. Integrating by parts again, we can further write

$$\begin{aligned}&{\langle \varphi ^2 D_\alpha ^hE\bar{v}^\lambda (s), D_\alpha ^h\bar{\sigma }^\lambda (s)\rangle }\\&\quad = - 2\sum _{\beta ,\gamma } \int _\omega \int _0^1 D_\beta \varphi ^2(x')\, (E\bar{v}^\lambda )_{\alpha \gamma }(s, x'+r he_\alpha )\, D_\alpha ^h\bar{\sigma }^\lambda _{\beta \gamma }(s,x')\, dr\, dx' \\&\qquad - \sum _{\beta ,\gamma } \int _\omega \int _0^1 D_\beta \varphi ^2(x')\, \bar{v}^\lambda _\alpha (s, x'+r he_\alpha )\, D_\alpha ^hD_\gamma \bar{\varrho }^\lambda _{\beta \gamma }(s,x')\, dr\, dx' \\&\qquad - \sum _{\beta ,\gamma } \int _\omega \int _0^1 D^2_{\beta \gamma }\varphi ^2(x')\, \bar{v}^\lambda _\alpha (s, x'+r he_\alpha )\, D_\alpha ^h\bar{\sigma }^\lambda _{\beta \gamma }(s,x')\, dr\, dx'\\&\qquad + \sum _{\beta ,\gamma } \langle D_\alpha ^{-h}\varphi ^2 \,\bar{v}^\lambda _\gamma (s), D_\alpha ^hD_\beta \bar{\varrho }_{\beta \gamma }(s) \rangle +\sum _{\beta ,\gamma } \langle \varphi ^2 \bar{v}^\lambda _\gamma (s), D_\alpha ^{-h}D_\alpha ^hD_\beta \bar{\varrho }_{\beta \gamma }(s) \rangle \end{aligned}$$

for a.e. $s\in [0,T]$. Arguing analogously for the first order moment $\hat{\sigma }^\lambda (s)$ and the vertical displacement $v_3^\lambda (s)$, and using the first equation in (4.13), we deduce that for a.e. $t\in [0,T]$ there holds

$$\begin{aligned}&{\langle \varphi ^2 D_\alpha ^hEv^\lambda (t), D_\alpha ^h\sigma ^\lambda (t)\rangle } \nonumber \\&\quad = - 2\sum _{\beta ,\gamma } \int _\varOmega \int _0^1 D_\beta \varphi ^2(x')\, ({\mathbb {A}}_r\dot{\sigma }^\lambda )_{\alpha \gamma }(t, x+r he_\alpha )\, D_\alpha ^h\sigma ^\lambda _{\beta \gamma }(t,x)\, dr\, dx \nonumber \\&\qquad - 2\sum _{\beta ,\gamma } \int _\varOmega \int _0^1 D_\beta \varphi ^2(x')\, D\psi _\lambda (\sigma ^\lambda )_{\alpha \gamma }(t, x+r he_\alpha )\, D_\alpha ^h\sigma ^\lambda _{\beta \gamma }(t,x)\, dr\, dx \nonumber \\&\qquad +\sum _{\beta ,\gamma } \int _\varOmega \int _0^1 v^\lambda _\alpha (t, x+r he_\alpha )\, D_\alpha ^{-h}D^2_{\beta \gamma } \varphi ^2(x')\, \sigma ^\lambda _{\beta \gamma }(t,x) \, dr\, dx \nonumber \\&\qquad +\sum _{\beta ,\gamma } \int _\varOmega \int _0^1\!\!\int _0^1 ({\mathbb {A}}_r\dot{\sigma }^\lambda )_{\alpha \alpha }(t, x+(r-\tilde{r}) he_\alpha )\, D^2_{\beta \gamma } \varphi ^2(x')\, \sigma ^\lambda _{\beta \gamma }(t,x) \, d\tilde{r}\,dr\, dx \nonumber \\&\qquad +\sum _{\beta ,\gamma } \int _\varOmega \int _0^1\!\!\int _0^1 D\psi _\lambda (\sigma ^\lambda )_{\alpha \alpha }(t, x+(r-\tilde{r}) he_\alpha )\, D^2_{\beta \gamma } \varphi ^2(x')\, \sigma ^\lambda _{\beta \gamma }(t,x) \, d\tilde{r}\,dr\, dx \nonumber \\&\qquad -\sum _{\beta ,\gamma } \int _\omega \int _0^1 \bar{v}^\lambda _\alpha (t, x'+r he_\alpha )\, D_\beta \varphi ^2(x')\, D_\alpha ^h D_\gamma \bar{\varrho }_{\beta \gamma }(t,x') \, dr\, dx' \nonumber \\&\qquad -\frac{1}{12}\sum _{\beta ,\gamma } \int _\omega \int _0^1 D_\alpha v^\lambda _3(t, x'+r he_\alpha )\, \varphi ^2(x')\, D_\alpha ^h D^2_{\beta \gamma }\hat{\varrho }_{\beta \gamma }(t,x') \, dr\, dx' \nonumber \\&\qquad + \sum _{\beta ,\gamma } \langle D_\alpha ^{-h}\varphi ^2 \,\bar{v}^\lambda _\gamma (t), D_\alpha ^hD_\beta \bar{\varrho }_{\beta \gamma }(t) \rangle + \sum _{\beta ,\gamma } \langle \varphi ^2 \bar{v}^\lambda _\gamma (t), D_\alpha ^{-h}D_\alpha ^hD_\beta \bar{\varrho }_{\beta \gamma }(t) \rangle . \end{aligned}$$

(4.40)

We now combine (4.39) and (4.40). From the definition of $\psi _\lambda$ we deduce the following estimate:

$$\begin{aligned} D^2\psi _\lambda (\xi )\, \zeta {\,:\,}\zeta \ge \frac{1}{\alpha _0^{N-1}}( |\xi |_r^{N-2}\wedge \lambda ^{N-2}) |\zeta |_r^2 \end{aligned}$$

(4.41)

for a.e. $\xi \in \mathbb {M}^{2\times 2}_{sym}$ and every $\zeta \in \mathbb {M}^{2\times 2}_{sym}$. In particular, this implies that the third term on the left-hand side of (4.39) is non negative. Moreover, using the inequality $|D\psi _\lambda (\xi )|\le \frac{1}{\alpha _0^{N-1}}\lambda ^{N-2}|\xi |$ for every $\xi \in \mathbb {M}^{2\times 2}_{sym}$, we obtain

$$\begin{aligned}&{\alpha _\mathbb {A}\int _\varOmega \varphi ^2 | D_\alpha ^h \sigma ^\lambda (t)|^2\, dx- \beta _\mathbb {A}\int _\varOmega \varphi ^2 | D_\alpha ^h \sigma _0|^2\, dx} \\&\quad \le C \int _0^t (\Vert \varphi \, D_\alpha ^h\sigma ^\lambda (s)\Vert _{L^2}+ \Vert \sigma ^\lambda (s)\Vert _{L^2}) \left( \Vert \dot{\sigma }^\lambda (s)\Vert _{L^2} + \frac{\lambda ^{N-2}}{\alpha _0^{N-1}} \Vert \sigma ^\lambda (s)\Vert _{L^2} \right) \, ds\\&\qquad + C \int _0^t \Vert v^\lambda (s)\Vert _{L^2} (\Vert \sigma ^\lambda (s) \Vert _{L^2} + 1)\, ds, \end{aligned}$$

where we used (4.36). Since we have $\sigma ^\lambda \in W^{1,2}(0,T;L^2(\varOmega ;\mathbb {R}^3))$ and $v^\lambda \in L^2(0,T;W^{1,2}(\varOmega ;\mathbb {R}^3))$, the previous inequality implies that $D_\alpha \sigma ^\lambda (t)\in L^2_{loc}(\omega \times [-\frac{1}{2},\frac{1}{2}];\mathbb {M}^{2\times 2}_{sym})$ for $\alpha =1,2$. Therefore, we can pass to the limit in (4.39)–(4.40), as $h\rightarrow 0$, and, using also (4.41), we obtain

$$\begin{aligned}&{\alpha _\mathbb {A}\int _\varOmega \varphi ^2 | D_\alpha \sigma ^\lambda (t)|^2\, dx -\beta _\mathbb {A}\int _\varOmega \varphi ^2 | D_\alpha \sigma _0|^2\, dx} \nonumber \\&\qquad + \frac{1}{\alpha _0^{N-1}} \int _0^t \int _\varOmega \varphi ^2\, ( |\sigma ^\lambda (s)|_r^{N-2}\wedge \lambda ^{N-2}) |D_\alpha \sigma ^\lambda (s)|_r^2 \,dx\,ds \nonumber \\&\quad \le - 2\sum _{\beta ,\gamma } \int _0^t \int _\varOmega D_\beta \varphi ^2\, ({\mathbb {A}}_r\dot{\sigma }^\lambda (s) +D\psi _\lambda (\sigma ^\lambda (s)))_{\alpha \gamma }\, D_\alpha \sigma ^\lambda _{\beta \gamma }(s)\, dx \, ds \nonumber \\&\qquad +\sum _{\beta ,\gamma } \int _0^t \int _\varOmega ({\mathbb {A}}_r\dot{\sigma }^\lambda (s) +D\psi _\lambda (\sigma ^\lambda (s)))_{\alpha \alpha }\, D^2_{\beta \gamma } \varphi ^2\, \sigma ^\lambda _{\beta \gamma }(s) \, dx\, ds \nonumber \\&\qquad +\sum _{\beta ,\gamma } \int _0^t \int _\varOmega v^\lambda _\alpha (s)\, D^3_{\alpha \beta \gamma } \varphi ^2\, \sigma ^\lambda _{\beta \gamma }(s) \, dx \, ds \nonumber \\&\qquad -\sum _{\beta ,\gamma } \int _0^t \int _\omega \bar{v}^\lambda _\alpha (s)\, D_\beta \varphi ^2\, D^2_{\alpha \gamma }\bar{\varrho }_{\beta \gamma }(s) \, dx \, ds \nonumber \\&\qquad -\frac{1}{12}\sum _{\beta ,\gamma } \int _0^t \int _\omega D_\alpha v^\lambda _3(s)\, \varphi ^2\, D^3_{\alpha \beta \gamma }\hat{\varrho }_{\beta \gamma }(s) \, dx \, ds \nonumber \\&\qquad + \sum _{\beta ,\gamma } \langle D_\alpha \varphi ^2 \,\bar{v}^\lambda _\gamma (t), D^2_{\alpha \beta } \bar{\varrho }_{\beta \gamma }(t) \rangle + \sum _{\beta ,\gamma } \langle \varphi ^2 \bar{v}^\lambda _\gamma (t), D^3_{\alpha \alpha \beta } \bar{\varrho }_{\beta \gamma }(t) \rangle . \end{aligned}$$

(4.42)

From this inequality we will deduce a uniform bound for $(D_\alpha \sigma ^\lambda )$ with respect to $\lambda$. We consider the first term on the right-hand side of (4.42). Using the expression of $D\psi _\lambda$, we have

$$\begin{aligned}&{\int _0^t \int _\varOmega | D_\beta \varphi ^2({\mathbb {A}}_r\dot{\sigma }^\lambda (s) +D\psi _\lambda (\sigma ^\lambda (s)))_{\alpha \gamma }\, D_\alpha \sigma ^\lambda _{\beta \gamma }(s)|\, dx \, ds}\\&\quad \le C \int _0^t \Vert \varphi D_\alpha \sigma ^\lambda (s)\Vert _{L^2}\Vert \dot{\sigma }^\lambda (s)\Vert _{L^2}\, ds\\&\qquad + \frac{C}{\alpha _0^{N-1}} \int _0^t \int _\varOmega ( |\sigma ^\lambda (s)|_r^{N-2}\wedge \lambda ^{N-2} ) |\sigma ^\lambda (s)|_r\,|\varphi D_\alpha \sigma ^\lambda (s)| \, dx \, ds\\&\quad \le C (\int _0^t \Vert \varphi D_\alpha \sigma ^\lambda (s)\Vert ^2_{L^2}\, ds )^\frac{1}{2}\\&\qquad + \frac{C}{\alpha _0^{\frac{N-1}{2}}} \left( \int _0^t \Vert \left( |\sigma ^\lambda (s)|_r^{N-2}\wedge \lambda ^{N-2} \right) ^{1/2} \varphi D_\alpha \sigma ^\lambda (s)\Vert ^2_{L^2}\, ds \right) ^\frac{1}{2} , \end{aligned}$$

where we have used (4.22) and (4.20).

Analogously, the second term on the right-hand side of (4.42) can be estimated as follows:

$$\begin{aligned}&{\int _0^t \int _\varOmega | D^2_{\beta \gamma } \varphi ^2\, ({\mathbb {A}}_r\dot{\sigma }^\lambda (s) +D\psi _\lambda (\sigma ^\lambda (s)))_{\alpha \alpha }\, \sigma ^\lambda _{\beta \gamma }(s)|\, dx\, ds} \\&\quad \le C \int _0^t \Vert \sigma ^\lambda (s)\Vert _{L^2}\Vert \dot{\sigma }^\lambda (s)\Vert _{L^2}\, ds\\&\qquad + \frac{C}{\alpha _0^{N-1}} \int _0^t \int _\varOmega \big ( |\sigma ^\lambda (s)|_r^{N-2}\wedge \lambda ^{N-2} \big ) |\sigma ^\lambda (s)|_r^2 \, dx \, ds, \end{aligned}$$

where the right-hand side is uniformly bounded with respect to $\lambda$, owing to (4.17), (4.22), and (4.20).

As for the remaining terms on the right-hand side of (4.42), we recall that $(v^\lambda )$ is uniformly bounded in $L^{N/(N-1)}(0,T;W^{1,N/(N-1)}(\varOmega ;\mathbb {R}^3))$, with respect to $\lambda$. Since $v^\lambda$ is a Kirchhoff–Love displacement for every $\lambda$, this implies that $(\bar{v}^\lambda )$ is uniformly bounded in $L^{N/(N-1)}(0,T;W^{1,N/(N-1)}(\omega ;\mathbb {R}^2))$, while $(v_3^\lambda )$ is uniformly bounded in $L^{N/(N-1)}(0,T;W^{2,N/(N-1)}(\omega ))$. By Sobolev embedding $(\bar{v}^\lambda )$ is thus uniformly bounded in $L^{N/(N-1)}(0,T;L^2(\omega ;\mathbb {R}^2))$ and $(v_3^\lambda )$ in $L^{N/(N-1)}(0,T;W^{1,2}(\omega ))$. Therefore, by (4.17)

$$\begin{aligned}&\Big |\int _0^t \int _\varOmega D^3_{\alpha \beta \gamma } \varphi ^2\, v^\lambda _\alpha (s)\, \sigma ^\lambda _{\beta \gamma }(s)\, dx \, ds \Big |\\&\quad \le C \int _0^t \Vert \bar{v}^\lambda (s)\Vert _{L^2}\, \Vert \bar{\sigma }^\lambda (s)\Vert _{L^2} \, ds +C \int _0^t \Vert D_{\alpha }v^\lambda _3(s)\Vert _{L^2}\, \Vert \hat{\sigma }^\lambda (s)\Vert _{L^2} \, ds \le C_N, \end{aligned}$$

where the last constant depends on N via the Sobolev embedding constants. The remaining terms in (4.42) can be estimated in a similar way, using the assumptions (4.36) on $\varrho$.

Combining all these estimates with (4.42), we conclude that for every open set $\omega '$ compactly contained in $\omega$ and for $\alpha =1,2$ the sequence $(D_\alpha \sigma ^\lambda )$ is uniformly bounded in $L^\infty (0,T; L^2(\omega '\times (-\frac{1}{2},\frac{1}{2});\mathbb {M}^{2\times 2}_{sym}))$, with respect to $\lambda$. By (4.24) this implies that $D_\alpha \sigma ^N$ belongs to $L^\infty (0,T;L^2(\omega '\times (-\frac{1}{2},\frac{1}{2});\mathbb {M}^{2\times 2}_{sym}))$ for $\alpha =1,2$.

To conclude the proof of (4.37), it remains to show that the norm of $D_\alpha \sigma ^N$ in the space $L^\infty (0,T;L^2(\omega '\times (-\frac{1}{2},\frac{1}{2});\mathbb {M}^{2\times 2}_{sym}))$ is uniformly bounded with respect to N. To this purpose, arguing exactly as in the proof of (4.42), we obtain

$$\begin{aligned}&{\alpha _\mathbb {A}\int _\varOmega \varphi ^2 | D_\alpha \sigma ^N(t)|^2\, dx -\beta _\mathbb {A}\int _\varOmega \varphi ^2 | D_\alpha \sigma _0|^2\, dx} \nonumber \\&\qquad + \int _0^t \int _\varOmega \varphi ^2 D^2\phi _N(\sigma ^N(s))\, D_\alpha \sigma ^N(s){\,:\,}D_\alpha \sigma ^N(s) \,dx\,ds \nonumber \\&\quad \le - 2\sum _{\beta ,\gamma } \int _0^t \int _\varOmega D_\beta \varphi ^2\, ({\mathbb {A}}_r\dot{\sigma }^N(s) +D\phi _N(\sigma ^N(s)))_{\alpha \gamma }\, D_\alpha \sigma ^N_{\beta \gamma }(s)\, dx \, ds \nonumber \\&\qquad +\sum _{\beta ,\gamma } \int _0^t \int _\varOmega ({\mathbb {A}}_r\dot{\sigma }^N(s) +D\phi _N(\sigma ^N(s)))_{\alpha \alpha }\, D^2_{\beta \gamma } \varphi ^2\, \sigma ^N_{\beta \gamma }(s) \, dx\, ds \nonumber \\&\qquad +\sum _{\beta ,\gamma } \int _0^t \int _\varOmega v^N_\alpha (s)\, D^3_{\alpha \beta \gamma } \varphi ^2\, \sigma ^N_{\beta \gamma }(s) \, dx \, ds \nonumber \\&\qquad -\sum _{\beta ,\gamma } \int _0^t \int _\omega \bar{v}^N_\alpha (s)\, D_\beta \varphi ^2\, D^2_{\alpha \gamma }\bar{\varrho }_{\beta \gamma }(s) \, dx \, ds \nonumber \\&\qquad -\frac{1}{12}\sum _{\beta ,\gamma } \int _0^t \int _\omega D_\alpha v^N_3(s)\, \varphi ^2\, D^3_{\alpha \beta \gamma }\hat{\varrho }_{\beta \gamma }(s) \, dx \, ds \nonumber \\&\qquad + \sum _{\beta ,\gamma } \langle D_\alpha \varphi ^2 \,\bar{v}^N_\gamma (t), D^2_{\alpha \beta } \bar{\varrho }_{\beta \gamma }(t) \rangle + \sum _{\beta ,\gamma } \langle \varphi ^2 \bar{v}^N_\gamma (t), D^3_{\alpha \alpha \beta } \bar{\varrho }_{\beta \gamma }(t) \rangle . \end{aligned}$$

(4.43)

We note that the third term on the left-hand side of (4.43) satisfies the following coercivity inequality:

$$\begin{aligned} D^2\phi _N(\sigma ^N(s))\, D_\alpha \sigma ^N(s){\,:\,}D_\alpha \sigma ^N(s) \ge \frac{1}{\alpha _0^{N-1}} |\sigma ^N(s)|_r^{N-2} |D_\alpha \sigma ^N(s)|_r^2. \end{aligned}$$

As for the right-hand side of (4.43), using the expression of $D\phi _N$, we have

$$\begin{aligned}&{\int _0^t \int _\varOmega | D_\beta \varphi ^2({\mathbb {A}}_r\dot{\sigma }^N(s) +D\phi _N(\sigma ^N(s)))_{\alpha \gamma }\, D_\alpha \sigma ^N_{\beta \gamma }(s)|\, dx \, ds} \\&\quad \le C \int _0^t \Vert \varphi \, D_\alpha \sigma ^N(s)\Vert _{L^2}\,\Vert \dot{\sigma }^N(s)\Vert _{L^2}\, ds \\&\qquad + \frac{C}{\alpha _0^{N-1}} \int _0^t \int _\varOmega |\sigma ^N(s)|_r^{N-1} \, |\varphi \, D_\alpha \sigma ^N(s)| \, dx \, ds \\&\quad \le C \left( \int _0^t \Vert \varphi \, D_\alpha \sigma ^N(s)\Vert ^2_{L^2}\, ds \right) ^\frac{1}{2} \\&\qquad + \frac{C}{\alpha _0^{\frac{N-1}{2}}} \left( \int _0^t \Vert |\sigma ^N(s)|_r^{\frac{N-2}{2}} \varphi \, D_\alpha \sigma ^N(s)\Vert ^2_{L^2}\, ds\right) ^\frac{1}{2} , \end{aligned}$$

where we have used (4.7) and (4.8). Analogously, the second term on the right-hand side of (4.43) can be estimated as follows:

$$\begin{aligned}&{\int _0^t \int _\varOmega | D^2_{\beta \gamma } \varphi ^2\, ({\mathbb {A}}_r\dot{\sigma }^N(s) +D\phi _N(\sigma ^N(s)))_{\alpha \alpha }\, \sigma ^N_{\beta \gamma }(s)|\, dx\, ds} \\&\quad \le C \int _0^t \Vert \sigma ^N(s)\Vert _{L^2}\,\Vert \dot{\sigma }^N(s)\Vert _{L^2}\, ds + \frac{C}{\alpha _0^{N-1}} \int _0^t \int _\varOmega |\sigma ^N(s)|_r^N\, dx \, ds, \end{aligned}$$

where the right-hand side is uniformly bounded with respect to N, owing to (4.7) and (4.8). As for the remaining terms on the right-hand side of (4.43), we observe that, in view of (4.9), the sequence $(v^N)$ is uniformly bounded in $L^2(0,T; BD(\varOmega ))$. Since $v^N$ is a Kirchhoff-Love displacement, this implies that $(\bar{v}^N)$ is uniformly bounded in $L^2(0,T; BD(\omega ))$ and $(v_3^N)$ is uniformly bounded in $L^2(0,T; BH(\omega ))$. By Sobolev embedding $(\bar{v}^N)$ is thus uniformly bounded in $L^2(0,T; L^2(\omega ;\mathbb {R}^2))$ and $(v_3^N)$ in $L^2(0,T; W^{1,2}(\omega ))$. Therefore, we have

$$\begin{aligned} \int _0^t \int _\varOmega | D^3_{\alpha \beta \gamma }\varphi ^2\, v^N_\alpha (s)\, \sigma ^N_{\beta \gamma }(s)| \, dx \, ds \le C \int _0^t \Vert v^N(s)\Vert _{L^2}\, \Vert \sigma ^N(s)\Vert _{L^2} \, ds, \end{aligned}$$

which is uniformly bounded with respect to N by (4.7) and (4.9). The remaining terms in (4.43) can be estimated similarly.

Combining these estimates with (4.43), we conclude that (4.37) is satisfied.

We now prove higher regularity with respect to $x_3$. Let $\varphi \in C^\infty _c(\varOmega )$. Multiplying the first equation in (4.6) by $D_3^{-h}(\varphi ^2 D_3^h\sigma ^N(t))$, we obtain

$$\begin{aligned}&\langle \varphi ^2 {\mathbb {A}}_rD_3^h\dot{\sigma }^N(t), D_3^h\sigma ^N(t)\rangle + \langle \varphi ^2 D_3^h(D\phi _N(\sigma ^N(t))), D_3^h\sigma ^N(t)\rangle \\&\quad = -\langle \varphi ^2 D^2v_3^N(t), D_3^h\sigma ^N(t)\rangle . \end{aligned}$$

Integrating this equation with respect to time and using (3.1), we deduce

$$\begin{aligned}&\alpha _\mathbb {A}\int _{\varOmega } \varphi ^2 |D_3^h\sigma ^{N}(t)|^2\,dx -\beta _\mathbb {A}\int _{\varOmega } \varphi ^2 |D_3^h\sigma _0|^2\,dx \nonumber \\&\qquad + \int _0^t \int _\varOmega \int _0^1 \varphi ^2 D^2\phi _N(\sigma ^N(s)+r h D^h_3\sigma ^N(s))\, D_3^h\sigma ^N(s) {\,:\,}D_3^h\sigma ^N(s)\, dr\,dx\,ds \nonumber \\&\quad \le - \int _0^t \langle \varphi ^2 D^2v_3^N(s), D_3^h\sigma ^N(s)\rangle \, ds. \end{aligned}$$

(4.44)

By integration by parts the right-hand side can be written as

$$\begin{aligned} -\int _0^t \langle \varphi ^2 D^2v_3^N(s), D_3^h\sigma ^N(s)\rangle \, ds= & {} -\int _0^t \langle D_3^{-h}(\varphi ^2)\, \nabla v_3^N(s), \mathrm {div}_{x'}\sigma ^N(s)\rangle \, ds \\&+\int _0^t \langle D_3^{-h}( \nabla _{x'}\varphi ^2)\odot \nabla v_3^N(s), \sigma ^N(s)\rangle \, ds. \end{aligned}$$

Combining the first estimate in (4.7), (4.37), and the uniform bound of $(v_3^N)$ in the space $L^2(0,T;W^{1,2}(\omega ))$, we deduce that the right-hand side of (4.44) is uniformly bounded with respect to h and N. Moreover, since $\phi _N$ is convex, the last term on the left-hand side of (4.44) is non-negative. Therefore, we have

$$\begin{aligned} \alpha _\mathbb {A}\int _{\varOmega } \varphi ^2 |D_3^h\sigma ^{N}(t)|^2\,dx \le \beta _\mathbb {A}\int _{\varOmega } \varphi ^2 |D_3^h\sigma _0|^2\,dx +C, \end{aligned}$$

(4.45)

where the constant C is independent of h and N. Using the assumptions on $\sigma _0$, this inequality implies that $D_3 \sigma ^{N}\in L^\infty (0,T;L^2_{loc}(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$ for every N. Therefore, we can pass to the limit in (4.45), as $h\rightarrow 0$, and we obtain

$$\begin{aligned} \alpha _\mathbb {A}\int _{\varOmega } \varphi ^2 |D_3\sigma ^{N}(t)|^2\,dx \le \beta _\mathbb {A}\int _{\varOmega } \varphi ^2 |D_3\sigma _0|^2\,dx+C, \end{aligned}$$

where the constant C is independent of N. This completes the proof of (4.38) and of the proposition. $\square$

We are now in a position to prove the main result of the paper, namely higher regularity for the stress component of the quasistatic evolutions. This will be established by showing convergence of the solutions to the Norton–Hoff problems (4.6) to a solution of the quasistatic evolution problem. As a by-product, we also prove existence of solutions to (qs1)–(qs3), under the assumptions (3.6)–(3.7) on the set $K_r$ of admissible stresses.

Theorem 2

Let the assumptions of Theorem 1 be satisfied with $\sigma _0=\mathbb {C}_re_0$, where $(u_0,e_0,p_0)\in {\mathcal A}_{KL}(w(0))$. Then there exists a solution

$$\begin{aligned} (u,e,p)\in W^{1,2}(0,T; BD(\varOmega ){\times } L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}){\times }M_b(\varOmega \cup \varGamma _d;\mathbb {M}^{2\times 2}_{sym})) \end{aligned}$$

of the quasistatic evolution problem (qs1)–(qs3) satisfying $(u(0),e(0), p(0))=(u_0,e_0,p_0)$. The stress component $\sigma (t):=\mathbb {C}_re(t)$ is unique and, under the assumptions of Proposition 5, it satisfies the following estimates:

• for every open set $\omega '$ compactly contained in $\omega$ there exists a constant $C_1(\omega ')>0$ such that for $\alpha =1,2$

  $$\begin{aligned} \sup _{t\in [0,T]}\Vert D_\alpha \sigma (t)\Vert _{L^2(\omega '\times (-\frac{1}{2},\frac{1}{2});\,\mathbb {M}^{2\times 2}_{sym})}\le C_1; \end{aligned}$$

  (4.46)

• for every open set $\varOmega '$ compactly contained in $\varOmega$ there exists a constant $C_2(\varOmega ')>0$ such that

  $$\begin{aligned} \sup _{t\in [0,T]}\Vert D_3\sigma (t)\Vert _{L^2(\varOmega ';\,\mathbb {M}^{2\times 2}_{sym})}\le C_2. \end{aligned}$$

  (4.47)

Proof

By applying the Ascoli–Arzelà Theorem we deduce from (4.7) that there exists $\sigma \in W^{1,2}(0,T;L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))$ such that, up to subsequences,

$$\begin{aligned} \sigma ^N(t)\rightharpoonup \sigma (t) \quad \text {weakly in } L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}), \end{aligned}$$

(4.48)

as $N\rightarrow \infty$, for every $t\in [0,T]$ and

$$\begin{aligned} \sigma ^N\rightharpoonup \sigma \quad \text {weakly in } W^{1,2}(0,T;L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})), \end{aligned}$$

(4.49)

as $N\rightarrow \infty$. By (4.48) it is clear that $\sigma (0)=\sigma _0$ and, in view of Proposition 2, that $-\mathrm {div}_{x'}\bar{\sigma }(t)=f(t)$, $-\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\sigma }(t)=g(t)$ in $\omega$, and $\sigma (t)\in \varTheta (\gamma _n,h(t), m(t))$ for every $t\in [0,T]$. From Proposition 5 and (4.49) it follows that (4.46) and (4.47) are satisfied. Passing to the limit in the first inequality of (4.8), as $N\rightarrow \infty$, we deduce that $\sigma (t)\in \mathcal {K}_r(\varOmega )$ for every $t\in [0,T]$.

We now set

$$\begin{aligned} u^N(t):=u_0+\int _0^t v^N(s)\, ds \quad \text { for every } t\in [0,T]. \end{aligned}$$

By (4.9) the sequences $(u^N)$ and $(\dot{u}^N)$ are bounded in $L^2(0,T; BD(\varOmega ))$. Thus, there exists $u\in W^{1,2}(0,T; BD(\varOmega ))$ such that, up to subsequences, $u^N\rightharpoonup u$ and $\dot{u}^N\rightharpoonup \dot{u}$ weakly$^*$ in $L^2(0,T;BD(\varOmega ))$, as $N\rightarrow \infty$. In particular, using the Kirchhoff–Love structure,

$$\begin{aligned} \begin{array}{c} \bar{v}^N=\dot{\bar{u}}^{N}\rightharpoonup \dot{\bar{u}} \quad \text {weakly in } L^2(0,T;L^2(\omega ;\mathbb {R}^2)),\\ v_3^N=\dot{u}_{3}^{N}\rightharpoonup \dot{u}_{3} \quad \text {weakly in } L^2(0,T;W^{1,2}(\omega )), \end{array} \end{aligned}$$

(4.50)

as $N\rightarrow \infty$.

We define $e(t):={\mathbb {A}}_r\sigma (t)$ and $p(t):=Eu(t)-e(t)$ in $\varOmega$, $p(t):=(w(t)-u(t))\odot \nu _{\partial \varOmega }\mathcal {H}^2$ on $\varGamma _d$. It is thus clear that $(u(t),e(t),p(t))\in {\mathcal {A}}_{KL}(w(t))$.

It remains to prove that the flow rule is satisfied. To this purpose, we will show that (4.3) holds. Let $\varphi \in C^2(\overline{\omega })$ with $\varphi \ge 0$ and let

$$\begin{aligned} \theta \in W^{1,2}(0,T;L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym}))\cap L^\infty (0,T;L^N(\varOmega ;\mathbb {M}^{2\times 2}_{sym})). \end{aligned}$$

Multiplying the first equation in (4.6) by $\varphi \,(\theta (t)-\sigma ^N(t))$, we obtain

$$\begin{aligned} \langle {\mathbb {A}}_r\dot{\sigma }^N(t)+D\phi _N(\sigma ^N(t))-Ev^N(t), \varphi \,(\theta (t)-\sigma ^N(t))\rangle =0. \end{aligned}$$

Using the convexity of $\phi _N$, this equality can be interpreted as the following minimality condition:

$$\begin{aligned}&\langle {\mathbb {A}}_r\dot{\sigma }^N(t)-Ev^N(t),\varphi \,\sigma ^N(t)\rangle + \int _\varOmega \varphi \, \phi _N(\sigma ^N(t))\, dx \nonumber \\&\quad \le \langle {\mathbb {A}}_r\dot{\sigma }^N(t)-Ev^N(t), \varphi \,\theta (t)\rangle + \int _\varOmega \varphi \,\phi _N(\theta (t))\, dx. \end{aligned}$$

(4.51)

We now choose $\theta =\sigma$ and $\varphi \equiv 1$, and integrate the inequality with respect to time on a time interval $[0,t_1]$. Using the equilibrium equations for $\sigma ^N(t)$ and $\sigma (t)$ and Remark 1 (note that $v^N(t)\in W^{1, N/(N-1)}(\varOmega ;\mathbb {R}^3)$ for a.e. $t\in [0,T]$, so we cannot apply Proposition 3), we have

$$\begin{aligned} \int _0^{t_1} \langle \sigma ^N(t)-\sigma (t), Ev^N(t)\rangle \, dt =\int _0^{t_1} \langle \sigma ^N(t)-\sigma (t), E\dot{w}(t)\rangle \, dt. \end{aligned}$$

Thus, since $\phi _N\ge 0$, we obtain

$$\begin{aligned}&\frac{1}{2} \langle {\mathbb {A}}_r\big (\sigma ^N(t_1)-\sigma (t_1)\big ), \sigma ^N(t_1)-\sigma (t_1)\rangle \\&\quad \le \int _0^{t_1} \langle \sigma ^N(t)-\sigma (t), E\dot{w}(t)-{\mathbb {A}}_r\dot{\sigma }(t)\rangle \,dt + \int _0^{t_1} \int _\varOmega \phi _N(\sigma (t))\, dx\,dt, \end{aligned}$$

hence, by the coercivity (3.1) of ${\mathbb {A}}_r$ we deduce

$$\begin{aligned} \alpha _\mathbb {A}\Vert \sigma ^N(t_1)-\sigma (t_1)\Vert ^2_{L^2}\le & {} \int _0^{t_1} \langle \sigma ^N(t)-\sigma (t), E\dot{w}(t)-{\mathbb {A}}_r\dot{\sigma }(t)\rangle \,dt \\&+ \int _0^{t_1} \int _\varOmega \phi _N(\sigma (t))\, dx\,dt. \end{aligned}$$

Since $\sigma (t)\in \mathcal {K}_r(\varOmega )$ for every $t\in [0,T]$, the last term in the previous expression tends to zero, as $N\rightarrow \infty$. Together with (4.48) and the first estimate in (4.7), this implies that

$$\begin{aligned} \sigma ^N\rightarrow \sigma \quad \text {strongly in } L^\infty (0,T;L^2(\varOmega ;\mathbb {M}^{2\times 2}_{sym})), \end{aligned}$$

(4.52)

as $N\rightarrow \infty$.

We now go back to Eq. (4.51), where we choose $\theta \in \mathcal {K}_r(\varOmega )\cap \varSigma (\varOmega )$ independent of time and $\varphi \in C^2(\overline{\omega })$, $\varphi \ge 0$, with $\varphi =0$ in a neighbourhood of $\gamma _n$. Since $\varphi (v^N(t)-\dot{w}(t))=0$ on $\partial \omega \times (-\frac{1}{2},\frac{1}{2})$, integration by parts yields

$$\begin{aligned}&{\langle Ev^N(t),\varphi \,(\sigma ^N(t)-\theta )\rangle }\\&\quad = \langle E\dot{w}(t),\varphi \,(\sigma ^N(t)-\theta )\rangle +\int _\omega \varphi \, (\bar{v}^N(t)-\dot{\bar{w}}(t))\cdot (f(t)+\mathrm {div}_{x'}\bar{\theta })\, dx'\\&\qquad -\int _\omega \nabla \varphi \odot (\bar{v}^N(t)-\dot{\bar{w}}(t)){\,:\,}(\bar{\sigma }^N(t)-\bar{\theta })\, dx'\\&\qquad +\frac{1}{12} \int _\omega \varphi \, (v_3^N(t)-\dot{w}_3(t))(g(t)+\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\theta })\, dx'\\&\qquad +\frac{1}{12} \int _\omega (v_3^N(t)-\dot{w}_3(t)) D^2\varphi {\,:\,}(\hat{\sigma }^N(t)-\hat{\theta })\, dx'\\&\qquad +\frac{1}{6} \int _\omega \nabla \varphi \odot (\nabla v_3^N(t)-\nabla \dot{w}_3(t)){\,:\,}(\hat{\sigma }^N(t)-\hat{\theta })\, dx'. \end{aligned}$$

We use this expression in (4.51), integrate with respect to time on an arbitrary time interval $[t_1,t_2]$, and observe that the established convergences (4.49), (4.50), and (4.52) are enough to pass to the limit, as $N\rightarrow \infty$. In this way we deduce

$$\begin{aligned}&{\int _{t_1}^{t_2} \langle {\mathbb {A}}_r\dot{\sigma } (t) -E\dot{w}(t) ,\varphi \,(\sigma (t)-\theta )\rangle \, dt}\\&\quad \le \int _{t_1}^{t_2} \int _\omega \varphi \, (\dot{\bar{u}}(t)-\dot{\bar{w}}(t))\cdot (f(t)+\mathrm {div}_{x'}\bar{\theta })\, dx'\, dt\\&\qquad -\int _{t_1}^{t_2} \int _\omega \nabla \varphi \odot (\dot{\bar{u}}(t)-\dot{\bar{w}}(t)){\,:\,}(\bar{\sigma }(t)-\bar{\theta })\, dx'\, dt\\&\qquad +\frac{1}{12} \int _{t_1}^{t_2} \int _\omega \varphi \, (\dot{u}_3(t)-\dot{w}_3(t))(g(t)+\mathrm {div}_{x'}\mathrm {div}_{x'}\hat{\theta })\, dx'\, dt\\&\qquad +\frac{1}{12} \int _{t_1}^{t_2} \int _\omega (\dot{u}_3(t)-\dot{w}_3(t)) D^2\varphi {\,:\,}(\hat{\sigma }(t)-\hat{\theta })\, dx'\, dt\\&\qquad +\frac{1}{6} \int _{t_1}^{t_2} \int _\omega \nabla \varphi \odot (\nabla \dot{u}_3(t)-\nabla \dot{w}_3(t)){\,:\,}(\hat{\sigma }(t)-\hat{\theta })\, dx'\, dt. \end{aligned}$$

By the integration by parts formula (3.18) this is equivalent to

$$\begin{aligned} \int _{t_1}^{t_2} \int _{\varOmega \cup \varGamma _d} \varphi \, d[(\theta -\sigma (t)){\,:\,}\dot{p}(t)]\, dt \le 0 \end{aligned}$$

(4.53)

for every $\theta \in \mathcal {K}_r(\varOmega )\cap \varSigma (\varOmega )$ and every $\varphi \in C^2(\overline{\omega })$, $\varphi \ge 0$, with $\varphi =0$ in a neighbourhood of $\gamma _n$. For every $\delta >0$ let now $\varphi _\delta \in C^2(\overline{\omega })$ be such that $0\le \varphi _\delta \le 1$, $\varphi _\delta =0$ on the set $\{x'\in \overline{\omega }:\ \mathrm {dist}(x',\gamma _n)<\delta \}$, and $\varphi _\delta =1$ on the set $\{x'\in \overline{\omega }:\ \mathrm {dist}(x',\gamma _n)>2\delta \}$. Using $\varphi _\delta$ as test function in (4.53) and sending $\delta$ to zero, we obtain

$$\begin{aligned} \int _{t_1}^{t_2}\langle \theta -\sigma (t), \dot{p}(t)\rangle \, dt\le 0. \end{aligned}$$

Since the time interval $[t_1,t_2]$ is arbitrary, this is equivalent to the flow rule in the form (4.3). $\square$

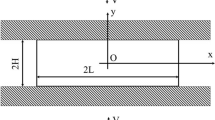
5 An example

In this section we show an explicit example of quasistatic evolution where the stress component $\sigma _\perp$ is different from zero.

We assume that the three-dimensional elasticity tensor $\mathbb {C}$ is isotropic, that is, of the form

$$\begin{aligned} \mathbb {C}\xi := 2\mu \, \xi +\lambda (\mathrm{tr}\,\xi )I_{3\times 3} \end{aligned}$$

for some $\lambda , \mu$ satisfying $\mu >0$, $\lambda +\mu \ge 0$, and every $\xi \in \mathbb {M}^{3\times 3}_{sym}$. From the results of [5, Sect. 3.2] it follows that the elasticity tensor of the reduced problem takes the form

$$\begin{aligned} \mathbb {C}_r\xi = 2\mu \,\xi +\frac{2\lambda \mu }{\lambda +2\mu }(\mathrm{tr}\,\xi )I_{2\times 2} \end{aligned}$$

for every $\xi \in \mathbb {M}^{2\times 2}_{sym}$. We also assume that $K_r$ is of the form (3.6)–(3.7). Finally we consider the boundary condition

$$\begin{aligned} w(t,x):=\left( \begin{array}{c} -tx_1x_3 \\ -tx_2x_3 \\ \frac{t}{2}(x_1^2+x_2^2) \end{array}\right) , \end{aligned}$$

for $t\in [0,T]$, prescribed on the whole lateral boundary $\partial \omega {\times }(-\frac{1}{2},\frac{1}{2})$; hence, $\gamma _d=\partial \omega$ and $\gamma _n=\emptyset$. We assume the body forces to be zero, that is, $f(t)=0$ and $g(t)=0$. We consider as initial datum $(u_0,e_0,p_0)=(0,0,0)$.

Let now

$$\begin{aligned} t_0:=\sqrt{\frac{3}{2}} \frac{\lambda +2\mu }{\mu (3\lambda +2\mu )}\alpha _0 \end{aligned}$$

(T is chosen large enough so that $t_0<T$). We define

$$\begin{aligned} u(t,x):=w(t,x) \end{aligned}$$

for every $t\in [0,T]$ and $x\in \varOmega$. For $t\le t_0$ and $x\in \varOmega$ we define

$$\begin{aligned} e(t,x)=-tx_3I_{2\times 2}, \qquad p(t,x):=0, \end{aligned}$$

while for $t>t_0$ and $x\in \varOmega$ we define

$$\begin{aligned} e(t,x)={\left\{ \begin{array}{ll} \quad \frac{t_0}{2}I_{2\times 2} &{} \text {for }\quad x_3<-\frac{t_0}{2t} , \\ -tx_3I_{2\times 2} &{} \text {for }\quad |x_3|\le \frac{t_0}{2t},\\ -\frac{t_0}{2}I_{2\times 2} &{} \text {for }\quad x_3>\frac{t_0}{2t} , \end{array}\right. } \qquad p(t,x):=Ew(t,x)-e(t,x). \end{aligned}$$

We claim that $t\mapsto (u(t),e(t),p(t))$ is a quasistatic evolution, that is, it satisfies conditions (qs1)–(qs3) in Definition 2.

It is easy to see that $t\mapsto (u(t),e(t),p(t))$ is absolutely continuous, that is, condition (qs1) holds. Clearly (u(t), e(t), p(t)) belongs to ${\mathcal {A}}_{KL}(w(t))$ for every $t\in [0,T]$. Setting $\sigma (t,x):=\mathbb {C}_re(t,x)$, we have that

$$\begin{aligned} \sigma (t,x)=-2\mu \frac{3\lambda +2\mu }{\lambda +2\mu }tx_3 I_{2\times 2} \end{aligned}$$

for $t\le t_0$, while

$$\begin{aligned} \sigma (t,x)={\left\{ \begin{array}{ll} \quad \mu \dfrac{3\lambda +2\mu }{\lambda +2\mu }t_0 I_{2\times 2} &{}\quad \text {for}\quad x_3<-\frac{t_0}{2t} , \\ -2\mu \dfrac{3\lambda +2\mu }{\lambda +2\mu }tx_3 I_{2\times 2} &{} \quad \text {for}\quad |x_3|\le \frac{t_0}{2t}, \\ -\mu \dfrac{3\lambda +2\mu }{\lambda +2\mu }t_0 I_{2\times 2} &{} \quad \text {for}\quad x_3>\frac{t_0}{2t} \end{array}\right. } \end{aligned}$$

for $t> t_0$. Using this expression and the definition of p, it is easy to check that also conditions (qs2) and (qs3) are satisfied. Thus, $t\mapsto (u(t),e(t),p(t))$ is a quasistatic evolution.

Note that $\bar{\sigma }(t)=0$ for every $t\in [0,T]$. For $t\le t_0$ we have $\sigma (t)=x_3\hat{\sigma }(t)$, while for $t>t_0$ we have $\sigma (t)=x_3\hat{\sigma }(t)+\sigma _\perp (t)$ with $\sigma _\perp (t)\ne 0$. Since the stress component is unique by Theorem 2, this is the expression of the stress for any solution to the quasistatic evolution problem with this choice of the data.

This example shows that the problem has a genuinely three-dimensional nature. Since the location of the plastic zone (that is, the region where the stress is on the yield surface) depends on the thickness variable $x_3$, reducing the problem to a two-dimensional setting is not possible. In particular, applying the classical plastic plate model to this set of data would mean to look for a solution that is linear with respect to $x_3$ both on e and p, and thus would lead to a wrong description of the plastic response.

We also point out that this example is a counterexample to the result of [5, Proposition 7.17], which is therefore false. It is in fact not true, in general, that if $\sigma \in K_r$ a.e. in $\varOmega$, then $\hat{\sigma }\in K_r$ a.e. in $\omega$.