Observer-based adaptive backstepping control for Mimo nonlinear systems with unknown hysteresis: a nonlinear gain feedback approach

Abstract

In this article, an adaptive neural network (NN) control problem is studied for nonstrict-feedback multi-input multi-output (MIMO) nonlinear systems with unmeasurable states and unknown hysteresis. Firstly, to estimate the unmeasurable states, a NN state observer is constructed. Additionally, the unknown nonlinear terms are online approximated by using radial basis function-neural networks (RBF-NNs). And then, the complexity problem is addressed by using the dynamic surface control (DSC), which is easy to overcome the problem of repeated differentiations for virtual control signals. Furthermore, a nonlinear gain feedback function is introduced into the backstepping design procedure to improve the dynamic performance of the closed-loop system. Meanwhile, to satisfy the practical engineering application, a prescribed performance control (PPC) technique is implemented to guarantee the tracking error can converge to a preassigned area. By using the proposed control scheme, all closed-loop signals are semi-global uniformly ultimately bounded (SGUUB). At last, the preponderance and usefulness of the proposed controller are indicated by simulation results.

1 Introduction

In recent years, the control problem for nonlinear systems has received much research attention in the past few years, and numerous control strategies have been developed, such as adaptive control [1]; sliding-mode control [2]; robust control [3]; etc. Since the backstepping control strategy is proposed [4], it has become a preeminent tool for stability analysis and control design of uncertain nonlinear systems. It is worth noting that the backstepping control strategy was first proposed to solve the problem of nonlinear systems subject to unmatched conditions, where the system nonlinearities are assumed to be known in advance. At the same time, the development of intelligent control theory, such as fuzzy logic systems (FLSs) and neural networks (NNs), becomes a useful tool to deal with the problem of control containing unknown nonlinear functions. Therefore, lots of adaptive backstepping-based NNs (and fuzzy) control strategies are developed for uncertain nonlinear systems [5,6,7,8]. Zuo [5] studied an adaptive backstepping control method for nonlinear multiagent systems by using the approximation ability of FLSs. Xu et al. [6] presented a fuzzy adaptive controller for SISO strict-feedback nonlinear systems with actuator quantization and mismatched external disturbances. Soon afterwards, the results in [6] were extended to solve the control problem of MIMO nonlinear systems in [7]. However, the complexity of computational, caused by repeated differentiation for virtual control laws, is unavoidable, which deteriorates obviously with the enlargement of the order for the backstepping-based nonlinear systems. Therefore, an advanced method called dynamic surface control (DSC) was reported to avoid such an issue by passing the intermediate control signals through the first-order filter, and in this way, the differentiations of intermediate control signals are not required in the process of the backstepping framework. Meanwhile, it should be noticed that the DSC technique relaxes the demands of the reference trajectories and the smoothness of nonlinear functions. Motivated by the DSC approach, on the basis of theoretical investigations and practical implementations, some original DSC-based results have been developed in [9,10,11].

Not all system states for actual engineering systems are easily quantifiable. Even if these states can be measured, more sensors are still needed, which raises the complexity of the control system. Therefore, it is necessary to explore deeply adaptive control strategies for nonlinear systems subject to unmeasurable states. In order to save the cost of control system, a series of observer-based adaptive output-feedback control methods have been published [12,13,14,15,16,17,18,19,20]. For example, the issue of adaptive output-feedback neural control for nonlinear systems in strict-feedback structure subject to input dead-zone constraints has been considered by [13]. By developing an extend state observer, a novel backstepping-based adaptive prescribed control approach has been proposed for the hydraulic systems under full-state constraints [14]. Zhang et al. [15] explained an adaptive formation containment control algorithm for linear multiagent systems with unmeasurable states and bounded unknown input. To estimate the unmeasured states in uncertain singular systems with unknown time-varying delay and nonlinear input, Tang et al. [16] proposed a simplified observer to give an adaptive sliding mode control method. A fuzzy observer-based adaptive control problem has been reported in [17] for nonstrict feedback systems under function constraints. Li et al. [18] investigated a learning-observer neural adaptive tracking problem of multiagent systems with quantized input. Wu et al. [19] focused on an adaptive quantized tracking control problem for nonlinear systems in nonstrict-feedback structure with sensor fault. In addition, based on a neural state observer and the command filter backstepping method, an adaptive control issue of pneumatic active suspension subject to sensor fault and vertical constraint has been studied in [20].

On the other hand, reducing tracking error for tracking control is a long-lasting yet challenging problem [21]. For the purpose of restricting system output within desired boundaries, Bechlioulis and Rovithakis originally proposed the prescribed control (PPC) technique in [22], which is a powerful tool to satisfy the high accuracy control requirements for different control systems. The work in [23] has studied an adaptive control problem for constrained nonlinear systems by using the barrier Lyapunov function method. Wang et al. [24] developed a finite-time adaptive PPC strategy for strict-feedback nonlinear systems with dynamic disturbances, actuator faults and time-varying parameters. By utilizing FLSs and PPC, an adaptive prescribe control strategy has been designed for nonlinear multiagent systems in [25]. Considering quantized input and tracking accuracy, a self-scrambling gain feedback controller has been proposed for MIMO nonlinear systems [26]. In [27], an adaptive control technique is developed for SISO nonlinear systems with hysteresis input, which guarantees the tracking error converges to the preassigned area by using PPC. The authors in [28] proposed a reinforcement learning-based control algorithm for an unmanned surface vehicle with prescribed performance.

Motivated by the above observations, this paper continues to focus on an adaptive PPC for a class of MIMO nonlinear systems with hysteresis input and unmeasurable states. Compared with the existing related results, the main advantages of this article are as follows.

• (1) It is a nontrivial work to investigate the adaptive control algorithm for MIMO nonstrict-feedback nonlinear systems with unmeasurable states and unknown hysteresis by using nonlinear error feedback. Moreover, compared with the MIMO strict (or pure)-feedback nonlinear systems [29, 30] and SISO nonlinear systems [31], the developed control approach in this paper can be used in more general situations.

• (2) Different from the case considered in [32,33,34], this article further studies the hysteresis input and the unmeasurable states that exist in actual engineering systems. Besides, the unmeasurable states of the system can be obtained by designing a NN state observer and the effect of the unknown hysteresis can be removed by constructing an adaptive update function.

• (3) In comparison to the traditional linear feedback control methods in [35,36,37], this study utilizes a novel nonlinear gain function in the backstepping design, which improves the dynamic performance of closed-loop system and also facilitates the closed-loop system stability analysis using its properties. Meanwhile, the computational explosion is addressed by applying DSC and the prescribed tracking error can be guaranteed.

2 Problem formulation and preliminaries

2.1 Plant description

The plant can be considered as the following nonstrict-feedback form

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}_{m,j}(t)&=x_{m,j+1}(t)+f_{m,j}(x_m)+d_{m,j}(t),\\ &~n=1,2,\dots ,N, j=1,\dots ,n_m-1\\ \dot{x}_{m,n_m}(t)&=u_m(v_m)+f_{m,n_m}(X)+d_{m,n_m}(t),\\ y_m(t)&=x_{m,1}(t),\\ \end{aligned} \right. \end{aligned}$$

(1)

where $n_m, m\in N_+$, $n_m>1$, $m>1$, $X=[x_1^\mathrm{T}, x_{2}^\mathrm{T}, \dots , x_m^\mathrm{T}]^\mathrm{T}$ with $x_m=[x_{m,1}, x_{m,2}, \dots , x_{m, n_m}]^\mathrm{T}$ is the state variable, $y_m\in \mathbb {R}$ indicates the system output, $f_{m,j}(\cdot )$ denotes the unknown smooth nonlinear function, $d_{m,j}(t)$ is the continuous time-varying disturbance, which is subject to $d_{m,j}(t)\le d_{m,j}^*$ with $d_{m,j}^*$ being an unknown constant. $u_m(v_m)$ represents the system input and the output of the backlash-like hysteresis with $v_m\in \mathbb {R}$ is the input of the backlash-like hysteresis.

Remark 1

It should be noticed that the nonlinear system (2) can be employed to represent many practical systems, such as unmanned surface vehicles [28], and connected inverted pendulums systems [10]. Thus, it is necessary to investigate the adaptive control problem for such MIMO nonlinear systems.

From [38], the hysteresis input $v_m$ and the system input $u_m(v_m)$ can be expressed as

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}u_m}{\mathrm{d}t}=\varrho _m|\frac{\mathrm{d}v_m}{\mathrm{d}t}|(c_mv_m-u_m)+D_m\frac{\mathrm{d}v_m}{\mathrm{d}t}, \end{aligned} \end{aligned}$$

(2)

where $\varrho _m$, $c_m$, and $D_m$ denote the unknown parameters and $\varrho _m>0$, $c_m>D_m$.

Furthermore, the solution of (2) can be solved as

$$\begin{aligned} \begin{aligned}&u_m(v_m)=c_mv_m(t)+h_m(v_m),\\&h_m(v_m)=[u_{m,0}-c_mv_{m,0}]e^{-\varrho _m(v_m-v_m(0))\text {sgn}(\dot{v}_m)}\\&+e^{-\varrho _mv_m\text {sgn}(\dot{v}_m)}\int _{v_{m,0}}^{v_m}[D_m-c_m]e^{-\varrho _m\kappa _m\text {sgn}(\dot{v}_m)}d\kappa _m, \end{aligned} \end{aligned}$$

(3)

where $v_{m,0}$ and $u_{m,0}$ are the initial conditions of $v_m$ and $u_m$, respectively. $h_m(v_m)$ is bounded, which satisfies $|h_m(v_m)|\le h_m^*$ and $h_m^*$ is the unknown bound.

From (3), it is easy to rewrite system (1) as the following matrix form

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}_m(t)\,=\,&A_mx_m(t)+L_my_m+\sum _{j=1}^{n_m}B_{m,j}f_{m,j}(X)\\ &+d_m+B_{m,n_m}v_m,\\ y_m(t)\,=\,&G_mx_m(t),\\ \end{aligned} \right. \end{aligned}$$

(4)

where

$$\begin{aligned} A= \quad \begin{bmatrix} -l_{m,1} & 1& \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ -l_{m,n_m-1} & 0 & \cdots & 1 \\ -l_{m,n_m} & 0 & \ldots & 0 \\ \end{bmatrix}_{n_m\times n_m} \end{aligned}$$

$L_m=[l_{m,1},\dots ,l_{m,n_m}]_{n_m\times 1}^\mathrm{T}$, $B_{m,j}=[\underbrace{0,\dots ,1}_{j},\dots ,0]_{n_m\times 1}^\mathrm{T}$, $d_m=[d_{m,1}(t), \dots , d_{m,n_m-1}(t), d_{m,n_m}(t)+h_m(v_m)]_{n_m\times 1}^\mathrm{T}$, $G_m=[1,\dots ,0]_{1\times n_m}$.

Some assumptions are made throughout this paper.

Assumption 1

For $\forall \imath _1, \imath _2$, there exists a positive constant $k_{m,j}$ such that the nonlinear function $f_{m,j}(\cdot )$ satisfies the following inequality

$$\begin{aligned} \begin{aligned} | f_{m,j}(\imath _1)-f_{m,j}(\imath _2)|&\le k_{m,j}| \imath _1-\imath _2|. \end{aligned} \end{aligned}$$

(5)

Assumption 2

The reference tracking signal $y_{m,d}(t)$, $\dot{y}_{m,d}(t)$ and $\ddot{y}_{m,d}(t)$ are bounded and continuous.

Lemma 1

[39] For $\forall (\ell _1, \ell _2)\in \mathbb {R}^2$, the following inequality can be obtained

$$\begin{aligned} \begin{aligned} \ell _1\ell _2\le \frac{\hbar ^p}{p}|\ell _1|^p+\frac{1}{q\hbar ^q}|\ell _2|^q, \end{aligned} \end{aligned}$$

where $\hbar >0$ and $1/p+1/q=1$ with $q>1$ and $p>1$.

2.2 Neural network

Due to the universal approximation property of RBF-NNs, it can be utilized to approximate the unknown nonlinearities [33]. As a consequence, for a continuous function $F_{nn}(\wp )$ over a compact set $\Omega _{\wp }\subset \mathbb {R}^q$, the NNs $W^{*\mathrm{T}}\varphi (\wp )$ can approximate it to a desired accuracy $\xi ^*>0$, which is expressed as

$$\begin{aligned} \begin{aligned} F_{nn}(\wp )=W^{*\mathrm{T}}\varphi (\wp )+\xi (\wp ), |\xi (\wp )|\le \xi ^* \end{aligned} \end{aligned}$$

where $W^*$ denotes the ideal constant weight vector and it is defined as $W^*=\arg \min _{W\in \mathbb {R}^i}[\sup _{\wp \in \Omega _\wp }|F_{nn}(\wp )-W^\mathrm{T}\varphi (\wp )|]$, $\wp \in \Omega _\wp$ is the input vector, $W=[W_1, \dots , W_i]^\mathrm{T}\in \mathbb {R}^i$ represents the ideal weight vector with the number of neural nodes $i>1$, and $\varphi (\wp )=[\varphi _1(\wp ),\dots ,\varphi _i(\wp )]^\mathrm{T}$ denotes the basis function vector with $\varphi _q(\wp )$ being chosen as the Gaussian function, which has the following form

$$\begin{aligned} \varphi _q(\wp )=\exp [\frac{\Vert \ \wp -\underline{\mu }_q\Vert ^2}{\bar{\sigma }_q^2}],~q=1,\dots ,i \end{aligned}$$

where $\underline{\mu }_q=[\underline{\mu }_{q1},\underline{\mu }_{i2}, \cdots ,\underline{\mu }_{il}]^\mathrm{T}$ and $\bar{\sigma }_q$ represent the center of the receptive field and the width of Gaussian function, respectively. Furthermore, it is worth noting that the Gaussian function satisfies $\varphi _{m,j}^\mathrm{T}(\cdot )\varphi _{m,j}(\cdot )\le \zeta _m$ with a positive constant $\zeta _m$.

3 Neural network observer

Due to the fact that only the system output is directly obtained, it is necessary to design an observer to estimate the unmeasurable state $x_{m,j},~i=1,\dots ,m, j=2,\dots , n_m$.

By utilizing the RBF-NNs, the following approximation result can be obtained

$$\begin{aligned} \begin{aligned} \hat{f}_{m,j}(\hat{X}|W_{m,j})=W_{m,j}^\mathrm{T}\varphi _{m,j}(\hat{X}), \end{aligned} \end{aligned}$$

(6)

where $\hat{X}$ and $W_{m,j}$ are the estimations of X and $W_{m,j}^*$. And $W_{m,j}^*$ is expressed as

$$\begin{aligned} \begin{aligned} W_{m,j}^*=\arg \min _{W_{m,j}\in \Omega _{m,j}}[\sup _{\hat{X}\in \hat{U}_{m,j}}|\hat{f}_{m,j}(\hat{X}|W_{m,j})-f_{m,j}(\hat{X})|], \end{aligned} \end{aligned}$$

where $\Omega _{m,j}$ and $\hat{U}_{m,j}$ represent compact regions of $W_{m,j}$, X and $\hat{X}$.

Similar to [17], we can design the following NN state observer

$$\begin{aligned} \left\{ \begin{aligned} \dot{\hat{x}}_m(t)\,=\,&A_m\hat{x}_m(t)+L_my_m+B_{m,n_m}\hat{c}_mv_m\\&+\sum _{j=1}^{n_m}B_{m,j}\hat{f}_{m,j}(\hat{X}|W_{m,j}),\\ \hat{y}_m(t)\,=\,&G_m\hat{x}_m(t),\\ \end{aligned} \right. \end{aligned}$$

(7)

where $c_m$ is estimated by $\hat{c}_m$.

The coefficient vector $L_m$ is selected, such that $A_m$ is Hurwitz. And then, for a given $Q_m$ with $Q_m=Q_m^\mathrm{T}>0$, there exists a positive definite matrix $P>0$ satisfying $A_m^\mathrm{T}P_m+P_m A_m=-Q_m$.

The observation error is defined as

$$\begin{aligned} \begin{aligned} \tilde{x}_m=x_m-\hat{x}_m \end{aligned} \end{aligned}$$

(8)

satisfies

$$\begin{aligned} \begin{aligned} \dot{\tilde{x}}_m(t)\,=\,&A_m\tilde{x}_m+\sum _{j=1}^{n_m} B_{m,j}\tilde{W}_{m,j}^\mathrm{T}\varphi _{m,j}(\hat{X})\\&+B_{m,n_m}\tilde{c}v_m+\xi _m+d_m+\triangle F_m, \end{aligned} \end{aligned}$$

(9)

where $\tilde{W}_{m,j}=W_{m,j}^*-W_{m,j}$, $\xi _m=[\xi _{m,1},\dots , \xi _{m,n_m}]^\mathrm{T}$, $\triangle F_m=[\triangle f_{m,1}, \dots , \triangle f_{m,n_m}]^\mathrm{T}$, $\triangle f_{m,j}= f_{m,j}(X)- f_{m,j}(\hat{X})$ and $\tilde{c}=c_m-\hat{c}_m$.

Consider the Lyapunov candidate as

$$\begin{aligned} \begin{aligned} V_{m,0}=\tilde{x}_m^\mathrm{T}P_m\tilde{x}_m. \end{aligned} \end{aligned}$$

(10)

Taking the time derivative of $V_{m,0}$ yields

$$\begin{aligned} \begin{aligned} \dot{V}_{m,0}\,=\,&-\tilde{x}_m^\mathrm{T}Q_m\tilde{x}_m+2\tilde{x}_m^\mathrm{T} P_m\sum _{j=1}^{n_m}B_{m,j}\tilde{W}_{m,j}\varphi _{m,j}(\hat{X})\\&+2\tilde{x}_m^\mathrm{T}P_m(\xi _m+\triangle F_m+d_m+B_{m,n_m}\tilde{c}v_m). \end{aligned} \end{aligned}$$

(11)

From Lemma 1, Assumption 2 and $\varphi _{m,j}^\mathrm{T}(\hat{X})\varphi _{m,j}(\hat{X})\le \zeta _m$, one gets

$$\begin{aligned}&2\tilde{x}_m^\mathrm{T}P_m\sum _{j=1}^{n_m}B_{m,j} \tilde{W}_{m,j}^\mathrm{T}\varphi _{m,j}(\hat{X})\\&\le \zeta _m\Vert P_m\Vert ^2\sum _{j=1}^{n_m}\tilde{W}_{m,j}^\mathrm{T}\tilde{W}_{m,j} +\Vert \tilde{x}_m\Vert ^2, \end{aligned}$$

(12)

$$\begin{aligned} &2\tilde{x}_m^\mathrm{T}P_m(\xi _m+d_m+\triangle F_m)\\&\le \Vert P_m\Vert ^2(\Vert \xi _m^*\Vert ^2+\Vert d_m^*\Vert ^2)+\left(\sum _{j=1}^{n_m}k_{m,j}^2+3\right)\Vert \tilde{x}_m\Vert ^2 \end{aligned}$$

(13)

where $\xi _m^*=[\xi _{m,1}^*,\dots ,\xi _{m,n_m}^*]^\mathrm{T}$, $d_m^*=[d_{m,1}^*,\dots ,d_{m,n_m}^*]^\mathrm{T}$.

Substituting (12) and (13) into (11), it produces

$$\begin{aligned} \dot{V}_{m,0}\le&-\tilde{x}_m^\mathrm{T}Q\tilde{x}_m+(\Vert P_m\Vert ^2\sum _{j=1}^{n_m} k_{m,j}^2+4)\Vert \tilde{x}_m\Vert ^2\\&+\Vert P_m\Vert ^2(\Vert \xi _m^*\Vert ^2+\Vert d_m^*\Vert ^2)+2\tilde{x}_m^\mathrm{T}P_m\\&\cdot B_{m,n_m}\tilde{c}_mv_m +\zeta _m\Vert P_m\Vert ^2\sum _{j=1}^{n_m}\tilde{W}_{m,j}^\mathrm{T}\tilde{W}_{m,j}\\ \le&-q_{m,0}\Vert \tilde{x}_m\Vert ^2 +2\tilde{x}_m^\mathrm{T}P_mB_{m,n_m}\tilde{c}_mv_m\\ &+\zeta _m\Vert P_m\Vert ^2\sum _{j=1}^{n_m}\tilde{W}_{m,j}^\mathrm{T}\tilde{W}_{m,j}+M_{m,0}, \end{aligned}$$

(14)

where $q_0=\lambda _{\min }(Q)-4-\Vert P_m\Vert ^2\sum _{j=1}^{n_m}k_{m,j}^2$, $M_{m,0}=\Vert P_m\Vert ^2\Vert d_m^*\Vert ^2+\Vert P_m\Vert ^2\Vert \xi _{i}^*\Vert ^2$.

4 Main results

In this section, the design procedure of backstepping controller will be presented, which contains the developed control strategy in four parts: the prescribed performance function and the nonlinear gain function with their properties are given, and the nonlinear gain-based adaptive NN controller is proposed by using the backstepping technique. And then, the design is augmented with a first-order filter and an adaptive function to solve the complexity explosion and the hysteresis input.

4.1 Prescribed performance

Define the following smooth monotone decreasing function

$$\begin{aligned} \mu _{m,1}(t)=(\mu _{0,m,1}-\mu _{\infty ,m,1})e^{-a_{m,1}t}+\mu _{\infty ,m,1}, \end{aligned}$$

(15)

where $\mu _{0,m,1}$ is the initial condition of $\mu _{m,1}(t)$, $\mu _{\infty ,m,1}$ is the ultimate value of $\mu _{m,1}(t)$ and $a_{m,1}$ is a positive constant. Furthermore, it is simple to obtain that $\lim _{t\rightarrow \infty }\mu _{m,1}(t)\rightarrow \mu _{\infty ,m,1}$. The prescribed steady-state and transient bounds can be defined by utilizing the following constraint conditions

$$\begin{aligned}-\lambda _{m,1}\mu _{m,1}(t)<e_{i}<\mu _{m,1}(t),~~~~\text {if}~~e_m(0)\ge 0 \end{aligned}$$

(16)

or

$$\begin{aligned} -\mu _{m,1}(t)<e_{i}<\lambda _{m,1}\mu _{m,1}(t),~~~~\text {if}~~e_m(0)<0\end{aligned}$$

(17)

where $0<\lambda _{m,1}\le 1$ and $e_m(t)$ means the tacking error.

Furthermore, the error transformation function is selected as

$$\begin{aligned} \digamma _{m,1}(t)\,=\,&\frac{e_m}{\phi _{m,1}(t)},\\ \phi _{m,1}(t)\,=\,&\iota \bar{\phi }_{m,1}(t)+(1-\iota )\underline{\phi }_{m,1}(t), \end{aligned}$$

(18)

where $\iota =1$, if $e_{i}\ge 0$ and 0 otherwise. $\bar{\phi }_{m,1}(t)$ and $\underline{\phi }_{m,1}(t)$ are chosen as: if $e_m(0)\ge 0$, $\bar{\phi }_{m,1}(t)=\mu _{m,1}(t)$, $\underline{\phi }_{m,1}(t)=-\lambda _{m,1}\mu _{m,1}(t)$, or else $\bar{\phi }_{m,1}(t)=\lambda _{m,1}\mu _{m,1}(t)$, $\underline{\phi }_{m,1}(t)=-\mu _{m,1}(t)$.

Lemma 2

[40] The introduced $\digamma _{m,j}$ satisfies $0<\digamma _{m,j}(t)<1$ is true if only if $\mu _{0,m,j}$, $\mu _{\infty ,m,j}$, $a_{m,j}$ and $\lambda _{m,j}$ satisfying (16) and (17).

4.2 Nonlinear gain function

Design a smooth nonlinear gain function, which can be described as

$$\begin{aligned} \Gamma (\imath )=\left\{ \begin{aligned}&\imath , |\imath |\le \nu \\&[\log _o(1-\ln o\cdot \nu + \ln o\cdot |\imath |)+\nu ]\text {sign}(\imath ), |\imath |>\nu \end{aligned} \right. \end{aligned}$$

(19)

where $\nu >0$ and $o>1$. $\nu$ means the joint point between the linear and nonlinear gain term in (19). If the variable $\imath$ is small $(|\imath |<\nu )$, $\Gamma (\imath )$ utilizes the linear part to realize the stable regulation. If the variable $\imath$ is large $(|\imath |>\nu )$, $\Gamma (\imath )$ takes nonlinear gain part to reject aggressive input. Moreover, o represents the damped coefficient. It is noteworthy that the slope can be changed by tuning o.

The properties of the nonlinear gain function (19) can be listed as follows

Property 1

The nonlinear gain function $\Gamma (\imath )$ is continuously differentiable monotonically increasing and its derivative along with $\imath$ satisfies

$$\begin{aligned} \Gamma _d(\imath )=\left\{ \begin{aligned}&1, |\imath |\le \nu \\&[(1-\ln o\cdot \nu +\ln o\cdot |\imath |)^{-1}],|\imath |<\nu \end{aligned} \right. \end{aligned}$$

(20)

Property 2

Let $\Gamma _f(\imath )=\Gamma _d(\imath )\cdot \imath +\Gamma (\imath )$, then $\Gamma _f(\imath )$ is a monotone increasing function. Furthermore, $\Gamma _f(\imath )\cdot \imath \ge \Gamma (\imath )\cdot \imath$ can be guaranteed.

Property 3

Define $\Gamma _h(\imath )=\frac{\Gamma _f(\imath )}{\imath }$, it is known that $\Gamma _h(\imath )>0$ is true for any $\imath \ne 0$. Let $\Gamma _h^+$ as

$$\begin{aligned} \Gamma _h^+(\imath )=\left\{ \begin{aligned}&\frac{\Gamma _d(\imath )}{\imath }, \imath \ne 0\\&2,\imath =0 \end{aligned} \right. \end{aligned}$$

(21)

As a result, if $\imath \ne 0$, $\Gamma _f(\imath )/\Gamma _h^+(\imath )=\imath$, and if $\imath =0$, $\Gamma _f(\imath )/\Gamma _h^+(\imath )=\Gamma _f(\imath )/2=\imath$.

To demonstrate the properties and the advantages of nonlinear function $\Gamma _f(\imath )$, the difference between linear feedback and nonlinear feedback has been given in Fig. 1. It is shown that when the error variable $\imath$ is small, $\Gamma _f(\imath )$ gives a big control gain, which ensures the closed-loop system has a faster transient response; when the error variable $\imath$ is large, $\Gamma _f(\imath )$ gives a small control gain and the nonlinear system can avoid the neglected effects of system disturbances. Nevertheless, the linear feedback only gives a linear control gain, which will generate the closed-loop system does not have a good dynamic performance.

Fig. 1

Trajectories of linear feedback and nonlinear gain feedback

Remark 2

By using the characteristic of small tracking error versus large control gain and large tracking error versus small control gain, the controller proposed in this article is more suitable for actual engineering applications. However, although nonlinear gain feedback has better dynamic performance than linear feedback, nonlinear gain feedback will produce composite functions, which will further create difficulties in the stability analysis compared with the stability analysis using general quadratic Lyapunov function.

Remark 3

If traditional Lyapunov function in quadratic form is utilized, the system stability can not be obtained. Thus, by employing the Property 1 and Property 2, a new Lyapunov function is proposed in the backstepping design procedure, in which $\Gamma (\imath )\imath$ is contained in the designed Lyapunov function. In addition, it should be noticed that $\Gamma (\imath )\imath$ derivatives with respect to time t yields its derivative $\Gamma _f(\imath )\dot{\imath }$. It will further facilitate the stability analysis.

4.3 Controller design

Define the change of coordinates as follows

$$\begin{aligned} \begin{aligned} e_{m}\,=\,&x_{m,1}-y_{m,d}, ~\digamma _{m,1}=\frac{e_1}{\phi _{m,1}},\\ s_{m,1}\,=\,&\frac{\digamma _{m,1}}{1-\digamma _{m,1}}, ~s_{m,j}=\hat{x}_{m,j}-\gamma _{m,j},\\ \varsigma _{m,j}\,=\,&\gamma _{m,j}-\alpha _{m,j-1}, \end{aligned} \end{aligned}$$

(22)

where $\alpha _{m,j-1}$ represents the virtual controller, $\gamma _{m,j}$ is the filter signal and $\varsigma _{m,j}$ means the output error surface with $j=2,\dots ,n_m$.

Step m, 1: According to (22), it yields

$$\begin{aligned} \begin{aligned} \dot{s}_{m,1}\,=\,&\frac{\dot{x}_{m,1}-\dot{y}_{m,d}-\digamma _{m,1} \dot{\phi }_{m,1}}{(1-\digamma _{m,1})^2\phi _{m,1}}\\ \,=\,&\frac{1}{(1-\digamma _{m,1})^2\phi _{m,1}}(x_{m,2}+f_{m,1}(x_m)\\&-\dot{y}_{m,d}+d_{m,1}-\digamma _{m,1}\dot{\phi }_{m,1})\\ \,=\,&\frac{1}{(1-\digamma _{m,1})^2\phi _{m,1}}(s_{m,2}+\varsigma _{m,2}+\alpha _{m,1}\\&+W_{m,1}^\mathrm{T}\varphi (\hat{x}_{m,1}) +W_{m,1}^{*\mathrm{T}}\varphi _{m,1}(\hat{x}_m))\\ &-W_{m,1}^{*\mathrm{T}}\varphi _{m,1} (\hat{x}_{m,1})+\tilde{W}_{m,1}^\mathrm{T}\varphi _{m,1}(\hat{x}_{m,1})\\&+\tilde{x}_{m,2}-\dot{y}_{m,d}+\xi _{m,1}+d_{m,1}- \digamma _{m,1}\dot{\phi }_{m,1}). \end{aligned} \end{aligned}$$

(23)

Consider a Lyapunov function as

$$\begin{aligned} \begin{aligned} V_{m,1}=V_{m,0}+\Gamma (s_{m,1})s_{m,1} +\frac{1}{2\delta _{m,1}}\tilde{W}_{m,1}^\mathrm{T}\tilde{W}_{m,1}, \end{aligned} \end{aligned}$$

(24)

where $\delta _{m,1}>0$ is the designed parameter.

The derivative of $V_{m,1}$ along with (24) yields

$$\begin{aligned} \begin{aligned} \dot{V}_{m,1}\,=\,&\dot{V}_{m,0}+\Gamma _f(s_{m,1})\dot{s}_{m,1} -\frac{1}{\delta _{m,1}}\tilde{W}_{m,1}^\mathrm{T}\dot{W}_{m,1}\\ \,=\,&\dot{V}_{m,0}+\frac{\Gamma _f(s_{m,1})}{(1-\digamma _{m,1})^2 \phi _{m,1}}(s_{m,2}+\varsigma _{m,2}\\ &+\alpha _{m,1} +W_{m,1}^\mathrm{T}\varphi (\hat{x}_{m,1})+W_{m,1}^{*\mathrm{T}} \varphi _{m,1}(\hat{x}_m)\\ &+\tilde{W}_{m,1}^\mathrm{T}\varphi _{m,1}(\hat{x}_{m,1}) -W_{m,1}^{*\mathrm{T}}\varphi _{m,1}(\hat{x}_{m,1})\\&-\dot{y}_{m,d}+\tilde{x}_{m,2} +\xi _{m,1}+d_{m,1}-\digamma _{m,1}\dot{\phi }_{m,1})\\&-\frac{1}{\delta _{m,1}}\tilde{W}_{m,1}^\mathrm{T}\dot{W}_{m,1}. \end{aligned} \end{aligned}$$

(25)

Based on Lemma 1, one gets

$$\begin{aligned} & \begin{aligned}&\frac{\Gamma _f(s_{m,1})}{(1-\digamma _{m,1})^2\phi _{m,1}}(\tilde{x}_{m,2} +\xi _{m,1}+d_{m,1})\\&\le \frac{3\Gamma _f^2(s_{m,1})}{2(1-\digamma _{m,1})^4\phi _{m,1}^2} +\frac{1}{2}\Vert \tilde{x}_m\Vert ^2+\frac{1}{2}\Vert \xi _m^*\Vert ^2+\frac{1}{2}\Vert d_m^*\Vert ^2, \end{aligned} \end{aligned}$$

(26)

$$\begin{aligned} & \begin{aligned}&\frac{\Gamma _f(s_{m,1})}{(1-\digamma _{m,1})^2\phi _{m,1}}\varsigma _{m,2} \le \frac{\Gamma _f^2(s_{m,1})}{2(1-\digamma _{m,1})^4\phi _{m,1}^2} +\frac{1}{2}\varsigma _{m,2}^2, \end{aligned} \end{aligned}$$

(27)

$$\begin{aligned} & \begin{aligned}&\frac{\Gamma _f(s_{m,1})}{(1-\digamma _{m,1})^2\phi _{m,1}}(W_{m,1}^{*\mathrm{T}} \varphi _{m,1}(\hat{x}_m) -W_{m,1}^{*\mathrm{T}}\varphi _{m,1}(\hat{x}_{m,1}))\\&\le \frac{\tau \Gamma _f^2(s_{m,1})}{2(1-\digamma _{m,1})^4\phi _{m,1}^2} +\frac{2\zeta _m}{\tau }\Vert W_{m,1}^*\Vert ^2, \end{aligned} \end{aligned}$$

(28)

where $\tau >0$ is a constant.

Select the intermediate controller $\alpha _{m,1}$, and adaptive updating law $\dot{W}_{m,1}$ as

$$\begin{aligned} \alpha _{m,1}=\, & -\epsilon _{m,1}\left(\Gamma _f(s_{m,1})\phi _{m,1}+\frac{(1-\digamma _{m,1})^2 \phi _{m,1}s_{m,1}}{m_{m,1}}\right)\nonumber \\ & +\digamma _{m,1}\dot{\phi }_{m,1} -(2+\frac{\tau }{2})\frac{\Gamma _f(s_{m,1})}{(1-\digamma _{m,1})^4\phi _{m,1}^2}\nonumber \\ & -W_{m,1}^\mathrm{T}\varphi (\hat{x}_{m,1})+\dot{y}_{m,d},\end{aligned}$$

(29)

$$\begin{aligned} \dot{W}_{m,1}=\, & \delta _{m,1}\frac{\Gamma _f(s_{m,1})\varphi _{m,1}(\hat{x}_{m,1})}{(1-\digamma _{m,1})^2\phi _{m,1}}-\sigma _{m,1}W_{m,1}, \end{aligned}$$

(30)

where $m_{m,1}$, $\epsilon _{m,1}$ and $\sigma _{m,1}0$ are positive design parameters.

Invoking (29), (30), we can deduce

$$\begin{aligned} \begin{aligned} \dot{V}_{m,1}\le&-q_{m,1}\Vert \tilde{x}_m\Vert ^2 +\zeta _m\Vert P_m\Vert ^2\sum _{j=1}^{n_m}\tilde{W}_{m,j}^\mathrm{T}\tilde{W}_{m,j}\\&-\epsilon _{m,1}(\frac{\Gamma _f^2(s_{m,1})}{(1-\digamma _{m,1})^2}+ \frac{s_{m,1}}{m_{m,1}}\Gamma _f(s_{m,1}))\\ &+M_{m,1}+\frac{1}{2}\varsigma _{m,2}^2 +\frac{\Gamma _f(s_{m,1})s_{m,2}}{(1-\digamma _{m,1})^2\phi _{m,1}}\\&+\frac{\sigma _{m,1}}{\delta _{m,1}}\tilde{W}_{m,1}^\mathrm{T}W_{m,1}, \end{aligned} \end{aligned}$$

(31)

where $q_{m,1}=q_{m,0}-\frac{1}{2}$, $M_{m,1}=M_{m,0}+\frac{1}{2}\Vert \xi _m^*\Vert ^2+\frac{1}{2}\Vert d_m^*\Vert ^2+\frac{2\zeta _m}{\tau }\Vert W_{m,1}^*\Vert ^2$.

The following filter is constructed

$$\begin{aligned} \begin{aligned} \varpi _{m,2}\dot{\gamma }_{m,2}+\gamma _{m,2}=\alpha _{m,1}, ~~\gamma _{m,2}(0)=\alpha _{m,1}(0). \end{aligned} \end{aligned}$$

(32)

According to (32), it is easy to know $\dot{\gamma }_{m,2}=-\frac{\varsigma _{m,2}}{\varpi _{m,2}}$, which implies

$$\begin{aligned} \begin{aligned} \dot{\varsigma }_{m,2}=\dot{\gamma }_{m,2}-\dot{\alpha }_{m,1}= \frac{\varsigma _{m,2}}{\varpi _{m,2}}+Y_{m,2}(\cdot ). \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} Y_{m,2}(\cdot )\,=\,&\frac{d(c_{m,1}(\Gamma _f(s_{m,1})+\frac{(1-\xi _{m,1})^2 \phi _{m,1}s_{m,1}}{m_{m,1}})}{\mathrm{d}t}\\ &+\frac{d(\frac{\Gamma _f(s_{m,1})}{(1-\xi _{m,1})^4\phi _{m,1}^2})}{\mathrm{d}t} -\frac{d(\xi _{m,1}\dot{\phi }_{m,1})}{\mathrm{d}t}\\ &+\dot{W}_{m,1}^\mathrm{T} \varphi _{m,1}(\hat{x}_{m,1}) +W_{m,1}^\mathrm{T}\dot{\varphi }_{m,1}(\hat{x}_{m,1})-\ddot{y}_{m,d} \end{aligned} \end{aligned}$$

is continuous function with a maximum value.

Remark 4

The first-order filter is proposed in (32) to address the repetitive derivation problem of the virtual control signal, which can alleviate the additional computation burden. However, it should be noticed that the developed first-order linear filter inevitably generates the filtering error.

Step m, 2: According to (1) and (22), $\dot{s}_{m,2}$ can be calculated as

$$\begin{aligned} \begin{aligned} \dot{s}_{m,2}\,=\,&\dot{\hat{x}}_{m,2}-\dot{\gamma }_{m,2}\\ \,=\,&s_{m,3}+\varsigma _{m,3}+\alpha _{m,2}+l_{m,2}\tilde{x}_{m,1}\\&+W_{m,2}^{\mathrm{T}}\varphi _{m,2}(\hat{\bar{x}}_m)+W_{m,2}^{*\mathrm{T}}\varphi _{m,2}(\hat{x}_m)\\&-W_{m,2}^{*\mathrm{T}}\varphi _{m,2}(\hat{\bar{x}}_{m,2})-\tilde{W}_{m,2}^\mathrm{T}\varphi _{m,2}(\hat{x}_m)\\&+\tilde{W}_{m,2}^\mathrm{T}\varphi _{m,2}(\hat{\bar{x}}_{m,2})-\dot{\gamma }_{m,2}. \end{aligned} \end{aligned}$$

(33)

Chose a Lyapunov function as

$$\begin{aligned} \begin{aligned} V_{m,2}\,=\,&V_{m,1}+\Gamma (s_{m,2})s_{m,2}\\&+\frac{1}{2}\varsigma _{m,2}^2+\frac{1}{2\delta _{m,2}} \tilde{W}_{m,2}^\mathrm{T}\tilde{W}_{m,2}, \end{aligned} \end{aligned}$$

(34)

where $\delta _{m,2}>0$ is the designed parameters.

By Lemma 2, (33) and (34), the time differentiation of $V_{m,2}$ can deduced as

$$\begin{aligned} \begin{aligned} \dot{V}_{m,2}\,=\,&\dot{V}_{m,1}+\Gamma _f(s_{m,2})\dot{s}_{m,2} +\varsigma _{m,2}\dot{\varsigma }_{m,2}\\&-\frac{1}{\delta _{m,2}}\tilde{W}_{m,2}^\mathrm{T}\dot{W}_{m,2}\\ \le&-q_{m,1}\Vert \tilde{x}_m\Vert ^2 +\zeta _m\Vert P_m\Vert ^2\sum _{j=1}^{n_m}\tilde{W}_{m,j}^\mathrm{T}\tilde{W}_{m,j}\\&-\epsilon _{m,1}(\Gamma _f^2(s_{m,1})+\frac{s_{m,1}}{m_{m,1}}\Gamma _f(s_{m,1}))\\&+\frac{1}{2}\varsigma _{m,2}^2+M_{m,1} +\frac{\Gamma _f(s_{m,1})s_{m,2}}{(1-\digamma _{m,1})^2\phi _{m,1}}\\&+\frac{\sigma _{m,1}}{\delta _{m,1}}\tilde{W}_{m,1}^\mathrm{T}W_{m,1} +\Gamma _f(s_{m,2})(s_{m,3}+\varsigma _{m,3}\\&+\alpha _{m,2}+l_{m,2}\tilde{x}_{m,1}+W_{m,2}^{\mathrm{T}}\varphi _{m,2}(\hat{\bar{x}}_m)\\&+W_{m,2}^{*\mathrm{T}}\varphi _{m,2}(\hat{x}_m)-W_{m,2}^{*\mathrm{T}} \varphi _{m,2}(\hat{\bar{x}}_{m,2})\\&-\tilde{W}_{m,2}^\mathrm{T}\varphi _{m,2}(\hat{x}_m) +\tilde{W}_{m,2}^\mathrm{T}\varphi _{m,2}(\hat{\bar{x}}_{m,2})\\&-\dot{\gamma }_{m,2})+\varsigma _{m,2}\dot{\varsigma }_{m,2} -\frac{1}{\delta _{m,2}}\tilde{W}_{m,2}^\mathrm{T}\dot{W}_{m,2}.\\ \end{aligned} \end{aligned}$$

(35)

According to Lemma 1, Assumptions 2 and 1, one has

$$\begin{aligned} & \begin{aligned}&\Gamma _f(s_{m,2})\varsigma _{m,3} \le \frac{1}{2}\Gamma _f^2(s_{m,2}) +\frac{1}{2}\varsigma _{m,3}^2, \end{aligned} \end{aligned}$$

(36)

$$\begin{aligned} & \begin{aligned}&-\Gamma _f(s_{m,2})W_{m,2}^{\mathrm{T}}\varphi _{m,2}(\hat{x}_m)\\&\le \frac{1}{2}\Gamma _f^2(s_{m,2})+\frac{\zeta _m}{2}\tilde{W}_{m,2}^{\mathrm{T}}\tilde{W}_{m,2}, \end{aligned} \end{aligned}$$

(37)

$$\begin{aligned} & \begin{aligned}&\Gamma _f(s_{m,2})(W_{m,2}^{*\mathrm{T}}\varphi _{m,2}(\hat{x}_m) -W_{m,2}^{*\mathrm{T}}\varphi _{m,2}(\hat{\bar{x}}_{m,2}))\\&\le \frac{\tau }{2}\Gamma _f^2(s_{m,2})+\frac{2\zeta _m}{\tau }\Vert W_{m,2}^*\Vert ^2. \end{aligned} \end{aligned}$$

(38)

The intermediate control signal $\alpha _{m,2}$ and the adaptive updating function $\dot{W}_{m,2}$ are designed as

$$\begin{aligned} \alpha _{m,2}=\, & -\epsilon _{m,2}\left(\Gamma _f(s_{m,2})+\frac{s_{m,2}}{m_{m,2}}\right)\nonumber \\ & -(1+\frac{\tau }{2})\Gamma _f(s_{m,2})+\dot{\gamma }_{m,2}\nonumber \\ & -l_{m,2}\tilde{x}_{m,1}-W_{m,2}^\mathrm{T}\varphi _{m,2}(\hat{\bar{x}}_{m,2})\nonumber \\ & -\frac{\Gamma _f(s_{m,1})}{(1-\digamma _{m,1})^2\phi _{m,1}\Gamma _h^+(s_{m,2})},\end{aligned}$$

(39)

$$\begin{aligned} & \dot{W}_{m,2}=\delta _{m,2}\Gamma _f(s_{m,2})\varphi _{m,2}(\hat{\bar{x}}_{m,2})-\sigma _{m,2}W_{m,2}, \end{aligned}$$

(40)

where $m_{m,2}$, $\epsilon _{m,2}$ and $\sigma _{m,2}$ are positive design parameters.

It follows from (34)–(40), one has

$$\begin{aligned} \begin{aligned} \dot{V}_{m,2}\le&-q_{m,1}\Vert \tilde{x}_m\Vert ^2 +\zeta _m\Vert P_m\Vert ^2\sum _{j=1}^{n_m}\tilde{W}_{m,j}^\mathrm{T}\tilde{W}_{m,j}\\&-\sum _{k=1}^{2} c_{m,k}(\Gamma _f^2(s_{m,k})+\frac{s_{m,k}}{m_{m,k}}\Gamma _f(s_{m,k}))\\&+\sum _{k=1}^{2}\frac{\sigma _{m,k}}{\delta _{m,k}}\tilde{W}_{m,k}^\mathrm{T}W_{m,k} +\frac{\zeta _m}{2}\tilde{W}_{m,2}^\mathrm{T}\tilde{W}_{m,2}\\&+\sum _{k=1}^{2}\frac{1}{2}\varsigma _{m,k+1}^2 +\Gamma _f(s_{m,2})s_{m,3}+M_{m,2}\\ &+\varsigma _{m,2}(-\frac{\varsigma _{m,2}}{\varpi _{m,2}}+Y_{m,2}(\cdot )), \end{aligned} \end{aligned}$$

(41)

where $M_{m,2}=M_{m,1}+\frac{2\zeta _m}{\tau }\Vert W_{m,2}^*\Vert ^2$

Define the following filter

$$\begin{aligned} \begin{aligned} \varpi _{m,3}\dot{\gamma }_{m,3}+\gamma _{m,3}=\alpha _{m,2}, ~ \gamma _{m,3}(0)=\alpha _{m,2}(0) \end{aligned} \end{aligned}$$

(42)

Defining $\varsigma _{m,3}=\dot{\gamma }_{m,3}-\alpha _{m,2}$, we can obtain $\dot{\gamma }_{m,3}=-\frac{\varsigma _{m,3}}{\varpi _{m,3}}$. Then, one has

$$\begin{aligned} \begin{aligned} \dot{\varsigma }_{m,3}\,=\,&\dot{\gamma }_{m,3}-\dot{\alpha }_{m,2} =-\frac{\varsigma _{m,3}}{\varpi _{m,3}}+Y_{m,3}(\cdot ), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} Y_{m,3}(\cdot )\,=\,&\frac{d(c_{m,2}(\Gamma _f(s_{m,2})+\frac{s_{m,2}}{m_{m,2}}))}{\mathrm{d}t}\\&+\frac{d((1+\frac{\tau }{2})\Gamma _f(s_{m,2}))}{\mathrm{d}t} +l_{m,2}\dot{\tilde{x}}_{m,1}\\ &+\dot{W}_{m,2}^\mathrm{T}\varphi _{m,2}(\hat{\bar{x}}_{m,2}) +W_{m,2}^\mathrm{T}\dot{\varphi }_{m,2}(\hat{\bar{x}}_{m,2})\\&-\frac{\dot{\varsigma }_{m,3}}{\varpi _{m,3}}+\frac{\frac{\mathrm{d}\Gamma _f(s_{m,1})}{\mathrm{d}s_{m,1}} \dot{s}_{m,1}\Gamma _h^+(s_{m,2})}{\Gamma _h^{+2}(s_{m,2})}\\&-\frac{\Gamma _f(s_{m,1})\frac{\mathrm{d}\Gamma _h^+(s_{m,2})}{\mathrm{d}s_{m,2}}\dot{s}_{m,2}}{\Gamma _h^{+2}(s_{m,2})} \end{aligned} \end{aligned}$$

(43)

is a continuous function with a maximum value.

Step m, j ($3\le j\le n_m-1$): By (1) and (22), $\dot{s}_{m,j}$ is calculated as

$$\begin{aligned} \begin{aligned} \dot{s}_{m,j}\,=\,&\dot{\hat{x}}_{m,j}-\dot{\gamma }_{m,j}\\ \,=\,&s_{m,j+1}+\varsigma _{m,j+1}+l_{m,j}\tilde{x}_{m,1}+\alpha _{m,j}\\&-W_{m,j}^{*\mathrm{T}}\varphi _{m,j}(\hat{\bar{x}}_{m,j}) +W_{m,j}^{*\mathrm{T}}\varphi _{m,j}(\hat{x}_m)\\ &-\tilde{W}_{m,j}^\mathrm{T}\varphi _{m,j}(\hat{x}_m) +W_{m,j}^\mathrm{T}\varphi _{m,j}(\hat{\bar{x}}_{m,j})\\&+\tilde{W}_{m,j}^\mathrm{T}\varphi _{m,j}(\hat{\bar{x}}_{m,j})-\dot{\gamma }_{m,j}, \end{aligned} \end{aligned}$$

(44)

where $\hat{\bar{x}}_{m,j}=[\hat{x}_{m,1},\dots ,\hat{x}_{m,j}]^\mathrm{T}$.

Consider the Lyapunov function candidate as

$$\begin{aligned} \begin{aligned} V_{m,j}\,=\,&V_{m,j-1}+\Gamma (s_{m,j})s_{m,j}\\ &+\frac{1}{2}\varsigma _{m,j}^2 +\frac{1}{2\delta _{m,j}}\tilde{W}_{m,j}^\mathrm{T}\tilde{W}_{m,j}, \end{aligned} \end{aligned}$$

(45)

where $\delta _{m,j}>0$ is the designed parameters.

In the same case of step m, 2, the following inequalities hold

$$\begin{aligned} & \begin{aligned}&\Gamma _f(s_{m,j})\varsigma _{m,j+1} \le \frac{1}{2}\Gamma _f^2(s_{m,j}) +\frac{1}{2}\varsigma _{m,j+1}^2, \end{aligned}\end{aligned}$$

(46)

$$\begin{aligned} & \begin{aligned}&-\Gamma _f(s_{m,j})W_{m,j}^{\mathrm{T}}\varphi _{m,j}(\hat{x}_m) \\ &\le \frac{1}{2}\Gamma _f^2(s_{m,j})+\frac{\zeta _m}{2}\tilde{W}_{m,j}^{\mathrm{T}}\tilde{W}_{m,j}, \end{aligned}\end{aligned}$$

(47)

$$\begin{aligned} & \begin{aligned}&\Gamma _f(s_{m,j})(W_{m,j}^{*\mathrm{T}}\varphi _{m,j}(\hat{x}_m) -W_{m,j}^{*\mathrm{T}}\varphi _{m,j}(\hat{\bar{x}}_{m,j}))\\&\le \frac{\tau }{2}\Gamma _f^2(s_{m,j})+\frac{2\zeta _m}{\tau }\Vert W_{m,j}^*\Vert ^2. \end{aligned} \end{aligned}$$

(48)

Select the intermediate controller $\alpha _{m,j}$, and adaptive updating law $\dot{W}_{m,j}$ as

$$\begin{aligned} & \begin{aligned} \alpha _{m,j}\,=\,&-\epsilon _{m,j}(\Gamma _f(s_{m,j})+\frac{s_{m,j}}{m_{m,j}})-l_{m,j}\tilde{x}_{m,1}\\ &-(1+\frac{\tau }{2})\Gamma _f(s_{m,j}) -W_{m,j}^\mathrm{T}\varphi _{m,j}(\hat{\bar{x}}_{m,j})\\ &+\dot{\gamma }_{m,j}-\frac{\Gamma _f(s_{m,j-1})}{\Gamma _h^+(s_{m,j})}, \end{aligned}\end{aligned}$$

(49)

$$\begin{aligned} & \begin{aligned} \dot{W}_{m,j}=\delta _{m,j}\Gamma _f(s_{m,j})\varphi _{m,j}(\hat{\bar{x}}_{m,j})-\sigma _{m,j}W_{m,j}, \end{aligned} \end{aligned}$$

(50)

where $m_{m,j}$, $\epsilon _{m,j}$ and $\sigma _{m,j}$ are positive design parameters.

According to (46)–(50), it procedures

$$\begin{aligned} \begin{aligned} \dot{V}_{m,j}\le&-q_{m,1}\Vert \tilde{x}_m\Vert ^2 +\zeta _m\Vert P_m\Vert ^2\sum _{j=1}^{n_m}\tilde{W}_{m,j}^\mathrm{T}\tilde{W}_{m,j}\\ &-\sum _{k=1}^{j} c_{m,k}(\Gamma _f^2(s_{m,k})+\frac{s_{m,k}}{m_{m,k}}\Gamma _f(s_{m,k}))\\ &+\Gamma _f(s_{m,j})s_{m,j+1} +\sum _{k=1}^{j}\frac{\sigma _{m,k}}{\delta _{m,k}}\tilde{W}_{m,k}^\mathrm{T}W_{m,k}\\ &+\frac{\zeta _m}{2}\sum _{k=2}^{j}\tilde{W}_{m,k}^\mathrm{T}\tilde{W}_{m,k}+\sum _{k=1}^{j}\frac{1}{2}\varsigma _{m,k+1}^2\\ &+M_{m,j}+\sum _{k=2}^{j}\varsigma _{m,k}(-\frac{\varsigma _{m,k}}{\varpi _{m,k}}+Y_{m,k}(\cdot )), \end{aligned} \end{aligned}$$

(51)

where $M_{m,j}=M_{m,j_1-1}+\frac{\zeta _m}{2}\Vert W_{m,j}^*\Vert ^2$.

Define the following filter

$$\begin{aligned} \begin{aligned} \varpi _{m,j+1}\dot{\gamma }_{m,j+1}+\gamma _{m,j+1}=\alpha _{m,j}, ~ \gamma _{m,j+1}(0)=\alpha _{m,j}(0) \end{aligned} \end{aligned}$$

(52)

Defining $\varsigma _{m,j+1}=\dot{\gamma }_{m,j+1}-\alpha _{m,j}$, $\dot{\gamma }_{m,j+1}=-\frac{\varsigma _{m,j+1}}{\varpi _{m,j+1}}$ can be obtained. Then, it easily procedures

$$\begin{aligned} \begin{aligned} \dot{\varsigma }_{m,j+1} =-\frac{\varsigma _{m,j+1}}{\varpi _{m,j+1}}+Y_{m,j+1}(\cdot ), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} Y_{m,j+1}(\cdot )\,=\,&\frac{d(c_{m,j}(\Gamma _f(s_{m,j})+\frac{s_{m,j}}{m_{m,j}}))}{\mathrm{d}t}\\ &+\frac{d((1+\frac{\tau }{2})\Gamma _f(s_{m,j}))}{\mathrm{d}t}\\ &+l_{m,j}\dot{\tilde{x}}_{m,1}+\dot{W}_{m,j}^\mathrm{T}\varphi _{m,j}(\hat{\bar{x}}_{m,j})\\ &+W_{m,j}^\mathrm{T}\dot{\varphi }_{m,j}(\hat{\bar{x}}_{m,j})-\frac{\dot{\varsigma }_{m,j+1}}{\varpi _{m,j+1}}\\ &+\frac{\frac{\mathrm{d}\Gamma _f(s_{m,j-1})}{\mathrm{d}s_{m,j-1}} \dot{s}_{m,j-1}\Gamma _h^+(s_{m,j})}{\Gamma _h^{+2}(s_{m,j})}\\ &-\frac{\Gamma _f(s_{m,j-1})\frac{\mathrm{d}\Gamma _h^+(s_{m,j})}{\mathrm{d}s_{m,j}}\dot{s}_{m,j}}{\Gamma _h^{+2}(s_{m,j})} \end{aligned} \end{aligned}$$

is a continuous function with a maximum value.

Step $m, n_m$: According to (22), we can obtain

$$\begin{aligned} \begin{aligned} \dot{s}_{m,n_m}\,=\,&\dot{\hat{x}}_{m,n_m}-\dot{\gamma }_{m,n_m}\\ \,=\,&l_{m,n_m}\tilde{x}_{m,1}+W_{m,n_m}^\mathrm{T}\varphi _{m,n_m}(\hat{x}_m)\\&+\tilde{W}_{m,n_m}\varphi _{m,n_m}(\hat{x}_m)+u_m\\ &-\tilde{W}_{m,n_m}^\mathrm{T}\varphi _{m,n_m}(\hat{x}_m)-\dot{\gamma }_{m,n_m}. \end{aligned} \end{aligned}$$

(53)

Define the Lyapunov function as

$$\begin{aligned} \begin{aligned} V_{m,n_m}\,=\,&V_{m,n_m-1}+\Gamma (s_{m,n_m})s_{m,n_m}+\frac{1}{2}\varsigma _{m,n_m}^2\\&+\frac{1}{2\varepsilon _m}\tilde{c}_m^2+\frac{1}{2\delta _{m,n_m}}\tilde{W}_{m,n_m}^\mathrm{T}\tilde{W}_{m,n_m}, \end{aligned} \end{aligned}$$

(54)

where $\delta _{m,n_m}$ and $\varepsilon _m$ are positive design parameters.

By using Lemma 1, one has

$$\begin{aligned} & \begin{aligned}&2\tilde{x}_m^\mathrm{T}P_mB_{m,n_m}\tilde{c}_mv_m\\ &\le \frac{1}{\rho _m}\Vert \tilde{x}_m \Vert ^2+\rho _m\tilde{c}_m(c_m-\hat{c}_m)\Vert P_m\Vert ^2v_m^2\\&\le \frac{1}{\rho _m}\Vert \tilde{x}_m\Vert ^2+\frac{\rho _m}{2}\tilde{c}_m^2\Vert P_m\Vert ^2v_m^2\\ &+\frac{\rho _m}{2}c_m^2\Vert P_m\Vert ^2v_m^2-\rho _m\tilde{c}_m\hat{c}_m\Vert P_m\Vert ^2v_m^2, \end{aligned}\end{aligned}$$

(55)

$$\begin{aligned} & \begin{aligned}&-\Gamma _f(s_{m,n_m})W_{m,n_m}^{\mathrm{T}}\varphi _{m,n_m}(\hat{x}_m)\\ &\le \frac{1}{2}\Gamma _f^2(s_{m,n_m})+\frac{\zeta _m}{2}\tilde{W}_{m,n_m}^{\mathrm{T}}\tilde{W}_{m,n_m}, \end{aligned} \end{aligned}$$

(56)

where $\rho _m$ is a positive constant.

Select the following control law and the adaptive laws as

$$\begin{aligned} v_m=\, & -\frac{1}{\hat{c}_m}(\epsilon _{m,n_m}(\Gamma _f(s_{m,n_m})+\frac{s_{m,n_m}}{m_{m,n_m}})\nonumber \\ & -\frac{1}{2}\Gamma _f(s_{m,n_m}) -l_{m,n_m}\tilde{x}_{m,1}+\dot{\gamma }_{m,n_m}\nonumber \\ & -W_{m,n_m}^\mathrm{T}\varphi _{m,n_m}(\hat{\bar{x}}_{m,n_m})-\frac{\Gamma _f(s_{m,n_m-1})}{\Gamma _h^+ (s_{m,n_m})}),\end{aligned}$$

(57)

$$\begin{aligned} \dot{W}_{m,n_m}=\, & \delta _{m,n_m}\Gamma _f(s_{m,n_m})\varphi _{m,n_m}(\hat{x}_m)\nonumber \\ & -\sigma _{m,n_m}W_{m,n_m}, \end{aligned}$$

(58)

$$\begin{aligned} \dot{\hat{c}}_{i}=\, & -\varepsilon _m\rho _m\hat{c}_m\Vert P_m\Vert ^2v_m^2-a_m\hat{c}_m, \end{aligned}$$

(59)

where $m_{m,n_m}$, $c_{m,n_m}$, $a_m$ and $\delta _{m,n_m}$ are positive designed parameters.

By using (55)–(59), one can obtain

$$\begin{aligned} \begin{aligned} \dot{V}_{m,n_m}\le&-q_{m,1}\Vert \tilde{x}_m\Vert ^2 +\zeta _m\Vert P_m\Vert ^2\sum _{j=1}^{n_m}\tilde{W}_{m,j}^\mathrm{T}\tilde{W}_{m,j}\\ &-\sum _{k=1}^{n_m} c_{m,k}(\Gamma _f^2(s_{m,k})+\frac{s_{m,k}}{m_{m,k}}\Gamma _f(s_{m,k}))\\ &+\frac{\zeta _m}{2}\sum _{k=2}^{n_m}\tilde{W}_{m,k}^\mathrm{T}\tilde{W}_{m,k}+\sum _{k=2}^{n_m}\frac{1}{2}\varsigma _{m,k}^2\\ &+\sum _{k=1}^{n_m}\frac{\sigma _{m,k}}{\delta _{m,k}}\tilde{W}_{m,k}^\mathrm{T}W_{m,k} +\frac{\epsilon _m}{\varepsilon _m}\tilde{c}_m\hat{c}_m\\ &+M_{m,n_m}+\sum _{k=2}^{n_m}\varsigma _{m,k}(-\frac{\varsigma _{m,k}}{\varpi _{m,k}}+Y_{m,k}(\cdot )),\\ &\end{aligned} \end{aligned}$$

(60)

where $M_{m,n_m}=M_{m,n_m-1}$.

According to the relationship $\tilde{W}_{m,j}=W_{m,j}^*-W_{m,j}$ and $\tilde{c}_m=c_m-\hat{c}_m$, the following inequality holds

$$\begin{aligned} & \begin{aligned} \sum _{k=1}^{n_m}\frac{\sigma _{m,k}}{\delta _{m,k}}\tilde{W}_{m,k}^\mathrm{T}W_{m,k}\le&-\sum _{k=1}^{n_m}\frac{\sigma _{m,k}}{2\delta _{m,k}}\tilde{W}_{m,k}^\mathrm{T}\tilde{W}_{m,k}\\ &+\sum _{k=1}^{n_m}\frac{\sigma _{m,k}}{2\delta _{m,k}}W_{m,k}^{\mathrm{T}}W_{m,k}, \end{aligned} \end{aligned}$$

(61)

$$\begin{aligned} & \begin{aligned} \frac{\epsilon _m}{\varepsilon _m}\tilde{c}_m\hat{c}_m\le -\frac{\epsilon _m}{\varepsilon _m}\tilde{c}_m^2 +\frac{\epsilon _m}{\varepsilon _m}c_m^{2}, \end{aligned} \end{aligned}$$

(62)

For any constants $\Re >0$ and $\aleph >0$, the set $\Omega _{y_{m,d}}=\{(y_{m,d}, \dot{y}_{m,d}, \ddot{y}_{m,d})^\mathrm{T}:y_{m,d}^2+\dot{y}_{m,d}^2+\ddot{y}_{m,d}\le \Re \}$ and $\Omega _{m,j}:=\{\tilde{x}^\mathrm{T}P\tilde{x}+\sum _{k=1}^{j} \Gamma (s_{m,j})s_{m,j}+\sum _{k=1}^{j}(1/\delta _{m,j}) \tilde{W}_{m,j}^\mathrm{T}\tilde{W}_{m,j}+ \sum _{k=2}^{j}\varsigma _{m,j}^2\le 2\aleph \}$ are compact in $\mathbb {R}^3$ and $\mathbb {R}^{3j}$, respectively. Thus, $\Omega _{y_{m,d}}\times \Omega _{m,j}$ is also compact in $\mathbb {R}^{3\times 3j}$. Therefore, $Y_{m,j}(\cdot )$ has a maximum $\bar{Y}_{m,j}>0$. such that $|Y_{m,j}(\cdot )|\le \bar{Y}_{m,j}$, and the following inequality holds

$$\begin{aligned} \begin{aligned} \sum _{k=2}^{n_m}\varsigma _{m,k}|Y_{m,k(\cdot )}|\le \sum _{k=2}^{n_m}\frac{\bar{Y}_{m,k}^2}{2\tau }\varsigma _{m,k}^2+2\tau . \end{aligned} \end{aligned}$$

(63)

Submitting (61)–(63) into (60), one can obtain

$$\begin{aligned} \begin{aligned} \dot{V}_{m,n_m}\le&-\sum _{k=1}^{n_m} c_{m,k}(\Gamma _f^2(s_{m,k})+\frac{s_{m,k}}{m_{m,k}}\Gamma _f(s_{m,k}))\\ &-\sum _{k=2}^{n_m}\frac{1}{2}(\frac{2}{\varpi _{m,k}}-1-\frac{\bar{Y}_{m,k}}{\tau })\varsigma _{m,k}^2\\ &-\frac{1}{2}(\frac{\sigma _{m,1}}{\delta _{m,1}}-2\Vert P_m\Vert ^2)\tilde{W}_{m,1}^\mathrm{T}\tilde{W}_{m,1}+M_{i}\\ &-\frac{1}{2}\sum _{k=2}^{n_m}(\frac{\sigma _{m,k}}{\gamma _{m,k}}-2\Vert P_m\Vert ^2-1)\tilde{W}_{m,k}^\mathrm{T}\tilde{W}_{m,k}\\ &-(\frac{\epsilon _m}{\varepsilon _m}-\frac{\rho _m}{2}\Vert P_m\Vert ^2v_m^2)\tilde{c}_m^2-q_{m,1}\Vert \tilde{x}_m\Vert ^2, \end{aligned} \end{aligned}$$

(64)

where $M_m=M_{m,n_m}+2\tau +\frac{\epsilon _m}{\varepsilon _m}c_m^{2}$.

Fig. 2

Control diagram

4.4 Stability analysis

Theorem 1

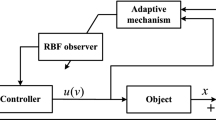
Consider the nonstrict-feedback MIMO systems (1). The actual control input (57) is designed with the NN observer (7) and the adaptive functions (30), (40), (50), (58) and (59), described in Fig. 2 and Algorithm 1. Furthermore, all the closed-loop variables can be adjusted to be bounded and the output of each subsystem can track the reference signals.

Proof: Choose a Lyapunov function $V=\sum _{i=1}^{m}V_m$ and calculate its time differentiation, one gets

$$\begin{aligned} \dot{V}\le&\sum _{i=1}^{m}\left\{ -C_m\sum _{k=1}^{n_m}\Gamma _f(s_{m,k})s_{m,k} -C_m\sum _{k=2}^{n_m}\frac{1}{2}\varsigma _{m,k}^2\right. \\&\left. -C_m\sum _{k=1}^{n_m}\frac{1}{2}\tilde{W}_{m,k}^\mathrm{T}\tilde{W}_{m,k}-C_m \frac{1}{\varepsilon _{i}}\tilde{c}_m^2+M_{i}\right\}, \end{aligned}$$

(65)

where

$$C_{m} = \min \left\{ {\frac{{q_{{m,1}} }}{{\lambda _{{\max }} (P_{m} )}},\frac{2}{{\varpi _{{m,k}} }} - 1 - \frac{{\bar{Y}_{{m,k}} }}{\tau },\frac{{\sigma _{{m,1}} }}{{\delta _{{m,1}} }} - 2\zeta _{m} P_{m} ^{2} ,\frac{{\sigma _{{m,k}} }}{{\gamma _{{m,k}} }} - 2\zeta _{m} P_{m} ^{2} - 1} \right\},\quad \frac{{\epsilon_{{m,k}} }}{{m_{{m,k}} }} \ge C_{m} > 0.$$

(66)

From Property 2, we can obtain the following inequality

$$\begin{aligned} \sum _{k=1}^{n_m}\Gamma (s_{m,k})s_{m,k}\le \sum _{k=1}^{n_m}\Gamma _f(s_{m,k})s_{m,k}, \end{aligned}$$

(67)

it gives

$$\begin{aligned}\dot{V}\le&\sum _{i=1}^{m}\left\{ -C_m\sum _{k=1}^{n_m}\Gamma (s_{m,k})s_{m,k} -C_m\sum _{k=2}^{n_m}\frac{1}{2}\varsigma _{m,k}^2\right. \\&\left. -C_m\sum _{k=1}^{n_m}\frac{1}{2}\tilde{W}_{m,k}^\mathrm{T}\tilde{W}_{m,k}-C_m \frac{1}{\varepsilon _{i}}\tilde{c}_m^2+M_{i}\right\}\\ \le&-CV+M,\end{aligned}$$

(68)

where $C=\min \left\{ C_1,C_2,\dots ,C_{n_m}\right\}$,

$M=\min \left\{ M_1, M_2,\dots ,M_{n_m}\right\}$.

Multiplying (68) by $e^{Ct}$ and integrating it over [0, t], one obtains

$$\begin{aligned} \begin{aligned} 0\le V\le (V(0)-\frac{M}{C})e^{-Ct}+\frac{M}{C}. \end{aligned} \end{aligned}$$

(69)

According to (69), we can learn that the output $y_m$ can track the reference trajectory $y_{m,d}$ with a minimal error. Meanwhile, if $s_{m,1}\le \nu$, $\Gamma (s_{m,1})s_{m,1}=s_{m,1}^2$, if not $\Gamma (s_{m,1})s_{m,1}=[\frac{\log _o(1-\ln o\cdot \nu +\ln o\cdot |s_{m,1}|)}{\ln o}+\nu ]|s_{m,1}|\ge \nu |s_{m,1}|$. Form the definition V, one has $\Gamma (s_{m,1})s_{m,1}\le V$, then, $|s_{m,1}|\le \sqrt{V(0)e^{-Ct}+\frac{M}{C}}$; if $|s_{m,1}|\le \nu$, otherwise, $|s_{m,1}(t)|\le \frac{V(0)e^{-Ct}}{\nu }+\frac{M}{C\nu }$. Finally, $s_{m,1}$ satisfies $|s_{m,1}|\le \max \left \{\frac{V(0)e^{-Ct}}{\nu }+\frac{M}{C\nu }, \min \left \{\sqrt{V(0)e^{-Ct}+\frac{M}{C}}\right\}\right\}$. Since $\lim _{t\rightarrow \infty }e^{-Ct}\rightarrow 0$, the ultimate bound of tracking error $e_m$ is $\lim _{t\rightarrow \infty }|e_m|\le \max \left \{\frac{V(0)e^{-Ct}}{\nu }+\frac{M}{C\nu }\right\}$. Thus, we can easily conclude that the error $e_m$ can be adjusted to arbitrarily small by choosing the appropriate parameters C, M and $\nu$.

Remark 5

For the tracking error, it should be noticed that if the performance function $\mu _{m,1}$ is a continuous function with $0<\mu _{m,1}(0)<1$, $\forall t>0$, $\mu _{m,1}$ satisfies $0<\mu _{m,1}(t)<1$ from Lemma 2. According to $\mu _{m,1}(t)=\frac{e_1}{\phi _{m,1}(t)}$, we can conclude that $|e_m(t)|\le |\phi _{m,1}(t)|$ holds. This further means that the steady-state and transient output tracking error $e_m(t)$ will not violate the predefined range by performance function.

Remark 6

Due to the fact that each subsystem nonlinear function $f_{m,j}(x_m)$ contains the whole states $x_m$, the nonlinear system (1) is said to be in nonstrict-feedback structure, which will increase the difficulty for controller design. In this paper, the approximation ability of RBF-NNs is utilized to estimate the nonlinear function $f_{m,j}(x_m)$. It should be noticed that the whole states $x_m$ appear in the j-th step backstepping design to further generate the algebraic loop problem. To deal with this obstacle, $W_{m,j}^{\mathrm{T}}\varphi _{m,j}(\hat{x}_m)=W_{m,j}^{*\mathrm{T}}\varphi _{m,j}(\hat{x}_m) -W_{m,j}^{*\mathrm{T}}\varphi _{m,j}(\hat{\bar{x}}_{m,j}) +W_{m,j}^\mathrm{T}\varphi _{m,j}(\hat{\bar{x}}_{m,j})+\tilde{W}_{m,j}^\mathrm{T}\varphi _{m,j}(\hat{\bar{x}}_{m,j})$ is transformed in (33). According to this variable separation technique, the algebraic loop problem can be solved.

Remark 7

It is noteworthy that some control approaches have been reported in [6, 29, 41] for nonlinear systems. The primary discrepancies between the results in [6, 29, 41] and our result are summarized as follows: (1) The reported control algorithms in [6, 29, 41] are in the sense of strict-feedback SISO systems. In contrast, we extend the strict-feedback SISO systems to nonstrict-feedback MIMO systems. And the nonlinear-gain based controller developed in our result can be employed to control the SISO systems. (2) It can be seen that the approximation ability of RBF-NNs is used to estimate the unknown packaged functions and the unknown functions in [42], which indicates $2n_m$ adaptive parameters should be online estimated, which will increase the computation burden. In order to save computing resources, we only utilize $n_m$ adaptive parameters to realize the controller design. Therefore, the complexity of computing can be alleviated.

Remark 8

The parameters of the proposed controller are chosen by the characteristics of the considered systems and the stability criteria. It is obvious that all designed parameters should be selected to ensure Theorem 1 holds. We can obtain the selection principles of these parameters and their impacts on the system performance. According to (65), the small error signals $e_m$, $s_{m,j}$ and $\tilde{W}_{m,j}$ may be obtained by choosing the larger $\epsilon _{m,j}$, $\tau$ and $\sigma _{m,j}$. Nevertheless, the larger $\epsilon _{m,j}$, $\tau$ and $\sigma _{m,j}$ may lead to the poor transient performance and the high control input. Hence, the trial-and-error method, a widely employed approach, can be utilized for parameter selection.

5 Simulation results

In order to demonstrate the effectiveness and application of the proposed control algorithm, this section provides two simulation examples.

Example 1

Consider the MIMO nonstrict-feedback nonlinear systems

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}_{1,1}=&x_{1,2}+f_{1,1}(X)+d_{1,1}(t),\\ \dot{x}_{1,2}=&u_{1}(v_1)+f_{1,2}(X)+d_{1,2}(t),\\ y_1=&x_{1,1},\\ \dot{x}_{2,1}=&x_{2,2}+f_{2,1}(X)+d_{2,1}(t),\\ \dot{x}_{2,2}=&u_{2}(v_2)+f_{2,2}(X)+d_{2,2}(t),\\ y_2=&x_{2,1},\\ \end{aligned} \right. \end{aligned}$$

(70)

where $f_{1,1}(X)=1-\cos (x_{1,1}x_{1,2}x_{2,1}x_{2,2})+x_{1,1}$, $f_{1,2}(X)=2x_{1,1}\cos (x_{1,1}x_{1,2})+x_{1,1}x_{1,2}x_{2,1}x_{2,2}e^{x_{1,2}}$, $f_{2,1}(X)=2-\cos (x_{1,1}x_{1,2}x_{2,1}x_{2,2})+3x_{1,1}x_{1,2}x_{2,1}x_{2,2}$, $f_{2,2}=x_{2,1}x_{2,2}e^{x_{2,2}}+x_{1,1}x_{1,2}x_{2,2}$. The tracking signals are selected as $y_{1,d}(t)=\frac{1}{2}\sin (t)+\frac{1}{2}\sin (\frac{t}{2})$, $y_{2,d}(t)=\frac{1}{2}\sin (t)-\frac{1}{4}\cos (2t)$. According to [38], the parameters of the hysteresis input are selected as $\varrho _m=1$, $c_m=5$ and $D_m=0.5$.

The basis vector function $\varphi _{m,j}$ is constructed by choosing the width of Gaussian functions and the centers of the receptive field as $\bar{\sigma }_m=2$ and $\underline{\mu }=[-1.5, -1, -0.5, 0, 0.5, 1, 1.5]^\mathrm{T}$. Prescribed performance function is $\mu _{1,1}=\mu _{2,1}=(0.5-0.015)e^{-2t}+0.015$ and it is easy to know $\mu _{0,m,1}=0.5$, $\mu _{\infty ,m,1}=0.05$, $a_{m,1}=2$, $\mu _{\infty ,m,1}=0.005$. The parameters of nonlinear gain function are selected as $o=10$ and $\nu =0.005$. Furthermore, all designed parameters are chosen as $l_{1,1}=l_{1,2}=25$, $l_{2,1}=l_{2,2}=20$, $\epsilon _{1,1}=\epsilon _{1,2}=1.5$, $\epsilon _{2,1}=\epsilon _{2,2}=2.5$ $\sigma _{1,1}=\sigma _{1,2}=1.2$, $\sigma _{2,1}=\sigma _{2,2}=1.5$, $\delta _{1,1}=\delta _{1,2}=1.5, \delta _{2,1}=\delta _{2,2}=1.8$, $\tau =1$. The initial values are given as $x_1(0)=[0.2, 0.01]^\mathrm{T}$, $x_2(0)=[-0.23, 0]^\mathrm{T}$, $\hat{x}_1(0)=[0.35, 0.35]^\mathrm{T}$, $\hat{x}_{2}(0)=[0.18, 0.18]^\mathrm{T}$, $\hat{c}_m(0)=0.05$, $W_{1,1}(0)=[0.2, 0.1, 0.1, 0, 0.1, 0, 0]^\mathrm{T}$, $W_{1,2}(0)=[0.2, 0.1, 0, 0.1, 0, 0, 0]^\mathrm{T}$, $W_{2,1}(0)=[0.2, 0.2, 0.2, 0.2, 0.2, 0, 0]^\mathrm{T}$, $W_{2,2}(0)=[0.15, 0, 0.15, 0.15, 0.15, 0.15, 0]^\mathrm{T}$. Figures 3, 4, 5, 6, 7, 8 and 9 illustrate the simulation results. According to Fig. 3, it is easy to conclude that the proposed control strategy can derive the output to track the reference signal. Figures 4 and Fig. 5 are described to show the tracking error, it can be seen that the nonlinear feedback control, the linear feedback (LF)-DSC and the LF-PPC have a similar control performance with a small tracking error. Compared with the LF control method, the nonlinear gain feedback control proposed in the paper can drive the tracking error retained within the predefined range with better tracking performance. Figures 6 and 7 are used to show the trajectories of states $x_{m,1}$ and $x_{m,2}$ and the NN observer values $\hat{x}_{m,1}$, $\hat{x}_{m,2}$. $\hat{x}_{m,1}$ and $\hat{x}_{m,2}$ are used to obtain the system states $x_{m,1}$ and $x_{m,2}$, respectively. The trajectories of $\Vert W_{m,j}\Vert ^2$ are given in Fig. 8. Figure 9 indicates the control signals $u_m(v_m)$ and $v_m$.

Fig. 3

Trajectories of $y_m(t)$ and $y_{m,d}(t)~(m=1,2)$

Fig. 4

Tracking error $e_1(t)$

Fig. 5

Tracking error $e_2(t)$

Fig. 6

Trajectories of $x_{1,j}(t)$ and $\hat{x}_{1,j}(t)~(j=1,2)$

Fig. 7

Trajectories of $x_{2,j}(t)$ and $\hat{x}_{2,j}(t)~(j=1,2)$

Fig. 8

Trajectories of $\Vert W_{1,1}\Vert ^2$, $\Vert W_{1,2}\Vert ^2$, $\Vert W_{2,1}\Vert ^2$ and $\left\| {W_{{2,2}} } \right\|^{2}$

Fig. 9

Trajectories of hysteresis input $v_1(t)$, v₂(t) and system input $u_1(t)$, u₂(t)

Fig. 10

The helicopter (CE-150) system

Table 1 Parameters of helicopter (CE-150)

Example 2

Consider the tracking error problem for a helicopter (CE-150) in [43], see Fig. 10. The helicopter system can be described as the following MIMO systems

$$\begin{aligned} \begin{aligned} \ddot{\varphi }\cos (\varphi I_{l_2})^2-2\cos (\theta )\sin (\theta )\dot{\theta }\dot{\varphi }I_{l_2}\,=\,&u_1(v_1),\\ I_{l_2}\ddot{\theta }+\cos (\theta )\sin (\theta )\dot{\varphi }^2I_{l_2}+mgI_{l_2}\cos (\theta )\,=\,&u_2(v_2). \end{aligned} \end{aligned}$$

(71)

where various parameters are shown in Table 1, $I_{l_2}$ and $I_c$ are defined as

$$\begin{aligned} \begin{aligned}&I_{l_2}=\frac{m_l(L_1^3+L_2^3)}{3(L_1+L_2)}+m_1L_1^2+m_2L_2^2,\\&I_c=\frac{(m_l(L_1-L_2)+m_1l_1-m_2l_2)}{m}, \end{aligned} \end{aligned}$$

(72)

where $m=m_l+m_1+m_2$.

By defining $x_{1,1}=\varphi$, $x_{1,2}=\dot{\varphi }$, $x_{2,1}=\theta$ and $x_{2,2}=\dot{\theta }$, (71) can be rewritten as

$$ \left\{ {\begin{array}{*{20}l} {\dot{x}_{{1,1}} = x_{{1,2}} + d_{{1,1}} (t),} \\ \begin{gathered} \dot{x}_{{1,2}} = \vartheta _{{1,2}} \left[ { - 0.5Fl\cos (x_{{1,1}} - \theta ) + m_{1} gl\sin x_{{1,1}} - T_{{f1}} } \right] \hfill \\ \quad \quad + u_{1} (v_{1} ) + d_{{1,2}} (t), \hfill \\ \end{gathered} \\ {y_{1} = x_{{1,1}} ,} \\ {\dot{x}_{{2,1}} = x_{{2,2}} + d_{{2,1}} (t),} \\ \begin{gathered} \dot{x}_{{2,2}} = \vartheta _{{2,2}} \left[ { - 0.5Fl\cos (x_{{2,1}} - \theta ) + m_{2} gl\sin x_{{2,1}} - T_{{f2}} } \right] \hfill \\ \quad \quad \; + u_{2} (v_{2} ) + d_{{2,2}} (t), \hfill \\ \end{gathered} \\ {y_{2} = x_{{2,1}} ,} \\ \end{array} } \right. $$

where $\vartheta _{1,2}=\frac{1}{J_1}$, $\vartheta _{2,2}=\frac{1}{J_2}$, $d_{1,1}(t)=d_{2,1}(t)=0$, $d_{2,1}(t)=0.01\cos (t)$, $d_{2,2}(t)=0.02\sin (t)$.

The target signals are chosen as $y_{1,d}(t)=\sin (t)$, $y_{2,d}(t)=\sin (t)$. The prescribe performance function and the nonlinear gain function are kept same with Example 1. And all designed parameters are selected as $l_{1,1}=l_{1,2}=15$, $l_{2,1}=l_{2,2}=10$, $\epsilon _{1,1}=\epsilon _{1,2}=1.2$, $\epsilon _{2,1}=\epsilon _{2,2}=1.6$ $\sigma _{1,1}=\sigma _{1,2}=1.8$, $\sigma _{2,1}=\sigma _{2,2}=2$, $\delta _{1,1}=\delta _{1,2}=1.5, \delta _{2,1}=\delta _{2,2}=1.8$, $\tau =1$, $x_1(0)=[0.25, 0]^\mathrm{T}$, $x_2(0)=[0.1, 0]^\mathrm{T}$, $\hat{x}_1(0)=[0.35, 0.35]^\mathrm{T}$, $\hat{x}_{2}(0)=[0.25, 0.25]^\mathrm{T}$, $\hat{c}_m(0)=0.1$. Figures 11, 12, 13, 11, 11, 11 and 17 show the effectiveness and the practicality of the proposed controller, which is employed to helicopter systems. The tracking results are demonstrated in Fig. 11 and the tracking errors are depicted in Figs 12 and 13. As shown in Figs. 14 and 15, the constructed observer can estimate the unmeasurable states to satisfy the controller design. Fig. 16 gives the curves of $\Vert W_{m,j}\Vert ^2$. Finally, Fig. 17 indicates the control signals $u_m(v_m)$ and $v_m$ under the hysteresis nonlinearity.

Fig. 11

Trajectories of $y_m(t)$ and $y_{m,d}(t)~(m=1,2)$

Fig. 12

Tracking error $e_1(t)$

Fig. 13

Tracking error $e_2(t)$

Fig. 14

Trajectories of $x_{1,j}(t)$ and $\hat{x}_{1,j}(t)~(j=1,2)$

Fig. 15

Trajectories of $x_{2,j}(t)$ and $\hat{x}_{2,j}(t)~(j=1,2)$

Fig. 16

Trajectories of $\Vert W_{1,1}\Vert ^2$, $\Vert W_{1,2}\Vert ^2$, $\Vert W_{2,1}\Vert ^2$ and $\Vert W_{2,2}\Vert ^2$

Fig. 17

Trajectories of hysteresis input v₁(t), v₂(t) and system input u₂(t)

6 Conclusion

In this paper, a tracking control problem of MIMO nonlinear systems with hysteresis input and unknown states is investigated and verified. The NN observer has been constructed to estimate the unmeasurable states. A nonlinear gain function is used in the process of backstepping design procedure, which brings a better dynamic performance for the closed-loop system. Meanwhile, by designing a novel Lyapunov function, we can easy to deal with the difficulties caused by the nonlinear gain function for stability analysis. Furthermore, the algebraic loop problem is addressed by using the property of the NNs. According to the benefits of DSC technique, an adaptive tracking control method is proposed, which guarantees that the closed-loop system is SGUUB and the tracking error converges to the prescribed bounds. Further work is considered to deal with the tracking control problem by using the fractional order control method the finite-time control method.