Disturbance-observer-based adaptive dynamic surface control for nonlinear systems with input dead-zone and delay using neural networks

Abstract

Disturbance-observer-based adaptive neural control approach is proposed for nonlinear systems. Considering the effect caused by long input delay and dead-zone, a novel auxiliary system has been introduced to degrade the design difficult. Based on the auxiliary system, a novel disturbance observer is developed to estimate the unknown time-varying external disturbance and the approximation error. What is more, the priori knowledge on the boundary of the disturbance and approximation error is not required for the disturbance observer. The “explosion of complexity” problem has been overcome by using dynamic surface control (DSC) scheme. By combing DSC scheme with backstepping technique, an adaptive neural dynamic surface controller is correctly devised to improve the disturbance rejection performance of the closed-loop system. Finally, the simulations of two examples show the superiority of the proposed scheme.

1 Introduction

Over the past years, many meaningful results have been proposed for nonlinear systems control in [1,2,3]. However, most of these results are obtained on the premise that the uncertain nonlinearity in system are known or bounded by known nonlinear functions. It should be pointed out that this assumption is not applicable to practical applications, because it is difficult to get the accurate system model or the information of the nonlinear term in practice. To overcome this drawback, the neural networks (NNS) and fuzzy logic systems (FLS) are introduced to construct the adaptive controller by combing the adaptive backstepping method in [4,5,6,7,8,9,10]. However, in the process of backstepping design, the “explosion of complexity” increases sharply with repeating differentiation of the virtual controller in the aforementioned results. Thus, the DSC scheme was proposed in [11] and many meaningful research results have been developed for strict-feedback nonlinear systems in [12,13,14,15,16,17]. However, some common phenomena such as external disturbance [18, 19], time delay [20, 21] and non-smooth nonlinearity [22, 23] bring great challenges to the controller design of strict-feedback nonlinear systems.

In general, many actual systems often suffer from different external disturbances. These disturbances are usually time-varying and unknown. As a result, it is difficult to obtain their accurate information, and the difficulty of system control increases sharply. The disturbance can break the control performance of the closed-loop system and even lead to disastrous results. Thus it is necessary to consider the external disturbance rejection performance of the closed-loop system. The authors in [24] first proposed the disturbance-observer-based control (DOBC) strategy. Unlike the general adaptive control approach, the disturbance observer (DO) can estimate the external disturbance and provide valuable information for control law design. Consequently, the robustness of the closed-loop system is improved effectively by using DOBC strategy. Inspired by the idea of DOBC, [25,26,27] proposed adaptive sliding terminal control scheme for strict-feedback nonlinear systems. Furthermore, considering mismatched disturbances, [28,29,30] proposed the disturbance rejection scheme for nonlinear systems. Recently, based on DOBC [31,32,33] proposed adaptive neural/fuzzy control for strict-feedback nonlinear systems, respectively. It should be noted that the imperfections are unavoidable in the practical production processes [34]. For instance, the authors in [35] proposed a control scheme for imperfect electromechanical round system. Furthermore, an optimal control approach for imperfect electronic circuits system was considered in [36]. Although the real devices still operate well in regimes far from ideality, the usual control approaches may useless. In addition, the dead-zone problem has not been considered in the aforementioned results. In contrast to time-varying external disturbance, the input dead-zone is a typical non-smooth nonlinearity problem, which often occurs in many physical components of control systems [37]. However, the control forces provided by the actuators are limited in practice. Thus, the output provided by the disturbance observer cannot be effective utilized by the control signal when the input dead-zone appears. As a result, the closed-loop systems will be unstable or even disastrous if the input dead-zone is ignored. Recently, in order to solve the problem of dead-zone in nonlinear systems, many meaningful results have been developed by the researchers in [38,39,40,41]. Although the input dead-zone problem has been widely studied by the researchers, these issues rarely considered in the DOBC scheme. In addition, the control schemes proposed in the aforementioned results cannot be extended to strict-feedback nonlinear systems with unknown time-varying external disturbance and input dead-zone.

On the other hand, as a kind of time delay, input delay is a common and inevitable phenomenon in practical control systems [42,43,44]. When input delay occurs, the performance of the closed-loop system will be damaged or even be disastrous if the control signal cannot feedback the information provided by the observer in time. However, the traditional state delay control methods proposed in [45,46,47] cannot be directly used to solve input delay. For nonlinear systems with input delay, the authors in [48] extended the predictor-based control approach to tackle input delay. However, for the predictor-based control method, the state of system is difficult to predict. In recent years, based on FLS and the idea of Pade approximation, [49] considered input delay and output constraint for strict-feedback nonlinear systems. Furthermore, considering strict-feedback nonlinear with state constrained and input delay, [50] proposed an adaptive tracking control approach by combing Pade approximation and NNS with adaptive backstepping technique. Later, the authors in [51, 52] developed a compensation mechanism or combing compensation mechanism with Pade approximation to degrade the effect of the input delay. Nevertheless, the Pade approximation approach is invalid for long input delay. In addition, most of existing results are invalid for strict-feedback nonlinear systems with time-varying external disturbance, input delay and dead-zone, simultaneously. Recently, [53] considered the input saturation, input delay and external disturbance for state constrained strict-feedback nonlinear systems. Unfortunately, if the long input delay or the dead-zone problem occurs the proposed method in [53] is invalid. Since input dead-zone and input delay are common phenomena in practical systems, the disturbance rejection ability is more in line with the robust performance requirements of the closed-loop system, it is a significant issue to consider strict-feedback nonlinear systems with time-varying external disturbance, input dead-zone and input delay. However, the aforementioned results cannot be directly generalized to this issue, which prompted us to carry out our research.

The aforementioned observation motivates us to discuss disturbance-observer-based adaptive neural dynamic surface control for strict-feedback nonlinear systems with time-varying external disturbance, input dead-zone and input delay. The main work of this paper is listed as follows:

• (1) Taking into account the effect caused by long input delay and dead-zone, a novel auxiliary system is introduced for the first time to degrade the design difficulty in each step. Compared with [49,50,51,52,53] the proposed method can tackle the long input delay.

• (2) DSC is introduced to tackle the “explosion of complexity” problem in each backstepping step, which can reduce the burden of computation. The radial basis function neural networks are introduced to approximate the unknown nonlinear functions.

• (3) Based on the proposed auxiliary system, a novel adaptive disturbance observer is introduced for the first time to estimate the unknown time-varying external disturbance and approximation error in each backstepping step. Unlike the usual disturbance observer, the boundary information of the time-varying external disturbance or approximate error is not required for the disturbance observer design. Compared with [28,29,30,31,32,33], the proposed method which not only estimates the unknown time-varying external disturbance and the approximation error caused by the NNS, but also eliminates the effect caused by input delay and dead zone. Furthermore, the closed-loop systems show better robust performance.

The reminder of this paper is organized as follows: Section 2 presents the problem and the preliminary results. Section 3 discusses the design process of the controller and the stability analysis. The simulation examples are considered in Sect. 4. Finally, a brief conclusion is given in Sect. 5.

2 Preliminary

2.1 Problem formulation

Consider the strict-feedback nonlinear system as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_i (t) = f_i ({\bar{x}}_{i}(t)) +x_{i + 1} (t) + d_i (t),\begin{array}{*{20}c} {} &{} {1 \le i \le } \\ \end{array}n - 1 \\ \dot{x}_n (t) = f_n ({\bar{x}}_{n}(t)) + D(v(t - \tau ) ) + d_n (t) \\ y(t) = x_1 (t) \\ \end{array} \right. \end{aligned}$$

(1)

where the state variable ${\bar{x}}_{i}(t) = [x_1 (t),x_2 (t), \cdots ,x_i (t)]^T \in R^{i}, i=1,2,\cdots ,n$, $D(v(t - \tau ) ) \in R$ denotes the control input with input dead-zone and delay, where $\tau$ represents the known constant or time-varying input delay, the system output $y(t) \in R$. For $1 \le i \le n$ , $f_i ( \cdot )$ is unknown smooth nonlinear function, $d_i(t)$ represents the unknown and time-varying external disturbance.

According to [38], D(v(t)) is defined as

$$\begin{aligned} D(v(t)) = \left\{ \begin{array}{l} m_r (v(t) - b_r ),\begin{array}{*{20}c} {} &{} {v(t) \ge b_r } \\ \end{array} \\ 0\begin{array}{*{20}c} {\begin{array}{*{20}c} , &{} {} \\ \end{array}} &{} {\begin{array}{*{20}c} {} &{} \ \ \ \ {b_l< v(t) < b_r } \\ \end{array}} \\ \end{array} \\ m_l (v(t) - b_l ),\begin{array}{*{20}c} {} &{} {v(t) \le b_l } \\ \end{array} \\ \end{array} \right. \end{aligned}$$

(2)

where $v(t) \in R$ denotes the input to the dead-zone, and D(.) denotes the output to the dead-zone.

Assumption 1

[38]: The dead-zone slopes $m_r=m_l=m$.

Assumption 2

[38]: The parameters m, $b_r$ and $b_l$ in (2) are bounded, i.e., $m_{min}< m < m_{max}$ , $b_{r_{\min }}<b_{r} < b_{r_{\max }}$ and $b_{l_{\min }}<b_{l} < b_{l_{\max }}$ with $m_{min}$, $m_{max}$, $b_{r_{\min }}$, $b_{r_{\max }}$, $b_{l_{\min }}$ and $b_{l_{\max }}$ being known constants.

Assumption 3

[38]: The signs for m, $b_r$ and $b_l$ are known, i.e., $m>0$, $b_r > 0$, $b_l< 0$.

Then, we redefine (2) as

$$\begin{aligned} D(v(t)) = mv(t) + d(v(t)) \end{aligned}$$

(3)

where

$$\begin{aligned} d(v(t)) = \left\{ \begin{array}{l} - mb_r , \ \ \ \ \ \ \ \ \ \ \ \ v(t) \ge b_r \\ - mv(t), \ \ \ \ \ \ \ b_l< v(t) < b_r \\ - mb_l , \ \ \ \ \ \ \ \ \ \ \ v(t) \le b_l \\ \end{array} \right. \end{aligned}$$

(4)

Based on Assumptions 1 and 2, the term d(v(t)) is bounded, i.e., $|d(v(t))| \le d^*$, with $d^*=max\{ mb_{r},-mb_{l} \}$.

Remark 1

In practice, many systems can be described or transform as the system (1), such as liquid level control system [53], power systems [54], maglev suspension systems [55, 56], and so on.

Remark 2

Compared with the works in [28,29,30,31,32,33] which only considered external disturbance, the effect of input dead-zone and input delay was unconsidered. Compared with the works in [49,50,51,52,53] which only focus on strict-feedback nonlinear systems with input delay, however, the effect of input dead-zone and the disturbance rejection ability of the closed-loop system are ignored. In addition, the developed method in [49,50,51,52,53] cannot work in long input delay.

The main idea of this research is to establish a unified framework of disturbance-observer-based adaptive neural dynamic surface control scheme for strict-feedback nonlinear systems with time-varying external disturbance, input dead-zone and input delay. Furthermore, the proposed controller can show effective tracking performance for the reference signal $y_d (t)$ and the closed-loop system shows better disturbance rejection performance.

Assumption 4

For 1 $\le i \le n$, the unknown time-varying external disturbances $d_i(t)$ and its derivative ${\dot{d}}_i(t)$ satisfy $|d_i(t) | \le \bar{d}_{iU}$ and $|{\dot{d}}_i(t) | \le \bar{d}_{iD}$, where $\bar{d}_{iU}$ and $\bar{d}_{iD}$ are unknown positive constants.

Assumption 5

[57]: The reference trajectory $y_d (t)$ and its time derivatives $\ddot{y}_d(t)$ are bounded, i.e., ${\varTheta _0 : = \{ (y_d ,\dot{y}_d ,\ddot{y}_d ):(y_d )^2 + (\dot{y}_d )^2 + (\ddot{y}_d )^2 \le B_0 \} }$, where $B_0$ is a positive constant.

2.2 Neural networks

In the process of controller design, the NNS are used to approximate the unknown nonlinear function $f\left( Z \right) :R^n \rightarrow R$. Assume that l represents the number of nodes in NNS, then $f\left( Z \right)$ can be modeled by

$$\begin{aligned} \begin{aligned} f_{nn} \left( Z \right) = W^T \varPhi (Z) \end{aligned} \end{aligned}$$

(5)

For Eq. (5), Z represents the input vector and $Z \in \varOmega _z \subset R^q$. $W \in R^l$ represents the weight vector and $W = \left[ {w_1 ,w_2 , . . . ,w_l } \right] ^T$. $\varPhi (Z) = \left[ {s_1 (Z),s_2 (Z), . . . ,s_l (Z)} \right] ^T \in R^l$ is the basis function vector with $s_i (Z)$ $( i=1,2, \cdots , l)$ being the Gaussian-like function, i.e.,

$$\begin{aligned} s_i (Z) = \exp \left[ { - \frac{{(Z - v_i )^T (Z - v_i )}}{{\eta ^2 }}} \right] \end{aligned}$$

(6)

where $\eta$ represents the width of the Gaussian function, and $v_i = \left[ {v_{i1} ,v_{i2} , . . . ,v_{iq} } \right] ^T$ denotes the center of the receptive domain.

For $f\left( Z \right)$ defined on a compact set $\varOmega _Z$, according to literature [7], there exists a suitable $W^{*T} \varPhi (Z)$ which satisfies

$$\begin{aligned} f\left( Z \right) = W^{*T} \varPhi (Z) + \delta (Z),\begin{array}{*{20}c} {} &{} {\forall z \in \varOmega _Z } \\ \end{array} \end{aligned}$$

(7)

with

$$\begin{aligned} W^* = \arg \mathop {\min }\limits _{W \in R^l } \left\{ {\mathop {\sup }\limits _{Z \in \varOmega _Z } |f\left( Z \right) - W^T \varPhi (Z)|} \right\} \end{aligned}$$

(8)

being the ideal weight vector and $|\delta (Z)| < \varepsilon$ $(\varepsilon > 0)$ being the approximation error.

3 Control design

In this section, we first introduce a novel compensation mechanism. Then, based on the compensation mechanism, we will focus on the system (1) to design the disturbance-observer-based adaptive tracking controller by using the idea of backstepping technique and the DSC technique.

3.1 Compensation design

Firstly, we present the following auxiliary system to compensate the effect caused by input delay and dead-zone

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{\mu }} _1= \mu _2 - h_1 \mu _1 \\ {\dot{\mu }} _i= \mu _{i + 1} - h_i \mu _i - g_{i - 1} \mu _{i - 1} , \ \ \ i = 2, 3, \cdots , n - 1 \\ {\dot{\mu }} _n= - h_n \mu _n - g_{n - 1} \mu _{n - 1} + D(v(t - \tau )) - D(v(t)) \\ \end{array} \right. \end{aligned}$$

(9)

where $h_1 - \frac{{|1 - g_1 |}}{2} > 0$ , $h_i - \frac{{|1 - g_i | + |1 - g_{i - 1} |}}{2} > 0$ , $i = 2,3,\; \cdots ,n - 1$ and $h_n - \frac{{|1 - g_{n - 1} |}}{2} -1> 0$.

Remark 3

It should be noted that, if input delay $\tau =0$, then $\mu _i ( i = 1,2,\; \cdots ,n)$ in (9) are zero when $\mu _i(0)=0$ .

Next, the following change of coordinate is employed in the process of backstepping designing

$$\begin{aligned} \begin{array}{l} z_1 = x_1 -y_d - \mu _1 \\ z_i = x_i -\omega _i - \mu _i ,\begin{array}{*{20}c} {} &{} {i = 2,3, \cdots ,n} \\ \end{array} \\ \end{array} \end{aligned}$$

(10)

where $\omega _i$ is the first-order filter output signal, which is defined as

$$\begin{aligned} \xi _i {\dot{\omega }} _i + \omega _i = \alpha _{i - 1}, \omega _i (0) = \alpha _{i - 1} (0) \end{aligned}$$

(11)

with $\xi _i$ being design parameter and $\alpha _i$ being the first-order filter input signals. The filter errors are given by

$$\begin{aligned} e_i = \omega _i - \alpha _{i - 1} \begin{array}{*{20}c} {} &{} {i = 2,3, \cdots ,n} \\ \end{array} \end{aligned}$$

(12)

Remark 4

In (10), the change of coordinate is a compensation mechanism, when the system has input delay the auxiliary signal $\mu _i$ will be utilized to compensate the effect caused by time delay at the last step.

3.2 Controller design

According to the previous compensation design, the specific design steps of the controller are described as follows.

Step 1: Based on (1) and (9), the time derivative of $z_1$ can be obtained that

$$\begin{aligned} \begin{aligned}&\dot{z}_1 = \dot{x}_1 - {\dot{\mu }} _1 - \dot{y}_d \\&\ \ \ \,= f_1 ({\bar{x}}) + x_2 + d_1 - \mu _2 + h_1 \mu _1 - \dot{y}_d \\ \end{aligned} \end{aligned}$$

(13)

Let $x_2$ be a desired virtual input, then we design the desired feedback signal $\alpha _{_1 }^*$ as

$$\begin{aligned} \alpha _{1 }^* = - k_1 z_1 -f_1 ({\bar{x}}) - d_1 -h_1 \mu _1 + \dot{y}_d \end{aligned}$$

(14)

Based on the idea of approximation by NNS, for given $\varepsilon _1 >0$, a suitable neural network $W_1 ^{*T} \varPhi _1 (Z_1 )$ can be selected to approximate the function $f_1 ({\bar{x}})$, which satisfies that

$$\begin{aligned} f_1 ({\bar{x}}) = W_1 ^{*T} \varPhi _1 (Z_1 ) + \delta _1 (Z_1 ),\begin{array}{*{20}c} {} &{} {|\delta _1 (Z_1 )| \le \varepsilon _1 } \\ \end{array} \end{aligned}$$

(15)

where $Z_1 = [x_1]^T$ and $\delta _1 (Z_1 )$ denote the input vector and the approximation error, respectively.

Then (14) can be rewritten as

$$\begin{aligned} \alpha _{1 }^* = - k_1 z_1 - W_1 ^{*T} \varPhi _1 (Z_1 ) - D_1 -h_1 \mu _1 + \dot{y}_d \end{aligned}$$

(16)

where $D_1 = \delta _1 (Z_1 ) + d_1 \le \varepsilon _1+ d_{1U} =\bar{ D}_1$. In addition, based on Assumption 4 and the idea of NNS approximation, $\dot{D}_1$ is bounded, i.e., $|\dot{D}_1 |\le \bar{\bar{D}}_1$ .

Owing to $W_1 ^{*}$ and $D_1$ are unknown, thus ${\hat{W}}_1$ and ${\hat{D}}_1$ are used to estimate $W_1 ^{*}$ and $D_1$, respectively. Then we design the virtual control law and the adaptive law as

$$\begin{aligned} \alpha _{1}=- k_1 z_1 - {\hat{W}}_1 ^{T} \varPhi _1 (Z_1 ) - {\hat{D}}_1 -h_1 \mu _1 + \dot{y}_d \end{aligned}$$

(17)

$$\begin{aligned} \dot{\hat{ W}}_1 = \Lambda _1 z_1 \varPhi _1 (Z_1 ) - \sigma _1 {\hat{W}}_1 \end{aligned}$$

(18)

where $\Lambda _1=\Lambda ^{T} _1 > 0$ and $\sigma _1 > 0$ are the design parameters.

To deal with the problem of “explosion of complexity” caused by repeatedly differentiating $\alpha _{1}$, let $\alpha _{1}$ pass through a given low-pass filter $\omega _2$, which defined in (11) with the filter time design parameter $\xi _2$ and the filter error $e_2$ defined in (12). Then one can get

$$\begin{aligned} {\dot{\omega }}_2=\frac{{ - e_2 }}{{\xi _2 }} \end{aligned}$$

(19)

and

$$\begin{aligned} \begin{aligned} \dot{e}_2 = {\dot{\omega }} _2 - {\dot{\alpha }} _1 = \frac{{ - e_2 }}{{\xi _2 }} - {\dot{\alpha }} _1 = \frac{{ - e_2 }}{{\xi _2 }} + M_2 (\cdot ) \end{aligned} \end{aligned}$$

(20)

where $M_2 (\cdot )$ is a continuous function, and $M_2 (z_1 ,z_2 ,e_2 ,{\hat{W}}_1 ,y_d ,\dot{y}_d ,\ddot{y}_d ,{\hat{D}}_1 ,\mu _1 )=- (\frac{{\partial \alpha _1 }}{{\partial x_1 }}\dot{x}_1$ $+ \frac{{\partial \alpha _1 }}{{\partial z_1 }}\dot{z}_1 + \frac{{\partial \alpha _1 }}{\partial {{\hat{W}} }}_1\dot{\hat{ W}}_1 + \frac{{\partial \alpha _1 }}{\partial {y_d }}\dot{y}_d + \frac{{\partial \alpha _1 }}{\partial {{\hat{D}}_1 }}\dot{\hat{ D}} _1 + \frac{{\partial \alpha _1 }}{\partial {\mu _1 }}{\dot{\mu }} _1)$. Furthermore, for any given $B_0$ and $\vartheta$, the sets $\varTheta _0 : = \{ (y_d ,\dot{y}_d ,\ddot{y}_d ):(y_d )^2 + (\dot{y}_d )^2 + (\ddot{y}_d )^2 \le B_0 \}$ is compact in $R^3$, and $\varTheta _2 : = \{ \sum \nolimits _{j = 1}^2 {z_j^2 + {{\tilde{W}}}_1^T \Lambda ^{-1} {{\tilde{W}}}_1 + e_2^2 } \le 2 \vartheta \}$ is compact in $R^{N_1+3}$ with $N_1$ being the dimension of ${{\tilde{W}}}_1^T$. According [57], $M_{2}$ has a maximum value $B_{2}$.

Based on (10), (12) and (17), we can have

$$\begin{aligned} \begin{aligned}&\dot{z}_1 = W_1 ^{*T} \varPhi _1 (Z_1 ) + z_2 + \alpha _1 + e_2 + D_1 + h_1 \mu _1 - \dot{y}_d \\&\ \ \ \,\,= - k_1 z_1 + {{\tilde{W}}}_1 ^T \varPhi _1 (Z_1 ) + \tilde{D}_1 + z_2 + e_2 \end{aligned} \end{aligned}$$

(21)

where ${{\tilde{W}}}_1 =W_1 ^{*}-\hat{ W_1}$ and ${{\tilde{D}}}_1 =D_1-\hat{ D}_1$ represent the estimation errors for $W_1 ^{*}$ and $D_1$, respectively.

Furthermore, in order to estimate $D_1$, an auxiliary variable $\gamma _1$ is introduced to design a DO, i.e.,

$$\begin{aligned} \gamma _1 = z_1 - o_1 \end{aligned}$$

(22)

with $o_1$ being an intermedial variable defined as

$$\begin{aligned} \dot{o} _1 = p_1 \gamma _1 + x_2 - \dot{y}_d - \mu _2 + h_1 \mu _1 \end{aligned}$$

(23)

where $p_1>0$ is a designed parameter.

According (21), (22) and (23), differentiating $\gamma _1$, then

$$\begin{aligned} \begin{array}{l} {\dot{\gamma }} _1 = \dot{z}_1 - {\dot{o}} _1 = W_1 ^{*T} \varPhi _1 (Z_1 ) + D_1 - p_1 \gamma _1 \\ \end{array} \end{aligned}$$

(24)

Defining the DO as

$$\begin{aligned} {\hat{D}}_1 = l_1 (\gamma _1 - \varphi _1 ) \end{aligned}$$

(25)

with $l_1>0$ being a design parameter, $\varphi _1$ being an intermedial variable defined as

$$\begin{aligned} \dot{\varphi {_1}}= - p_1 \gamma _1 + {\hat{D}}_1 \end{aligned}$$

(26)

Based on (24) and (26), differentiating ${\hat{D}}_1$, then

$$\begin{aligned} \dot{\hat{D}}_1 = l_1 W_1^{*T} \varPhi _1 (Z_1 ) + l_1 {{\tilde{D}}}_1 \end{aligned}$$

(27)

Furthermore, one can get

$$\begin{aligned} \dot{{\tilde{D}}}_1 = \dot{D}_1 - l_1 W_1^{*T} \varPhi _1 (Z_1 ) - l_1 {{\tilde{D}}}_1 \end{aligned}$$

(28)

From (24), (28) and (20), according to Young’s inequality and Assumption 4, one can get the following inequalities (29), (30) and (31) .

$$\begin{aligned} \begin{aligned}&\gamma _1 {\dot{\gamma }} _1 = \gamma _1 W_1 ^{*T} \varPhi _1 (Z_1 ) + \gamma _1 D_1 - p_1 \gamma _1^2 \\&\ \ \ \ \ \ \le r_1 \phi _1^2 \gamma _1^2 + \frac{1}{{r_1 }}||W_1 ^{*T} ||^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}}\gamma _1^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}} D_1^2 - p_1 \gamma _1^2 \\&\ \ \ \ \ \ \le - (p_1 - r_1 \phi _1^2 - \frac{{\mathrm{1}}}{{\mathrm{2}}})\gamma _1^2 + \frac{1}{{r_1 }}||W_1^{*T}||^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}}{\bar{D}}_1^2 \\ \end{aligned} \end{aligned}$$

(29)

$$\begin{aligned} \begin{aligned}&{{\tilde{D}}}_1 \dot{{\tilde{D}}}_1 = {{\tilde{D}}}_1 \dot{D}_1 - l_1 {{\tilde{D}}}_1 W_1^{*T} \varPhi _1 (Z_1 )- l_1 {{\tilde{D}}}_1 {{\tilde{D}}}_1 \\&\ \ \ \ \ \ \ \ \ \le \frac{1}{2}{{\tilde{D}}}_1^2 + \frac{1}{2}\dot{D}_1^2 + r_1 \phi _1^2 {{\tilde{D}}}_1^2 + \frac{{l_1^2 }}{{r_1 }}||W_1^{*T}||^2 - l_1 {{\tilde{D}}}_1^2 \\&\ \ \ \ \ \ \ \ \ \le - ( - \frac{1}{2} - r_1 \phi _1^2 + l_1 ){{\tilde{D}}}_1^2 + \frac{1}{2} \bar{\bar{D}}_1^2 + \frac{{l_1^2 }}{{r_1 }}||W_1^{*T} ||^2 \\ \end{aligned} \end{aligned}$$

(30)

where $|\varPhi _1 (Z_1 )| \le \phi _1$, $r_1>0$ is a design parameter.

$$\begin{aligned} \begin{aligned}&e_2 \dot{e}_2 = e_2 (\frac{{ - e_2 }}{{\xi _2 }}) + e_2 M_2 (z_1 ,z_2 ,e_2 ,{\hat{W}}_1 ,y_d ,\dot{y}_d ,\ddot{y}_d ,{\hat{D}}_1 ,\mu _1 ) \\&\ \ \ \ \ \ \ \le - \frac{1}{{\xi _2 }}e_{_2 }^2 + \frac{1}{2}e_{_2 }^2 + \frac{1}{2}B_{_2 }^2 \\ \end{aligned} \end{aligned}$$

(31)

Now, the Lyapunov function is taken as

$$\begin{aligned} V_1 = \frac{1}{2}z_1^2 + \frac{1}{{2 }}{{\tilde{W}}}_1^T {\Lambda ^{-1}_1}{{\tilde{W}}}_1 + \frac{1}{2}\gamma _1^2 + \frac{1}{2}{{\tilde{D}}}_1^2 + \frac{1}{2}e_2^2 \end{aligned}$$

(32)

It should be noted that the factor $\frac{1}{2}$ is employed in the Lyapunov function $V_1$, which is often employed in the backstepping design process. The main reason is that the Lyapunov function takes the form of square, thus the employed factor $\frac{1}{2}$ is convenient for us to carry out the theoretical derivation in the process of backstepping design and stability analysis. In other words, the factor $\frac{1}{2}$ can be chosen the other positive constant, which might cause inconvenience to the design process.

Differentiating $V_1$, then

$$\begin{aligned} \begin{aligned}&\dot{V}_1 = z_1 ( - k_1 z_1 + {{\tilde{W}}}_1 ^T \varPhi _1 (Z_1 ) + {{\tilde{D}}}_1 + z_2 + e_2 ) - {{\tilde{W}}}_1 ^T{\Lambda ^{-1}_1} \dot{\hat{W}} _1 \\&\quad + \gamma _1 {\dot{\gamma }} _1 + {{\tilde{D}}}_1 \dot{{\tilde{D}}}_1 + e_2 \dot{e}_2 \\&= - k_1 z_1^2 + z_1 z_2 + z_1 e_2 + z_1 {{\tilde{D}}}_1 + \sigma _1 {{\tilde{W}}}_{_1 }^T {\hat{W}}_1 + \gamma _1 {\dot{\gamma }} _1 \\&\quad + {{\tilde{D}}}_1 \dot{{\tilde{D}}}_1 + e_2 \dot{e}_2 \\ \end{aligned} \end{aligned}$$

(33)

Substituting (29), (30) and (31) into (33), and using the complete squares formula, then

$$\begin{aligned} \begin{aligned}&\dot{V}_1 \le - k_1 z_1^2 + z_1 z_2 + \frac{1}{2}z_1^2 + \frac{1}{2}e_2^2 + \frac{1}{2}z_1^2 + \frac{1}{2} {{\tilde{D}}}_1^2 \\&\qquad - \sigma _1 {{\tilde{W}}}_{_1 }^T {\hat{W}}_1 + \gamma _1 {\dot{\gamma }} _1 + {{\tilde{D}}}_1 \dot{{\tilde{D}}}_1 + e_2 \dot{e}_2 \\&\quad \le - (k_1 - 1)z_1^2 - (p_1 - r_1 \phi _1^2 - \frac{{\mathrm{1}}}{{\mathrm{2}}})\gamma _1^2 \\&\qquad - ( - 1 - r_1 \phi _1^2 + l_1 ){{\tilde{D}}}_1^2 \\&\qquad - (\frac{1}{{\xi _2 }} - 1)e_{_2 }^2 \\&\qquad + z_1 z_2 + \sigma _1 {{\tilde{W}}}_{_1 }^T {\hat{W}}_1 + \frac{{l_1^2 + 1}}{{r_1 }}||W_1^{*T} ||^2 \\&\qquad + \frac{{\mathrm{1}}}{{\mathrm{2}}}{\bar{D}}_1^2 + \frac{1}{2}\bar{\bar{D}}_1^2 + \frac{1}{2}B_{_2 }^2 \\ \end{aligned} \end{aligned}$$

(34)

Step i ($2 \le i \le n - 1$): Based on (1) and (9), differentiating $z_i = x_i - \omega _i - \mu _i$, then

$$\begin{aligned} \begin{aligned} \dot{z}_i = f_i ({\bar{x}}) + x_{i + 1} + d_i - {\dot{\omega }} _i - \mu _{{\mathrm{i + 1}}} + h_i \mu _i + g_{i - 1} \mu _{i - 1} \end{aligned} \end{aligned}$$

(35)

Let $x_{i+1}$ be a desired virtual input, we define the desired feedback signal $\alpha _{_i}^*$ as

$$\begin{aligned} \alpha _{i}^* =-z_{i-1} -k_i z_i -f_i ({\bar{x}}) - d_i - h_i \mu _i - g_{i - 1} \mu _{i - 1} + {\dot{\omega }} _i \end{aligned}$$

(36)

As the first step, based on the idea of approximation, the nonlinear function $f_i ({\bar{x}})$ can be approximated by $W_i ^{*T} \varPhi _i (Z_i)$, which yields

$$\begin{aligned} f_i ({\bar{x}}) = W_i ^{*T} \varPhi _i (Z_i ) + \delta _i (Z_i ),\begin{array}{*{20}c} {} &{} {|\delta _i (Z_i )| \le \varepsilon _i } \\ \end{array} \end{aligned}$$

(37)

where $\delta _i (Z_i )$ and $Z_i = [x_1 ,x_2 , \cdots ,x_i]^T$ denote the approximation error and input vector, respectively.

Substituting (37) into (36), then $\alpha _i^*$ can be rewritten as

$$\begin{aligned} \alpha _i^* =-z_{i-1} - k_i z_i - W_i ^{*T} \varPhi _i (Z_i ) - D_i - h_i \mu _i - g_{i - 1} \mu _{i - 1} + {\dot{\omega }} _i \end{aligned}$$

(38)

where $D_i = \delta _i (Z_i ) + d_i \le {\varepsilon _i}+ d_{iU} =\bar{ D}_i$. Based on Assumption 4 and the idea of NNS approximation, $\dot{D}_i$ is bounded, i.e., $|\dot{D}_i |\le \bar{\bar{D}}_i$ .

Because $W_i ^{*}$ and $D_i$ are unknown, thus we use ${\hat{W}}_i$ and ${\hat{D}}_i$ to estimate $W_i ^{*}$ and $D_i$, respectively. Then, we design the virtual control law and the adaptive law as

$$\begin{aligned} \alpha _{i}&=-z_{i-1}- k_i z_i - {\hat{W}}_i ^{T} \varPhi _i (Z_i ) - {\hat{D}}_i - h_i \mu _i - g_{i - 1} \mu _{i - 1} + {\dot{\omega }} _i \end{aligned}$$

(39)

$$\begin{aligned} \dot{\hat{ W_i}}&= \Lambda _i z_i \varPhi _i (Z_i ) - \sigma _i {\hat{W}}_i \end{aligned}$$

(40)

with $\Lambda _i=\Lambda ^{T} _i > 0$ and $\sigma _i > 0$ being the design parameters.

To deal with the “explosion of complexity” problem caused by repeatedly differentiating $\alpha _{i}$, let $\alpha _{i}$ pass through the low-pass filter $\omega _{i+1}$ defined in (11) with the filter time design parameter $\xi _{i+1}$ and the filter error $e_{i+1}$ defined in (12). Thus, one can have

$$\begin{aligned} {\dot{\omega }}_{i+1}=\frac{{ -e_{i+1} }}{{\xi _{i+1} }} \end{aligned}$$

(41)

and

$$\begin{aligned} \begin{aligned}&\dot{e}_{i+1} = {\dot{\omega }} _{i+1} - {\dot{\alpha }} _i = \frac{{ - e_{i+1} }}{{\xi _{i+1} }} - {\dot{\alpha }} _i = \frac{{ - e_{i+1} }}{{\xi _{i+1} }} + M_{i+1}(\cdot ) \end{aligned} \end{aligned}$$

(42)

where $M_{i+1}(\cdot )$ is a continuous function, and $M_{i+1}(\cdot ) =M_{i+1} (z_1, \cdots ,z_{i+1}, e_{2}, \cdots , e_{i+1},$ ${\hat{W}}_1, \cdots , {\hat{W}}_i ,$ $y_d , \dot{y}_d , \ddot{y}_d , {\hat{D}}_1, \cdots , {\hat{D}}_{i} , \mu _1, \cdots , \mu _{i} ) \mathrm{= } - (\frac{{\partial \alpha _i }}{\partial {x_i }}\dot{x}_i + \frac{{\partial \alpha _i }}{\partial {z_i }}\dot{z}_i + \frac{{\partial \alpha _i }}{\partial {{\hat{W}}_i }}\dot{\hat{ W_i}} + \frac{{\partial \alpha _i }}{\partial {y_d }}\dot{y}_d + \frac{{\partial \alpha _i }}{\partial {{\hat{D}}_i }}\dot{\hat{ D_i}} + \frac{{\partial \alpha _i }}{\partial {\mu _i }}{\dot{\mu }} _i)$. For any given $B_0$ and $\vartheta$, the sets $\varTheta _0 : = \{ (y_d ,\dot{y}_d ,\ddot{y}_d ):(y_d )^2 + (\dot{y}_d )^2 + (\ddot{y}_d )^2 \le B_0 \}$ is compact in $R^3$ and $\varTheta _{i} : = \{ \sum \nolimits _{j = 1}^{i} {z_j^2 + {{\tilde{W}}}_1^T \Lambda ^{-1} {{\tilde{W}}}_1 + e_{i+1}^2 } \le 2 \vartheta \}$ is in $R^{\sum \nolimits _{j = 1}^{i}N_i+2i-1}$ with $N_i$ being the dimension of ${{\tilde{W}}}_i^T$. According [57], $M_{i+1}$ has a maximum value $B_{i+1}$.

With the aid of $x_{i+1} = z_{i+1} + \alpha _{i} + e_{i+1} + \mu _{i+1}$ and based on (39), then (35) can be rewritten as

$$\begin{aligned} \begin{aligned}&\dot{z}_i =-z_{i-1}- k_i z_i + {{\tilde{W}}}_i ^T \varPhi _i (Z_i ) + {{\tilde{D}}}_i + z_{i + 1} + e_{i + 1} \end{aligned} \end{aligned}$$

(43)

where ${{\tilde{W}}}_i =W_i ^{*}-\hat{ W_i}$ and ${{\tilde{D}}}_i =D_i ^{*}-\hat{ D_i}$ represent the estimation errors for $W_i^{*}$ and $D_i$, respectively.

In what follows, to estimate $D_i$, an auxiliary variable $\gamma _i$ is introduced to design a DO, i.e.,

$$\begin{aligned} \gamma _i = z_i - o_i \end{aligned}$$

(44)

with $o_i$ being an intermedial variable defined as

$$\begin{aligned} \dot{o} _i = p_i \gamma _i + x_{i + 1} - {\dot{\omega }} _i - \mu _{i + 1} + h_i \mu _i + g_{i - 1} \mu _{i - 1} \end{aligned}$$

(45)

where $p_i>0$ is a designed parameter.

Based on (43), (44) and (45), differentiating $\gamma _i$, then

$$\begin{aligned} \begin{array}{l} {\dot{\gamma }} _i = W_i^{*T} \varPhi _i (Z_i ) + D_i - p_i \gamma _i \\ \end{array} \end{aligned}$$

(46)

Let the DO be designed as

$$\begin{aligned} {\hat{D}}_i = l_i (\gamma _i - \varphi _i ) \end{aligned}$$

(47)

with $l_i>0$ being a design parameter, $\varphi _i$ being an intermedial variable defined as

$$\begin{aligned} \dot{\varphi {_i}}= - p_i \gamma _i + {\hat{D}}_i \end{aligned}$$

(48)

According (46) and (48), differentiating ${\hat{D}}_i$, then

$$\begin{aligned} \dot{\hat{ D}}_i = l_i W_i^{*T} \varPhi _i (Z_i ) + l_i {{\tilde{D}}}_i \end{aligned}$$

(49)

Furthermore, one can get

$$\begin{aligned} \dot{{\tilde{D}}}_i = \dot{D}_i - l_i W_i^{*T} \varPhi _i (Z_i) - l_i{{\tilde{D}}}_i \end{aligned}$$

(50)

Based on (46), (50) and (42), according to Young’s inequality and Assumption 4, one can get the following inequalities (51), (52) and (53).

$$\begin{aligned} \begin{aligned}&\gamma _i {\dot{\gamma }} _i = \gamma _i W_i ^{*T} \varPhi _i (Z_i ) + \gamma _i D_i - p_i \gamma _i^2 \\&\ \ \ \ \ \le r_i \phi _i^2 \gamma _i^2 + \frac{1}{{r_i }}||W_i ^{*T} ||^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}}\gamma _i^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}} D_i^2 - p_i \gamma _i^2 \\&\ \ \ \ \ \le - (p_i - r_i \phi _i^2 - \frac{{\mathrm{1}}}{{\mathrm{2}}})\gamma _i^2 + \frac{1}{{r_i }}||W_i^{*T}||^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}}{\bar{D}}_i^2 \\ \end{aligned} \end{aligned}$$

(51)

$$\begin{aligned} \begin{aligned}&{{\tilde{D}}}_i \dot{{\tilde{D}}}_i = {{\tilde{D}}}_i \dot{D}_i - l_i {{\tilde{D}}}_i W_i^{*T} \varPhi _i (Z_i )- l_i {{\tilde{D}}}_i {{\tilde{D}}}_i \\&\ \ \ \ \ \ \ \ \le \frac{1}{2}{{\tilde{D}}}_i^2 + \frac{1}{2}\dot{D}_i^2 + r_i \phi _i^2 {{\tilde{D}}}_i^2 + \frac{{l_i^2 }}{{r_i }}||W_i^{*T}||^2 - l_i {{\tilde{D}}}_i^2 \\&\ \ \ \ \ \ \ \ \le - ( - \frac{1}{2} - r_i \phi _i^2 + l_i ){{\tilde{D}}}_i^2 + \frac{1}{2} \bar{\bar{D}}_i^2 + \frac{{l_i^2 }}{{r_i }}||W_i^{*T} ||^2 \\ \end{aligned} \end{aligned}$$

(52)

where $|\varPhi _i (Z_i )| \le \phi _i$, $r_i>0$ is a design parameter.

$$\begin{aligned} \begin{aligned}&e_{i+1} \dot{e}_{i+1}= e_{i+1} (\frac{{ - e_{i+1} }}{{\xi _{i+1} }}) + e_{i+1} M_{i+1}(\cdot ) \\&\ \ \ \ \ \ \ \ \ \ \ \ \ \le - \frac{1}{{\xi _{i+1} }}e_{{i+1} }^2 + \frac{1}{2}e_{{i+1} }^2 + \frac{1}{2}B_{{i+1} }^2 \\ \end{aligned} \end{aligned}$$

(53)

Considering the Lyapunov function candidate be

$$\begin{aligned} V_i = \frac{1}{2}z_i^2 + \frac{1}{{2 }}{{\tilde{W}}}_i^T {\Lambda ^{-1}_i}{{\tilde{W}}}_i + \frac{1}{2}\gamma _i^2 + \frac{1}{2}{{\tilde{D}}}_i^2 + \frac{1}{2}e_{i+1}^2 \end{aligned}$$

(54)

Differentiating $V_i$

$$\begin{aligned} \begin{aligned}&\dot{V}_{i} = -z_{i-1}z_i - k_{i} z_{i}^2 + z_{i} z_{i+1} + z_{i} e_{i+1} + z_{i} {{\tilde{D}}}_{i} \\&\ \ \ \ \ \ \ \ + \sigma _{i} {{\tilde{W}}}_{i}^T {\hat{W}}_{i} + \gamma _{i} {\dot{\gamma }} _{i} + {{\tilde{D}}}_{i} \dot{{\tilde{D}}}_{i} + e_{i+1} \dot{e}_{i+1} \\ \end{aligned} \end{aligned}$$

(55)

Now, substituting (51), (52) and (53) into (55), one can get

$$\begin{aligned} \begin{aligned}&\dot{V}_i \le -z_{i-1}z_i - k_i z_i^2 + z_i z_{i+1} + z_i^2 + \frac{1}{2}e_{i+1}^2 + \frac{1}{2} {{\tilde{D}}}_i^2 + \sigma _i {{\tilde{W}}}_i^T {\hat{W}}_i \\&\qquad + \gamma _i {\dot{\gamma }} _i + {{\tilde{D}}}_i \dot{{\tilde{D}}}_i + e_{i+1} \dot{e}_{i+1} \\&\quad \le - (k_i - 1)z_i^2 - (p_i - r_i \phi _i^2 - \frac{{\mathrm{1}}}{{\mathrm{2}}})\gamma _i^2 - ( - 1 - r_i \phi _i^2 + l_i ){{\tilde{D}}}_i^2 \\&\qquad - (\frac{1}{{\xi _{i+1} }} - 1)e_{i+1}^2 -z_{i-1}z_i+ z_i z_{i+1} + \sigma _i {{\tilde{W}}}_{i}^T {\hat{W}}_i \\&\qquad + \frac{{l_i^2 + 1}}{{r_i }}||W_i^{*T} ||^2 \\&\qquad + \frac{{\mathrm{1}}}{{\mathrm{2}}}{\bar{D}}_i^2 + \frac{1}{2}\bar{\bar{D}}_i^2 + \frac{1}{2}B_{i+1}^2 \end{aligned} \end{aligned}$$

(56)

Step n: According (1) and (9), the time derivative of $z_n$ as

$$\begin{aligned} \begin{aligned}&\dot{z}_n = \dot{x}_n - {\dot{\omega }} _n - {\dot{\mu }} _n\\&\ \ \ \,= f_n ({\bar{x}}) + d_n - {\dot{\omega }} _n + h_n \mu _n + g_{n - 1} \mu _{n - 1} + mv(t)+d(v(t)) \end{aligned} \end{aligned}$$

(57)

As in step i, for given $\varepsilon _n > 0$, $f_n ({\bar{x}})$ can be modeled by a suitable $W_n ^{*T} \varPhi _n (Z_n)$, i.e.,

$$\begin{aligned} f_n ({\bar{x}}) = W_n ^{*T} \varPhi _n (Z_n ) + \delta _n (Z_n ),\begin{array}{*{20}c} {} &{} {|\delta _n (Z_n )| \le \varepsilon _n } \\ \end{array} \end{aligned}$$

(58)

where $\delta _n (Z_n )$ and $Z_n = [x_1 ,x_2 , \cdots ,x_n]^T$ denote the approximation error and input vector, respectively.

Substituting (58) into (57), then (57) can be rewritten as

$$\begin{aligned} \dot{z}_n&= W_n ^{*T} \varPhi _n (Z_n ) + \delta _n (Z_n ) + d_n - {\dot{\omega }} _n \nonumber \\&\quad + h_n \mu _n + g_{n - 1} \mu _{n - 1} + mv(t)+d(v(t)) \end{aligned}$$

(59)

Now, design the desired feedback control $v^*$ as

$$\begin{aligned} v^*&= \frac{1}{{m}}(-z_{n-1} - k_n z_n - W_n ^{*T} \varPhi _n (Z_n )\nonumber \\&\quad - D_n - h_n \mu _n - g_{n - 1} \mu _{n - 1} + {\dot{\omega }} _n) \end{aligned}$$

(60)

where $D_n = \delta _n (Z_n ) + d_n +d(v(t))$. By using Assumption  4, the idea of NNS approximation, and taking $|d(v(t))| \le d^*$ into account, one can get $D_n \le {\varepsilon _n}+ d_{nU}+ d^* =\bar{ D}_n$ and $|\dot{D}_n |$ is bounded, i.e., $|\dot{D}_n |\le \bar{\bar{D}}_n$ .

Since $W_n ^{*}$ and $D_n$ are unknown, we use ${\hat{W}}_n$ and ${\hat{D}}_n$ to estimate $W_n ^{*}$ and $D_n$, respectively. Then, the desired feedback control is designed as

$$\begin{aligned} v&= \frac{1}{{m}}(-z_{n-1} - k_n z_n -\hat{W_n}^{T} \varPhi _n (Z_n ) \nonumber \\&\quad - {\hat{D}}_n - h_n \mu _n - g_{n - 1} \mu _{n - 1} + \dot{\omega }_n) \end{aligned}$$

(61)

and the adaptive law is designed as

$$\begin{aligned} \dot{\hat{ W}}_n = \Lambda _n z_n \varPhi _n (Z_n ) - \sigma _n {\hat{W}}_n \end{aligned}$$

(62)

where $\Lambda _n=\Lambda ^{T}_n > 0$ and $\sigma _n > 0$ the design parameters.

Substituting (61) into (59), one can get

$$\begin{aligned} \dot{z}_n=-z_{n-1} - k_n z_n + {{\tilde{W}}}_n^T \varPhi _n (Z_n ) + {{\tilde{D}}}_n \end{aligned}$$

(63)

where ${{\tilde{W}}}_n =W_n ^{*}-\hat{ W}_n$ and ${{\tilde{D}}}_n =D_n ^{*}-\hat{ D}_n$ represent the estimation errors for $W_n ^{*}$ and $D_n$, respectively.

Next, to estimate $D_n$, an auxiliary variable $\gamma _n$ is proposed to design a DO, i.e.,

$$\begin{aligned} \gamma _n = z_n - o_n \end{aligned}$$

(64)

with $o_n$ being an intermedial variable defined as

$$\begin{aligned} \dot{o}_n= p_n \gamma _n + mv - {\dot{\omega }} _n + h_n \mu _n + g_{n - 1} \mu _{n - 1} \end{aligned}$$

(65)

where $p_n>0$ is a designed parameter.

Based on (63), (64) and (65), differentiating $\gamma _n$, then

$$\begin{aligned} \begin{array}{l} {\dot{\gamma }} _n =W_n ^{*T} \varPhi _n (Z_n ) + D_n - p_n \gamma _n \\ \end{array} \end{aligned}$$

(66)

Let the DO be designed as

$$\begin{aligned} {\hat{D}}_n = l_n (\gamma _n - \varphi _n ) \end{aligned}$$

(67)

with $l_n>0$ being a design parameter, $\varphi _n$ being an intermedial variable defined as

$$\begin{aligned} \dot{\varphi {_n}}= - p_n \gamma _n + {\hat{D}}_n \end{aligned}$$

(68)

Based on (66) and (68), differentiating ${\hat{D}}_n$, then

$$\begin{aligned} \dot{\hat{D}}_n = l_n W_n^{*T} \varPhi _n (Z_n ) + l_n {{\tilde{D}}}_n \end{aligned}$$

(69)

Furthermore, one can get

$$\begin{aligned} \dot{{\tilde{D}}} _n = \dot{D}_n - l_n W_n^{*T} \varPhi _n(Z_n ) - l_n {{\tilde{D}}}_n \end{aligned}$$

(70)

Similar to Step i, according to (66) and (69) and according to Young’s inequality and Assumption 4, one can get the following inequalities (71) and (72).

$$\begin{aligned} \begin{aligned}&\gamma _n {\dot{\gamma }} _n = \gamma _n W_n ^{*T} \varPhi _n (Z_n ) + \gamma _n D_n - p_n \gamma _n^2 \\&\ \ \ \ \ \ \, \le r_n \phi _n^2 \gamma _n^2 + \frac{1}{{r_n }}||W_n ^{*T} ||^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}}\gamma _n^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}} D_n^2 - p_n \gamma _n^2 \\&\ \ \ \ \ \ \, \le - (p_n - r_n \phi _n^2 - \frac{{\mathrm{1}}}{{\mathrm{2}}})\gamma _n^2 + \frac{1}{{r_n }}||W_n^{*T}||^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}}{\bar{D}}_n^2 \\ \end{aligned} \end{aligned}$$

(71)

$$\begin{aligned} \begin{aligned}&{{\tilde{D}}}_n \dot{{\tilde{D}}} _n = {{\tilde{D}}}_n \dot{D}_n - l_n {{\tilde{D}}}_n W_n^{*T} \varPhi _n (Z_n )- l_n {{\tilde{D}}}_n {{\tilde{D}}}_n \\&\ \ \ \ \ \ \ \ \ \le \frac{1}{2}{{\tilde{D}}}_n^2 + \frac{1}{2}\dot{D}_n^2 + r_n \phi _n^2 {{\tilde{D}}}_n^2 + \frac{{l_n^2 }}{{r_n }}||W_n^{*T}||^2 - l_n {{\tilde{D}}}_n^2 \\&\ \ \ \ \ \ \ \ \ \le - ( - \frac{1}{2} - r_n \phi _n^2 + l_n ){{\tilde{D}}}_n^2 + \frac{1}{2} \bar{\bar{D}}_n^2 + \frac{{l_n^2 }}{{r_n }}||W_n^{*T} ||^2 \\ \end{aligned} \end{aligned}$$

(72)

where $|\varPhi _n (Z_n )| \le \phi _n$, $r_n>0$ is a design parameter.

Then, the Lyapunov function is taken as

$$\begin{aligned} V_n = \frac{1}{2}z_n^2 + \frac{1}{{2 }}{{\tilde{W}}}_n^T {\Lambda ^{-1}_n}{{\tilde{W}}}_n + \frac{1}{2}\gamma _n^2 + \frac{1}{2}{{\tilde{D}}}_n^2 \end{aligned}$$

(73)

Differentiating $V_n$

$$\begin{aligned} \begin{aligned}&\dot{V}_{n} = z_{n} ( -z_{n-1}- k_{n} z_{n} + {{\tilde{W}}}_{n} ^T \varPhi _{n} (Z_{n} ) + {{\tilde{D}}}_{n} ) \\&\qquad - {{\tilde{W}}}_{n} ^T{\Lambda ^{-1}_{n}} \dot{\hat{W}}_{n} + \gamma _{n} {\dot{\gamma }} _{n} + {{\tilde{D}}}_{n} \dot{{\tilde{D}}}_{n} \\&\quad\,\,\, = -z_{n-1}z_n - k_{n} z_{n}^2 + z_{n} {{\tilde{D}}}_{n} + \sigma _{n} {{\tilde{W}}}_{n}^T {\hat{W}}_{n} + \gamma _{n} {\dot{\gamma }} _{n} + {{\tilde{D}}}_{n} \dot{{\tilde{D}}}_{n} \\ \end{aligned} \end{aligned}$$

(74)

Consequently, substituting (63), (71) and (72) into (74), we can have the following result

$$\begin{aligned} \begin{aligned}&\dot{V}_n \le -z_{n-1}z_n - k_n z_n^2 + z_n^2 + \frac{1}{2} {{\tilde{D}}}_n^2 + \sigma _n {{\tilde{W}}}_n^T {\hat{W}}_n + \gamma _n {\dot{\gamma }} _n + {{\tilde{D}}}_n \dot{{\tilde{D}}}_n \\&\quad \le - (k_n - 1)z_n^2 - (p_n - r_n \phi _n^2 - \frac{{\mathrm{1}}}{{\mathrm{2}}})\gamma _n^2 \\&\qquad - ( - 1 - r_n \phi _n^2 + l_n ){{\tilde{D}}}_n^2 \\&\qquad -z_{n-1}z_n + \sigma _n {{\tilde{W}}}_{n}^T {\hat{W}}_n + \frac{{l_n^2 + 1}}{{r_n }}||W_n^{*T} ||^2 \\&\qquad + \frac{{\mathrm{1}}}{{\mathrm{2}}}{\bar{D}}_n^2 + \frac{1}{2}\bar{\bar{D}}_n^2 \end{aligned} \end{aligned}$$

(75)

3.3 Main result

Based on the above detailed design procedures, now the main result can be described by the following theorem.

Theorem 1

Based on Assumptions 1–5, for system (1) the disturbance observer is designed in (25), (47), (67), the virtual signals defined in (17), (39) for $1 \le i \le n - 1$ , the real controller defined in (61), and the adaptive law defined in (40) for $1 \le i \le n$, which can ensure that all the signals of the closed-loop system are bounded, and the tracking error converges to a bounded compact set near the origin.

Proof

Firstly, we design the following Lyapunov function candidate to discuss the stability of the closed-loop system.

$$\begin{aligned} \begin{aligned}&V = \sum \limits _{i = 1}^n {V_n } = \sum \limits _{i=1}^{n} {\left( \frac{1}{2}z_i^2 + \frac{1}{{2 }}{{\tilde{W}}}_i^T {\Lambda ^{-1}_i}{{\tilde{W}}}_i + \frac{1}{2}\gamma _i^2 + \frac{1}{2}{{\tilde{D}}}_i^2 \right) } \\&\quad +\sum \limits _{i=1}^{n-1} {\left( \frac{1}{2}e_{i+1}^2 \right) } \end{aligned} \end{aligned}$$

(76)

Based on the fact ${{\tilde{W}}}_{i}^T {\hat{W}}_i \le \frac{{1 }}{2}||W _i^*||^2 - \frac{1}{2}{||{{\tilde{W}}} _i||^2 }$ for $i=1,\cdots ,n$, and differentiating $V_n$, then

$$\begin{aligned} \begin{aligned}&\dot{V} \le - \sum \limits _{i = 1}^{n } (k_i - 1)z_i^2 + \sum \limits _{i = 1}^n \sigma _i {{\tilde{W}}}_{i}^T {\hat{W}}_i - \sum \limits _{i = 1}^n (p_i - r_i \phi _i^2 - \frac{{\mathrm{1}}}{{\mathrm{2}}})\gamma _i^2 \\&\qquad - \sum \limits _{i = 1}^n ( - 1 - r_i \phi _i^2 + l_i ){{\tilde{D}}}_i^2 - \sum \limits _{i = 1}^{n-1} (\frac{1}{{\xi _{i+1} }} - 1)e_{i+1}^2 \\&\qquad + \sum \limits _{i = 1}^n {\left( \frac{{l_i^2 + 1}}{{r_i }}||W_i^{*T} ||^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}}{\bar{D}}_i^2 + \frac{1}{2}\bar{\bar{D}}_i^2 \right) } + \sum \limits _{i = 1}^{n-1} { \frac{1}{2}B_{i+1}^2 }\\&\quad \le - \sum \limits _{i = 1}^{n } (k_i - 1)z_i^2 - \sum \limits _{i = 1}^n \frac{{\sigma _i }}{2} ||{{\tilde{W}}}_{i}||^2 - \sum \limits _{i = 1}^n (p_i - r_i \phi _i^2 - \frac{{\mathrm{1}}}{{\mathrm{2}}})\gamma _i^2 \\&\qquad - \sum \limits _{i = 1}^n ( - 1 - r_i \phi _i^2 + l_i ){{\tilde{D}}}_i^2 - \sum \limits _{i = 1}^{n-1} (\frac{1}{{\xi _{i+1} }} - 1)e_{i+1}^2 \\&\qquad + \sum \limits _{i = 1}^n {\left( \left( \frac{{\sigma _i }}{2} +\frac{{l_i^2 + 1}}{{r_i }} \right) ||W_i^{*T} ||^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}}{\bar{D}}_i^2 + \frac{1}{2}\bar{\bar{D}}_i^2 \right) } \\&\qquad + \sum \limits _{i = 1}^{n-1} { \frac{1}{2}B_{i+1}^2 }\\&\quad = - cV + d \\ \end{aligned} \end{aligned}$$

(77)

where $c = \min \{ 2(k_{\mathrm{{i}}}-1) :1 \le i \le {\mathrm{n}} ,\frac{{\sigma _i }}{{\lambda _{\max } (\Lambda _i^{ - 1} )}} :1 \le i \le {\mathrm{n}} , 2(p_i - r_i \phi _i^2 - \frac{{\mathrm{1}}}{{\mathrm{2}}}) :1 \le i \le {\mathrm{n}}, 2( - 1 - r_i \phi _i^2 + l_i ) :1 \le i \le {\mathrm{n}} , (\frac{1}{{\xi _{i+1} }} - 1) :1 \le i \le {\mathrm{n}-1}\}$, and

$$\begin{aligned} d= & {} \sum \limits _{i = 1}^n {\left( \left( \frac{{\sigma _i }}{2} +\frac{{l_i^2 + 1}}{{r_i }} \right) ||W_i^{*T} ||^2 + \frac{{\mathrm{1}}}{{\mathrm{2}}}{\bar{D}}_i^2 + \frac{1}{2}\bar{\bar{D}}_i^2 \right) } \\&+ \sum \limits _{i = 1}^{n-1} { \frac{1}{2}B_{i+1}^2 } \end{aligned}$$

Multiplying (77) by $e^{ct}$ on both sides, and integrating from 0 to t, one can get

$$\begin{aligned} V(t) \le \left( V(0)-\frac{d}{c} \right) e^{-ct}+\frac{d}{c} \end{aligned}$$

(78)

For (78), if $t \rightarrow \infty$, then $e^{-ct} \rightarrow 0$ and V is convergent. This means that all the signals $z_i$, ${\tilde{W}}_i$, $\gamma _i$, ${{\tilde{D}}}_i$ and $e_{i+1}$ are all bounded.

In what follows, we consider the boundedness of $\mu _i$. Let the Lyapunov function defined as

$$\begin{aligned} V_{\mu _0 } = \frac{1}{2}\sum \limits _{i = 1}^n {\mu _i^2 } + \frac{1}{\beta }\int _{t - \tau }^t {\int _\theta ^t {||\dot{v}(s)} ||^2 dsd\theta } \end{aligned}$$

(79)

Thus, the derivative of $V_{\mu _0 }$ satisfies that

$$\begin{aligned} \begin{aligned}&\dot{V}_{\mu _0 } \le \mu _1 (\mu _2 - p_1 \mu _1 ) + \sum \limits _{i = 2}^{n - 1} {\mu _i (\mu _{i + 1} - p_i \mu _i - g_{i - 1} \mu _{i - 1} )} \\&\qquad + \mu _n ( - p_n \mu _n \\&\qquad - g_{n - 1} \mu _{n - 1} + D(v(t - \tau )) - D(v(t)))\\&\qquad + \frac{\tau }{\beta }||\dot{v}(t)||^2 - \frac{1}{\beta }\int _{t - \tau }^t {||\dot{v}(s)||^2 ds} \\&\quad =\sum \limits _{i = 1}^{n - 1} {((1 - g_i )\mu _i \mu _{i + 1} )} \\&\qquad + \sum \limits _{i = 1}^n {( - p_i \mu _i^2 )} + (D(v(t - \tau )) - D(v(t)))\mu _n \\&\qquad + \frac{\tau }{\beta }||\dot{v}(t)||^2 - \frac{1}{\beta }\int _{t - \tau }^t {||\dot{v}(s)||^2 ds} \\&\quad \le \sum \limits _{i = 1}^{n - 1} {\frac{{|1 - g_i |}}{2}(\mu _i^2 + \mu _{i + 1}^2 )} \\&\qquad + \sum \limits _{i = 1}^{n - 1} {( - p_i \mu _i^2 ) + ( - p_n \mu _n^2 )} + (mv(t - \tau ) \\&\qquad - mv(t))\mu _n + (dv(t - \tau ) - dv(t))\mu _n + \frac{\tau }{\beta }||\dot{v}(t)||^2 \\&\qquad - \frac{1}{\beta }\int _{t - \tau }^t {||\dot{v}(s)||^2 ds} \\&\quad \le - (p_1 - \frac{{|1 - g_1 |}}{2})\mu _1^2 \\&\qquad - \sum \limits _{i = 2}^{n - 1} {(p_i - \frac{{|1 - g_{i - 1} |}}{2} - \frac{{|1 - g_i |}}{2})\mu _i^2 } - (p_n \\&\qquad - \frac{{|1 - g_{n - 1} |}}{2} - 1)\mu _n^2 + \frac{{m^2 }}{{2 }}||v(t - \tau ) - v(t)||^2 \\&\qquad + \frac{1}{2}||dv(t - \tau ) - dv(t)||^2 \\&\qquad + \frac{\tau }{\beta }||\dot{v}(t)||^2 - \frac{1}{\beta }\int _{t - \tau }^t {||\dot{v}(s)||^2 ds} \\ \end{aligned} \end{aligned}$$

(80)

Based on Assumption 3, we have

$$\begin{aligned} \frac{1}{2}||dv(t - \tau ) - dv(t)||^2 \le \frac{1}{2}(||dv(t - \tau )||^2 + ||dv(t)||^2) \le d^{*2} \end{aligned}$$

(81)

According to the Cauchy–Schwarz inequality, then

$$\begin{aligned} \frac{1}{{2}}||v(t - \tau ) - v(t)||^2 \le \frac{\tau }{{2 }}\int _{t - \tau }^t {||\dot{v}(s)||^2 ds} \end{aligned}$$

(82)

Furthermore, substituting (81) and (82) into (80), one has

$$\begin{aligned}&\dot{V}_{\mu _0 } \le - \sum \limits _{i = 1}^n {{\bar{h}}_i \mu _i^2 } - \left( {\frac{1}{\beta } - \frac{m \tau }{{2 }}} \right) \int _{t - \tau }^t {||\dot{v}(s)||^2 ds} \nonumber \\&\quad + \frac{\tau }{\beta }||\dot{v}(t)||^2 + d^{*2} \end{aligned}$$

(83)

where ${\bar{h}}_1 = h_1 - \frac{{|1 - g_1 |}}{2}$ , ${\bar{h}}_i = h_i - \frac{{|1 - g_i | + |1 - g_{i - 1} |}}{2}$ , $i = 2,3,\; \cdots ,n - 1$, and ${\bar{h}}_n = h_n - \frac{{|1 - g_{n - 1} | }}{2}-1$.

In what follows, we consider the boundedness of $\frac{\tau }{\beta }||\dot{v}(t)||^2$ in (83).

According to (10), (17), (18), (39),(40),(61) and (62), we describe v(t) and $\dot{v}(t)$ as

$$\begin{aligned} v(t) = \zeta _1 (z_{n-1}, z_n ,{\hat{W}}_n , {\hat{D}}_n) + \zeta _2 \mu _{n} + \zeta _3 \mu _{n - 1} + \zeta _4 (e_n ) \end{aligned}$$

(84)

$$\begin{aligned} \begin{aligned}&\dot{v}(t) = \zeta _5 (z_{n - 2} ,z_{n - 1}, z_n ,{\hat{W}}_{n - 1}, {\hat{W}}_n , {{\tilde{D}}}_{n}) + \sum \limits _{j = 1}^n {\zeta _{8j} (z,{\hat{W}} )\mu _j} \\&\ \ \ \ \ \ \ \ \ \ + \zeta _6(M_n(.), e_n )+\zeta _7 (z,{\hat{W}} )v(t - \tau )\\ \end{aligned} \end{aligned}$$

(85)

where $\zeta _1 (.), \zeta _2 (.), \cdots , \zeta _7 (.)$ and $\zeta _{8j} (.)(1 \le j \le n)$ are $C^1$ functions. Due to the fact that $z_{n-2}$, $z_{n-1}$, $z_{n}$, ${\hat{W}}_{n-1}$, ${\hat{W}}_n$, ${\hat{D}}_n$ , ${{\tilde{D}}}_n$, $e_n$ and $M_n(.)$ are all bounded, therefore, one can obtain that

$$\begin{aligned} |\zeta _i || \le \kappa _i ,i = 1,2,\cdots ,7 \ \text {and} \ ||\zeta _{ik} || \le \kappa _{jk} \end{aligned}$$

(86)

where $\kappa _i$ and $\kappa _{jk} ,(j = 8; 1 \le k \le n)$ are the positive constants.

$$\begin{aligned} \begin{aligned}&||v(t)||^2 \le (||\zeta _1 || + ||\zeta _2|| \mu _{n-1} + ||\zeta _3|| \mu _{n} + ||\zeta _4 (e_n)|| )^2 \\&\ \ \ \ \ \ \ \ \ \ \ \ \le ( \kappa _1 + \kappa _2 \mu _n + \kappa _3 \mu _{n - 1} + \kappa _4)^2\\&\ \ \ \ \ \ \ \ \ \ \ \ \le 4\kappa _1^2 + 4\kappa _2^2 \mu _n^2 + 4\kappa _3^2 \mu _{n - 1}^2 + 4\kappa _4^2 \\&\ \ \ \ \ \ \ \ \ \ \ \ \le \kappa '_1 + \kappa '_2 \mu _n^2 + \kappa '_{3} \mu _{n - 1}^2 + \kappa '_4 \\ \end{aligned} \end{aligned}$$

(87)

where $\kappa '_1 = 4\kappa _1^2$, $\kappa '_2 = 4\kappa _2^2$, $\kappa '_3 = 4\kappa _3^2$, and $\kappa '_4= 4\kappa _4^2$. Furthermore, for $v(t - \tau )$ it satisfies that

$$\begin{aligned} ||v(t - \tau )||^2 \le \kappa '_1 + \kappa '_2 \mu _n^2(t - \tau ) + \kappa '_{3} \mu _{n - 1}^2(t - \tau ) + \kappa '_4 \end{aligned}$$

(88)

From (85) and (88), the upper boundedness of $\frac{\tau }{\beta }||\dot{v}(t)||^2$ can be estimated by

$$\begin{aligned} \begin{aligned}&\frac{\tau }{\beta }||\dot{v}(t)||^2 \le \frac{\tau }{\beta }|| \zeta _5 + \sum \limits _{j = 1}^n {\zeta _{8j} (z,{\hat{W}} )\mu _j} \\&\qquad + \zeta _6(M_n(.), e_n )+\zeta _7 (z,{\hat{W}} )v(t - \tau )||^2 \\&\quad \le \frac{\tau }{\beta }4(\kappa _5^2 + n\sum \limits _{j = 1}^n {\kappa _{8j}^2 \mu _j^2 } + \kappa _6^2 + \kappa _7^2 v^2 (t - \tau )) \\&\quad \le \frac{\tau }{\beta }(4\kappa _5^2 + 4\kappa _7^2 (\kappa '_1+\kappa '_4) + \kappa _6^2 + 4n\sum \limits _{j = 1}^n {\kappa _{8j}^2 \mu _j^2 } \\&\qquad + 4\kappa _7^2 \kappa '_2 \mu _n^2 (t - \tau ) + 4\kappa _7^2 \kappa '_3 \mu _{n - 1}^2 (t - \tau )) \\&\quad \le \frac{\tau }{\beta }(\kappa '_5 + \sum \limits _{j = 1}^n {\kappa '_{8j} \mu _j^2 } + \kappa '_6 \mu _n^2 (t - \tau ) + \kappa _7 ' \mu _{n - 1}^2 (t - \tau )) \\ \end{aligned} \end{aligned}$$

(89)

where $\kappa '_5 = 4\kappa _5^2 + 4\kappa ^2_7( \kappa '_1+\kappa '_4)+\kappa ^2_6$ , $\kappa '_{8j} =4n\kappa _{8j}^2$, $\kappa '_6 = 4\kappa _7^2 \kappa '_2$ and $\kappa '_7 = 4\kappa _7^2 \kappa '_3$.

According to (89) and rewriting (83) as

$$\begin{aligned} \begin{aligned}&\dot{V}_{\mu _0 } \le - \sum \limits _{i = 1}^n {{{\tilde{h}}}_i \mu _i^2 } - \left( {\frac{1}{\beta } - \frac{m \tau }{{2 }}} \right) \int _{t - \tau }^t {||\dot{v}(s)||^2 ds} + \frac{{\tau \kappa '_6 }}{\beta }\mu _n^2 (t - \tau ) \\&\ \ \ \ \ \ \ \ \ + \frac{{\tau \kappa '_7 }}{\beta }\mu _{n-1}^2 (t - \tau ) + d^{*2}+ \frac{\tau }{\beta }\kappa '_5 \end{aligned} \end{aligned}$$

(90)

where ${{\tilde{h}}}_i = {\bar{h}}_i - \frac{\tau }{\beta }\kappa '_{8i}$ ,$1 \le i \le n$.

For the auxiliary system (9), let the Lyapunov function candidate be

$$\begin{aligned} \begin{aligned} V_\mu = V_{\mu 0} + \frac{{\tau \kappa '_{6} }}{\beta }\int _{t - \tau }^t {\mu _n^2 (s)ds + \frac{1}{v_1}\int _{t- \tau }^{t } {\int _\theta ^t {\mu _n^2 (s)dsd\theta } } } \\ \ \ \ \ \ \ \ \ {\mathrm{}} + \frac{{\tau \kappa '_{7} }}{\beta }\int _{t - \tau }^t {\mu _{n-1}^2 (s)ds} +{ \frac{1}{v_2}\int _{t- \tau }^{t} {\int _\theta ^t {\mu _{n-1}^2 (s)dsd\theta } } } \end{aligned} \end{aligned}$$

(91)

Differentiating $V_\mu$, then

$$\begin{aligned} \begin{aligned}&\dot{V}_\mu \le - \sum \limits _{i = 1}^n {{\hat{h}}_i \mu _i^2 } - \left( {\frac{1}{\beta } - \frac{m \tau }{{2}}} \right) \int _{t - \tau }^t {||\dot{v}(s)||^2 ds} - \frac{1}{v_1}\int _{t - \tau }^t {\mu _n^2 (s)ds} \\&\ \ \ \ \ \ \ \ - \frac{1}{v_2}\int _{t - \tau }^t {\mu _{n-1}^2 (s)ds} + \frac{\tau }{\beta }\kappa '_4 + d^{*2}+ \frac{\tau }{\beta }\kappa '_5 \end{aligned} \end{aligned}$$

(92)

where ${\hat{h}}_i = {{\tilde{h}}}_i$ $(1 \le i \le n - 2)$, ${\hat{h}}_{n-1} = {{\tilde{h}}}_{n-1} + \frac{\tau }{\beta }\kappa '_7 - \frac{\tau }{v_2}$, and ${\hat{h}}_n = {{\tilde{h}}}_n + \frac{\tau }{\beta }\kappa '_6 - \frac{\tau }{v_1}$.

By designing the parameters $h_i, \beta$ , $v_1$ and $v_2$, we can have

$$\begin{aligned} {\hat{h}}_i> 0, \ \frac{1}{\beta } - \frac{m \tau }{{2}} > 0 \end{aligned}$$

(93)

Furthermore, one can get

$$\begin{aligned}&\int _{t - \tau }^t {\int _\theta ^t {||\dot{v}(s)||^2 dsd\theta } }\nonumber \\&\quad \le \tau \mathop {\sup }\limits _{\theta \in [t - \tau ,t]} \int _{t - \tau }^t {||\dot{v}(s)||^2 ds}= \tau \int _{t - \tau }^t {||\dot{v}(s)||^2 ds} \end{aligned}$$

(94)

$$\begin{aligned}&\int _{t - \tau }^t {\int _\theta ^t { {\mu _k^2 (s)} dsd\theta } }\nonumber \\&\quad \le \tau \mathop {\sup }\limits _{\theta \in [t - \tau ,t]} \int _{t - \tau }^t { {\mu _k^2 (s)} ds}= \tau \int _{t - \tau }^t { {\mu _k^2 (s)} ds} , \ \ \ k=n-1, n. \end{aligned}$$

(95)

Consequently, the derivative of $V_\mu$ satisfies that

$$\begin{aligned} \begin{aligned}&\dot{V}_\mu \le - \sum \limits _{i = 1}^n {{\hat{h}}_i \mu _i^2 } - \left( {\frac{1}{\beta } - \frac{m \tau }{{2}}} \right) \int _{t - \tau }^t {||\dot{v}(s)||^2 ds} \\&\qquad - \left( {\frac{1}{v_{1}} - \frac{{\tau \kappa '_6 }}{\beta }} \right) \int _{t - \tau }^t {\mu _n^2 (s)ds} \\&\qquad - \frac{{\tau \kappa '_6 }}{\beta }\int _{t - \tau }^t {\mu _n^2 (s)ds} - \left( {\frac{1}{v_{2}} - \frac{{\tau \kappa '_7 }}{\beta }} \right) \int _{t - \tau }^t {\mu _{n-1}^2 (s)ds} \\&\qquad - \frac{{\tau \kappa '_7 }}{\beta }\int _{t - \tau }^t {\mu _{n-1}^2 (s)ds} + \frac{\tau }{\beta }\kappa '_4 + d^{*2}+ \frac{\tau }{\beta } \kappa '_5\\&\quad \le - \sum \limits _{i = 1}^n {{\hat{h}}_i \mu _i^2 } - \left( {\frac{1}{\tau } - \frac{m \beta }{{2 }}} \right) \frac{1}{\beta }\int _{t - \tau }^t {\int _\theta ^t {||\dot{v}(s)||^2 dsd\theta } } \\&\qquad - \left( {\frac{1}{\tau } - \frac{{v_1 \kappa '_6 }}{\beta }} \right) \frac{1}{v_1}\int _{t - \tau }^t {\int _\theta ^t {\mu _n^2 dsd\theta } } - \frac{{\tau \kappa '_6 }}{\beta }\int _{t - \tau }^t {\mu _n^2 (s)ds} \\&\qquad - \left( {\frac{1}{\tau } - \frac{{v_2 \kappa '_7 }}{\beta }} \right) \frac{1}{v_2}\int _{t - \tau }^t {\int _\theta ^t {\mu _{n-1}^2 dsd\theta } } - \frac{{\tau \kappa '_7 }}{\beta }\int _{t - \tau }^t {\mu _{n-1}^2 (s)ds} \\&\qquad + \frac{\tau }{\beta }\kappa '_4 + d^{*2}+ \frac{\tau }{\beta } \kappa '_5 \\&\quad \le - \varrho V_\mu + \kappa \\ \end{aligned} \end{aligned}$$

(96)

where $\varrho = \min \{ 2{\hat{h}}_i ,\frac{1}{\tau } - \frac{m \beta }{{2}},\frac{1}{\tau } - \frac{{v_1\kappa '_6 }}{\beta } , 1 ,\frac{1}{\tau } - \frac{{v_2\kappa '_7 }}{\beta }, i = 1,2, \cdots ,n\}$ and $\kappa = \frac{\tau }{\beta }\kappa '_4 + d^{*2}+ \frac{\tau }{\beta } \kappa '_5$.

By integrating (96) on both sides over [0, t], one can obtain that

$$\begin{aligned} V_\mu (t) \le (V_\mu (0) - \frac{\kappa }{\varrho })e^{ - \varrho t} + \frac{\kappa }{\varrho } \end{aligned}$$

(97)

From (98), we can conclude that $\mu _i$ is bounded, i.e.,

$$\begin{aligned} | \mu _i | \le \sqrt{2 (V_\mu (0) - \kappa /\varrho )e^{ - \varrho t} + \kappa /\varrho } \ \ \ \ i=1,2, \cdots , n. \end{aligned}$$

(98)

According to (78), the signals $z_i$, ${\tilde{W}}_i$, $\gamma _i$, ${{\tilde{D}}}_i$ and $e_{i+1}$ for $1 \le i \le n$ are all bounded. Furthermore, from (17), (39), (61) and (98) one can get $\alpha _i$ and v are also bounded. Thus, $\omega _i$ is bounded which can be derived from the fact that $e_{i+1}$ and $\alpha _i$. Consequently, based on the boundedness of $z_i$, $\mu _i$, $\omega _i$, $\alpha _i$ and v, one can get $x_i$ is also bounded. In particular, one can get $|y - y_d| \le |z_1|+|\mu _1|$ which means that the tracking error is bounded. From above discussions, we can get that for $1 \le i \le n$, all the signals of the closed-loop system are all bounded. The proof is completed.

Remark 5

From above discussions, the tracking error can be minimized by adjusting the design parameters $k_i$, $h_i$, $g_i$, $\sigma _i$, $p_i$, $l_i$ and $\xi _i$, such that a good robust performance of the closed-loop systems can be obtained. In particular, if we increase the parameters $k_i$, $h_i$, $g_i$, $p_i$ and $l_i$, the tracking errors will be decreased. On the other hand, if we decrease the parameters of $\xi _i$, $\sigma _i$, then the tracking errors will also be decreased.

Remark 6

Based on the auxiliary system, the disturbance observer is introduced to estimate the approximation error and unknown time-varying external disturbance. There is no need to know the boundary of the approximation error or time-varying external disturbance.

Remark 7

The output information of the disturbance observer is employed to construct the virtual control signal and the real control signal. Then the control signal can be adaptive adjusted according to the output of the disturbance observer. Compared with the existing results in [28,29,30,31,32,33, 49,50,51,52,53], the proposed adaptive neural dynamic surface control scheme in this paper which not only estimates the unknown time-varying external disturbance and the approximation error caused by the NNS, but also eliminates the effect caused by input delay and dead-zone. Consequently, the disturbance rejection performance of the closed-loop system can be effectively improved.

Remark 8

In practical applications, the proposed auxiliary system can be constructed easily according to the number of system state variables. The compensation signal $\mu _i {\mathrm{(i = 1,2,}} \cdots {\mathrm{,n)}}$ in the auxiliary system can be used in the virtual signals and real control signal. The stability of the closed-loop system can also be guaranteed by choosing the appropriate Lyapunov function and the setting parameters.

4 Simulation

In this section, two examples of strict-feedback nonlinear systems are given to show the effectiveness and characteristics of the proposed method. Example 1 is a third-order numerical example with constant input delay and dead-zone used for a comparison with the proposed method in [53]. Example 2 is an application example of third-order one-link robot system with time-varying input delay and dead-zone used to show the superiority of the proposed approach.

Example 1

A third-order nonlinear system with time-varying external disturbance, input dead-zone and input delay described as the following form:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_1 = - x_1^2-sin(x_1) + x_2 + d_1(t) \\ \dot{x}_2 = x_1^2+ x_1 x_2 +x_2 cos(x_1) + x_3 +d_2(t) \\ \dot{x}_3 = 0.1x_1 x_2 e^{x_3 } + 0.5x_3 \cos (x_1 x_2 ) +D(v(t - \tau )) +d_3(t)\\ y = x_1 \\ \end{array} \right. \end{aligned}$$

where $d_1(t)=0.5cos(t)$, $d_2(t)=sin(0.5t)$ and $d_3(t)=sin(0.2t)+0.5cos(0.1t)$ are time-varying external disturbance. The initial conditions $x (0)=[0.5, 0,0]^T$.

The control object is to make the output to track the reference signal $y_d=0.5sin(t)+0.5cos(0.5t)$ with the input delay being $\tau =1s$, and the dead-zone parameters being $m=1$, $b_r=2$, $b_l=-2$.

Firstly, in order to verify the effectiveness of the proposed method in this paper, a comparison with the proposed method in [53] is carried out to test the tracking performance for the reference signal.

The simulation parameters in [53] (please see [53]) which are selected as $k_1=20$, $k_2=30$, $k_3=40$, $\Lambda _1=0.01I$, $\Lambda _2=0.02I$, $\Lambda _3=0.01I$, $\sigma _1=5$, $\sigma _2=8$, $\sigma _3=15$, $c_1=8$, $c_2=10$, $c_3=15$, $l_1=20$, $l_2=20$, $l_3=50$, $\beta _1=0.015$, $\beta _2=0.01$. The simulation result is shown in Fig. 1.

Fig. 1

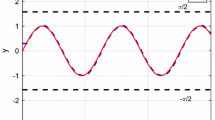
The trajectories of $x_1$ and $y_d$ with input delay $\tau =1s$ using the method [53] in example 1

From Fig. 1, one can observe that the system trajectory $x_1$ can not track the reference signal $y_d$, and the system trajectory $x_1$ is unstable when the input delay $\tau =1s$, input dead-zone, and external disturbances appear. The simulation result shows that the control signal is completely invalid when the input delay occurs. This means that, the Pade approximation method is invalid for long input delay.

In what follows, we test the effectiveness of the proposed method in this article. In the simulation, some parameters are selected as above, let the parameters be ${\hat{W}} _1(0)$= ${\hat{W}}_2(0)$= ${\hat{W}}_3(0)=0.1$, $\gamma _1(0)=\gamma _2(0)=\gamma _3(0)=0$, $\mu _1(0)$=$\mu _2(0)$=$\mu _3(0)=0$, $\omega _1(0)=\omega _2(0)=0$, $o_1(0)=o_2(0)=o_3(0)=0$, $k_1=20$, $k_2=30$, $k_3=40$, $h_1=2$, $h_2 =4$, $h_3=3$, $g_1=1$, $g_2=1$, $\Lambda _1=0.01I$, $\Lambda _2=0.02I$, $\Lambda _3=0.01I$, $\sigma _1=5$, $\sigma _2=8$, $\sigma _3=15$, $p_1=8$, $p_2=10$, $p_3=15$, $l_1=20$, $l_2=20$, $l_3=50$, $\xi _1=0.015$, $\xi _2=0.01$. The Gaussian NNS are employed in the simulation, and the center of the receptive field is $v=[-5,-4,-3,-2,-1,0,1,2,3,4,5]^T$ with the width $\eta =1$. The simulation time is 30s, and the simulation results are shown in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10.

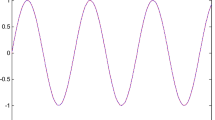
Figure 2 draws the trajectories of the state $x_1$ and $y_d$.

Fig. 2

The trajectories of $x_1$ and $y_d$ with input delay $\tau =1s$ in example 1

From Fig. 2, one can observe that under the input delay $\tau =1s$, input dead-zone and external disturbances, the system state trajectory of $x_1$ can track $y_d$ quickly.

Figure 3 draws the state trajectories of $x _2$ and $x _3$, respectively. From Fig.3 one can observe that the state trajectories of $x _2$ and $x _3$ are all bounded with input delay $\tau =1s$, input dead-zone, and time-varying external disturbances.

Fig. 3

The trajectories of $x_2$ with input delay $\tau =1s$ in example 1

Figure 4 depicts the trajectories of $z_1$, $z_2$ and $z_3$ are all bounded with input delay $\tau =1s$, input dead-zone and time-varying external disturbances. This means that the proposed adaptive controller can ensure that the tracking errors converge to a compact set of the origin.

Fig. 4

The trajectories of $z_1$,$z_2$ and $z_3$ in example 1

Figure 5 depicts the state trajectories of auxiliary system $\mu _1$, $\mu _2$ and $\mu _3$

Fig. 5

The auxiliary system’s states $\mu _1$, $\mu _2$ and $\mu _3$ in example 1

From Fig. 5, one can observe that the auxiliary systems $\mu _1$, $\mu _2$ and $\mu _3$ are asymptotically stable. Therefore, the compensation signals are bounded, which verifies the correctness of the theoretical analysis.

Figure 6 displays the adaptive laws $\hat{W} _1$, $\hat{W}_2$ and $\hat{W}_3$ are bounded.

Fig. 6

The adaptive laws’ trajectories $\hat{W} _1$, $\hat{W}_2$ and $\hat{W}_3$ in example 1

From the simulation result in Fig.6, although the input delay and input dead zone exist in practical system, one can conclude that the adaptive laws are all bounded. This demonstrates the effectiveness of the proposed compensation mechanism.

Figures 7, 8 and 9 depict the trajectories of ${\hat{D}}_1$, $D_1$, ${\hat{D}}_2$, $D_2$, ${\hat{D}}_3$, $D_3$, respectively.

Fig. 7

The adaptive laws’ trajectories ${\hat{D}}_1$, and $D_1$ in example 1

Fig. 8

The adaptive laws’ trajectories ${\hat{D}}_2$, and $D_2$ in example 1

Fig. 9

The adaptive laws’ trajectories ${\hat{D}}_3$, and $D_3$ in example 1

From Figs. 7, 8, 9, one can observe that the proposed disturbance observer can estimate the approximation error and the external time-varying disturbance accurately and quickly. This means that the proposed disturbance observer can effectively provide the estimation information for the adaptive controller, thus improving the disturbance rejection performance of the closed-loop system.

The control signal $D(v(t- \tau ))$ with $\tau =1s$ is shown in Fig. 10. It can be seen from Fig. 10 that the input signal is bounded.

Fig. 10

The control signal $D(v(t - \tau ))$ with $\tau =1s$ in example 1

From Fig. 10, one can observe that the proposed controller is bounded by using the compensation mechanism, although the input delay and input dead zone exist in practical system.

From the simulation results in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10 one can obtain that for input delay $\tau = 1s$ and the time-varying external disturbance $d_1(t)=0.5cos(t)$, $d_2(t)=sin(0.5t)$ and $d_3(t)=sin(0.2t)+0.5cos(0.1t)$, and input dead-zone, all the signals of the closed-loop systems are bounded by using the proposed adaptive neural controller.

From the comparative results of Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, one can observe that the proposed method in this paper can tackle disturbance-observer-based adaptive control for strict-feedback systems with long input delay and dead-zone. At the same time, the proposed scheme shows excellent tracking performance.

Example 2

Consider a one-link robot system used in [58]. The dynamics model of the system with input dead-zone and time-varying delay is described as follows:

$$\begin{aligned} \left\{ \begin{aligned}&D\ddot{q} + B\dot{q} + N \sin (q) = I \\&M \dot{I} +JI= - K_m \dot{q} + D(v(t - \tau )) \\&y = q \\ \end{aligned} \right. \end{aligned}$$

where q represents the link position, $\dot{q}$ represents the angular velocity, and $\ddot{q}$ represents the angular acceleration. I denotes the motor shaft angle and $\dot{I}$ denotes the velocity. v is the motor torque, and $D(v(t - \tau ))$ represents the input dead-zone and delay for control input v.

Let $x_1=q$, $x_2=\dot{q}$ and $x_3=I/D$, we add the external disturbances $d_1(t)=0.3sin(t)$, $d_2(t)=0.2sin(2t)$ and $d_3(t)=0.3cos(t)$ and rewrite the system as

$$\begin{aligned} \left\{ \begin{aligned}&\dot{x}_1 = x_2 + d_1(t) \\&\dot{x}_2 = - \frac{N}{D}\sin (x_1 ) - \frac{B}{D}x_2 + x_3 + d_2(t) \\&\dot{x}_3 = - \frac{{K_m }}{M}x_2 - \frac{DJ}{M}x_3 + \frac{1}{M}D(v(t - \tau ) )+ d_3(t) \\&y = x_1 \\ \end{aligned} \right. \end{aligned}$$

where $D=1$, $B=1$, $M=1$, $K_m=10$, $J=0.5$, $N=10$ and $x (0)=[0, 0,0]^T$.

The control object is to make the output to track the reference signal $y_d=0.5sin(t)$ with the time-varying input delay being $\tau =0.8+0.5sin(t)s$, and the dead-zone parameters being $m=2.5$, $b_r=2$, $b_l=-2$.

Let the initial conditions ${\hat{W}} _1(0)$= ${\hat{W}}_2(0)$= ${\hat{W}}_3(0)=0.01$, $\gamma _1(0)=\gamma _2(0)=\gamma _3(0)=0$, $\mu _1(0)$=$\mu _2(0)$=$\mu _3(0)=0$, $\omega _1(0)=\omega _2(0)=0$, $o_1(0)=o_2(0)=o_3(0)=0$, $k_1=20$, $k_2=10$, $k_3=10$, $h_1=8$, $h_2 =8$, $h_3=5$, $g_1=2$, $g_2=2$, $\Lambda _1=0.0001I$, $\Lambda _2=0.0001I$, $\Lambda _3=0.0001I$, $\sigma _1=1$, $\sigma _2=1$, $\sigma _3=1$, $p_1=9$, $p_2=9$, $p_3=9$, $l_1=18$, $l_2=18$, $l_3=18$, $\xi _1=0.015$, $\xi _2=0.01$. The Gaussian NNS are employed in the simulation, and the center of the receptive field is $v=[-5, -4, -3, -2, -1, 0, 1,$ $2, 3, 4, 5]^T$ with the width $\eta =1$. The simulation time is 30s, and the simulation results are shown in Figs. 11, 12, 13, 14, 15, 16, 17, 18, 19. The trajectories of the state $x_1$ and $y_d$ are depicted in Fig. 11.

Fig. 11

The trajectories of $x_1$ and $y_d$ with time-varying input delay $\tau =0.8+0.5sin(t)s$ in example 2

From Fig. 11, one can observe that under the input delay $\tau =0.8+0.5sin(t)s$, input dead-zone and external disturbances, the system state trajectory of $x_1$ can track the reference signal $y_d$.

Figure 12 draws the state trajectories of $x _2$ and $x _3$.

Fig. 12

The state trajectory of $x _2$ and $x _3$ with input delay $\tau =0.8+0.5sin(t)s$ in example 2

From Fig.12 we can see that the state trajectories of $x _2$ and $x_3$ are bounded with input delay $\tau =0.8+0.5sin(t)s$, input dead-zone and external disturbances.

Figure 13 depicts the trajectories of $z_1$, $z_2$ and $z_3$.

Fig. 13

The trajectory of $z_1$, $z_2$ and $z_3$ in example 2

From Fig. 13, we can observe that all the signals of the tracking errors are bounded by using the proposed adaptive controller with input delay $\tau =0.8+0.5sin(t)s$, input dead-zone and time-varying external disturbances.

Figure 14 shows the state trajectories of auxiliary system $\mu _1, \mu _2$ and $\mu _3$ are asymptotically stable.

Fig. 14

The auxiliary system’s states $\mu _1$, $\mu _2$ and $\mu _3$ in example 2

Figure 15 displays the adaptive laws $\hat{W} _1$, $\hat{W}_2$ and $\hat{W}_3$ are bounded with time-varying input delay, input dead-zone and time-varying external disturbances.

Fig. 15

The adaptive laws’ trajectories $\hat{W} _1$, $\hat{W}_2$ and $\hat{W}_3$ in example 2

Figures 16, 17 and 18 depict the trajectories of ${\hat{D}}_1$, $D_1$, ${\hat{D}}_2$, $D_2$, ${\hat{D}}_3$, $D_3$, respectively.

Fig. 16

The adaptive laws’ trajectories ${\hat{D}}_1$, and $D_1$ in example 1

Fig. 17

The adaptive laws’ trajectories ${\hat{D}}_2$, and $D_2$ in example 1

Fig. 18

The adaptive laws’ trajectories ${\hat{D}}_3$, and $D_3$ in example 1

From Figs. 16, 17, 18, one can observe that the proposed disturbance observer can estimate the approximation error and the external time-varying disturbance accurately and quickly.

The control signal $D(v(t- \tau ))$ with $\tau =0.8+0.5sin(t)s$ is shown in Fig.19.

Fig. 19

The control signal $D(v(t - \tau ) )$ with $\tau =0.8+0.5sin(t)s$ in example 2

From the simulation results in Figs. 11, 12, 13, 14, 15, 16, 17, 18, 19, one can conclude that for the time-varying input delay $\tau =0.8+0.5sin(t)s$, input dead-zone and the time-varying external disturbance $d_1(t)=0.3sin(t)$, $d_2(t)=0.2sin(2t)$ and $d_3(t)=0.3cos(t)$, all the signals of the closed-loop systems are bounded by using the proposed adaptive neural controller.

In order to illustrate the superiority of the proposed method in this paper, a comparison with [52] and [53] is carried out to test the effectiveness of the method in handling different input delays. The reference signal is selected as above, and the comparison results are shown in Table 1. In Table 1, the mark $\checkmark$ denotes the output signal can track the reference signal, and the mark $\times$ denotes the output signal cannot track the reference signal.

Table 1 The comparison between different methods

From the results in Table 1, one can observe that for the smallest input delay, all proposed method are effectiveness. However, if the input delay $\tau \ge 0.1s$, the method in [52] is completely invalid, and the output signal of the system cannot track the reference signal. The method in [53] is superior to the method in [52]. However, if the input delay $\tau \ge 1.5s$, then the closed-loop system become unstable for the method in [53]. For the proposed method in this paper, the system state variables are still controllable when $\tau \le 2.0s$. From the results in Table 1, one can conclude that the proposed method in this paper is super to the methods in [52, 53].

4.1 Comparative explanations

The proposed method in this paper gives an effective way for strict-feedback nonlinear systems with time-varying external disturbance, input dead-zone and input delay. Compared with the existing results in [13,14,15,16, 28,29,30,31,32,33, 49,50,53], the main advantages of the proposed method can be summarized in the following three aspects.

• (1) The proposed compensation mechanism is convenient to overcome the design difficulty on the input-delay systems theoretically. Unlike the Pade approximation method which is invalid once the input delay is long, the proposed method can tackle long input delay.

• (2) Different from [28,29,30,31,32,33], the proposed control scheme can not only estimate the unknown time-varying external disturbance and the approximation error caused by the NNS, but also eliminate the effect caused by input delay and dead-zone.

• (3) Compared with the existing results in [13,14,15,16] [49,50,51,52,53], the disturbance rejection performance of the closed-loop system can be effectively improved. Especially, when the system has input delay and dead zone, the robust performance of the system can be effectively guaranteed.

5 Conclusions

In this article, based on the idea of DSC scheme and by combing NNS with backstepping technique, we consider disturbance-observer-based adaptive tracking control for strict-feedback nonlinear systems with time-varying external disturbance, input dead-zone and input delay. To degrade the complexity and difficulty of controller design, a novel compensation mechanism is developed to exclude the effect caused by input dead-zone and input delay. Based on the auxiliary system, a disturbance observer is constructed to estimate the approximation error and the unknown external time-varying disturbance in each backstepping step, and the effect of input dead zone and delay can be eliminated. The “explosion of complexity” problem has been avoided by DSC scheme. Finally, the simulation results show that the proposed scheme has better tracking performance. In the future, we will discuss the problem of nonlinear systems control with unknown input delay in depth.