1 Introduction

Clustering is a hot topic in machine learning [1], which groups similar data into a same cluster while different data are assigned distinct clusters. With the development of media technology, image clustering is a significant problem and has wide applications such as face recognition [2], image annotation [3], image retrieval [4], and image segmentation [5]. Many different clustering algorithms are applied in image clustering, like the partition-based method [6], the density-based method [7], and the hierarchical method [8]. However, the high dimension of a picture always causes the “curse of dimension” phenomenon. So, in image clustering, the dimension reduction method plays an essential role. Principal component analysis (PCA) [9] and linear discriminant analysis (LDA) [10] are traditional and representative algorithms in dimension reduction. However, the results may contain negative elements in PCA and LDA. This phenomenon weakens their interpretability because the input image data are nonnegative. For this phenomenon, nonnegative matrix factorization (NMF) [11] is a better dimension reduction method. The nonnegative property makes the NMF more comprehensible. NMF and its variants can be roughly divided into two categories.

The first category is unsupervised. Without supervised information, the intrinsic data structure is vital for performance improvements. However, lossing data inherent structure is a drawback of NMF. Many scholars proposed different methods to maintain the original structure in the reduced space. Cai et al. [12] proposed the graph regularized nonnegative matrix factorization (GNMF). In GNMF, if data are near in original space, their representations would be close in the reduced space. Shang et al. [13] developed the graph dual regularization NMF (DNMF). More than the local structure of data space, DNMF maintains the local structure of feature space. Ding et al. [14] developed the convex nonnegative matrix factorization (CNMF). In CNMF, a factor matrix is reconstructed by the convex combinations of data. In other words, in CNMF, the center of a cluster should be represented by data. Hu et al. [15] developed the graph regularized and convex nonnegative matrix factorization (GCNMF). Compared with CNMF, a graph regularized term is employed in GCNMF. Cui et al. [16] proposed the subspace clustering guided convex nonnegative matrix factorization (SCCNMF). Subspace clustering can reconstruct a sample by other samples. The above methods investigate how to maintain the structure in the reduced space in various ways.

Another drawback of NMF is the error measure. The square of Frobenius norm is sensitive to noise and outliers. To address this problem, researchers have adopted different error measures. Kong et al. [17] used the \(\ell _{2,1}\) norm (\(\ell _{2,1}\)NMF). Li et al [18] employed the \(\ell _{2,p}\) norm (\(\ell _{2,p}\)NMF). Compared with the square of Frobenius norm, these two norms are more robust. Except for above methods, different norms can be applied to data representations. Zhang et al. [19] and Xing et al. [20] added a regularized term in the NMF. [19] used the \(\ell _{1/2}\) norm on data representations while [20] employed the \(\ell _{2,1}\) norm.

The second category is semisupervised. Here is a brief introduction. Because the cost of collecting a little supervised information is affordable, some semisupervised methods are developed. Generally, there are two types of supervised information. The first type is label constraints, and the second type is pairwise constraints. Label constraints mean the data belong to known classes, while the pairwise constraints restrict data relationships. Based on label constraints, Babaee et al. [21] proposed the discriminative nonnegative matrix factorization (DNMF). When data have the same label, DNMF tries to set them on the same axis. Different from [21], Liu et al. [22] proposed the constrained nonnegative matrix factorization (CNMF). CNMF lets samples in the same class to have the same representation. Based on pairwise constraints, Wang et al. [23] proposed the penalized matrix factorization (PMF). PMF adds a penalized term to mitigate the situation that the factorization violates constraints. Yang et al. [24] developed the pairwise constraints guided nonnegative matrix factorization (PCNMF). Must links and cannot links generate two different regularized terms in PCNMF.

In this paper, the main focus is the unsupervised NMF. Above unsupervised methods achieved notable improvements. However, there still exist some drawbacks. The first drawback is that the method of calculating similarities is always basing the Euclidean distance. However, the Euclidean distance is sensitive to outliers and noise. This phenomenon may lead to a low-accurate clustering result. Second, there is no direct way to keep the global similarity in data representations. Keeping the global similarity by neighbors always causes information loss. A new nonnegative matrix factorization under structure constraints (SNMF) is proposed to handle these drawbacks.

The main contributions are concluded as follows:

  1. 1.

    A direct way to keep the global structure similarity in data representations is introduced into SNMF. Meanwhile, combined with a graph regularized term to save the local structure information, SNMF eases the structure information loss.

  2. 2.

    To make data representations more discriminative, the \(\ell _2\) norm constraints are employed in SNMF. Based on \(\ell _2\) norm constraints, the dot measure, which is equivalent to cosine measure, is used in data representations to avoid the drawback of Euclidean distance.

  3. 3.

    New updating rules are given, and experiments confirm the effectiveness of updating rules.

The rest of this paper is organized as follows. In Sect. 2, a brief introduction to related work is given. Section 3 introduces the details of SNMF. Section 4 concludes the experiment results to show the effectiveness of SNMF on clustering. Section 5 makes conclusions about this paper.

2 Related work

2.1 NMF algorithm and GNMF algorithm

Lee et al. [11] proposed the nonnegative matrix factorization (NMF). Here is a brief introduction.

The model of NMF in the Euclidean distance is as follows:

$$\begin{aligned} \min \limits _{U\ge 0, V\ge 0} \Vert X - UV^T \Vert _F^2. \end{aligned}$$
(1)

In (1), \(X\in R^{m \times n}_+\) is a dataset. \(U \in R^{m \times k}_+\) and \(V \in R^{n \times k}_+\) are factorization results, which are called basis matrix and data representations (or encoding matrix). Each row in V represents a sample in the reduced k-dimension space spanned by U. The number k is predetermined, which is the number of clusters expected in most situations.

The updating formulations of (1) are as follows:

$$\begin{aligned} U_{mk} \leftarrow U_{mk} \dfrac{(XV)_{mk}}{(UV^T V)_{mk}},\\ V_{nk} \leftarrow V_{nk} \dfrac{(X^T U)_{nk}}{(VU^T U)_{nk}}. \end{aligned}$$

Cai et al. [12] pointed out that (1) focused on factorization results while losing the local structure information. However, the local structure information is vital for clustering. To address this drawback, Cai et al. [12] proposed the graph regularized nonnegative matrix factorization (GNMF). The GNMF model is as follows:

$$\begin{aligned} \min \limits _{U\ge 0, V\ge 0} \Vert X - UV^T \Vert _F^2 + \lambda tr(V^T LV). \end{aligned}$$
(2)

\(\lambda\) is a balanced parameter. The second term in (2) is called graph regularized term, and the matrix L in this term is the Laplacian matrix. With the help of this graph regularized term, when samples in the original space are near, their representations in the reduced space will be close. The calculation of this Laplacian matrix L is the following equation:

$$\begin{aligned} L=D-W. \end{aligned}$$
(3)

In (3), D is a diagonal matrix, and the element \(D_{ii}=\sum ^n_{j=1} W_{ij}\). W is the similarity matrix which is calculated from a graph \(G_G=(V_G, E)\). \(V_G\) represents the set of samples in the dataset X, and E is the edge set. The formulation for W is as follows.

$$\begin{aligned} W_{ij}=\left\{ \begin{aligned} 1, &\quad i\in \kappa (j)\ or\ j\in \kappa (i), \\ 0,&\quad otherwise. \end{aligned} \right. \end{aligned}$$
(4)

\(\kappa (i)\) is a set, which contains the \(\kappa\) nearest neighbors of sample i and does not contain itself. These \(\kappa\) nearest neighbors are generated by Euclidean distances.

Updating rules of (2) are given as follows:

$$\begin{aligned} U_{mk} \leftarrow U_{mk} \dfrac{(XV)_{mk}}{(UV^T V)_{mk}},\\ V_{nk} \leftarrow V_{nk} \dfrac{(X^T U)_{nk} + \lambda (WV)_{nk}}{(VU^T U)_{nk} + \lambda (DV)_{nk}}. \end{aligned}$$

2.2 NMF with \(\ell _2\) norm constraints

The \(\ell _2\) norm constraint has excellent potential to feature extraction and data representations [25]. Yang et al. [25] proposed an algorithm to solve the following problem:

$$\begin{aligned} \begin{array}{lll} \text {min}& \frac{1}{2}\Vert X - UV^T \Vert _F^2, \\ \text {subject to}& U\ge 0, &V\ge 0, \\ & \Vert U_{*i} \Vert _2^2 = 1, & i=1,2,3,\ldots ,k. \\ \end{array} \end{aligned}$$
(5)

\(U_{*i}\) represents the ith column in U.

Compared with (1), (5) has no other constraints on V. Therefore, the same updating rule is adopted for V. For U, Yang et al. [25] proposed a new updating rule which updated U by columns. Next is a description of updating a column of U [25].

x represents the ith column of U. The partial derivative of x is denoted as a. So, \(a=(UV^TV)_{*i}-(XV)_{*i}\). Let \(c_1=(UV^TV)_{*i}\), and \(c_2=(XV)_{*i}\). Therefore, \(a=c_1-c_2\). To update x under the constraint \(\Vert x\Vert _2^2 = 1\), following auxiliary variables need to be calculated [25].

$$\begin{aligned} \begin{aligned} T1&=x^Txc_1^Txc_2+x^txc_2^Txc_1+x^Txx^Tc_1c_1+x^Txx^Tc_2c_2, \\ T2&=x^Txc_1^Txc_1+x^txc_2^Txc_2+x^Txx^Tc_1c_2+x^Txx^Tc_2c_1, \\ P1&=c_1^Txx^Tc_2x+c_2^Txx^Tc_1x+x^Txc_1^Tc_1x+x^Txc_2^Tc_2x, \\ P2&=c_1^Txx^Tc_1x+c_2^Txx^Tc_2x+x^Txc_1^Tc_2x+x^Txc_2^Tc_1x, \\ M&=(a^Tx)^2-\Vert a\Vert _2^2\Vert x\Vert _2^2, \\ B&=2T1+2P1+Mx, \\ C&=4(x^Txc_1+x^Tc_2x), \\ D&=-4x. \\ \end{aligned} \end{aligned}$$
(6)

Then, calculate \(\tau\) and q.

$$\begin{aligned} & \begin{aligned} \tau&=min\left\{ \frac{\sqrt{C_i^2-4B_iD_i}-C_i}{2B_i},\quad if \quad B_i\ne 0; \right. \\&\quad \left. -\frac{D_i}{C_i},\quad if \quad B_i=0.\right\} ,\quad i=1,2,3,\ldots ,m, \\ \end{aligned} \end{aligned}$$
(7)
$$\begin{aligned} & q=1-\left( \frac{\tau }{2}\right) ^2(a^Tx)^2+\left( \frac{\tau }{2}\right) ^2\Vert a\Vert _2^2\Vert x\Vert _2^2. \end{aligned}$$
(8)

Now the updating rule of the ith column of U is (9).

$$\begin{aligned} & U_{*i} \leftarrow x-\frac{\tau }{q}\left( x^Txc_1+\frac{\tau }{2}T1+x^Tc_2x+\frac{\tau }{2}P1\right) \nonumber \\ & \qquad +\frac{\tau }{q}\left( x^Txc_2+\frac{\tau }{2}T2+x^Tc_1x+\frac{\tau }{2}P2\right) . \end{aligned}$$
(9)

There is a subtraction operation in (9). However, the theoretical analysis in [25] guarantees results’ nonnegativity.

2.3 Cosine similarity

Suppose \(x_i\) and \(x_j\in R^{m\times 1}\) are two samples. The cosine similarity between \(x_i\) and \(x_j\) is following:

$$\begin{aligned} cos(x_i,x_j) = \frac{x_i^T x_j}{\Vert x_i\Vert _2 \Vert x_j\Vert _2}. \end{aligned}$$
(10)

If \(\Vert x_i\Vert _2=1\) and \(\Vert x_j \Vert _2=1\), (10) can be reduced to (11).

$$\begin{aligned} cos(x_i,x_j)=x_i^Tx_j. \end{aligned}$$
(11)

Given a dataset \(A\in R^{m\times n}\), each column \(A_{*i} (i \in {1,2,\ldots ,n})\) represents a sample. If \(\Vert A_{*i}\Vert _2=1(i\in {1,2,\ldots ,n})\), (12) saves cosine similarities between samples.

$$\begin{aligned} B=A^TA. \end{aligned}$$
(12)

Clearly, B is a symmetric matrix, and \(B_{ij}\) is the cosine similarity between ith sample and jth sample. The matrix B is called cosine matrix of A.

3 Nonnegative matrix factorization under structure constraints

First, some symbols are given in Table 1.

Table 1 Definitions of symbols
Full size table

3.1 Saving the global structure information in data representations

For dataset \(X\in R_+^{m\times n}\), each column represents a sample. Normalization, which is used to eliminate some differences between samples, is a necessary operation in machine learning. Different normalizations have various influences on similarity, and the impacts of normalizations will be investigated in Sect. 4.3.

\(X^N\) represents the data after a normalization. The local similarity always is reflected by neighbors in (4) which discards similarities with other samples. This operation may cause information loss.

Define the global similarity matrix measured by the dot measure as follows:

$$\begin{aligned} G={X^N}^TX^N. \end{aligned}$$
(13)

\(G_{ij}\) reflects the global similarity between samples i and j, and a great value means a high similarity.

For data representations, the \(\ell _2\) norm could make them more discriminative [25]. Thus, the \(\ell _2\) norm constraint is added on the row of V. Meanwhile, the global structure should be kept in the coding matrix V. Thus, the same global similarity calculation is adopted on the coding matrix V. Because of \(\ell _2\) norm constraints, the dot measure on V could be seen as the cosine measure. Then a global structure regularized term is proposed as follows:

$$\begin{aligned} \begin{array}{lll} \text {min}& \Vert G-VV^T \Vert _F^2, \\ \text {subject to} & \Vert V_{i*} \Vert _2^2 = 1, &i=1,2,3\ldots ,n. \\ \end{array} \end{aligned}$$
(14)

Although the objective function of (14) has a same form as [26] and [27], the purpose of (14) is different from these two works. Compared with [26], (14) has a more precise and distinct sense. Equation (14) represents that the global similarity matrices, which are based on dot measures, of original space and reduced space should be similar. In [26], G only captures the local information, and the purpose of \(VV^T\) does not have a clear explanation. In [27], G is a similarity matrix, while V is the cluster index matrix. Clustering results are determined by the biggest value of each row in V. However, in (14), V is a coding matrix, which is related to the factorization. Moreover, the \(\ell _2\) norm constraints of V in (14) do not exist in [26, 27].

The conventional method of exploring the structure information is always through neighbors of each sample. To find neighbors, calculating similarities and ranking similarities are all necessary. It is an indirect method to save similarities. Selecting neighbors will discard some similarities. Different from the conventional method, Eq. (14) is a direct way to keep the global structure. Equation (14) requires that the global similarity of data representations should reflect the original global similarity directly. That operation will capture the global structure information more effectively. In addition, compared with the conventional method, (13) reduces calculations because (13) does not need the similarity ranking. By minimizing this term, the global similarity in the reduced space will be approximately equal to the original global similarity.

3.2 Proposed method

This subsection describes details of the nonnegative matrix factorization under structure constraints (SNMF).

X is a given nonnegative dataset. After normalization, \(X^N\) is the dataset. Then calculate G and L on \(X^N\). G is the global similarity matrix which is calculated by (13). L is the Laplacian matrix which stores local structure information, and is calculated by (3).

As paper [12], minimizing the following term will keep the local information in the reduced space.

$$\begin{aligned} \begin{aligned} \frac{1}{2}\sum _{i,j}^n\Vert V_{i*}-V_{j*}\Vert ^2W_{ij}&=\sum _i^n V_{i*}V_{j*}^TD_{ii}-\sum _{i,j}^nV_{i*}V_{j*}^TW_{ij} \\&=tr(V^TLV). \end{aligned} \end{aligned}$$
(15)

The reason is that the value of \(\Vert V_{i*}-V_{j*}\Vert ^2\) should be small when \(W_{ij}\) is 1. Thus, (15) requires data representations to be similar if the samples are neighbors in the original space. As the popular way [12], \(\kappa\) is set as 5 for W.

Therefore, to keep the global and local structure in the reduced space, the model of SNMF is as follows:

$$\begin{aligned} \begin{array}{ll} \text {min}&{\frac{1}{2}\Vert X^N - UV^T \Vert _F^2+\frac{\alpha }{2}\Vert G-VV^T \Vert _F^2+\frac{\beta }{2} tr(V^TLV)} \\ \text {subject to}& U\ge 0,\ \ \ \ \ V\ge 0, \\ & \Vert V_{i*} \Vert _2^2 = 1, i=1,2,3\ldots ,n. \\ \end{array} \end{aligned}$$
(16)

In (16), the global structure regularized term stores the global similarities information. Meanwhile, the graph regularized term is employed to keep the local structure in data representations V. \(\ell _2\) norm constraints are utilized to make data representations more discriminative. \(\alpha\) and \(\beta\) are balanced parameters. \(\alpha\) is related to the global data structure, and \(\beta\) has a relation to local data structure. These two regularized terms make SNMF to keep more data intrinsic structure information in the reduced space. They are beneficial to the clustering performance. Section 4.4 displays influences of \(\alpha\) and \(\beta\).

Different from (5), (16) pursues discriminative data representations. Meanwhile, the original structure information is maintained in the reduced space by these two regularized terms on V.

3.3 Optimization on (16)

For (16), an iterative algorithm is given to solve it. The Lagrange function of model (16) is as follows.

$$\begin{aligned} \begin{aligned}&O =\frac{1}{2}\Vert X^N - UV^T \Vert _F^2+\frac{\alpha }{2} \Vert G-VV^T\Vert _F^2 \\&\qquad +\frac{\beta }{2} tr(V^TLV)+tr(\Psi U^T)+tr(\Phi V^T)\\&\qquad +\sum _{i=1}^n\gamma _i(V_{i*}V_{i*}^T-1) \\&\quad =\frac{1}{2}tr({X^N}^TX^N-{X^N}^TUV^T-VU^TX^N+VU^TUV^T) \\&\qquad +\frac{\alpha }{2} tr(G^TG-G^TVV^T-VV^TG+VV^TVV^T) \\&\qquad +\frac{\beta }{2} tr(V^TLV)+tr(\Psi U^T)+tr(\Phi V^T)\\&\qquad +\sum _{i=1}^n \gamma _i(V_{i*}V_{i*}^T-1) \\&\quad =\frac{1}{2}(tr({X^N}^TX^N)-tr({X^N}^TUV^T)-tr(VU^TX^N)\\&\qquad +tr(VU^TUV^T)) \\&\qquad +\frac{\alpha }{2}(tr(G^TG)-tr(G^TVV^T)-tr(VV^TG)\\&\qquad +tr(VV^TVV^T)) \\&\qquad +\frac{\beta }{2} tr(V^TLV)+tr(\Psi U^T)+tr(\Phi V^T)\\&\qquad +\sum _{i=1}^n \gamma _i(V_{i*}V_{i*}^T-1) \\&\quad =\frac{1}{2}(tr({X^N}^TX^N)-2tr(VU^TX^N)+tr(VU^TUV^T)) \\&\qquad +\frac{\alpha }{2} (tr(G^TG)-2tr(G^TVV^T)+tr(VV^TVV^T)) \\&\qquad +\frac{\beta }{2}tr(V^TLV)+tr(\Psi U^T)+tr(\Phi V^T)\\&\qquad +\sum _{i=1}^n \gamma _i(V_{i*}V_{i*}^T-1). \end{aligned} \end{aligned}$$
(17)

In Eq. (17), \(\Psi _{mk}\), \(\Phi _{kn}\), and \(\gamma _i\) are the Lagrange multipliers for \(U_{mk} \ge 0\), \(V_{kn}\ge 0\), and \(\Vert V_{i*}\Vert ^2_2=1\), respectively. \(\Vert A\Vert _F^2=tr(A^TA)\), \(tr(AB)=tr(BA)\) and \(tr(A)=tr(A^T)\) are used in (17).

For O, the partial derivative respect to \(U_{mk}\) is as follows:

$$\begin{aligned} \dfrac{\partial O}{\partial U_{mk}}=-(X^NV)_{mk}+(UV^TV)_{mk}+\Psi _{mk}. \end{aligned}$$

By the KKT condition \(\Psi _{mk}U_{mk}=0\), when

$$\begin{aligned} \dfrac{\partial O}{\partial U_{mk}}=0, \end{aligned}$$

we get the following equation:

$$\begin{aligned} (-X^NV+UV^TV)_{mk} U_{mk}=0. \end{aligned}$$

Then the updating rule for U is given.

$$\begin{aligned} U_{mk}\leftarrow U_{mk}\dfrac{(X^NV)_{mk}}{(UV^TV)_{mk}}, \end{aligned}$$
(18)

For V, because of the \(\ell _2\) norm constraints, updating rules are given based Yang et al. [25]. The updating rules for V in (16) are one row by one row. The following are details.

In the tth iteration, \(x_r\) represents the ith row of V. In (16), let F represent the objective function and calculate the partial derivative on \(x_r\) which is the following.

$$\begin{aligned} \dfrac{\partial F}{\partial x_r}= & (-X^{N^T}U)_{i*}+(VU^TU)_{i*}-2\alpha (GV)_{i*}\\ & +2\alpha (VV^TV)_{i*}+\beta (DV)_{i*}-\beta (WV)_{i*}. \end{aligned}$$

Denote

$$\begin{aligned} h=\dfrac{\partial F}{\partial x_r}. \end{aligned}$$

Let

$$\begin{aligned} & l_1=(VU^TU)_{i*}+2\alpha (VV^TV)_{i*}+\beta (DV)_{i*},\\ & l_2=(X^{N^T}U)_{i*}+2\alpha (GV)_{i*}+\beta (WV)_{i*}. \end{aligned}$$

Thus, \(h=l_1-l_2.\)

Let

$$\begin{aligned} x=x_r^T, a=h^T, c_1=l_1^T, c_2=l_2^T. \end{aligned}$$

Then the same method introduced in Sect. 2.2 is used. Calculate the other auxiliary variables by (6), (7) and (8). Note that B, C, D are vectors. So, the \(B_i,C_i\) and \(D_i\) are the ith element in vectors.

To get the updating rule, a transpose operation should be carried out on the obtained result. So, the updating rule of ith row in V is given as follows:

$$\begin{aligned} & V_{i*} \leftarrow \left( x-\frac{\tau }{q}\left( x^Txc_1+\frac{\tau }{2}T1+x^Tc_2x+\frac{\tau }{2}P1\right) \right. \nonumber \\ & \qquad \left. +\frac{\tau }{q}\left( x^Txc_2+\frac{\tau }{2}T2+x^Tc_1x+\frac{\tau }{2}P2\right) \right) ^T. \end{aligned}$$
(19)

Although there is a subtraction in Eq. (19), a theoretical analysis in the appendix guarantees the nonnegativity of V. After updating every row in V, the tth iteration finishes.

Algorithm 1 summarizes the SNMF algorithm.

figure a

3.4 Complexity analysis

The computational complexity of SNMF mainly depends on the updating of U and V. The complexities of updating U and V are \(O(mnk^2)\) and \(O(n^2k^2+nk^2)\), respectively. Constructing the graph of \(X^N\) needs \(O(n^2m)\), and calculating the global similarity matrix G occupies \(O(n^2m)\). Therefore, the complexity of SNMF is \(O(tmnk^2+tn^2k^2+tnk^2+2n^2m)\), where t is the number of iterations.

4 Experimental results

4.1 Data sets and comparison algorithms

Three image datasets are used to show the effectiveness of the SNMF, which are USPSFootnote 1, YaleBFootnote 2, and ORL\(^2\) [28]. USPS contains hand-written number pictures, while human face pictures are the samples in YaleB and ORL. For USPS, its original dataset has too many instances. Thus, 200 samples are selected from each class randomly to form the USPS dataset in experiments. Each sample in these datasets is stretched to be a vector. Details of each dataset are shown in Table 2.

Table 2 Details of datasets
Full size table

Comparison algorithms are:

  1. 1.

    NMF [11]

  2. 2.

    GNMF [12]

  3. 3.

    \(\ell _{2,1}\)NMF [17]

  4. 4.

    \(\ell _{2,p}\)NMF [18]

  5. 5.

    SCCNMF-1[16]

  6. 6.

    FR-NMF[29]

For these comparison algorithms, parameters are set according to the author’s suggestion.

4.2 Evaluation metrics

Four widely used metrics are adopted to evaluate clustering results: cluster accuracy (ACC) [30], normalized mutual information (NMI) [30], F-measure (F*) [31], and adjusted rand index (ARI) [32].

ACC is calculated by Eq. (20):

$$\begin{aligned} ACC=\dfrac{\sum _{i = 1}^n \delta (map(r_i),l_i)}{n}, \end{aligned}$$
(20)

where \(r_i\) is the clustering label after a clustering algorithm. \(l_i\) is the true class label for ith sample. \(map(\cdot )\) is a function to map a clustering label into the true class label set. \(\delta (a,b)\) is a function that equals 1 when \(a=b\) and 0 otherwise. n is the number of samples.

NMI is established on mutual information (MI). MI [30] is calculated by (21).

$$\begin{aligned} M I\left( C, C^{\prime }\right) =\sum _{c_i \in C, c_j^{\prime } \in C^{\prime }} p\left( c_{i}, c_{j}^{\prime }\right) \cdot \log _{2} \frac{p\left( c_{i}, c_{j}^{\prime }\right) }{p\left( c_{i}\right) \cdot p\left( c_{j}^{\prime }\right) }. \end{aligned}$$
(21)

C denotes the set of clusters obtained from the ground truth and \(C^{\prime }\) is obtained from a clustering algorithm. \(p(c_i)\) and \(p(c_j^{\prime })\) are the probabilities that a sample arbitrarily selected from the dataset belongs to the clusters \(c_i\) and \(c_j^{\prime }\), respectively. \(p(c_i, c_j^{\prime })\) is the joint probability that the arbitrarily selected sample belongs to the clusters \(c_i\) as well as \(c_j^{\prime }\) at the same time. [30].

Then NMI is calculated through Eq. (22).

$$\begin{aligned} NMI\left( C, C^{\prime }\right) =\frac{M I\left( C, C^{\prime }\right) }{\max \left( H(C), H\left( C^{\prime }\right) \right) }. \end{aligned}$$
(22)

H(C) and \(H(C^{\prime })\) are entropies of C and \(C^{\prime }\) [30].

Let \(n_c\) represent the number of samples of the cth cluster. \(n_c^p\) represents the number of common samples between the cth cluster and the pth class. F* and ARI are defined as follows.

$$\begin{aligned} & F*=\frac{2\cdot \frac{n_c^p}{n_c} \cdot \frac{n_c^p}{n_p}}{\frac{n_c^p}{n_c} + \frac{n_c^p}{n_p}}, \end{aligned}$$
(23)
$$\begin{aligned} & ARI=\frac{{\sum }_{c,p} \left(\begin{array}{c}n^p_c\\ 2\end{array}\right)- {\sum }_c\left(\begin{array}{c}q_c\\ 2\end{array}\right){\sum }_p \left(\begin{array}{c}s_p\\ 2\end{array}\right)/ \left(\begin{array}{c}n\\ 2\end{array}\right)}{\frac{1}{2} \left( {\sum }_c \left(\begin{array}{c}q_c\\ 2\end{array}\right) + {\sum }_p \left(\begin{array}{c}q_c\\ 2\end{array}\right)\right) -{\sum }_c \left(\begin{array}{c}q_c\\ 2\end{array}\right) {\sum }_p \left(\begin{array}{c}s_p\\ 2\end{array}\right) / \left(\begin{array}{c}2\\ 2\end{array}\right)}, \end{aligned}$$
(24)

where \(\left(\begin{array}{c}n\\ k\end{array}\right) = \frac{n!}{k!(n-k)!},\) \(q_c = \sum _p n^p_c, s_p = \sum _c n^p_c.\)

The value range is [0,1] for ACC, NMI, and F* while [−1,1] for ARI. High values of these metrics represent satisfactory clustering results.

4.3 Normalization influence on similarity

Different normalizations will have multiple effects on similarity matrices G and W. To show normalizations’ various effects directly, an example is displayed in Fig. 1 on ORL [28].

Fig. 1
figure 1

Different normalization methods and their effects on the similarity based ORL. Method 1 represents the \(\ell _2\) norm of each sample equals 1 and method 2 represents the \(\ell _1\) norm of each feature equals 1

Full size image

Figure 1a is an ideal situation, which is generated by labels. When two samples are in a same class, the similarity for them is 1, and equals 0 otherwise. Basing the samples’ indexes, only the submatrices on the main diagonal have values of 1, and each yellow square represents a class.

Two different normalizations are selected. The first normalization, denoted as method 1, will normalize the \(\ell _2\) norm of samples to be 1, which is widely used. The second normalization, marked as method 2, normalizes the \(\ell _1\) norm of each feature to be 1. For nonnegative data, these two normalizations will keep data nonnegative. Figure 1b–e displays the effects on global similarity G and local similarity W of these two methods. In an ideal situation, Fig. 1b–e should be similar to Fig. 1a.

It is clear that Fig. 1b–e has differences. From Fig. 1b, method 1 makes the elements on the main diagonal 1. However, method 1 also assigns high similarities between different classes, which is reflected by that too many yellow pixels are not in the submatrices on the main diagonal. In Fig. 1c, method 2 assigns high values on the submatrices on the main diagonal in most situations. Comparing Fig. 1d, e, which reflect the local similarity, we find that pixels in yellow are more concentrated in submatrices on the main diagonal in Fig. 1e. This phenomenon verifies that method 2 has advantages on the local similarity over method 1.

More than Fig. 1, Table 3 displays the proportion of same classes similarities in overall similarities. Values in Table 3 represents the proportion of the sum of similarity values in submatrices on the main diagonal to overall similarities for global similarity G and local similarity W. From Table 3, proportions of method 2 are higher than method 1 in both global similarities and local similarities. This phenomenon means that the correct information takes a high proportion in method 2, and confirms that method 2 is superior to method 1.

Table 3 Proportion of same classes similarities in overall similarities
Full size table

From the above analysis, method 2 could reflect the data similarity well, and this normalization is selected as the normalization in this paper.

4.4 Parameter selection

The trynumber and \(\varepsilon\) for SNMF are 200 and 10\(^{-6}\), respectively. The value of k equals the number of classes in the ground truth. Now, only \(\alpha\) and \(\beta\) are not determined. Obviously, \(\alpha\) and \(\beta\) have influences on clustering results at the same time. Thus, a same changing set [0.001, 0.01, 0.1, 1.0, 10, 100, 1000] is adopted for \(\alpha\) and \(\beta\). Clustering results of tuning \(\alpha\) and \(\beta\) are displayed in Figs. 2, 3 and 4.

Figure 2 shows that 4 combinations, which are (1.0, 1000), (0.1, 100), (0.01, 10), (0.001, 1.0), have the satisfactory results on ORL. Basing Figs. 3 and 4, satisfactory combinations are (0.1, 1000), (0.01, 100), (0.001, 10) on USPS and YaleB. The combinations of ORL have poor performance on USPS and YaleB. However, combinations of USPS and YaleB have adequate performance on ORL. So, in the next experiments, we set \(\alpha = 0.01\) and \(\beta = 100\).

From these results, when the ratio of \(\frac{\beta }{\alpha }\) between 1000 and 10,000, the performance of SNMF is satisfactory. When emphasizing local structure too much (which leads to the ratio being too big), SNMF has poor performance on ORL and YaleB. When emphasizing global structure too much (which leads to the ratio being too small), SNMF has worse performance through all datasets. This phenomenon means that the ratio of local structure information and global structure information should be suitable. SNMF only employs local and global structure information effectively when the ratio is proper.

Fig. 2
figure 2

clustering results (ACC, NMI, F* and ARI) on dataset ORL

Full size image
Fig. 3
figure 3

clustering results (ACC, NMI, F* and ARI) on dataset USPS

Full size image
Fig. 4
figure 4

clustering results (ACC, NMI, F* and ARI) on dataset YaleB

Full size image

4.5 Experimental results and analysis

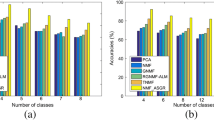
The clustering results of SNMF and other comparison algorithms are shown in Table 4. Kmeans is used on data representations to get final clustering results. To eliminate accidents’ impacts, each algorithm is carried out 20 times. Because all these algorithms need random initializations, the same random seed is adopted for each algorithm at each time. Mean values and standard deviations are reported in Table 4. Bold numbers represent the best results. ‘–’ represents that the time of this algorithm is too long to get results. SNMF-A represents \(\beta =0\) in SNMF.

Table 4 Results (mean(std)) on datasets
Full size table

From Table 4, we have the following conclusions.

First, SNMF has the best results. These results confirm that data intrinsic structure information plays a crucial role in clustering. Sufficiently using data structure information is beneficial for clustering.

Second, using global structure information solely does not provide enough structure information for clustering. In Table 4, the performance of SNMF-A is the worst. This phenomenon shows that the global structure information is not enough to promote clustering without local structure information.

Third, the performance of SNMF is better than GNMF and SNMF-A. This result means that using local and global structure information simultaneously is beneficial to clustering. Although only using the global structure is not enough to elevate clustering results, there is still some valuable information for clustering. The absence of either of these two kinds of structure information will weaken clustering results, which are confirmed by the performance of NMF, GNMF and SNMF-A.

4.6 Time cost analysis

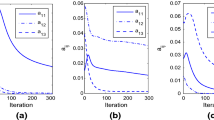
In this section, the time costs of one iteration for NMF, GNMF, \(\ell _{2,1}\)NMF, \(\ell _{2,p}\)NMF, SCCNMF-1, FR-NMF, and SNMF are displayed in Table 5. The notion ‘–’ in Table 5 represents that the time is too long to finish one iteration. From this table, it is clear that time costs of SNMF are not the least. For SNMF, maintaining data structure information in the reduced space will augment the computational burden.

Table 5 Time costs (seconds) of one iteration on three data sets
Full size table

In addition to the cost of one iteration, the number of iterations to get a convergence result is a crucial factor for time costs. Figure 5 displays the convergence curves on USPS, and other convergence curves on the remaining datasets have similar tendencies as USPS. Figure 5 shows that almost all methods will be stable after 100 iterations, except FR-NMF. For FR-NMF, it will be stable after 200 iterations. Figure 5 reveals that SNMF does not need more iterations to get a stable result compared with other methods.

The above analysis confirms that SNMF takes a little more time to get a stable result. However, SNMF makes satisfactory promotions compared with the extra time costs. Thus, the time cost of SNMF is acceptable.

Fig. 5
figure 5

convergence curves on USPS

Full size image

4.7 Robustness analysis

To evaluate the robustness of SNMF, Gaussian noise and Poisson noise are added to the data, respectively. For Gaussian noise, the mean and standard deviation are 0 and 0.1, respectively. If some elements become negative after adding Gaussian noise, they are mapped to be 0. Some noisy data under these two different noises are shown in Fig. 6. Clustering results on noisy datasets are shown in Tables 6 and 7.

From Tables 6 and 7, results show that SNMF has the best results on noisy datasets. The performance of SNMF confirms that global and local structure information is beneficial for clustering when noise exists. Only considering local structure information is not enough, which is demonstrated by the performance of GNMF and SNMF.

Fig. 6
figure 6

Noisy data: first column is USPS dataset, second column is ORL dataset, and third column is YaleB dataset

Full size image
Table 6 Results (mean(std)) on Gaussian noisy datasets
Full size table
Table 7 Results (mean(std)) on Poisson noisy datasets
Full size table

5 Conclusion

In this paper, a nonnegative matrix factorization under structure constraints is proposed. Different from previous works, the global structure is considered in SNMF. To accomplish this aim, a new global structure regulation term is presented. The \(\ell _2\) norm constraints are applied to get discriminative data representations. In addition, SNMF employs a graph Laplacian term to keep the local structure. Effective updating rules, which guarantee SNMF non-increasing, are given. The effects of different normalizations on similarity are investigated by experiments.

However, there are still some problems. First, capturing the global structure is still a problem. In Table 3, we find that the proportion of correct information on global similarity is low. There should be some better methods for generating global similarity. Second, there is no relationship between global similarities and local similarities in this work. However, if an algorithm could establish a framework to connect global similarities and local similarities to refine the quality of these similarities, it may be beneficial for clustering. All these problems need deeper investigations.