Non-negative Matrix Factorization with Symmetric Manifold Regularization

Abstract

Non-negative matrix factorization (NMF) is becoming an important tool for information retrieval and pattern recognition. However, in the applications of image decomposition, it is not enough to discover the intrinsic geometrical structure of the observation samples by only considering the similarity of different images. In this paper, symmetric manifold regularized objective functions are proposed to develop NMF based learning algorithms (called SMNMF), which explore both the global and local features of the manifold structures for image clustering and at the same time improve the convergence of the graph regularized NMF algorithms. For different initializations, simulations are utilized to confirm the theoretical results obtained in the convergence analysis of the new algorithms. Experimental results on COIL20, ORL, and JAFFE data sets demonstrate the clustering effectiveness of the proposed algorithms by comparing with the state-of-the-art algorithms.

1 Introduction

Nonnegative matrix factorization (NMF) algorithms were developed to separate data into factors with nonnegative entries. This method allowed only additive combinations of elements [1, 2], which aimed to capture a parts-based representation of sample observations. Currently, the NMF has been applied in many fields, including signal processing, pattern recognition, and neuroscience [3,4,5,6,7,8]. Lee and Seung proposed NMF to decompose images for feature representation [2], and they further proved that in the updates, the objective functions of the algorithms were non-increasing [9]. However, in general, the non-increasing of objective functions cannot guarantee the convergence of learning rules. For this class of algorithms, researchers obtained the convergence of their algorithms by proving that the algorithms can converge to their local minima. Studies showed that Lee and Seung’s NMF learning algorithms may not converge or converge to saddle points [10,11,12]. To solve this problem, some slight modifications of existing NMF update rules were proposed by Lin [13]. Recently, the stability and the local minima of the NMF related learning algorithms were investigated [14,15,16,17,18], from which, the local and global convergent properties of this class of algorithms can be guaranteed.

For non-linear dimensionality reduction, learning performance can be significantly enhanced if the geometrical structure of observed data is considered. Up to now, many manifold learning algorithms have been proposed for handling of the geometrical structures of image data. Classical manifold learning algorithms including the Laplacian eigenmap (LE) [19, 20], the Roweis and Saul proposed locally linear embedding (LLE) [21], and the isometric feature mapping (ISOMAP) for discovering the non-linear degrees of freedom hiding in human handwriting or face images [22]. From these basic methods, many interesting learning algorithms were derived for the applications of intrinsic structure extracting of image data [23,24,25,26,27].

By combining manifold features with NMF, some important graph regularized nonnegative matrix factorization learning algorithms, such as non-negative graph embedding (NGE) [28], graph regularized non-negative matrix factorization (GNMF) [29,30,31,32], and Group Sparse graph algorithms (GS) [33] have been proposed recently, which explicitly considered the intrinsic geometrical information of data space. The graph regularized NMF is only a class of one-sided clustering methods and the redundant solutions may be generated by its graph regularization [34, 35]. Based on the duality between data points and features, several co-clustering algorithms have been proposed [36,37,38]. Graph dual regularized NMF (DNMF) algorithms simultaneously considered the geometric structures of the data manifold as well as the feature manifold [38]. In semi-supervised and structured NMF algorithms [39, 40], both the labelled and unlabelled data were simultaneously learned to explore the the block-diagonal structure for data classifying, which was time consuming for data labeling. Comparing with GNMF, DNMF can be applied to learn a sparser parts-based data representation. However, our study will show that the graph dual regularized NMF learning algorithms may have divergent points, which will degrade their performance in data clustering [41].

In this paper, based on the extended KL divergence and Euclidian distance, learning algorithms of NMF with symmetric manifold regularization (SMNMF) are derived, in which both the global and local geometric features of sample data will be regularized. Convergence properties of the novel learning algorithms are also analyzed. Comparing with other NMF related algorithms, our analysis results show that the proposed NMF algorithms have the best convergent feature. Experimental results on three different image datasets confirm that the new algorithms can learn the state of art performance on parts-based representations.

The rest of this paper is organized as follows: In Sect. 2, the objective functions and their related definitions of important terms are presented. Section 3, the proposed learning algorithms are derived. In Sect. 4, the convergence of the proposed algorithms is analyzed. In Sect. 5, experimental results are presented. In Sect. 6 conclusion and future works are given.

2 Preliminaries

In the original NMF algorithms, the sample data matrix $\mathbf{Y } =[{\mathbf {y}}_{1}, {\mathbf {y}}_{2},\ldots , {\mathbf {y}}_{N}] \in {\mathbb {R}}^{m\times N}$ was decomposed into matrices $\mathbf{A }=[{\mathbf {a}}_{1}, {\mathbf {a}}_{2},\ldots , {\mathbf {a}}_{m}]^{T} \in {\mathbb {R}}^{m\times n}$ and $\mathbf{X } =[{\mathbf {x}}_{1}, {\mathbf {x}}_{2},\ldots , {\mathbf {x}}_{N}]^T\in {\mathbb {R}}^{N\times n}$ with only nonnegative components in the matrices. To incorporate the decomposition with manifold regularization, the decomposition model was defined as the following:

$$\begin{aligned} \mathbf{Y } \approx \mathbf{A }\mathbf{X }^T. \end{aligned}$$

(1)

In the convergence studies, a detailed scalar form of the model was used:

$$\begin{aligned} y_{ik} \approx \sum _{j=1}^{n} a_{ij}x_{kj},\quad (i = 1, \ldots , m; \ k = 1, \ldots , N) \end{aligned}$$

or

$$\begin{aligned} {\mathbf {y}}_{k} \approx \sum _{j=1}^{n} {\mathbf {a}}_{j}x_{kj},\quad ( k = 1, \ldots , N), \end{aligned}$$

(2)

where ${\mathbf {y}}_{k} = [y_{1k}$, $y_{2k},\ldots , y_{mk}]^{T}$ is a vector of the k-th sample data; We called ${\mathbf {A}}$ the basis of the sample matrix ${\mathbf {Y}}$. Each column of ${\mathbf {X}}^T$ is a representation of the sample in the low dimensional space.

For NMF, imposing nonnegativity constraint can provide sparseness of its components. We can increase sparseness and smoothness by adding to the loss function suitable regularization or penalty terms [8]. Thus, the regularized general KL divergence and the Euclidian distance (Frobenius norm) in the following can be used as the cost functions:

$$\begin{aligned} D_{KL}(\mathbf{Y }||\mathbf AX ^T)= & {} \sum _{i=1}^{m}\sum _{k=1}^{N}\left( y_{ik}\log \frac{y_{ik}}{[\mathbf AX ^T]_{ik}} + [\mathbf AX ^T]_{ik}-y_{ik}\right) \nonumber \\&\quad +\frac{1}{2}\lambda _{\mathbf{X }}J(\mathbf{X }) +\frac{1}{2}\lambda _{\mathbf{A }}J(\mathbf{A }) \nonumber \\&s.t.\quad a_{ij} \ge 0,\quad x_{kj} \ge 0,\quad \nonumber \\&\sum _{i=1}^m a_{ij} = 1, \quad i, j, k\in N,\quad \end{aligned}$$

(3)

$$\begin{aligned} D_{F}(\mathbf{Y },\mathbf AX ^T)= & {} \frac{1}{2}||\mathbf{Y }-\mathbf AX ^T||_{F}^2 + \frac{1}{2}\lambda _{\mathbf{X }}J(\mathbf{X }) +\frac{1}{2}\lambda _{\mathbf{A }}J(\mathbf{A }) \nonumber \\&s.t.\quad a_{ij} \ge 0,\quad x_{kj} \ge 0,\quad \quad \quad \nonumber \\&\sum _{i=1}^m a_{ij}^2 = 1, \quad i, j, k\in N. \end{aligned}$$

(4)

Applying gradient descent approach to cost function (3), it follows that

$$\begin{aligned}&x_{kj} \leftarrow x_{kj} -\eta _{kj}\frac{\partial D_{KL}(\mathbf{Y }||\mathbf AX ^T)}{\partial x_{kj}},\\&a_{ij} \leftarrow a_{ij} -\delta _{ij}\frac{\partial D_{KL}(\mathbf{Y }||\mathbf AX ^T)}{\partial a_{ij}}, \end{aligned}$$

where $\eta _{kj}$ and $\delta _{ij}$ are learning rates. The partial derivatives of cost function with respect to components in matrices $\mathbf{X }$ and $\mathbf{A }$ are:

$$\begin{aligned}&\frac{\partial D_{KL}(\mathbf{Y }||\mathbf AX ^T)}{\partial x_{kj}}=\sum _{i=1}^{m}\left( a_{ij}-\frac{a_{ij}y_{ik}}{[\mathbf {AX}^T]_{ik}}\right) +\frac{\lambda _{X}}{2}\frac{\partial J(\mathbf{X }^T)}{\partial x_{kj}},\\&\frac{\partial D_{KL}(\mathbf{Y }||\mathbf AX ^T)}{\partial a_{ij}}=\sum _{k=1}^{N}\left( x_{kj}-\frac{x_{kj}y_{ik}}{[\mathbf {AX}^T]_{ik}}\right) +\frac{\lambda _{A}}{2}\frac{\partial J(\mathbf{A })}{\partial a_{ij}}. \end{aligned}$$

Assuming

$$\begin{aligned} \eta _{kj}= & {} \frac{x_{kj}}{\displaystyle \sum \nolimits _{i=1}^{m}a_{ij}+\frac{1}{2}\lambda _{X}\frac{\partial J(\mathbf{X }^T)}{\partial x_{kj}}},\\ \delta _{ij}= & {} \frac{a_{ij}}{\displaystyle \sum \nolimits _{k=1}^{N}x_{kj}+\frac{1}{2}\lambda _{A}\frac{\partial J(\mathbf{A })}{\partial a_{ij}}}, \end{aligned}$$

the following learning rules can be proposed:

$$\begin{aligned}&x_{kj} \leftarrow x_{kj} \frac{\displaystyle \sum \nolimits _{i=1}^{m}a_{ij}(y_{ik}/[\mathbf AX ^T]_{ik})}{\displaystyle \sum \nolimits _{q=1}^{m}a_{qj} +\frac{1}{2}\lambda _{\mathbf{X }} \frac{\partial J(\mathbf{X }^T)}{\partial {x_{kj}}}}, \end{aligned}$$

(5)

$$\begin{aligned}&a_{ij} \leftarrow a_{ij} \frac{\displaystyle \sum \nolimits _{k=1}^{N}x_{kj}(y_{ik}/[\mathbf AX ^T]_{ik})}{\displaystyle \sum \nolimits _{p=1}^{N}x_{pj} +\frac{1}{2}\lambda _{\mathbf{A }} \frac{\partial J(\mathbf{A })}{\partial {a_{ij}}}}. \end{aligned}$$

(6)

Experimental results in [8] showed that, for some given additional constraint terms $J(\mathbf{A })$ and $J(\mathbf{X })$, this class of learning algorithms can learn very good sparseness and smoothness features in the applications of blind source separation.

To apply rules (5) and (6) to manifold learning, we need to choose suitable new constraint functions $J(\mathbf{X })$ and $J(\mathbf{A })$. NMF is a type of dimensionality reduction algorithm. For the column vector ${\mathbf {y}}_{j}$ ($j = 1, 2,\ldots , N$) of matrix ${\mathbf {Y}}$, the low dimensional representation corresponding to the new basis is ${\mathbf {x}}_{j} = [x_{j1},\ldots , x_{jn}]^{T}$. NMF algorithms are designed to learn a set of basis vectors that can be used to best approximate the sample data [29]. If we consider to obtain the geometric structure of images in the learning, a general assumption is, for any two manifold data points ${\mathbf {y}}_{j}$ and ${\mathbf {y}}_{k}$, if they are close in their geometric structures, then their respective representations ${\mathbf {x}}_{j}$ and ${\mathbf {x}}_{k}$ will also be close to each other. For basis vectors ${\mathbf {a}}_{i}$ and ${\mathbf {a}}_{j}$ of matrix ${\mathbf {A}}$, we have similar assumption.

Assume that each vertex of an N vertex graph is represented by a data point. If each point ${\mathbf {y}}_{j}$ has p nearest neighbors, then edges are added between node ${\mathbf {y}}_{j}$ and its neighbors. Each edge has a corresponding weight. We have different choices to define the $N\times N$ weight matrix ${\mathbf {W}}$ for these edges. Assuming $w_{jk}$ is the jk-th element of matrix $\mathbf{W }$, usually the following three weights defined in [19, 29] can be used.

• 1. 0–1 weighting: if nodes j and k connected, $w_{jk} = 1$; otherwise $w_{jk} = 0$.

• 2. Heat kernel weighting: if nodes j and k connected, $w_{jk} = e^{-\frac{||{\mathbf {y}}_{j}-{\mathbf {y}}_{k}||}{t}}$, $t\in {\mathbb {R}}$, $t\ne 0$; otherwise $w_{jk} = 0$.

• 3. Dot-product weighting: if nodes j and k connected, $w_{jk} = {\mathbf {y}}^{T}_{j} {\mathbf {y}}_{k}$; otherwise $w_{jk}$ = 0.

In fact, $w_{jk}$ is employed to measure the closeness of two nodes ${\mathbf {y}}_{j}$ and ${\mathbf {y}}_{k}$. Usually, the dot-product weighting is used for document analysis and the heat kernel weight is one of the most popular choices for image data factorization.

In image feature extraction, experimental results in [2] showed that each column of sample matrix ${\mathbf {Y}}$ represents a single image. Clearly, it is not enough for the feature extracting of manifold structures by only considering the column vectors of ${\mathbf {Y}}$ and ${\mathbf {X}}^T$. For example, alignment of the input image is essential for face classification and recognition. In this type of sample decompositions, we often consider both matrices ${\mathbf {A}}$ and ${\mathbf {X}}^T$ in a symmetric way. Each column vector of ${\mathbf {A}}$ is a representation of some global features of all the observation samples. Thus, if p nearest row vectors of images have similar features, then their corresponding representations in ${\mathbf {A}}$ will also be close.

Assume ${\bar{\mathbf {y}}}_{i}$ and ${\bar{\mathbf {y}}}_{j}$ are the row vectors of $\mathbf{Y }$. The row vectors ${\mathbf {a}}_{i}$ and ${\mathbf {a}}_{j}$ of ${\mathbf {A}}$ are used to measure the closeness of two points ${\bar{\mathbf {y}}}_{i}$ and ${\bar{\mathbf {y}}}_{j}$ of graph. Similar to the computing of $w_{ij}$, the weight $h_{ij}$ can be computed from ${\bar{\mathbf {y}}}_{i}$ and ${\bar{\mathbf {y}}}_{j}$. For all i and j, $h_{ij}$ compose an $m\times m$ weight matrix ${\mathbf {H}}$.

The disadvantage of p nearest neighbors is that the computation results are less geometrically intuitive. To overcome this problem, we can use $\epsilon$-neighborhoods to define the closeness of two points in a graph. The $\epsilon$-neighborhoods definition is as follows:

For any two nodes ${\mathbf {y}}_{i}$ and ${\mathbf {y}}_{j}$, if the Euclidian distance

$$\begin{aligned} ||{\mathbf {y}}_{i}-{\mathbf {y}}_{j}||^{2} <\epsilon , \quad \epsilon \in {\mathbb {R}}, \end{aligned}$$

then these two nodes are close and an edge can be put between them. The only problem is, for each application, we need different tests to find a suitable $\epsilon$.

3 The Proposed Algorithms

For the extended KL-divergence in (3), we need an effective approach to define sparse and smooth terms. Usually, Euclidian distance is one of the most popular choices for measuring the geometrical structures of a graph. Thus, $J({\mathbf {A}})$ and $J({\mathbf {X}})$ are defined as follows:

$$\begin{aligned} J(\mathbf{X })= & {} \frac{1}{2}\sum _{j=1}^{N}\sum _{k=1}^{N}||\mathbf{x }_{j}-\mathbf{x }_{k}||^{2}w_{jk} =Tr(\mathbf{X }^T\mathbf{L }\mathbf{X }), \end{aligned}$$

(7)

$$\begin{aligned} J(\mathbf{A })= & {} \frac{1}{2}\sum _{i=1}^{m}\sum _{j=1}^{m}||\mathbf{a }_{j}-\mathbf{a }_{k}||^{2}h_{ij} =Tr(\mathbf{A }\mathbf{A }^T\mathbf{M }), \end{aligned}$$

(8)

where Tr(.) is the trace of a matrix, ${\mathbf {L}}={\mathbf {D}}_{X}-{\mathbf {W}}$ is called a graph Laplacian, ${\mathbf {D}}_{X}$ is a diagonal matrix with $d_{x_{jj}} = \sum _{k} w_{jk}$, and similarly, ${\mathbf {M}}={\mathbf {D}}_{A}-{\mathbf {H}}$, ${\mathbf {D}}_{A}$ is a diagonal matrix with $d_{a_{ii}} = \sum _{j} h_{ij}$.

From (5), (6), (7), and (8), the following manifold structure modelled NMF learning rules can be proposed:

$$\begin{aligned}&x_{kj} \leftarrow x_{kj} \frac{\sum \nolimits _{i=1}^{m}a_{ij}(y_{ik}/[\mathbf AX ^T]_{ik})}{\sum \nolimits _{q=1}^{m}a_{qj} +\lambda _{\mathbf{X }}[\mathbf{L }\mathbf{X }]_{kj}}, \end{aligned}$$

(9)

$$\begin{aligned}&a_{ij} \leftarrow a_{ij} \frac{\sum \nolimits _{k=1}^{N}x_{kj}(y_{ik}/[\mathbf AX ^T]_{ik})}{\sum \nolimits _{p=1}^{N}x_{pj} +\lambda _{\mathbf{A }}[\mathbf{M }\mathbf{A }]_{ij}}, \end{aligned}$$

(10)

where $a_{ij}$ is normalized in each update step as $a_{ij} = a_{ij}/\sum _{p}a_{pj}$. Learning algorithm (9) is employed to obtain the update result of matrix ${\mathbf {X}}^T$. Since the above definitions show that elements in matrices $\mathbf{L }\mathbf{X }$ and $\mathbf{M }\mathbf{A }$ may be negative, we can use a small positive number $\varepsilon > 0$ to replace these non-positive terms in the learning rules. Thus, for any i, j, and k, if $\sum _{q=1}^{m}a_{qj} +\lambda _{\mathbf{X }}[\mathbf{L }\mathbf{X }]_{kj} \le \varepsilon$ or $\sum _{p=1}^{N}x_{pj} +\lambda _{\mathbf{A }}[\mathbf{M }\mathbf{A }]_{ij} \le \varepsilon$, we can set them equal to $\varepsilon$. Typically we can set $\varepsilon$ = $10^{-5}$.

The objective of the learning algorithms is, for all i, j, and k, the NMF learning can obtain some points $a_{ij}$ and $x_{kj}$ such that

$$\begin{aligned}&x_{kj}=x_{kj}\frac{\sum \nolimits _{i=1}^{m}a_{ij}(y_{ik}/[\mathbf AX ^T]_{ik})}{\sum \nolimits _{q=1}^{m}a_{qj} +\lambda _{\mathbf{X }}[\mathbf{L }\mathbf{X }]_{kj}}, \end{aligned}$$

(11)

$$\begin{aligned}&a_{ij}=a_{ij}\frac{\sum \nolimits _{k=1}^{N}x_{kj}(y_{ik}/[\mathbf AX ^T]_{ik})}{\sum \nolimits _{p=1}^{N}x_{pj} +\lambda _{\mathbf{A }}[\mathbf{M }\mathbf{A }]_{ij}}, \end{aligned}$$

(12)

where $y_{ik}$ are elements of observation samples, $a_{ij} \in [0, 1]$, $x_{kj} \in [0, +\infty )$.

Equations (11) and (12) can be rewritten as

$$\begin{aligned} x_{kj}= & {} x_{kj} \frac{\sum \nolimits _{i=1}^{m}a_{ij}(y_{ik}/[\mathbf AX ^T]_{ik})+ \lambda _{\mathbf{X }}[\mathbf{W }\mathbf{X }]_{kj}}{\sum \nolimits _{q=1}^{m}a_{qj} +\lambda _{\mathbf{X }}[\mathbf{D }_{X}\mathbf{X }]_{kj}},\\ a_{ij}= & {} a_{ij} \frac{\sum \nolimits _{k=1}^{N}x_{kj}(y_{ik}/[\mathbf AX ^T]_{ik})+ \lambda _{\mathbf{A }}[\mathbf{H }\mathbf{A }]_{ij}}{\sum \nolimits _{p=1}^{N}x_{pj} +\lambda _{\mathbf{A }}[\mathbf{D }_{A}\mathbf{A }]_{ij}}. \end{aligned}$$

Thus, (9) and (10) can be modified as additive learning algorithms:

$$\begin{aligned}&x_{kj} \leftarrow x_{kj} \frac{\sum _{i=1}^{m}a_{ij}(y_{ik}/[\mathbf AX ^T]_{ik})+\lambda _{\mathbf{X }}[\mathbf{W }\mathbf{X }]_{kj}}{\sum _{q=1}^{m}a_{qj} +\lambda _{\mathbf{X }}[\mathbf{D }_{X}\mathbf{X }]_{kj}},\end{aligned}$$

(13)

$$\begin{aligned}&a_{ij} \leftarrow a_{ij} \frac{\sum _{k=1}^{N}x_{kj}(y_{ik}/[\mathbf AX ^T]_{ik})+\lambda _{\mathbf{A }}[\mathbf{H }\mathbf{A }]_{ij}}{\sum _{p=1}^{N}x_{pj} +\lambda _{\mathbf{A }}[\mathbf{D }_{A}\mathbf{A }]_{ij}}, \end{aligned}$$

(14)

Similar to (9) and (10), from the cost function in (4), the following learning rules can be proposed:

$$\begin{aligned}&x_{kj} \leftarrow x_{kj} \frac{[\mathbf{Y }^{T}\mathbf{A }-\lambda _{\mathbf{X }}\mathbf{L }\mathbf{X }]_{kj}}{[{\mathbf {X}}{\mathbf {A}}^{T}\mathbf{A }]_{kj}}, \end{aligned}$$

(15)

$$\begin{aligned}&a_{ij} \leftarrow a_{ij} \frac{[\mathbf YX -\lambda _{\mathbf{A }}\mathbf{M }\mathbf{A }]_{ij}}{[\mathbf AX ^T{\mathbf {X}}]_{ij}}. \end{aligned}$$

(16)

where $a_{ij}$ is normalized in each step as $a_{ij} = a_{ij}/\sqrt{\sum _{p}a_{pj}^2}$. To ensure the nonnegativity of elements in the learning rules, if for some i, j, and k, $[\mathbf{Y }^{T}\mathbf{A }-\lambda _{\mathbf{X }}\mathbf{L }\mathbf{X }]_{kj}\le \varepsilon$ or $[\mathbf YX -\lambda _{\mathbf{A }}\mathbf{M }\mathbf{A }]_{ij}\le \varepsilon$, $\varepsilon$ can be used to replace them.

Same to (13) and (14), update rules (15) and (16) are equivalent to the following additive learning algorithms:

$$\begin{aligned}&x_{kj} \leftarrow x_{kj} \frac{[\mathbf{Y }^{T}\mathbf{A }+\lambda _{\mathbf{X }}\mathbf{W }\mathbf{X }]_{kj}}{[{\mathbf {X}}{\mathbf {A}}^{T}\mathbf{A }+\lambda _{\mathbf{X }}\mathbf{D }_{X}\mathbf{X }]_{kj}}, \end{aligned}$$

(17)

$$\begin{aligned}&a_{ij} \leftarrow a_{ij} \frac{[\mathbf YX +\lambda _{\mathbf{A }}\mathbf{H }\mathbf{A }]_{ij}}{[\mathbf AX ^T{\mathbf {X}}+\lambda _{\mathbf{A }}\mathbf{D }_{A}\mathbf{A }]_{ij}}. \end{aligned}$$

(18)

The advantage of the learning rules (17) and (18) is that in the learning we don’t need to test the nonnegativity of $a_{ij}$ and $x_{kj}$ since all terms in these two rules are nonnegative. However, (17) and (18) are similar to the learning rules in DNMF. Our analysis in the next section will show that the another type of expressions of these two rules in (15) and (16) can be non-divergent under a specific condition. From this condition, the convergence of this algorithm can be controlled in the learning.

From Eq. (2), we can see that the learning can obtain the feature representation ${\mathbf {x}}_{k}$ of each sample vector ${\mathbf {y}}_{k}$ and their corresponding basis vectors ${\mathbf {a}}_{j}$ ($j=1, 2,\ldots , n$). Thus, we consider that $\mathbf LX$ is used for the local manifold regularization and $\mathbf MA$ is used for the global manifold regularization of sample data. Comparing with the algorithms (15) and (16), our analysis will show that the learning algorithms (9) and (10) have better convergent properties. We only focus on the convergence analysis of these two learning rules in this paper.

4 Convergence Analysis of the Learning Algorithms

To present the convergence properties of the learning algorithms (9) and (10), let us introduce the concept of fixed point first.

Definition 1

For the learning algorithm (9), a point $x_{kj} \in {\mathbb {R}}$ is called a fixed point of the update iterations, if and only if Eq. (11) holds. Similarly, for the learning algorithm (10), a point $a_{ij} \in {\mathbb {R}}$ is called a fixed point of the update iterations, if and only if Eq. (12) holds.

The point $x_{kj}$ satisfying Eq. (11) or the point $a_{ij}$ satisfying Eq. (12) is also called an equilibrium point of the corresponding learning algorithm. At the fixed points, we can say that the learning algorithms reach their equilibrium state.

For all i, j, and k, if a point $(a_{11}$, $a_{12},\ldots , a_{mn}, x_{11}, x_{12},\ldots , x_{nN})$ satisfies Eqs. (11) and (12), then it is called the fixed point of its corresponding algorithms.

At the fixed point, Eq. (11) can be rewritten as

$$\begin{aligned} x_{kj}= & {} x_{kj}\frac{\sum _{i=1}^{m}a_{ij}\left( y_{ik}/\sum _{p=1}^{n}a_{ip}x_{kp}\right) }{\sum _{q=1}^{m}a_{qj}+\lambda _{{\mathbf {X}}}\sum _{p=1}^{N}l_{kp}x_{pj}} \nonumber \\= & {} \frac{x_{kj}\sum _{i=1}^{m}a_{ij}y_{ik}/\left( a_{ij}x_{kj}+\sum _{p=1,\ne j}^{n}a_{ip}x_{kp}\right) }{\lambda _{{\mathbf {X}}}l_{kk}x_{kj}+\sum _{q=1}^{m}a_{qj}+\lambda _{{\mathbf {X}}}\sum _{p=1, p\ne k}^{N}l_{kp}x_{pj}}. \end{aligned}$$

(19)

Assuming

$$\begin{aligned}&a_{j}=\sum _{q=1}^{m}a_{qj}+\lambda _{{\mathbf {X}}}\sum _{p=1, p\ne k}^{N}l_{kp}x_{pj},\quad b_{k} = \lambda _{{\mathbf {X}}}l_{kk},\nonumber \\&c_{i}=a_{ij}y_{ik},\quad d_{i}=\sum _{p=1,\ne j}^{n}a_{ip}x_{kp}, \quad e_{i} = a_{ij}, \end{aligned}$$

(20)

Equation (11) can be simplified to

$$\begin{aligned} x_{kj}=\frac{x_{kj}}{a_{j}+b_{k}x_{kj}}\sum _{i=1}^{m}\frac{c_{i}}{d_{i}+e_{i}x_{kj} }, \end{aligned}$$

(21)

where $x_{kj}$ is the only variable in a single update computing and for all i, j, and k, $a_{j}$, $b_{k}$, $d_{i}$, and $e_{i}$ cannot be zeros at the same time. Here we must know that in the learning, $x_{kj}$, $a_{j}$, and $b_{k}$ are all variables. In any update step, the only constants are $\lambda _{\mathbf{A }}$, $\lambda _{\mathbf{X }}$, $y_{ik}$, and $l_{kp}$.

From Eq. (21), the $t+1$-th update is

$$\begin{aligned} x_{kj}(t+1)\leftarrow \frac{x_{kj}(t)}{a_{j}+b_{k}x_{kj}(t)}\sum _{i=1}^{m}\frac{c_{i}}{d_{i}+e_{i}x_{kj}(t)}. \end{aligned}$$

(22)

From (22), it is clear that $t+1$-th update has the following possible results:

$$\begin{aligned} x_{kj}(t+1)=\left\{ \begin{array}{ll} 0, &{}\quad { if}\quad x_{kj}(t)\rightarrow 0, \\ 1/b_{k}, &{}\quad { if}\quad x_{kj}(t)\rightarrow \infty .\\ { constant}, &{}\quad { otherwise}. \end{array} \right. \end{aligned}$$

Since $l_{kk}>0$, if $\lambda >0$, it always holds that $b_{k}>0$. Thus, in any cases, if the learning is convergent, the update will converge to a constant.

It is clear that update rules (17) and (18) are similar to DNMF learning rules. For this class of learning algorithms, the update result at the fixed point can be rewritten as

$$\begin{aligned} x_{kj}(t+1)= & {} x_{kj}(t)\frac{[\mathbf{Y }^{T}\mathbf{A }-\lambda _{\mathbf{X }}\mathbf{L }\mathbf{X }]_{kj}}{[{\mathbf {X}}{\mathbf {A}}^{T}\mathbf{A }]_{kj}}\\= & {} x_{kj}(t)\frac{\sum _{i=1}^{n}a_{ik}(t)y_{ik}-\lambda _{\mathbf{X }}\sum _{p=1}^{N}l_{kp}x_{pj}(t)}{\sum _{p=1}^{n}\sum _{i=1}^mx_{kp}(t)a_{ip}(t)a_{ij}(t)}. \end{aligned}$$

Therefore, similar to update rule (22), (15) can be simplified to

$$\begin{aligned} x_{kj}(t+1)\leftarrow x_{kj}(t)\frac{{\hat{a}}_{k}+{\hat{b}}_{k}x_{kj}(t)}{{\hat{c}}_{j}+{\hat{d}}_{k}x_{kj}(t)}. \end{aligned}$$

(23)

From update rule (23), if $\lambda _{\mathbf{X }} >0$, it follows that

$$\begin{aligned} x_{kj}(t+1)=\left\{ \begin{array}{ll} 0, &{}\quad { if}\quad x_{kj}(t)\rightarrow 0, \\ \infty , &{}\quad { if}\quad x_{kj}(t)\rightarrow \infty ,\\ { constant},&{}\quad { otherwise}. \end{array}\right. \end{aligned}$$

Thus, for this class of learning algorithms, the convergence can not be guaranteed, which indicates that for the GNMF and DNMF learning algorithms, the divergent points may exist. We will analyze the detail convergent properties of all the learning algorithms later. For those learning rules which may be divergent, we will find the the non-divergent conditions for them.

For the update algorithm of $a_{ij}$, the terms in Eq. (12) can also be rewritten; then we have similar results as follows:

$$\begin{aligned} \sum _{k=1}^{N}x_{kj}(y_{ik}/[\mathbf AX ^T]_{ik})= & {} \sum _{k=1}^{N}\frac{x_{kj}y_{ik}}{\sum _{p=1}^{n}a_{ip}x_{kp}}\\= & {} \sum _{k=1}^{N}\frac{x_{kj}y_{ik}}{a_{ij}x_{kj}+\sum _{p=1, p\ne j}^{n}a_{ip}x_{kp}} \end{aligned}$$

and

$$\begin{aligned} \sum _{p=1}^{N}x_{pj} +\lambda _{\mathbf{A }}[\mathbf{M }\mathbf{A }]_{ij}= & {} \sum _{p=1}^{N}x_{pj}+\lambda _{\mathbf{A }}\sum _{p=1}^{m}m_{ip}a_{pj}\\= & {} \lambda _{\mathbf{A }}m_{ii}a_{ij}+\sum _{p=1}^{N}x_{pj}+\lambda _{\mathbf{A }}\sum _{p=1,p\ne i}^{m}m_{ip}a_{pj}. \end{aligned}$$

Assuming

$$\begin{aligned}&{\tilde{a}}_{j}=\sum _{p=1}^{N}x_{pj}+\lambda _{\mathbf{A }}\sum _{p=1,p\ne i}^{m}m_{ip}a_{pj},\quad {\tilde{b}}_{i}=\lambda _{\mathbf{A }}m_{ii},\nonumber \\&{\tilde{c}}_{k}=x_{kj}y_{ik},\quad {\tilde{d}}_{k}=\sum _{p=1, p\ne j}^na_{ip}x_{pj},\quad {\tilde{e}}_{k} =x_{kj}, \end{aligned}$$

(24)

Equation (12) can be simply written as

$$\begin{aligned} a_{ij}=\frac{a_{ij}}{{\tilde{a}}_{j}+{\tilde{b}}_{i}a_{ij}}\sum _{k=1}^N\frac{{\tilde{c}}_{k}}{{\tilde{d}}_{k}+{\tilde{e}}_{k}a_{ij}}, \end{aligned}$$

(25)

where $a_{ij}$ is the only variable for a single update step of $a_{ij}$.

From Eqs. (21) and (25), we can see that the updates of $a_{ij}$ and $x_{kj}$ have similar convergent features. For the update of $a_{ij}$, the only difference is the normalization of $a_{ij}$ in each update step. Thus, $a_{ij}$ will not diverge to $+\,\infty$ in the learning anyway.

4.1 Non-divergence of the Learning Algorithms

For NMF algorithms, previous studies have shown that the non-increasing of divergence functions cannot guarantee the convergence of the learning algorithms. It is necessary to show that the proposed algorithms will converge to the local minima of their corresponding cost functions.

Theorem 1

For any initializations, $a_{ij}$ and $x_{kj}$ of update rules (9) and (10) are always upper bounded by constants in the learning, $i=1,2,\ldots , m$, $j=1,2,\ldots , n$, $k= 1, 2,\ldots ,N$; thus, update algorithm (9) and (10) are non-divergent.

Theorem 1 guarantees that any trajectories of the algorithms (9) and (10) starting from any limited points will be always bounded by a positive constant.

For the matrix $\mathbf{L }$ and $\mathbf{X }$, we use vector $\mathbf{x }_{\cdot j}=(x_{1j}, x_{2j},\ldots , x_{Nj})^T$ to represent the j-th column vector of $\mathbf{X }$ and $\mathbf{l }_{k\cdot }=(l_{k1}, l_{k2},\ldots , l_{kN})$ to represent the k-th row vector of $\mathbf{L }$. We have the following theorem for update rule (15) to guarantee the non-divergence in the learning.

Theorem 2

In the learning, if at any update step t, $x_{kj}$ in update rule (15) satisfies

$$\begin{aligned} x_{kj}(t)\le ||{\mathbf {x}}_{\cdot j}(t)||\le \frac{\sqrt{N}\sum _{i=1}^{m}y_{ij}}{1-\sqrt{N}\lambda _{X}||{\mathbf {l}}_{k\cdot }||}, \end{aligned}$$

(26)

then $x_{kj}$ are always upper bounded in the updates; thus, the update algorithm (15) will be always non-divergent under the given condition.

In the test, if there exists a small enough $\lambda _{\mathbf{X }}$ such that $1-\lambda _{\mathbf{X }}||{\mathbf {l}}_{k\cdot }||>0$, then the non-divergence of the learning can be guaranteed by choosing suitable initializations of ${\mathbf {A}}$ and ${\mathbf {X}}$. On the other hand, if the condition in (26) is not met, it is possible to find initial data which leads the divergence of the learning algorithms. For example, if in the applications we have some $\lambda _{\mathbf{X }}$ and initial ${\mathbf {A}}$ and ${\mathbf {X}}$ such that $1-\lambda _{\mathbf{X }}||{\mathbf {l}}_{k\cdot }||<0$, then it may have the result that $x_{kj}$ will diverge in the learning.

The learning rules proposed in DNMF are similar to (17) and (18), which have the same convergence problem. Thus, the proposed learning algorithms in (9) and (10) will have advantages in the applications.

For the updates of $a_{ij}$, because of the normalization, it always holds that $a_{ij}\le 1$. Meanwhile, because of the symmetry, we can give similar initial constraint such that the learning converging to their local minima. Thus, under the condition (26), the learning algorithms (17) and (18) will be always non-divergent.

4.2 Existence of Fixed Points

For the NMF related learning algorithms, the objective function is non-convex for both variables ${\mathbf {A}}$ and ${\mathbf {X}}$, but if we only consider a single variable ${\mathbf {A}}$ or ${\mathbf {X}}$, then the objective function is convex. For the update rules (9) and (10), Theorems 1 and 2 can only guarantee the non-divergence of the learning algorithms. If each learning algorithm has multiple fixed points, the learning may vibrate between these fixed points. We have the following theorems to guarantee the convergence of the algorithms. In the proof of the theorem, we will show that in the updates, for given initializations, each learning rule has a unique fixed point.

Theorem 3

For any initializations of ${\mathbf {A}}$ and ${\mathbf {X}}$, there exists points $x_{kj0}$ and $a_{ij0}$ to be the fixed points of the update algorithms (9) and (10) respectively. For any i, j, $k\in N$, $x_{kj0}$ will be the unique fixed point of the learning algorithm (9) and $a_{ij0}$ will be the unique fixed point of the learning algorithm (10).

Learning algorithms (15) and (16) have the same results. Generally, for the proposed learning algorithms (9) and (10), the following results hold:

• 1. At any update step t, $a_{ij}(t)$ and $x_{kj}(t)$ are always upper bounded by a constant. Each algorithm has unique fixed point, and the update algorithms will converge to their corresponding fixed points.

• 2. If $\exists \, t$ such that $x_{kj}(t)=0$, the update will converge to zero fixed point. The update of $a_{ij}$ has the same result.

  For the proposed learning algorithms (15) and (16), the following result holds:

• 3. For any given initializations, the fixed point is unique. Under the condition (26), the updates of $a_{ij}(t)$ and $x_{kj}(t)$ will always converge to their corresponding fixed points.

Therefore, for any initializations, the NMF updates (9) and (10) will converge to either zero or nonzero constants. However, since each learning algorithm has infinite groups of fixed points, the learning can only obtain a local minimum of the objective function.

5 Simulations

Numerical tests in this section will confirm the convergent properties and the effectiveness of the proposed learning algorithms (9) and (10), and structures in the [35] are used in the tests so that the redundant solutions caused by graph regularization can be eliminated. Four existing methods are also employed to test, including: Normalized cut (NCut) [42], Lee and Seung’s nonnegative matrix factorization (NMF) [2], graph regularized nonnegative matrix factorization (GNMF) [29], and the graph dual regularization nonnegative matrix factorization (DNMF) [36].

We perform experiments on the following three image data sets: COIL20 image library [43], which contains total 1440 images of 20 classes. ORL face dataset [44], which contains total 400 images of 40 classes, and JAFFE facial expression database [45], which contains total 213 images of 10 classes. All the images are resized to $32\times 32$ pixels. 0–1 weighting is used in all the tests. At last, heat kernel weighting is also employed to compute $w_{jk}$ and $h_{ij}$. When we set $t=5.1$, $\lambda =1\sim 200$, similar test results can be obtained. The experiments are conducted on a Windows 10 system with i5-6200U CPU, 2.3 GHz, 4 Processors. Matlab programming is utilized to run all the algorithms.

To test the convergent properties of the proposed learning algorithms, we only choose a single $128\times 128$ image to run the algorithms so that we can take the shortest time to obtain the convergence.

Figures 1 and 2 show the convergent results of $a_{ij}$ and $x_{kj}$ in the decomposition of the single image. Since the learning of $a_{ij}$ and $x_{kj}$ are non-increasing, they will eventually converge to constants. In this test, $\mathbf{A }$ and $\mathbf{X }$ are randomly initialized, $\lambda _{\mathbf{A }} = 0.0375$, $\lambda _{\mathbf{X }}=0.15$, and $n=50$; thus, the image is separated into a $128 \times 50$ matrix ${\mathbf {A}}$ and a $50\times 128$ matrix ${\mathbf {X}}$.

Fig. 1

For random initial matrices ${\mathbf {X}}$ and ${\mathbf {A}}$, all the updates of $a_{ij}$ converge to constants in the updates. The convergent results of $a_{ij}$ for different NMF learning algorithms: a Lee and Seung’s NMF, b the proposed SMNMF, and c the Euclidian distance based DNMF algorithms

Fig. 2

For random initial matrices ${\mathbf {X}}$ and ${\mathbf {A}}$ with $a_{ij}>0$, $x_{kj}>0$, all $x_{kj}$ converge to constants in the updates. Trajectories show the convergent results of $x_{kj}$ for different NMF learning algorithms: a Lee and Seung’s NMF, b the proposed SMNMF, and c the Euclidian distance based DNMF algorithms

Since we initialize components in ${\mathbf {A}}$ and ${\mathbf {X}}$ with $a_{ij}>0$ and $x_{kj}>0$, although the Fig. 1 shows that some $a_{ij}$ ($i, j = 1, 2,\ldots$) converge to zeros, the practical data show that the convergent results are just very close to zero.

From Fig. 3, we can see the non-increasing and converging to zero of KL-divergence and Euclidian distance for different types of NMF algorithms. This figure also shows that for this group of initializations, all the learning methods converge almost at the same time: at about the update iteration 50, all of them begin to converge.

Fig. 3

For random initial matrices ${\mathbf {X}}$ and ${\mathbf {A}}$, the trajectories show the convergent results of KL-divergence and Euclidian distance for different NMF learning algorithms: a Lee and Seung’s NMF, b the proposed SMNMF, and c the Euclidian distance based DNMF algorithms

From Figs. 1, 2 and 3, we can see the convergent properties of the discussed algorithms. For these learning algorithms, there always exist initializations such that the learning will converge to constants.

However, Fig. 4 shows some different update results for $x_{kj}$. In this test, we set $\lambda _{\mathbf{A }}$ = 0.11, $\lambda _{\mathbf{X }}=0.5$, and $\epsilon =200$. The image is still separated into a $128 \times 50$ matrix ${\mathbf {A}}$ and a $50 \times 128$ matrix ${\mathbf {X}}$. For Lee and Seung’s NMF and our proposed algorithms, Fig. 4a, b show the convergence of $x_{kj}$; but Fig. 4c shows the update result for DNMF. Since the computing result shows that in this case, it has $1-\sqrt{N}\lambda _{\mathbf{X }}||{\mathbf {l}}_{\cdot k}||<0$, the condition in (26) is not met; there exists the situation that $x_{kj}$ are diverging even after 600 learning iterations. Therefore, for the DNMF, the divergent points exist.

Fig. 4

In a $128 \times 128$ face image factorization, for random initialization matrices ${\mathbf {X}}$ and ${\mathbf {A}}$, the trajectories show the update results of $x_{kj}$ for different NMF learning algorithms: a Lee and Seung’s NMF, b the proposed SMNMF, and c DNMF algorithms

For this test, Fig. 5 shows the trajectories of Euclidian distance. For Lee and Seung’ NMF and our proposed SMNMF, the Fig. 5a, b show that the objective function converges to zero very fast. For the DNMF, however, since Fig. 4c indicates that for this group of initializations, the divergent points exist, comparing with Fig. 5a–c shows that the corresponding cost function has bigger errors although it is non-increasing in the learning. Thus, the results in Figs. 4c and 5c confirm that the non-increasing of objective functions cannot guarantee the convergence of each learning update.

Fig. 5

In a $128\times 128$ face image factorization, for random initialization matrices ${\mathbf {X}}$ and ${\mathbf {A}}$ with $a_{ij} \ge 0$, $x_{kj} \ge 0$, the trajectories show the convergent results of Euclidian distance for different NMF learning algorithms: a Lee and Seung’s NMF, b the proposed SMNMF, and c DNMF algorithms

However, in practical data decomposition, since matrix $\mathbf{A }$ and ${\mathbf {X}}$ are initialized randomly, to test the condition (26) for each element in the learning is rather time-consuming. Thus, the proposed SMNMF algorithms (9) and (10) are the best choice for manifold learning.

To further test the effectiveness of the proposed learning algorithms, we utilize the algorithms to perform image clustering. In the experiments, different methods are employed so that we can compare their clustering results.

Each image consists of $32\times 32$ pixels. For the COIL20 image dataset, a $1024\times 1440$ sample matrix can be used for learning. Figure 6 shows the basis images learned by different NMF based methods on COIL20 dataset. In this figure, we only show four $5\times 5$ basis image pictures. Figure 6c indicates that the proposed learning algorithms can learn sparser basis vectors since $\lambda _{\mathbf{A }}$ and $\lambda _{\mathbf{X }}$ are used to increase the sparseness of the row vectors. Figure 6d shows that the sparseness will decrease if we decrease $\lambda _{\mathbf{A }}$.

Fig. 6

The basis vectors learned by different NMF algorithms in the COIL20 images decomposition: a Lee and Seung’s NMF learned basis vectors, b the Euclidian distance based GNMF learned basis vectors with $\lambda _{\mathbf{A }} = 0$, $\lambda _{\mathbf{X }} = 0.015$. c The proposed SMNMF learned basis vectors with $\lambda _{\mathbf{A }} = 0.245$, $\lambda _{\mathbf{X }} = 0.015$, and d the proposed SMNMF learned basis vectors with $\lambda _{\mathbf{A }} = 0.0245$, $\lambda _{\mathbf{X }} = 0.015$

Figure 7 shows part of the COIL20 and JAFFE images clustering results performed by the proposed learning algorithms. For COIL20 images, we only choose 10 images from each class to show the clustering effectiveness. From Fig. 7a, b we can see that the proposed method can learn very high accuracy in image clustering. For the presented clustering results, only three face images are clustered to wrong clusters for each dataset.

Fig. 7

The clustered COIL20 and JAFFE images from the proposed learning algorithms with $\lambda _{\mathbf{A }} = 0.0245$, $\lambda _{\mathbf{X }} = 56$, and $n=150$: a The clustered COIL20 images, b the clustered JAFFE images

To show the performance of the learning algorithms, 30 runs were conducted on a given data set for each learning method. The average accuracy results are presented on the following figures.

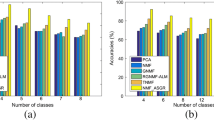
The left figure in Fig. 8 shows the variations of accuracy on the test of COIL20 data set for different values of $\lambda _{\mathbf{A }}$. In this test, we have $p=3$, $\lambda _{\mathbf{X }} = 56$. For different methods, the test results show that the highest accuracy is obtained at $\lambda _{\mathbf{A }}=0.1$. The right figure shows the average clustering accuracy on COIL20 data set for different values of $\lambda _{\mathbf{X }}$. In this test, $p=3$, $\lambda _{\mathbf{A }} = 0.1$. For different types of learning algorithms, the tests show that the highest accuracy is obtained at $\lambda _{\mathbf{X }}=50$.

Fig. 8

The performance of different learning algorithms on COIL20 dataset versus the variations of $\lambda _{\mathbf{A }}$ (left) and $\lambda _{\mathbf{X }}$ (right)

Figure 9 shows the variations of clustering accuracy on COIL20 data set for different settings of nearest neighbor number p. In this test, $\lambda _{\mathbf{A }} = 0.1$, $\lambda _{\mathbf{X }} = 59$. The test results show that the highest accuracy is obtained at $p=3$.

Fig. 9

The performance of learning algorithms on COIL20 dataset versus the variations of p

Fig. 10

The performance of learning algorithms on JAFFE (left) and ORL (right). Datasets for different values of $\lambda _{\mathbf{A }}$

The left figure in Fig. 10 shows the clustering efficiency on JAFFE data set for different values of $\lambda _{\mathbf{A }}$. In this test, we have $p = 3$, $\lambda _{\mathbf{X }} = 56$. Totally $1024\times 213$ samples are used for image clustering. The test results show that, for different types of learning algorithms, the highest accuracy is obtained at $\lambda _{\mathbf{A }}=0.1$. The right shows the average clustering results on ORL data set for different values of $\lambda _{\mathbf{A }}$. In this test, we set $p = 5$, $\lambda _{\mathbf{X }} = 65$. $1024\times 400$ sample images are used for clustering. The test results show that the highest accuracy is obtained at $\lambda _{\mathbf{A }}=0.1$.

Comparing with different types of algorithms, test results in Figs. 8, 9 and 10 show that our proposed algorithms have the best average accuracy in data clustering. Although DNMF and SMNMF have similar structures, they have different convergent features. Comparing with DNMF, the detail test data show that the proposed algorithms have better stability in image clustering. Clearly, algorithms that have better convergence can produce more stable image recognition results.

6 Discussion and Future Work

In the learning, NMF based algorithms switch between two different updates of factors ${\mathbf {A}}$ and ${\mathbf {X}}$. Thus, all the elements in ${\mathbf {A}}$ and ${\mathbf {X}}$ will be modified in each iteration, which greatly increases the difficulties of convergence analysis of the learning algorithms.

For any given initializations, the fixed points of the proposed SMNMF algorithms can be uniquely determined in the learning. Therefore, the non-divergence of the proposed SMNMF algorithms can be guaranteed. For the proposed algorithms, we have the following important results:

• 1. For any initial values, learning updates (9) and (10) are always non-divergent.

• 2. In the learning, since a small positive number $\varepsilon >0$ is added to ensure that all the denominator terms in the learning algorithms will not be zero or negative, the update algorithms will converge to their unique fixed points for any initializations. This problem can also be solved by using the update rule (13) and (14).

• 3. The non-divergence of the learning algorithm in (15) can be guaranteed if we control the initial setting to a predefined value.

In general, because of their unconditional non-divergence, it is clear that the proposed algorithms (9) and (10) can be safely applied to a wide range of manifold learning problems.

The future work in this research includes: Suitable values of $\lambda _{A}$ and $\lambda _{X}$ are critical to the proposed algorithm. Theoretically, it is difficult to determine the efficient selections of these parameters in the learning. The proof shows that our algorithms are non-divergent, but we still cannot prove the convergence of the proposed algorithms.

Appendix: Proofs of theorems

For matrix $\mathbf{A }$, its row number m and column number n are limited numbers. Thus in the proofs of theorems, m and n can be considered as constants. Because of the normalization, we have $\sum _{i=1}^{m}a_{ij}=1$ or $\sum _{i=1}^{m}a_{ij}^2=1$. For all i, $a_{ij}\le 1$, from (20), it holds that there always exists i, such that $e_{i}>0$. For the update algorithm of $x_{kj}$, if $x_{kj} > 0$, $c_{i} > 0$, from (20) and (21), $\forall \, i$, $d_{i}\ge 0$, it holds that

$$\begin{aligned} 0\le x_{kj}(t)\sum _{i=1}^m\frac{c_{i}}{d_{i}+e_{i}x_{kj}(t)}\le \sum _{i=1}^m\frac{c_{i}}{e_{i}}. \end{aligned}$$

If $\exists i$, such that $e_{i} =0$, then $c_{i}= 0$, it follows that

$$\begin{aligned}&d_{i}> 0, \quad \frac{c_{i}}{d_{i}+e_{i}x_{kj}(t)}=0,\\&x_{kj}(t)\sum _{i=1}^m\frac{c_{i}}{d_{i}+e_{i}x_{kj}(t)}\le \sum _{i=1}^m\frac{c_{i}}{e_{i}}=\sum _{r=1, r\ne i}^m\frac{c_{r}}{e_{r}} \le \sum _{i=1}^m y_{ik}. \end{aligned}$$

From (20), if $\forall \, i$, $e_{i} \ne 0$, then $a_{ij}>0$; it holds that

$$\begin{aligned} \sum _{i=1}^m\frac{c_{i}}{e_{i}} =\sum _{i=1}^m\frac{a_{ij}y_{ik}}{a_{ij}}= \sum _{i=1}^my_{ik}. \end{aligned}$$

(27)

For all i, k, and p, $y_{ik}$ and $l_{kp}$ are constants and $y_{ik}$ are nonnegative. Therefore, for all i and p, there always exist some $y_{ik}$ and $l_{kp}$ such that $y_{ik}>0$ and $l_{pk}\ne 0$. Denote

$$\begin{aligned}&Y_{k} = \max _{i}\left\{ y_{ik}|y_{ik}>0, \ i=1, 2,\ldots , m\right\} ,\nonumber \\&y_{k} = \min _{i}\left\{ y_{ik}|y_{ik}>0, \ i=1, 2,\ldots , m \right\} ,\nonumber \\&Z_{p} = \max _{k}\left\{ |l_{kp}|\left| l_{kp}\ne 0\right. , \ k=1, 2,\ldots , N \right\} . \end{aligned}$$

(28)

Proof of Theorem 1

From (21) and (27), for the $t+1$-th update, if $x_{kj}(t) = 0$, then $x_{kj}(t+1) = 0$, Thus $x_{kj}(t+1)$ is bounded by any positive constant. If $x_{kj}(t) > 0$, it follows that

$$\begin{aligned} x_{kj}(t+1)= & {} \frac{x_{kj}(t)}{a_{j}+b_{k}x_{kj}(t)}\sum _{i=1}^m\frac{c_{i}}{(d_{i}+e_{i}x_{kj}(t))}\nonumber \\= & {} \frac{1}{a_{j}+b_{k}x_{kj}(t)}\sum _{i=1}^m\frac{x_{kj}(t)c_{i}}{(d_{i}+e_{i}x_{kj}(t))}\nonumber \\\le & {} \frac{1}{a_{j}+b_{k}x_{kj}(t)}\sum _{i=1}^m\frac{x_{kj}(t)c_{i}}{e_{i}x_{kj}(t)}\nonumber \\= & {} \frac{1}{a_{j}+b_{k}x_{kj}(t)}\sum _{i=1}^m\frac{c_{i}}{e_{i}}\nonumber \\\le & {} \frac{\sum _{i=1}^{m}y_{ik}}{\sum _{q=1}^{m}a_{qj}+\lambda _{\mathbf{X }}\sum _{p=1 }^{N}l_{kp}x_{pj}(t)}\nonumber \\\le & {} \frac{\sum _{i=1}^{m}y_{ik}}{\varepsilon }. \end{aligned}$$

(29)

From the definition of matrix $\mathbf{L }$, if $\lambda _{\mathbf{X }}$ is small enough, we have $\lambda _{\mathbf{X }}\sum _{p=1 }^{N}l_{kp}x_{pj}(t)< \sum _{q=1}^{m}a_{qj}$. Thus $x_{kj}(t+1)$ will be upper bounded by $\sum _{i=1}^{m}y_{ik}$.

Inequality (29) shows that in any update step, $x_{kj}$ is always upper bounded by a positive constant.

On the other hand, assuming that $C_{0}$ is a nonnegative constant, if $x_{kj}(t)\ge C_{0}$, from Eq. (19), it follows that:

$$\begin{aligned} x_{kj}(t+1)= & {} x_{kj}(t)\frac{\sum _{i=1}^{m}a_{ij}(y_{ik}/\sum _{p=1}^{n}a_{ip}x_{kp}(t))}{\sum _{q=1}^{m}a_{qj}+\lambda _{\mathbf{X }}\sum _{p=1}^{N}l_{kp}x_{pj}(t)}\nonumber \\\ge & {} \frac{x_{kj}(t)y_{k}/\left( \frac{n\sum _{i=1}^{m}y_{ik}}{\varepsilon }\right) }{1+\lambda _{\mathbf{X }}Z_{p}\sum _{k=1}^{N}\sum _{i=1}^{m}y_{ik}}\nonumber \\= & {} \frac{x_{kj}(t)y_{k}}{ \left( 1+\lambda _{\mathbf{X }}Z_{p}\sum _{k=1}^{N}\sum _{i=1}^{m}y_{ik} \right) \frac{n\sum _{i=1}^{m}y_{ik}}{\varepsilon }} \end{aligned}$$

(30)

$$\begin{aligned}\ge & {} \frac{C_{0}y_{k}}{n\left( 1+\lambda _{\mathbf{X }}Z_{p} \sum _{k=1}^{N}Y_{k}\right) \frac{\sum _{i=1}^{m}y_{ik}}{\varepsilon }}>0. \end{aligned}$$

(31)

From (31), assume

$$\begin{aligned} M_{0}=\frac{C_{0}y_{k}}{n\left( 1+\lambda _{\mathbf{X }}Z_{p}\sum _{k=1}^{N}Y_{k}\right) \frac{\sum _{i=1}^{m}y_{ik}}{\varepsilon }}. \end{aligned}$$

For any update step t, if $x_{kj}(t)\ge C_{0}$, then it holds that

$$\begin{aligned} x_{kj}(t+1) \ge M_{0}. \end{aligned}$$

(32)

Inequality (32) shows for any update of $x_{kj}$, if initialization $x_{kj}(0)>0$, then in any update step t, it holds that $x_{kj}(t)>0$; if initialization $x_{kj}(0)=0$, then in any update step t, it holds that $x_{kj}(t)=0$. The update of $a_{ij}$ has the similar result; to save page, we omit the detail analysis steps here.

For the update of $a_{ij}$, since $m_{ii}\ge 0$, from (24), (25), and (32), it follows that

$$\begin{aligned} a_{ij}(t+1)= & {} \frac{1}{{\tilde{a}}_{j}+{\tilde{b}}_{i}a_{ij}(t)}\sum _{k=1}^N\frac{a_{ij}(t){\tilde{c}}_{k}}{{\tilde{d}}_{k}+{\tilde{e}}_{k}a_{ij}}\nonumber \\\le & {} \frac{1}{{\tilde{a}}_{j}+{\tilde{b}}_{i}a_{ij}(t)}\sum _{k=1}^N\frac{a_{ij}(t){\tilde{c}}_{k}}{{\tilde{e}}_{k}a_{ij}(t)}\nonumber \\= & {} \frac{1}{\lambda _{\mathbf{A }}\sum _{p=1}^{m}m_{ip}a_{pj}+\sum _{p=1}^Nx_{pj}}\sum _{k=1}^N\frac{{\tilde{c}}_{k}}{{\tilde{e}}_{k}}\nonumber \\= & {} \frac{1}{\lambda _{\mathbf{A }}\sum _{p=1}^{m}m_{ip}a_{pj}+\sum _{p=1}^Nx_{pj}}\sum _{k=1}^N\frac{x_{kj}y_{ik}}{x_{kj}}\nonumber \\\le & {} \frac{\sum _{k=1}^{N}y_{ik}}{\lambda _{\mathbf{A }}\sum _{p=1, p\ne i}^{m}m_{ip}+NM_{0}}. \end{aligned}$$

(33)

If $\lambda _{\mathbf{A }}\sum _{p=1, p\ne i}^{m}m_{ip}+NM_{0} \le 0$, it holds that

$$\begin{aligned} a_{ij}(t+1)\le \frac{\sum _{k=1}^{N}y_{ik}}{\varepsilon }. \end{aligned}$$

Inequality (33) shows that after the t+1-th update, $a_{ij}$ will be a limited number under the condition (32). But in the update the denominator may become zero if we don’t have the constraint $\sum _{p=1}^{N}x_{pj} +\lambda _{\mathbf{A }}[\mathbf{M }\mathbf{A }]_{ij} \ge \varepsilon$. Thus, we cannot guarantee the non-divergence of the learning update of $a_{ij}$. With this constraint, the normalization of $a_{ij}$ in each update iteration can guarantee $a_{ij} \le 1$ for any i and j. Thus, the proof of Theorem 1 is complete. $\square$

Proof of Theorem 2

Assume

$$\begin{aligned} x_{rj} = \max \left\{ x_{1j}, x_{2j},\ldots , x_{Nj} \right\} . \end{aligned}$$

For the updates of $x_{kj}$, at any update step t, if

$$\begin{aligned} x_{kj}(t)\le ||{\mathbf {x}}_{\cdot j}(t)||\le \frac{\sqrt{N}\sum _{i=1}^{m}y_{ij}}{1-\sqrt{N}\lambda _{X}||{\mathbf {l}}_{k\cdot }||}, \end{aligned}$$

then it follows that

$$\begin{aligned} ||{\mathbf {x}}_{\cdot j}(t+1)||= & {} \sqrt{x_{1j}^2(t+1)+x_{2j}^2(t+1)+\cdots +x_{Nj}^2(t+1)}\nonumber \\\le & {} \sqrt{Nx_{rj}^2(t+1)}\nonumber \\= & {} x_{rj}(t+1)\nonumber \\= & {} \sqrt{N}x_{rj}(t)\frac{[\mathbf{Y }^{T}\mathbf{A }-\lambda _{\mathbf{X }}\mathbf{L }\mathbf{X }]_{rj}}{[{\mathbf {X}}{\mathbf {A}}^{T}\mathbf{A }]_{rj}}\nonumber \\= & {} \sqrt{N}x_{rj}(t)\frac{\sum _{i=1}^{n}a_{ik}(t)y_{ij}-\lambda _{\mathbf{X }} \left( \sum _{p=1}^{N}l_{rp}x_{pj}(t)\right) }{\sum _{i=1}^n\sum _{p=1}^{m}x_{ri}(t)a_{pi}(t)a_{pj}(t)}\nonumber \\= & {} \sqrt{N}x_{rj}(t)\frac{\sum _{i=1}^{m}y_{ij}+\lambda _{\mathbf{X }}\mathbf{l }_{r\cdot }(-\mathbf{x }_{\cdot j}(t))}{\sum _{i=1}^n\sum _{p}^{m}a_{pi}(t)a_{pj}(t)x_{ri}(t)}\nonumber \\\le & {} \sqrt{N}\frac{\sum _{i=1}^{m}y_{ij}+\lambda _{\mathbf{X }}||\mathbf{l }_{r\cdot }||||\mathbf{x }_{\cdot j}(t)|||\cos \theta _{t}|)}{\sum _{p}^{m}a_{pj}^2(t)}\nonumber \\= & {} \sqrt{N}\left( \sum _{i=1}^{m}y_{ij}+\lambda _{\mathbf{X }}||\mathbf{l }_{r\cdot }||||\mathbf{x }_{\cdot j}(t)|||\cos \theta _{t}|\right) \nonumber \\\le & {} \sqrt{N}\left( \sum _{i=1}^{m}y_{ij}+\lambda _{\mathbf{X }}||\mathbf{l }_{r\cdot }||||\mathbf{x }_{\cdot j}(t)||\right) \nonumber \\\le & {} \frac{\sqrt{N}\sum _{i=1}^{m}y_{ij}}{1-\sqrt{N}\lambda _{\mathbf{X }}||{\mathbf {l}}_{r\cdot }||}. \end{aligned}$$

(34)

Since $\frac{\sqrt{N}\sum _{i=1}^{m}y_{ij}}{1-\sqrt{N}\lambda _{\mathbf{X }}||{\mathbf {l}}_{r\cdot }||}$ is a constant, if the initialization $||{\mathbf {x}}_{\cdot j}(0)||\le \frac{\sqrt{N}\sum _{i=1}^{m}y_{ij}}{1-\sqrt{N}\lambda _{X}||{\mathbf {l}}_{k\cdot }||}$, (34) shows that $x_{kj}$ is always upper bounded. Thus, the proof is complete. $\square$

Proof of Theorem 3

The update algorithms (9) and (10) show that for each update iteration, all the elements in ${\mathbf {A}}$ and ${\mathbf {X}}^T$ will be updated. However the updates of $x_{kj}$ can be considered column by column and the updates of $a_{ij}$ can be considered row by row. Assuming ${\mathbf {x}}_{k\cdot }=(x_{k1}, x_{k2},\ldots , x_{kn})^T$, ${\mathbf {a}}_{i\cdot }=(a_{i1}, a_{i2},\ldots , a_{in})$, we have the following update systems for $x_{kj}$ and $a_{ij}$:

$$\begin{aligned}&{\mathbf {x}}_{k\cdot }=\left[ \begin{matrix} x_{k1}\\ x_{k2} \\ \cdots \\ x_{kn}\\ \end{matrix}\right] \leftarrow \left[ \begin{matrix} x_{k1}\frac{\sum _{i=1}^{m}a_{i1} \frac{y_{ik}}{{\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }}}{\sum _{q=1}^{m}a_{q1}+\lambda _{{\mathbf {X}}}\sum _{p=1}^{N}l_{kp}x_{p1}}\\ \\ x_{k2}\frac{\sum _{i=1}^{m}a_{i2} \frac{y_{ik}}{{\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }}}{\sum _{q=1}^{m}a_{q2}+\lambda _{{\mathbf {X}}}\sum _{p=1}^{N}l_{kp}x_{p2}}\\ \cdots \\ \\ x_{kn}\frac{\sum _{i=1}^{m}a_{in} \frac{y_{ik}}{{\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }}}{\sum _{q=1}^{m}a_{qn}+\lambda _{{\mathbf {X}}}\sum _{p=1}^{N}l_{kp}x_{pn}}\\ \end{matrix}\right] , \end{aligned}$$

(35)

$$\begin{aligned}&{\mathbf {a}}_{i\cdot }=\left[ \begin{matrix} a_{i1}\\ a_{i2} \\ \cdots \\ a_{in}\\ \end{matrix}\right] ^{T}\leftarrow \left[ \begin{matrix} a_{i1}\frac{\sum _{k=1}^{N}x_{1k} \frac{y_{ik}}{{\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }}}{\sum _{p=1}^{N}x_{p1}+\lambda _{{\mathbf {A}}}\sum _{p=1}^{m}m_{ip}a_{p1}}\\ \\ a_{i2}\frac{\sum _{k=1}^{N}x_{2k} \frac{y_{ik}}{{\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }}}{\sum _{p=1}^{N}x_{p2}+\lambda _{{\mathbf {A}}}\sum _{p=1}^{m}m_{ip}a_{p2}}\\ \cdots \\ \\ a_{in}\frac{\sum _{k=1}^{N}x_{nk} \frac{y_{ik}}{{\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }}}{\sum _{p=1}^{N}x_{pn}+\lambda _{{\mathbf {A}}}\sum _{p=1}^{m}m_{ip}a_{pn}}\\ \end{matrix}\right] ^{T}. \end{aligned}$$

(36)

From systems (35) and (36), it is clear that for the update rules of $x_{kj}$, if $\lambda _{\mathbf{X }}=0$, they only include the column vector ${\mathbf {x}}_{k\cdot }$ of matrix ${\mathbf {X}}^T$ as a variable, and for the update rules of $a_{ij}$, if $\lambda _{\mathbf{A }}=0$, they only include the row vector ${\mathbf {a}}_{i\cdot }$ of matrix ${\mathbf {A}}$ as a variable. Denoting

$$\begin{aligned} v_{i}= & {} v_{i}(x_{k1}, x_{k2},\ldots , x_{kn})= \frac{y_{ik}}{{\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }}, \end{aligned}$$

(37)

$$\begin{aligned} s_{k}= & {} s_{k}(a_{i1}, a_{i2},\ldots , a_{in})= \frac{y_{ik}}{{\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }}, \end{aligned}$$

(38)

the following two systems hold:

$$\begin{aligned}&\left[ \begin{matrix} x_{k1}\\ x_{k2} \\ \cdots \\ x_{kn}\\ \end{matrix}\right] \leftarrow \left[ \begin{matrix} x_{k1}\frac{\sum _{i=1}^{m}a_{i1}v_{i}(x_{k1}, x_{k2},\ldots , x_{kn})}{\sum _{q=1}^{m}a_{q1}+\lambda _{{\mathbf {X}}}\sum _{p=1}^{N}l_{kp}x_{p1}}\\ \\ x_{k2}\frac{\sum _{i=1}^{m}a_{i2}v_{i}(x_{k1}, x_{k2},\ldots , x_{kn})}{\sum _{q=1}^{m}a_{q2} +\lambda _{{\mathbf {X}}}\sum _{p=1}^{N}l_{kp}x_{p2}}\\ \cdots \\ \\ x_{kn}\frac{\sum _{i=1}^{m}a_{in}v_{i}(x_{k1}, x_{k2},\ldots , x_{kn})}{\sum _{q=1}^{m}a_{qn} +\lambda _{{\mathbf {X}}}\sum _{p=1}^{N}l_{kp}x_{pn}}\\ \end{matrix}\right] , \end{aligned}$$

(39)

$$\begin{aligned}&\left[ \begin{matrix} a_{i1}\\ a_{i2} \\ \cdots \\ a_{in}\\ \end{matrix}\right] ^{T}\leftarrow \left[ \begin{matrix} a_{i1}\frac{\sum _{k=1}^{N}x_{k1}s_{k}(a_{i1}, a_{i2},\ldots , a_{in})}{\sum _{p=1}^{N}x_{p1}+\lambda _{{\mathbf {A}}}\sum _{p=1}^{m}m_{ip}a_{p1}}\\ \\ a_{i2}\frac{\sum _{k=1}^{N}x_{k2}s_{k}(a_{i1}, a_{i2},\ldots , a_{in})}{\sum _{p=1}^{N}x_{p2} +\lambda _{{\mathbf {A}}}\sum _{p=1}^{m}m_{ip}a_{p2}}\\ \cdots \\ \\ a_{in}\frac{\sum _{k=1}^{N}x_{kn}s_{k}(a_{i1}, a_{i2},\ldots , a_{in})}{\sum _{p=1}^{N}x_{pn} +\lambda _{{\mathbf {A}}}\sum _{p=1}^{m}m_{ip}a_{pn}}\\ \end{matrix}\right] ^{T}. \end{aligned}$$

(40)

For NMF, since ${\mathbf {A}}$ and ${\mathbf {X}}$ are variables, the objective functions are not convex in both variables together. Therefore, the learning algorithms have multiple fixed points if all the elements in ${\mathbf {A}}$ and ${\mathbf {X}}$ are updated at the same time. However, in the practical data decomposition, updates for matrix ${\mathbf {A}}$ and ${\mathbf {X}}$ are computed alternately. A reasonable assumption is that update system (39) is used to find a group fixed points $x_{kj0}$, $j = 1, 2,\ldots , n$ for some given matrix ${\mathbf {A}}$, and elements in ${\mathbf {A}}$ are not changed in the updates of $x_{kj}$. Thus, we can temporarily consider ${\mathbf {A}}$ as a constant matrix in the study of fixed point $x_{kj0}$. For the update of $a_{ij}$, we have similar assumption.

For the kj-th update, if $x_{kj}=0$ is a solution of Eq. (11), then $x_{kj}=0$ is a fixed point of the kj-th update in (9). However, elements in ${\mathbf {x}}_{k\cdot }$ cannot be all zeros, otherwise the denominators in the learning algorithms may be zeros. In fact, inequality (31) shows that for any point $x_{kj}$, it its initial point $x_{kj}(0)>0$, then at any update step t, it always holds that $x_{kj}(t)>0$. $a_{ij}$ has the similar result.

Let us find all the nonnegative fixed points for the kj-th update. From Eqs. (11) and (12), if all the solutions $x_{kj0}$ and $a_{ij0}$ are nonzero, they are included in the following two linear equation systems separately:

$$\begin{aligned} \left\{ \begin{matrix} \sum \nolimits _{i=1}^{m}a_{i1}v_{i}=\sum \nolimits _{q=1}^{m}a_{q1} +\lambda _{{\mathbf {X}}}\sum \nolimits _{p=1}^{N}l_{kp}x_{p1}\\ \\ \sum \nolimits _{i=1}^{m}a_{i2}v_{i}={\sum \nolimits _{q=1}^{m}a_{q2}} +\lambda _{{\mathbf {X}}}\sum \nolimits _{p=1}^{N}l_{kp}x_{p2}\\ \cdots \\ \\ \sum \nolimits _{i=1}^{m}a_{in}v_{i}={\sum \nolimits _{q=1}^{m}a_{qn}} +\lambda _{{\mathbf {X}}}\sum \nolimits _{p=1}^{N}l_{kp}x_{pn}\\ \end{matrix} \right. , \end{aligned}$$

(41)

and

$$\begin{aligned} \left\{ \begin{matrix} \sum \nolimits _{k=1}^{N}x_{k1}s_{k}= {\sum \nolimits _{p=1}^{N}x_{p1}+\lambda _{{\mathbf {A}}}\sum \nolimits _{p=1}^{m}m_{ip}a_{p1}}\\ \\ \sum \nolimits _{k=1}^{N}x_{k2}s_{k}={\sum \nolimits _{p=1}^{N}x_{p2} +\lambda _{{\mathbf {A}}}\sum \nolimits _{p=1}^{m}m_{ip}a_{p2}}\\ \cdots \\ \\ \sum \nolimits _{k=1}^{N}x_{kn}s_{k}={\sum \nolimits _{p=1}^{N}x_{pn} +\lambda _{{\mathbf {A}}}\sum \nolimits _{p=1}^{m}m_{ip}a_{pn}}\\ \end{matrix}\right. . \end{aligned}$$

(42)

For linear equation system (41), only $x_{kj}$ (j = $1,2,3,\ldots , N$) are considered as variables of the system. Denoting $v_{i}(x_{k1}, x_{k2},\ldots , x_{kn})= v_{i}$, linear equation system (41) can be simplified to

$$\begin{aligned} \left\{ \begin{matrix} \sum \nolimits _{i=1}^{m}a_{i1}v_{i}=1+\lambda _{{\mathbf {X}}}{\mathbf {l}}_{k\cdot }{\mathbf {x}}_{k\cdot }\\ \\ \sum \nolimits _{i=1}^{m}a_{i2}v_{i}=1+\lambda _{{\mathbf {X}}}{\mathbf {l}}_{k\cdot }{\mathbf {x}}_{k\cdot }\\ \cdots \\ \\ {\sum \nolimits _{i=1}^{m}a_{in}v_{i}}=1+\lambda _{{\mathbf {X}}}{\mathbf {l}}_{k\cdot }{\mathbf {x}}_{k\cdot }\\ \end{matrix} \right. , \end{aligned}$$

(43)

which can be rewritten as

$$\begin{aligned} {\mathbf {A}}^{T}\left( \begin{matrix} v_{1}\\ v_{2}\\ \cdots \\ v_{m} \end{matrix} \right) = \left( \begin{matrix} 1+\lambda _{{\mathbf {X}}}{\mathbf {l}}_{k\cdot }{\mathbf {x}}_{k\cdot }\\ 1+\lambda _{{\mathbf {X}}}{\mathbf {l}}_{k\cdot }{\mathbf {x}}_{k\cdot }\\ \cdots \\ 1+\lambda _{{\mathbf {X}}}{\mathbf {l}}_{k\cdot }{\mathbf {x}}_{k\cdot } \end{matrix} \right) . \end{aligned}$$

(44)

Assuming $(v_{10}, v_{20},\ldots , v_{m0})$ is a solution of the equation system (44), if there exists some i, such that $y_{ik}=0$, then $v_{i0} =0$; the number of variables will reduce to $m-1$. Thus, we can always assume for any i, $v_{i0} >0$. From (37), it holds that

$$\begin{aligned} \left\{ \begin{array}{l} \sum \nolimits _{p=1}^{n}a_{1p}x_{kp}=\frac{y_{1k}}{v_{10}}\\ \\ {\sum \nolimits _{p=1}^{m}a_{2p}x_{kp}}=\frac{y_{2k}}{v_{20}}\\ \cdots \\ \\ {\sum \nolimits _{p=1}^{n}a_{mp}x_{kp}}=\frac{y_{mk}}{v_{m0}}\\ \end{array} \right. , \end{aligned}$$

(45)

which can be rewritten as

$$\begin{aligned} \mathbf {Ax}_{k\cdot }={\mathbf {A}}\left( \begin{matrix} x_{k1}\\ \\ x_{k2}\\ \cdots \\ \\ x_{kn} \end{matrix} \right) = \left( \begin{array}{l} \frac{y_{1k}}{v_{10}}\\ \\ \frac{y_{2k}}{v_{20}}\\ \cdots \\ \\ \frac{y_{mk}}{v_{m0}} \end{array} \right) . \end{aligned}$$

(46)

If for some $\mathbf{A }$, linear equation systems (44) and (46) have nonnegative solutions, then update algorithm (9) will have nonnegative fixed points.

Similarly for the update of $a_{ij}$, from (38) and (40), we have the following linear equation systems.

$$\begin{aligned} {\mathbf {X}}\left( \begin{matrix} s_{1}\\ s_{2}\\ \cdots \\ s_{N} \end{matrix} \right) = \left( \begin{matrix} \sum \nolimits _{p=1}^{N}x_{p1}+\lambda _{{\mathbf {A}}}{\mathbf {m}}_{1\cdot }{\mathbf {a}}_{\cdot k}\\ \\ \sum \nolimits _{p=1}^{N}x_{p2}+\lambda _{{\mathbf {A}}}{\mathbf {m}}_{2\cdot }{\mathbf {a}}_{\cdot k}\\ \cdots \\ \\ \sum \nolimits _{p=1}^{N}x_{pn}+\lambda _{{\mathbf {A}}}{\mathbf {m}}_{n\cdot }{\mathbf {a}}_{\cdot k} \end{matrix} \right) . \end{aligned}$$

(47)

Assuming $(s_{10}, s_{20},\ldots , s_{N0})$ is a solution of the equation system (47), it follows that

$$\begin{aligned} {\mathbf {a}}_{i\cdot }{\mathbf {X}}=(a_{i1}, a_{i2},\ldots , a_{in}){\mathbf {X}}= \left( \begin{array}{l} \frac{y_{i1}}{s_{10}}\\ \\ \frac{y_{i2}}{s_{20}}\\ \cdots \\ \\ \frac{y_{iN}}{s_{N0}} \end{array} \right) ^{T}. \end{aligned}$$

(48)

(48) is equivalent to

$$\begin{aligned} {\mathbf {X}}^{T}\left( \begin{matrix} a_{i1}\\ a_{i2}\\ \cdots \\ a_{in} \end{matrix} \right) =\left( \begin{array}{l} \frac{y_{i1}}{s_{10}}\\ \\ \frac{y_{i2}}{s_{20}}\\ \cdots \\ \\ \frac{y_{iN}}{s_{N0}} \end{array} \right) . \end{aligned}$$

(49)

Thus, if for some $\mathbf{X }$, linear equation systems (47) and (49) have nonnegative solutions, then update algorithm (10) will have nonnegative fixed points.

For the given initializations and observation sample matrix $\mathbf{Y }$, the process of the NMF learning is equivalent to solve linear systems Eqs. (44), (46) and (47), (49) alternately. When solving Eqs. (44), (46), matrix $\mathbf{A }$ is temporarily considered as a constant. Similarly, when solving Eqs. (47), (49), $\mathbf{X }^T$ is considered temporarily as a constant. When the learning converges, the fixed points of the learning algorithms are obtained, which indicates that the solutions of these systems are obtained.

If $\lambda _{{\mathbf {A}}} = \lambda _{{\mathbf {X}}}=0$, systems (41) and (42) can be rewritten as

$$\begin{aligned} \left\{ \begin{matrix} \sum \nolimits _{i=1}^{m}a_{i1}v_{i}=\sum \nolimits _{q=1}^{m}a_{q1}\\ \\ \sum \nolimits _{i=1}^{m}a_{i2}v_{i}={\sum \nolimits _{q=1}^{m}a_{q2}}\\ \cdots \\ \\ \sum \nolimits _{i=1}^{m}a_{in}v_{i}={\sum \nolimits _{q=1}^{m}a_{qn}},\\ \end{matrix} \right. \end{aligned}$$

(50)

and

$$\begin{aligned} \left\{ \begin{matrix} \sum \nolimits _{k=1}^{N}x_{k1}s_{k}= \sum \nolimits _{p=1}^{N}x_{p1}\\ \\ \sum \nolimits _{k=1}^{N}x_{k2}s_{k}=\sum \nolimits _{p=1}^{N}x_{p2}\\ \cdots \\ \\ \sum \nolimits _{k=1}^{N}x_{kn}s_{k}=\sum \nolimits _{p=1}^{N}x_{pn} \\ \end{matrix}\right. . \end{aligned}$$

(51)

For any ${\mathbf {a}}_{i\cdot }$ and ${\mathbf {x}}_{k\cdot }$, the only solutions for systems (50) and (51) are $v_{1} = v_{2} =\ldots , = v_{m} = s_{1} = s_{2} =\ldots , = s_{N} = 1$. From Eqs. (37) and (38), it follows that

$$\begin{aligned} \left\{ \begin{matrix} s_{k}=1 \Longrightarrow {\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot } =y_{ik}, \quad k = 1, 2,\ldots , N\\ v_{i}=1 \Longrightarrow {\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot } =y_{ik}, \quad i = 1, 2,\ldots , m\\ \end{matrix}\right. \end{aligned}$$

Thus, For sample matrix $\mathbf{Y }$, NMF learning is to find matrices $\mathbf{A }$ and $\mathbf{X }$ such that $\mathbf{Y }=\mathbf AX ^T$. Clearly, this type of matrices $\mathbf{A }$ and $\mathbf{X }$ exists. The conditions of the solution existing are:

• (a) For variables $x_{kj}$, $j=1, 2,\ldots , n$, if the ranks of matrix ${\mathbf {A}}$ and the augmented matrix of Eq. (46) are equal, then Eq. (46) has one or more groups of nonzero solutions.

• (b) For variables $a_{ij}$, $j=1, 2,\ldots , n$, if the ranks of matrix ${\mathbf {X}}^{T}$ and the augmented matrix of Eq. (49) are equal, then Eq. (49) has one or more groups of nonzero solutions.

Clearly, only if the conditions in both (a) and (b) are satisfied, the NMF learning algorithms can reach their equilibrium state. At this state, we can say that the learning algorithms converge.

In fact, for all k, if ${\mathbf {X}}$ is a group solution of Eq. (46), then the corresponding ${\mathbf {A}}$ is a group solution of Eq. (49). For $a_{ij}$, we have the same result.

At the equilibrium state, to simplify the expression, $x_{1}$, $x_{2},\ldots , x_{n}$ are used to replace variables $x_{k1}$, $x_{k2}\ldots , x_{kn}$ in the following linear equation system. For the case of $\lambda _{\mathbf{X }}=0$, ($v_{1}$, $v_{2},\ldots , v_{m}) = {\mathbf {1}}$ is the only solution of Eq. (50). In the update of $x_{kj}$, $\mathbf{A }$ is temporarily considered as a constant matrix. From (46), for any given matrix ${\mathbf {A}}$, assume $r = \hbox {rank}({\mathbf {A}})$. Using Gaussian elimination, the following equivalent linear equation system holds:

$$\begin{aligned} \left\{ \begin{matrix} g_{11}x_{1} +\cdots + g_{1r}x_{r}={\bar{d}}_{1} - g_{1r+1}x_{r+1} -\cdots - g_{1n}x_{n}\\ g_{22}x_{2} +\cdots + g_{2r}x_{r}= {\bar{d}}_{2} - g_{2r+1}x_{r+1} -\cdots - g_{2n}x_{n}\\ \cdots \quad \quad \quad \quad \quad \\ \quad \quad \quad \quad \quad g_{rr}x_{r}= {\bar{d}}_{r} - g_{rr+1}x_{r+1} -\cdots - g_{rr}x_{n}\\ \quad \quad \quad x_{r+1}= x_{r+1} \quad \quad \quad \quad \quad \quad \quad \quad \\ \cdots \quad \quad \quad \quad \quad \\ \quad \quad \quad x_{n}= x_{n} \quad \quad \quad \quad \quad \quad \quad \quad \\ \end{matrix}, \right. \end{aligned}$$

(52)

where $g_{ii}\ne 0$ ($i=1, 2,\ldots , r$), $x_{r+1},x_{r+2},\ldots , x_{n}$ are the free variables of the system, and (${\bar{d}}_{1}$, ${\bar{d}}_{2},\ldots , {\bar{d}}_{r}$) is uniquely determined by ${\mathbf {v}}= (v_{1}, v_{2},\ldots , v_{m})$. Clearly, system (52) has infinite number of solutions since usually we have $n \ge r$ in the NMF applications. The solutions of system (52) depend on the values of $x_{r+1},x_{r+2},\ldots , x_{n}$. For each group of determined values of $x_{r+1},x_{r+2}, \ldots , x_{n}$, the linear equation system has only one group solution. However, $x_{r+1},x_{r+2},\ldots , x_{n}$ can be uniquely determined by the initializations in the learning. Thus for a group of given initializations, the solution vector of system (52) ${\mathbf {x}} = (x_{1},x_{2},\ldots , x_{n})$ is unique. Thus, the update will converge to the unique fixed point of the learning algorithm.

For the SMNMF, it always holds that $\lambda _{\mathbf{A }}\ne 0$ and/or $\lambda _{\mathbf{X }}\ne 0$. Thus, we have the following different cases:

If $\lambda _{{\mathbf {A}}}=0$, $\lambda _{{\mathbf {X}}}\ne 0$, it holds that

$$\begin{aligned} \left\{ \begin{matrix} s_{k}=1 \Longrightarrow {\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot } =y_{ik}, \quad k = 1, 2,\ldots , N\\ v_{i}>1 \Longrightarrow {\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot } <y_{ik}, \quad i = 1, 2,\ldots , m\\ \end{matrix}\right. . \end{aligned}$$

(53)

If $\lambda _{{\mathbf {A}}}\ne 0$, $\lambda _{{\mathbf {X}}}=0$, it holds that

$$\begin{aligned} \left\{ \begin{matrix} s_{k}>1 \Longrightarrow {\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot } <y_{ik}, \quad k = 1, 2,\ldots , N\\ v_{i}=1 \Longrightarrow {\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot } =y_{ik}, \quad i = 1, 2,\ldots , m\\ \end{matrix}\right. \end{aligned}$$

(54)

In these two cases, the fixed points that simultaneously satisfy Eqs. (11) and (12) do not exist. Therefore, the learning algorithms can only obtain their fixed points approximately.

If both $\lambda _{{\mathbf {A}}}>0$ and $\lambda _{{\mathbf {X}}}>0$, then it holds that

$$\begin{aligned} \left\{ \begin{matrix} s_{k}>1 \Longrightarrow {\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }<y_{ik}, \quad k = 1, 2,\ldots , N\\ v_{i}>1 \Longrightarrow {\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot } <y_{ik}, \quad i = 1, 2,\ldots , m\\ \end{matrix}\right. \end{aligned}$$

(55)

Although the separation results have $\mathbf {AX}^T<{\mathbf {Y}}$, systems (44) and (46) may have solutions, which are the fixed points of the learning algorithms (9) and (10) and at the same time the sparseness is imposed. Assuming the ik-th error is $d_{ik}$, it follows that

$$\begin{aligned} \left\{ \begin{matrix} s_{k}>1 \Longrightarrow {\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }+d_{ik} =y_{ik}, \quad k = 1, 2,\ldots , N\\ v_{i}>1 \Longrightarrow {\mathbf {a}}_{i\cdot }{\mathbf {x}}_{k\cdot }+d_{ik} =y_{ik}, \quad i = 1, 2,\ldots , m\\ \end{matrix}\right. \end{aligned}$$

Combining Eqs. (44), (46), (47) and (49), we have $v_{i}\ge 1$ and $s_{k}\ge 1$. Thus, a unique separation result $\mathbf{Y }$ = $\mathbf AX ^T$ + $\mathbf{d }$ can be achieved, where $\mathbf{d }$ is a displacement matrix. The proof is complete. $\square$